[Trouble Shooting] Sympy

Activation Function 카테고리를 정리하면서 각 acitvation function 들을 직접 graph 로 그리고 도함수의 graph 도 그려봤는데, 이 과정에서 도함수를 쉽게 구할 수 있게 해주는 sympy 라이브러리를 사용했다. 자주 사용하지는 않겠지만, 이 포스트에 정리해두고 간간히 참고하고자 한다.

Sympy 란?

• Python 에서 수학 기호 연산을 다룰 수 있도록 돕는 라이브러리다. 다양한 수학 연산을 심볼릭 형태로 처리할 수 있으며, 복잡한 수식을 다루는 데 유용하다.
• 즉 수학에서 사용하는 것처럼 $x$ 와 $y$ 를 Python 의 변수가 아니라 방정식의 표현으로 사용할 수 있다.

from sympy import Symbol

# 변수 x 와 y 를 정의하고 x + y 를 정의
x = Symbol('x')
y = Symbol('y')

expr = x + y
print(expr)  # x + y

Sympy 의 장점

• 수학적인 표현식을 간단하게 처리할 수 있다.
• 수치 계산보다는 수식의 기호적 변형 및 해석에 강점이 있으며, 복잡한 수학적 연산을 심볼릭 연산으로 효율적으로 수행할 수 있다.
• 미적분, 선형대수, 방정식 풀이, 극한 등의 연산을 손쉽게 수행할 수 있다. 아래 예시를 보자.

# Sympy 를 이용한 미분 계산
from sympy import Symbol, diff

x = Symbol('x')
f = x**2 + 2*x + 1

f_prime = diff(f, x)
print(f_prime)  # 2*x + 2

Symbol

• Sympy 의 Symbol 클래스는 변수를 기호 형태로 표현하여 다양한 수식을 생성하고 계산할 수 있도록 돕는다.
• 위 예시들에서 봤듯 Symbol 을 사용하여 수식을 표현하면, 이를 기반으로 미분, 적분, 단순화 등의 기호적 계산을 할 수 있다.

# x 와 y 라는 Symbol 을 정의
x = Symbol('x')
y = Symbol('y')

• 그러나 Sympy 에서는 자주 사용하는 기호를 미리 정의해 제공하고 있다. sympy.abc 에는 $x, y, a, b$ 등의 자주 사용하는 기호에 접근할 수 있다.

from sympy import diff
from sympy.abc import x, y

# 수식 작성
expr = x**2 + y**3 + 20*x + y
print(expr) # x**2 + 20*x + y**3 + y

# x에 대한 도함수
diff_expr = diff(expr, x)
print(diff_expr) # 2*x + 20

자주 사용하는 함수

• Sympy 에서 자주 사용하는 함수들은 수식을 다루거나, 계산 결과를 실수로 반환하는 등의 작업에 유용하다.
• 여기에 대표적인 함수들을 정리해보자.

diff

• diff 는 미분(도함수)을 구하는 함수로, 특정 변수에 대해 기호적 미분을 수행한다.

# x 에 대한 f 의 도함수
f = x**3 + 3*x**2 + x + 1
f_prime = diff(f, x)
print(f_prime) # 3*x**2 + 6*x + 1

evalf

• evalf 는 수식을 수치값으로 계산하는 함수로, 표현된 수식을 실수값으로 평가하여 반환한다.

result = (x + y).evalf(subs={x: 1.5, y: 2.5})
print(result) # 4.00000000000000

sigmoid = (1 / (1 + sympy.exp(-x))).evalf(subs={x:0})
print(sigmoid) # 0.500000000000000

simplify

• simplify 는 주어진 수식을 가능한 가장 간단한 형태로 변환하는 함수다.

from sympy import simplify, cos, sin
from sympy.abc import x, y
a = (x + x**2)/(x*sin(y)**2 + x*cos(y)**2)

print(a) # (x**2 + x)/(x*sin(y)**2 + x*cos(y)**2)
simplify(a) # x+1

• 위 예제는 삼각함수 공식에 의해 간단하게 정리할 수 있는 식을 simplify 로 간소화한 것이다.

expand

• expand 는 곱셈과 분배 법칙을 적용하여 수식을 펼치는 함수이다.

from sympy import expand

expr = (x + 1)**2
expanded_expr = expand(expr)
print(expanded_expr)  # x**2 + 2*x + 1

Eq

• Eq 는 Sympy 에서 방정식을 정의할 때 사용하는 함수로, 방정식의 좌변과 우변을 설정하여 두 식이 같음을 나타낸다. solve 함수와 함께 방정식의 해를 구하는 데 자주 쓰인다.
• 즉 Python 에서 == 연산자와 같은 역할을 하며, Sympy 에서는 Eq 를 사용해 기호적 방정식을 표현한다.

from sympy import Symbol, Eq, solve
from sympy.abc import x

# x**2 - 4 = 0
equation = Eq(x**2 - 4, 0)

solutions = solve(equation, x)
print(solutions) # [-2, 2]

solve

• solve 는 방정식을 풀기 위한 함수이다. 주어진 수식을 특정 변수에 대해 풀어준다.

from sympy import Eq, solve
from sympy.abc import x

equation = Eq(x**2 - 9, 0)
solutions = solve(equation, x)
print(solutions) # [-3, 3]

lambdify

• lambdify 는 심볼릭 수식을 Python 함수로 변환해주는 함수로, Sympy 에서 만든 수식을 빠르게 평가하고자 할 때 유용하다.
• Numpy, Scipy 와 함께 사용할 수 있어 벡터화 연산에 적합하다.

from sympy import lambdify
from sympy.abc import x
import numpy as np

# Sympy 수식을 람다 함수로 변환
f = x**2 + 2*x + 1
f_lambda = lambdify(x, f, 'numpy')

# 변환한 함수에 배열을 넣어 평가
print(f_lambda(np.array([1, 2, 3]))) # [ 4  9 16]

• 이를 활용하여 특정 활성화함수의 미분식을 구하고, 도함수 그래프를 그릴 수 있다. 아래 예제는 $\text{Mish}$ 함수에 대한 그래프와 그 도함수에 대한 그래프를 그리는 코드다.

import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
plt.style.use('default')

# Mish 함수 정의
def mish(x):
    return x * np.tanh(np.log(1 + np.exp(x)))

x_vals = np.linspace(-5, 5, 100)

plt.figure(figsize=(12, 6))

x = sym.symbols('x')
mish_expr = x * sym.tanh(sym.log(1 + sym.exp(x)))
mish_derivative = sym.diff(mish_expr, x)  # 도함수 계산
mish_deriv_np = sym.lambdify(x, mish_derivative, 'numpy')  # numpy 로 변환
y = mish(x_vals)  # Mish 함수 값
y_deriv = mish_deriv_np(x_vals)  # 도함수 값

# Mish 함수 시각화
plt.subplot(1, 2, 1)
plt.plot(x_vals, y)
plt.title('Mish Function')
plt.grid(True)

# 도함수 시각화
plt.subplot(1, 2, 2)
plt.plot(x_vals, y_deriv)
plt.title('Mish Derivative')
plt.grid(True)

plt.tight_layout()
plt.show()

• 아래와 같이 Sympy 를 통해 미분식을 만들고, numpy.ndarray 를 통과시켜 vectorize 연산이 잘 작동함을 확인할 수 있다.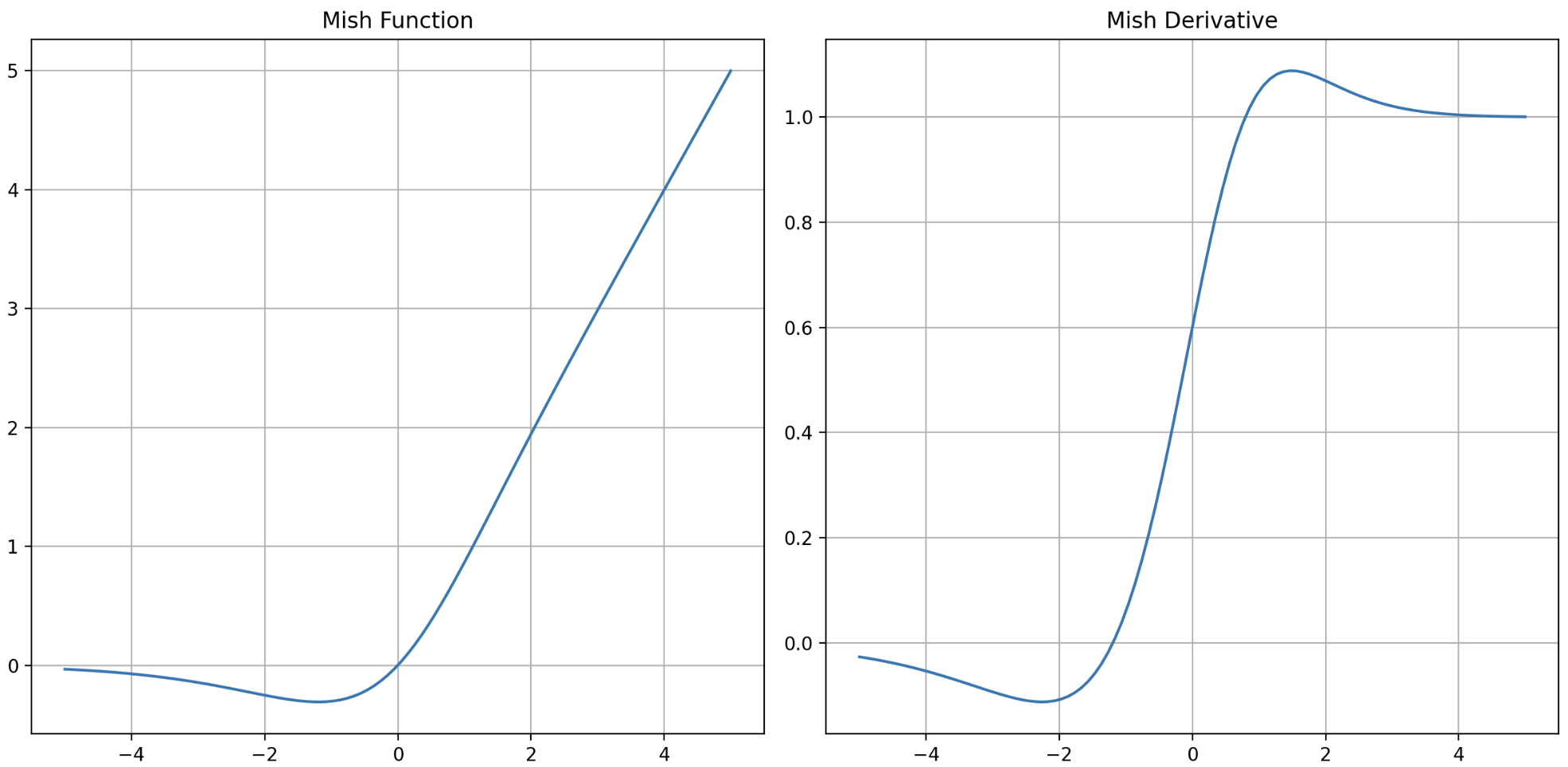

  

integrate

• integrate 는 적분을 구하는 함수로, 정적분 및 부정적분을 수행할 수 있다.

from sympy import integrate
from sympy.abc import x

# x 에 대한 부정적분 계산
f = x**2 + 3*x + 1
integral = integrate(f, x)
print(integral) # x**3/3 + 3*x**2/2 + x

# 정적분 계산 (0에서 2까지)
integral_def = integrate(f, (x, 0, 2))
print(integral_def) # 32/3

Matrix

• Sympy 를 사용하여 행렬의 고유값과 고유벡터를 구할 수도 있다.
• Matrix 의 eigenvals 함수를 통해 고유값을, eigenvects 함수를 통해 고유벡터와 고유값을 함께 구할 수 있다. 이를 사용하면 행렬의 고유값 문제를 쉽게 해결할 수 있다.

from sympy import Matrix

# 2x2 행렬 정의
A = Matrix([[3, 1], [0, 2]])

# 고유값 계산
eigenvalues = A.eigenvals()
print(eigenvalues) # {2: 1, 3: 1}

# 고유값과 고유벡터 계산
eigenvectors = A.eigenvects()
print(eigenvectors)
# [(2, 1, [Matrix([
# [-1],
# [ 1]])]),
# (3, 1, [Matrix([
# [1],
# [0]])])]

• eigenvals 는 {eigenval: multiplicity} 형식의 딕셔너리를 반환한다.
• eigenvects 는 [(eigenval, multiplicity, eigenspace), ...] 형식으로 반환한다.

그 외 연산

• Sympy 에서는 tanh, log, exp 를 포함한 다양한 수학 함수를 사용할 수 있다.
• 각각의 함수는 기호 계산을 쉽게 만들어주며, 복잡한 방정식이나 표현식에 사용될 때 유용하다. 위에서 정리한 것들을 활용하여 아래 예시를 보자.

from sympy import symbols, tanh, sin, cos, log, exp

x = symbols('x')

# Hyperbolic tangent
tanh_expr = tanh(x)

# Trigonometric functions
sin_expr = sin(x)
cos_expr = cos(x)

# Logarithmic function
log_expr = log(x)

# Exponential function
exp_expr = exp(x)

# 각 함수의 도함수 구하기
tanh_derivative = tanh_expr.diff(x)
sin_derivative = sin_expr.diff(x)
log_derivative = log_expr.diff(x)
exp_derivative = exp_expr.diff(x)

print(tanh_derivative) # 1 - tanh(x)**2
print(sin_derivative)  # cos(x)
print(log_derivative)  # 1/x
print(exp_derivative)  # exp(x)

# 특정 값 대입 해보기
exp_value = exp_expr.evalf(subs={x: 1})
print("Exponential of 1:", exp_value)  # 2.71828182845905

Reference

• https://docs.sympy.org/latest/index.html

맨 위로 이동 ↑