[Trouble Shooting] WX + b vs. XW + b

WX + b vs. XW + b

• 블로그에 그간 배운 것들을 정리하다가 문득 궁금증이 생겼다. “왜 교재에서는 $\mathbf{W}\mathbf{X} + \mathbf{b}$ 로 표현하는데, Pytorch 나 Tensorflow 같은 딥러닝 프레임워크에서는 $\mathbf{X}\mathbf{W} + \mathbf{b}$ 로 표현할까?”

  

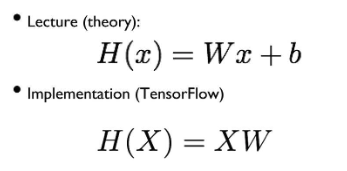
• 먼저, 우리가 머신러닝/딥러닝을 할 때 가지고 있는 것은 parameter 인 $W$ 보다는 데이터인 $X$ 를 가지고 있다.
• 그리고 $X$ 는 행의 개수가 데이터의 개수 $n$ (혹은 batch_size), 열의 개수가 feature 의 개수 $d$ 를 나타낸다. 따라서 $X$ 는 $(n, d)$ 가 되며 이는 데이터 분석에서의 관습이다.
  • 데이터 사이언스 스쿨에서는 다음과 같이 이야기한다.

    하나의 데이터 레코드를 단독으로 벡터로 나타낼 때는 하나의 열(column)로 나타내고 복수의 데이터 레코드 집합을 행렬로 나타낼 때는 하나의 데이터 레코드가 하나의 행(row)으로 표기하는 것은 얼핏 보기에는 일관성이 없어 보이지만 추후 다른 연산을 할 때 이런 모양이 필요하기 때문이다. 데이터 분석에서 쓰는 일반적인 관례이므로 외워두어야 한다.

• 또한 딥러닝의 근간을 이루는 연산은 행렬연산, 즉 행렬곱이다.
• 이러한 이유를 종합해볼 때, 행렬곱은 A 행렬의 행벡터와 B 행렬의 열벡터 사이의 내적이고, 관례적으로 하나의 데이터 레코드는 열벡터로 나타내므로, 이론상 $Wx + b$ 로 나타낼 수 있다.
• 또한 1) 우리가 가지고 있는 데이터 $\mathbf{X}$ 는 일반적으로 여러 개의 데이터 레코드를 모은 행렬이며, 2) neural network diagram 이나 computational graph 를 보면 알겠지만 모델의 입장에서 $\mathbf{X}$ 를 건네받고 $\mathbf{W}$ 와 내적을 통한 행렬곱이 이뤄지기 때문에 딥러닝 프레임워크에서 $\mathbf{X}\mathbf{W}$ 로 나타내는 것은 타당하다.
• 이외에 기술적인 이유도 있다.

• torch.nn.linear() 를 공식문서에서 보면 argument 로 받는 weight 의 shape 이 아래 그림과 같이 $(\text{out_features, in_features})$ 다.

  

• input 이 $(\text{*, in_features})$ 이므로 일반적인 행렬곱 규칙에 따르면 위와 같은 shpae 의 weight 를 전치(transpose)해야 한다.
• 그러나 내가 weight 에 대한 shape 을 결정할 수 있다면, 굳이 transpose 연산을 쓸 것이 아니라 맨 처음부터 $(\text{in_features, out_features})$ 로 weight 의 shape 을 미리 transpose 취한 형태로 주면, 연산도 알맞게 되고 transpose 연산도 할 필요가 없지 않을까?

• 그러나 transpose 를 하는 이유는 메모리 효율을 위한 것이다.

  

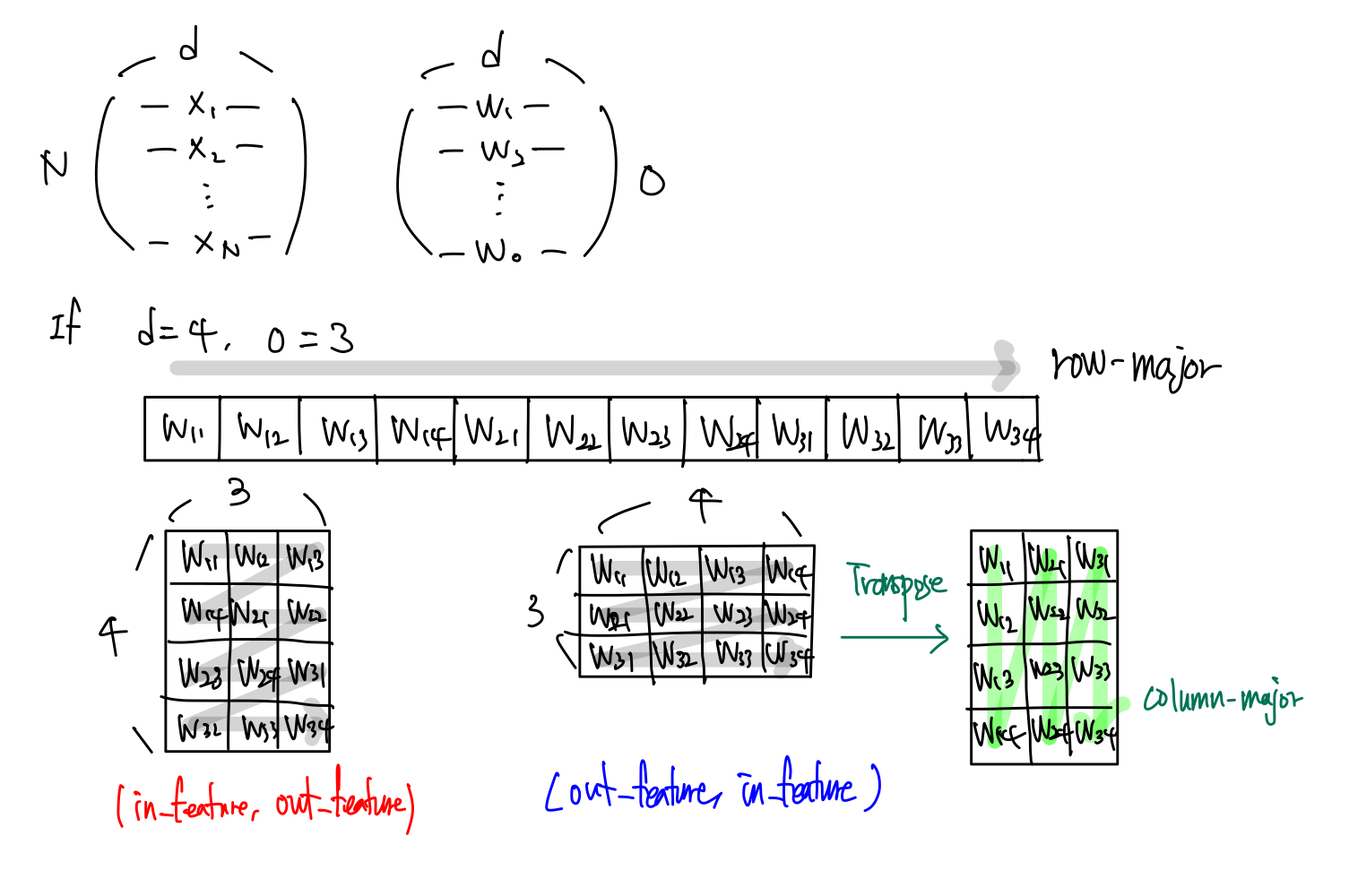
• 위 그림처럼 메모리는 1d array 로 이루어져 있고, torch 에서는 row-major 로 데이터를 읽는다. 이 때 transpose 를 미리 취한 shape $(\text{in_features, out_features})$ 을 해주면 행렬곱 연산에서 잘못된 값을 불러오게 된다.
• 즉 row-major contiguous 로 읽기 때문에 열벡터인 $(w_{11}, w_{21}, w_{31}, w_{41})$ 로 읽는 것이 아니라 $(w_{11}, w_{12}, w_{13})$ 의 순서로 읽는다.
• 만약 이 상태에서 $(w_{11}, w_{12}, w_{13}, w_{14})$ 를 순서대로 읽는다 하더라도 일관성 없이 row 를 읽기 때문에 matrix 의 구조가 무의미하게 된다.
• 따라서 오른쪽 그림처럼 $(\text{out_features, in_features})$ 로 weight 의 shape 을 주고 transpose 를 하면 row-major 가 column-major 가 되어 읽는 방향이 달라지기 때문에 더 효율적으로 데이터를 읽게 된다.
• 또한 실제로, 이 링크에서 잘 설명이 되어 있는데, transpose 는 BLAS 를 기반으로 한 연산에서 overhead 가 없다고 한다.
• 그리고 transpose 가 들어간 matrix multiplication routine 이 5 배는 더 빠르다고 한다. 물론 torch 에서는 이미 최적화가 되어 있어 별로 차이가 없다고 한다.
• 위처럼 weight 의 shape 이 $(\text{out_features, in_features})$ 라고 했을 때, $XW$ 와 $WX$ 는 어떤 차이가 있을까?

  • 우선 행렬곱 규칙에 따라 transpose 되는 행렬이 달라진다. $XW$ 는 $W$ 가 transpose 되고, $WX$ 는 $X$ 가 transpose 된다.

    

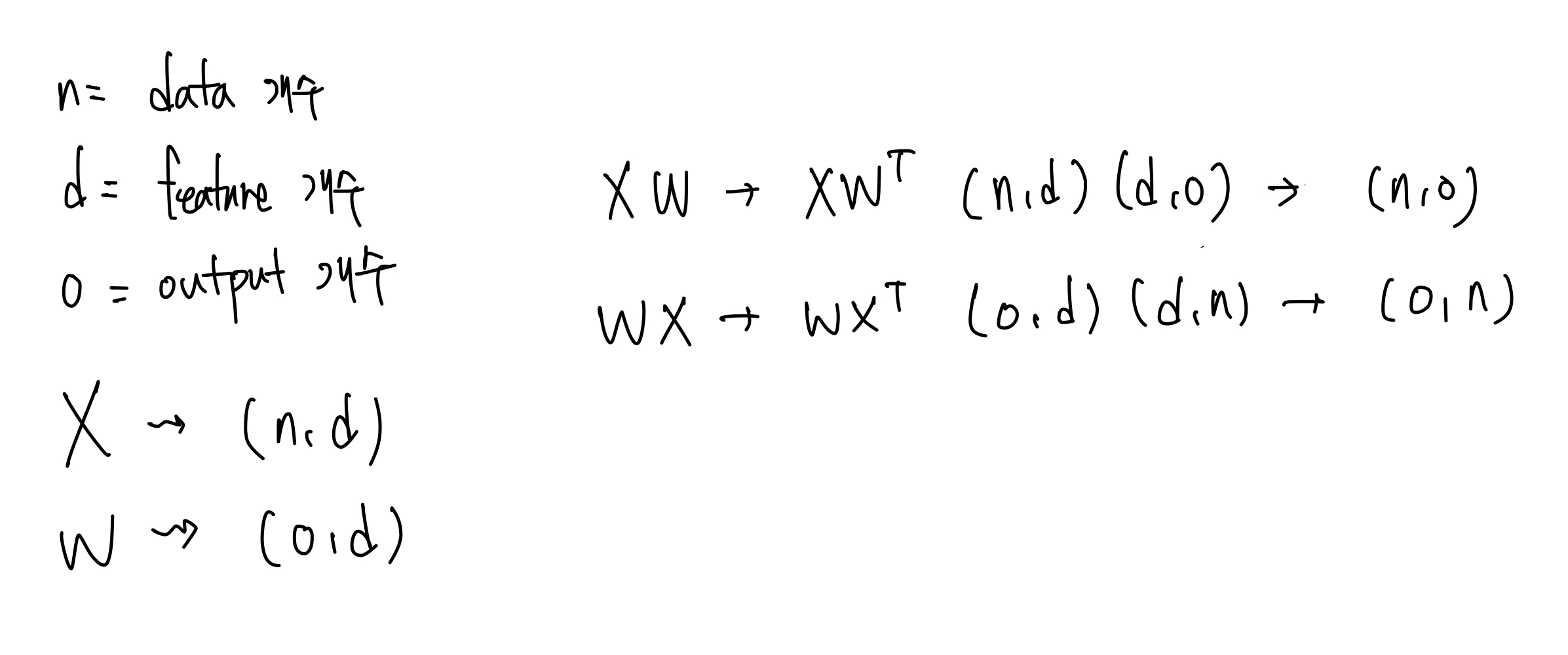
  • 따라서 $WX$ 의 형식으로 구현하게 되면 $X$ 를 transpose 해야 한다. 그러나 이렇게 되면 비효율적인 점이 발생한다.
  • $X$ 에 transpose 연산을 취하여 column-major 로 데이터를 읽는다면 메모리는 그대로 있고 읽는 방향만 바뀌는 것이기 때문에, 이후 $X$ 에 대한 수정이 어려울 수 있다. 딥러닝에서 데이터를 추가하거나 삭제하는 경우는 흔하다.
  • 즉 실제 딥러닝에서는 augmentation 이나 전처리 등 데이터의 추가와 삭제가 필요할 수 있기 때문에, 고정된 transpose view 보다 일반적인 row-major 형태의 $X$ 를 그대로 사용하고 $W$ 만 transpose 하는 것이 유연한 접근 방식이다.
• 또한 딥러닝 작업에서는 원본 데이터를 보존한 상태에서 연산을 효율적으로 수행하고, 유연한 데이터 수정이 가능해야 한다. $X$ 를 transpose 하는 방식은 이러한 요구 사항에 맞지 않기 때문에, $XW$ 방식이 구현적으로 더 유리하다고 볼 수 있다.

결론

• 이론적으로 $Wx + b$ 라고 표기하는 것은 아래와 같은 선형 연립방정식의 일반화된 표현이다.

  \[{\displaystyle {\begin{pmatrix}w_{11}&w_{12}&w_{13}&\cdots &w_{1n}\\w_{21}&w_{22}&w_{23}&\cdots &w_{2n}\\w_{31}&w_{32}&w_{33}&\cdots &w_{3n}\\\vdots &\vdots &\vdots &&\vdots \\w_{m1}&w_{m2}&w_{m3}&\cdots &w_{mn}\\\end{pmatrix}}{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\\\vdots \\x_{n}\end{pmatrix}}={\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\\\vdots \\b_{m}\end{pmatrix}}}\]
• 그리고 우리는 아래의 것들을 확인했다.
  1. 우리는 관습으로 하나의 데이터 포인트 $x$ 는 열벡터로 표현되지만 여러 데이터 포인트가 모인 $X$ 에서는 $x$ 가 행벡터로 표현된다.
  2. 그리고 Pytorch 와 같은 딥러닝 프레임워크에서는 일반적으로 data size $n$ 이 있는 데이터 행렬 $X$ 를 활용한다.
  3. 딥러닝 프레임워크, 특히 Pytorch 의 특성상 메모리에 올라가 있는 데이터를 row-major 로 읽는다. 그리고 weight 는 $(\text{out_features, in_features})$ 의 shape 을 가진다. 이는 transpose 연산을 했을 때 행렬곱 규칙에 딱 알맞게 되고 메모리를 읽는 순서만 바꿔 효율적으로 계산할 수 있다.
  4. $WX$ 로 구현하게 되면 데이터 행렬 $X$ 가 transpose 되어야 하며, 데이터의 추가/삭제/수정이나 shape 가 쉽게 수정될 수 있는 데이터 행렬 특성상 비효율적이다.
• 따라서 딥러닝 프레임워크에서 선형모델 $XW + b$ 를 이론과 같은 형태로 구현하지 않는 이유는 관습적인 이유와 계산과 메모리의 효율성 때문이다.
• 즉 이론상 $WX + b$ 표기법이 선형 방정식의 일반화된 표현이지만, 연산 효율성 면에서 $XW + b$ 가 더 유리하다는 것을 딥러닝 모델의 구현 측면으로 잘 반영한 것이라 볼 수 있다.

맨 위로 이동 ↑