[Transformer] 1. Summary of Transformer

Transformer

• transformer 는 기본적으로 sequential 데이터를 다루는 방법론이다.
• 그러나 vanila RNN, LSTM, GRU 와는 풀려고 하는 것은 비슷하지만 조금 다른 방법론이다.

• sequential 데이터의 대표적 예인 문장은 항상 길이가 달라질 수 있다.

  

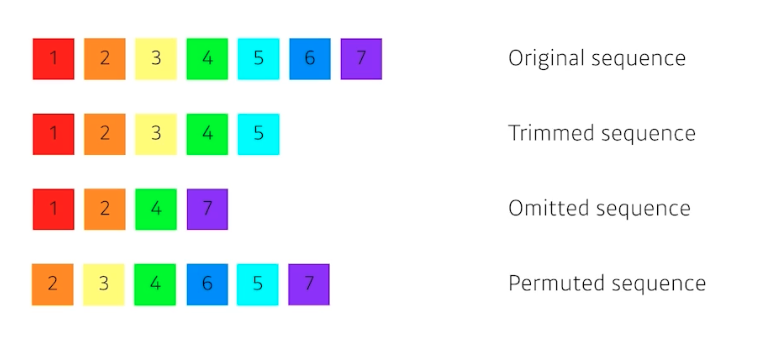
• 즉 위 그림처럼 중간에 뭐가 빠지거나 순서가 달라지면 모델링하기 많이 어려워진다.
• 이런 문제를 해결하고자 transformer 가 등장했다.
• transformer 구조는 기본적으로 self-attention 이라는 구조를 사용한다.
  • transformer 를 소개한 논문의 이름도 “Attention is all you need” 다.
  • 사실 attention 이라는 것은 LSTM, GRU 와 같은 seq2seq 모델의 추가적인 add one 모듈로 사용된 바 있다.
  • 그러나 transformer 에서는 attention 만으로 LSTM, GRU 등을 대체할 수 있고 attention 만으로 sequence data 를 입력으로 받고 sequence 형태의 데이터를 예측할 수 있는 형태의 모델 구조를 가지고 있다.

• transformer 라는 구조가 어떤 것인지 보자! 어떻게 돌아가는지 이해하면 큰 자산이 될 것이다.

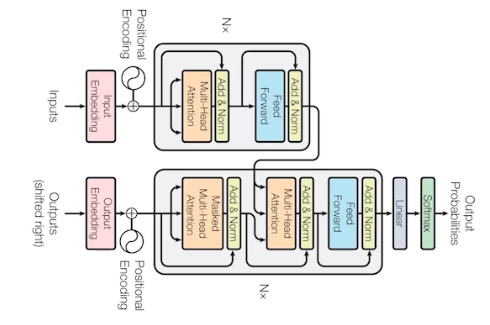  transformer

• RNN 은 입력이 2개다. 이전 RNN 에서 가지고 있던 cell state 가 다시 다음 번으로 들어가는 식으로 반복해서 재귀적으로 돌아간다.
• transformer 는 이런 재귀적인 구조가 없고, attention 이라는 구조를 활용한다.
• ‘Attention Mechanism’
  • 이 메커니즘은 모델이 입력 시퀀스의 각 부분에 얼마나 주의를 기울일지 결정하게 해준다.
  • 특히, transformer 에서 사용되는 ‘Self-Attention’ 은 각 입력 요소가 시퀀스 내의 다른 모든 요소와의 관계를 이해하는 데 도움을 줄 수 있다.
• 기계어 번역(NMT) 문제에 transformer 가 어떻게 적용되는지 보자.
  • 먼저, transformer 방법론은 sequential 한 데이터를 처리하고 이 데이터를 Encoding 하는 방법이기 때문에 NMT 문제에만 적용되는 것은 아니다.
  • 실제로 transformer 가 image classification, image detection, ViT 등 다양한 분야에서 활용되고 있다.
  • 문장이 주어지면 문장에 맞는 이미지를 생성해주는 DALL-E 라는 방법론도 있다. 이는 GPT-3 기반이긴 하지만, 내부를 들어가면 결국에는 self-attention 이 사용된다.
• 결국 transformer 가 하려고 하는 것은 sequence 2 sequence 다.
• 입력 시퀀스와 출력 시퀀스는 숫자, 도메인이 다를 수 있다. 그러나 모델은 하나다.
  • 원래 RNN 에서는 3개의 input 이 있으면 3번의 Network 가 돌아간다.
  • 그런데 transformer 의 encoder 부분은 몇 개의 데이터가 들어가든 재귀적으로 돌지 않는다. 한번에 그 단어들을 encoding 한다.
  • 물론 출력을 생성할 때는 autoregressive 하게 한 단어씩 만들게 된다.
• encoder 혹은 self-attention 이라 불리는 구조에서는 한번에 N 개의 단어를 처리할 수 있다.

Transformer 의 구조

• transformer 는 네트워크 파라미터가 다르게 학습되는 encoder 와 decoder 가 stack 되어 있다.
• encoder 에 N 개의 벡터가 한 번에 들어간다.
• 하나의 encoder 는 self-attention 과 feed forward neural network 를 거친다.
• 그렇게 출력되는 N 개의 출력값이 2번째 layer 의 encoder 에 들어가는 방식이다.
• self-attention 은 transformer 가 왜 잘 작동하는지를 나타낼 수 있다.
• 뒷단의 FFN(feed forward network) 은 MLP 와 동일하다. 따라서 self-attention 이 새로운 부분이다.
• 앞으로 transformer 로 NMT 문제를 푼다고 가정하자.
• N 개의 단어가 들어왔을 때, 기계가 번역할 수 있도록 각 단어마다 특정 숫자의 벡터로 표현한다. 즉 N 개의 벡터로 표현한다.

• self-attention 은 3개의 단어(벡터)가 주어지면 3개의 벡터로 찾아주고 4개가 주어지면 4개가 나온다.

  

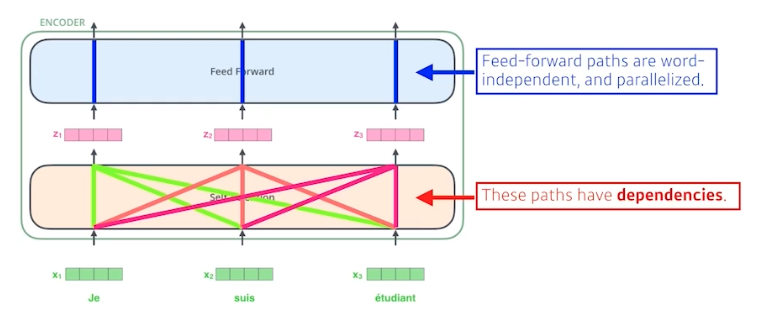
• 위 그림을 보면 FFN 은 서로 단어에 대해서 dependency 가 없다. 즉, FFN 은 같은 벡터에서 같은 벡터로 가는 것이라 볼 수 있다.
• 반면에 self-attention 은 3개의 벡터($x_1, x_2, x_3$)가 들어왔을 때 이를 3개의 벡터($z_1, z_2, z_3$)로 찾을 때, 모든 벡터($x_1, x_2, x_3$)를 같이 고려한다. 즉 dependency 가 있다.
• 어떤 문장을 이해하려면 어떤 단어를 그 자체로 이해하는 게 아니라 그 단어가 문장 속에서 다른 단어들과 어떻게 interaction 이 있는지 이해하는 것이 중요하다.

• 이처럼 transformer 는 단어들 사이의 관계성을 본다. 그래서 대명사 같은 것들이 뭘 가리키는지를 잘 알도록 학습되어 있다. 그래서 모델이 문장 전체 구조 속에서 단어를 잘 이해할 수 있다.

  Self-Attention (SA)

  • self-attention 구조는 3가지 벡터 Q(query), K(key), V(value) 를 만들어낸다.

  • 각 단어마다 $Q_1, K_1, V_1$ 를 만들어내는 것이다. 이들 각각을 만들어내는 3개의 NN(inear 변환, $W$) 가 있는 것이라 이해하면 편하다.

    

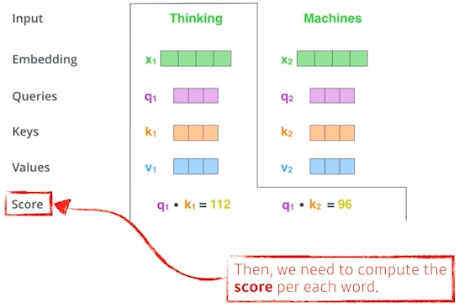
  • 하나의 단어(입력)가 주어지면, 3개의 벡터($Q, K, V$)를 만들게 되고, 이 3개의 벡터를 통해서 원래의 단어에 대한 임베딩 벡터($X_i$)를 새로운 벡터로 바꿔준다.
  • 각각의 단어마다 $Q, K, V$ 벡터를 만든 이후 Score 벡터를 만든다.
  • $i$ 번째 단어에 대한 score 벡터를 계산할 때, transformer 의 인코더를 통과시키는 벡터($X_i$)의 $Q$ 벡터와 나머지 모든 단어에 대한 $K$ 벡터를 내적한다.
  • 바꿔 말하면, 이 두 벡터가 얼마나 align 이 잘 되어있는지를 본다. 즉, $i$ 번째 단어가 나머지 N 개의 단어와 얼마나 관계가 있는지를 정한다.

  • 즉 내가 encoding 하고자 하는 벡터의 쿼리 벡터($Q$)와, 자기 자신을 포함한 나머지 벡터들의 키 벡터($K$)들을 다 구하고 그 두 벡터 사이에서 내적을 하는 것이다.

    $\text{Attention}(Q,K,V) = \text{softmax} \left( \frac{QK^T}{\sqrt{d_K}}\right)V \in \mathbb{R}^{n \times d_V}$
  • 그렇게 내적한 것($QK^T$)은 결국 $i$ 번째 단어와 나머지 단어들 사이에 얼마나 interaction 을 해야하는지를 학습하는 것이다. 이것이 바로 attention 이다.
  • 원래 attention 은 어떤 task 를 수행할 때 특정 time step 의 어떤 입력들을 더 주의깊게 볼지 해당한다. transformer 에서도 마찬가지다.

  • 어떤 단어들(나머지 혹은 자기자신)과 더 많이 interaction 이 일어나야 하는지를 쿼리벡터($Q$)와 나머지 벡터들의 키벡터($K$) 사이의 내적으로 표현하는 것이다.

    

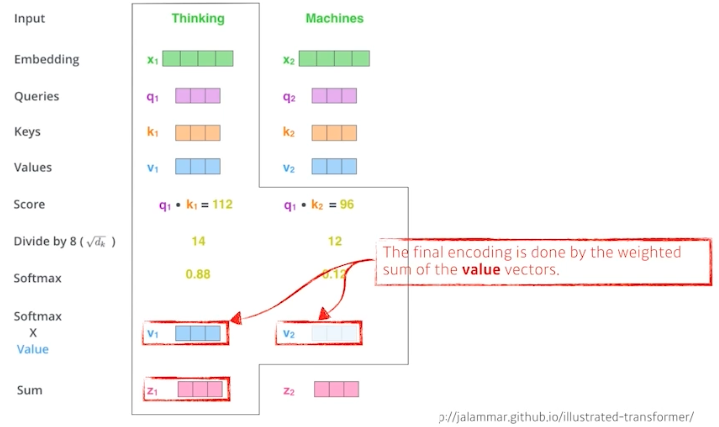
  • score 벡터($QK^T$)가 나오면 한번 normalize 를 해준다.
    • 위 예시에서 8로 나눠주는 것에 해당한다.
    • 여기서 8은 키 벡터의 dim($d_K$) 에 dependent 하다.
    • 키 벡터의 dim 에 루트를 취한 것($\sqrt{d_k}$)으로 normalize 를 해준다. key 벡터를 몇 차원으로 만들지는 하이퍼 파라미터다.
    • 이 normalize 과정은 값 자체가 너무 커지지 않게 만들어준다.
    • score 가 특정 range 안에 들어갈 수 있게 키 벡터의 차원 혹은 쿼리벡터의 차원(같은 차원이기 때문)의 루트로 나눠준다.
  • 이후 normalized score 가 0~1 값이 되도록 하기 위해서 소프트맥스를 취한다.
  • 그러면 어떤 단어와 특정 단어(나머지 혹은 자기 자신) 사이의 attention 즉 interaction 에 해당하는 값이 나온다. 이것이 바로 attention weights 에 해당한다.
  • attention weight 는 각각의 단어가 다른 단어 혹은 자기 자신과 얼마나 attention 을 해야하는지를 나타내는 스칼라 값이다.
  • 지금까지의 과정을 정리하면,
    1. 임베딩 벡터가 주어지면 각각 벡터마다 각각의 NN(neural network)을 통해서 $Q, K, V$ 벡터를 만든다.
    2. $Q, K$ 벡터의 내적(score 벡터)과 normalize, softmax 로 score scalar 즉, attention weight 를 만든다.
  • 최종 값은 이 attention weight 를 각각의 단어 임베딩에서 나오는 $V$ 벡터들에 weighted sum 하는 것이다.
  • 즉 각 단어에서 나오는 $Q, K$ 벡터 사이의 내적을 normalize, softmax 해서 attention 을 구하고, 그것을 value 벡터와 weighted sum 을 한 것이 최종적으로 나오는 인코딩된 벡터($z$)가 되는 것이다.
  • 이렇게 다 거치면 하나의 단어 임베딩 벡터($x$)에 대한 인코딩 벡터($z$)가 나온다.
  • 중요한 점은 $Q$ 와 $K$ 벡터는 항상 차원이 같아야 한다. 내적해야 하기 때문이다.
  • 하지만 $V$ 벡터는 차원이 달라도 된다. 왜냐하면 마지막에 attention weight 와 weighted sum 만 하면 되기 때문이다.
  • 최종적으로 나오는 인코딩 벡터의 차원은 여기에서는(multi-head attention 에 가서는 달라진다.) $V$ 벡터 차원과 동일하다.

  • 이제 이 과정을 행렬을 활용해서 보자.

    

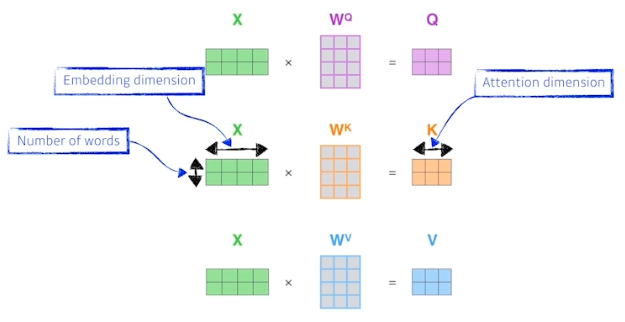
  • $X$ 의 spatial dimension 이 (2,4) 인 것은 단어가 2개, 각 단어마다 4차원 임베딩된 것을 뜻한다.
  • 3개의 weight matrix($W^Q, W^K, W^V$) 를 찾는다. 각 matrix 는 $Q, K, V$ 를 구하기 위한 각각의 MLP 의 weight matrix 다. 이 MLP 는 인코딩된 단어마다 다 shared 된다.
  • $Q, K$ 벡터를 내적해서 스칼라(score)를 뽑고, 그것을 $\sqrt{d_k}$ 로 normalize 한다. 이후 소프트맥스를 취하여 attenion weight 를 구하고, $V$ 에 대해서 weighted sum(그냥 곱) 한다.

  • 위 과정이 아래의 그림으로 표현될 수 있다.

    

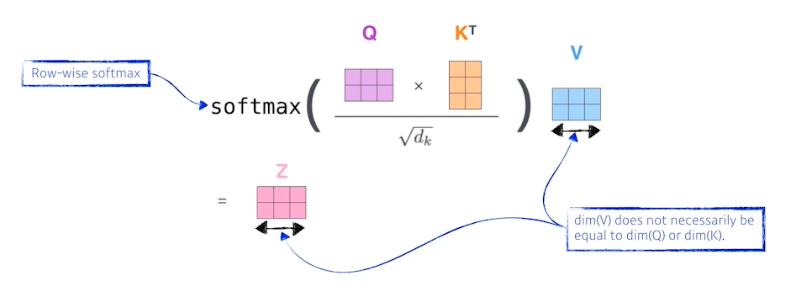
  • 중요한 점은, $Q, K$ 벡터의 차원은 내적해야 하기 때문에 항상 같아야 하고 $V$ 의 차원은 $Q, K$ 벡터와 달라도 된다는 점이다. 하지만 편의상 $V$ 벡터까지 같게 해주기는 한다.
  • 왜 이게 잘될까? 를 생각해보자.
  • 이미지 하나가 주어졌을 때 CNN 이나 MLP 을 돌리면, 같은 input 에 같은 출력이 고정된다.
  • transformer 는 input 이 고정되고 network 가 고정되어 있더라도, 인코딩하려는 단어와 그 옆에 있는 단어들에 따라서 인코딩된 값이 달라진다.
  • 어떻게 보면 MLP 보다 좀 더 flexible 한 모델인 것이다. 입력이 고정되더라도 내 옆에 주어진 다른 입력들이 달라짐에 따라서 출력이 달라질 여지가 있는 것이다.
  • 그래서 훨씬 많은 것을 표현할 수 있다. 그렇기 때문에 바꿔 말하면, 더 많은 computation 이 필요하다.
  • transformer 에서 N 개의 단어가 주어지면 N x N attention map 을 만들어야 한다. 즉 1000 개를 한번에 처리하려면, 1000 x 1000 을 처리해야 한다.
  • 따라서 단어 개수가 길어지면 한계가 생기고 메모리를 많이 먹는다. 그러나, 훨씬 flexible 하고 더 많은 것을 표현할 수 있는 네트워크를 만들 수 있다.

  Multi-head attention (MHA)

  • 이름 그대로 attention 을 여러 번 하는 것이다.
  • 왜냐하면 하나의 문장에서도 얻을 수 있는 정보가 관점에 따라 다르기 때문이다. 예를 들어 “나는 집에서 쉬고 있다” 라는 문장에서 행위의 관점에서는 쉬고 있는 것이고, 위치의 관점에서는 집에 있는 것이다.
  • 이처럼 여러 관점에서의 정보를 더 잘 취합하기 위해서 여러 개의 self-attention 을 사용한다.
  • 여기서 head 는 각 단어를 $Q, K, V$ 로 만들어주는 linear 변환 ($W^Q, W^K, W^V$) 을 뜻하며 각 self-attention 모두 다르게 적용된다.
  • 하나의 입력, 임베딩 벡터에 대해서 $Q, K, V$ 를 하나씩이 아니라 여러 개를 만든다.
  • N 개의 attention 을 반복하게 되면 N 개의 인코딩된 벡터가 나온다. transformer 에서는 8개의 head 가 사용된다. 즉 하나의 임베딩 벡터에 대해서 8개의 인코딩 벡터가 나오게 된다.
  • 여기서 고려해야 할 것은 인코딩이 되면 다음 번 인코딩으로 또 넘어간다는 점이다.
  • 이 때 필요한 것은 입력과 출력의 차원을 맞춰줘야 한다. 임베딩된 벡터의 차원(입력)과 인코딩되어서 self-attention 으로 나오는 벡터(출력)가 항상 같은 차원이어야 한다.
  • 또한 transformer 는 Add 라는 residual connection 이 있기 때문에 input 의 차원과 output 의 차원이 같아야 한다.
  • 어떻게 인코딩된 벡터를 다음 층으로 넘길까?

  • 차원을 줄여서 넘겨야 한다. 원래 dim 으로 줄여주는 linear layer($W^O$) 를 붙혀서 input 과 dim 을 맞춰주는 것이다.

    

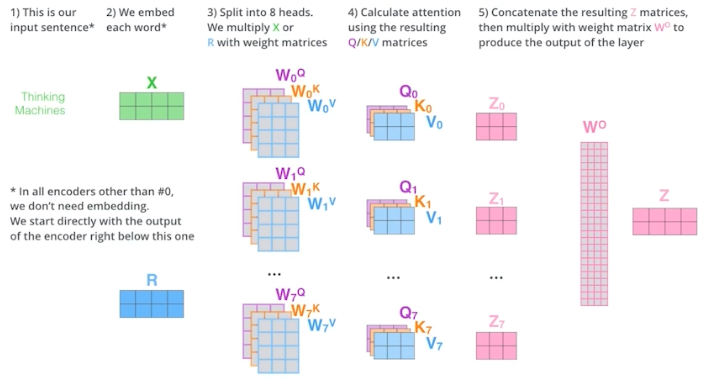
  • 실제 구현체를 보면, 위처럼 구현되지 않는다.
  • 100 dim 의 임베딩 벡터에 10 개의 head를 사용한다고 하면, 100 dim 을 10 개로 나눈다. 실제로 $Q, K, V$ 를 만드는 것에 10 dim 임베딩 벡터를 사용하는 것이다.

  Add & Norm

  • MHA 을 통과한 인코딩된 벡터들은 Add(residual connection) 와 Norm(Layer Normalization) 을 거치게 된다.
  • Add 는 residual connection 을 뜻하는 것으로, input 을 그대로 더해준다.
  • 이는 층이 깊을수록 gradient vanishing 에 의해 학습이 잘 되지 않는 문제를 방지하고, 학습에 안정성을 가져다 준다.
  • 이 관점에서 MHA 에서 구하는 것은, Add 를 통과한 인코딩된 벡터와 input 벡터의 차이를 구하는 것이다.
  • Norm 은 Layer Normalization 을 뜻한다.
  • 인코딩된 단어 벡터 별로 평균을 0, 분산을 1로 만들어준 뒤 affine tranformation 을 통해서 원하는 평균과 분산을 주입해줄 수 있다.
  • Batch Normalization 과 세부적인 부분에서는 다르지만, 큰 틀에서 이 또한 학습을 안정화하고 최종적인 성능을 끌어올리는데 중요한 역할을 하게 된다.

  Positional Encoding

  

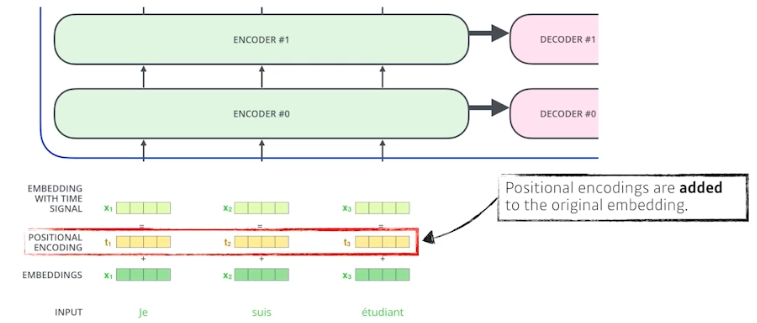
  • 입력에 특정값을 더해주는 bias 라고 볼 수 있다.
  • 왜 positional encoding 이 필요할까?
    • transformer 를 보면, N 개의 단어를 sequential 하게 넣었다고 하지만 이 안에 sequential 한 정보가 있지는 않다.
    • 순서가 바뀌더라도 각각 단어가 인코딩 되는 값은 달라질 수 없다. 왜 그럴까?
    • RNN 과 달리 transformer 의 self-attention 은 순서에 independent 하기 때문이다.
    • 각 단어는 독립적으로 $Q$ 벡터가 되고 자기 자신을 포함한 $K$ 벡터와 내적한 후 normalize, softmax 를 취하여 $V$ 와 weighted sum 이 된다. 이 때 교환법칙이 성립한다. 왜냐하면 $V$ 와 weighted sum 될 때 $Q$ 벡터와 같은 단어가 되기 때문이다.
    • 즉, “I go home” 에서의 I 나 “go I home” 에서의 I 나 self-attention 을 취하면 똑같은 값이 나온다.
    • 그러나 문장을 만들 때는 어떤 단어가 먼저 나왔는지가 중요하다. 따라서 positional encoding 이 필요하다.
    • positional encoding 은 predefined 된 방법으로, 그냥 몇 번째 단어인지 그 $i$ 를 그대로 더해줄 수 있다.일종의 offset 처럼 작용하는 것이다.
    • transformer 에서는 sin, cos 함수를 이용해서 벡터들을 만들고, 단어의 위치 별로 서로 다른 벡터가 더해지도록 만든다.
    • 정리하면, transformer 모델은 기본적으로 입력 시퀀스의 순서 정보를 고려하지 않는 구조이고, ‘Positional Encoding’은 각 단어나 토큰의 위치 정보를 모델에 전달하기 위해 도입되었으며, 이를 통해 Transformer는 시퀀스 내에서 각 단어의 위치를 이해하고, 이에 기반하여 더 정확한 컨텍스트 해석이 가능해진다.
    • 즉, Positional Encoding 의 주요 목적은 시퀀스의 각 위치에 고유한 정보를 제공하여 위치 정보를 포함시키는 것이다.

  Encoder

  • self-attention, multi-head attention 은 N 개의 단어가 주어지면 N 개의 인코딩된 단어를 만든다.
  • self-attention 메커니즘은 시퀀스 내의 각 원소가 다른 모든 원소와의 관계를 모델링할 수 있게 해준다.
  • 다시 말해, 각 위치의 원소는 시퀀스 내의 모든 다른 위치로부터 정보를 얻을 수 있으며, 문장 내에서 단어 간의 관계나 문맥을 이해하는 데 매우 유용하다.

  • 즉 self-attention 은 입력 시퀀스의 각 위치에서 모든 위치로의 의존성을 계산하고, 이러한 관계를 수치화하여 모델이 각 단어나 토큰에 주어진 정보를 최적으로 활용할 수 있도록 한다.

    

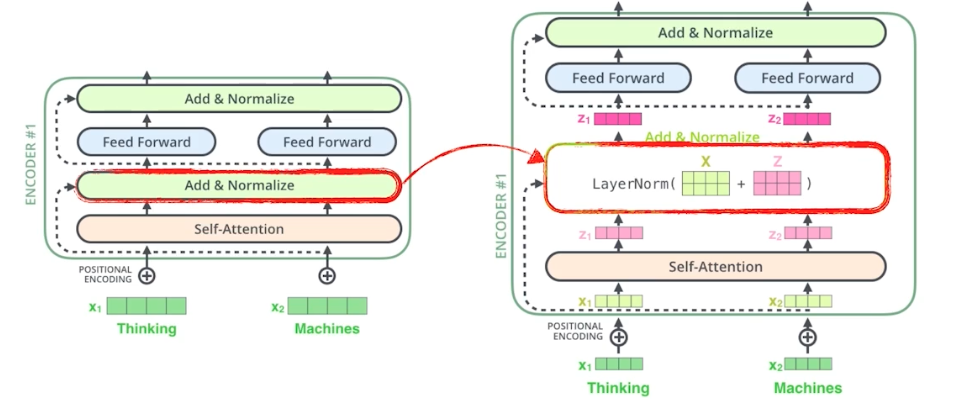
  • 인코더 안에는 self-attention, add & normalize(identity connection, layer norm), FFN(각각의 인코딩된 $z$ 벡터에 대해서 독립적으로 동일한 NN가 동작함) 이것을 계속 반복한다.
  • 각각에 대해서는 따로 정리하자.

  Decoder

  

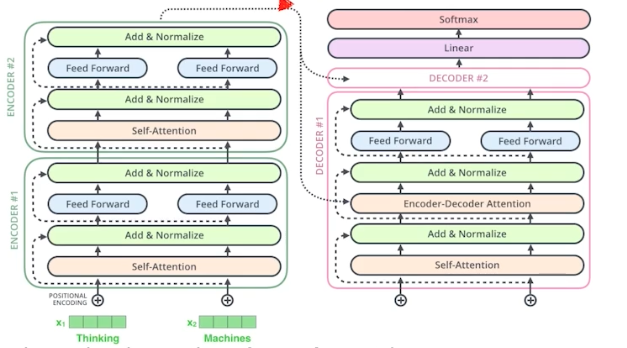
  • 인코더는 attention 을 통해 주어진 단어를 표현하는 것이고, 디코더는 그것을 가지고 생성하는 것이다.

  • 인코더에서 디코더로 어떤 정보가 전해질까?

    

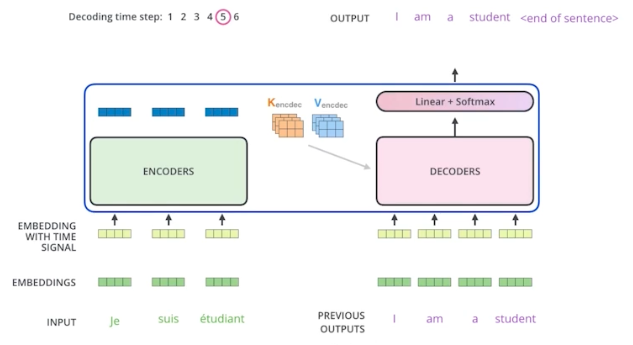
  • 인코더는 결국 $K, V$ 를 보냄. $i$ 번째 단어의 인코딩 벡터를 만들 때 $i$ 번째 단어의 $Q$ 벡터와 나머지 단어들의 $K$ 벡터를 내적해서 attention 을 만들고 거기에 $V$ 벡터를 weighted sum 한다.
  • input 에 있는 단어들을 디코더에 있는 출력하고자 하는 단어들에 대해서 attention map 을 만들려면, input 에 해당하는 단어들의 $K, V$ 가 필요하다.
  • 이 인코더에서 전달되는 $K, V$ 와 디코더에 들어가는 단어들로 만들어지는 $Q$ 벡터를 가지고 최종값을 만든다.
  • 이 때 디코더의 입력인 $Q$ 와 인코더에서 전달된 $K, V$ 는 수가 달라도 된다.

  • 그리고 최종 출력은 autoregressive 하게 하나의 단어씩 만들게 된다.

    

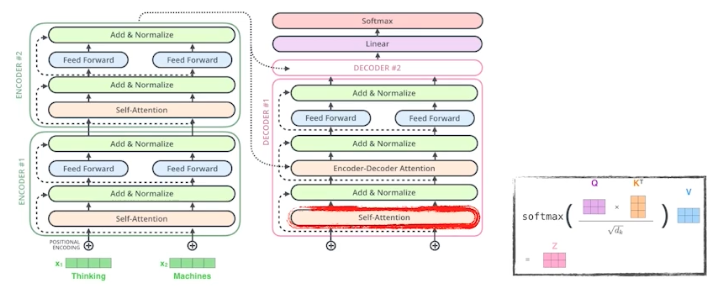
  • 학습할 때는 입력과 정답을 알고 있다. 따라서 학습 단계에서 마스킹을 함. 미래에 있는 정보를 활용하지 않도록 하는 것이다.

    

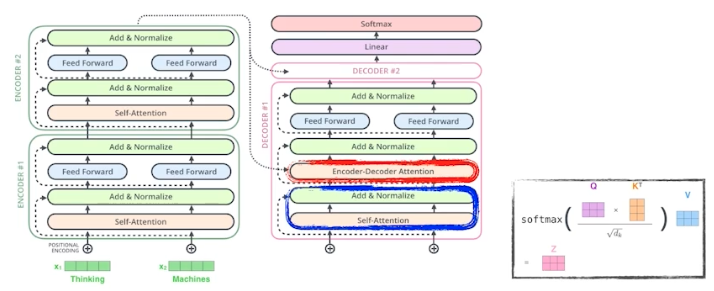
  • encoder-decoder attention 은 인코더와 디코더 사이의 관계를 나타낸다. 이전까지 생성한 단어들만 가지고 $Q$ 를 만들고 $K, V$ 는 인코더에서 주어진 벡터를 활용한다.

Transformer 의 활용

• attention 이 단어들의 시퀀스를 처리하는 것 뿐만 아니라 이미지 혹은 다른 영역에도 많이 활용되고 있다.

• ViT (Vision Transformer)

  

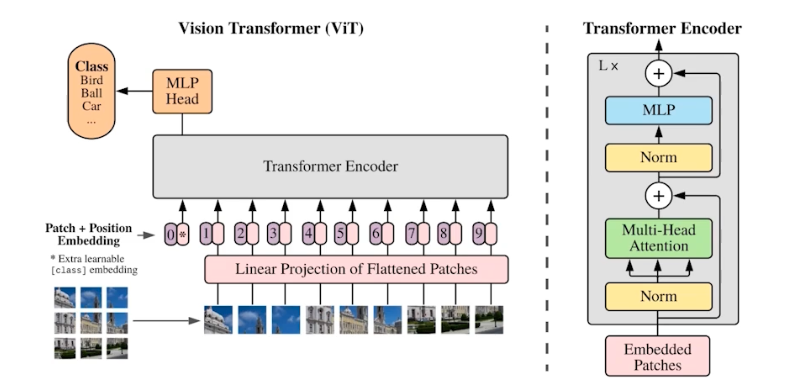
  • self-attention, attention 은 이미지 에서도 활용되고 있다.
  • ViT 는 인코더만 활용했다. 인코더에서 나오는 인코딩 벡터를 분류기에 집어넣는 구조다.
  • 원래 NMT 에서는 단어들의 시퀀스가 들어오는데, 이미지도 이와 맞추기 위해 이미지를 특정 영역(패치)으로 나누고 각각 영역을 하나의 입력처럼 취한다.
  • 마찬가지로 attention 구조 자체는 input 순서에 independent 하기 때문에 positional embedding 도 들어간다.
• DALL-E
  • open-ai 에서 만든 이미지 생성 모델이다.
  • 문장이 주어지면 문장에 대한 이미지를 만들어낸다.
  • GPT-3 를 활용했다.

맨 위로 이동 ↑