[Segmentation] 1. Segmentation Overview

• Segmentation Overview
  • segmentation 은 기존 분류와는 다르게 픽셀 단위의 분류 문제.
  • 픽셀 단위로 클래스를 부여함.
  • semantic segmentation → 같은 object 별 구분하지 않음
  • instance segmentation → 같은 object 도 구분함.

  

  

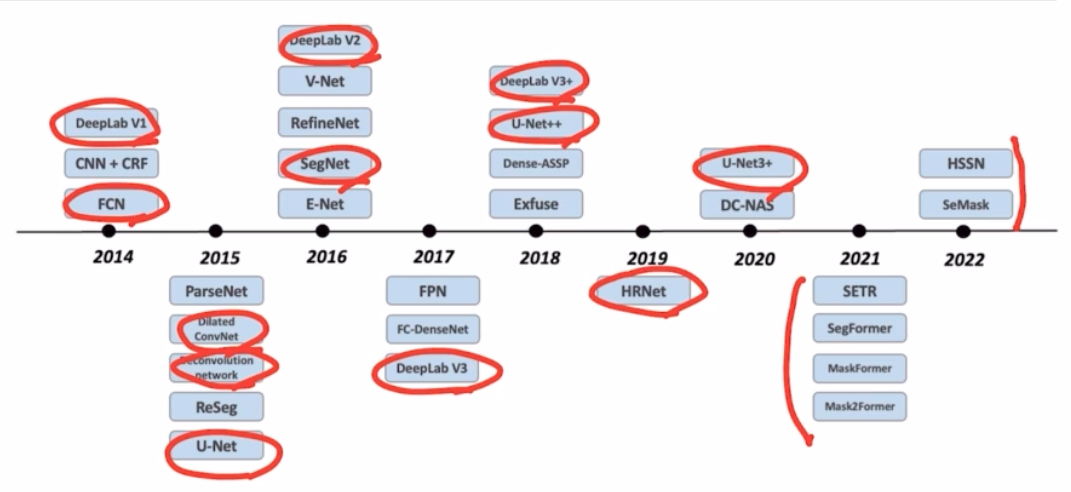
  • FCN 모델이 어떻게 개선되었는지를 중점적으로 보면서 segmentation 모델에 대한 동향성을 볼 것.
  • semantic segmentation 에 대한 기초를 살펴보고,
  • 논문에 대한 정확한 이해보다는 논문이 나온 배경과 방법론에 대한 이해를 하고,
  • 모델의 구조를 살펴보면서 어떤 식으로 코드를 작성할 지에 대한 실력을 향상시키고,
  • 대회에서 사용되는 기법에 대해서 살펴보면서 많은 스킬들을 습득하는 것을 목표로 강의를 듣자!
• Semantic Segmentation의 기초와 이해
  • FCN 부터 시작해서 최근 연구인 HRNet 까지 살펴보자
  • 대표적 end-to-end 의 semantic seg 를 시작한 FCN.
  • FCN(Fully Convolutional Networks)
    • 3가지 특징

      • vgg 를 backbone으로 사용(backbone : feature extracting network)

        

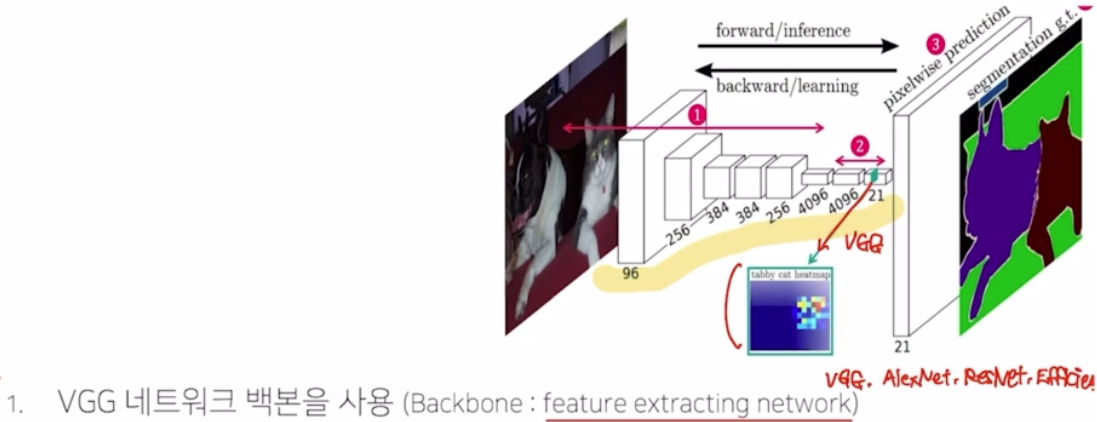
      • vgg 의 fc layer(nn.Linear)를 convolution 으로 대체
      • transposed convolution 을 이용해서 pixel wise prediction 을 수행 → 각 픽셀이 어떤 class 를 가지는지 prediction 할 때 사용함
    • VGG
      • 3x3 conv 를 딥하게 쌓아서 적은 파라미터로 효과적으로 receptive field 를 넓히면서 높은 성능을 가져옴.

      

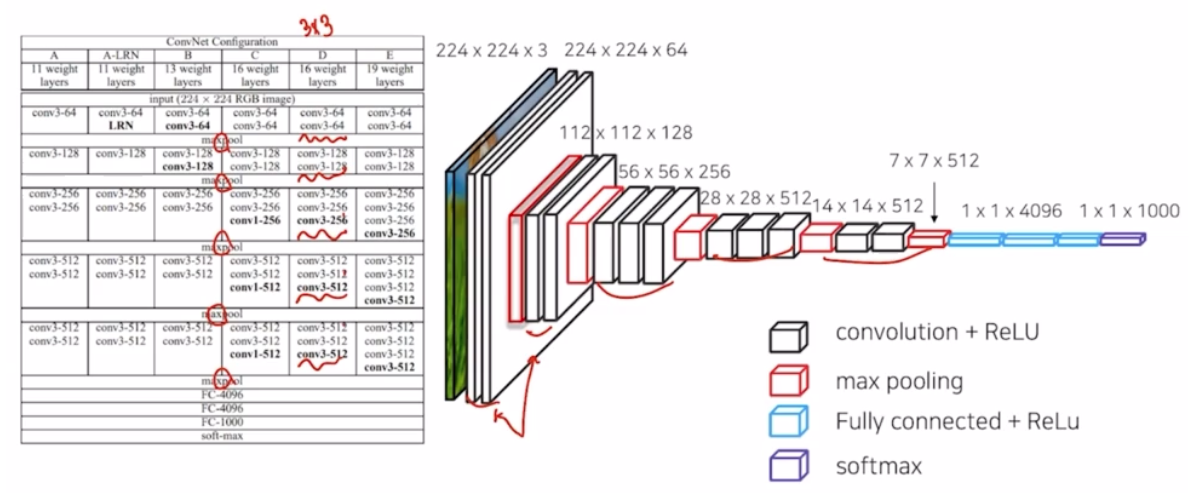
      • FCN 의 특징 중 하나가 이 VGG net 을 backbone 으로 사용했는데, 그것이 어떤 의미를 가질까?
      • pre-trained 된 net 을 그대로 사용할 수 있음. 새로운 네트워크를 만들면 네트워크 가중치 학습을 새로 시작해야 하는데, pre-trained 를 사용하면 이미 어느정도 학습된 가중치를 사용할 수 있음. resnet, efficientnet 도 사용할 수 있음.
      • 각 픽셀의 위치 정보를 해치지 않은채로 특징을 추출할 수 있음. fc layer 는 flatten 하게 되는데 이게 각 픽셀의 위치 정보를 해칠 수 있음.
  • Fully Connected layer vs. Fully Convolution Layer
    • linear → conv2d 로 바꿀 때 얻는 의미는?

    

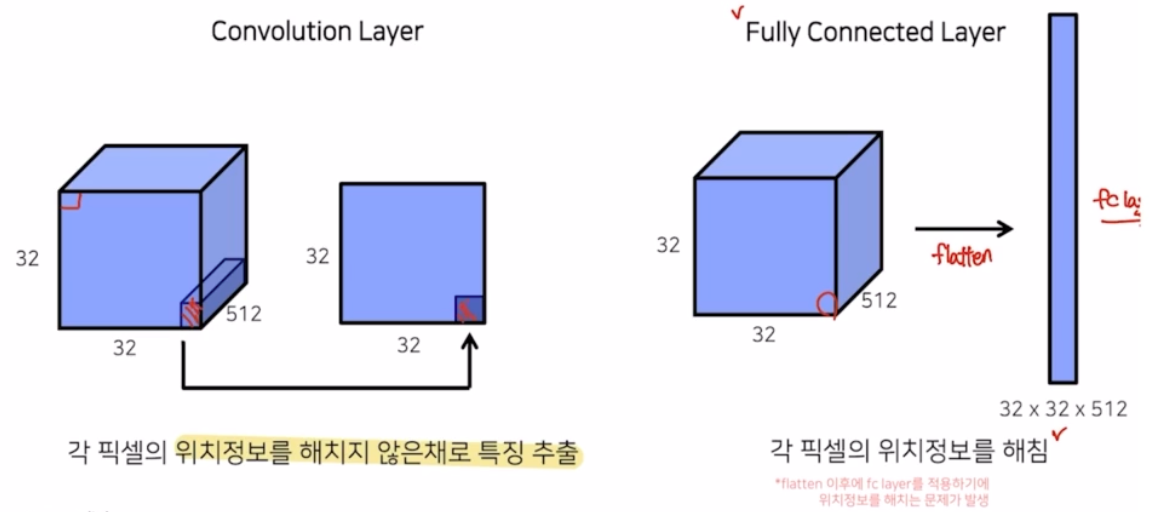
    • 기존의 classification 은 flatten 한 후 fc layer 를 적용해서 위치정보를 없애도 문제가 없었던 이유는 하나의 이미지 내에 어떤 object 가 존재하는지만 관심있었기 때문. → 위치 정보는 관심이 없었음. 그래서 translation invariance 라고 해서 입력의 위치가 변해도 출력의 결과는 바뀌지 않는 효과를 낼 수 있었음. 그러나 seg task의 경우 각 픽셀마다 어떤 클래스를 가지는지 정보가 중요하기 때문에 위치 정보가 중요함. 따라서 fc layer 를 제거하고 conv layer 로 교체해서 문제점을 해결함.
    • 즉 flatten 을 하고 fc layer 를 취하면 label 에 대한 정보 밖에 알 수 없음.

    • 또한, conv layer 를 사용하면 임의의 입력값에 대해서도 학습을 진행할 때 파라미터 변경이 필요없어지는 장점이 있음.

      

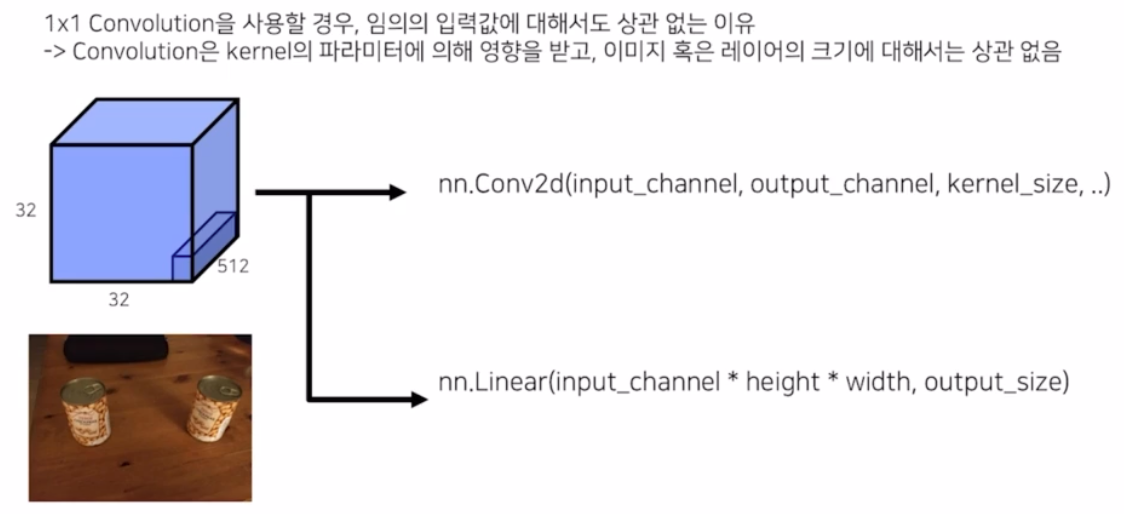
      • Conv2d 는 파라미터 인자로 입력의 채널, 출력의 채널, 커널 사이즈를 가짐. Linear 는 입력 채널, h, w 에 대한 정보를 받음. 이는 flatten과 관련 있는 것(hwc)
      • conv 는 입력 인자에 h, w 가 없기 때문에 입력 사이즈가 달라지더라도 상관 없음. linear 는 사이즈가 달라지면 학습이 불가능해짐.
      • 따라서 conv 를 사용하면 위치정보도 해치지 않고, 임의의 입력값에 대해서도 상관없이 학습이 가능하다는 장점이 있는 것
  • Transposed Conv
    • max pooling 에 의해 줄어든 이미지를 복원해주기 위한 upsampling 의 종류. 이를 통해서 원본 이미지의 크기로 복원해줄 수 있음. 학습 가능한 conv 임.
    • 출력에서 각 픽셀마다 어떤 클래스를 가지는지 정보를 가지고 있어야 함.
    • vgg 에서 max pooling 을 5번 거쳐 입력 이미지 사이즈에 1/32 가 되는데, 이를 원본 이미지 사이즈에 맞게 늘려줘야 함.
    • 이 때 upsampling 을 하고, seg 에서 가장 중요하게 생각하는 부분 중 하나.
    • FCN 에서는 upsampling 방법 중 transposed conv 를 이용함.

    • conv 는 kernel size 에 맞게 element-wise 로 곱하고 summation 함.

      

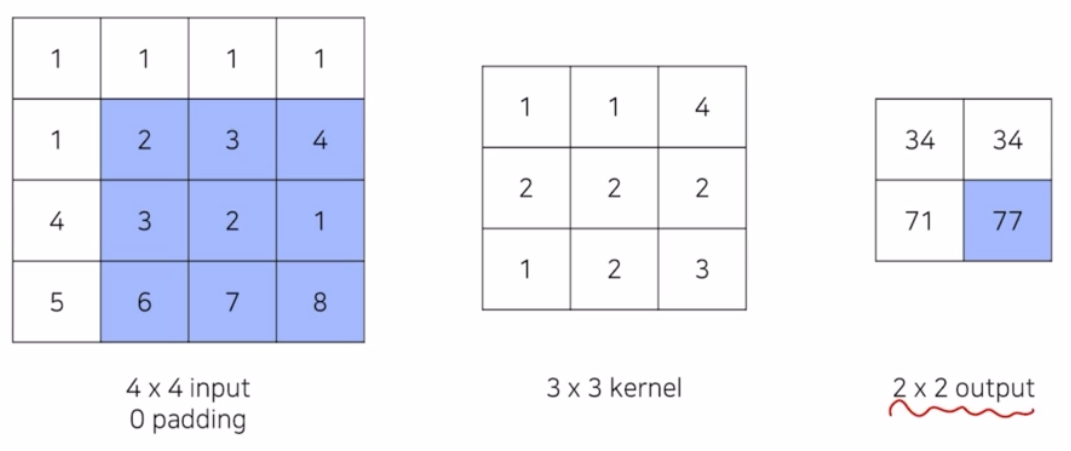
    • 위 예제를 transposed conv 하면, 입력 이미지를 upsampling 하는 과정이기 때문에, 2x2 input 에 3x3 의 transposed conv 를 적용하면 어떻게 되는지 보자
    • transposed conv 는 즉 아래 예제에서 3x3 의 kernel 은 학습이 가능한 파라미터. 학습과정을 통해 더 잘 upsampling 하도록 하는 weight 를 찾아가는 과정임.

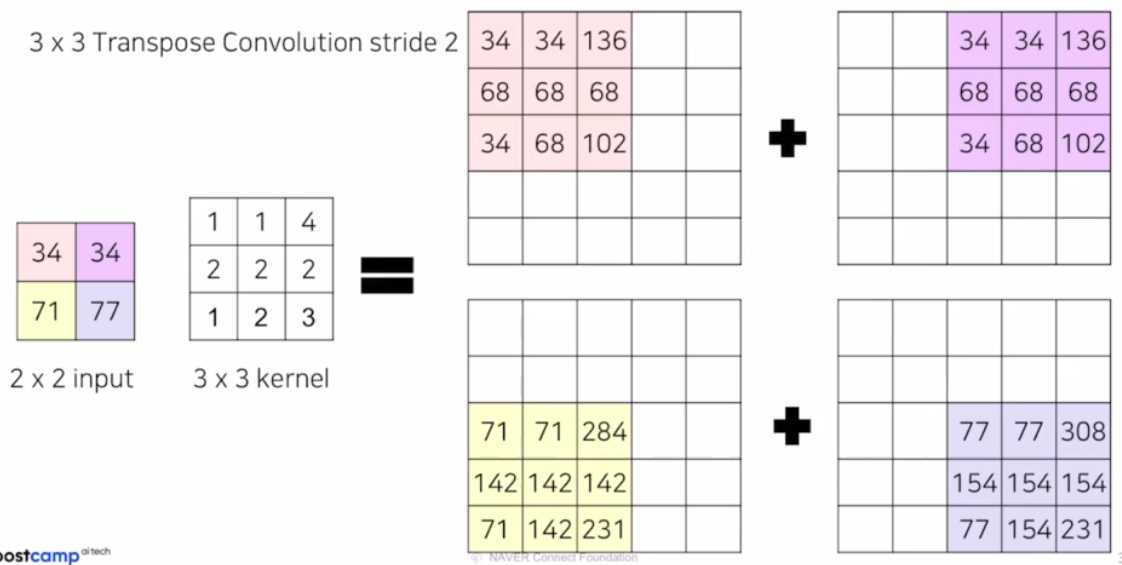
    • 입력 인자 하나가 3x3 의 transposed conv 에 각각 곱해져 결과가 나옴.

      

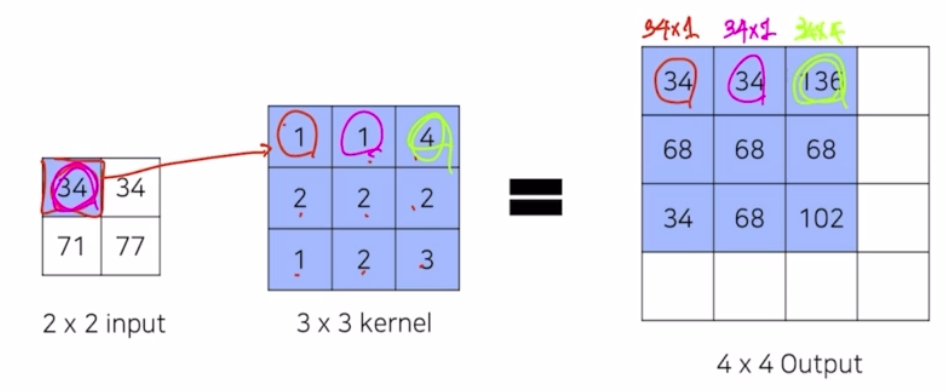
    • 각 영역에 대해서 결과가 나오면, 몇몇 부분들은 겹치는 영역이 있음. 이렇게 겹친 영역에 대해서는 summation 과정을 통해서 output 을 생성함

      

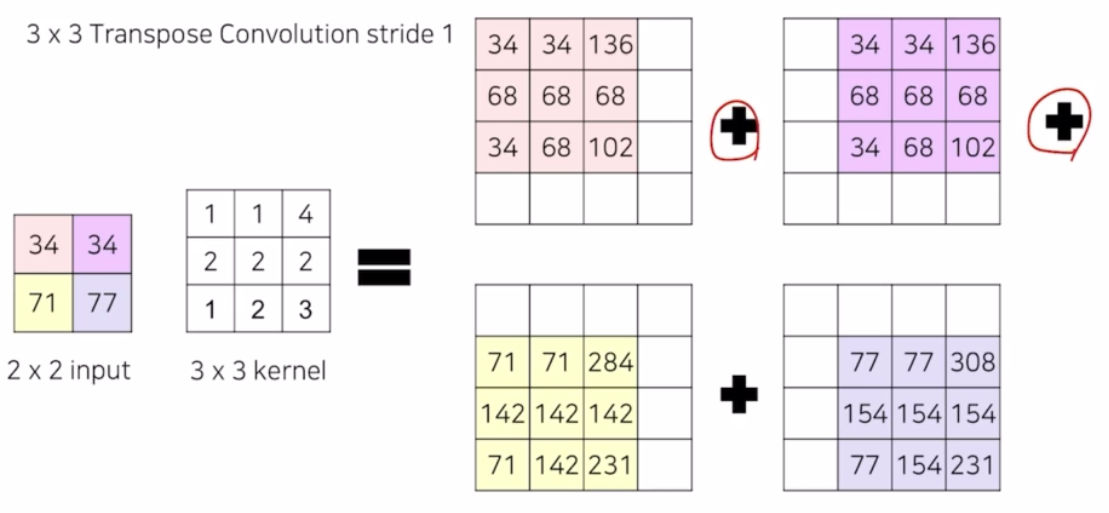
    • 만일 output 사이즈를 더 늘리고 싶으면, stride 를 늘림. 위 예제는 stride 1 이었고, stride 를 2 로 변경하면 됨.

      

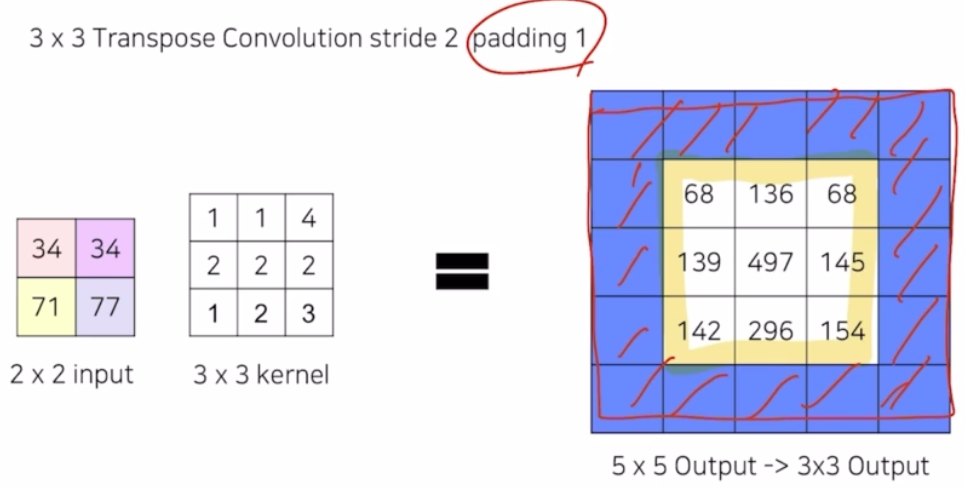
    • padding 에 대해서는 stride 2에서 padding 1 을 넣어주면, 외곽 영역이 지워져서 최종 결과가 내부만 남음.

      

    • 왜 transposed conv 라는 용어로 불릴까?
    • transposed conv 는 부르는 명칭이 많음. 주어진 이미지 크기를 복원하는 과정이어서 upsampling 이라 부르기도 하고, conv 연산을 거꾸로 하기 때문에 deconvolution 이라 부르기도 함. conv 자체를 transposed 해서 transposed conv 라고 부르기도 함.

    • 실제 엄밀히 맞는 명칭은 transposed conv.

      

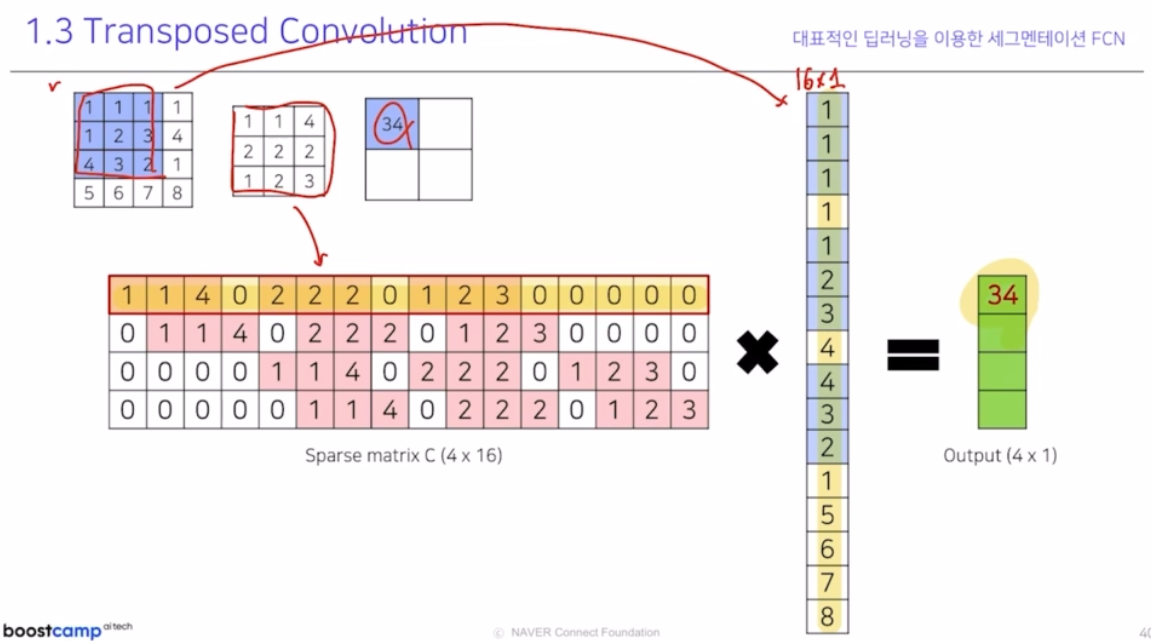
    • 위 처럼 동일한 연산값을 가지는 것을 보면, matrix 를 transpose 시킬 때를 생각해볼 수 있음. matrix 인 conv kernel 을 동일하게 transpose 만 해서 연산하면 알 수 있음.

      

      

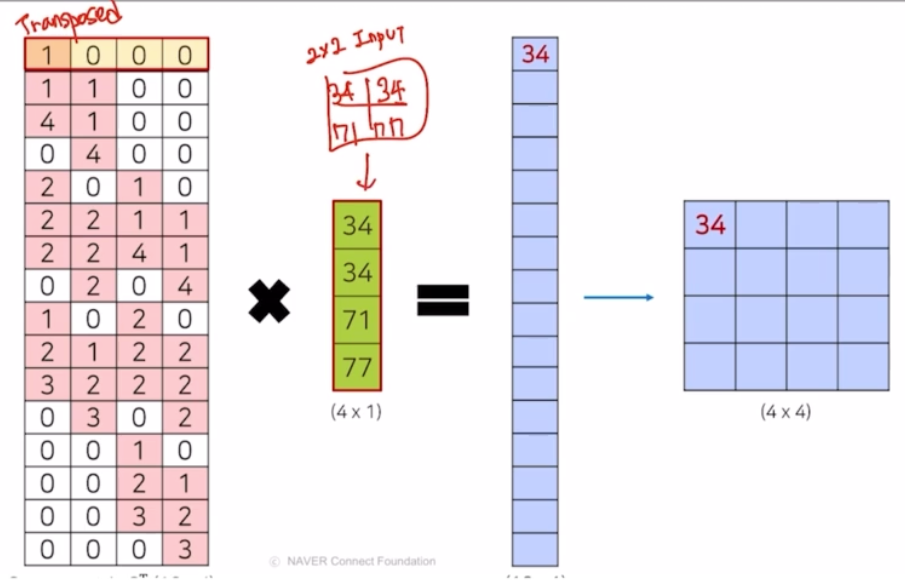
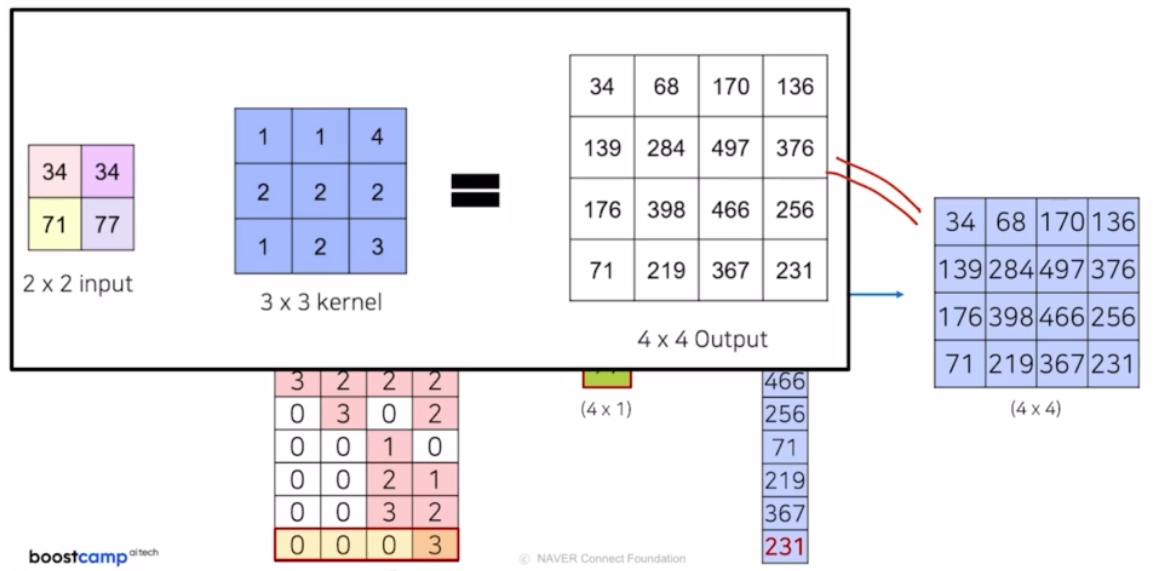
    • 따라서 transposed conv 라는 명칭이 가장 알맞음을 알 수 있다.

    • 그런 conv 연산 후 나온 output 을 transposed conv 했을 때 맨 처음 input 과 output 이 동일하지 않음을 알 수 있다.

      

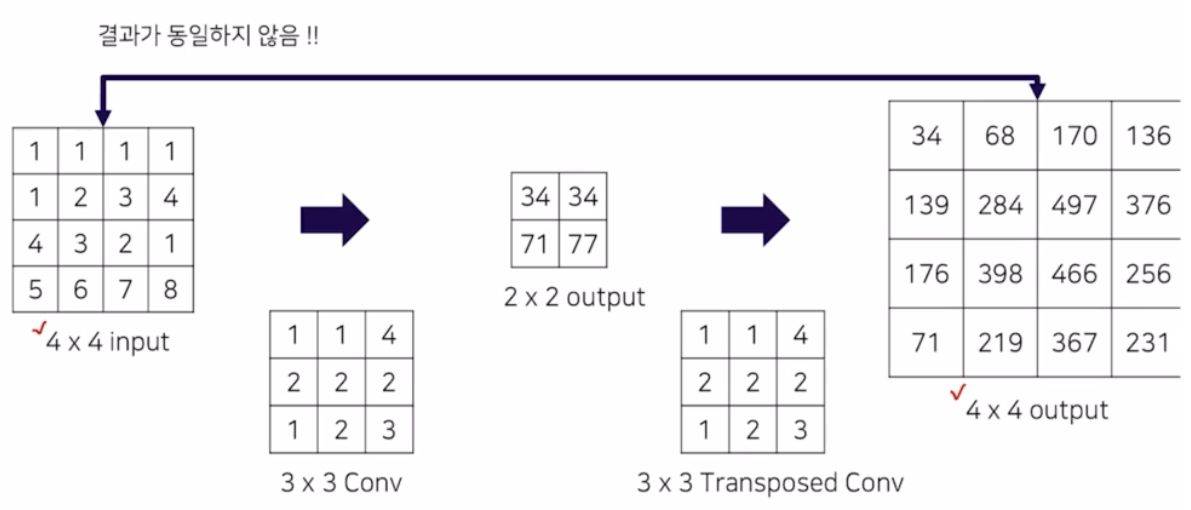
    • 따라서 CS231 강의에서는 transposed conv 를 deconvolution 이라 표현하는 것이 잘못되었다고 얘기하는 것. conv 의 정확한 역에 대한 연산이 아니기 때문. 원래 input 을 복원해내는 연산이 아니기 때문.
    • conv 의 matrix 를 tranpose 해서 연산하는 과정이라 transposed conv 라고 표현하는 것이 정확. 그러나 논문, 다른 강의에서는 해당 표현을 혼용해서 쓰고 있음. 따라서 우리 강의에서는 deconv 와 transposed conv 를 혼용해서 사용할 예정이고 이게 지금껏 배운 transposed conv 를 의미한다고 알아두면 좋음.
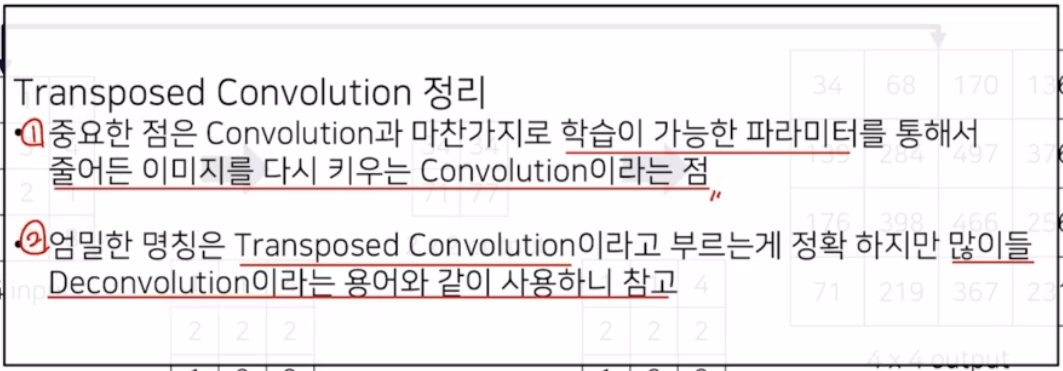
    • 가장 중요한 것은 transposed conv 는 학습이 가능한 weight 로서 학습하는 과정에 따라서 더 좋은 output 을 만들도록 업데이트 되는 값임을 기억

    

  • FCN 에서 성능을 향상시키기 위한 방법

    

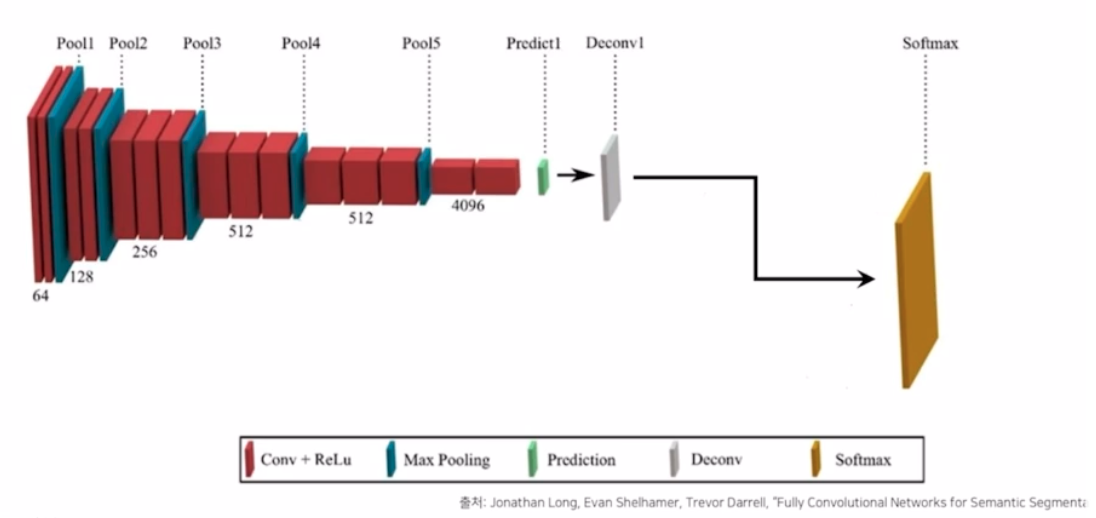
    • FCN 은 vgg16 을 backbone 으로 사용

    

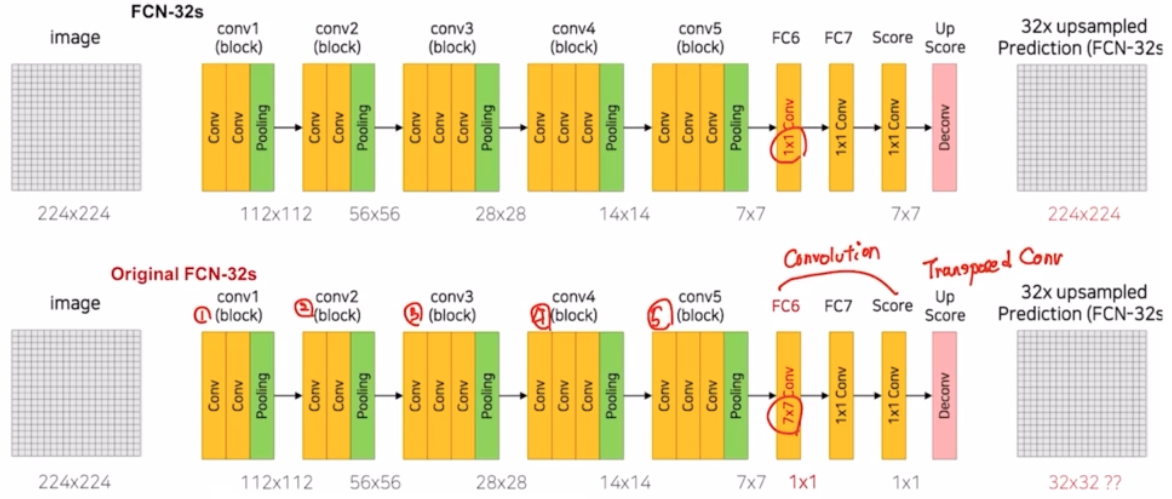
    • 7x7 conv 를 사용하면 이슈가 생김. 따라서 1x1 conv 로 먼저 설명
      • 하나의 conv block 은 conv 과 relu 가 같이 있음. padding, stride 는 각각 1, 1. 따라서 크기 사이즈 변동은 일어나지 않음. max pooling 에서 kernel size 2, stride 2 라서 크기가 1/2 만큼 감소함.
    • fc layer 부분을 linear 가 아닌 conv 을 사용. kernel size 를 1을 이용. 이후 drop out 으로 모델을 좀 더 robust 하게 만들어줌.
    • score 부분에서는 동일하게 1x1 conv 를 적용하지만, 이 때 score 함수 같은 경우는 prediction 즉 classification 을 픽셀 단위로 수행하는 역할을 담당함.
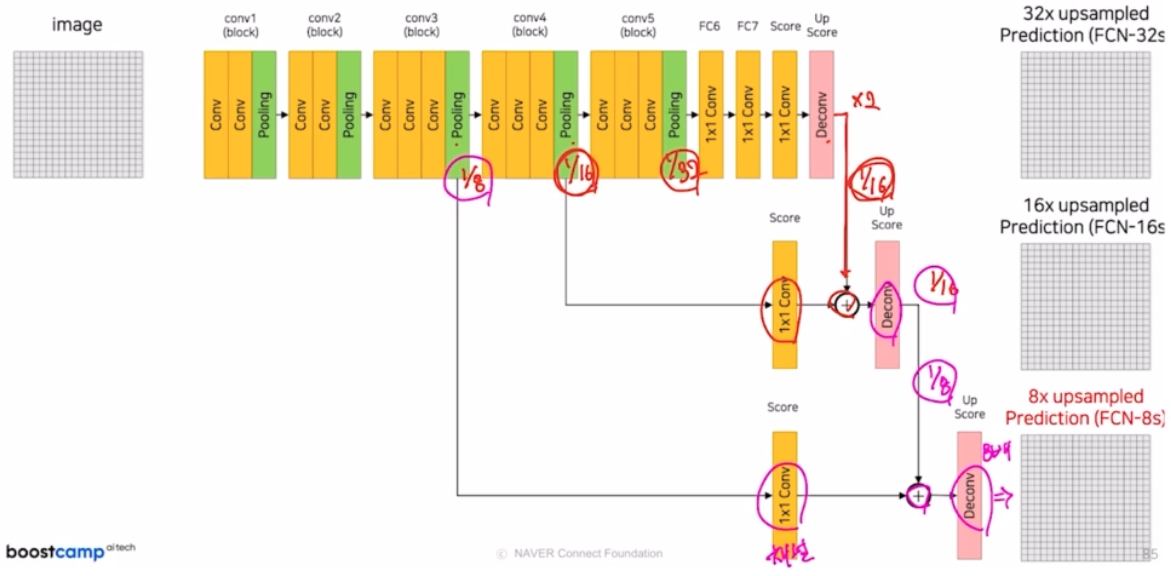
    • 5번의 max pooling 으로 줄어든 크기를 복원하기 위해 Deconv(ConvTranspose2d) 사용. 즉 32배 만큼 복원해줌. kernel size 64, stride 32, padding 16을 주어서 동일하게 32배만큼 키워줌. FCN-32s 는 32의 stride 를 적용한 것을 의미함.
    • 그러나 한번에 32의 stride로 32배로 키우면 결과가 좋지 않음.

    

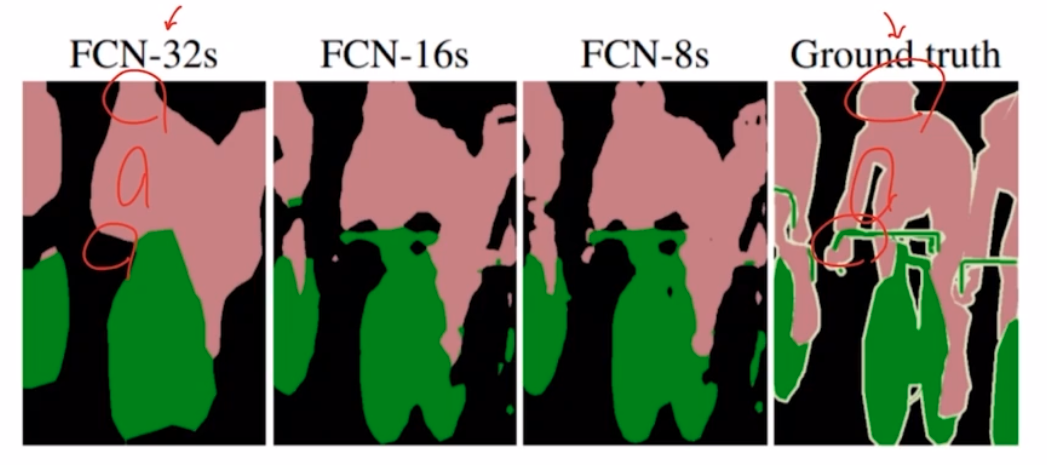
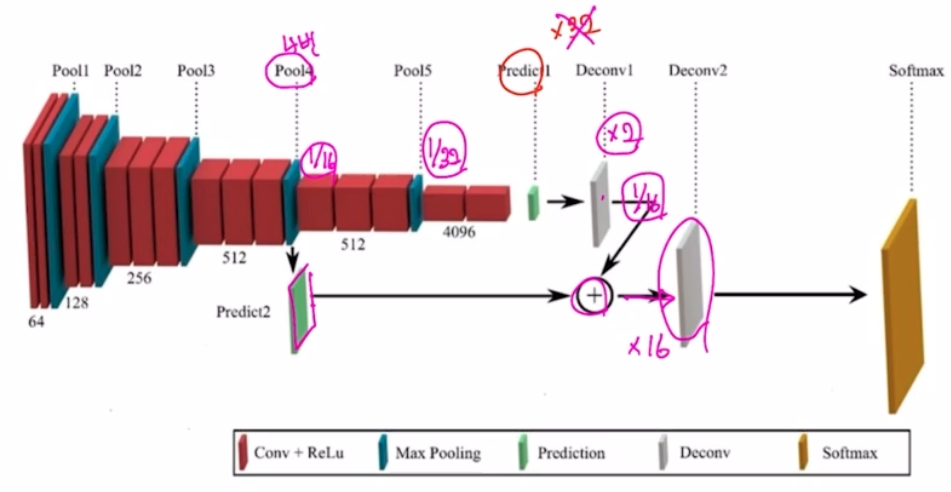
    • 이를 위해 논문에서는 stride size 는 줄이고 이전의 output feature map 과 summation 하는 skip connection 을 적용함. 즉 아래 그림처럼 skip connection 으로 deconv 를 순차적으로 적용함.

    

    • max pooling 에 의해 잃어버린 정보를 복원해주는 작업을 진행함. max pooling 은 feature map 에서 가장 중요한 정보만을 추출해주는 과정임. 이 과정에서 어느정도 정보 손실이 발생함. 이 손실이 발생하기 전의 정보를 summation 하여 정보 복원 작업을 진행하는 것.
    • upsampling size 를 32배가 아니라 2배, 16배로 순차적으로 적용해주는 구조로, 좀 더 효율적으로 이미지 복원이 가능함.
    • summation 을 위해 resolution(h, w)을 맞춰줌.
    • 즉 pooling 에 의해 잃어버릴 수 있는 정보를 보존한 것을 마지막 score 에 더해주어 결과를 좋게 만드는 것.
    • 16s 뿐 아니라 8s 도 있음.

    

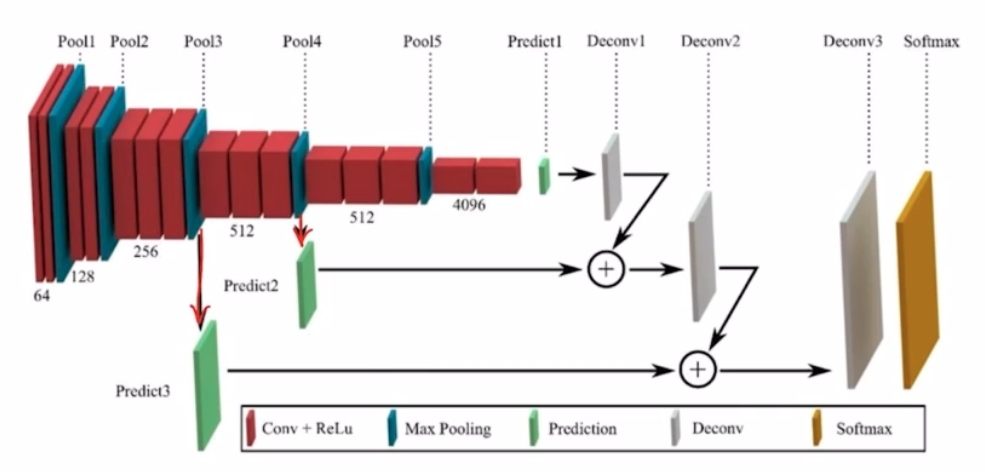
    • 각 skip connection 에서는 pooling 후 나온 feature 와 deconv 를 통과한 score의 채널이 맞지 않기 때문에 1x1 conv 를 통해 채널을 맞춰줌. 그리고 deconv 에서는 resolution(h, w) 를 맞춤. 그 이후 summation 함. 맨 마지막에는 원래 이미지의 크기와 맞춰주기 위해서 deconv 를 함.

      

    • pixel acc 와 mean IoU

      

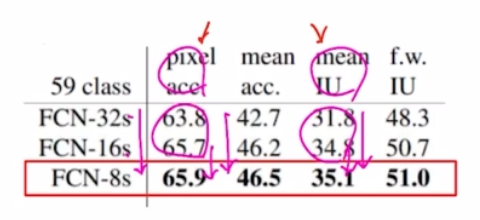
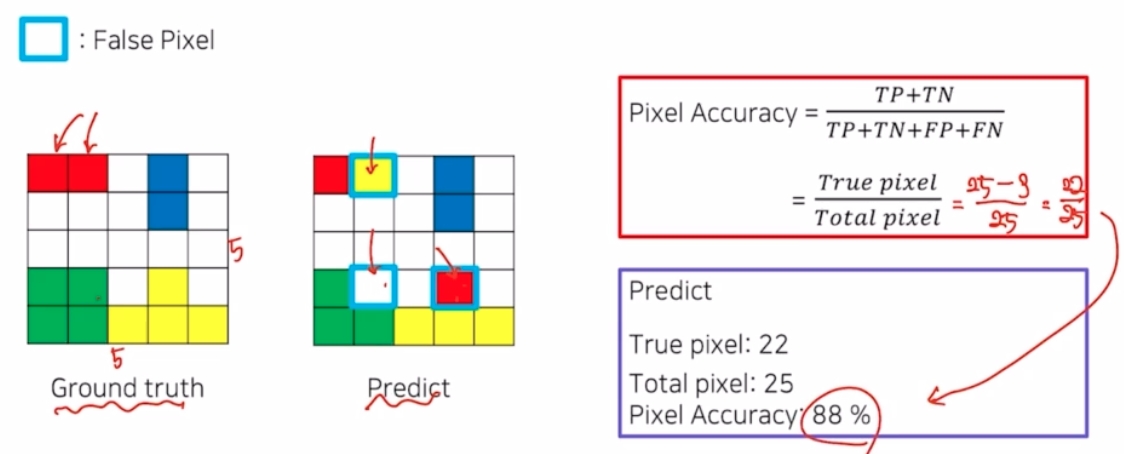
      • pixel acc 는 pixel 단위로 acc 를 계산

      

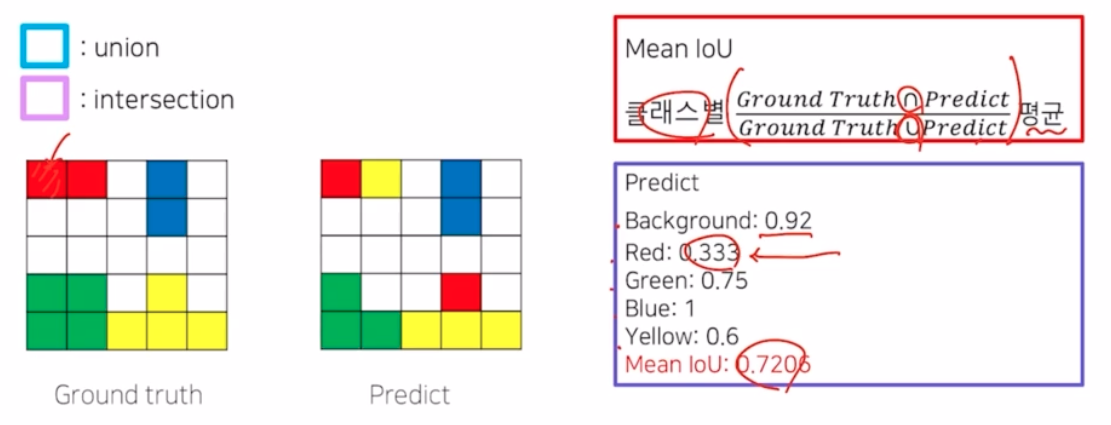
      • Mean IoU

      

  • Further Reading
    • FC6 부분을 7x7 conv 가 아닌 1x1 conv 로 바꿔 설명함. 실제 논문은 vgg 16 구조를 그대로 가져와서 1x1 이 아니라 7x7 kernel size 임.
    • 1x1 이 아니라 7x7 이면, 입력 이미지의 크기가 변동되는 문제가 발생함. 그러면 입력값과 output size 가 서로 크기 매칭이 안됨.
    • 그래서 원 논문의 저자 코드는 이러한 문제를 해결해주기 위해서 첫번째 conv padding 을 100으로 적용하여 입력이미지의 크기를 엄청 크게 키우고 conv 를 수행함.
    • 그럼에도 입력 이미지 크기와 output size 가 달라짐.

    • 이를 해결해주기 위해서 외곽 부분을 crop 해서 크기를 맞춰주는 작업을 수행해줌. 즉 transposed conv 에서 padding size 를 조절해서 외곽의 영역을 제거할 수도 있고, 함수를 직접만들어서 제거해줄 수도 있음. 그 함수는 직접 slicing 을 이용해서 입력 이미지 크기에 맞게 잘라내는 것. crop 을 해주면 transposed conv2d 에서 padding 은 0으로 줌

      

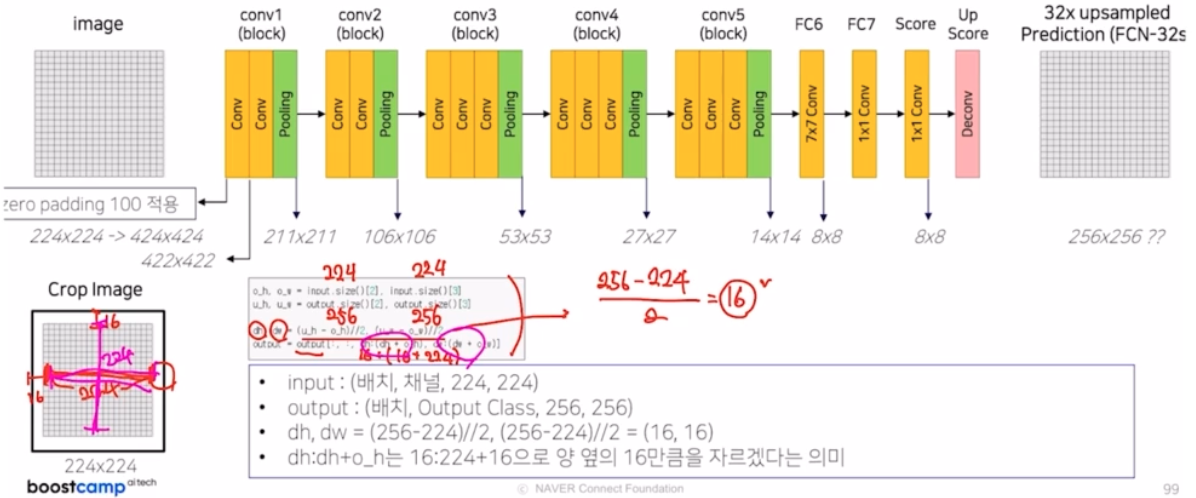
    • 1x1 을 사용하지 않으면 FCN 32s 가 아닌 FCN 16s 에서도 동일한 문제가 발생. 따라서 skip connection 부분 마다 crop 해주는 방법을 사용함. 또한 최종 결과에서도 crop 을 해줌.

맨 위로 이동 ↑