[RNN] 1. RNN(Recurrent Nueral Network)

Sequential Data

• RNN 은 주어지는 입력 자체가 sequential 데이터다.
• 우리가 결국 얻고 싶은 것은 하나의 라벨 혹은 어떤 정보이다. 그러나 sequential 데이터는 그 정의상 길이가 언제 끝날지 모른다. 이것이 sequential 데이터를 처리하는 데 있어서 가장 큰 어려움이다.
• 즉 내가 받아들여야 하는 입력의 차원을 알 수 없다. 따라서 fully connected layer 나 fully convolution layer 를 사용할 수 없다. 몇 개의 데이터가 주어질 지 모르기 때문이다.
• sequential 데이터를 처리하기 위해서 몇 개의 입력들이 들어오든 상관없이 모델이 동작할 수 있어야 한다.
• 가장 기본적인 sequential 모델은 입력이 여러 개 들어왔을 때 다음 번 입력에 대한 예측을 하는 것이다. 이는 언어모델이 가장 간단한 예시가 된다.
• 그러나 sequential 데이터의 특징은 이전 데이터들, 즉 고려해야 하는 과거의 정보량이 점점 늘어난다. 따라서 내가 고려해야 하는 conditioning vector 의 숫자가 점점 늘어난다.
• 이를 간단히 만들기 위해서 제일 쉽게 할 수 있는 것은 fixed timespan 으로, 과거의 몇 개만 보는 방법이 있다.

Markov model(first-order autoregressive model)

• markov assumption 을 가지는 모델이다.

  

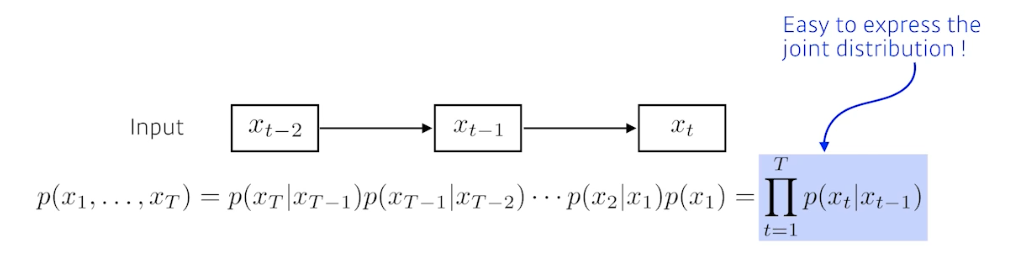
• 강화학습에서도 MDP(markov decision process) 가 있다.
• 이 모델은 사실 말은 안되지만, 현재는 바로 전 과거에만 dependent 하다는 가정을 한다.
• 그래서 되게 많은 정보를 버릴 수 밖에 없다. 그러나 가장 큰 장점은 joint distribution 을 표현하기 쉬워진다는 점이다.
• 이 부분은 Generative 모델(autoregressive model)에서 굉장히 많이 활용된다.

Latent autoregressive model

• ar model(autoregressive, markov model)의 가장 큰 단점은 모델의 가정 때문에, 과거의 많은 정보를 고려해야 하는데 그럴 수 없다는 것이다.
• 그래서 latent ar model 은 중간에 hidden state 가 들어간다. 이 hidden state 가 과거의 정보를 요약하고 있다고 보는 것이다.
• 다음 번 타임 스텝은 바로 전 hidden state 하나에만 dependent 하다.
• 그래서 모델만 봐서는 하나의 과거 정보에만 의존적으로 보이지만, 그 과거 정보가 이전의 정보들을 다 요약하는 hidden state 이자 Latent state 인 것이다.
• 여기서 어떻게 Latent space 를 만드느냐에 따라 다르긴 하지만, 중요한 것은 중간에 hidden state 를 추가해줌으로써 이것이 과거 정보를 요약한다고 볼 수 있는 것이다.

RNN (Recurrent Neural Network)

• 이런 컨셉들을 가장 쉽게 구현한 방법이 바로 RNN 이다.

• RNN 의 구조는 MLP 에 자기 자신으로 돌아오는 구조를 더한 모습이다.

  

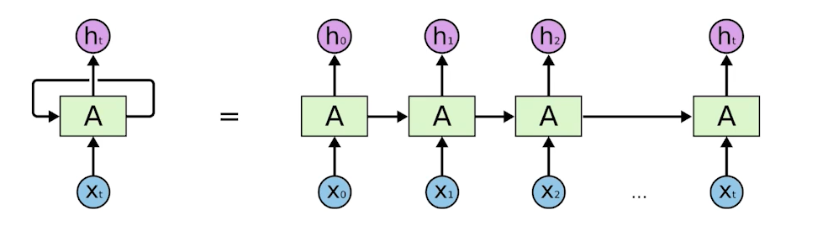
• $t$ 에서의 hidden state 는 $x_t$ 에만 dependent 한 게 아니라 $t-1$ 에서 얻어진 state 에 dependent 하게 된다.
• RNN 은 시간 순으로 푼다고 말할 수 있다. 현재 입력과 함께 이전의 정보가 recurrent 하게 들어온다. 즉 내가 $t$ 에서 보고 있는 것은 $t-1$ 에서 전달된 정보도 같이 있다는 것이다.
• 여기서 중요한 사실은 recurrent 구조를 시간 순으로 풀게 되면 입력이 굉장히 많은 fully connected layer 로 표현될 수 있다는 점이다. 이것은 RNN 을 학습하는 것과 동일하다.
• 즉 timespan 을 고정시키고 시간 순으로 풀게 되면 input 의 width 가 매우 크고 각각의 네트워크의 파라미터가 share 되는 큰 네트워크가 된다.
• 실제로 RNN 은 모든 시간 단계에서 동일한 가중치를 재사용한다. 이러한 특성은 RNN 이 시계열 데이터를 처리하는 데 효과적이라고 생각되는 이유 중 하나이다.
• RNN 의 제일 큰 단점은 short-term dependencies다.
  • 과거에 얻어진 정보들이 다 취합되어서 미래에서 그것을 고려해야 하는데, RNN 자체는 어떤 하나의 fixed rule 로 이 정보들을 계속 취합하기 때문에 이전 과거의 정보가 미래까지 살아남기 힘들다.
  • 그래서 현재에서 몇 스텝 전의 정보는 잘 고려되지만 한참 멀리 있는 정보는 현재에서 고려가 잘 되지 않는다.
• 따라서 Long-term dependencies 를 잡는 것이 RNN 에서 어려운 문제다.
• 이러한 단점을 해결하고자 나온 것이 바로 다음 포스트에서 볼 LSTM 이다.

RNN 학습이 어려운 이유

• 위에서 봤듯 네트워크를 풀어서 보면 input 의 폭이 타임스텝 만큼 굉장히 커지는 네트워크가 된다.

  

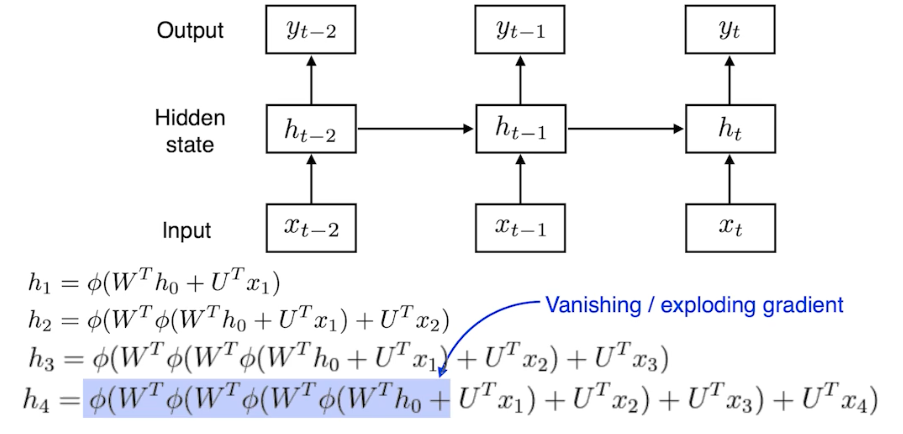
• $W$ 와 $U$ 는 weight 이고 $\phi$ 는 non-linear activation func 이다.
• RNN 은 cell state dim 과 output dim 이 같아야 한다. 왜냐하면 중첩되는 구조가 들어가기 때문이다.
• 또한 $h_0$ 에서 $h_4$ 까지 가기 위해서는 굉장히 많은 똑같은 weight 를 곱하고 non-linear activate func 을 통과시키는 일이 발생한다.
• 이 때 non-linear activate func 이 시그모이드 함수라면 정보가 계속 흘러가면서 값이 의미가 없어진다.
  • 시그모이드는 값을 0~1 로 바꿔서 정보를 줄인다.
  • 그러면 0단계에서부터 흘러가는 정보가 값이 계속 줄어들면서 의미가 없어지는 것이다.
• 만약 시그모이드를 바꿔서 ReLU 를 쓴다면 값이 엄청 커지게 된다.
  • ReLU 특성상 $w$ 가 양수일 때 $w$ 라는 숫자가 계속해서 곱해지게 된다.
• 즉 $\phi$ 가 시그모이드면 정보가 죽어서 학습이 안되는 vanishing gradient 가 발생하는 것이다.
• 또, $\phi$ 가 ReLU 면 weight 를 곱하는 게 계속 반복되어서 exploding gradient 가 발생하고 학습이 잘 안된다.

맨 위로 이동 ↑