[Optimization] Optimization for DL
용어
- 최적화라는 문제에서는 여러가지 용어가 나온다. 이 용어들에 대해서 명확히 정의를 짚고 넘어가지 않으면 다른 개념을 배울 때 많은 오해가 생길 수 있다. 용어가 통일되어야 큰 문제를 막을 수 있기 때문에, 용어들에 대해서 명확한 컨셉을 잡자! 동시에, 아래 용어들은 최적화에서 중요한 컨셉들이다.
-
Gradient Descent
- 줄어들었을 때 optimal에 이를 것이라 기대하는 loss func 이 존재하고, 내가 찾고자 하는 파라미터를 가지고 loss func 을 미분한 편미분을 가지고 학습한다. 1차 미분값만 사용하고, 반복적으로 최적화 시킨다. 그렇게 되면 local minimum 으로 갈 수밖에 없다. 국소적으로 봤을 때 좋은 local minimum 을 찾는 것이 바로 Gradient Descent 다.
-
Generalization
- 딥러닝은 많은 경우 일반화 성능을 높이는 것이 목적이다.
- 일반화란? 학습 에러가 0 이라고 해서 우리가 원하는 최적값은 아니다. 학습에 사용하지 않은 데이터(test data)에 대해서는 성능이 떨어질 수 있기 때문.
- 따라서 일반화 성능이 좋다는 것은, 이 네트워크의 성능이 학습데이터와 비슷하게 나올거라는 보장을 해주는 것. 즉, Generalization Gap 이 적은 것을 의미한다.
-
Under fitting vs. over-fitting
- 학습 데이터에서는 잘 동작하지만 테스트 데이터에서 잘 동작하지 않는 것이 over-fitting 혹은 과적합이라고 한다.
- 네트워크의 구조가 간단하거나 학습이 부족한 이유로, 학습 데이터 조차 잘 못 맞추는 것이 under-fitting 이다.
- 모델이 학습 데이터에 너무 완벽하게 맞춰짐으로써 training error가 0이 되었을때, over-fitting 되었다고 표현한다. over-fitting 은 모델이 상당히 복잡하게 구성되어있는데, 학습 데이터를 표현하는 정보가 적을때 즉 학습데이터가 단순할 때 발생한다.
- 이와 반대 현상은 under-fitting 이라고 하는데, 모델은 단순하고 학습 데이터를 표현하는 정보가 너무 많을 때 단순한 모델이 많은 정보들을 학습할 수가 없어서 under-fitting 이 되는 것이다.
- 이렇게 모델의 Complexity 와 데이터를 표현하는 정보의 규모가 서로 매칭되지 않을 때 under-fitting, over-fitting 이 일어나는 것을 Bad generalization 이다.
-
Cross Validation
- 학습 데이터를 다시 train data - validation data 로 나누는 것.
- train data 로 학습 시킨 모델이 validation data 기준으로 얼마나 잘되는 지를 판단한다.
- k-fold validation
- 학습데이터를 k 개로 나누고, 이 k 개 중 k-1개로 학습하고 나머지 한 개로 validation 을 진행하는 것.
- 하이퍼 파라미터(내가 정하는 값. lr rate, loss func 등) vs. 파라미터(내가 최적해에서 찾고 싶은 값. weight, bias 등)
- 어떤 하이퍼 파라미터가 좋을지 모르니 cross-validation 으로 최적의 하이퍼 파라미터를 찾는다.
- test 데이터는 어떤 방법으로든 학습에 사용되어서는 안된다.
-
Bias-Variance trade off
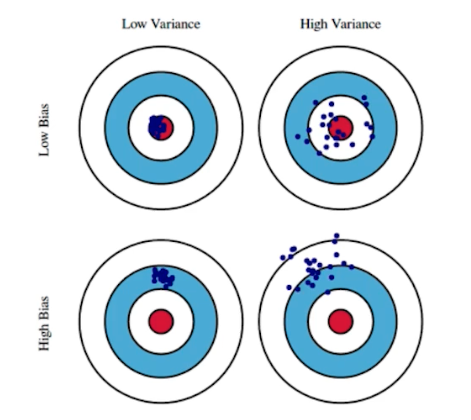
- under-fitting, over-fitting 과 이어지는 개념이다.
- variance 라는 것은 입력에 따라 출력이 얼마나 일관적으로 나오는지를 뜻한다.
- 정답이거나 정답이 아니더라도 같은 곳에 모여있는 것이 low-variance.
- variance 가 낮다고 다 좋은 것이 아니라 구조가 간단한 모델일 수 있다.
- variance 가 크면 비슷한 입력이 들어와도 출력이 많이 달라질 수 있다. 즉, over-fitting 될 가능성이 크다.
- bias 라는 것은 평균적으로 봤을 때, 출력이 많이 분산되더라도 true target 에 접근하면 bias 가 낮은 것이다.
- bias 가 높으면 타겟과 많이 벗어나는 것.
-
비용 함수(loss)를 최소화하는 하는 것은 3가지 파트로 나눌 수 있다. 즉 최소화 하는 것은 1가지 값인데, 이것이 3가지 컴포넌트로 이루어진 것. (bias, variance, noise)

- bias 와 variance 는 하나가 줄어들면 하나가 커지는 trade-off 관계이다.
- bias 를 줄이면 variance가 높아질 가능성이 크다. 반대도 마찬가지.
- 즉, 근본적으로 학습 데이터에 noise 가 껴있을 경우, bias 와 variance 를 둘 다 줄일 수 없는 것이 근본적 한계이다.
-
Bootstrapping
- 통계학 기반
- 학습 데이터 중 몇 개만 활용하여 모델을 여러 개 만든다. 이 여러 개의 모델이 하나의 입력에 대해서 예측한 값들의 일치를 이루는 정도를 보고 전체적인 모델의 uncertainty 를 예측하고자 한다.
- 학습데이터가 고정되어 있을 때, 그 안에서 sub-sampling 으로 여러 개를 만들고, 그걸 가지고 여러 모델 혹은 metric 을 만들어서 하겠다는 것.
-
Bagging and boosting
- Bagging(Bootstrapping aggregating)
- 여러 개의 모델을 만들고, 이 여러 모델들을 가지고 output 의 평균 내는 것. 일반적인 앙상블을 뜻한다.
- N개의 모든 모델을 돌리고 돌린 값들의 평균이나 voting을 이용하는 것이 1개의 단일 모델을 쓰는 것보다 성능이 좋을 때가 많다. 이처럼 앙상블은 배깅에 속할 때가 많다.
- Boosting
- Bagging 과 다른 점은 여러 개의 모델을 sequential 하게 바라본다.
- 여러 개의 모델을 만드는 것은 맞지만 구체적으로 잘 안되는 데이터에 대해서만 모델을 추가적으로 만들고 이 모델들을 합치는 것.
- 이것이 독립적인 N 개의 결과를 만드는 것이 아니라, week learner(하나하나의 모델들) 들을 순차적으로 합쳐서 하나의 strong learner 를 만드는 것. 즉, 추가적인 후처리를 통해서 결과적으로 한 개의 모델이 나오게 된다.
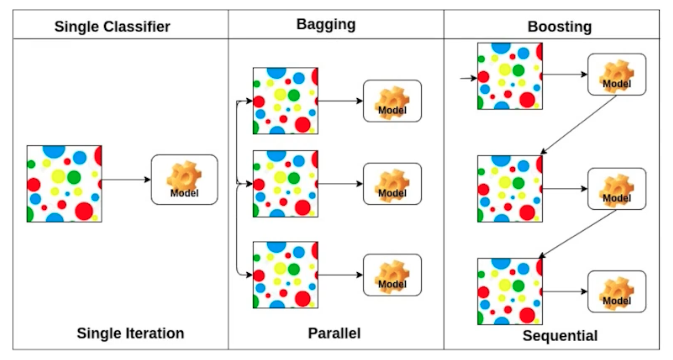
- Bagging(Bootstrapping aggregating)
Gradient Descent Methods
- SGD(Stochastic gradient descent)
- 내가 찾고자 하는 파라미터(최적의 파라미터) 를 찾기 위해서는 정해진 Step size(lr rate) 만큼 파라미터를 업데이트하는 과정을 여러번 반복해야 하는데, 이 경우 gradient 를 정확히 계산할 수는 있지만 전체 데이터에 대한 loss func 을 매 iteration 마다 계산해야 하기 때문에 엄청난 계산량이 필요하다.
- 이를 개선한 방법으로, 한번의 iteration 에 single sample 로 가중치를 업데이트 한다.
- Mini-batch gradient descent
- 일반적으로 말하는 batch size 를 활용해서 gradient를 구하고 이것을 가지고 가중치를 업데이트 한다.
- SGD 가 각 iteration 의 계산은 훨씬 빠른 반면 gradient 의 추정값이 너무 noise 해진다는 단점을 보완한 방법이다.
- 딥러닝에서 가장 일반적으로 사용되는 기법.
- Batch gradient descent
- 데이터를 한번에 다 사용해서 모든 gradient의 평균을 가지고 업데이트 한다.
- Gradient Descent 의 자세한 개념은 AI Math 카테고리에서 정리하고, 각각의 Optimizer 는 Optimizer & Scheduler 에서 정리하자.
Batch Size Matters
- Batch Size 는 중요한 하이퍼 파라미터이다.
-
Batch Size 가 Gradient Descent(일반적으로 mini-batch SGD) 에 끼치는 영향은 아래와 같다.
큰 Batch size 작은 Btach Size gradient 에 대한 정확한 추정(low variance) gradient 에 대한 noisy 한 추정(high variance) iteration 마다 많은 계산량 iteration 마다 적은 계산량 빠른 학습(parellel computation에 용이하다) 느린 학습 -
Revisiting Small Batch Training for Deep Neural Networks, 2018
- 아래 두 식을 비교해보면, 작은 batch size 의 경우(위 식) 파라미터 공간 상에서 보다 최신 상태의 gradient 를 사용할 수 있는 반면, 큰 batch size 의 경우(아래 식)는 오래 전 상태의 gradient 를 계속 사용해야 한다.
Batch size m을 이용하여 n steps의 weight update를 진행한 이후의 weight 값
batch size를 n배 증가시키고, 같은 개수의 training example에 해당하는 weight update
- Deep Learning 의 loss func 과 같은 non-convex func(convex 는 global minimum 을 가지는 것) 일수록 gradient 값은 파라미터 상태에 따라 크게 변한다.
- 큰 batch size 를 사용하면 오래전 gradient로 부정확한 weight update를 하게 될 위험이 커지게 되고, base learning rate 를 크게 가져가지 못하는 원인이 될 수 있다.
 Batch Normalization 없는 실험결과
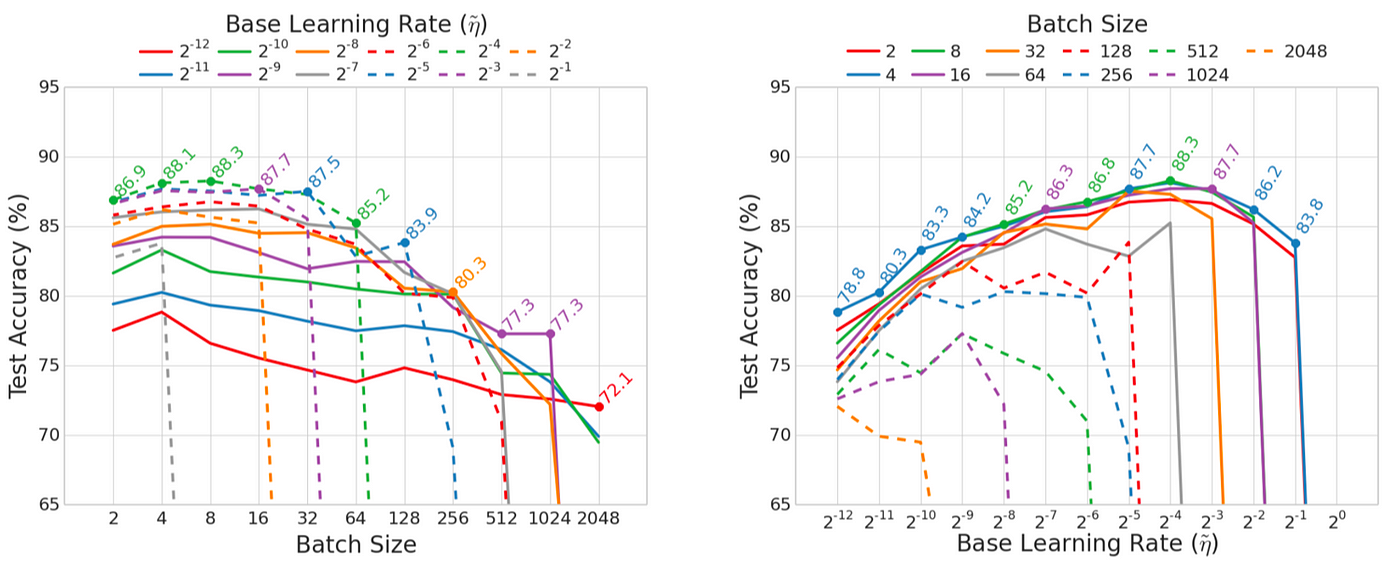
Batch Normalization 없는 실험결과- Learning rate 를 고정하고 batch size를 변화시킨 그래프 (왼쪽)는 작은 batch size에서 보다 높은 test accuracy를 얻을 수 있음을 보여준다.
- 또한 batch size 를 고정하고 learning rate 를 변화시킨 그래프 (오른쪽)를 보면, 작은 batch size 를 사용할 경우 더 넓은 범위의 learning rate 에서 안정적인 학습이 가능함을 알 수 있다.
 Batch Normalization 을 적용한 실험 결과
Batch Normalization 을 적용한 실험 결과- Batch Normalization(BN) 을 사용할 경우 batch size 가 너무 작으면(< 8) batch statistics가 부정확해져서 약간의 성능저하가 생김을 관찰할 수 있다.
 SGD의 batch size 와 BN의 batch size를 분리하여 (multi-GPU를 사용하는 일반적인 상황) 학습한 실험 결과
SGD의 batch size 와 BN의 batch size를 분리하여 (multi-GPU를 사용하는 일반적인 상황) 학습한 실험 결과- SGD의 batch size와 무관하게 BN의 batch size가 8 정도 일 때 최적의 성능이 얻어짐을 보여준다.
- 정리하면, 작은 Batch Size 는 1) 일반화 성능이 좋고, 2) 보다 안정적인 학습을 가능하게 하여 넓은 범위의 learning rate 로 학습이 가능하다.
-
On Large-batch Training for DL: Generalization Gap and Sharp Minima, 2017
- 큰 Batch Size 를 활용하면 sharp minimumr 에 도달하게 된다. 반면에 작은 Batch Size 는 flat minimum 에 도달하게 된다.
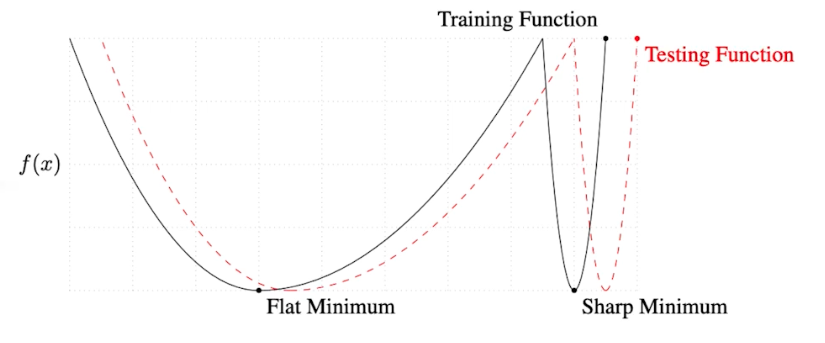 이렇게 생긴 loss func 을 생각 해 볼때, sharp minima는 loss func 의 작은 변화에도 민감하게 반응하기 때문에
이렇게 생긴 loss func 을 생각 해 볼때, sharp minima는 loss func 의 작은 변화에도 민감하게 반응하기 때문에
flat minima 에 비해 generalization 측면에서 훨씬 불리하다고 볼 수 있다.- Flat Minimum 에 도달했다는 것은 train 데이터에서 잘 되면 test 에서 어느정도 잘 되는 것을 의미한다. 즉, Flat Minimum 에 도달한 모델은 일반화 성능이 좋은 것.
- 그런데 Sharp Minimum 에 도달한 모델의 경우는 학습에서 최소값에 도달했어도 테스트에서 높은 값일 수 있다. 즉 일반화 성능이 떨어진다.
 batch size 에 따른 test accuracy 와 sharpness 를 그래프로 나타낸 결과
batch size 에 따른 test accuracy 와 sharpness 를 그래프로 나타낸 결과- batch size가 커짐에 따라 sharpness가 증가하고 test accuracy가 감소함을 확인할 수 있다.
- 이 논문에서는 Batch Size 를 작게 쓰는 것이 일반적으로 일반화 성능이 좋다는 것을 말하고 있다. 즉 flat minimum 에 도달하는 게 좋다는 것.
- 위 논문은, Batch Size 를 줄이면 일반적으로 일반화 성능이 좋다는 것을 sharpness of minima의 관점에서 설명하고 실험적으로 확인했다.
- small batch 를 사용할 경우 gradient의 noise가 커지기 때문에 sharp minimizer에서 쉽게 벗어날 수 있고 noise에 둔감한 flat minimizer로 수렴하게 된다.
- 정리하면, 작은 Batch Size 는 1) 일반화 성능이 좋고, 2) 보다 넓은 범위의 learning rate 로 학습이 가능하며, 3) gradient noise 가 커서 sharp minimum 을 쉽게 벗어나 flat minimum 으로 수렴할 수 있다.
💡 딥러닝이 푸는 문제는 수학적으로 무엇일까? convex optimization 문제인 것처럼 보인다. 딥러닝은 convex optimization 을 사용하는 non-convex optimization 라고 할 수 있다. 우리의 loss-func 은 convex 가 아니다. 즉 항상 감소하는 것이 아니다. 다시 말하면 ultra high-dimensional non-convex optimization = optimal 한 포인트를 알 수 없다! 따라서 loss-func 의 minimum 값을 절대 알 수 없다. 그러나 다행히도 딥러닝에서 알려진 사실 중 하나는 적당한 local minima 는 아주 깊은 낮은 곳에 있는 optimal point 와 그렇게 큰 차이가 있지 않다고 알려져 있다. 따라서 1) 적당한 곳에서 optimal point 라고 여겨도 된다고 알려져 있다. 2) 실험적으로 local 한 optima와 sharp 한 optima 중에는 flat 한 optimal point 가 훨씬 안정적인 값을 가질 확률이 높다. 즉, flat 한 local minima 를 찾는 것이 딥러닝인 것이다. 위에서 내린 결론은 결국 작은 batch size 가 좋다는 것이다. 이 질문은 우리가 풀고자 하는 문제가 뭔지를 짚어내고 있다. 우리가 convex optimization(SGD, Adam) 을 사용하는 이유는, data size 가 커지면 연산속도를 고려하지 않을 수 없는데, 연산 속도를 고려했을 때 적당한 성능을 낼 수 있으면서 충분히 시간이 주어진다면 더 복잡한 optimizer 보다 부족하지 않은 것들이 SGD 계열이기 때문이다.
-
실제로 최적의 성능을 얻기 위한 batch size 는 모델과 task의 특성에 따라 크게 달라지며, 학습 시간을 단축하기 위한 측면에서는 batch size 를 최대한 크게 키우면서 성능을 향상시키는 것이 훨씬 좋은 접근법이라고 볼 수 있다.
-
실제적으로 모델을 학습시킬 때 loss func 을 정의하고 나면, 편미분을 구하는데 이것은 torch 등 라이브러리에서 자동 미분을 해준다. 그러면 이제 Optimizer 를 골라야 한다. 각각의 Optimizer가 왜 제안이 되었고 어떤 성질을 가지는 지를 알면 좋다.
Reference
https://medium.com/lunit/batch-size-in-deep-learning-696e1b57764f
맨 위로 이동 ↑
댓글 남기기