[Object Detection] 7. Advanced Object Detection (1)

• Advanced Object Detection 1

  💡 Cascade RCNN은 학습할 bouding box의 IOU threshold를 0.5에서 더 높여보면 어떨까라는 아이디어에서 출발했다. Cascade RCNN은 Iterative BBox at Inference와 Intergral loss를 결합하여 기존의 Faster RCNN보다 더 좋은 성능을 나타낸다. → Cascade RCNN은 Iterative bbox at Inference와 Intergral Loss를 사용해서 1) bbox pooling을 반복 수행할 시 성능 향상되는 것 2) IOU threshold를 다르게 가지는 Classifier가 반복될 때 성능 향상 되는 것 3) IOU threshold를 다르게 가지는 RoI head를 cascade로 쌓을 시 성능 향상되는 것 을 증명했다.

  ViT를 사용하는 Detection network

  • ViT 를 사용하는 network의 예시로는 DeTR, Swin 등이 있다.
  • Swin의 경우 Shifted Window Multi-Head Attention 를 사용하여 window안에서만 self attention 을 작동하여 receptive field 가 제한되는 단점을 해결했다.
  • DeTR 에서는 각 예측 값이 N개 unique하게 나타나 post-process 과정이 필요 없다.
  • Swin 은 position embedding은 사용하나 class embedding 은 사용하지 않는다.
  • Swin의 경우 Shifted Window Multi-Head Attention 와 Window Multi-Head Attention 를 동시에 사용한다.

  Transformer 와 ViT

  • Transformer 는 self attention 메커니즘을 활용 NLP에서 long range dependency를 해결한다.
  • Self attention mechaism 의 attention 수식에는 softmax를 포함한다.
  • ViT는 image를 flatten해 2d로 변형 후 learnable embedding 처리를 한다.
  • ViT는 learnable embedding앞에 class embedding 을 추가 해준다.

  • MLP head에는 class embedding vector를 입력하여 최종 결과를 추출한다.

  • 앞서 basic 한 내용을 다 다뤘으면, 여기서부터는 Object detection 을 수행하면서 알면 더 도움이 많이 되는 모델들에 대해서 알아보자.
  • Cascade RCNN
    • 그 전에 Faster RCNN 에 대해 한 번 더 복습하자.

    • Faster RCNN Pipeline

      

      • 입력 이미지가 CNN 을 통과해서 feature map 을 만든다. 이 feature map 으로부터 RPN 을 통과시킨다. RPN 에 여러가지 region proposal 들이 나온다. Region proposal 들을 feature map 에 projection 시켜서 최종적으로 RoI 를 뽑아낸다.
      • RoI 를 Pooling 과정을 거치게 되면 고정된 feature vector 가 나온다. 이 고정된 feature vector 를 cls head, regressor head 두 가지 head 에 통과시키면 최종적으로 RoI 가 어떤 object 를 가지게 될 것인지 또는 RoI 가 구체적으로 어떤 위치에 존재하는지 Detection task 를 수행할 수 있게 된다.
      • 이런 과정이 inference 과정이다. inference 과정을 위해서는 먼저 모델 training 을 진행해야 한다. Faster RCNN 에서는 어떤 모듈들을 위주로 학습할까?
      • 첫번째로 backbone 인 CNN 이 있고, 두번째로 RPN, 세번째로 head network 이다.
      • 그중에서 backbone 은 RPN 과 head 두 가지 모두에서 공통적으로 사용되는 네트워크이다.
      • 그렇다면 크게 RPN 과 Head 를 학습하기 위해 데이터셋을 구성해줘야 한다.
      • 학습을 위해서는 데이터셋을 positive dataset 과 negative dataset 으로 나눠준다.
      • Faster RCNN 에서는 RPN 학습을 위해서 0.7 이상의 IoU 를 갖는 anchor box 를 positive 로, 0.7 미만의 IoU 를 갖는 anchor box 를 negative sample 로 정했다.
      • 또 Head 학습을 위해서 0.5 이상의 RoI 를 positive 로, 0.5 미만의 RoI 를 negative sample 로 할당했다.
    • Cascade RCNN 의 경우, Faster RCNN 에서 postive 와 negative sample 을 나누는 기준에 집중했다. 이 기준을 0.5 로 정한 이유가 없었는데, Cascade RCNN 에서는 0.5 가 아니라 0.6 으로 했을때는? 이런 부분에 집중을 해서 실험이나 연구를 진행했다.

    

    • 0.5 를 기준으로 positive/negative sample 을 나누고 head network 를 training 시켰을 때가 (a) 이고, 0.7 을 기준으로 positive/negative 를 나누고 training 후 detection task 를 수행했을 때 (b) 와 같은 결과가 나왔다.
    • (a) 를 보면 상당히 퀄리티가 낮은 그림들이 많이 보인다. 정확히 예측한 box 도 있지만 빈 box 도 있는 등 이상한 box 들이 보인다. 즉 false positive 가 상당히 많은 것을 확인해볼 수 있다.
    • (b) 의 경우는 0.7 이상을 positive, 0.7 미만을 negative 로 한 경우이다. (a) 보다 훨씬 더 false positive 가 줄어든 것을 확인할 수 있다.

    • 또한 연구진은 IoU 기준(thr)을 0.5, 0.6, 0.7 세 가지로 2 stage detector 들을 학습했다.

      

    • 왼쪽 그래프의 경우는 Localization 을 얼마나 잘 수행했는지를 나타낸다.
      • GT 와 IoU 를 가지는 RoI 가 detection 을 통과했을 때 어떤 IoU 를 가질까에 대한 실험이다. 다시 말해서 x 축이 RPN 결과 나온 RoI 들이 GT 와 어떤 IoU 값을 가질까에 대한 값이고, y 축은 box head 를 통과한 box prediction 이 GT 와 IoU 가 어떻게 될까에 대한 예측이다.

      

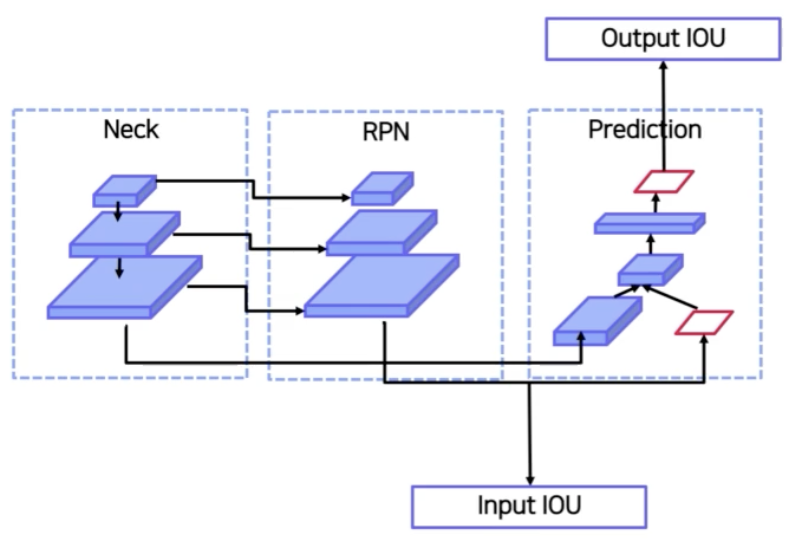
      • input IoU(x축) 은 RPN 통과하면 box 가 나오는데, 그렇게 box 가 나왔을 때 이 box 가 GT 와 어떤 IoU 값을 가질까에 대한 부분
      • output IoU(y축) 은 box 를 head 통과시켰을 때 최종적으로 box 가 한번 더 나오는데, 이 box 에 대해서 GT 와 IoU 를 계산했을 때 IoU 값이 어떨까가 y축 값이다.
      • 즉, RPN 에서 특정 IoU 값(x)을 가질 때, head Network 를 통과했더니 IoU 값(y)이 바뀌는 것을 나타내는 그림이다.
      • 그래프 결과를 해석하면, IoU thr 에 따라 다르게 학습되었을 때 결과가 다르다. 또한 input IoU 가 높을수록 높은 IoU thr 에서 학습된 모델이 더 좋은 localization 결과를 낸다.
      • 반면에 낮은 IoU input 에 대해서는 낮은 IoU thr 로 학습된 모델이 더 좋은 localization 성능을 보여준다는 결과를 알 수 있다.
    • 또한 학습된 IoU thr 에 따라서 detection 성능은 어떻게 바뀔지도 실험했다.(오른쪽 그래프)
      • AP 를 계산하기 위해서는 예측 box 와 GT box 사이에 IoU 를 계산하고, 그 IoU 가 특정 기준 이상이면 true, 특정 기준 미만이면 false 로 labeling 한 뒤 AP 를 계산한다.
      • 이 때 각 x 축이 특정 기준이 된다. 즉 IoU thr 0.5 에 대해서는 예측된 box 들 중에서 GT 와 IoU 를 계산했을 때 0.5 면 잘 예측한 것이고 0.5 미만이면 틀린 것이다.
      • 그렇다면 0.5 는 AP50 이 되고, 0.75 는 AP75, 0.9 는 AP90 이 된다.
      • 이 때 실험결과를 보면, 마찬가지로 IoU thr 에 따라 다르게 학습되었을 때 결과가 다르다.
      • 전반적인 AP 의 경우, 즉 AP 의 평균은 IoU thr 0.5 로 학습된 모델이 성능이 가장 좋다.
      • 그러나 AP 의 IoU thr(x축)가 높아질수록(ex. AP70, AP90) IoU thr 0.6, 0.7 로 학습된 모델의 성능이 좋다.
    • 즉 두 가지 실험으로 아래와 같은 motivation 을 얻을 수 있다.
      • 학습되는 IoU 값에 따라서 대응 가능한 IoU 박스가 달라진다. 즉, 작은 IoU thr 로 학습된 모델은 GT 와 작은 IoU 를 가지는 box 를 예측하는데 유리하고, 높은 IoU thr 로 학습된 모델은 GT 와 높은 IoU 를 가지는 box 를 예측하는데 유리하다.
      • 그래프와 같이 high quality detection 을 수행하기 위해서는 IoU threshold 를 높여 학습할 필요가 있다. 즉, IoU 가 높은 수준으로 detection 하기 위해서는, 학습단계에서 IoU 를 높게 잡을 필요가 있다. localization 실험에서도 높은 IoU thr 에서, 높은 input IoU 에서 높은 output IoU 가 높았다.
      • 그러나, 단순하게 IoU 만 높이면 높은 IoU 점수를 가지는 box 에 대해서는 어느정도 잘 잡을 수 있지만, IoU 가 낮은 부분에서는 성능이 떨어진다. 즉, 성능이 하락하는 문제가 존재한다. 예를들어, detection performance 실험에서 IoU thr 를 0.7 로 학습했을 때 GT 와 IoU 가 작은 부분을 잘 잡아내지 못했다.
      • 이렇게 IoU thr 를 높여서만 학습하면 성능이 하락하는 문제가 존재하기 때문에 이 paper 에서는 단순히 IoU 를 높여서 positive/negative 를 나누고 학습을 하는 것은 성능면에서 좋지 않다고 밝힘.
      • 따라서 이를 해결할 수 있는 Cascade RCNN 방법론을 제안했다.
      • Cascade 뜻은 폭포. 폭포가 위에서 아래로 순서를 가지고 떨어지듯이, IoU 를 0.5, 0.6, 0.7 이렇게 순서를 가지고 학습하는 방법론을 제안했다.
    • Method
      • 어떤 방법으로 Cascade RCNN 을 구현했을까?

      

      • Faster R-CNN
        • paper 에서 사용한 Faster R-CNN 이다.
        • I 는 input image 이고 conv 는 backbone network 를 의미한다.
        • conv → H0 의 화살표는 RPN 로 가는 화살표를 의미하고, H0 는 RPN 결과로 나온 proposal 들을 의미한다.
        • 이 proposal 이 cls head C0, box head B0 를 통과해서 region proposal 에 대한 inference 나 학습이 이루어진다.
        • 이 때 각 proposal 에 대한 박스 정보 B0 를 다시 conv feature map 에 projection 을 한다.
        • projection 후 RoI Pooling 을 통해 고정된 feature vec 로 바꾼다. 이렇게 pooling 된 고정된 size 의 feature vec 을 H1 이라 한다.
        • 이를 cls head C1, box head B1 에 통과시킨다.
        • C0 는 RPN 에서의 classification 이기 때문에 어떤 object 인지 예측하지는 않고 단순히 배경인지 아닌지 여부를 예측한다.
        • C1 은 구체적으로 배경 여부를 포함해서 어떤 객체를 갖는지 예측을 한다.
      • Iterative BBox at inference
        • faster RCNN 에서 RPN 결과로 나온 box 정보(B0)를 이용해서 RoI Projection 를 진행했었다.
        • B0 가 아닌 다른 박스가 존재한다면 그 박스로 RoI Projection 을 시키는 것도 가능하다.
        • 따라서 Faster RCNN 과 비슷하게 최종 head 로부터 B1 을 얻고, 이 B1 을 다시 Projection 을 진행한다. 그렇게 얻은 RoI 가 RoI Pooling 후 head 를 통과해서 B2 를 만들어낸다. 또 이 B2 를 Projection 및 RoI Pooling 을 하고 B3 를 만들 수 있다.
        • 즉, inference 단계에서 head 에서 예측된 bbox 를 다시 RoI Projection 에 이용하는 iterative bbox 가 존재할 수 있다.
        • 이 방법을 이용했을 때, RPN 만 이용했을 때보다 box 가 훨씬 더 정확하게 생기게 되고, 이 정확해진 box 로부터 head network 를 통과할 수 있다. 그러나 성능의 향상은 그렇게 크게 없었다고 한다.
      • Integral Loss
        • 아예 학습 단계일 때 head 를 여러 개 만들 수도 있다.
        • RPN 으로부터 나온 bbox B0 를 이용해서 RoI Projection 을 진행해서 head network 를 통과할 RoI 를 계산한다.
        • 이 때 RoI 를 특정 IoU thr 기준으로 positive / negative sample 로 나눠서 head network 를 학습시킨다.
        • IoU thr 를 여러개 두고 각 thr 마다 head 를 따로 구성할 수 있다. (H1, H2, H3)
        • 이 때 각 head 에서 class 와 bbox 가 나오는데, 각각 loss 를 계산한 뒤 summation 을 한다. $L_{cls}(h(x),y) = \displaystyle\sum_{u \in U}L_{cls}(h_u(x),y_u)$ 이렇게 학습을 진행한다.
        • inference 할 때는 각각 head (H1, H2, H3) 의 결과를 앙상블하는 방법을 사용할 수 있다.
        • 그러나, RPN 에서 나온 box 인 B0 를 RPN proposal 로 동일하게 RoI Projection 후 RoI pooling 해서 사용했기 때문에 성능 향상은 크게 없다고 한다.
      • Cascade R-CNN
        • 따라서 iterative 방식과 integral 방식 두 가지를 혼합한 새로운 방식에 대해 제안했다.
        • 이 방법이 바로 Cascade 방식이다.

        

        • integral 방식처럼 IoU thr 에 따라서 head 를 여러개(H1, H2, H3) 둔다. 이 때, head 에 들어갈 feature vec 를 만들 때 사용되는 box 를 RPN 결과를 이용하는 것이 아니라 이전 thr 의 head 의 결과를 이용하는 방식을 채택했다.
        • 즉, 처음에는 RPN 으로부터 B0 를 얻고 Projection, Pooling 후 head 를 통과시켜서 B1 을 얻는다. 그 이후 B1 의 box 를 projection 후 head 를 통과시켜 B2 를 얻는다. B3 도 B2를 이용해서 마찬가지 과정을 거친다.
        • 이는 폭포수 같은 Cascade 라고 할 수 있다.
        • C3, B3 가 최종 결과이다.
      • Cascade 방식으로 학습했을 때 각 head 별 결과를 살펴보자.

      

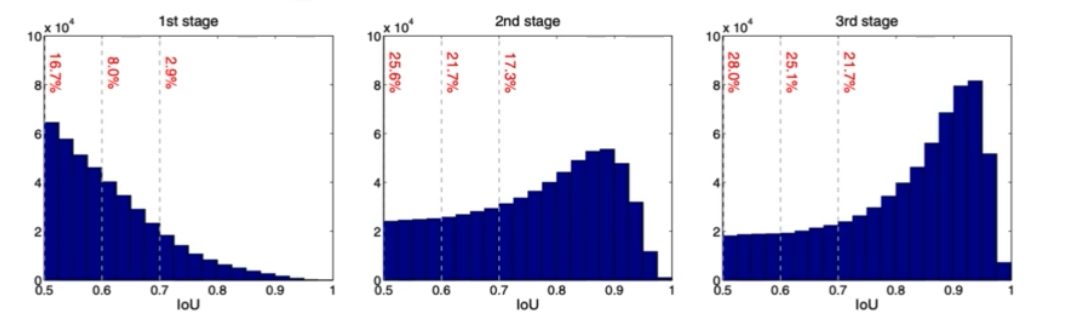
      • 학습이 진행되면 진행될수록 IoU 가 좋아진다.

    • 그렇다면 각 head 별 IoU thr 를 어떻게 정할 수 있을까?

      

      • 위 그래프를 보면 처음 head 는 0.5, 두번째 head 는 0.6 이 성능이 가장 좋다. 따라서 thr 는 0.5, 0.6, 0.7 이 된다.
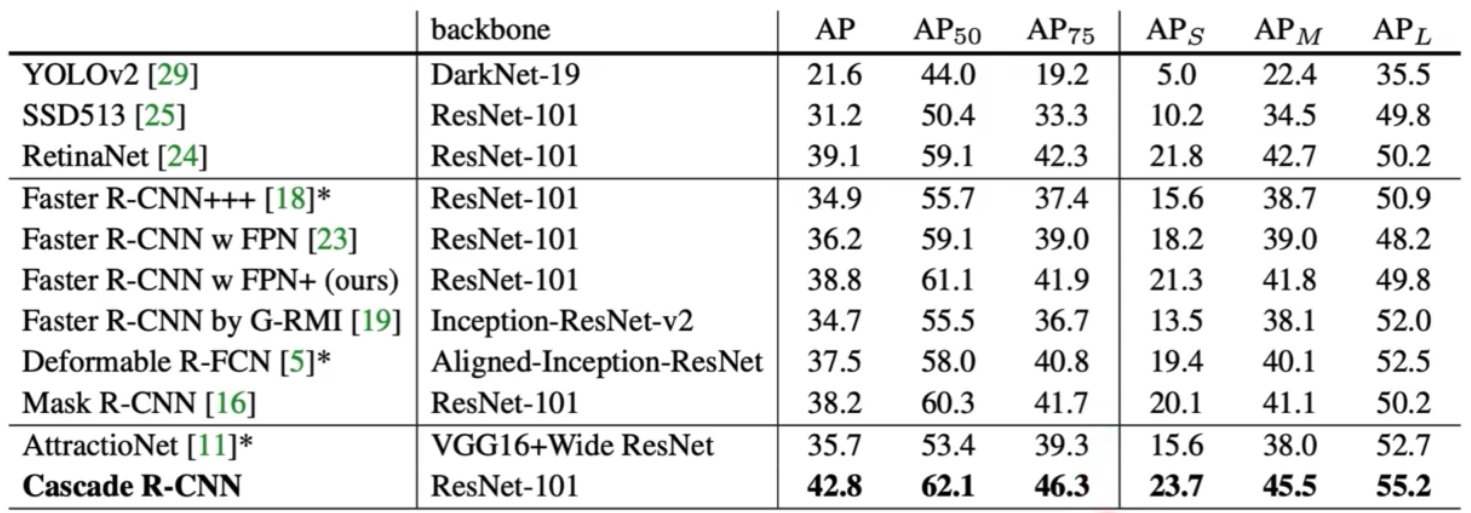
    • 실험결과는 가장 기본적인 Faster RCNN 부터 iterative, integral loss, cascade 방식을 비교한다.

    

    • 재밌는 결과는, AP50, 즉 IoU 가 0.5 일 때 기존 Faster RCNN 과 크게 성능 차이가 없는데(0.8), IoU 가 점점 커지게 되면서, 즉 high quality prediction 에 대해서 성능향상이 많이 됐다.
    • AP 가 높다는 것은 엄청 좋은 퀄리티의 prediction 이다. 즉 Cascade R-CNN 을 하니 high quality box 를 잘 예측하게 되는 것이다.
    • 다른 모델들과 비교했을 때에도, AP75 의 high quality 일 때 많은 성능향상을 가져왔다.

    

    • 정리
      • Cascade 는 bbox pooling 을 반복 수행할 시 성능 향상이 되는 것을 증명했다. (iterative)
      • IoU thr 에 따라 head 를 다르게 둘 때 성능 향상이 발생함을 보였다. 즉 IoU thr 가 다른 classifier 가 반복될 때 성능 향상이 증명됐다. (integral)
      • IoU thr 에 따라서 서로 RoI head 를 다르게 두고 cascade 방식을 사용하면 성능향상이 됨을 실험적으로 보였다. (cascade)
  • Deformable Convolutional Networks(DCN)
    • 기존 CNN 의 문제점
      • 일정한 패턴을 지닌 CNN 은 geometric transformation 에 한계를 지녔다.
      • nxn filter 를 sliding window 방식으로 이미지를 이동시키면서 filter 와 이미지의 곱, 그리고 summation 으로 계산한다. 이 때 filter 는 kernel 이라고 하며 size, stride, dilation 등 여러가지 요소가 영향을 미친다.
      • 이 conv 연산이 한계점을 지니는데, filter 의 모양을 보면 nxn 고정적 사이즈를 가진다. 즉 사이즈가 생긴 모양이 정사각형 모양이고 정사각형 모양의 filter 는 geometric transform 에 대해서 한계점이 존재한다.
    • geometric transform
      • 이미지의 spatial 연산을 가하는 것을 의미한다.
      • 정상적 이미지가 있을 때 affine 같이 기울기를 조절하는 연산을 수행할 수 있다.
      • 또 다른 예시로 같은 이미지를 다른 관점에서 보는 것도 geometric transform 이라 할 수 있다.
      • 또 같은 사진을 pose 만 다르게 취해서 촬영하는 것도 geometric transform 이라 할 수 있다.
    • 이처럼 일반적인 Conv 연산만 이용하면 고정된 filter size 를 갖기 때문에 특정 이미지를 geometric transform 하게 되면 같은 이미지를 다른 이미지로 인식하게 되는 문제가 있다.
    • 이런 문제를 해결하기 위해서 기존에는 Geometric augmentation 과 Geometric invariant feature engineering 을 수행했다. 즉 Geometric transform 된 이미지를 추가해서 학습 데이터셋을 구성하면 사람이 추가한 geometric 연산을 모델이 충분히 이해할 수 있을 것이라 본 것.
    • Geometric augmentation
      • 이미지가 회전하는 Rotate 나 이미지를 기울이는 Shift 연산도 geometric transform 이라 할 수 있는데, 일반적으로 data augmentation 을 할 때 많이 넣어주는 augmentation 이다.
      • 이런 transform 을 추가해주면 모델들이 geometric transform 에 대해서 이해하면서 좀 더 일반화된 모델이 될 수 있다.
      • 그러나 이런 augmentation 들 역시 geometric transform 을 완벽히 이해했다고 보기 어렵다.
      • 그 이유는 우리가 추가해준 augmentation 에 대해서만 모델이 학습이 가능하다는 점이다.
      • 예를 들어 flip 은 horizontal 과 vertical 이 가능한데, 이 중 하나만 추가해서 모델을 학습 시키면 추가된 transform 에 대해서는 모델이 robust 해지지만, 그렇지 않은 transform 에 대해서는 학습한 적이 없기 때문에 robust 하지 못하다.
      • 즉, 휴리스틱하게 사람이 어떤 geometric 이 있을지 먼저 이해를 하고 geometric 연산을 넣어줘야 한다는 점이 geometric augmentation 의 단점이라고 보면 된다.

    • Geometric invariant feature selection

      

      • geometric invariant feature 는 위 그림과 같이 이미지의 geometric transform 과는 무관하게 어떤 feature 들을 뽑을 수 있다.
      • David G. Lowe 의 “Distinctive image Features from Scale-invariant Keypoints” 에 위 그림과 같은 feature 를 뽑는 과정을 알 수 있다.

      

      • 이렇게 뽑힌 feature 들은 geometric transform 에 영향을 받지 않는다는 장점이 있지만 결국 이런 feature 를 뽑아내는 과정도 사람의 머리에서 나온 알고리즘이기 때문에 사람이 인지하지 못한 geometric 연산에 대해서는 feature 를 뽑는 과정이 없을 것이고 따라서 그런 연산들에 대해서는 robust 하지 못하다.
      • 결론적으로 사람이 휴리스틱하게 연산을 넣어주면 사람이 넣어준 연산에 대해서만 모델이 학습할 수 있다는 것이다. 즉 사람이 모르는 연산들에 대해서는 모델이 학습할 수 없다.
    • 그래서 이 DCN paper 는 위 문제를 해결하기 위해서 Deformable 이라는 새로운 모듈에 대해서 제안했다.
    • Deformable Convolution
      • Deformable 이란 “변형할 수 있는” 을 뜻한다.
      • 즉 기존의 conv filter size 가 정사각형의 고정된 size 였다면 정사각형이 아니라 다양한 shape 을 가질 수 있게 제안됐다.
      • 어떤 이미지가 있고, 사람은 이해하지 못하지만, 컴퓨터가 이해할 수 있는 geometric 연산을 스스로 찾아서 그 연산에 맞춰서 conv filter size 를 변형할 수 있게끔 한다는 것이 DCN 의 메인 아이디어이고 가장 큰 contribution 이다.
      • 특히, classification, object detection, segmentation 에서 deformable 이라는 개념이 엄청난 성능 향상을 가져왔다.

      

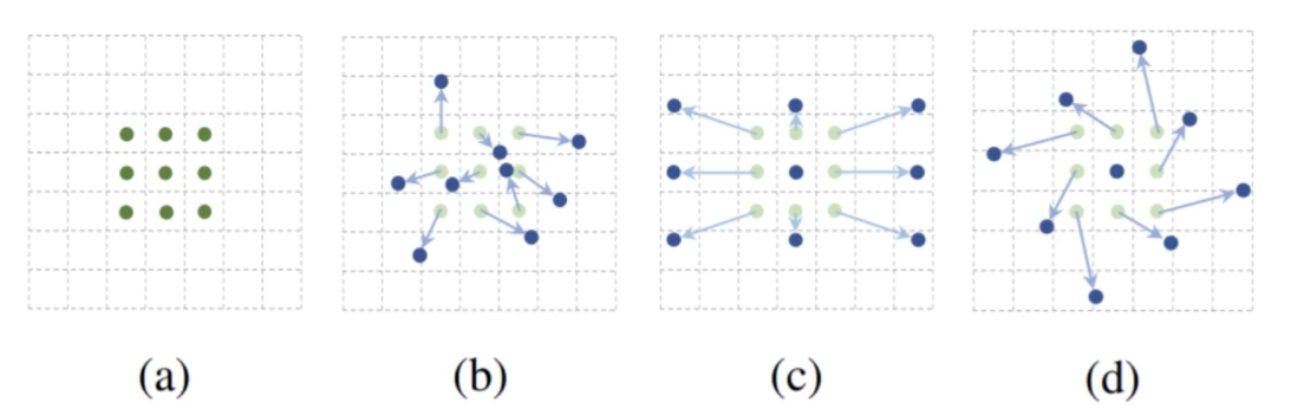
      • (a) 는 일반적인 Conv 연산이다. kernel size 가 nxn 이고, kernel 의 각 값이 이미지의 픽셀값과 element wise 하게 곱해진 다음에, 곱해진 값의 summation 을 계산을 해서 feature vector 가 탄생하게 된다.
      • 이 때 kernel size 는 그대로 두고 각 kernel 이 바로 뒤에 있는 이미지 픽셀에 곱해지는 것이 아니라, 특정 kernel 의 cell 이 왼쪽 혹은 위로 몇 칸 가서 곱한다는 offset 을 추가를 해서 conv 연산을 수행할 수 있다.
      • 즉, 기존에는 offset 의 개념이 없는데, offset 을 추가해서 그 픽셀과 kernel 의 값과 element wise 하게 곱한다는 것이다.
      • 예를 들어서, (b) 같은 경우 그런 offset 을 각 kernel 의 cell 마다 랜덤으로 부여한 경우이다. 바로 뒤에 있는 이미지의 픽셀과 곱해지는 것이 아니라 offset 만큼 이동해서 그 픽셀과 곱하는 것이다.
      • (b) 같이 offset 이 각 kernel 의 값마다 random 하게 부여될 수 있고, (c) 처럼 기존 kernel 이 팽창하게 둘 수도 있다. 만약에 모델이 (c) 의 offset 을 학습했다는 것은 여기에 이미지를 확대하는 geometric transform 이 존재한다고 생각해볼 수 있다. 그렇게 기존의 conv 연산보다 receptive field 를 더 크게 갖게 하는 geometric transform 이 적용된 것처럼 볼 수 있는 것이다.
      • (d) 의 경우처럼 offset 이 적용됐다면, 왼쪽으로 45도 rotate 하는 transform 일 확률이 크다. 그러면 모델이 rotate 라는 transform 을 이해할 수 있다고 생각할 수 있다.

      

      • input feature map 이 존재하고 conv 연산이 있다면, 원래대로라면 conv kernel 이 바로 뒤에 있는 이미지 픽셀 값과 곱해지게 된다. 그러나 새롭게 바로 뒤에 있는 값이 아니라 다른 위치에 있는 픽셀값과 곱하도록 하는 offset vector 를 새롭게 추가할 수 있다.
      • 즉, conv kernel 각각의 값에 offset 을 추가해서, 추가된 offset 만큼 이동한 위치의 이미지 픽셀과 계산을 하게끔 하는 것이다.
      • 일반적인 conv 부터 offset 컨셉에서 다시 한번 이해해보자.

      

      • 기존 conv 연산은 filter 가 존재하고 그 filter 가 곱해질 픽셀의 위치를 정하고, 그렇게 정해진 위치에서 filter 와 element-wise 하게 곱해진다고 생각할 수 있다.
      • 위처럼 kernel size 가 3x3 이고 상대적인 위치를 grid 안에 표시했다고 생각할 수 있다. 중심점이 (0, 0) 이고, 왼쪽 1칸 위쪽 1칸으로 가면 (-1, -1) 이 되는 것이다.
      • 이 때 구체적인 conv 연산은 $\mathbf{y}(\mathbf{p}0) = \displaystyle\sum{\mathbf{p}_n \in \mathcal{R}}\mathbf{w}(\mathbf{p}_n) \cdot \mathbf{x}(\mathbf{p}_0 + \mathbf{p}_n)$ 로 계산할 수 있다.
      • 아래처럼 conv 연산을 수행한 output feature map 이 존재할 때, $\mathbf{y}(\mathbf{p}_0)$ 는 output feature map 의 한 픽셀이라고 생각할 수 있다.

      

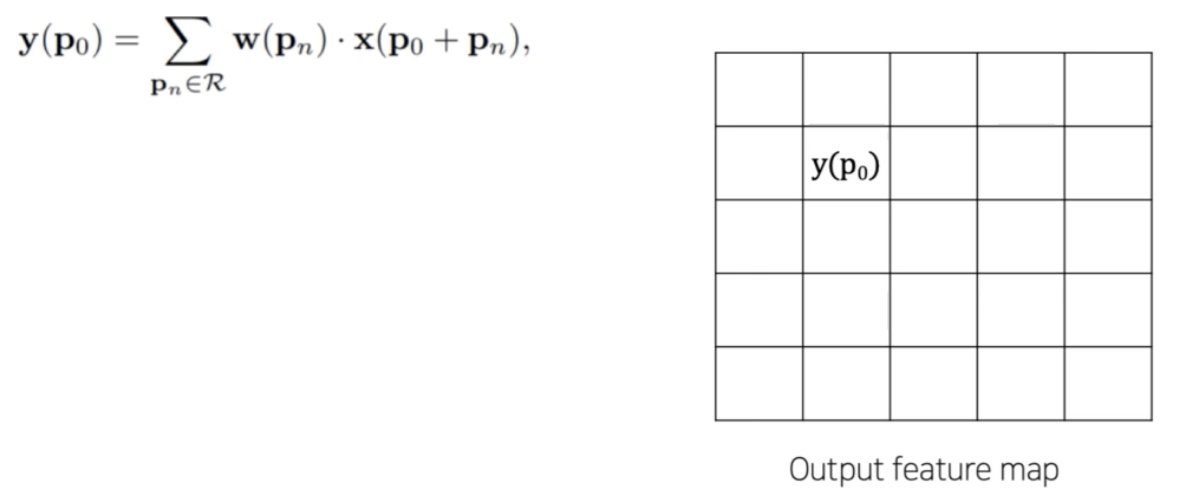
      • $\mathbf{y}(\mathbf{p}_0)$ 는 다음과 같이 계산될 수 있다.

      

      • input feature map 과 weight 가 존재하고 $\mathbf{p}_0$ 의 위치가 중심이라고 했을 때, weight 의 값이 input feature map 에서 어떤 값과 곱해져야 하는지를 $\mathcal{R}$ 에서 얻을 수 있다.
      • 즉, $\mathcal{R}$ 의 위치에 있는 픽셀 weight 와 곱해라! 라는 것이다.
      • 그러면 $\mathcal{R}$ 의 (-1, -1) 은 kernel 의 중심점으로부터 위로 1칸, 왼쪽으로 1칸 이동한 input feature map 의 픽셀값으로 연산하라는 것이다.
      • 즉 weight 가 input feature map 의 어떤 픽셀과 곱해져야 하는지 $\mathcal{R}$ 을 참고한다는 것이다. 이렇게 참고해가면서 input feature map 에서 어떤 픽셀값과 곱해질지 결정할 수 있다.
      • 이게 일반적인 conv 연산이다. 다만 위 설명은 offset 이라는 정의를 빌려서 일반적인 conv 연산을 설명한 것이다.
      • 그렇다면 Deformable conv 는 간단해진다. $\mathcal{R}$ 의 값을 바꾸면 되는 것이다.
      • 예를 들어 kernel 의 weight 는 input feature map 의 어느 부분과 곱해질까에 대해서 $\mathcal{R}$ 을 참고한다고 했는데, 기존의 (-1, -1) 인 부분이 (1, 1) 로 바뀌면 그 위치의 weight 는 input feature map 의 (1, 1) 위치의 픽셀값과 곱해지게 되는 것이다.
      • 이런 식으로 $\mathcal{R}$ 에 변화를 줘서 weight 가 곱해질 위치를 조절할 수 있다.
      • 그 과정이 바로 Deformable Convolution 이다.
      • Deformable Conv 를 식으로 나타내면 $\mathbf{y}(\mathbf{p}0) = \displaystyle\sum{\mathbf{p}_n \in \mathcal{R}}\mathbf{w}(\mathbf{p}_n) \cdot \mathbf{x}(\mathbf{p}_0 + \mathbf{p}_n + \Delta\mathbf{p}_n)$ 가 된다.
      • $\mathbf{p}_n$ 이 $\mathcal{R}$ 인데, 그 위치에 offset 인 $\Delta\mathbf{p}_n$ 만큼 더해줌으로써 바뀐 위치로부터 나온 픽셀값과 weight 를 곱하라는 것이다.
      • 그렇게 offset 을 주면 input feature 를 뽑을 위치가 그 offset 만큼 변형되게 된다.

      

      • 이와 같이 model 이 offset 을 배우면서 학습하면 geometric transform 에 대해서 충분히 대응할 수 있다.
      • 실제로 이런 deformable conv 로 학습한 feature map 을 실제 이미지에 mapping 시켜보면 아래 그림과 같다.
      • 왼쪽은 일반적으로 offset 이 존재하지 않는 고정된 conv 이다. conv 가 고정된 위치에서 수행되는 것을 볼 수 있다.
      • 반면에 offset 이 추가되면 conv 들이 고정된 정사각형에서 feature 를 뽑는 게 아니라 훨씬 더 객체가 있을 법한 위치에서 conv 를 수행한다.

      

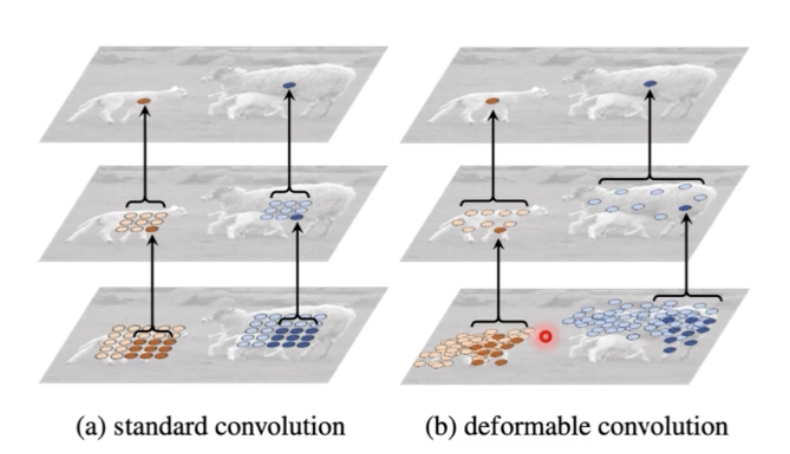
      • 즉 offset 을 통해서 객체가 있을법한 위치를 더 잘 학습하게 되고 conv 연산 결과 훨씬 더 유의미한 결과를 뽑아내게 되는 것이다.
      • 배경과 작은 객체, 큰 객체를 비교해보면, 고정된 정사각형이 아니라 배경은 펼쳐져 이고, 작은 객체, 큰 객체에 모여있다.

      

      

    • 결과를 보면, none 은 deformable conv 가 아니라 일반 conv 를 진행했을 때이다. 점점 deformable conv 를 진행했을 때 일반 conv 에 비해서 mAP 가 높아지고 있다. object detection 보다는 segmentation 에서 성능이 훨씬 많이 향상된다.

    

    • 최종 정리
      • deformable conv 가 등장하게 된 배경은 일정한 패턴을 지닌 CNN 은 geometric transform 에 한계가 있었기 때문에, 정사각형의 일정한 패턴이 아니라 곱해질 픽셀의 위치를 찾아주는 새로운 offset 이라는 개념을 제안.
      • 그 offset 을 학습시키면서 feature 를 뽑을 위치를 유동적으로 변환을 시킬 수 있다.
      • object detection, segmentation 에서 많은 성능 향상을 이뤘다.
  • Transformer
    • Transformer
      • NLP 에서 LSTM 이나 GRU 같은 RNN 계열들이 text 가 길어질수록 성능이 떨어지는 문제(long range dependency)가 있었는데 이를 해결하기 위해서 각 word 로부터 중요한 것을 뽑아내는 attention 개념을 사용했다.
      • LSTM 에 attention 이 복합적으로 이용되다가, attention 기반의 새로운 네트워크를 제안하는데 그것이 바로 Transformer. (Attention is all you need)
      • Transformer 를 Vision 쪽에 적용시키려는 많은 시도가 있었다.
      • ViT, DETR 등이 있다.
      • Swin Transformer 는 detection 의 SOTA 를 갈아치우고 있다.

    • Self Attention

      

      • input text 를 딥러닝 모델이 이해할 수 있는 format 으로 변환해야 한다. 딥러닝이 이해할 수 있는 format 은 vector 이다. 따라서 text 를 특정 vector 형태로 변환해줘야 한다.
      • vector 로 바꾸는 과정은 TF/IDF, word2vec, BERT embedding 등 다양한 방법이 있다.
      • input 의 순서를 담당하는 positional encoding 을 embedding 된 text 에 더해주고, 이를 attention network 에 넣어준다.

    • Multi-head Attention Network

      

      • transformer 의 꽃
      • multi-head 를 이해하기 위해서 single-head 인 Scaled-dot product attention 을 이해할 필요가 있다.

      • Scaled-dot product attention

        

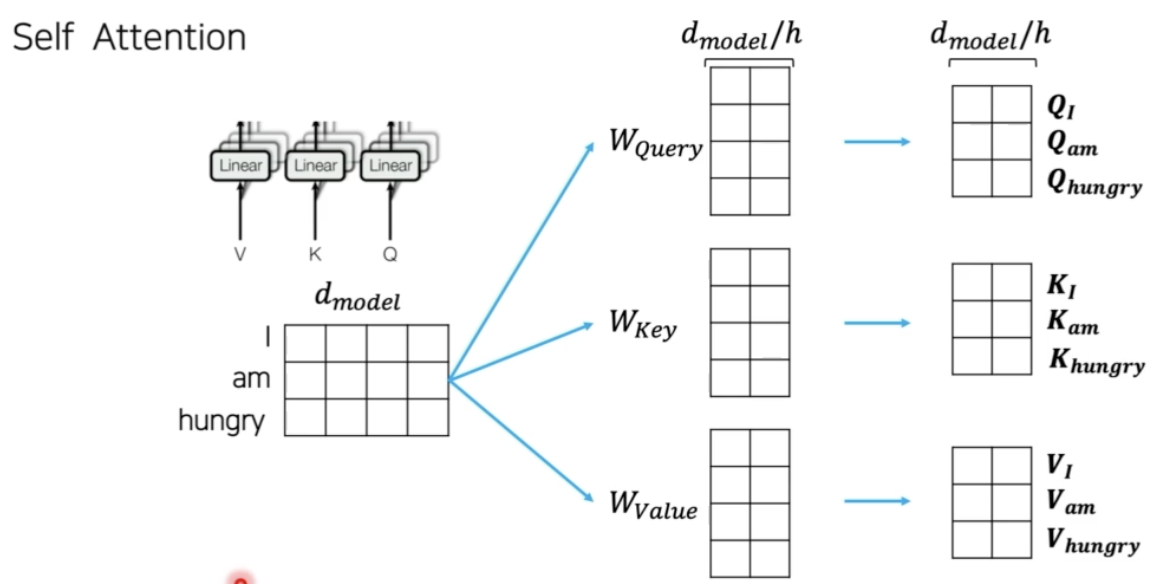
        • 각 단어들은 embedding 과정을 통해서 총 $d$ 개의 차원을 가지는 embedding vector 로 변환된다.
        • 이 때 embedding vector 를 3가지 vector 형태로 새롭게 연산을 수행한다. 각각 Query, Key, Value vector 이다.
        • 자세한 것은 transformer 에 대해 따로 포스트를 마련하여 정리할 것이다.
        • Q, K, V vector 를 만들면, 각 단어들의 중요도, Attention 을 계산해주어야 한다. 그러기 위하여 attention map 을 구성해준다.
        • Q 와 K의 transpose 를 곱해줘서 matrix 를 만든다. 이 matrix 를 $d$ 의 크기로 normalization 을 해준다. normalization 을 해주는 이유는 Q, K, V 가 내적 연산을 통해서 구해지기 때문에 $d$ 가 커질수록 matrix 안의 값이 절대적으로 커지기 때문이다.
        • normalize 후 softmax 연산을 취해주게 되면 총합은 1 이고 0~1 사이의 값을 가지게 된다.

        

        • 그렇게 softmax 를 취한 matrix 에서 각각의 값은 각 단어의 중요도를 담당하게 된다. 이 attention matrix 와 V 를 행렬곱 해주게 되면 각 word 가 이 문장에서 어느정도 중요도를 가지고 있는지 중요도가 반영된 새로운 value vector 가 나오게 된다.
      • 이제 head 의 개수를 여러개 줄 수 있다. 그러면 Multihead attention 을 수행할 수 있다.

      

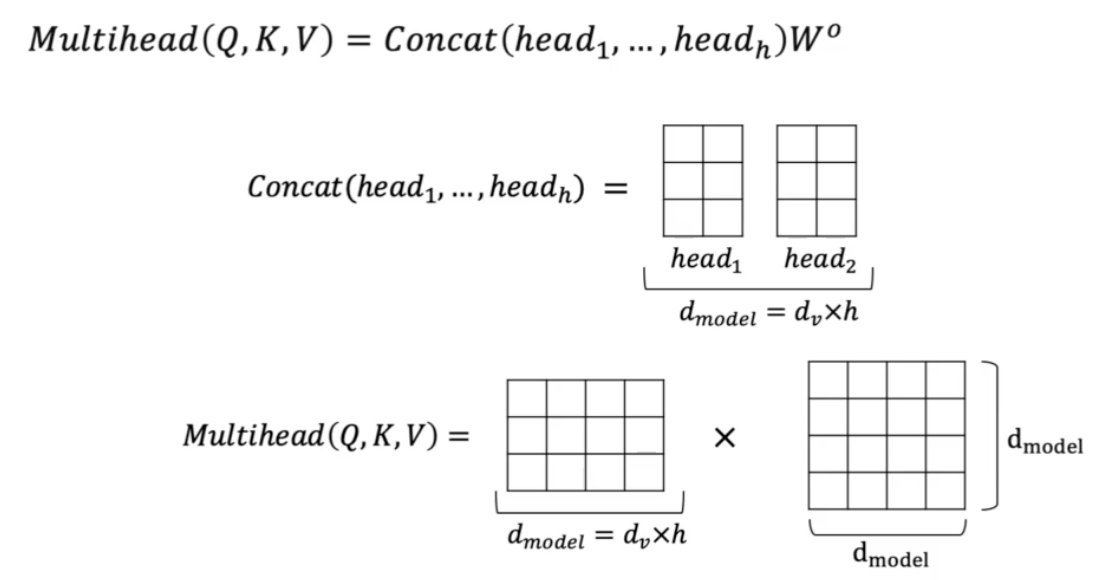
    • ViT
      • transformer 를 이미지 데이터에 적용하기 위해서는 이미지 데이터를 자연어 데이터처럼 sequencial 한 input 으로 바꿔줘야 한다.
      • 이후 sequencial 한 input 들이 embedding 을 가져야하고 몇 가지 encoding 을 추가해서 transformer encoder 에 input 을 넣어주면 된다.
      • 이를 Vision Transformer 라고 한다.
      • Image Classification 에서 ViT 는 5가지 절차로 이루어진다.

      

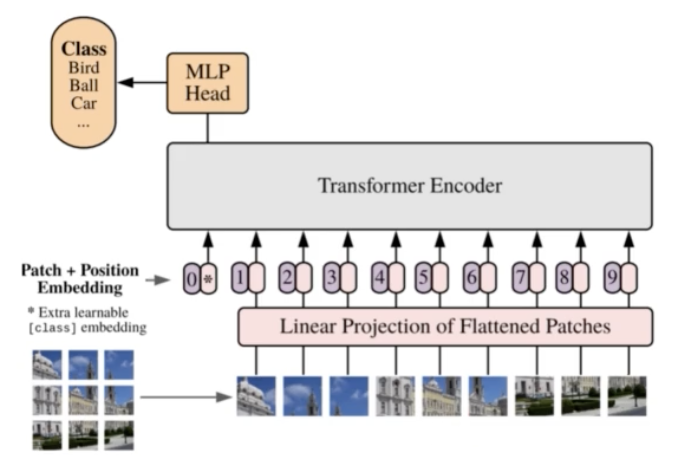
      1) 하나의 이미지가 transformer 에 들어가기 위해 이미지를 word 같은 형태로 바꿔준다. 이를 위해 3D 형태를 flatten 하여 2D 형태로 만든다. 즉 Patch 단위로 나누는 것이다.

      2) 학습가능한 embedding 처리를 해준다.

      3) cls 토큰과 positional embedding 을 추가해준다.

      4) Transformer 연산을 수행한다.

      5) cls 토큰으로부터 Prediction을 수행한다.

      • Flatten 3D to 2D (Patch 단위로 나누기)

        

        • 하나의 이미지를 word 같은 형태로, sequential 한 포맷으로 바꿔준다.
        • 이미지 하나의 픽셀을 하나의 word 로 볼 수 있다. 그러나 그렇게 되면 word 의 개수가 많아져 sentence 의 길이가 긴 경우가 된다. 그러면 mutli head attention 의 연산 cost 가 매우 많이 늘어날 것이다.
        • 따라서 word 의 개수를 줄이기 위해서 grid 형태의 patch 를 이용한다.
        • 예를 들어 16x16 이미지가 있을 때 8x8 grid 를 사용하게 된다면 4개의 patch 가 생기게 된다.
        • 이 때 각 patch 를 flatten 해줄 수 있다. 그렇게 되면 Patch 의 개수 x (HWC) 의 shape 을 가지게 된다. 즉 patch 로 나누고 flatten 을 해주게 되면 하나의 이미지가 word 처럼 변하게 된다.

      • Learnable 한 embedding 처리

        

        • 이미지 patch 들을 학습가능한 embedding matrix($E$)에 통과시킨다.

      • Add class embedding, position embedding

        

        • 앞서 4개의 patch 가 만들어졌는데, BERT 에서 [CLS] token 과 같이 4개의 patch 에서 맨 앞에 하나의 새로운 patch 를 추가해준다. 이 임의의 patch 를 추가해서 총 input 이 5개의 word 즉 5개의 patch 를 가지도록 만들어준다.
        • 이 [CLS] token 을 class embedding 이라고도 한다.
        • 이를 왜 추가해주냐면, 하나의 이미지에 대해서 classification 을 수행해줘야 하는데, [CLS] token 으로부터 classification 을 수행할 수 있게끔 처리해주기 위해서이다.
        • 이후 transformer 와 마찬가지로 이미지의 위치에 따라 학습하기 위해 position embedding 을 추가해준다.
      • Transformer
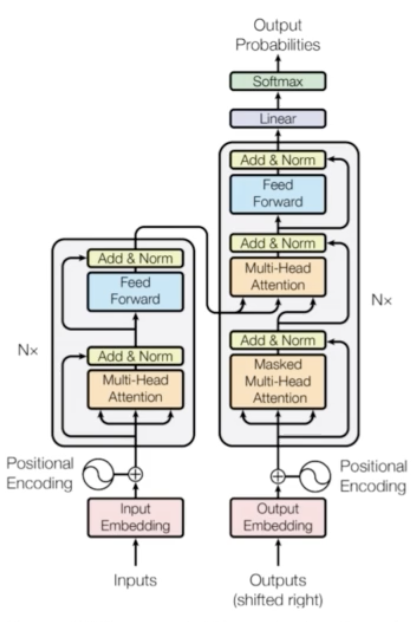
        • 이렇게 구성된 embedding 을 transformer 에 input 으로 넣어주면 된다.
        • 첫번째 token 이 [CLS] token 이다.
        • transformer output 을 생각해보면 input 이 10개 들어갔기 때문에 output 도 10개가 나오게 되는데, 그 중에서 첫번째 output 인 [CLS] token 으로부터 MLP head 를 통과해서 최종적으로 classification 을 수행한다.
        • 구체적으로 아키텍처를 살펴보자.

        

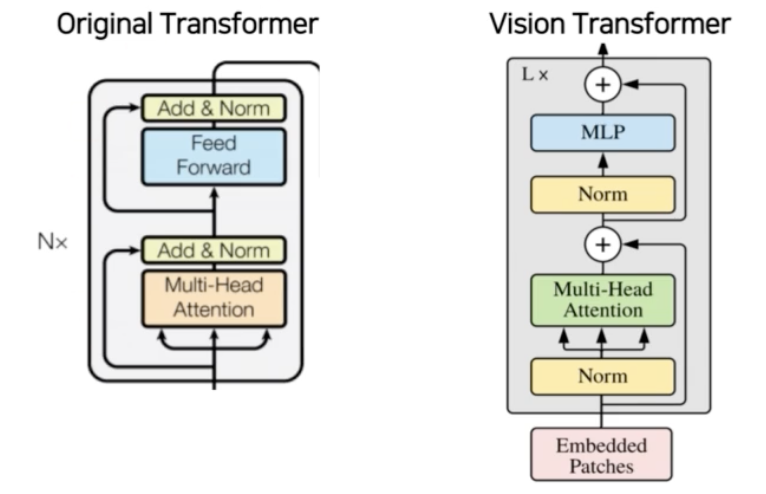
        • original transformer 와 세부적으로 다른 부분은 있지만 전체적으로 유사하다.
      • Predict
        • 이렇게 transformer 연산을 수행했을 때 나오는 output 중 [CLS] token 이 MLP 를 통과해서 최종 class 를 예측하게 된다.
      • 이러한 ViT 는 Conv 를 완전히 벗어났다. 그리고 어느정도 성능 향상이 있었다.
      • ViT 의 문제점
        • ViT 의 실험부분을 보면 굉장히 많은 양의 Data 를 학습해야 성능이 나온다. ImageNet 뿐만 아니라 구글의 큰 자체 데이터셋도 활용했기 때문에 학습의 난이도가 높은 편이다.
        • transformer 특성 상 computational cost 가 굉장히 크다. 특히 detection 에서는 resolution이 큰 편이기 때문에 이 computational cost 가 훨씬 critical 하게 다가온다.
        • 기존 CNN은 backbone 으로 활용했을 때 backbone 중간 단계에서 feature map 을 추출해서 FPN 같은 Neck 으로 feature map 의 정보를 풍부하게 만들어줬었는데, ViT 는 output 이 바로 나오기 때문에 detection, seg backbone 으로 사용하기에 어려움이 있다.
    • DETR
      • transformer 를 detection 에 처음으로 적용한 모델이다.
      • 기존의 Detection 은 NMS 와 같은 hand-crafted post process 단계를 시행했는데, 이 DETR 에서는 transformer 를 사용해서 post process 과정을 완벽하게 생략했다.
      • 기존의 detection 에서는 최종 head 를 통과하고 나온 output 은 많은 bbox 를 가지고 있기 때문에 NMS 와 같은 메소드로 후처리를 진행했었다.

      

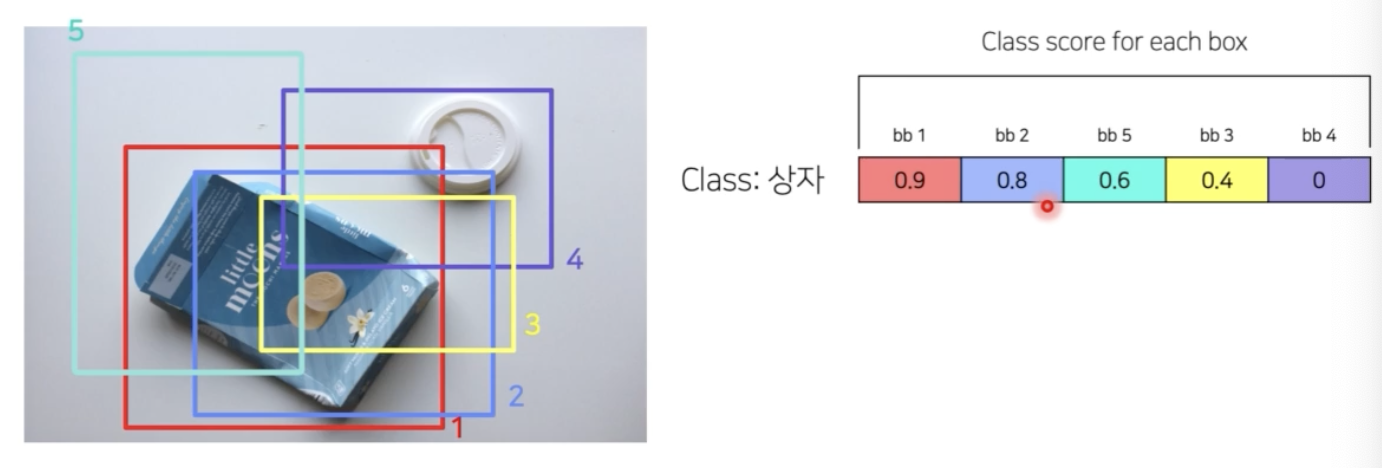
      • NMS 는 class score 가 가장 큰 상자를 기준으로 나머지 상자와 IoU 를 계산했을 때 IoU 가 thr 이상이면 같은 상자라고 보고, 겹치는 상자를 제거하는 후처리였다.

      • DETR Architecture

        

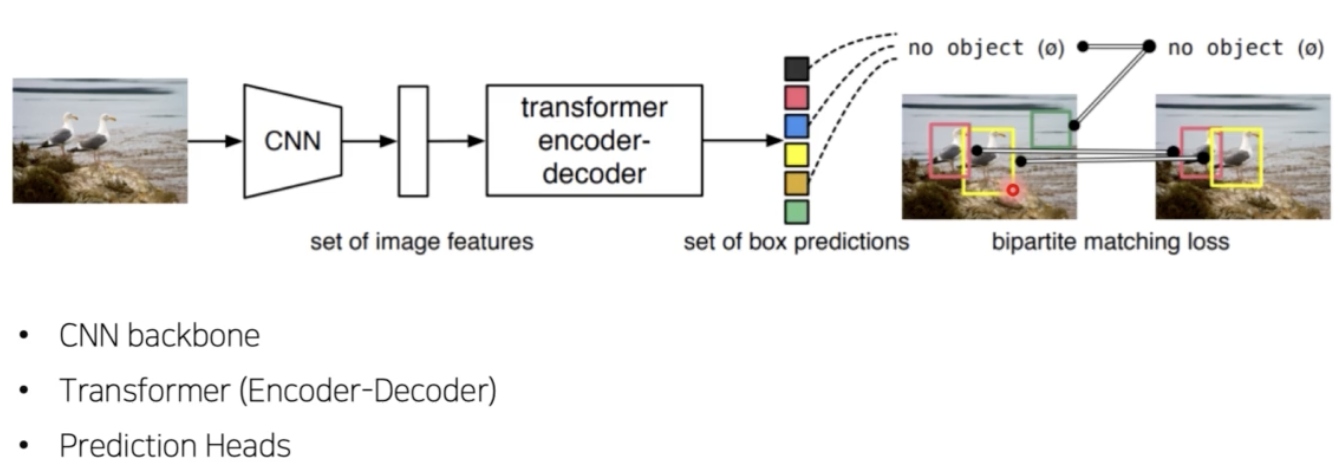
        • DETR 의 detection 구조는 1 stage detection 구조이다.
        • backbone network 를 사용해 feature map 을 뽑는다. 이 부분은 기존과 동일하다.
        • 이후 이 feature map 을 transformer encoder, decoder 에 통과시키고 사용자가 정한 decoder의 output 개수만큼 최종 예측이 나온다.
        • 이 최종 예측으로부터 bbox 와 object 여부, object 라면 class 여부를 예측하게 된다.
        • 여기서 Neck 구조는 없다.

        

        • feature map 의 경우 transformer 가 연산량이 매우 많기 때문에 가장 높은 레벨의 feature map 을 사용한다.
        • 이후 ViT 처럼 feature map 을 2D 형태로 flatten 하고 positional embedding 을 추가한 후 transformer 연산을 수행하게 된다.
        • 이 때 input size 는 224x224 이고, backbone 연산을 수행한 feature map 의 사이즈는 7x7 이기 때문에, 따로 patch 를 구분해주지 않고 이 7x7 feature map 을 그대로 flatten 해서 49개의 feature vector 를 encoder 의 입력값으로 사용했다.

        

        • 다음으로 encoder 를 통과한 vector 를 transformer decoder 에 통과시킨다.
        • decoder 는 encoder 와 구조상으로 크게 다르지 않다.
        • output 개수를 사람이 정할 수 있다.
        • 이 때 output 개수는 한 이미지에 존재하는 object 개수보다 높게 설정해야 한다.
        • N 개의 output vector 들은 최종 Feed Forward Network(FFN) 을 통과해서 클래스와 box 를 예측하게 된다.
      • Train 시 중점을 둘 사항들
        • output vector 개수를 N 개로 정했는데, 한 이미지 당 적지도 않고 많지도 않고 딱 N 개의 객체가 예측된다.
        • 이 때 GT 와 prediction 을 N:N 매핑을 한다.
        • prediction 은 무조건 N 개인데, GT 는 N개가 아닐 수 있다. 이미지에 존재하는 객체보다 더 크게 N 을 정했기 때문이다.
        • 따라서 GT 에 부족한 object 개수가 있을 수 있다. 이 개수 만큼 no object 로 padding 처리를 해줘야 한다.
        • 이렇게 padding 처리를 하게 되면 GT 와 prediction 사이에 N:N 매핑이 이루어지고, N 개의 예측이 유니크하게 나타나기 때문에 예측되는 박스 개수만큼 객체의 박스 개수가 나오게 된다. 이는 post-process 과정이 필요 없음을 의미한다.
      • 결과를 보면 Faster R-CNN 보다 조금 더 좋은 성능을 낸다.
      • 또한 전체적으로 AP 가 상승했지만, DETR 에서는 가장 high level 의 feature map 만을 사용했기 때문에 $AP_s$ 로 대표되는 작은 객체들에 대한 성능이 하락했다.
    • Swin Transformer
      • DETR
        • 마지막 feature map 만을 사용하고 이후 head 부터는 transformer 를 사용했다.
        • conv 연산 한 feature map 이후 transformer 를 적용해서 객체를 뽑아냈다.
        • backbone 으로 transformer 를 사용한 것이 아니다.
        • Swin-T 는 backbone 에 transformer 를 적용했다.
      • ViT 의 문제점
        • ViT 의 실험부분을 보면 굉장히 많은 양의 data 를 학습해야 성능이 나온다.
        • transformer 특성 상 computational cost 가 크다.
        • 일반적인 backbone 으로 사용하기 힘들다.
      • Swin-T 는 transformer 를 CNN 과 유사한 구조로 설계했고, transformer 는 cost 가 매우 큰 편인데 새롭게 Window 라는 컨셉을 도입해서 cost 를 줄이는 방법을 제안했다.

      • Architecture

        

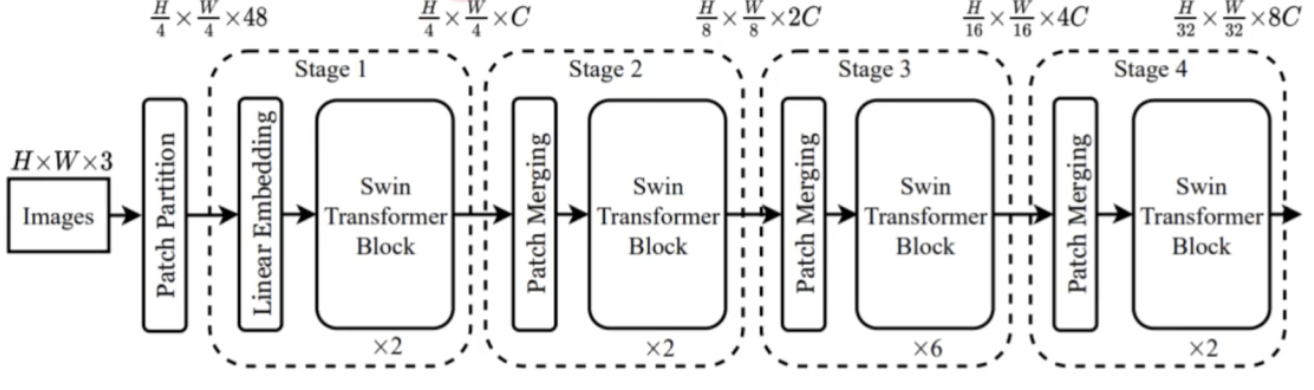
        • 이미지를 patch 로 나누는 과정은 동일하다.
        • 이후 transformer N 개로 나눠서 각 stage 별로 transformer 를 수행할 수 있게끔 아키텍처를 구성했다.
        • 앞 stage 에서 다음 stage 로 넘어갈 때 feature map 의 size 를 줄여준다. 이런 점이 CNN backbone 과 유사한 점이다.
        • 전체적인 과정을 정리하면 크게 5가지 과정으로 구분할 수 있다.
          • Patch Partitioning: 이미지를 patch 로 나눠주는 과정
          • Linear Embedding: patch 에 embedding 을 더해주는 과정
          • Swin Transformer Block: transformer 과정
          • Window Multi-head Attention: transformer block 에서 cost 를 줄이는 과정
          • Patch Merging: feature map 의 size 를 2의 제곱수로 줄이는 과정

        • Patch Partitioning

          

          • ViT 와 같이 patch size 를 줘서 이미지를 N 개의 patch 로 나눈다.

        • Linear Embedding

          

          • ViT 방식처럼 학습가능한 embedding 을 통과시킨다.
          • 차이점은 classification task 가 아니라 detection task 이기 때문에 class embedding 은 제거한다.

        • Swin Transformer Block

          

          • ViT 은 attention layer 를 1번 수행하는데, Swin-T 는 attention 을 1번 수행한 뒤 그 결과를 한 번 더 attention 을 통과시켜준다.
          • 즉 2번의 attention 이 하나의 transformer block 으로 묶인다.
          • 이 때 ViT 는 Multi-head attention 을 사용하지만, Swin-T 는 MHA 가 아닌 Window Multi-head Self Attention(W-MSA) 을 이용한다.
          • 첫번째 attention 연산에서는 W-MSA 을 이용하고, 두번째 attention 연산에서 Shifted W-MSA 을 이용한다.
          • 즉 하나의 Swin Transformer Block 은 두 가지 transformer 연산으로 이루어져 있다. (W-MSA, SW-MSA)

        • Window Multi-Head Attention(W-MSA)

          

          • W-MSA 는 임베딩을 window 단위로 나누는 것이다.
          • 기존 ViT 는 모든 임베딩이 transformer 에 입력됐는데, Swin-T 는 각 window 안에서만 transformer 연산을 수행한다.
          • ViT 는 이미지 크기에 따라서 점점 computational cost 가 증가하는데 window 안에서만 transformer 를 진행하기 때문에 cost 를 조절이 가능해지게 된다. 즉 window 크기에 따라 조절이 가능하다.
          • 다만 단점은 window 안에서만 transformer 를 진행하기 때문에 receptive field, 즉 transformer 가 볼 수 있는 이미지 영역 크기가 제한된다.

        • Shifted Window Multi-Head Attention(SW-MSA)

          

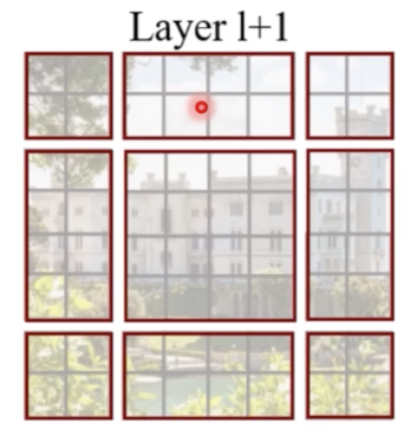
          • W-MSA 의 단점을 해결하기 위해서, 즉 receptive field 를 다양하게 해주기 위해서 한번 더 transformer layer 를 통과하는데, 이 때는 그냥 window 가 아니라 window 를 위 아래로 shift(이동) 해준 shift window 를 사용하게 된다.
          • 이렇게 되면 transformer 마다 receptive field 가 다양해진다는 장점이 있을 수 있다.
          • 다만 이 경우에는 가운데 window 는 문제 없지만, 가장자리에 window 조각들이 생기게 되어서, window 조각들에 대한 정의가 필요해진다.

          

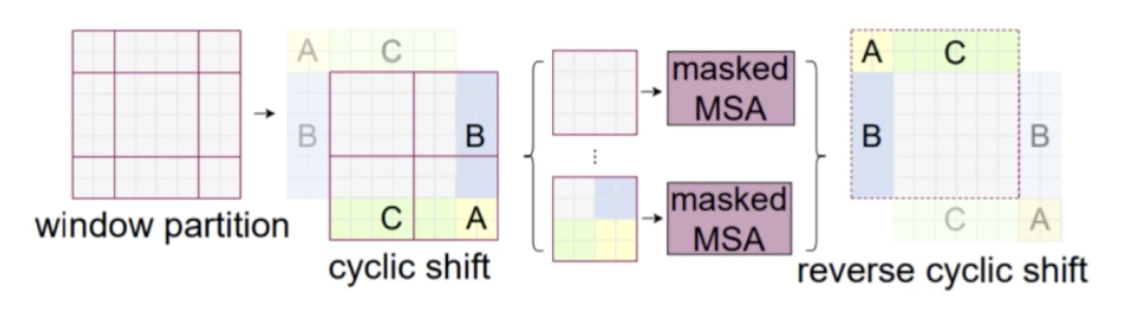
          • 이를 위해 조각들이 하나의 window 를 형성할 수 있도록 위치를 대칭 형태로 옮겨주게 된다(cyclic shift).
          • 이 때 남는 부분들은 마스킹 처리를 해서 self-attention 연산에서 제거해준다.
          • 이렇게 남는 부분을 옮겨가면서 작은 window 조각을 하나의 window 로 만들어준 뒤 attention 연산을 수행하면 SW-MSA 가 수행된다.

        • Patch Merging

          

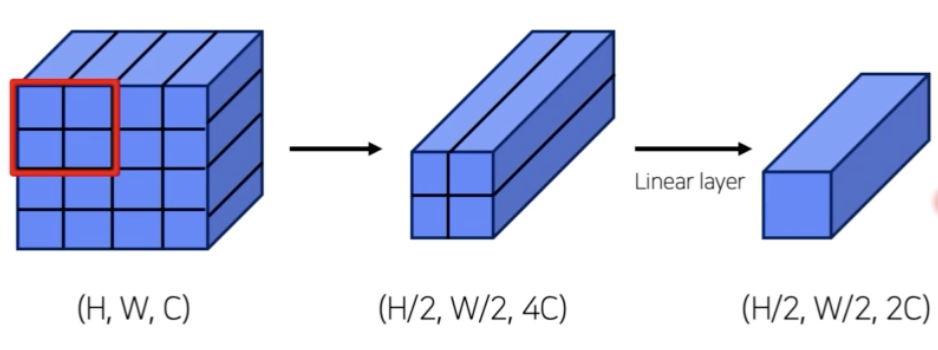
          • 각각의 stage 별로 transformer 연산을 수행하는데, stage 가 넘어갈 때마다 feature size 를 줄여주는 Patch Merging 이 실행된다.
          • Patch Partitioning 과 비슷하게 feature size 를 줄이고 channel 을 늘리는데 중요한 역할을 한다.
          • 즉 Merging 단계에서는 feature size 를 줄이고 channel-wise 하게 concat 해서 linear layer 를 통과시킨다.
      • 이렇게 backbone 단계에서 transformer 를 적용한 Swin-T 에 대해서 리뷰했다.

      • 결과를 보면 AP 가 Swin-T 가 가장 잘 나온다.

        

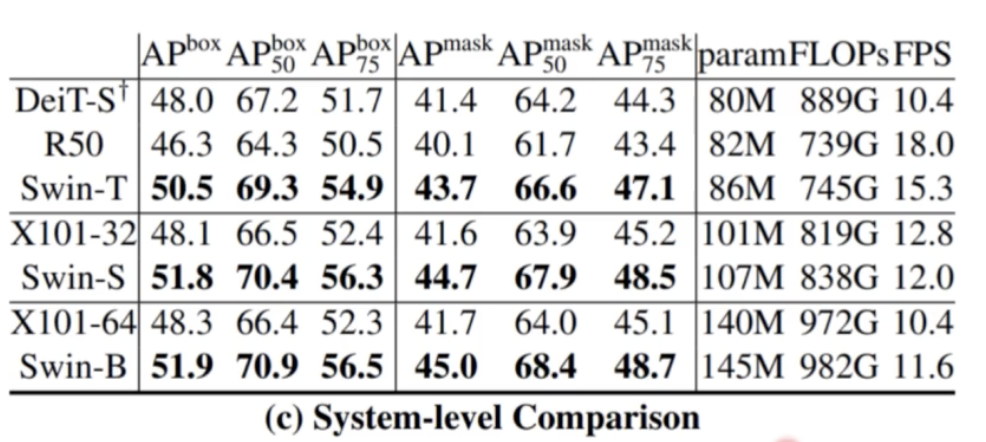
      • Segmentation task 에서도 큰 성능 향상을 가져왔다.
      • 정리
        • 적은 data 에도 학습이 잘 이루어진다.
        • window 라는 unit 을 사용해서 computational cost 를 대폭 줄였다.
        • CNN 과 비슷한 stage 구조를 사용해서 기존의 FPN, PANet 이런 모듈들과 호환이 정말 잘 된다. 따라서 Object detection, Segmentation 에서 backbone 으로 general 하게 활용될 수 있다.
        • 가장 좋은 것은 성능이 정말 좋다는 것!

맨 위로 이동 ↑