[Metric] 1. Accuracy, Precision, Recall, F1-score
- 머신러닝/딥러닝에서 사용되는 대표적인 Metric 에 대해 알아보자.
Confusion Matrix
-
실제 라벨과 예측 라벨의 일치 갯수를 matrix 로 표현하는 방법이다.
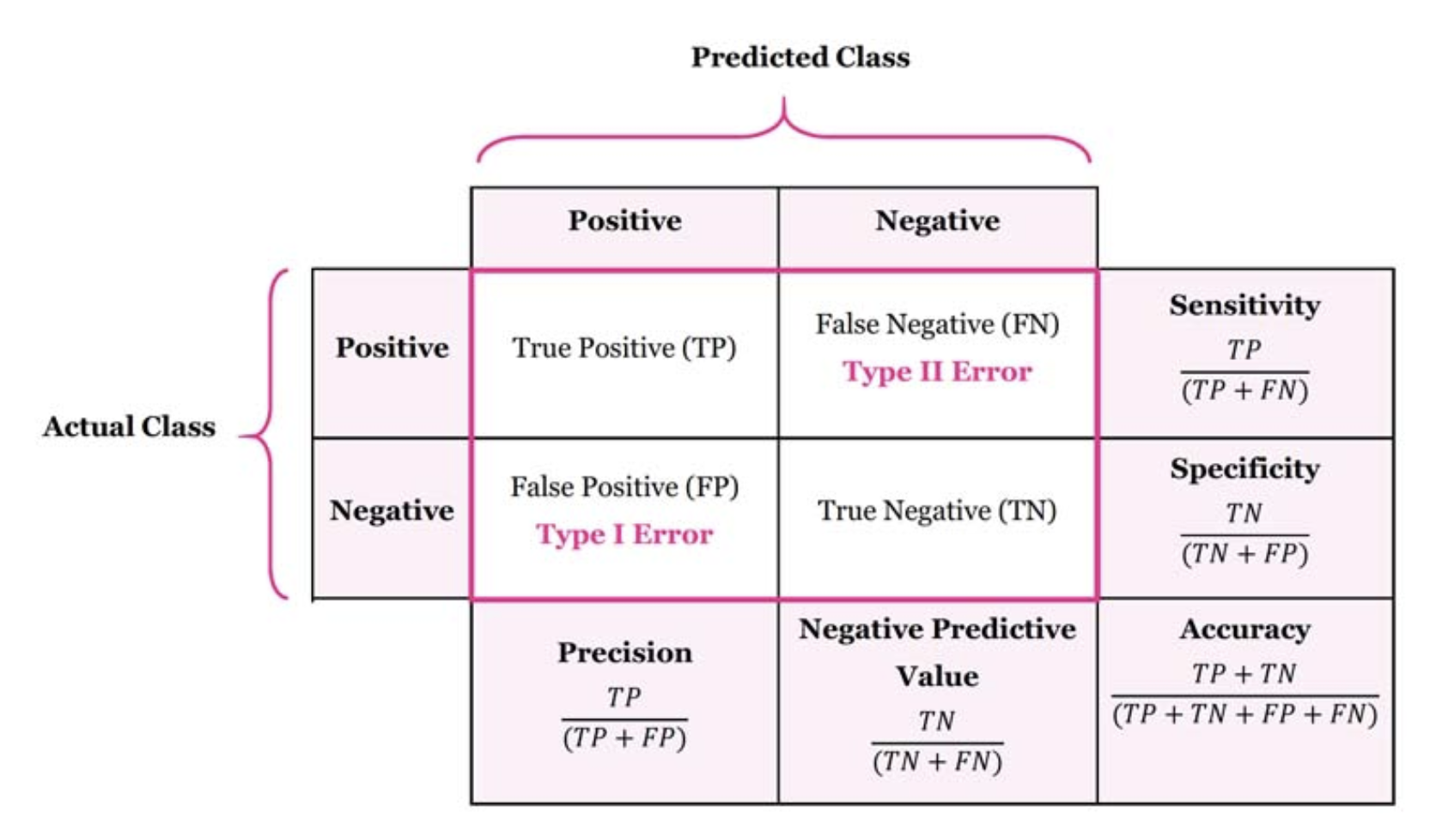
- TP(True Positive)
- 실제 맞는 것을 맞다고 예측하여 맞는 경우
- True : 예측이 맞음
- Positive : 예측값이 Positive(1)
- FP(False Positive)
- 실제 아닌데 맞다고 예측하여 틀린 경우
- False : 예측이 틀림
- Positive : 예측값이 Positive(1)인 경우
- FN(False Negative)
- 실제 맞는데 틀리다고 예측하여 틀린 경우
- False : 예측이 틀림
- Nagative : 예측값이 Negative(0)인 경우
- TN(True Negative)
- 실제 아닌 것을 아니라고 예측하여 맞는 경우
- True : 예측이 맞음
- Negative : 예측값이 Negative(0)인 경우
Accuracy
- 전체 대비 정확하게 예측한 개수의 비율이다.
-
위 confusion matrix 의 값을 이용하여 표현할 수 있다.
$$\text{Accuracy} = \frac{TP + TN}{TP + FP + FN + TN}$$ - Accuracy 를 metric 으로 사용할 때는 주의해야하는 점이 있다.
- 불균형한 데이터셋에서 Accuracy 를 사용한다면 그 결과는 상당회 왜곡될 수 있다.
- 예를 들어 시험 합격률이 2%일 때, 모든 수험자가 불합격 한다고 하면 98%의 정확도를 가지게 되어 정확도는 높지만 쓸모없는 모델이 만들어진다.
- 이 때, Accuracy 대신 사용할 수 있는 지표가 Precision 과 Recall 이다.
Precision
- Presicion 은 Positive 라고 예측한 비율 중 실제 True 의 비율을 나타낸다.
-
즉, Positive 라고 예측한 것 중에서 얼마나 잘 맞았는지에 대한 비율이다.
$$\text{Precision} = \frac{TP}{TP + FP}$$ - Precision Score 는 average 옵션에 따라 micro 와 macro 로 구분할 수 있다.
- None : 라벨 별 각 평균을 그대로 구한다.
- micro : 전체 평균
- average 를 micro 로 두면 전체 평균으로 모든 열에서 맞은 것 즉, 대각선 성분의 총 합을 총 갯수로 나눈 값이다.
- macro : 라벨 별 각 합의 평균
- macro 는 각 열(라벨 별)에 대한 precision 값을 모두 더한 다음 열의 갯수로 나눈다.
- 즉 average 를 None 으로 두었을 때 구한 각 열의 Precision 들을 산술 평균한 값이 macro 가 된다.
Recall
- 실제 True 데이터 중 Positive 라고 예측한 비율이다.
- Presicion 의 기준은 모델이 예측한 것인 반면, Recall 의 기준은 데이터다.
-
따라서 실제 True 한 것 중에서 얼마나 잘 예측하였는지 비율이 Recall 이다.
$$\text{Recall} = \frac{TP}{TP + FN}$$ - Precision 과 Recall 은 어느정도 Trade off 가 발생한다.
- 왜냐하면 Recall 을 높이려면 FN 을 줄여야 하고 Precision 을 높이려면 FP를 줄여야 하기 때문이다.
- Precision 과 마찬가지로 micro 는 전체 평균, macro 는 각 열의 산술 평균이다.
Precision-Recall Graph(PR Curve)
- 대부분의 시스템을 모델링 할 때에는 Precions 과 Recall 중 하나를 선택하는 것이 아니라 두 지표 모두를 사용해야 하는 경우가 많다.
- 예시를 들어보자.
- A 와 B 라는 기술이 있다.
- A 는 이미지에 있는 사람을 99.99% 잡아내지만 이미지 1장 당 평균 10건 정도의 오검출이 발생한다. 즉, 사람이 아닌 부분도 사람이라고 검출하는 경우가 발생한다.
- 반면에 B 는 이미지에 있는 사람들 중 50% 밖에 못 잡아내지만 오검출은 발생하지 않는다.
- 이 때 A 와 B 중 어느 기술이 뛰어난 기술일까?
- 사용 용도에 따라 어느 기술이 좋은지 차이가 나겠지만, 중요한 것은 검출율 만으로 기술을 평가하는 것은 바람직 하지 않다는 것이다.
- 예를 들어 모든 입력에 대하여 물체가 검출된 것으로 반환하면 검출률 100%의 물체인식 기술이 된다.
- Recall 은 실제 대상 물체들을 빠뜨리지 않고 얼마나 잘 잡아내는지를 나타내는 지표다.
- Precision 은 검출된 결과가 얼마나 정확한지 즉, 검출 결과들 중 실제 물체가 얼마나 포함되어 있는지를 나타낸다.
- 어떤 알고리즘의 Recall 과 Precision 은 알고리즘의 파라미터 조절에 따라 유동적으로 변하는 값이기 때문에 어느 한 값으로는 알고리즘 전체의 성능을 제대로 표현할 수 없다.
- 일반적으로 알고리즘의 Recall 과 Precision 은 서로 반비례 관계(Trade-Off)를 가진다. 즉 알고리즘의 파라미터를 조절해서 Recall 을 높이면 Precision 이 감소하고 반대로 Precision 을 높이면 Recall 이 떨어진다.
- 위 예시에서 우리는 알고리즘/모델의 성능을 제대로 비교하고 평가하기 위해 Precision 과 Recall 의 성능 변화 전체를 살펴봐야 함을 알 수 있다.
-
그 대표적인 방법이 precision-recall 그래프를 이용하는 것이다.
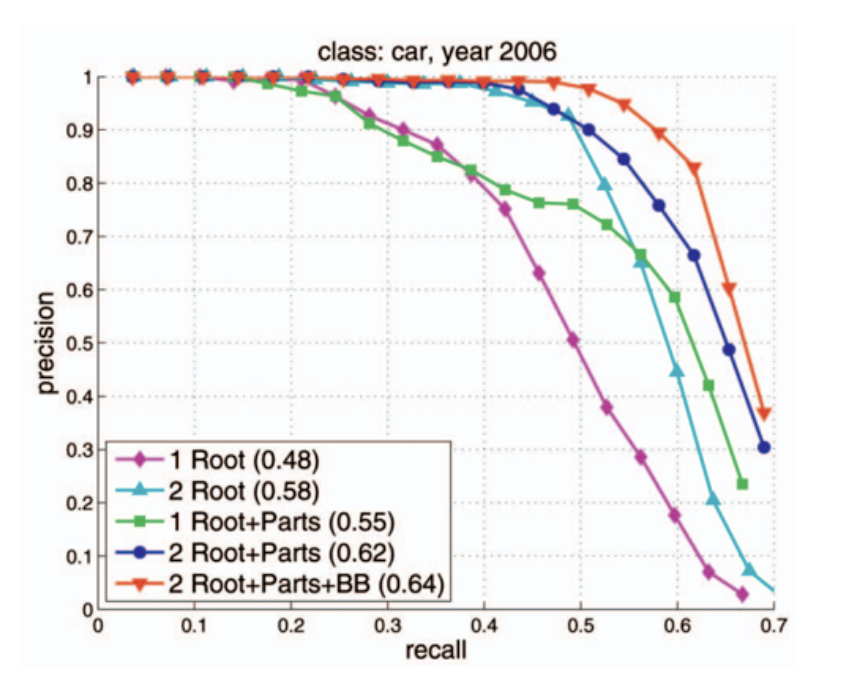
- 알고리즘의 파라미터 조절에 따른 Precision 과 Recall 값의 변화를 그래프로 표현하면 위와 같다.
- 상황에 따라, Recall 대신 miss rate(1- Recall)을 사용할 수 있고, Precision 대신에 false alarm(1 - Precision)을 사용할 수 있다.
Average Precision(AP)
- Precision-Recall 그래프는 어떤 알고리즘의 성능을 전반적으로 파악하기에는 좋으나 서로 다른 두 알고리즘의 성능을 정량적으로 비교하기에는 불편한 점이 있다.
- 이 때 Average Precision(AP)을 이용하면 비교하기 용이하다.
- AP 는 Precision-Recall 그래프에서 그래프 선 아래쪽의 면적을 계산하는 방식이다.
-
이 면적의 값 즉, AP 가 클수록 성능이 좋은 알고리즘이라고 할 수 있다.
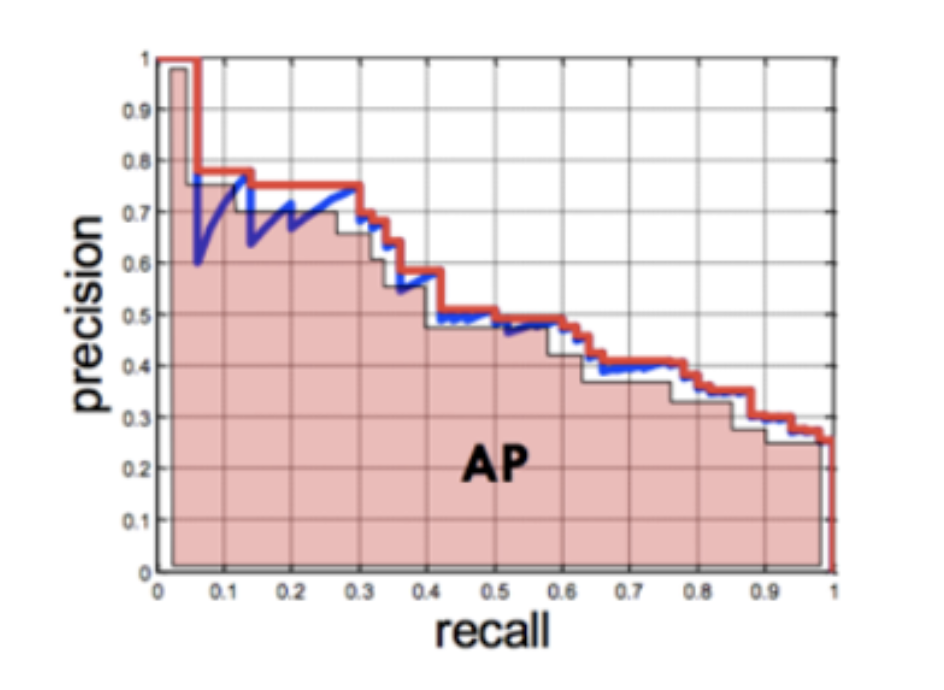
- 위 그래프의 아랫 면적의 총 합이 AP 가 된다. 이 AP 값을 이용하여 다른 모델과의 정량적 비교가 가능해진다.
F1-score
- Precision 과 Recall 은 서로 Trade-off 관계를 가진다.
- 거기다 접근하는 방식도 Precision 은 모델의 예측 관점, Recall 은 정답 데이터 관점이므로 서로 상이하다.
- 그러나 두 지표 모두 모델의 성능을 확인하는 데 중요하므로 둘 다 사용되어야 한다. 따라서 두 지표를 평균값을 통해 하나의 값으로 나타낼 수 있는데, 이를 F1 score 라고 한다.
- 이 때, 사용되는 방법은 조화 평균이다.
- 조화 평균을 사용하는 이유는 평균이 Precision 과 Recall 중 낮은 값에 가깝도록 만들기 위함이다.
-
조화 평균의 경우 평균 계산에 사용된 값, 즉 여기서 Precion 과 Recall 이 불균형할수록 Penalty 가 가해져서 작은 값에 가깝도록 평균이 계산된다.
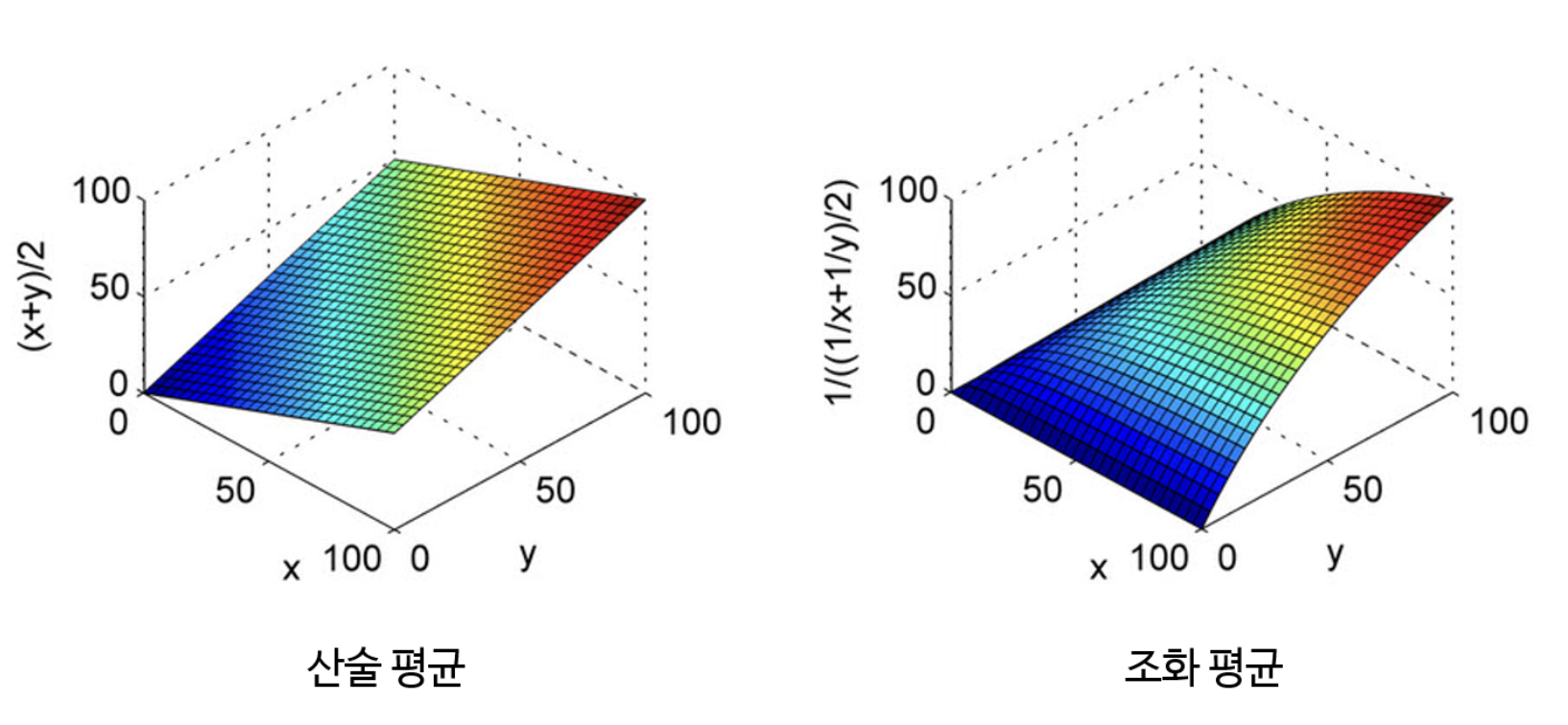
- 위 그래프 분포를 살펴보면 조화 평균의 경우 $X, Y$ 값의 차이가 크면 $Z$ 축의 값이 작은 것을 확인할 수 있다.
- 따라서 극단적으로 Precision 과 Recall 중 한 쪽이 1 에 가깝고 한 쪽이 0 에 가까운 경우 산술 평균과 같이 0.5가 아니라 0 에 가깝도록 만들어준다.
-
F1 score 를 높게 하려면 Precision 과 Recall 이 균일한 값이 필요하기 때문에 두 지표 성능 모두를 높일 수 있도록 해야한다.
$$\text{F1 Score} = 2 \; \cdot \; \frac{\text{precision} \times \text{recall}}{\text{precision + recall}}$$ - 물론 데이터셋 마다 특성이 다르므로, Precision, Recall, F1 score 를 비교하며 가장 적합한 것을 사용해야 한다.

댓글 남기기