[AI Math] 9. 정보이론, 엔트로피

클로드 엘우드 섀넌(Claude Elwood Shannon)으로부터 시작된 정보이론(Information Theory)과 엔트로피(Entropy)의 개념을 알아보자.

엔트로피

• 엔트로피(entropy)는 확률분포가 가지는 정보의 확신도 혹은 정보량을 수치로 표현한 것이다.
  • 확률분포에서 특정한 값이 나올 확률이 높아지고 나머지 값의 확률은 낮아진다면 엔트로피가 작아진다.
  • 빈대로 여러가지 값이 나올 확률이 대부분 비슷한 경우에는 엔트로피가 높아진다.
• 엔트로피는 확률분포의 모양이 어떤지를 나타내는 특성값 중 하나로 볼 수도 있다.
  • 확률 또는 확률밀도가 특정값에 몰려있으면 엔트로피가 작다고 하고 반대로 여러가지 값에 골고루 퍼져 있다면 엔트로피가 크다고 한다.
• 확률분포의 엔트로피는 물리학의 엔트로피 용어를 빌려온 것이다. 물리학에서는 물질의 상태가 분산되는 정도를 엔트로피로 정의한다. 물체의 상태가 여러가지로 고루 분산되어 있으면 엔트로피가 높고 특정한 하나의 상태로 몰려있으면 엔트로피가 낮다.
• 수학적으로 엔트로피는 확률분포함수를 입력으로 받아 숫자를 출력하는 범함수(functional)로 정의한다. $H[]$ 기호로 표기한다.

• 확률변수 $Y$ 가 카테고리분포와 같은 이산확률변수이면 다음처럼 정의한다.

  \[H[Y] = - \sum^K_{k=1}P(y_k)\log_2P(y_k)\]
• 이 식에서 $K$ 는 $X$ 가 가질 수 있는 클래스의 수이고 $P(y)$ 는 확률질량함수다. 확률의 로그값이 항상 음수이므로 음수 기호를 붙여서 양수로 만들었다.

• 확률변수 $Y$ 가 정규분포와 같은 연속확률변수이면 다음처럼 정의한다.

  \[H[Y] = - \int^\infty_{\infty}P(y)\log_2P(y)\text{d}y\]
• 이 식에서 $P(y)$ 는 확률밀도함수다.
• 로그의 밑(base)이 2 로 정의된 것은 정보통신과 관련을 가지는 역사적인 이유 때문이다.
• 이론적인 확률밀도함수가 없고 실제 데이터가 주어진 경우에는 데이터에서 확률질량함수를 추정한 후, 이를 기반으로 엔트로피를 계산한다.

엔트로피에 대한 이해

• 이 엔트로피에 대해 이해해보자.

알파벳 맞추기 게임

• 간단한 게임을 하나 생각해보도록 하자. 게임의 규칙은 다음과 같다.
  • A 는 알파벳 a,b,c,d 가 각각 적혀 있는 카드 중 하나를 뽑아 본인만 확인한다.
  • B 는 A 에게 YES 또는 NO 의 대답이 나올 수 있는 질문만을 할 수 있다.
  • B 는 최소한의 질문을 통해 A 가 뽑은 카드의 알파벳을 맞춰야 한다.
• 만약 내가 B 라면 어떤 전략을 써서 A 의 카드를 맞출 것인가? 다음과 같은 간단한 전략을 짤 수 있다.
  • [전략 1]
    1. a 인지 물어본다. YES 면 a 이다.
    2. a 가 아니면 b 인지 물어본다. YES 면 b 이다.
    3. b 가 아니면 c 인지 물어본다. YES 면 c, NO 면 d 이다.
• 과연 효과적인 전략일까?

• 이제부터 어떤 전략이 효과적인 전략인지 알아보기 위해서 질문 횟수의 기댓값($E[X]$)을 구해서 평균적으로 몇 회의 질문을 거쳐야 하는지를 알아보자.

  

• 기대값의 수식에 따라 위 전략의 기대값은 아래와 같이 구해진다.

  \[E[X] = \sum^4_{i=1}p_ix_i = \frac{1}{4} \times 1 + \frac{1}{4} \times 2 + \frac{1}{4} \times 3 + \frac{1}{4} \times 3 = 2.25\]
• 따라서 위 전략을 사용할 경우 평균적으로 2.25 회의 질문을 해야만 답을 얻을 수 있다.
• 이제 안정성을 추구하는 사람이라면 아래와 같은 전략을 생각해 낼 수 있다. 반씩 쪼개서 물어보는 것이다.
  • [전략 2]
    1. {a,b} 중에 있는지 물어본다.
    2. {a,b} 중에 있다면 a 인지 물어보고, 그렇지 않다면 c 인지 물어본다.

• 이 전략의 경우, a,b,c,d 중 어떤 카드가 뽑히더라도 2 번의 질문으로 그 카드의 정체를 알 수 있다. 즉 질문 횟수의 기댓값은 굳이 계산하지 않아도 2 임을 알 수 있다.

  

  \[E[X] = \sum^4_{i=1}p_ix_i = \frac{1}{4} \times 2 + \frac{1}{4} \times 2 + \frac{1}{4} \times 2 + \frac{1}{4} \times 2 = 2\]
• 이 전략은 첫 번째 전략에 비해 효과적이다. 평균 0.25회의 질문을 아낄 수 있기 때문이다.
• Shannon 의 정보이론에 따르면, 모든 카드가 뽑힐 확률이 동일할 경우 위의 두번째 전략과 같이 반씩 쪼개 먹는 전략이 가장 효과적이다.

• 그래서 일반적으로 $N$ 개의 카드가 존재할 경우, 이 전략을 사용할 시 질문의 횟수($I$)는 결국 반씩 쪼갠 횟수와 같기 때문에 로그를 이용하여 다음과 같이 표현한다.

  \[I = \log_2N\]

• 위 예시에서 $N$ 이 4 이기 때문에 $\log_2 4 = 2$ 만큼의 질문이 필요한 것이다. 여기서 $N$ 은 각 카드가 뽑힐 확률의 역수라고 볼 수 있으므로 다음과 같이 쓸 수 있다.

  \[I(s_i) = \log_2\frac{1}{P(s_i)} = -\log_2P(s_i) = -\log_2p_i\]
• 이 식은 ‘가장 안전한 전략’인 ‘반씩 쪼개기 전략’을 쓴 경우의 질문의 횟수를 계산하는 식이 된다.
• 갑자기 식에 $s_i$ 를 명시한 이유는 A가 뽑은 카드에 어떤 알파벳이 써 있었느냐에 따라 질문의 횟수가 달라질 수도 있기 때문이다. 즉 지금은 모든 카드가 뽑힐 확률이 동일하여 그런 일이 발생하지 않지만 카드가 뽑힐 확률이 달라질 수 있다는 것이다.

확률이 같지 않은 경우

• 이번에는 각 카드가 뽑힐 확률이 다음과 같다고 가정하자.

  

• 방금 전에 했던 게임과는 다르게 각 알파벳이 뽑힐 확률이 같지 않다. a 가 뽑힐 확률이 다른 알파벳에 비해 무려 3배나 높다.
• 이 경우에도 앞에서 했던 것 처럼 ‘반씩 쪼개기 전략’을 이용할 것인가?
• a 가 뽑힐 확률이 더 높다는 이 귀한 정보를 활용하면 이득을 볼 수 있다. a 가 나올 확률이 높으니, 다음과 같이 a 를 먼저 물어보고, 맞으면 좋고 틀리면 나머지 b,c,d 중에서 해결을 보는 전략을 택할 수 있다.
  • [전략 3]
    1. a 인지 물어본다. YES 면 a 이다.
    2. a 가 아니면 {b,c} 중에 있는지 물어본다.
    3. {b,c} 중에 있다면 b 인지 물어보고, 그렇지 않다면 정답은 d 이다.

• a의 확률이 가장 높으니 {a} 와 {b,c,d} 로 쪼갠 다음, {b,c,d} 는 홀수개라 2 개와 1 개로 쪼갠 것이다. 이 경우 질문 횟수의 기댓값을 계산하면 아래와 같다.

  

  \[E[X] = \sum^4_{i=1}p_ix_i = \frac{1}{2} \times 1 + \frac{1}{6} \times 3 + \frac{1}{6} \times 3 + \frac{1}{6} \times 2 = 1.8333\ldots\]
• 모든 카드가 뽑힐 확률이 전부 동일했던 상황과는 달리, 평균 2회보다 적은 질문으로 게임을 완료할 수 있게 되었다.
• 4개의 카드가 뽑힐 확률이 같지 않을 경우의 가장 효율적인 이 전략은 ‘반씩 쪼개기’이긴 하지만 정확히 말하면 ‘확률을 반씩 쪼개기’ 전략이다.
• [전략 2]에서와 같이 a,b,c,d 의 확률이 전부 동일한 경우에 {a,b} 와 {c,d} 로 쪼갰었던 이유는 {a,b} 중에 정답이 있을 확률과 {c,d} 중에 정답이 있을 확률이 같기 때문이다.
• 만약 이 상황에서 {a}, {b,c,d} 로 쪼갰었다면 이 전략은 도박성이 증가한다. 만약 정답이 a 일 경우엔 이득이지만 b,c,d 중에 있었을 경우에는 손해를 보게 된다. 그리고 실험을 통해 확인해봤듯이, 안전한 전략을 택하는 쪽이 질문 횟수의 기댓값이 작다.
• 그렇다면 왜 [전략 3]과 같이 a,b,c,d 의 확률이 다른 경우에는 반반 쪼개지 않고 {a}, {b,c,d} 로 쪼갰을까? 이 경우도 역시 {a} 중에 정답이 있을 확률과 {b,c,d} 중에 정답이 있을 확률이 같기 때문이다. {a,b}, {c,d} 로 쪼갠 경우에 비해 안전하다.
• 이제 각 알파벳이 나올 확률이 같지 않은 경우에 알파벳에 따라 질문의 횟수가 다를 수 있음을 이해할 수 있다. 이 예시만 봐도 정답이 a 였다면 1번의 질문으로 게임을 끝낼 수 있지만 b,c,d 였다면 그렇지 않다.

• 이제 위에서 질문의 횟수 $I(s_i)$ 를 구하는 식을 이용해보자. 먼저 정답이 a였을 경우에는 다음과 같다.

  \[I(a) = -\log_2\frac{1}{2} = 1\]
• 실제로 [전략 3]에 따라 정답이 a 일 경우 1번의 질문만 하면 정답을 알아낼 수 있었다.

• 그렇다면 b,c,d 인 경우는 어떻게 되는지 계산해보자.

  \[I(b) = I(c) = I(d) = -\log_2\frac{1}{6} = 2.5850\ldots\]
• 여기서는 실제 질문의 횟수와 일치하지 않는 값이 나왔다. 심지어 ‘횟수’라고 하기도 애매하게 자연수도 아닌 값이 나왔다.
• 그 이유는 바로 b,c,d 를 정확히 반으로 쪼갤 수 있는 방법이 존재하지 않기 때문이다.
• 로그를 이용한 계산은 모든 경우에 대해서 확률이 정확히 반으로 쪼개지도록 할 수 있다는 가정 하에 진행된다. 그래서 사실 위에서 제시한 [전략 3]은 이론적으로는 ‘가장’ 효율적인 전략이라고는 볼 수 없다.
• 그러나 [전략 3]의 경우 이론적인 최적점에 도달하는 것은 불가능한 상황이기 때문에, 가능한 전략 중에서는 그나마 최선이다.

• 그러면, 어차피 도달하는 것은 불가능하지만, 로그를 이용해 기댓값을 계산하면 이론적으로 가장 적은 질문 횟수의 기댓값을 구할 수 있지 않을까?

  

  \[E[X] = \sum^4_{i=1}p_ix_i = \frac{1}{2} \times 1 + \frac{1}{6} \times \log_2 6 + \frac{1}{6} \times \log_2 6 + \frac{1}{6} \times \log_2 6 = 1.7925\ldots\]
• 이 값은 카드의 개수 즉 카드가 뽑힐 확률에 따라서 도달할 수도, 도달하지 못할 수도 있는 값이다.
• 지금의 경우는 도달하지 못하는 값이고, 맨 처음 봤던 a,b,c,d 의 확률이 모두 동일한 경우는 도달 가능한 값이다.
• 하지만 이 값은 우리에게 의미가 있다. 무슨 수를 쓰건, 이렇게 구한 값보다 질문 횟수의 기댓값이 적은 전략은 존재하지 않는다.

• 이 값을 우리는 엔트로피(Entropy)라고 부르고, 식으로는 다음과 같이 계산한다.

  \[H = \sum_ip_iI(s_i) = -\sum_ip_i\log_2(p_i)\]

엔트로피와 불확실성

• 이제 각 카드의 확률 분포가 어떻게 되는지에 따라서 최소의 질문 횟수가 존재한다는 사실을 알게 되었으며, 구할 수도 있다.
• 그리고 엔트로피가 그 최소의 질문 횟수를 의미한다.
• 그러나 왜 a,b,c,d 의 확률이 동일할 때보다 a 의 확률이 더 높은 경우에 엔트로피가 더 작은 것일까?
• 이 질문을 해결하기 위해서는 먼저, 엔트로피가 갖는 의미에 대해서 더 생각해볼 필요가 있다.
  • 물리학에서는 엔트로피를 ‘무질서도’라고 한다.
  • 정보이론에서 엔트로피가 갖는 의미를 한 마디로 표현하자면, ‘불확실성(uncertainty)’이라고 볼 수 있다.
• 왜 엔트로피가 불확실성일까?
• 엔트로피가 크다는 것은 A 가 들고 있는 카드에 적힌 알파벳을 맞추기 위해 더 많은 질문을 필요로 한다는 것이고, 결국 A 가 들고 있는 카드의 알파벳을 알아내기가 더 힘들다는 뜻이다. 즉 불확실하다는 뜻이다.
• 그러면 왜 a,b,c,d 의 확률이 전부 동일한 경우가 특정 알파벳의 확률이 높은 경우보다 불확실성이 크다는 것일까?

• 극단적인 예를 들어보면 쉽다. a,b,c,d 의 확률이 다음과 같다고 가정하자.

  

• 위 예시에서는 질문을 하지 않고 그냥 a 라고 찍기만 해도 100번 중 97번꼴로 정답을 맞출 수 있다. A 가 들고 있는 카드가 a라는 사실은 ‘거의 확실’하기 때문이다.
• 하지만 a,b,c,d 의 확률이 전부 동일한 경우에는 우리는 그 카드에 어떤 알파벳이 적혀 있는지 조금의 확신도 할 수 없다.
• 그렇기 때문에 특정 알파벳의 확률이 커지는 순간, 우리는 그 정보를 활용하여 게임을 유리하게 이끌어나갈 수 있으며, 이는 게임의 불확실성, 즉 엔트로피를 감소시킨다.

• 위 예제에서 엔트로피를 계산하면 아래와 같다. 그리고 예상했던 대로 엔트로피 값이 매우 작다.

  \[H = -\sum_ip_i\log_2(p_i) = 0.97\log_2 0.97 + 3 \times 0.01\log_2 0.01 = 0.2149\]

정보량과 부호화(Coding)

• 엔트로피를 구성하는 $I(s_i)$ 에 조금 더 집중해보자.
• $I(s_i)$ 는 정답이 $s_i$ 인 경우 ‘반씩 쪼개기 전략’을 썼을 때 필요한 이상적인 최소 질문 횟수이다.
• 하지만 이 의미는 우리가 가정한 알파벳 맞추기 게임에서만 통용될 수 있고, 일반적인 정보 이론에서는 $I$ 를 정보량이라고 한다. 왜 정보량이라고 할까?
• $I$ 가 클수록 정보를 많이 담고 있음을 뜻한다. 이를 이해하기 위해 알파벳 맞추기 게임으로 돌아가보자.
• 카드에 적혀 있는 알파벳은 사실 그냥 보기에는 다 똑같아 보이지만, 어떤 전략을 쓰느냐에 따라 다른 의미를 갖는다.
• 스무고개의 예를 들어보자. ‘한국’이 정답이고 다음 질문들을 통해 한국이 정답임을 알아냈다고 가정하자.
  1. {한국, 중국, 일본} 중의 하나인가? YES
  2. 인구가 5억명 미만인가? YES
  3. 섬으로 구성된 나라인가? NO
• 이렇게 YES, YES, NO 의 패턴이 나오는 나라는 한국밖에 없으므로 우리는 답을 구할 수 있다.
• 우리는 한국이라는 단어를 다양한 말로 표현할 수 있다. ‘자본주의 국가이다’, ‘한국어를 사용하는 국가이다’, ‘UN 회원국이다’ 등등이다.
• 그러나 이 스무고개 게임에서만큼은 한국은 ‘한국, 중국, 일본중에 하나이며 인구가 5억명 미만이고, 섬나라가 아닌 나라’, 더 짧게 쓰면, ‘위 세 질문에 대해 YES, YES, NO 가 나오는 나라’로 정의할 수 있다.
• 즉, 각 질문에 대한 YES, NO의 패턴으로 한 대상을 정의할 수가 있게 되는 것이다.
• 이제 위에서의 [전략 3]을 보도록 하자. 스무고개에서 한국을 정의한 것 처럼 [전략 3]의 질문들에 대한 대답으로 a,b,c,d 를 정의하면 다음과 같다.
  • a: YES
  • b: NO, YES, YES
  • c: NO, YES, NO
  • d: NO, NO
• 각 알파벳을 알아내기 위해 필요한 질문의 개수가 달랐기 때문에, 정의의 길이가 다른 것도 당연하다. 여기서 정의의 길이가 바로 정보량이 된다.
• b,c 를 표현하기 위해서는 YES 또는 NO 가 3개씩 필요하지만 a 를 표현하기 위해서는 YES 또는 NO 가 1개만 있으면 된다. 즉, 질문의 개수가 많으면 그 대상이 지니는 정보량은 많다.
• 확률적인 관점에서 보더라도 마찬가지이다.
• $I(s_i) = − \log_2 p_i$ 이 식을 보면 확률이 작을수록 정보량이 크다는 사실을 알 수 있다.
• 사실 직관적으로 생각해봐도 매번 나오는 값들 보다는 어쩌다 한 번 나오는 값이 더 가치 있으며, 우리에게 더 큰 정보를 줄 수 있다.
• 무심하던 친구가 평소답지 않게 격식을 차리고 나에게 잘해준다면 뭔가 바라는 바가 있다는 메세지를 담고 있는 것과 비슷하다.
• 주의할 것은 정보량과 엔트로피는 다른 개념이다.
  • 엔트로피는 가능한 모든 경우에 해당하는 정보량들의 기댓값이다. 불확실성으로도 해석할 수 있다.
  • 발생 확률이 작은 사건의 정보량이 더 크다. 두 사건으로 구성된 경우 한 사건의 확률이 작으면 나머지 한 사건의 확률은 그만큼 크다. 즉 정보량이 작다.
  • 이렇게 정보량이 한 사건으로 몰려있을 경우 정보량의 기댓값인 엔트로피는 작게 된다.
  • 엔트로피를 불확실성으로 해석할 때, 두 사건의 확률이 정확히 반반으로 어떤 사건이 일어날지 모르겠는 상황의 불확실성이, 특정 사건이 일어날 확률이 너무 커서 예상이 가능한 상황의 불확실성보다 크다.
  • 따라서 모든 사건의 발생 확률이 동일한 상황은 모든 사건의 정보량이 같은 상황이며, 불확실성, 즉 엔트로피가 가장 높다.
• 위에서 a,b,c,d 를 YES 와 NO 의 집합으로 나타내는 과정이 바로 ‘부호화(Coding)’의 방식이다.
• 컴퓨터는 정보를 전송하기 위해서 숫자든 알파벳이든 그림이든 모든 신호를 0과 1의 조합으로 만들 필요가 있는데, a,b,c,d 를 YES 는 1로, NO 는 0으로 바꿔서 부호화 하면 다음과 같이 된다.
  • a: 1
  • b: 011
  • c: 010
  • d: 00
• 위에서 살펴본 바에 의하면, 특정 알파벳의 등장 확률이 작을수록 질문 횟수가 많이 필요하고, 이로 인해 정보량이 많아져서 부호화 결과 비트 수가 많아진다.
• 이 방식을 이용하여 부호화를 했을 경우, 자연스럽게 많이 등장하는 신호에는 적은 비트가 할당되고, 적게 등장하는 비트에는 많은 비트가 할당되어 전체 부호의 길이가 줄어들게 된다. 그렇기 때문에 매우 효율적인 코딩이 가능하다.
• 이 원리를 이용한 부호화에는 허프만 부호화(huffman coding)가 있다.
• 참고로, [전략 3]에서 직면했던 ‘알파벳들의 집합이 완벽하게 똑같이 쪼개지지 않음으로 인해 발생한 문제’를 해결하기 위해 실수 도메인으로 부호화를 하는 방식이 있는데, 이 방식을 산술 부호화(arithmetic coding)라고 하며, 이 방식을 통해 이상적으로 구한 Entropy 에 더 가깝게 부호화 하는 것이 가능하다.

엔트로피와 딥러닝

• 머신러닝/딥러닝은 대부분 정답 분포를 모사하는것이 목표가 되고, 얼마나 근접했는지를 수치화해서 피드백을 주는 방식으로 구성되어 있다.
• 즉, 어떤 문제를 풀고 싶고, 그 문제에는 정확히는 알 수 없으나 어떠한 미지의 진분포라는게 존재하며, 머신러닝/딥러닝 모델은 그 진분포를 모사해주는 확률 모델인 것이다.
• 따라서 딥러닝 모델은 실제 분포인 $P$ 를 모르고, 모델링하여 예측한 분포 $Q$ 를 $P$ 에 근사시키는 것이다.
• 이제 다시 한번 엔트로피를 떠올려보자.

  • 엔트로피(Entropy)는 확률 분포의 불확실성을 측정하는 지표다. 주어진 확률 분포 $P$ 에 대해 엔트로피 $H(P)$ 는 아래와 같이 정의한다.

    \[H(P) = - \sum_i p_i \log p_i\]
  • ​여기서 $p_i$ 는 확률 분포 $P$ 의 각 사건 $i$ 가 발생할 확률이다.

  • 엔트로피는 분포가 얼마나 고르게 퍼져 있는지도 알 수 있다. 분포가 퍼져 있어 불확실성이 클수록 엔트로피는 높아진다.

    

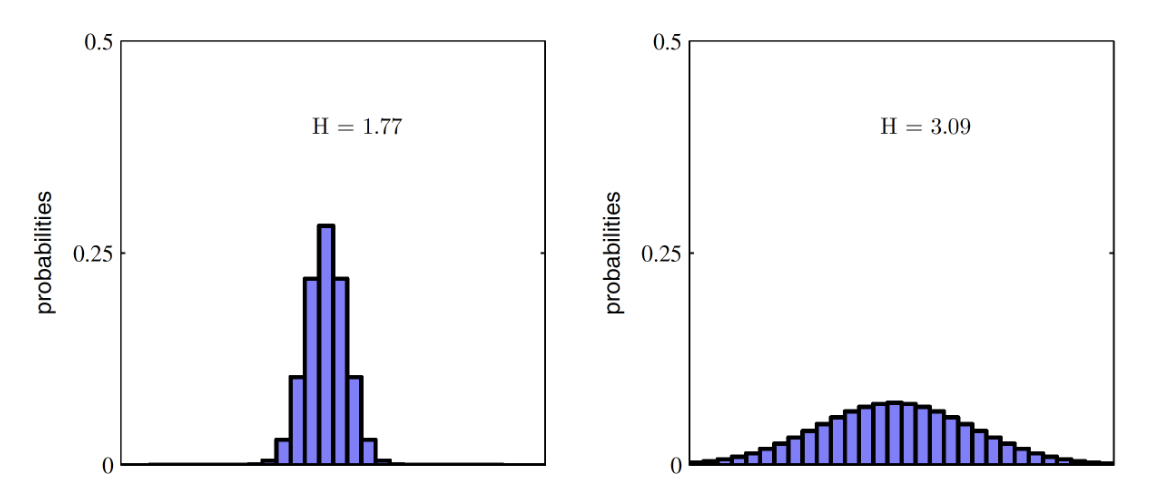
  • 이러한 엔트로피는 한 개의 분포에 대해 구할 수 있다. $p$ 분포면 $p$, $q$ 분포면 $q$ 에 대한 엔트로피, 이렇게 하나의 상황에 대한 엔트로피를 구하는 것이다.
  • 그리고 엔트로피는 정보량의 기대값도 나타내면서 동시에 어떤 분포를 표현하는데 필요한 최소 평균 자원(bit 등) 수다.
• 딥러닝에서는 두 분포를 다뤄야 한다. 여기서 두 개의 분포를 비교하는 크로스 엔트로피가 사용된다.
• 크로스 엔트로피는 확률분포로 된 어떤 문제 $P$ 에 확률분포로 된 어떤 전략 $Q$ 를 사용할 때의 질문횟수(정보량)의 기대값이다.

• 머신러닝/딥러닝을 통한 예측 모형에서 학습 데이터에서는 실제 분포인 $P$ 를 알 수 있기 때문에 크로스 엔트로피를 계산할 수 있다.

  \[H(P, Q) = -\sum^K_{k=1}P(y_k)\log_2Q(y_k)\]
• $P$ 는 실제 분포(또는 실제 레이블)이고, $Q$ 는 모델이 예측한 분포다. 위에서 $Q(y_k)$ 는 모델이 예측한 분포에서 클래스 $k$ 에 대한 확률이다.
• 이처럼 크로스 엔트로피는 두 개의 확률분포 $P$ 와 $Q$ 에 대해 정의된다. 이는 실제 분포 $P$ 에 대해 모델이 예측한 분포 $Q$ 의 정보량을 평균(기대값)낸 것으로 볼 수 있다.
• 즉, 실제 분포 $P$ 를 기준으로 $Q$ 가 예측한 사건의 정보량을 평가하는 것이다.
• $P$는 실제 데이터의 분포이고, $Q$는 모델의 예측 분포이기 때문에 $Q$ 가 $P$ 와 다를 수 있으며, 크로스 엔트로피는 이 차이를 반영하여 모델 예측의 효율성을 측정한다.
• 크로스 엔트로피 값이 작을수록 모델의 예측이 실제 분포에 더 잘 맞는다는 의미고, 크로스 엔트로피 값이 클수록 모델의 예측이 실제 분포와 더 많이 다르다는 것을 의미한다.

• 우리는 앞서 두 확률 분포의 차이를 다룰 때 확률분포 사이의 거리 중 KL-divergence 를 사용했다.

  \[\small{\mathbb{KL}(P\Vert Q) = \sum_{\mathbf{x} \in \mathcal{X}}P(\mathbf{x})\log\left(\frac{P(\mathbf{x})}{Q(\mathbf{x})}\right) \quad \mathbb{KL}(P\Vert Q) = \int_ \mathcal{X}P(\mathbf{x})\log\left(\frac{P(\mathbf{x})}{Q(\mathbf{x})}\right)}\text{d}\mathbf{x}\]

• 그리고 이 KL-div 는 기대값의 정의를 활용하여 두 개의 term 으로 분리할 수 있었다.

  \[\mathbb{KL}(P\Vert Q) = -\mathbb{E}_{\mathbf{x}\sim P(\mathbf{x})}[\log Q(\mathbf{x})] + \mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[\log P(\mathbf{x})]\]

• 이를 잘보면, KL-div 의 두 항은 각각 크로스 엔트로피, 엔트로피와 대응되는 것을 알 수 있다.

  \[\begin{aligned} \mathbb{KL}(P\Vert Q) &= -\mathbb{E}_{\mathbf{x}\sim P(\mathbf{x})}[\log Q(\mathbf{x})] + \mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[\log P(\mathbf{x})] \\ &= -\sum_{\mathbf{x} \in \mathcal{X}}P(\mathbf{x})\log Q(\mathbf{x}) + \sum_{\mathbf{x} \in \mathcal{X}}P(\mathbf{x})\log Q(\mathbf{x}) \\ &= H(P, Q) - H(P) \end{aligned}\]
• KL-div 의 중요한 성질은 항상 0 이상이라는 것이다. $\mathbb{KL}(P\Vert Q)=0$일 때는 오직 $P=Q$ 인 경우에만 성립한다. 이 성질은 Jensen’s inequality(젠센부등식)에 의해 증명된다.
• 따라서 항상 $\mathbb{KL}(P\Vert Q) \geq 0$ 이므로 크로스 엔트로피 $H(P, Q)$ 는 항상 엔트로피 $H(P)$ 보다 크거나 같다.
• 크로스 엔트로피는 분류 문제에서 loss function 으로 많이 쓰인다. 따라서 딥러닝 모델을 학습할 때 크로스 엔트로피를 최소화하는 방향으로 파라미터(가중치)들을 업데이트 한다.
• 크로스 엔트로피 $H(P, Q)$ 를 최소화한다는 것은 KL-div 를 최소화하는 것과 그 의미가 완전히 같다(equivalent).
• 왜냐하면 데이터 분포 $P(\mathbf{X})$ 는 학습 과정에서 바뀌지 않기 때문이다.
• 결과적으로 크로스 엔트로피의 최소화는 우리가 가지고 있는 데이터의 분포 $P(\mathbf{X})$ 와 모델이 추정한 데이터의 분포 $Q(X)$ 간의 차이를 최소화하는 것이다.
• 따라서 딥러닝에서 크로스 엔트로피를 최소화하는 것은 모델이 실제 데이터 분포 $P$ 를 잘 예측하도록 학습하는 과정이다. 이는 모델의 불확실성을 줄이고, 실제 분포와 더 일치하도록 만드는 것이 목표이다. 크로스 엔트로피를 최소화하면, 모델의 예측이 실제 데이터에 더 근접하게 되고, 결과적으로 불확실성이 제어된다.
• 이 크로스 엔트로피에 대해서는 Loss 카테고리에서 더 자세하게 다룰 것이다.

Reference

• https://hyeongminlee.github.io/post/prob001_information_theory/
• https://hyunw.kim/blog/2017/10/14/Entropy.html

맨 위로 이동 ↑