[AI Math] 8. Frequentist vs. Bayesian 딥러닝
앞서 MLE 를 통해 loss function 을 유도하고 경사하강법을 통해 파라미터를 최적화하는 방법을 살펴봤고, 베이즈 정리를 통해 사전확률을 사후확률로 지속적으로 업데이트 하는 방법도 살펴봤다. 딥러닝에서 두 개념이 어떻게 쓰이고, 어떤 차이가 있는 것일까?
빈도주의(Frequentist) vs. 베이지안(Bayesian)
- 통계학의 두 가지 주요 접근법인 Bayesian 확률과 Frequentist 확률은 머신러닝과 딥러닝에서 중요한 역할을 하므로 깊이 있는 이해가 필요하다.
- 확률은 불확실한 사건의 발생 가능성을 수치화한 것이다. 일상에서 “확률적으로”, “확률이 높다” 등의 표현을 자주 사용하지만, 확률을 해석하는 방식에는 크게 두 가지 접근법이 있다.
- 바로 Frequentist(빈도주의)와 Bayesian(베이지안) 접근법이다.
- “주사위를 던졌을 때 1이 나올 확률은 1/6이다.”라는 명제에 대해 각 접근은 다음과 같이 해석한다.
- Frequentist 해석: 주사위를 매우 많이 (이론적으로는 무한히) 던지면, 1 이 나오는 횟수의 비율이 1/6 에 수렴한다.
- Bayesian 해석: 주사위의 공정성에 대한 우리의 믿음을 바탕으로, 다음 던지기에서 1 이 나올 것이라고 믿는 정도가 1/6 이다.
- 이처럼 두 접근법에는 확률을 해석하는 차이가 존재하며, 이는 통계적 추론과 의사결정 과정에도 큰 영향을 미친다.
- 머신러닝과 딥러닝에서는 문제의 특성과 목적에 따라 두 접근법을 적절히 선택하거나 결합하여 사용한다.
- 결론적으로 Frequentist 딥러닝과 Bayesian 딥러닝의 구분은 모델 parameter 에 대한 해석과 불확실성 처리 방식에 관한 구분이다.
Frequentist 확률
- 사건의 발생 빈도에 기반한 객관적인 확률 해석이다.
- 주요 특징은 아래와 같다.
- 반복 가능한 실험이나 관찰을 통해 확률을 정의한다.
- 장기적인 상대 빈도를 확률로 간주한다.
- 객관적이고 데이터 중심적인 접근 방식이다.
- 고정된 모수(parameter)를 가정한다.
- 동전 던지기를 예로 들어보자. 동전을 2~3 번 던지면 앞면이 나올 확률 0.5 이 아닐 수 있다.
- 그러나 우리가 앞면이 나올 확률이 0.5 라고 말할 수 있는 것은 “동전을 무한히 많이 던지면, 앞면이 나오는 비율이 0.5 에 수렴한다”라는 빈도주의적 관점에서 말하는 것이다.
- 주요 이론은 아래와 같다.
- 대수의 법칙(Law of Large Numbers)
- 표본의 크기가 커질수록 표본 평균이 모집단의 실제 평균에 수렴한다는 이론
- 실험을 충분히 많이 반복하면 관찰된 빈도가 실제 확률에 가까워진다.
- 중심극한정리(Central Limit Theorem)
- 독립적이고 동일한 분포를 가진 확률변수들의 평균은 표본의 크기가 커질수록 정규분포에 가까워진다.
- 많은 통계적 추론의 기초가 되며, 정규분포의 가정을 정당화한다.
- 최대우도추정(Maximum Likelihood Estimation, MLE)
- 관측된 데이터를 가장 잘 설명하는 모수(parameter)를 추정하는 방법이다.
- 가능도 함수를 최대화하는 모수 값을 찾는다.
- 대수의 법칙(Law of Large Numbers)
- 장점
- 객관성: 데이터에만 기반하여 추론하므로 주관적 판단의 영향이 적다.
- 계산의 단순성: 많은 경우에 계산이 상대적으로 간단하다.
- 대규모 데이터에서의 효율성: 대량의 데이터를 다룰 때 계산적으로 효율적일 수 있다.
- 널리 사용되는 방법론: 많은 통계적 기법과 소프트웨어가 빈도주의 접근법을 기반으로 한다.
- 단점
- 사전 정보 활용의 한계: 이전 지식이나 전문가의 의견을 명시적으로 모델에 포함시키기 어렵다.
- 소규모 데이터셋에서의 한계: 데이터가 부족한 경우 신뢰할 만한 추론이 어렵다.
- 점 추정의 한계: 불확실성을 완전히 표현하기 어려울 수 있다.
- 반복 가능한 실험 가정: 모든 상황이 반복 가능한 실험으로 모델링되기 어려운 경우가 있다.
Bayesian 확률
- 주관적 믿음의 정도를 나타내는 확률 해석이다.
- 주요 특징은 아래와 같다.
- 사전 지식이나 믿음을 바탕으로 초기 확률(사전 확률)을 설정한다.
- 새로운 증거나 데이터를 통해 확률을 갱신(사후 확률)한다.
- 주관적이며 지식이나 믿음의 정도를 반영한다.
- 불확실성을 다루는 데 유용하다.
- 마찬가지로 동전 던지기에서, 앞면이 나올 확률 0.5 라는 것을 베이지안 확률 관점 측면에서 해석하면 “이 동전이 공정하다는 우리의 현재 믿음 상태”를 의미한다.
- 주요 이론은 아래와 같다.
- 사전 확률(Prior Probability, $P(\theta)$)
- 가능도 (Likelihood, $P(\mathcal{D}\vert \theta)$)
- 사후 확률 (Posterior Probability, $P(\theta \vert \mathcal{D})$)
- 베이즈 정리(Bayes’ Theorem)
- 사전확률, 가능도, evidence 를 이용해서 사후확률을 계산할 수 있다. 앞 포스트를 참고하자.
- 베이지안 추론(Bayesian Inference)
- 과정: 사전 분포 → 데이터 관찰 → 가능도 계산 → 사후 분포 도출
- 점 추정 대신 확률 분포로 결과를 표현하여 불확실성을 명시적으로 나타낸다.
- 장점
- 사전 지식의 통합: 도메인 전문가의 지식이나 이전 연구 결과를 모델에 명시적으로 포함할 수 있다.
- 불확실성의 자연스러운 표현: 파라미터의 전체 확률 분포를 제공하여 불확실성을 더 잘 표현한다.
- 점진적 학습: 새로운 데이터가 도착할 때마다 모델을 자연스럽게 업데이트할 수 있다.
- 소규모 데이터셋에서의 강점: 사전 정보를 활용하여 데이터가 적은 상황에서도 의미 있는 추론이 가능하다.
- 단점
- 계산 복잡성: 복잡한 모델의 경우 사후 분포 계산이 어려울 수 있다.
- 사전 분포 선택의 주관성: 부적절한 사전 분포 선택이 결과를 왜곡할 수 있다.
- 해석의 어려움: 비전문가에게 베이지안 결과의 해석이 직관적이지 않을 수 있다.
어떤 접근법?
- Bayesian 접근법과 Frequentist 접근법은 각각 고유한 장단점을 가지고 있으며, 상황에 따라 적절한 방법을 선택하는 것이 중요하다.
- 많은 경우, 두 접근법을 보완적으로 사용하는 것이 가장 효과적일 수 있다.
- Bayesian 방법은 불확실성을 명시적으로 다루고, 사전 지식을 통합하며, 점진적 학습에 유리하다. 따라서 데이터가 제한적이거나, 도메인 지식이 중요하거나, 불확실성의 정확한 추정이 필요한 경우에 특히 유용하다.
- Frequentist 방법은 계산이 간단하고, 대규모 데이터셋에서 효율적이며, 널리 사용되는 많은 통계적 도구와 호환된다. 따라서 대량의 데이터가 있거나, 계산 효율성이 중요하거나, 표준화된 보고가 필요한 경우에 적합할 수 있다.
- 머신러닝과 딥러닝 분야에서는 두 접근법의 장점을 결합한 하이브리드 방법론도 점차 발전하고 있다.
- 예를 들어, SGD 등의 기법은 Bayesian 추론의 장점을 유지하면서도 대규모 데이터셋에 적용 가능한 효율성을 제공한다.
- 요약하자면 특정 문제와 상황에 가장 적합한 접근법을 선택하거나 두 접근법을 적절히 조합하는 것이 최선의 결과를 얻는 데 중요하다.
- 두 접근법에 대한 깊이 있는 이해는 데이터 과학자와 머신러닝 실무자들에게 더 풍부한 도구 세트를 제공하며, 다양한 상황에서 더 나은 의사결정을 할 수 있게 해준다.
빈도주의 딥러닝 vs. 베이지안 딥러닝
- 빈도주의 딥러닝
- 모델의 파라미터를 단일 값으로 추정하고, 데이터를 통해 최적의 파라미터를 찾는 방법.
- 대부분의 딥러닝 모델은 빈도주의적 접근을 따른다.
- 베이지안 딥러닝
- 모델의 파라미터를 확률 분포로 추정하고, 사전 확률(prior)을 설정한 후 데이터에 의해 사후 확률(posterior)을 업데이트하는 방법
- 불확실성을 명시적으로 다루며, 파라미터와 예측의 불확실성을 계산한다.
주요 비교
- 아래는 빈도주의 딥러닝과 베이지안 딥러닝을 주요 개념마다 비교해본 것이다.
- 이러한 비교는 공부한 것들을 헷갈리지 않고 명확히 방향을 잡기 위함이며 너무 구속되지는 말자.
-
파라미터
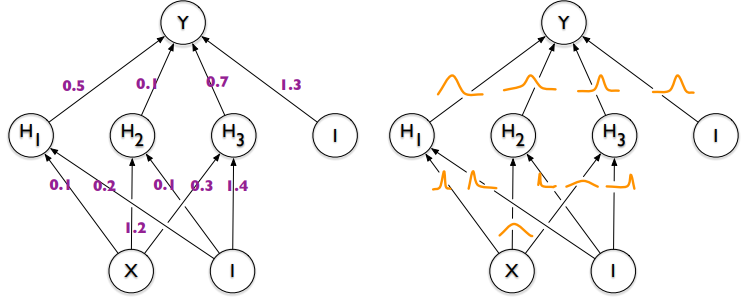
- 빈도주의 딥러닝
- 파라미터는 단일 값으로 표현되며, 학습을 통해 고정된 값을 갖게 된다.
- 가중치 $W$ 와 편향 $b$ 는 고정된 값으로 최적화된다.
- 베이지안 딥러닝
- 파라미터는 확률 분포로 표현된다.
- 파라미터 $W$ 와 $b$ 는 사전 확률 분포를 가지며, 데이터에 의해 사후 확률로 업데이트된다.
- 빈도주의 딥러닝
- 최적화 방식
- 빈도주의 딥러닝
- 주로 경사 하강법(Gradient Descent)과 그 변형을 사용하여 손실 함수를 최소화한다.
- 여기서 최적화는 단일 최적 파라미터 값을 찾는 데 초점을 맞춘다.
- 베이지안 딥러닝
- 변분 추론(Variational Inference)이나 MCMC(Markov Chain Monte Carlo)와 같은 방법을 사용하여 파라미터의 사후 분포를 근사한다.
- 최적화는 파라미터 분포를 추정하는 데 초점을 둔다.
- 빈도주의 딥러닝
- 학습 방법
- 빈도주의 딥러닝
- 데이터에 대해 손실 함수(MSE, Cross-Entropy 등)를 최소화하여 파라미터를 학습한다.
- 일반적으로 점 추정(point estimation)을 사용하며, 학습 과정은 하나의 고정된 모델을 생성한다.
- 베이지안 딥러닝
- 사전 확률을 기반으로 데이터에 의한 사후 확률을 계산하여 파라미터를 학습한다.
- 학습 과정에서 모델의 불확실성을 반영하며, 여러 분포 샘플을 통해 다양한 모델을 생성할 수 있다.
- 빈도주의 딥러닝
- 불확실성 처리
- 빈도주의 딥러닝
- 불확실성을 명시적으로 다루지 않는다.
- 모델은 단일 예측값을 반환하며, 불확실성에 대한 정보는 제공되지 않는다.
- 머신러닝에서 불확실성을 처리하려면 부트스트래핑과 같은 별도의 방법이 필요하다.
- 베이지안 딥러닝
- 불확실성을 명시적으로 처리한다.
- 예측값의 분포를 제공하여 모델이 얼마나 확신하는지를 평가할 수 있다.
- 예측의 신뢰도를 추정하고, 모델 불확실성과 데이터 불확실성을 모두 고려한다.
- 빈도주의 딥러닝
- 모델 복잡성 및 일반화
- 빈도주의 딥러닝
- 모델 복잡성은 주로 하이퍼 파라미터 튜닝과 Regularization 기법으로 제어한다.
- 일반화를 위해 Regularization, Dropout, Early Stopping 등의 방법을 사용한다.
- 베이지안 딥러닝
- 사전 확률의 설정을 통해 모델 복잡성을 자연스럽게 제어할 수 있다.
- 베이지안 접근은 과적합을 방지하고, 데이터가 부족한 상황에서도 일반화 성능을 유지하는 데 유리하다.
- 빈도주의 딥러닝
- 계산 복잡도 및 구현
- 빈도주의 딥러닝
- 상대적으로 계산이 효율적이고, GPU 를 활용한 대규모 병렬화가 용이하다.
- 일반적인 딥러닝 라이브러리와 도구들을 사용하여 쉽게 구현할 수 있다.
- 베이지안 딥러닝
- 계산이 복잡하고, 특히 사후 분포를 계산하는 데 높은 계산 비용이 요구된다.
- 변분 추론이나 MCMC 와 같은 근사 기법이 필요하며, 구현이 더 복잡하다.
- 빈도주의 딥러닝
- 적용 분야
- 빈도주의 딥러닝
- 이미지 분류, 자연어 처리, 음성 인식, 추천 시스템 등 대규모 데이터와 빠른 예측이 필요한 응용에 널리 사용된다.
- 대부분의 상업적 및 산업적 응용에서 사용된다.
- 베이지안 딥러닝
- 의료 진단, 자율주행, 금융 예측 등 불확실성을 명시적으로 고려해야 하는 분야에서 유용하다.
- 데이터가 부족하거나, 사전 지식을 잘 활용해야 하는 상황에서도 효과적이다.
- 빈도주의 딥러닝
- MLE 사용 방식
- 빈도주의 딥러닝
- 최대우도추정(MLE, Maximum Likelihood Estimation)은 빈도주의 딥러닝의 핵심이다.
- MLE 를 사용해서 모델 파라미터 $\theta$ 를 학습 데이터 $\mathbf{X}$ 에 대해 가능도(likelihood, $P(\mathbf{X} \vert \theta)$) 를 최대화하는 방식으로 최적화한다.
- 손실 함수는 데이터에 대한 negative log-likelihood 를 최소화하는 방식으로 설정된다.
- 회귀 모델에서는 평균 제곱 오차(MSE)를 최소화하거나, 분류 문제에서는 크로스 엔트로피 손실을 최소화한다.
- 베이지안 딥러닝
- 베이지안 딥러닝에서도 MLE 를 사용할 수 있지만, 이는 모델 파라미터를 단일 값으로 추정하는 데 국한된다.
- MLE 는 베이지안 방법의 사후 확률을 근사할 때 참고로 사용될 수 있지만, 베이지안 접근에서는 MLE 가 아닌 사후 확률을 최적화하는 데 중점을 둔다.
- MLE 는 베이지안 프레임워크에서 사전 확률(prior)을 무시한 최대가능도 추정값으로 사용될 수 있지만, 일반적으로는 베이지안 추론에서의 근사 기법 중 하나로만 활용된다.
- 빈도주의 딥러닝
- 베이즈 정리 사용 방식
- 빈도주의 딥러닝
- 베이즈 정리는 빈도주의 딥러닝에서 명시적으로 사용되지 않는다.
- 사전 정보를 활용하지 않고 주로 현재 데이터에만 의존한다.
- 빈도주의적 접근에서는 파라미터 추정을 위한 확률적 추론을 하지 않기 때문에, 베이즈 정리가 학습 과정에 직접적으로 적용되지 않는다.
- 즉 빈도주의적 접근에서 파라미터 자체를 확률변수가 아닌 데이터에 대한 단일 추정값으로 최적화되며, 모델은 확률적 관점보다는 함수 최적화 문제로 접근한다.
- 여기서 헷갈릴 수 있는데, MLE 에는 확률적 개념이 들어가 있지만 주어진 $\theta$ 에서 데이터 $\mathbf{X}$ 가 관측될 확률을 구하는 것이기 때문에, $\theta$ 는 고정된 값이자 데이터가 관측될 가능성을 최대화하는 단일 값으로 추정되는 것이다.
- 베이지안 딥러닝
- 베이즈 정리는 베이지안 딥러닝의 핵심이다.
- 사전 확률 $P(\theta)$ 와 데이터로부터 계산된 가능도 $P(\mathbf{X} \vert \theta)$ 를 결합하여 사후 확률 $P(\theta \vert \mathbf{X})$ 을 계산한다.
- 베이지안 딥러닝에서는 사후 확률 $P(\theta \vert \mathbf{X})$ 를 근사하기 위해 변분 추론 또는 MCMC 와 같은 방법을 사용하며, 이 사후 확률을 통해 모델 파라미터의 불확실성을 표현하고 업데이트한다.
- 모델 학습 과정에서 각 학습 스텝 마다 사후 확률을 업데이트하고, 이로부터 새로운 예측값을 도출한다.
- 빈도주의 딥러닝
- Gradient
- 빈도주의 딥러닝
- 손실 함수(loss function)를 최소화하여 모델 파라미터를 최적화하기 위해 사용된다.
- 이 손실 함수는 데이터와 모델 간의 차이를 측정하며, 경사 하강법은 이 손실 함수의 기울기(gradient)를 따라 내려가면서 파라미터를 업데이트한다.
- 주로 경사 하강법(Gradient Descent), 확률적 경사 하강법(Stochastic Gradient Descent, SGD), 모멘텀(Momentum), Adam 등의 최적화 알고리즘을 사용하여 손실 함수를 최소화한다.
- 베이지안 딥러닝
- 파라미터의 사후 확률 분포를 최적화하는데 사용된다.
- 베이지안 딥러닝에서 gradient 는 주로 변분 추론(Variational Inference)이나 하이브리드 MCMC 방법을 통해 사후 분포의 근사치를 찾기 위해 사용된다.
- 변분 추론(Variational Inference): 변분 손실 함수(변분 바운드, ELBO)를 최적화하기 위해 경사 하강법을 사용한다. 이 과정에서 파라미터 분포를 근사하는 데 사용되는 변분 파라미터를 최적화한다.
- 즉 두 접근법 모두 gradient 를 사용하여 최적화한다. 빈도주의 딥러닝에서는 손실 함수를 최소화하기 위해, 베이지안 딥러닝에서는 사후 확률 분포를 최적화하거나 근사하기 위해 사용된다.
- 빈도주의 딥러닝
- 확률분포 사이의 거리
- 주로 베이지안 딥러닝에서 사용된다. 그러나 특정 상황에서는 빈도주의 딥러닝에서도 사용된다.
- 빈도주의 딥러닝
- KL-divergence
- 빈도주의 딥러닝에서 KL-divergence 가 사용될 수 있지만, 이는 주로 특정 응용에서 확률적 출력 분포를 비교할 때 사용된다.
- 예를 들어, 정보 이론적 정규화(Information-theoretic regularization)나 distillation 에서 두 모델의 출력 확률 분포 간의 차이를 측정하기 위해 사용된다.
- GAN(Generative Adversarial Networks)에서 두 분포(실제 데이터 분포와 생성된 데이터 분포)를 비교하는 데 사용될 수 있다. 다만, GAN 에서는 주로 JSD 를 통해 두 분포 간의 유사성을 측정한다.
- JSD
- GAN 의 학습에서 중요한 역할을 한다.
- JSD 는 실제 데이터 분포와 생성된 데이터 분포 사이의 유사성을 평가하는 데 사용된다.
- GAN 의 목적은 이 JSD 를 최소화하여 생성된 데이터가 실제 데이터와 최대한 유사하도록 만드는 것이다.
- KL-divergence
- 베이지안 딥러닝
- KL-divergence
- 변분 추론(Variational Inference)에서 사후 확률 분포를 근사할 때 KL-div 가 주요한 역할을 한다.
- 변분 추론의 목적은 실제 사후 확률 분포 $P(\theta \vert \mathbf{X})$ 와 이를 근사하는 분포 $Q(\theta)$ 간의 KL-div 를 최소화하는 것이다.
- 이 KL-divergence 는 ELBO 를 유도하는 과정에서 사용된다.
- ELBO 는 근사 분포가 실제 사후 분포와 얼마나 가까운지를 측정하며, 이를 통해 베이지안 딥러닝에서 파라미터의 불확실성을 더 잘 반영할 수 있다.
- JSD
- JSD는 두 확률 분포 간의 유사성을 측정할 때 사용될 수 있다.
- 베이지안 방법을 사용하여 모델의 예측 불확실성을 평가할 때, 서로 다른 예측 분포들 간의 차이를 평가하는 데 JSD 가 사용될 수 있다.
- KL-divergence
- 대표 모델
- 빈도주의 딥러닝
- Convolutional Neural Networks (CNNs)
- Recurrent Neural Networks (RNNs)
- Transformers
- GANs (Generative Adversarial Networks)
- 베이지안 딥러닝
- Bayesian Neural Networks (BNNs)
- Variational Autoencoders (VAEs)
- Bayesian Convolutional Neural Networks
- Bayesian RNNs
- 빈도주의 딥러닝
결론
- 머신 러닝 정의는, 관측된 Data(=Training Sample) 로부터 Model 을 설계하는 것이다. 여기서의 Model 이 바로 확률 분포가 된다.
- MLE 는 확률 분포에서 어떠한 Parameter $\theta$ 일 때, Data $\mathbf{X}$ 가 가장 잘 설명 될까? 이다. 따라서 “주어진 Data를 보고” 최적의 $\theta$ 를 찾아 내야 하는 것이다.
- 이것이 MLE 이며 관점이며 딥러닝의 학습법이다. 이 때 미분이 0이 되는 값을 찾기가 어려우므로 Gradient Descent 를 사용하는 것이다.
- 물론 Prior 를 고려해서 최적의 Parameter 를 찾는 Maximum a Posterior(MAP) 방법도 있다. 그러나 대부분의 경우 Likelihood 를 고려하면 잘 해결이 된다.
- 결국 모든 머신러닝, 딥러닝은 확률 모델의 파라미터를 찾는 것으로 귀결된다.
- 파라미터를 추정할 때 대부분 Maximum Likelihood Estimation 방법을 사용한다.
- 또한 파라미터 역시 Random 하다는(확률변수) 것으로 보는 Bayesian View 의 Approach 도 존재한다.
- 물론 파라미터를 추정하지 않고 답을 찾는 Non-parametric 방법들도 존재한다.

댓글 남기기