[AI Math] 7. 베이즈 통계학

앞 포스트에서 베이즈 정리 수식의 notation 인 Posterior, Prior, Likelihood 에 대해 알아보았다. 이제 이 베이즈정리가 딥러닝에서 어떻게 사용될 수 있을지 좀 더 알아보자.

베이즈 통계학

• 앞 포스트에서 공부한 통계학은 빈도주의 또는 frequentest statistics 에 해당하는 내용들이다.
• 여기서는 베이즈 통계학이 어떤 식으로 모델의 모수를 추정하고, 모델을 추정할 때 사용되는 베이즈 정리에 대해서 이해해보자.
• 베이즈 정리는 데이터가 새로 추가될 때 정보를 업데이트하는 방식에 대해서 이론적 기반을 소개하는 내용이다.
  • 베이즈 정리는 데이터라는 조건이 주어졌을 때의 조건부확률을 구하는 공식이다.
  • 베이즈 정리를 쓰면 데이터가 주어지기 전의 사전확률값이 데이터가 주어지면서 어떻게 변하는지 계산할 수 있다.
  • 따라서 데이터가 주어지기 전에 이미 어느 정도 확률값을 예측하고 있을 때 이를 새로 수집한 데이터와 합쳐서 최종 결과에 반영할 수 있다.
  • 이러한 이유로 데이터의 개수가 부족한 경우 아주 유용하다. 데이터를 매일 추가적으로 얻는 상황에서도 매일 전체 데이터를 대상으로 새로 분석작업을 할 필요없이 어제 분석결과에 오늘 들어온 데이터를 합쳐서 업데이트만 하면 되므로 유용하게 활용할 수 있다.
• 오늘날 기계학습을 사용하는 예측 모형의 방법론에서 굉장히 많이 사용되는 철학이기도 하고 방법론이기도 하다.
• 베이즈 통계학을 통해 기계학습에서 데이터가 새로 추가될 때마다 정보를 업데이트하는 베이즈 정리의 내용들을 이해할 수 있고, 실제로 데이터를 분석할 때 어떤 식으로 이용할 수 있는지를 이해할 수 있다.

조건부확률

• 베이즈 통계학을 이해하기 위해서는 조건부확률의 개념을 이해해야 한다.

  \[P(A \cap B) = P(B)P(A\vert B)\]
• 조건부확률을 계산하는 방법은 두 개의 사건 $A, B$ 가 있을 때, 두 사건의 교집합이 일어날 확률을 조건부에 들어가는 사건의 확률로 나눠주면 계산할 수 있다.
• 위 수식은 나누지 않고 곱하는 형태로 표현한 것이다. 어떤 사건 $B$ 가 일어난다는 조건부 상황에서 조건부확률 $P(A\vert B)$ 를 계산하려면, 그 조건부확률에다가 조건부에 들어가는 사건 $B$ 의 확률 $P(B)$ 를 곱했을 때 교집합에 해당하는 확률을 계산할 수 있다는 정의에서 출발한다.
• 즉 위 정의가 나타내는 것은 조건부확률($P(A \vert B)$)이라는 것은 특정 사건 $B$ 가 일어난 상황을 분모로 넣고, 그 사건 $B$ 와 동시에 사건 $A$ 가 발생할 확률인 교집합의 사건을 분자로 넣었을 때 조건부확률을 계산할 수 있다.
• 이러한 조건부확률의 개념을 이용해서 베이즈 정리를 유추할 수 있다.

• 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려준다. 아래의 수식을 보자.

  \[{\color{red}{P(B\vert A)}} = \frac{P(A \cap B)}{P(A)} = {\color{red}{P(B)}}\frac{P(A\vert B)}{P(A)}\]
• 사건 $A$ 가 주어졌을 때 $B$ 가 일어날 확률, 즉 $P(B\vert A)$ 인 확률을 계산할 때는 위 정의와 마찬가지로 $A, B$ 가 동시에 일어날 확률인 교집합의 확률을 조건부에 들어가는 사건 $A$ 의 확률로 나눴을 때 구할 수 있다.
• 이 때 $A, B$ 가 동시에 일어날 교집합의 사건을 $B$ 가 주어져있는 경우의 조건부확률로 표시할 수 있다. 그렇게 하면 위 수식 중 두번째 수식과 같은 베이즈 정리를 유도할 수 있다.
• 따라서 $A$ 가 조건부로 주어져있을 때 $B$ 의 사건을 구할 확률은, $B$ 가 조건부로 주어졌을 때 $A$ 가 일어날 확률($P(A\vert B)$)에다가 $P(A)$ 와 $P(B)$ 를 각각 나누고 곱해주는 형태로 계산할 수 있다.
• 수식에서 빨간색으로 표시한 부분에 집중해보자.
  • $B$ 가 일어날 확률($P(B)$)이 주어져 있을 때, $B$ 를 조건부로 $A$ 가 일어날 확률 $P(A\vert B)$ 와 $A$ 자체가 일어날 확률 $P(A)$ 를 각각 분자 분모로 해서 곱한다.
  • 이를 통해 $A$ 라는 정보가 추가적으로 주어졌을 때, $B$ 라는 사건이 일어날 확률을 계산할 수 있게 된다.
• 다시 말해서, $A$ 라는 정보가 새로 주어졌을 때 $P(B)$ 로부터 $P(B \vert A)$ 를 계산하는 것이다.
• 이렇게 $A$ 가 조건으로 주어졌을 때 $B$ 라는 사건이 일어날 확률을 계산하는 방법을 제공해주는 것이 바로 베이즈 정리의 공식이 의미하는 것이다.

베이즈 정리

• 예제를 통해 베이즈 정리를 이해해보자. 그전에 베이즈 정리에서 사용하는 용어를 구분해야 한다.

  \[P(\theta\vert\mathcal{D}) = P(\theta)\frac{P(\mathcal{D}\vert\theta)}{P(\mathcal{D})}\]
• $\mathcal{D}$ 는 관찰하는 데이터이다.
• $\theta$ 는 어떤 가정이나 모델링하는 이벤트 또는 모델에서 계산하고 싶은 모수(parameter)다.
• 위 수식의 왼쪽 식 $P(\theta\vert\mathcal{D})$ 를 사후확률(posterior) 이라고 한다.
  • 이것은 데이터를 관찰했을 때 이 파라미터가 성립할 확률을 의미한다.
  • 왜 사후확률이냐면, 데이터를 관찰한 이후에 측정하는 확률이기 때문이다.
• $P(\theta)$ 는 사전확률(prior) 이라고 한다.
  • 사전확률은 데이터가 주어지지 않은 상황에서 $\theta$ 에 대한 모델링을 하기 이전에 사전에 주어진 확률로 이해할 수 있다.
  • 사전확률은 데이터를 분석하기 전에 어떤 모수나 가정 등 이런 모델링하고자 하는 타겟에 대해서 사전에 미리 가정을 깔아두고, 모델링 하기 이전에 설정하는 확률분포이다.
• 이렇게 사전확률을 설정하고 모델링하여 데이터를 관찰한 후 나오는 사후확률을 업데이트할 때는 베이즈 정리 공식을 이용해서 업데이트 할 수 있다.
• 베이즈 정리에 사용되는 수식을 잘 보면, 가능도(likelihood, $P(\mathcal{D}\vert\theta)$) 와 Evidence($P(\mathcal{D})$) 가 있다.
  • 가능도(likelihood)는 현재 주어진 파라미터, 모수 또는 가정에서 이 데이터가 관찰될 확률을 계산하는 것이다. 이 가능도는 분자에 들어가게 된다.
  • Evidence 의 역할은 데이터 전체의 분포에 해당한다. 따라서 어떠한 데이터들을 관찰할 때, 그 데이터 자체의 분포를 Evidence 라고 부른다.
• 데이터를 통해서 모델을 학습하거나 예측할 때, $\theta$ 가 주어진 상황에서 데이터가 관찰될 확률을 의미하는 가능도와 관찰하는 데이터 자체의 분포 evidence 를 통해서 사전확률을 사후확률로 업데이트할 수 있게 되는 것이다.

• 이처럼 베이즈 정리의 데이터와 파라미터 또는 가정의 관계를 알면, 굉장히 많은 데이터 분석에 활용할 수 있다.

  베이즈 정리 예제

  • COVID-99 이라는 새로운 바이러스가 있다. 이 바이러스의 발병률은 10% 로 알려져있다. COVID-99 에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 1% 라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-99 에 감염되었을 확률은?
  • 이 문제는 사전확률과 Recall(민감도), False Alarm(오탐율)을 가지고 Precision(정밀도)를 계산하는 문제다.
  • 발병률은 사전확률로 사용할 수 있다. 따라서 실제 데이터를 관측하기 이전의 발병률인 10% 을 사전확률로 설정할 수 있다.
  • 문제에서 주어진 검진 테스트의 효과는 바이러스에 실제로 감염되었을 때 검진될 확률이 99% 이고 실제로 걸리지 않았을 때 오검진될 확률이 1% 라고 했다. 이 때 실제로 병에 걸리는 경우를 $\theta$ 라고 표시하고, 테스트 하여 검진된 것으로 관측이 된 것을 $\mathcal{D}$ 라고 표시할 수 있다.
  • 즉, $\theta$ 를 COVID-99 발병 사건으로 정의(관찰 불가)하고, $\mathcal{D}$ 를 테스트 결과라고 정의(관찰 가능)한다.
  • $\theta$ 가 조건부로 주어졌을 때 검진될 확률을 $P(\mathcal{D}\vert\theta)$ 로 표시할 수 있다. 이 값이 0.99 가 된다.
  • 또한 실제로 걸리지 않았을 때 $\mathcal{D}$ 가 관찰될 확률(검진될 확률)을 $P(\mathcal{D}\vert\neg\theta)$ 로 표시할 수 있다.

  • 위 두 가지 확률 모두 likelihood 가 된다.

    \[\begin{aligned} P(\theta) = 0.1 \quad &P(\mathcal{D}\vert\theta) = 0.99 \\ &P(\mathcal{D}\vert\neg\theta) = 0.01 \end{aligned}\]
  • 이제 사전확률과 가능도가 주어져있기 때문에 사후확률을 계산하기 위해서 Evidence 를 계산해야 한다.

  • Evidence 는 가지고 있는 가능도를 가지고 계산할 수 있다. Marginal distribution(주변확률분포)을 계산하는 방법과 조건부확률의 정의를 이용하면 Evidence 를 계산하는 공식을 도출할 수 있다.

    \[\begin{aligned} P(A, B) &= P(A \cap B) = P(B)P(A\vert B) \\P(\mathcal{D})&= \sum_\theta P(\mathcal{D}, \theta)\\ &= \sum_\theta P(\theta)P(\mathcal{D}\vert\theta) \end{aligned}\]

  • 사전확률인 $\theta$ 가 일어날 확률은 0.1 이기 때문에 $\neg\theta$ 의 확률($\theta$ 가 아닌 확률)은 0.9 가 된다. 이 두 확률을 가능도에 각각 곱해서 더해주게 되면 Evidence 의 확률을 계산할 수 있게 된다.

    \[\begin{aligned} P(\mathcal{D}) = \sum_\theta P(\theta)P(\mathcal{D}\vert\theta) &= \underset{P(\mathcal{D}\vert\theta)}{0.99} \times \underset{P(\theta)}{0.1} + \underset{P(\mathcal{D}\vert\neg\theta)}{0.01} \times \underset{P(\neg\theta)}{0.9} \\ &= 0.108 \end{aligned}\]
  • 만약 $\theta$ 를 부정했을 때 $\mathcal{D}$ 가 일어날 확률, 즉 $P(\mathcal{D}\vert\neg\theta)$ 를 모른다면 이 문제는 풀기 어렵다. 즉, 두 가능도 중 하나라도 모르게 되면 이 문제를 풀기 어려워진다.

  • 이제 사전확률과 가능도(likelihood)와 Evidence 를 가지고 사후확률을 계산해볼 수 있다.

    \[P(\theta\vert\mathcal{D}) = P(\theta)\frac{P(\mathcal{D}\vert\theta)}{P(\mathcal{D})} = 0.1 \times \frac{0.99}{0.108} \approx 0.916\]
  • 0.916 은 질병에 걸렸다고 검진결과가 나왔을 때($\mathcal{D}$) 실제로 감염($\theta$)되었을 확률, 즉 사후확률을 뜻한다.
  • 이렇게 높은 확률이 나온 이유는, 실제로 걸렸을 때 검진될 확률(가능도)이 99%이고 실제로 걸리지 않았을 때 오검진될 확률이 1% 로 낮기 때문이다.

  • 만약 오검진률(1종 오류, $P(\mathcal{D}\vert\neg\theta)$)이 1% 가 아니라 10% 가 되면 아래와 같이 값이 달라진다.

    \[\small P(\mathcal{D}) = \sum_\theta P(\theta)P(\mathcal{D}\vert\theta) = \underset{P(\mathcal{D}\vert\theta)}{0.99} \times \underset{P(\theta)}{0.1} + \underset{P(\mathcal{D}\vert\neg\theta)}{\color{red}{0.1}} \times \underset{P(\neg\theta)}{0.9} = 0.189 \\ P(\theta\vert\mathcal{D}) = P(\theta)\frac{P(\mathcal{D}\vert\theta)}{P(\mathcal{D})} = 0.1 \times \frac{0.99}{\color{red}{0.189}} \approx \color{red}{0.524}\]
  • 따라서 베이즈 정리를 통해, 오검진 확률$(P(\mathcal{D}\vert\neg\theta))$, 즉 오탐률이 오르면 테스트의 정밀도(Precision)가 떨어짐을 관찰할 수 있다.
  • 즉 베이즈 정리와 데이터를 통해서 가설의 검정이나 가설의 신뢰도를 측정할 수 있다.

조건부확률의 시각화

• 오탐률과 정밀도의 관계를 잘 알아보기 위해서 시각화를 해볼 수 있다.

• 이를 confusion matrix 라고 한다.

  

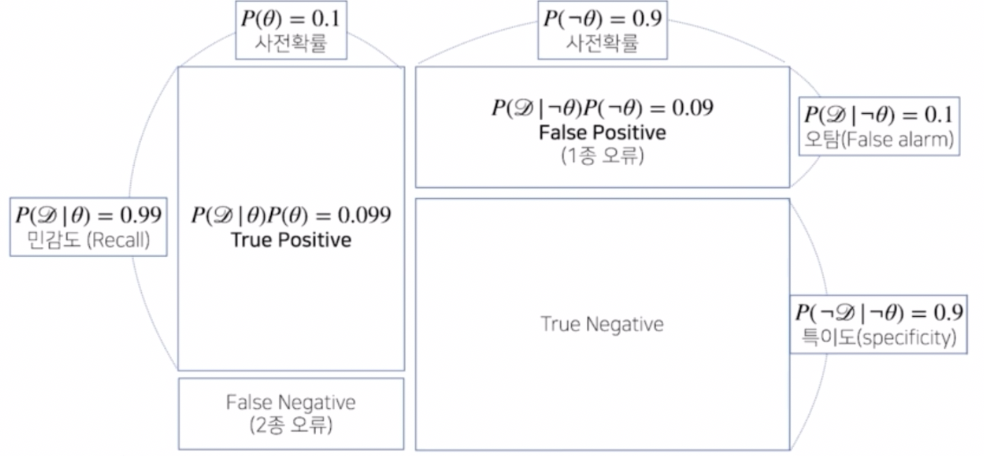
• 조건부 확률로 계산되는 경우는 총 4 가지 경우다.
  • 양성이 나왔을 때 진짜 양성인 경우
  • 음성이 나왔을 때 진짜 음성인 경우
  • 양성이 나왔을 때 실제 양성이 아니라 음성인 경우
  • 음성이 나왔을 때 실제 음성이 아니라 양성인 경우
• 첫번째로 양성이 나왔을 때 실제 그 질병으로 관찰될 확률을 true positive 라고 부른다. 또한 음성이 나왔을 때 실제 그 질병에 걸리지 않은 경우를 true negative 라고 분류한다.
• 반대로 양성이 나왔을 때 실제로 병에 걸리지 않은 경우 false positive 라고 부르고, 이 경우를 1종 오류라고 부른다. 이것은 앞에서 관찰된 false alarm 과 관계가 있다.
• 또한 음성이 나왔는데 실제로 병에 걸린 경우 false negative 라고 하고 2종 오류라 부르게 된다.
• 데이터 분석의 성격에 따라서 1종 오류를 줄이는 게 중요할지 2종 오류를 줄이는 게 중요할지 민감하게 된다. 가령 암 환자를 진단내릴 때 조직 검사의 효과가 1종 오류, 2종 오류 어디에 초점을 두냐에 따라 달라진다.
• 1종 오류의 효과도 막심하지만 2종 오류의 경우, ‘질병이 아니다’라고 판정 내렸을 때 실제로 질병인 경우를 말하는 오류이기 때문에 false negative 는 실제 의료 문제에서 많이 신경쓰는 metric 이다.
• 의료 문제의 경우 false positive 는 상대적으로는 2종 오류에 비해 심각도가 떨어질 수 있기 때문에 false alarm 은 조금 희생하더라도 false negative 를 줄이는 형식으로 테스트의 설계를 한다.
• 위 그림을 보면 질병에 실제로 걸렸을 때 데이터가 관찰될 확률이 민감도(Recall)에 해당하는 값이다. 이 때 해당 영역의 가로축에 해당하는 지표가 사전확률이다.
• 사전확률은 실제 질병의 발생률이고, 이는 데이터 분석을 하기 전에 사전에 주어진 정보이다.
• 사전확률 없이는 베이즈 통계학에서 분석을 하기 어렵다. 만약 사전확률을 모르는 경우에는 임의로 사전확률을 설정하는 경우도 있겠으나, 이 경우에는 베이즈 통계학에서 분석의 신뢰도가 떨어질 수 있다.

• 위 문제에서 사전확률이 0.1 이고, 오탐지율이 0.1 이었을 때, 1종 오류(false positive)와 true positive 를 가지고 정밀도(precision)을 계산하면 0.524 가 나왔다.

  

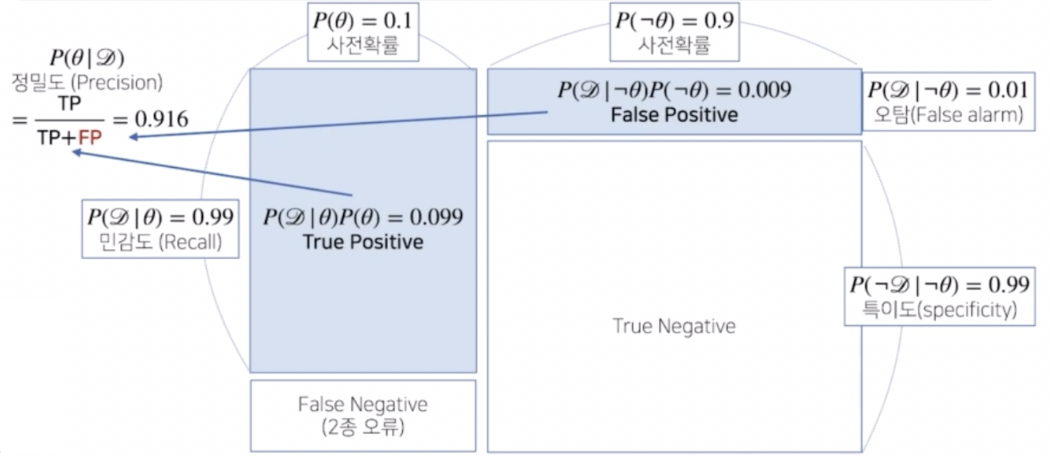
• 만약 오탐지율 즉 false alarm 을 줄이게 되면, 정밀도를 구하는 공식에서 분모에 들어가는 false positive(FP) term 이 줄어들기 때문에 정밀도가 높아지게 된다.
• 이처럼 정밀도를 계산할 때는 false negative 나 true negative 로 계산하지 않고 true positive 와 false positive 로 계산한다. 따라서 위 그림에서 볼 수 있듯 오탐지율과 민감도가 반영되어 정밀도를 계산할 수 있게 된다.

베이즈 정리를 통한 정보의 갱신

• 베이즈 정리를 이용했을 때 이러한 정밀도(precision)만 계산하는 것이 아니라, 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산하는 것이 가능하다.
• 즉, 데이터가 새로 들어왔을 때 정보를 갱신하는 것을 베이즈 정리를 사용해서 가능하다는 것이다.

• 이 프로세스에 대해 좀 더 알아보자.

  

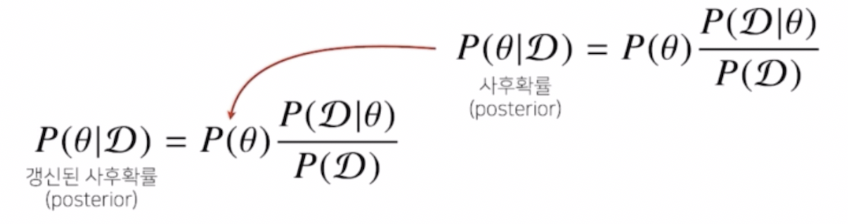
• 위 식처럼 사전확률과 주어진 데이터를 가지고 한 번 계산한 사후확률을, 그 다음 계산에서 사전확률에 대입하고 그 전에 사용했던 가능도와 evidence 를 다시 한번 활용해서 업데이트된 사후확률을 계산하는데 사용할 수 있다.
• 데이터를 새로 관찰할 때마다 사후확률을 계산하는 이 프로세스를 반복하여, 가정이나 모델의 파라미터 $\theta$ 를 점점 업데이트하는 형태로 모델링을 하고 이 모델의 정확도 또는 예측력을 향상시킬 수 있다.
• 이 방식을 통해서 앞서 COVID-99 판정을 받은 사람이 두 번째 검진을 받았을 때도 양성이 나왔을 때 진짜 COVID-99 에 걸렸을 확률을 구해보자.
• 오탐지율이 0.1 라서 이 검진의 신뢰도가 0.524 밖에 안나온 상황에서 과연 양성이 두 번 연속으로 나오게 됐을 때 이 사람이 COVID-99 에 걸렸을 확률은 얼마나 될까?

• 이 검진의 신뢰도가 0.524 기 때문에 두번째 판정도 믿을 수 없다고 생각할 수 있다.

  \[P(\mathcal{D}\vert\theta) = 0.99, \quad P(\mathcal{D}\vert\neg\theta) = 0.1 \\ P(\theta\vert\mathcal{D}) = P(\theta)\frac{P(\mathcal{D}\vert\theta)}{P(\mathcal{D})} = 0.1 \times \frac{0.99}{0.189} \approx 0.524\]
• 이번에는 앞에서 계산한 사후확률 0.524 를 0.1 의 사전확률 대신에 대입하면 된다.

• 그렇게 되면 evidence 를 갱신해서 계산할 수 있다. 가능도는 그대로 두되 앞에서 계산한 사후확률을 가지고 사전확률에 대입하여 갱신하는 것이다.

  \[\underset{\tiny\text{갱신된 Evidence}}{P(\mathcal{D}^\ast)} = 0.99 \times {\color{red}{0.524}} + 0.1 \times {\color{red}{0.476}} \approx 0.566\]

• 이 Evidence 를 통해서 새롭게 갱신된 사후확률(Posterior)을 계산할 수 있다.

  \[P(\theta\vert\mathcal{D}^\ast) = {\color{red}{0.524}} \times \frac{0.99}{\color{red}{0.566}} \approx 0.917\]
• 91.7% 라는 높은 정밀도가 나오게 된다. 세번째 검사에도 양성이 나오면 정밀도가 99.1% 까지 갱신된다.
• 즉 베이즈 정리, 베이즈 통계학의 굉장히 큰 장점은 데이터가 새로 들어올 때마다 이런식으로 사후확률을 업데이트할 수 있고, 그럴 때마다 좀 더 업데이트된 정보를 가지고 모델링을 할 수가 있기 때문에 실제로 굉장히 유효한 테스트를 할 수가 있다는 점이다.

조건부확률, 인과관계

• 조건부 확률의 개념을 이용한 베이즈 정리를 통해 데이터가 새롭게 들어올 때마다 정보를 업데이트하는 방식으로 통계적 해석을 하거나 통계적 검정을 하거나 또는 통계 모델에서 모수를 추정할 때 좀 더 정확하게 예측 모델을 만드는 방법을 봤다.
• 한 가지 조심해야 할 점은, 조건부확률은 유용한 통계적 해석을 제공해주지만 이를 가지고 인과관계(causality)를 추론할 때 함부로 사용해서는 안된다.
• 실제 두 사건 $A, B$ 가 있을 때 $A$ 가 $B$ 의 원인인가를 판단할 때 보통 조건부확률로 많이 해석하는데, 조건부확률을 가지고 계산하는 것도 가능은 하지만 그것은 실제로 $A$ 가 $B$ 의 원인일 때 그렇게 해석할 수 있는 것이다.
• 인과관계를 추론할 때는 조건부확률을 만능으로 사용해서는 안된다. 상당히 많은 데이터 분석 문제에서 이런 오류를 많이 저지른다. 조건부확률을 가지고 인과관계를 해석하는 것은 주의해야한다.
• 또한 조건부확률만 가지고 인과관계를 추론하는 것이 불가능하기 때문에 데이터가 아무리 많아져도 해결되는 문제는 아니다.

• 인과관계를 예측모형에서 고려해야 하는 이유는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요하기 때문이다.

  

• 조건부확률 기반의 예측모형을 인과관계를 고려하지 않고 만들게 되면, 실제 테스트 시에는 높은 예측 정확도를 가지는 모델을 얻을 수 있다. 오늘날 기계학습 모형들은 많이 발달하여 테스트 데이터에서 높은 예측 정확도를 가지도록 학습시키는 것이 가능한 상황이다.
• 문제는 이런 상황에서 데이터 분포가 바뀌게 되는 경우다. 즉 데이터가 유입되는 상황이 바뀌거나 또는 새로운 정책을 도입, 새로운 치료법을 도입했을 때 유입되는 데이터 분포가 변하는 경우가 굉장히 많다.
• 이런 경우에는 조건부확률만 가지고 예측모형을 만들었을 때 시나리오에 따라서 예측 확률이 크게 변할 수 있다.
• 만약 데이터 분포의 변화에 강건한 예측모형을 만들고 싶을 때는 인과관계를 기반해서 예측모형을 만드는 것이 필요하다.
• 위 그림을 보자.
  • 조건부확률만 가지고 예측모형을 만들었을 때는 어떤 시나리오에서는 정확도가 유지되지만, 어떤 시나리오에서는 정확도가 낮게 떨어지는 경우가 많다.
  • 그러나 인과관계를 도입하게 되면 예측 정확도를 조건부확률 기반 예측모형만큼 가져오지는 않는다. 즉 인과관계만 고려해서 예측모형을 만들게 되면 높은 예측 정확도를 담보하기는 어렵다.
  • 다만 데이터 분포의 변화에 강건한 예측모형을 만드는 것은 가능하기 때문에 여러 시나리오가 발생했을 때 예측 정확도가 크게 변하지 않는 상황을 보장하는 것이 가능하다.

• 인과관계를 실제로 알아내기 위해서는 조건부확률만 가지고 계산해서는 안되고, 두 개의 변수가 있을 때 이 두 개의 변수에 동시에 영향을 주는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다.

  

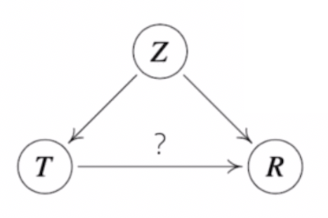
• 위 그림에서 $Z$ 에 해당하는 중첩요인의 효과를 제거하지 않으면 가짜 연관성(spurious correlation)이 나온다.
• 즉 원인과 결과에 해당하는 인과관계, 위 그림에서 ? 에 해당하는 관계를 계산할 때는 $Z$ 가 $T, R$ 둘 다 영향을 주기 때문에, $Z$ 의 효과를 제거하지 않으면 가짜 연관성이 계산될 수 있다.
• $Z$ 가 예측모형에서 데이터 분포의 변화가 생겼을 때 예측 모델의 정확도를 떨어뜨리는 가장 큰 요인이 될 수가 있다.
• 간단한 예제를 들어보자.
  • $R$ 을 지능지수라고 하고 $T$ 를 키라고 해보자.
  • 키에 따라서 지능지수를 분석한다고 했을 때 일반적인 상식에 따르면 키와 지능지수는 관계가 없을 것 같지만, 데이터 분석을 해보면 키가 클수록 지능지수가 높다는 분석이 나오게 된다.
  • 이는 바로 연령이라는 중첩효과를 제거하지 않았기 때문이다.
  • 당연히 나이가 들면 들수록 키가 크다. 나이에 따른 키의 효과를 제거하지 않게 되면 보통 어린아이가 어른보다 지능지수가 낮기 때문에 연령이 높을수록 지능지수가 높게 나오게 된다.
  • 따라서 연령이 중첩요인이 되어서 마치 키가 크면 지능지수가 높다는 식의 데이터 분석을 하게 된다.
• 이처럼 중첩요인의 효과를 제거하지 않고 변수들 간의 예측모형을 분석하게 되면 잘못된 가짜연관성을 관찰할 확률이 높다.
• 이런 중첩요인을 제거하는 방법을 알아야만 인과관계를 통해서 좀 더 정확한 예측 모델의 구조를 알 수 있게 되고, 이를 통해서 좀 더 강건한 예측 모형을 만드는 것이 가능하다.

인과관계 추론 예제

• 신장 결석에 따라서 치료법을 선택하는 예제다. 치료법은 $a, b$ 가 있고 각각 개복수술, 주사를 통해 치료하는 시술이라 하자.
• 이제 어떤 치료법이 신장결석이 발생했을 때 완치율이 더 높은지 분석해보자. 즉 치료법에 따른 완치율의 원인과 결과를 분석하고 싶은 것이다.

• 이 때 각각의 치료법에 따른 통계치는 아래와 같다.

  

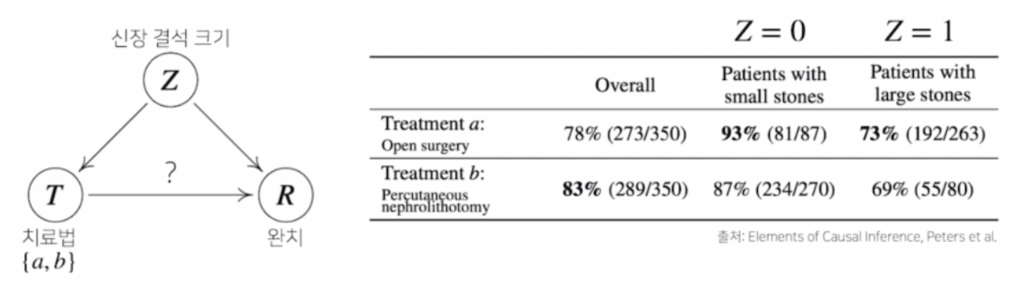
• 위 통계치는 어떤 환자군이 작은 신장결석 크기를 가지고 있을 때와 큰 신장결석 크기를 가지고 있을 때 치료법에 따라 완치율을 기록한 것이다.
• 잘 보면 전체적으로 봤을 때 83% 의 치료법 $b$ 가 좀 더 높은 완치율을 가지고 있는 것으로 보인다.
• 그러나 각각의 환자군에 따라서 보면, 신장결석 크기가 작을 때도 $a$ 가 완치율이 높고 신장결석 크기가 클 때도 $a$ 가 완치율이 더 높다.
• 전체적으로 볼 땐 $b$ 가 완치율이 높은데, 각각의 환자군에서 봤을 때는 $a$ 가 더 높은 것이다. 어떻게 이런 결과가 나왔을까?
• 이는 Simpson’s paradox 라고 부르는 통계적 역설 문제다.
• 이 역설 문제를 해결하기 위해서는 그냥 조건부확률만 가지고, 즉 $a$ 를 조건부로 했을 때의 완치율 또는 $b$ 를 조건부로 했을 때의 완치율만 가지고는 안된다.

• 신장결석 크기($Z$)에 따른 $a, b$ 의 중첩효과를 제거해야만 실제 정확한 치료법에 따른 완치율을 계산하는 것이 가능하다.

  

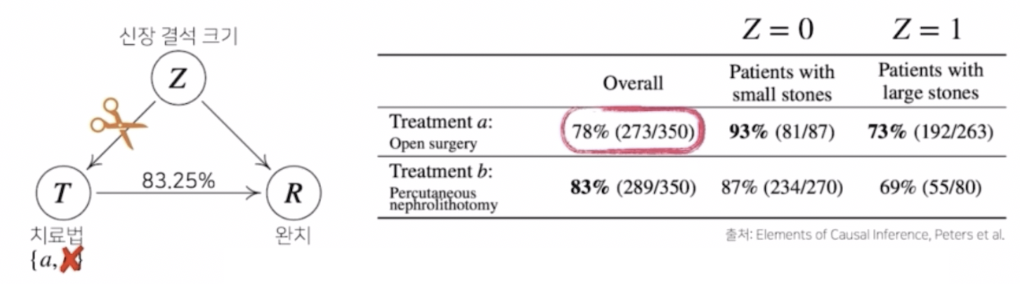
• 이를 위해 신장결석 크기에 따른 치료법의 선택을 제거하는 것으로 중첩효과를 제거해 볼 수 있다.
• 모든 환자가 신장결석 크기에 상관없이 치료법 $a$ 를 선택했을 때의 완치율과, 거꾸로 치료법 $b$ 를 선택했을 때 완치율을 계산하는 것이다.

• 따라서 베이즈 정리를 통해 계산하는 것과는 다른 방식의 계산 공식이 필요하다.

  \[\begin{aligned} P^{\mathfrak{C}_{\color{red}a}}(R=1) &= \sum_{z \in \{0,1\}}P^\mathfrak{C}(R=1\vert T={\color{red}a},Z=z)P^\mathfrak{C}(Z=z) \\ &= \frac{81}{87} \times \frac{(87+270)}{700} + \frac{192}{263} \times \frac{(263+80)}{700} \approx 0.8325 \end{aligned}\]
• 위 공식처럼 $\text{do}(T=a)$ 라는 조정(intervention)효과를 통해 중첩효과를 가지는 변수 $Z$의 효과를 제거하는 방식으로 계산할 수 있다.
• 본래 조건부로 계산했을 때 78% 로 나왔던 치료법 $a$의 완치율이 83.25% 라는 높은 완치율로 계산된다.
• 모든 환자가 신장결석 크기와 상관없이 치료법 $b$ 를 선택하는 경우에도 조건부확률에서 계산했을 때는 83% 가 나오지만 중첩효과를 제거했을 때는 77.89% 효과를 얻게 된다.
• 다시 말해서, 치료법 $a, b$ 에 따른 인과관계 분석을 했을 때 조건부확률을 계산하는 것과 달리 실제로 중첩효과를 제거한 인과관계로 계산한 확률이기 때문에 훨씬 더 믿을만한 결과로 해석할 수 있다.
• 이렇게 인과관계를 고려해서 중첩효과를 제거한 데이터 분석을 했을 때 좀 더 안정적인 분석이나 예측 모형 설계가 가능하다.
• 이 예제를 통해서 단순히 조건부확률로 데이터 분석을 하는 것은 위험한 것임을 알 수 있다.
• 데이터에서 추론할 수 있는 사실관계, 데이터가 생성되는 관계, 도메인 지식을 활용해서 변수들끼리의 관계를 실제로 파악을 해야만 인과관계 추론이 가능하다.
• 따라서 데이터분석을 할 때 인과관계도 고려하는 것이 중요하다. 즉 강건한 데이터 모형을 만들 때 인과관계가 중요하다는 사실을 이해하자.

맨 위로 이동 ↑