[AI Math] 6. 베이즈 정리
Bayes’ rule (베이즈 정리)
- Bayes Rule 은 Bayesian Deep Learning 에서 가장 기본이 되는 개념이다.
- 어떤 값을 예측하기 위한 수단으로서 딥러닝 이전부터 굉장히 많이 쓰여 왔던 방식이기 때문에 Bayesian Deep Learning 이 아니더라도 알아두면 굉장히 유용한 정리다.
- 그만큼 유명한 정리고, 딥러닝에서 loss function 을 정의하는데 중요한 역할을 하는 MLE(Maximum Likelihood Estimation)와 그 학습방법에도 이 베이즈 정리가 많이 녹아있다.
- 베이즈 정리를 아주 잘 정리해놓은 글을 토대로, 이 포스트를 작성하면서 베이즈 정리 수식의 notation 에 대해 이해해보자.
Bayesian Deep Learning
- Deep Learning 을 비롯한 대부분의 머신러닝 알고리즘들은 주어진 문제를 해결하기 위해 필요한 다양한 파라미터들을 주어진 데이터를 통해 학습한다. 그래서 머신러닝은 최적의 파라미터를 찾는 일이라고 볼 수 있다.
- 이 파라미터를 보는 관점에는 크게 두 가지가 존재한다.
- Frequentest View : Model 의 파라미터들을 Fixed Value 로 취급하여 데이터로부터 그 값을 구해낸다.
- Bayesian View : Model 의 파라미터들을 각각 하나의 Random Variable 로 취급하여 그 Distribution 을 구해 낸다.
- 예를 들어 전국 대학생의 평균 연령을 알기 위해 전국적으로 100명의 대학생을 Sampling 하여 평균 연령을 구했고, 그 결과 23살이라는 값이 나왔다고 해보자.
- Frequentest View 에서는 “전국 대학생의 평균 연령을 23살이라고 하면 되겠군!“이라고 대답할 것이고, Bayesian View 에서는 “전국 대학생의 평균 연령이 23살일 확률이 높겠지만, 아닐 확률도 존재 한다. 그 확률 분포는 다음과 같다.“라는 이야기를 할 것이다.
- 이처럼 Bayesian View 에서는 우리가 구하고자 하는 값을 정확히 구하지 않고, 어떤 값일 확률이 어느 정도인지에 대한 확률 분포로 대답한다.
- 우리가 일반적으로 사용하는 Deep Learning 은 Frequentest View 다. Model 의 Parameter 들이 하나의 값으로 정해져 있고, 그에 따라 output 도 하나의 값으로 출력하기 때문이다.
- 그러나 Bayesian Deep Learning 은 Bayesian View 에 해당한다. 즉 정답 뿐만 아니라 정답이 어느 값일 확률이 높은지에 대한 distribution 을 출력한다.
- 이렇게 distribution 을 출력할 경우 얻을 수 있는 이득 중의 하나는 Uncertainty 를 알 수 있다는 점이다.
- Model 이 특정 값을 예측함에 있어서 그 대답이 얼마나 확실한지, 믿을만 한지를 알게 되면 여러 분야에 활용 가능하다.
- 특히 자율주행과 같이 안전이 우선시되는 분야에서는 인공지능이 스스로 내린 결정이 정말 믿을만 한지에 대한 정보를 알 필요가 있다.
농어 vs. 연어
-
많은 Pattern Recognition 수업에서는 Bayes Rule 을 설명하기 위해 농어(Sea Bass)와 연어(Salmon)를 구분하는 문제를 예로 많이 든다.
농어(a) 와 연어(b) - 우리가 할 일은 간단하다. 낚시를 통해 건져 올린 물고기를 보고 농어인지 연어인지 맞추기만 하면 되는 것이다.
- 이 때 우리가 물고기를 분류하는 기준은 피부의 밝기이다. 즉 물고기의 피부 밝기 정보를 이용해서 그 물고기가 농어인지 연어인지 맞추는 Task 를 진행한다.
수식적 표현
- 물고기의 피부 밝기 정보가 주어졌을 때 그 물고기가 농어인지 연어인지 맞추기 위해서 이 문제를 수학적으로 모델링 할 것이다.
- 먼저 우리에게 주어진 물고기의 피부 색의 밝기를 $x$ 라고 하자. 물고기의 종류를 $w$라고 하고, 그 물고기가 농어일 사건을 $w=w_1$, 그리고 연어일 사건을 $w=w_2$ 라고 하자.
-
즉 물고기의 피부 밝기가 0.5일 때, 그 물고기가 농어일 확률은 다음과 같은 조건부 확률로 표현할 수 있다.
$$P(w=w_1 \vert x=0.5) = P(w_1 \vert x=0.5)$$ - 만약 모든 $x$ 에 대해서 $P(w_1 \vert x)$ 와 $P(w_2 \vert x)$ 의 값이 주어진다면, 어떤 $x$ 가 주어지더라도 아래와 같은 방법으로 농어인지 연어인지를 구분할 수 있다.
- $P(w_1 \vert x) > P(w_2 \vert x)$ 라면 농어로 분류한다.
- $P(w_1 \vert x) < P(w_2 \vert x)$ 라면 연어로 분류한다.
- 이는 단순히 농어일 확률이 높으면 농어, 연어일 확률이 높으면 연어로 분류하는 전략이다.
- 그렇다면 물고기 분류 문제는 $P(w_i \vert x)$, 즉 피부 밝기 $x$ 가 주어졌을 때 그 물고기가 class $w_i$ 에 속할 확률만 구하면 풀 수 있다.
- 여기서 우리가 구해야 할 확률 $P(w_i \vert x)$ 를 사후확률(Posterior)이라고 부른다.
관찰하기
- 그렇다면 Posterior, 즉 $P(w_i \vert x)$ 를 어떻게 구할 수 있을까? 우리는 전체 농어와 연어를 모르기 때문에 구할 수 없다.
- 하지만 $P(x \vert w_i)$ 는 구할 수 있다. $P(x \vert w_i)$ 는 물고기의 종류가 $w_i$ 일 경우 피부 밝기가 $x$ 일 확률이라고 해석할 수 있다.
- 이 때 $x$ 는 continuous 하기 때문에 확률 보다는 확률밀도 가 맞는 표현이다.
- 즉 $P(x \vert w_1)$ 는 농어의 피부 밝기 분포이고, $P(x \vert w_2)$ 는 연어의 피부 밝기 분포라고 할 수 있다.
- 그렇다면 $P(x \vert w_i)$ 를 어떻게 구할 수 있을까? 바로 관찰 이다.
- 농어를 충분히 잡아서 어떤 피부 밝기를 가진 농어들이 많은지에 대한 분포를 구하는 것이다. 연어도 마찬가지다.
- 이렇게 관찰을 통해서 얻은 확률분포 $P(x \vert w_i)$ 를 가능도(Likelihood) 라고 부른다.
-
열심히 물고기들을 관찰하고 피부 밝기를 측정한 결과, 아래와 같은 분포를 얻을 수 있다.
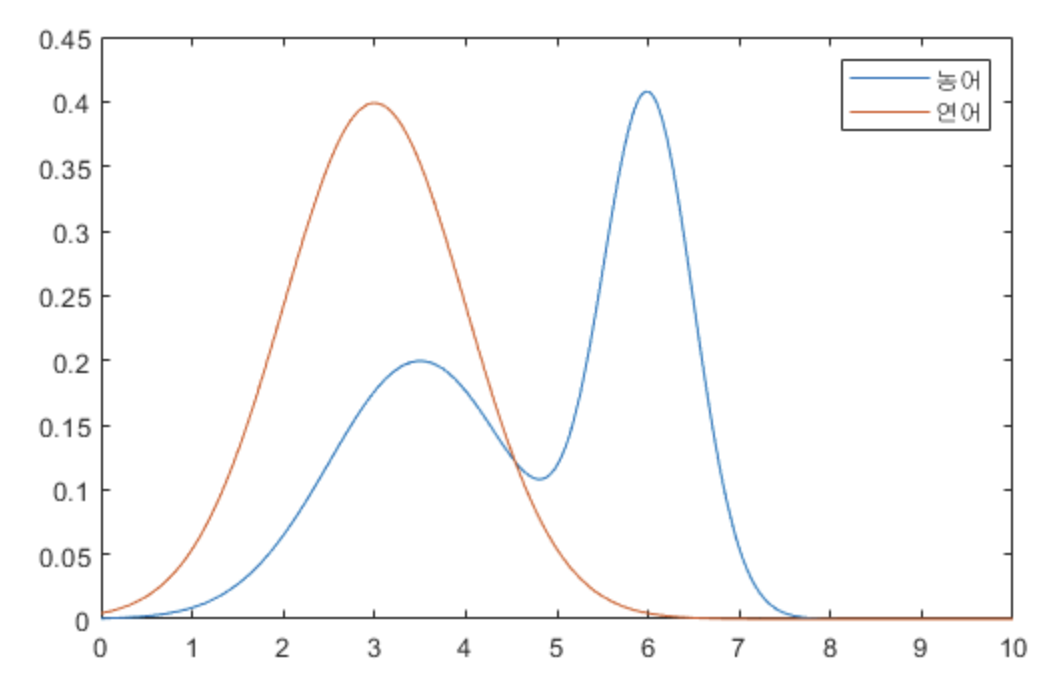농어와 연어의 피부 밝기 분포 - 분포를 해석해보면, 농어의 피부 밝기가 전체적으로 연어에 비해 밝다는 사실을 알 수 있다.
- 이렇게 우리는 Likelihood 를 얻었다. 그리고 Likelihood 의 그래프를 보고 이런 생각이 들 수 있다. 그냥 지금 가지고 있는 Likelihood 분포에서 두 곡선이 만나는 지점의 $x$ 를 기준으로 $x$ 가 그 값보다 작으면 연어, 크면 농어로 분류하면 되지 않을까?
- 즉 Posterior 까지 구할 필요 없이 Likelihood 만 가지고도 분류할 수 있지 않을까 생각할 수 있다. 결론은 그렇지 않다.
- 왜냐면 Likelihood 에는 애초에 연어와 농어가 잡힐 확률이 반영돼 있지 않기 때문이다.
- 즉 Likelihood 만으로 분류를 하기 위해서는 농어와 연어가 똑같은 비율로 바다에 살고 있다는 가정이 있어야 한다.
- 예를 들어 $x=5$ 가 나왔다고 하자. 그래프 대로라면 우리는 이 물고기를 농어로 분류해야 한다. 그런데 만약 농어가 많이 희귀해서 농어가 잡힐 확률 자체가 1%도 안된다면, 아무리 $x=5$ 라고 해도 그 물고기가 농어일 확률은 현저히 낮다.
Prior
- 지금까지 본 결과, 물고기의 피부 밝기 $x$ 가 주어졌을 때 그 물고기가 농어인지 연어인지 구분하기 위해서는 Posterior($P(w_i \vert x)$) 를 알아야 한다.
- 그러나 이 Posterior 는 바로 알 수 없기 때문에 관찰을 통해서 Likelihood($P(x \vert w_i)$) 를 먼저 구한다.
- 하지만 Likelihood 만으로는 Posterior 를 알 수 없다. 바다에 살고 있는 농어와 연어의 비율이 반영되지 않았기 때문이다.
- 아무리 특정 $x$ 에 대해 연어의 Likelihood 가 농어의 Likelihood 보다 크다 하더라도 애초에 연어가 매우 희귀하다면 이 물고기가 농어일 가능성도 생가해 볼 필요가 있다.
- 결론은, $x$ 에 관계없이 애초에 농어가 잡힐 확률($P(w_1)$) 과 연어가 잡힐 확률($P(w_2)$)을 알아야 한다.
- 이 값을 사전확률(Prior)이라고 하며, 이름 그대로 우리가 이미 가지고 있는 사전 지식에 해당한다.
- 농어와 연어 문제에서는 물고기를 많이 잡아서 농어와 연어의 비율을 추정할 수 있지만, 보통은 주어지거나 우리가 정해줘야 하는 경우가 많다.
- 예를 들어 농어와 연어의 실제 비율을 모를 경우, 우리는 편의상 농어와 연어의 비율이 같다고 가정할 수도 있다.
- 이렇게 Prior 는 보통 우리가 사전 지식을 이용해서 정해주는 값에 해당한다.
- 이 다음부터는 편의상 $P(w_1) = 0.7$, $P(w_2) = 0.3$ 이라고 하자. 즉 연어가 농어에 비해 희귀하다고 가정하는 것이다.
Bayes’ Rule
- 지금까지 세 가지 확률을 알아봤다.
- Posterior(사후확률, $P(w_i \vert x)$) : 피부 밝기 $x$ 가 주어졌을 때 그 물고기가 농어 또는 연어일 확률이다. 즉 단서가 주어졌을 때, 대상이 특정 클래스에 속할 확률이다. 우리가 최종적으로 구해야 하는 값이다.
- Likelihood(가능도, $P(x \vert w_i)$) : 농어 또는 연어의 피부 밝기 $x$ 가 어느 정도로 분포되어 있는지의 정보다. 즉 각 클래스에서 우리가 활용할 단서가 어떤 형태로 분포되어 있는지를 알려준다. Posterior 를 구하는데 있어서 매우 중요한 단서가 된다.
- Prior(사전확률, $P(w_i)$) : 피부 밝기 $x$ 에 관계없이 농어와 연어의 비율이 얼마나 되는지에 대한 값이다. 보통 사전 정보로 주어지거나, 주어지지 않는다면 연구자의 사전 지식을 통해 정해줘야 하는 값이다.
- 우리의 목적은 Posterior $P(w_i \vert x)$ 를 구하는 것이며, 이 값은 Likelihood $P(x \vert w_i)$ 와 Prior $P(w_i)$ 를 이용하면 구할 수 있다.
- 조건부 확률의 정의를 활용하면 아래의 식을 유도할 수 있다.
- 베이지안 확률론은 두 사건 $A$ 와 $B$ 의 관계를 알고 있다면 사건 $B$ 가 발생했다는 사실로부터 기존에 알고 있는 사건 $A$ 에 대한 확률 $P(A)$ 를 좀 더 정확한 확률로 바꿀 수 있는 방법을 알려준다.
-
결합확률(joint probability)은 사건 $A$ 와 $B$ 가 동시에 발생할 확률로, 사건 $A$ 도 진실이고 사건 $B$ 도 진실이므로 사건 $A$ 와 $B$ 의 교집합의 확률을 계산하는 것과 같다.
$$P(A \cap B) \; \text{or} \; P(A, B)$$ - 결합확률과 대비되는 개념으로 결합되지 않는 개별 사건의 확률 $P(A)$ 또는 $P(B)$ 를 주변확률(marginal probability) 이라고 한다.
-
또한 $B$ 가 사실일 경우의 사건 $A$ 에 대한 확률을 사건 $B$ 에 대한 사건 $A$ 의 조건부확률(conditional probability) 이라고 한다.
$$P(A \vert B) = \text{new} \; P(A) \; \text{if} \; P(B) = 1$$ -
이 조건부확률은 다음과 같이 정의된다.
$$P(A \vert B) = \frac{P(A, B)}{P(B)}$$ - 그 근거는 다음과 같다.
- 사건 $B$ 가 사실이므로 모든 가능한 표본은 사건 $B$ 에 포함되어야 한다. 따라서 새로운 실질적 표본공간이 $B$ 가 된다.
- 사건 $A$ 의 원소는 모두 사건 $B$ 의 원소도 되므로 사실상 사건 $A \cap B$ 의 원소가 된다. 즉 $A$ 가 실질적으로 $A \cap B$ 가 된다.
- 따라서 조건부확률은 결합확률을 새로운 표본공간으로 정규화(normalization)한 값이라고 할 수 있다.
-
결합확률, 즉 $A$ 와 $B$ 가 모두 발생할 확률을 “$B$ 라는 사건이 발생할 확률과 그 사건이 발생한 경우 다시 $A$ 가 발생할 경우의 곱” 이라는 관점으로 볼 수 있다. $A$ 와 $B$ 를 바꿔도 마찬가지다.
$$P(A, B) = P(A \vert B)P(B) = P(B \vert A)P(A)$$
-
위 결합확률의 식을 살짝 변형하면 다음과 같은 식을 얻을 수 있다. 이 공식이 조건부 확률을 구하는 베이즈 정리(Bayesian rule)다.
$$P(A \vert B) = \frac{P(B \vert A)P(A)}{P(B)} = \frac{P(B \vert A)P(A)}{\sum_A P(B \vert A)P(A)}$$ -
이 때 분모의 식은 전체 확률의 법칙에 의해 구해진다.
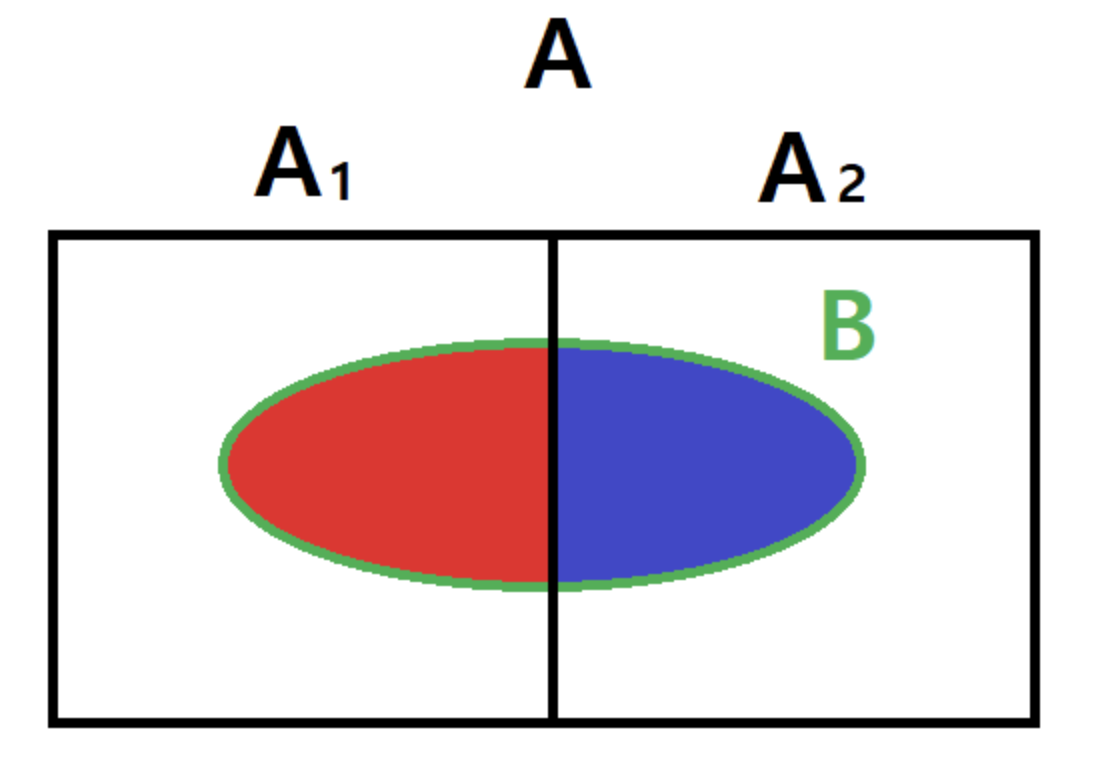
- 위 그림과 같이 사건 $A_i$ 가 서로 배타적($A_1 \cap A_2 = \emptyset$)이고, 완전(합집합이 표본공간, $A_1 \cup A_2 = A$)하다면 전체 확률의 법칙을 이용해 베이즈 정리를 확장할 수 있다.
-
즉, 위 그림에서 아래의 식이 성립한다.
$$ \begin{aligned} P(B) &= P(B \cap A) \\ &= P(B \cap A_1) + P(B \cap A_2) \\ &= P(B \vert A_1)P(A_1) + P(B \vert A_2)P(A_2) \end{aligned} $$
-
이제 $A$ 대신 $w$, $B$ 대신 $x$ 를 넣으면 아래와 같이 된다.
$$P(w_i \vert x) = \frac{P(x \vert w_i)P(w_i)}{\sum_j P(x \vert w_j)P(w_j)}$$ - 좌변은 우리가 구하고자 하는 Posterior 이고, 우변의 분자는 Likelihood 와 Prior 의 곱이며, 우변의 분모는 Evidence 라고 보통 부른다. Evidence 또한 Likelihood 와 Prior 들을 통해 구할 수 있다.
-
즉, 우리는 이 식을 이용하면 Posterior 를 구할 수 있고, 이 식을 우리는 Bayes’ Rule 또는 Bayesian Equation 등으로 부른다.
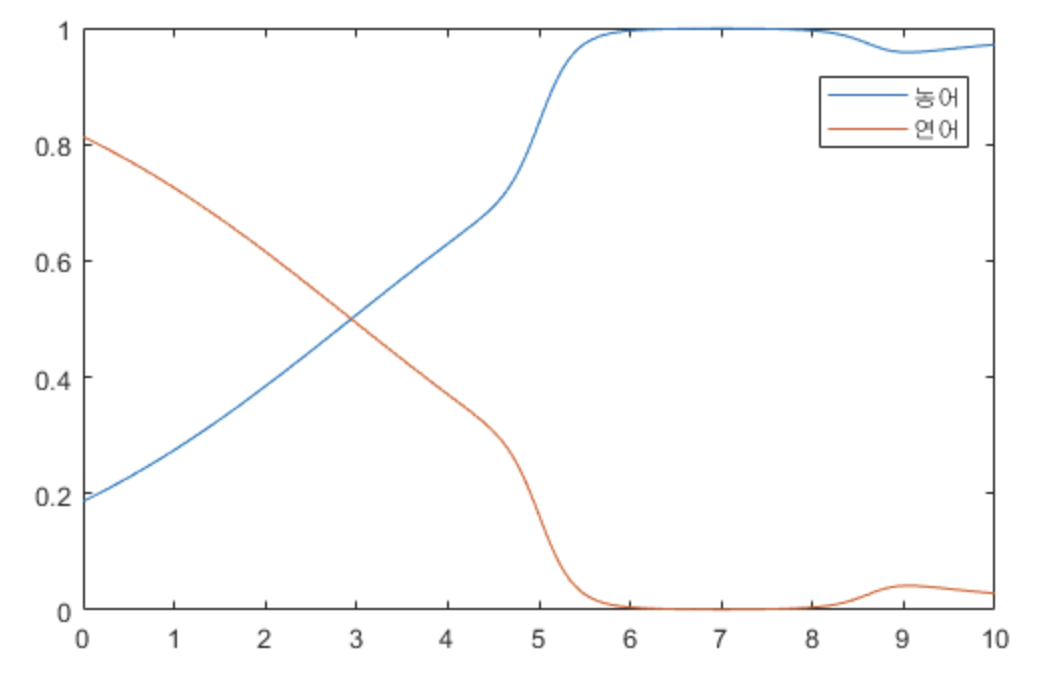피부 밝기에 따른, 농어일 확률과 연어일 확률. 즉 Posterior - 위 그래프는 Bayes’ Rule 에 따라 농어와 연어의 Posterior 를 구한 결과이다.
- 이제 $x$ 가 주어지면 Posterior 가 큰 쪽을 고르면 된다. 농어와 연어를 구분하는 $x$ 의 전환점을 보면, Likelihood 그래프에서는 전환점이 $x = 4.5$ 부근에 형성되었지만 Posterior 그래프에서는 $x = 3$ 부근에 형성된다.
- 연어가 더 희귀하다는 사전 정보(Prior)가 반영되기 때문이다.
댓글 남기기