[AI Math] 5. 통계

통계

• 통계학에서의 통계적 모델링은 적절한 가정 위에서 데이터를 표현하는 확률분포를 추정(inference)하는 것이 목표이며, 기계학습과 통계학이 공통적으로 추구하는 목표다.

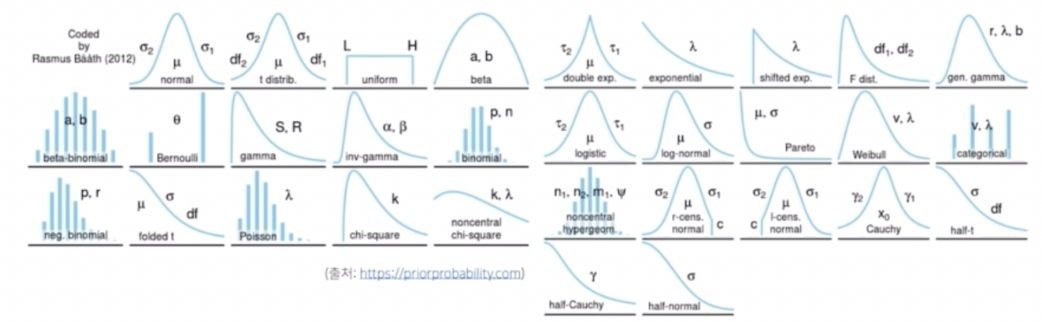  다양한 종류의 확률분포

• 문제는 데이터를 통해서 관찰할 수 있는 분포로 정답의 분포를 확실히 알 수는 없다.
• 또한 실제로 사용할 수 있는 분포의 종류에도 굉장히 다양한 종류의 확률분포가 있다. 따라서 어떤 확률분포를 사용해서 모델링 하느냐가 중요한 선택의 문제가 된다.
• 중요한 것은 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하다는 것이다.
• 컴퓨터를 이용해서 실험적으로 만들어 낸 데이터의 정답 확률분포를 알 수 있는 것이지, 실제 문제 또는 현장에서의 데이터에 대한 확률분포를 데이터만 가지고 정확하게 알아내는 것은 거의 불가능하다.
• 따라서 이 경우엔 근사적으로 확률분포를 추정할 수밖에 없다. 이게 가능한 이유는, 예측 모형을 만드는 것의 목적은 분포를 정확하게 맞추는 것 보다는 데이터와 추정 방법의 불확실성을 고려한 상태에서 예측의 위험을 최소화하는 방향으로 학습을 하는 것만으로도 충분하기 때문이다.
• 즉 데이터 분석이나 딥러닝 목적 하에서는 확률분포를 추정하는 것으로 충분히 예측을 할 수 있다는 것이다.
• 데이터가 어떤 특정 확률분포를 따른다고 선험적으로(a priori) 먼저 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적(parametric) 방법론이라고 한다.
  • 가령 정규분포를 가지고 확률분포를 모델링한다면, 정규분포의 모수인 평균, 분산을 추정하는 방법을 통해 데이터를 학습한다. 이 방법이 모수적 방법론이다.
• 만약 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조와 모수의 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론이라고 부른다.
  • 기계학습의 많은 방법론은 비모수 방법론에 속한다.
  • 주의할 점은 비모수 방법론이라고 해서 모수가 없는 것이 아니다. 비모수 방법론은 모수가 무한히 많거나, 모수의 개수가 데이터에 따라서 바뀌는 경우에 비모수 방법론이라 부른다. 따라서 모수를 쓰지 않는다고 이해하면 안된다.
• 모수적 방법론과 비모수 방법론의 차이는 어떤 가정을 미리 부여를 하는지 또는 아닌지에 따라서 구별된다.
• 기본적으로 어떤 확률분포에는 모수(parameter)라는 것이 적용되기 마련이고, 어떤 확률분포를 가지고 모델링을 할 때는 항상 모수가 뒤따라온다는 것을 기억하자.

확률분포 가정

• 데이터를 보고 특정 확률분포를 가정할 때 아무렇게나 가정하지 않는다.
• 히스토그램, 통계치 등의 형태를 통해서 데이터의 전체적인 모양을 관찰하고 이를 통해 확률분포를 가정해야 한다.
  • 가령 데이터가 2개의 값(0 또는 1)만 가지는 경우 베르누이 분포로 모델링 해볼 수 있다.
  • 데이터가 n 개의 이산적인 값을 가지는 경우 카테고리 분포 또는 다항분포로 모델링 해볼 수 있다.
  • 데이터가 이산적인 값이 아니라 0과 1 사이의 실수값을 가지는 경우에는 베타분포로 표현해볼 수 있다.
  • 데이터가 특정 구간이 아니라 0 이상의 값을 가지는 경우 감마분포, 로그정규분포 등을 이용해볼 수 있다.
  • 데이터가 실수 전체에서 값을 가지는 경우에는 정규분포, 라플라스분포 같은 다양한 연속확률분포를 사용해 볼 수 있다.
• 따라서 관찰되는 데이터의 분포를 보고 이산확률분포와 연속확률분포를 결정할 수 있는 것이다.
• 주의할 점은 기계적으로 확률분포를 가정하는 것은 금물이다. 항상 데이터가 어떤 원리로 생성되었는지를 먼저 관찰해보고, 데이터 생성 원리에 따라서 확률분포를 가정해야 한다.
• 그리고 항상 데이터를 먼저 관찰한 후에 어떤 확률분포가 적절한지를 분석가가 보고 선택해야 한다. 이 원칙은 통계적 분석 또는 기계학습에 상관없이 중요한 원칙이다.
• 또한 어떤 확률분포를 가지고 모델링 했을 때, 모수만 추정하는 것 보다는 모수를 추정한 후에 통계적 검정을 통해서 적절하게 예측을 하고 있는지를 검정해야 한다.

데이터로 모수 추정: 정규분포

• 데이터의 확률분포를 가정했다면 여러가지 모수(parameter)를 추정해볼 수 있다.
• 가령 가장 흔히 사용하는 정규분포를 예로 들어보자.

• 정규분포의 모수는 평균 $\mu$ 와 분산 $\sigma^2$ 으로, 이 두가지 모수를 추정하는 통계량(statistic)은 아래와 같다. 즉 모집단의 평균과 분산을 추정하는 통계량인 표본평균과 표본분산을 아래와 같이 공식으로 나타낼 수 있다.

  

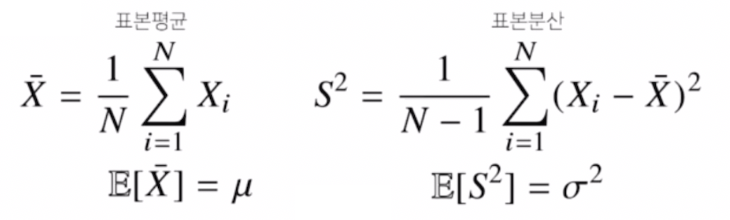
• 표본평균($\bar{X}$)을 보면 주어진 데이터($X_i$)들의 산술평균으로 정의된다. 이 표본평균의 기대값은 원래 데이터에서 관찰되는 모집단의 평균($\mu$)과 일치하게 된다.
• 이 표본평균을 사용해서 표본분산도 정의할 수 있다. 표본분산은 주어진 데이터에서 표본평균을 빼서 제곱을 한 뒤 여기에 산술평균을 취한다. 이 때 $N$ 이 아니라 $N-1$ 로 나누어서 표본분산을 정의한다. 이 표본분산의 기대값이 원래 모집단의 분산($\sigma^2$)과 일치하게 된다.
• 표본분산을 구할 때 $N-1$ 로 나눠주는 이유는 불편(unbiased)추정량을 구하기 위해서다.
  • 기대값을 취했을 때 원래 모집단을 대표하는 통계치와 일치하는 것을 유도하기 위해서 사용되는 것이다.
  • 추정량을 구할 때 통계적으로 중요한 성질들에 따라서 다른 통계량을 사용할 수도 있다.
• 이런 식으로 표본평균과 표본분산을 정의하게 되면, 주어진 데이터를 가지고 데이터의 확률분포의 모수를 추정해볼 수 있다.
• 이후 추정된 모수를 가지고 원래 데이터에서의 성질, 정보들을 취합해볼 수 있다. 이를 통해 예측을 하거나 의사결정을 내릴 때 사용할 수 있다.
• 통계량의 확률분포를 표집분포(sampling distribution)라고 부른다. 조심할 점은 표본분포(sample distribution) 와 표집분포는 다른 용어다.
  • 표본들의 분포가 아니라 통계량인 표본 평균과 표본 분산의 확률분포를 표집분포라고 부른다.
  • 이 표본평균(sample distribution)의 표집분포(sampling distribution)는 $N$ 이 커질수록, 즉 데이터를 많이 모을수록 정규분포 $\mathcal{N}(\mu, \sigma^2/N)$ 를 따른다.
  • 이를 중심극한정리(Central Limit Theorem)라고 부른다.
  • 모집단의 분포가 정규분포를 따르지 않아도, 표본평균의 표집분포는 정규분포를 따른다는 것이다.
• 다시 한번 정리하면, 표본평균과 표집분포는 다르다.
• 원래 모집단의 분포가 정규분포를 따르지 않는다면, 표본분포(sample dist)는 당연히 데이터를 많이 모아도 정규분포가 될 수는 없다.

• 그러나 통계량의 확률분포, 즉 표본평균의 확률분포가 정규분포를 따른다는 것이고, 표본에 대한 분포는 정규분포를 따르지 않을 수 있다. 이 차이를 이해해야 중심극한정리에 대해서 틀리지 않게 이해할 수 있다.

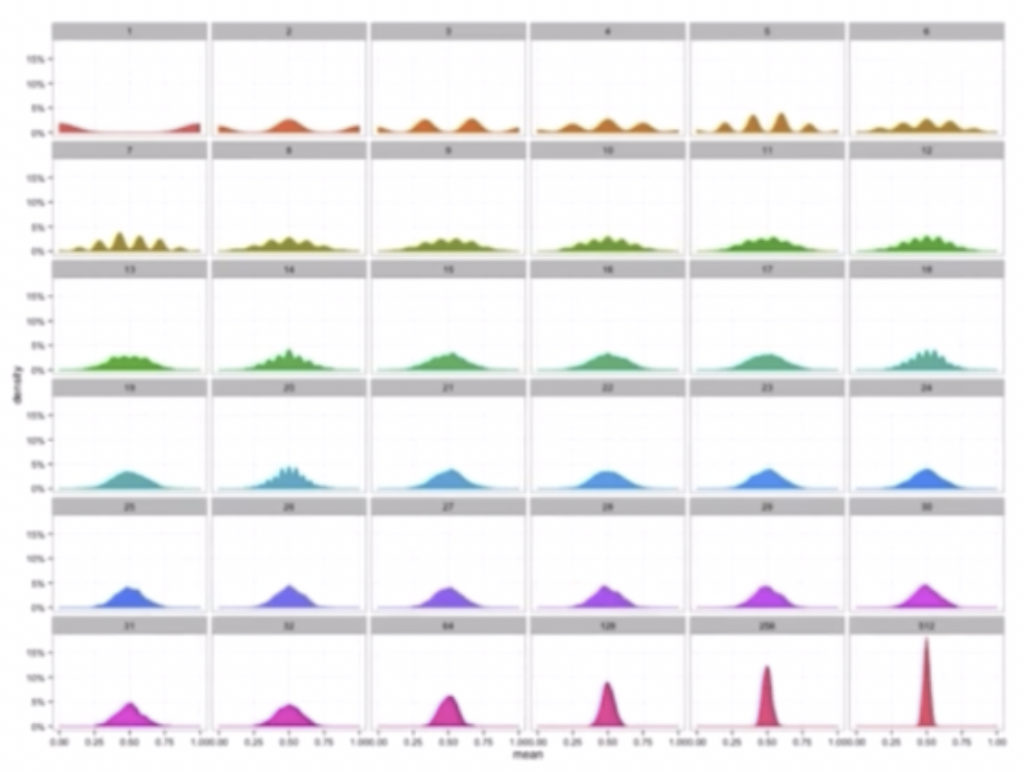  중심극한정리

• 위 그림은 베르누이 확률분포를 따르는 확률변수들의 분포를 그린 것이다.
• 처음 데이터를 모았을 때 표본평균의 분포를 찍어보면 좌측 맨 위의 그래프처럼 양 극단으로 나뉜 것이 관찰된다. 그러나 데이터를 모으면 모을수록 표본평균들의 분포가 점점 더 정규분포가 된다.
• 또한 평균값은 하나의 값으로 물려있는 반면, 분산이 점점 작아지는 모양을 보인다.
• 표본평균의 분산에 해당하는 값이 $\sigma^2/n$ 기 때문에 데이터의 개수인 $n$ 이 늘어나게 되면 표본평균의 분산이 0으로 가게 된다.
• 그래서 위 그림처럼 데이터를 많이 모을수록 표본평균의 분포가 정규분포가 되는데, 분산값이 점점 0으로 가기 때문에 하나의 값으로 몰리는 양상을 관찰할 수 있다.
• 다시 정리해보자.
  • 위 그림에서 원래 확률분포는 이항분포, 즉 베르누이 확률분포이다.
  • 여기서 이항분포의 표본 분포는 당연히 아무리 데이터를 많이 모아도 정규분포가 되지 않는다.
  • 하지만 이 이항분포에서 계산한 통계량 즉 표본평균의 확률분포는 위 그림과 같이 데이터가 많을수록 정규분포로 가고, 이렇게 정규분포로 가는 현상을 중심극한정리라고 한다.

  중심극한정리

  • 중심극한정리란 i.i.d. 확률변수 $X_1, X_2, \ldots$ 가 표본의 크기 $n$ 이 $\inf$ 에 다가가면, 표본평균 $\bar{X}$ 의 분포가 정규분포에 수렴한다는 정리다.
  • 만약 표본 평균이 표준화(standardization)된 상태라면 $\mu = 0, \sigma^2=1$ 인 표준정규분포에 수렴한다.
  • 대수의 법칙은 데이터가 많을수록 표본평균이 모집단의 평균에 수렴한다는 것으로, 표본평균의 분포에 대해서는 정보가 없다.
  • 그러나 중심극한정리는 표본평균의 분포를 설명할 수 있다.
  • 중심극한정리가 중요한 점은, i.i.d. 가정이 충족되고 유한한 평균 $\mu$ 및 분산 $\sigma^2$ 만 정의된다면 원래의 분포 $X_j$ 의 어떠한 정보가 없더라도 표본평균의 분포가 평균이 $\mu$ 이고 분산이 $\sigma^2/\sqrt{n}$ 인 정규분포에 가까워진다는 것을 알려준다는 것이다.
  • 따라서 중심극한정리에 기반하여, 표본의 크기가 충분하다면 내가 수집한 표본의 표본평균이 발생할 확률을 정규 분포에서 계산할 수 있게 된다.
  • 특히 이러한 통계적 추론은 모집단의 분포가 어떤 모양이든지 관계없이 가능하다는 점에서 엄청난 편의성을 제공한다.
  • 정리하자면, 중심극한정리는 표본평균과 모집단 간의 관계를 나타냄으로써 표본 통계량(statistics)를 이용해 모수(parameter)를 추정할 수 있는 수학적 근거를 제시한다. 따라서 중심극한정리는 통계에서 가장 중요한 이론적 근거 중 하나다.
  • 중심극한정리의 증명에 대해서는 이 글에 잘 정의되어 있다. 참고하자.

최대가능도 추정법(Maximum Likelihood Estimation)

• 표본평균이나 표본분산은 정규분포 뿐 아니라 다른 분포에서도 계산할 수 있는 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로 적절한 통계량, 즉 확률분포의 성질을 결정하는 모수를 추정하는 적절한 통계량이 달라지게 된다.
• 그렇기 때문에 기계적으로 표본평균, 표본분산만 가지고 확률분포를 추정하는 것은 위험하다.

• 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법(maximum likelihood estimation, MLE)이다.

  \[\hat{\theta}_{\text{MLE}} = \underset{\theta}{\text{argmax}} \; L(\theta \text{;} \mathbf{x}) = \underset{\theta}{\text{argmax}} \; P(\mathbf{x}\vert\theta)\]
• 확률분포를 어떤 식으로 가정하냐에 따라 상관없이, MLE 를 이론적으로 가장 가능성이 높은 모수(parameter)를 추정하는 방법론으로 사용할 수 있다. 따라서 MLE 는 기계학습에서 여러모로 활용될 수 있다.
• 가능도(likelihood) 함수는 위 수식에서 $L(\theta \text{;} \mathbf{x})$ 로 정의된다. 이 함수는 사실 확률밀도함수나 확률질량함수와 같은 것이다. 단지, 관점의 차이다.
• 확률질량함수 또는 확률밀도함수($P(\mathbf{x}\vert\theta)$)는 모수 $\theta$ 가 주어졌을 때 $\mathbf{x}$ 에 대한 함수로 해석한다.
• 가능도 함수($L(\theta;\mathbf{x})$)는 주어진 데이터 $\mathbf{x}$ 에 대해서 모수 $\theta$ 를 변수로 둔 함수로 해석하면 된다. 다시 말해서 데이터($\mathbf{x}$)가 주어진 상황에서 $\theta$ 를 변형시킴에 따라 값이 바뀌는 함수다.
• 이처럼 가능도(likelihood) 함수는 모수 $\theta$ 를 따르는 분포가 데이터 $\mathbf{x}$ 를 관찰할 가능성을 뜻하지만 확률로 해석해서는 안된다.
• 다시 말해서 확률밀도함수나 확률질량함수와 같은 공식을 쓰게 되지만, $\theta$ 에 대해서 적분을 해줬을 때 1 이 되거나 또는 $\theta$ 에 대해서 다 더했을 때 1 이 되는 개념이 아니기 때문에, $\theta$ 에 대한 확률로 해석하면 안된다.
• 가능도 함수는 오로지 $\theta$ 에 대해서 크고 작음에 따른 대소비교가 가능한 그런 함수로 이해하면 좀 더 명확하다.

• 이러한 가능도 함수는 만약 데이터 집합 $\mathbf{X}$ 의 각 행벡터가 독립적으로 추출되었을 경우 아래와 같이 확률밀도함수 또는 확률질량함수들의 곱으로 표현할 수 있다.

  \[L(\theta;\mathbf{X}) = \prod^n_{i=1}P(\mathbf{x}_i\vert\theta) \quad \Rightarrow \quad \text{log}\;L(\theta;\mathbf{X}) = \sum^n_{i=1}\text{log}\;P(\mathbf{x}_i\vert\theta)\]
• 이렇게 곱으로 표현되는 것은 데이터 집합의 확률분포가 독립적으로 추출되었을 경우에, 즉 데이터가 독립적으로 추출되었을 경우에 가능한 공식이다. 데이터가 독립적으로 추출되었을 경우에는 $\prod$ 로 표현된다.
• 이 때 로그함수의 성질을 이용한다.
  • 로그함수는 곱을 덧셈으로 바꿔준다.
  • 로그함수의 이러한 성질을 이용해서 가능도 함수에 로그를 씌워주면 log likelihood 라고 부르게 되고, 확률분포 함수들의 곱셈을 로그와 확률분포들의 덧셈으로 바꿔줄 수 있다.
• 이 로그가능도를 최적화할 때, 곱셈으로 계산되는 공식이 아니라 덧셈으로 정의된 공식을 최적화할 수 있다.

로그가능도

• 로그가능도(log likelihood)를 사용하는 이유는 뭘까?
• 로그가능도를 최적화하는 모수나 원래 가능도를 최적화하는 모수나 똑같이 MLE 가 된다. 즉 로그가능도를 최적화하는 모수 $\theta$ 는 가능도를 최적화하는 MLE 가 된다.
• 데이터의 숫자가 적으면 상관없지만 만일 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로 가능도를 계산하는 것은 불가능하다.
  • 가령 0에서 1 사이의 확률값을 수억번 곱한다고 가정한다면, 보통 수학적으로는 낮은 자리수의 단위까지 계산할 수 있지만 컴퓨터는 너무 낮은 자리수까지 표현할 수 없고 연산 오차 때문에 계산이 불가능하게 된다.
• 그렇기 때문에 원래 가능도를 가지고 MLE 를 사용하는 것이 쉽지 않다.
• 만약 데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있기 때문에 이 때부터 컴퓨터로 연산이 가능해진다. 따라서 이 경우에는 최적화를 할 수가 있게 된다.
• 데이터가 수억개라 하더라도 덧셈으로 표현되는 경우에는 곱셈에서 부딪히게 되는 연산의 오차가 너무 작아지게 되는 것을 방지할 수 있다.
• 따라서 로그가능도를 사용하면 원하고자 하는 목적식을 최적화하는 것이 가능해지게 된다.
• 또한 로그가능도를 경사하강법으로 최적화하게 되는데, 경사하강법을 사용한다는 것은 미분을 사용한다는 의미다.
• 원래 가능도를 가지고 미분을 사용하게 되면 연산량이 $O(n^2)$ 에 비례하는 연산을 해주어야 하는데, 로그가능도를 사용하게 되면 이 연산량을 $O(n)$ 으로 줄일 수 있다.
• 다시 말해서, 연산의 복잡도가 선형적으로 변환이 되기 때문에 훨씬 더 효율적으로, 빠른 속도로 연산이 가능하다.
• 또한 연산의 오차 범위 내에서 계산할 수 있기 때문에, 로그가능도를 사용하는 이유는 최적화 관점에서 중요한 이유로 사용하는 것이다.
• 대게의 손실함수의 경우, 경사하강법을 사용하므로 목적식을 최대화시키는 것이 아니라 목적식을 최소화하게 된다.
• 그러나 로그가능도는 보통 maximum 을 찾아주게 된다. 따라서 이를 목적식을 최소화하는 것으로 바꿔주기 위해서 그냥 로그가능도가 아니라 음의 로그가능도(negative log-likelihood)를 최적화하게 된다.

최대가능도 추정법 예제 : 정규분포

• 정규분포를 따르는 확률변수 $X$ 로부터 독립적인 표본 ${x_1, \cdots, x_n}$ 을 얻었을 때, 이 표본(데이터)을 가지고 MLE 를 사용하여 모수를 추정하면 어떻게 될까?

  \[\hat{\theta}_{\text{MLE}} = \underset{\theta}{\text{argmax}} \; L(\theta \text{;} \mathbf{x}) = \underset{\theta}{\text{argmax}} \; P(\mathbf{x}\vert\theta)\]
• MLE 는 주어진 데이터($\mathbf{x}$)를 가지고, 가능도 함수 $L(\theta;\mathbf{x})$ 를 최적화하는 $\theta$ 를 찾는 것이다.

• 정규분포이기 때문에, 두 개의 모수를 가진다. 평균과 분산 이 두가지 모수(parameter)를 가지고 정규분포를 표현한다. 따라서 아래와 같이 식이 표현된다.

  \[\hat{\theta}_{\text{MLE}} = \underset{\theta}{\text{argmax}} \; L(\theta \text{;} \mathbf{x}) = \underset{\mu, \sigma^2}{\text{argmax}} \; P(\mathbf{X}\vert\mu,\sigma^2)\]

• 이를 이용해서 가능도를 계산해보자. 특히 그냥 가능도 대신 로그가능도를 이용한다.

  \[\begin{aligned} \text{log}\;L(\theta;\mathbf{X}) = \sum^n_{i=1}\text{log}\;P(x_i\vert\mu, \sigma^2) &= \sum^n_{i=1}\text{log}\;\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{\vert x_i-\mu \vert^2}{2\sigma^2}} \\ &= -\frac{n}{2}\text{log}\;2\pi\sigma^2-\sum^n_{i=1}\frac{\vert x_i - \mu \vert^2}{2\sigma^2} \end{aligned}\]
• 로그가능도로 정규분포의 가능도를 계산해보면, 정규분포의 확률밀도함수에 로그를 씌운 것으로 계산할 수 있다.
• 정규분포의 확률밀도함수는 두가지 곱셈의 형태다. 하나는 분산항만 들어있는 $1/\sqrt{2\pi\sigma^2}$ term 과, 지수함수 term 이다.
• 이 정규분포의 확률밀도함수에 로그를 씌우게 되면 두 항을 덧셈으로 쪼갤 수 있다.
• 맨 하단 수식의 왼쪽 term 은 오로지 분산만 들어가 있는 term 이고, 오른쪽 term 은 분산과 평균 두 가지가 동시에 존재하는 term 이다.

• 모수인 평균과 분산에 대해서, 즉 $\theta = (\mu, \sigma)$ 에 대해서 위 수식을 미분해서 최적화를 할 수 있다.

  \[\begin{aligned} \frac{\partial \text{log}\;L}{\partial \mu} &= -\sum^n_{i=1}\frac{x_i-\mu}{\sigma^2} = 0 \\ \frac{\partial \text{log}\;L}{\partial \sigma} &= -\frac{n}{\sigma} + \frac{1}{\sigma^3}\sum^n_{i=1}\vert x_i - \mu \vert^2 = 0 \end{aligned}\]
• 주어진 로그가능도를 $\mu, \sigma$ 로 미분해주게 되면, 위 수식을 얻게 된다.
• 먼저 $\mu$ 로 로그가능도를 미분해주면, 두 term 중에서 오른쪽에 있는 term 만 살아남게 된다. 분자에 있던 제곱과 분모에 있던 2가 서로 상쇄되어 위와 같이 표현된다.
• 표준편차 $\sigma$로 로그가능도를 미분해주면, 두가지 term 모두 $\sigma$ 가 존재하기 때문에 미분을 계산해보면 위 수식 중 아래와 같은 식을 얻을 수 있다.
• 미분을 사용해서 MLE 를 하고 싶다면, 미분을 했을 때 각각의 파라미터에 대해서 0 이 되는 점을 찾아주면 된다. 즉 위 수식의 두 미분이 모두 0 이 되는 $\mu,\sigma$ 를 찾아주게 되면 결론적으로 로그가능도를 최대화해주는 모수를 찾게 된다.

• 주어진 수식들에 대해서 이 값들이 0 이 되는 $\mu, \sigma$ 를 풀어주게 되면 아래와 같다.

  \[\begin{aligned} \hat{\mu}_{\text{MLE}} &= \frac{1}{n}\sum^n_{i=1}x_i \\ \hat{\sigma}^2_{\text{MLE}} &= \frac{1}{n}\sum^n_{i=1}(x_i - \mu)^2 \end{aligned}\]
• MLE 로 추정한 모수 $\mu$ 는 데이터($x_i$)가 주어진 상황에서 산술평균이 된다.
• MLE 로 추정한 모수 $\sigma$ 는 데이터에 평균을 빼준 후 제곱하여 산술평균을 계산한 값이다.
• 이 결론은 모수를 추정하는 통계량(statistic)과 유사한 결과다.
  • 즉, 데이터들의 표본평균과 최대가능도 추정법과 일치한다.
  • 분산의 경우, 표본분산은 $n-1$ 로 나눴는데 MLE 로 구한 분산은 $n-1$ 이 아니라 $n$ 으로 나눠준다.
• 즉 통계량으로 추정된 모수와 다른 추정량이 될 수도 있다. 사실 통계량은 하나만 사용할 필요가 없고, 여러가지 통계량을 사용해 볼 수 있다.
• MLE 의 경우 가능도를 최적화하는 통계량에 해당하지만 불편추정량을 보장하지는 않는다. 그러나 통계학에서 얘기하는 consistency 는 보장할 수 있기 때문에 MLE 의 장점도 있다.
• 참고로 $\sigma^2$ 의 MLE 에 들어가는 $\mu$ 자리에는 위에서 구한 $\mu$ 의 MLE 를 넣어도 된다.
• 주어진 가능도를 최적화하는 모수는 이 두가지 MLE 에 사용된 $\mu, \sigma^2$ 를 사용했을 때 결론적으로 가능도를 최적화시키는 모수를 구했다고 얘기할 수 있다.

최대가능도 추정법 예제 : 카테고리 분포

• 위에서 연속확률변수에 해당하는 정규분포에서의 MLE 를 이용한 모수 추정 방법을 봤다. 이번에는 이산확률변수에 해당하는 카테고리 분포에서의 MLE 를 사용하는 예제를 보자.
• 카테고리 분포는 두 개의 값 중 하나를 선택하는 베르누이 분포를 다차원으로, 즉 $d$ 차원으로 확장한 개념이다.
• $d$ 개의 각 차원에서 어떤 하나의 값을 선택하게 되는 확률변수로서, 하나의 값을 선택한 경우에는 선택된 값은 1이고, 나머지는 0으로 주어진다. 즉 one-hot 벡터로 $\mathbf{x}$ 값이 표현된다.

• 이러한 카테고리 분포 $\text{Multinoulli}(\mathbf{x};p_1,\cdots,p_d)$ 를 따르는 확률변수 $X$ 로부터 독립적인 표본 ${\mathbf{x}_1, \cdots, \mathbf{x}_n}$ 을 얻었을 때 MLE 를 이용하여 카테고리 분포의 모수 $p_1$ 부터 $p_d$ 를 추정해보자.

  \[\hat{\theta}_{\text{MLE}} = \underset{p_1, \ldots, p_d}{\text{argmax}} \; \text{log} \; P(\mathbf{x}_i \vert \theta) = \underset{p_1, \ldots, p_d}{\text{argmax}} \; \text{log} \left(\prod^n_{i=1}\prod^d_{k=1}p^{x_{i, k}}_k\right)\]
• 조심할 점은 카테고리 분포의 모수 $p_1, \ldots, p_d$ 는 정규분포의 모수와 다르다.
• 정규분포의 모수는 평균과 분산이라는 통계량에 해당했지만, 카테고리 분포의 모수인 $p_1, \ldots, p_d$ 는 1 부터 $d$ 차원까지 각각의 차원에서 값이 1 또는 0 이 될 확률을 의미하는 모수이다.

• 따라서 카테고리 분포에서 추정하는 모수 $p_1, \ldots, p_d$ 는 주어진 카테고리 분포의 확률질량함수에 해당하는 모수이기 때문에, 모수들을 다 더했을 때 반드시 1 이 되어야 한다 제약식이 존재한다.

  \[\sum^d_{k=1}p_k = 1\]
• 이렇게 제약식이 주어진 상황에서 MLE 를 어떻게 사용하여 최대 가능도를 최적화하는지 보자.
• 먼저 카테고리 분포의 가능도함수를 표현할 때, 모수 $p_k$ 에 $x_{i, k}$, 즉 주어진 데이터 $x_i$ 의 $k$ 번째 차원에 해당하는 값을 승수를 취해주는 형태로 계산해주게 된다.
• 만약 $x_{i, k}$ 가 0 이 되면 \(p^{x_{i,k}}_k\) 은 \(p^{0}_k\) 이 되기 때문에 그냥 1 이 되고, \(p^{x_{i,k}}_k\) 에서 \(x_{i,k}\) 가 1 이면 이 값은 $p_k$ 라는 값을 가지게 된다.
• 따라서 $x_{i,k}$ 가 0 과 1 두 가지 값만 가짐으로 인해서, 카테고리 분포의 가능도함수는 $p_k$ 가 1 또는 $p_k$ 로 사용되는 형태로 정의되고, 이를 이용해서 최대가능도를 추정하게 된다.

• 이렇게 주어진 가능도함수에 로그를 씌우게 되면, 곱셈으로 표현된 가능도이기 때문에 덧셈으로 표현할 수 있다.

  \[\hat{\theta}_{\text{MLE}} = \underset{p_1, \ldots, p_d}{\text{argmax}} \; \text{log} \; P(\mathbf{x}_i \vert \theta) = \underset{p_1, \ldots, p_d}{\text{argmax}} \; \text{log} \left(\prod^n_{i=1}\prod^d_{k=1}p^{x_{i, k}}_k\right) \\ \text{log} \left(\prod^n_{i=1}\prod^d_{k=1}p^{x_{i, k}}_k\right) = \sum^d_{k=1}\left(\sum^n_{i=1}x_{i,k}\right)\text{log}\;p_k\]
• 주어진 가능도함수에 로그를 씌우면 로그 연산의 성질에 의해서 곱셈을 덧셈으로 바꿀 수 있다. 그러면 $x_{i,k}$ 는 로그 바깥으로 나오게 되고, $p_k$ 는 $\text{log}\;p_k$ 로 바뀌게 된다.
• 이제 곱셈을 전부 다 덧셈으로 바꿔주게 되면, $x_{i,k}$ 에 대해서 데이터 개수($i=1 \sim n$)만큼 더해주는 덧셈 연산을 먼저 해준 후, 그 다음 각 차원별($d$)로 덧셈을 표현해줄 수 있다.

• 이 때 $x_{i,k}$ 는 전부 0 또는 1 이기 때문에, 각각의 $i=1 \sim n$ 까지의 $x_{i,k}$ 를 더해주는 개념은 주어진 각 데이터들에 대해서 $k$ 번째 값이 1 인 개수를 카운팅하는 $n_k$ 로 대체해서 표현할 수 있다.

  \[n_k = \sum^n_{i=1}x_{i,k}\]

• 즉 $n_k$ 는 주어진 데이터 $x_i$ 에 대해서 $k$ 번째 값이 1 인 데이터의 개수를 세는 개념으로 이해할 수 있다. 따라서 모수들에 대해서 전부 다 더했을 때 1 이 된다는 제약식과 아래의 식이 도출된다.

  \[\text{log} \left(\prod^n_{i=1}\prod^d_{k=1}p^{x_{i, k}}_k\right) = \sum^d_{k=1}n_k\;\text{log}\;p_k \quad \text{with} \quad \sum^d_{k=1}p_k=1\]
• 오른쪽 제약식을 만족하면서 왼쪽 목적식을 최대화하는 것이 우리가 구하는 카테고리 분포에서의 MLE 다.
• 목적식에 제약식이 추가된 상황에서는, 앞에서와 같이 그냥 미분 했을 때 0 이 되는 값을 구하는 것이 아니고, 라그랑주 승수법을 이용해서 제약식의 등식을 양변으로 넘겨준 상태에서 라그랑주 승수에 해당하는 $\lambda$ 를 곱해준 식을 목적식에 더해줘서 새로운 목적식을 만들어줄 수 있다.

  • 라그랑주 승수법(Lagrange multiplier method)은 프랑스의 수학자 조세프루이 라그랑주 (Joseph-Louis Lagrange)가 제약 조건이 있는 최적화 문제를 풀기 위해 고안한 방법이다.

    \[\begin{aligned} \text{log} \left(\prod^n_{i=1}\prod^d_{k=1}p^{x_{i, k}}_k\right) &= \sum^d_{k=1}n_k\;\text{log}\;p_k \quad \text{with} \quad \sum^d_{k=1}p_k=1 \\ \Rightarrow \mathcal{L}(p_1, \ldots, p_d, \lambda) &= \sum^d_{k=1}n_k\log p_k + \lambda(1-\sum_kp_k) \end{aligned}\]
• 이 새로운 목적식을 최적화함을 통해서, 제약식도 만족하면서 주어진 원래 로그 가능도 함수를 최대화시키는 모수 $p_1, \ldots, p_d$ 까지를 구할 수 있다.

• 우선 주어진 라그랑주 목적식($\mathcal{L}$)을 각각의 모수 $p_k$ 에 대해서 미분해주고, 라그랑주 승수인 $\lambda$ 에 대해서도 미분을 해준다.

  \[\mathcal{L}(p_1, \ldots, p_d, \lambda) = \sum^d_{k=1}n_k\log p_k + \lambda(1-\sum_kp_k) \\ 0 = \frac{\partial\mathcal{L}}{\partial p_k} = \frac{n_k}{p_k} - \lambda, \quad 0 = \frac{\partial\mathcal{L}}{\partial \lambda} = 1-\sum^d_{k=1}p_k\]
• 그러면 각각의 모수에 대해서 미분을 취해준 결과값은 로그의 미분은 분모로 가게 되기 때문에 왼쪽 수식이 된다. 이 값이 0 이 되어야 한다.
• 마찬가지로 $\lambda$ 에 대해서 미분을 취해준 값도 0 을 만족해야 한다. 잘 보면 이 식은 원래 주어진 제약식과 똑같다.
• 왼쪽의 수식을 잘보면 $n_k/p_k$ 가 모두 $\lambda$ 를 만족해야 한다는 점을 알 수 있다.

• 이 두가지 사실을 조합해보면, 아래의 식을 도출할 수 있다.

  \[\frac{n_k}{p_k} = \lambda \; \rightarrow \; p_k = \frac{n_k}{\lambda}, \quad \sum^d_{k=1}p_k = 1 \\ \begin{aligned} \sum^d_{k=1}\frac{n_k}{\lambda} &= 1 \; \rightarrow \; \sum^d_{k=1}n_k = \lambda = n \\ \therefore \; p_k &= \frac{n_k}{\lambda} = \frac{n_k}{\Sigma^d_{k=1}n_k} = \frac{n_k}{n} \end{aligned}\]
• 즉 $p_k$ 는 $n_k$ 를 모두 다 더해준 것이 분모가 되고, $n_k$ 가 분자로 들어간다.
• 이 때 분모 term 을 잘보면, $n_k$ 를 $k=1 \sim d$ 까지 전부 다 더해준 것이 바로 데이터 개수인 $n$ 과 똑같다. 왜냐하면 모든 데이터마다 1 을 하나씩 가지고 있을 것이기 때문이다. 따라서 최종적으로 $p_k$ 는 $n_k/n$ 과 같다는 결론을 얻을 수 있다.
• 따라서 카테고리 분포의 MLE 는 각각의 차원에 해당하는 데이터의 개수, 즉 경우의 수를 세서 비율을 구하는 것이다. 이를 통해 최대가능도를 달성하는 모수를 추정하는 것이 가능하다.

딥러닝에서의 최대가능도 추정법

• 지금까지 확률분포의 모수를 MLE 로 추정하는 방법을 봤다. MLE 는 굉장히 폭 넓은 범주 내에서 사용할 수 있다.
• 이러한 MLE 는 기계학습 모델의 학습에서도 사용할 수 있다.
• MLP 에서 가중치를 layer 에 따라 $(\mathbf{W}^{(1)}, \ldots, \mathbf{W}^{(L)})$ 로 표현할 수 있다.
• 딥러닝 모델의 가중치를 $\theta = (\mathbf{W}^{(1)}, \ldots, \mathbf{W}^{(L)})$ 이라 표기했을 때, 분류 문제에 딥러닝 모델을 적용하게 되는 경우에는 맨 마지막 층에서 소프트맥스 벡터를 이용해서 조건부확률분포를 계산해볼 수 있었다.
• 이 소프트맥스 확률 벡터가 카테고리 분포의 모수 $(p_1, \ldots, p_k)$ 를 모델링하는데 사용될 수 있다. 즉 one-hot 벡터로 표현되는 정답레이블 $\mathbf{y} = (y_1, \ldots, y_K)$ 을 관찰데이터로 사용해서 확률분포인 소프트맥스 벡터의 로그가능도를 최적화하는 방향으로 딥러닝의 모수인 $\theta$ 를 학습 시킬 수 있다.

• 이런 식으로 주어진 MLP 의 $\theta$ 를 최적화시킬 때, 위에서 본 MLE 의 수식과 유사한 수식으로 표현할 수 있다.

  \[\hat{\theta}_{\text{MLE}} = \underset{\theta}{\text{argmax}}\;\frac{1}{n}\sum^n_{i=1}\sum^K_{k=1}y_{i,k}\log(\text{MLP}_\theta(\mathbf{x}_i)_k)\]
• 위 수식을 잘 보면 $k = 1 \sim K$ 까지 모든 클래스의 개수에 대해서, 데이터 $i=1\sim n$ 까지 모든 데이터를 입력으로 하는 MLP 의 예측값의 $k$ 번째 값의 로그값과 정답레이블에 해당하는 $y$ 의 $k$ 번째 주소값을 곱해준 것들의 덧셈으로 해석할 수 있다. 이 수식을 잘 기억하자.

확률분포의 거리

• 기계학습에서 사용되는 손실함수들은 사실 아무렇게나 사용되는 손실함수들이 아니다.
• 기계학습에서 사용되는 손실함수들은 기계학습 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도할 수 있다.
• 통계학에서 MLE 로 추정하게 되는 많은 모델 학습방법론이 확률분포의 거리를 최적화하는 것과 밀접하게 관련이 있다.
• 데이터 공간에 두 개의 확률분포 $P(\mathbf{x}), Q(\mathbf{x})$ 가 있을 경우, 두 확률분포 사이의 거리(distance) 를 계산하는 방법에는 여러가지 방법이 있다.
  • 총변동 거리(Total Variation Distance, TV)
  • 쿨백-라이블러 발산(Kullback-Leibler Divergence, KL)
  • 바슈타인 거리(Wasserstein Distance)

쿨백-라이블러 발산(KL-div)

• KL-div 는 아래와 같이 정의한다.

  \[\small{\mathbb{KL}(P\Vert Q) = \sum_{\mathbf{x} \in \mathcal{X}}P(\mathbf{x})\log\left(\frac{P(\mathbf{x})}{Q(\mathbf{x})}\right) \quad \mathbb{KL}(P\Vert Q) = \int_ \mathcal{X}P(\mathbf{x})\log\left(\frac{P(\mathbf{x})}{Q(\mathbf{x})}\right)}\text{d}\mathbf{x}\]
• 이산확률변수의 경우 두 개의 확률변수 $P(\mathbf{x}), Q(\mathbf{x})$ 에 대해 먼저 뒷자리에 들어가게 되는 $Q(\mathbf{x})$ 를 로그의 분모에 집어넣게 되고, 앞자리에 들어가는 $P(\mathbf{x})$ 를 로그의 분자와 로그값으로 계산되는 것에 곱한다.
• 연속확률변수의 경우 같은 함수를 적분하는 형태로 정의한다.

• 이 때 KL-div 는 기대값의 정의에 따라 아래와 같이 두 개의 항으로 분해할 수 있다.

  \[\mathbb{KL}(P\Vert Q) = -\mathbb{E}_{\mathbf{x}\sim P(\mathbf{x})}[\log Q(\mathbf{x})] + \mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[\log P(\mathbf{x})]\]
• $\log Q(\mathbf{x})$ 에 대한 기대값에 - 를 붙인 term 과, $\log P(\mathbf{x})$ 에 대한 기대값을 더해주는 형태로 표현할 수 있다.
• 앞에 있는 term 은 크로스 엔트로피이고, 뒤에 있는 term 은 엔트로피다. 즉 KL-div 함수는 두 개의 엔트로피 함수로 표현할 수 있는 것이다.
• 위에서 MLP 와 정답레이블에 대해서 표현되는 MLE 함수를 다시 한번 떠올리자.
  • 분류 문제에서 정답레이블을 $P$, 모델 예측을 $Q$ 라 두면 MLE 에서 사용되는 손실함수가 KL-div 에서의 첫번째 term 인 크로스 엔트로피에 - 를 붙인 것과 똑같게 된다.
  • $P, Q$ 를 MLE 수식에 대입하고, 위 KL-div 에서의 첫번째 term 을 기대값 수식으로 전개하면 두 식이 부호만 다른 것임을 알 수 있다.
  • 다시 말해서, 최대가능도 추정법에서 로그 가능도를 최대화시키는 것과 정답 레이블에 해당되는 확률분포 $P$ 와 모델 예측의 확률분포 $Q$ 사이에 거리, 다시 말해서 KL-div 을 최소화하는 것과 동일하게 된다.
• 확률분포 사이의 거리를 최소화하는 개념과 로그가능도 함수를 최대화시킨다는 개념이 굉장히 밀접하게 연결되어 있다는 것이다.
• 따라서 두 개의 확률 분포의 거리를 최소화한다는 개념과 주어진 데이터를 통해서 목적으로 하는 확률분포의 최적화된 모수를 구하는 것은 동일한 개념이다.
• 이를 이해하면 기계학습의 원리가 데이터로부터 확률분포 사이의 거리를 최소화하는 것과 동일한 것임을 이해할 수 있다. 즉 통계학적으로 기계학습 모형에서 적절한 학습 방법론을 사용하는 것이다.
• 많은 딥러닝의 논문을 보면서 손실함수(loss function)가 어떻게 또는 이 최적화 모형이 어떻게 나왔는지를 고민할 때, MLE 라는 관점에서 많이 유도되었음을 기억하자.
• 또한 통계학적인 방법론에 기반해서 기계학습 모형들이 학습을 하게 된다는 것을 기억하자.
• 이에 대한 것은 Loss 카테고리에서 자세하게 정리할 것이다.

맨 위로 이동 ↑