[AI Math] 3. Deep Learning 학습방법

2024-04-08

딥러닝

단순한 데이터를 해석할 때는 선형모델이 도움이 되지만, 분류 문제를 풀거나 복잡한 패턴을 가진 문제를 푸는 경우에는 선형모델만 가지고는 높은 예측을 가지는 모델을 만들기는 어렵다.
딥러닝에서는 Neural Network 라는 신경망 모델을 이용하는데, 신경망 모델은 기본적으로 선형모델이 아닌 비선형 모델이다.
그러나 비선형 모델인 신경망을 수학적으로 분해해보면 선형 모델이 그 안에 숨겨져 있다. 즉 선형 모델과 비선형 함수들의 결합으로 이루어져 있다.
신경망을 수식으로 분해해보고, 선형모델의 동작 방식과 신경망이 선형모델을 기반으로 어떻게 하면 비선형 패턴을 배울 수 있는지를 보자.

선형 모델

각 행벡터 $\mathbf{o}_i$ 는 데이터 $\mathbf{x}_i$ 와 가중치 행렬 $\mathbf{W}$ 사이의 행렬곱과 절편 $\mathbf{b}$ 벡터의 합으로 표현될 수 있다.

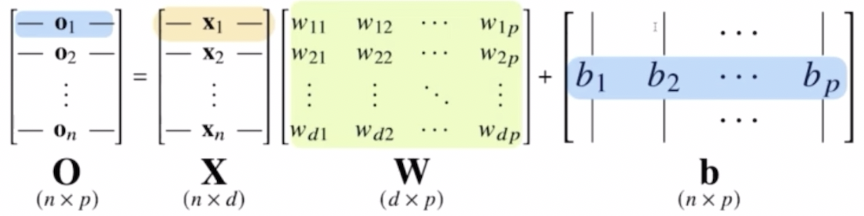
$image.png$
전체 데이터들로 구성된 행렬 $\mathbf{X}$ 가 있다. 이 행렬 $\mathbf{X}$ 의 각각의 행벡터들은 각각의 데이터 포인트들, 데이터 공간으로 치면 한 점으로 표현되는 데이터들이다. 또한 데이터 포인트들을 출력으로 뱉어주는 가중치 행렬 $\mathbf{W}$ 가 있다.
행렬은 두 가지 의미로 해석할 수 있는데, 1) 첫번째로 $\mathbf{X}$ 처럼 데이터를 모아놓은 행렬이 될 수 있고, 2) 가중치 행렬 $\mathbf{W}$ 처럼 데이터를 다른 데이터 공간으로 보내주는 행렬이다.
선형모델은 데이터를 모아 놓은 행렬과 그 행렬을 다른 벡터 공간으로 보내주는 가중치 행렬의 곱을 통해서 표현할 수 있다.
맨 오른쪽의 $\mathbf{b}$ 라는 행렬은 y 절편에 해당하는 벡터들을 모든 행에 대해서 다 똑같이 복제한 것이다. 따라서 $\mathbf{b}$ 라는 행렬은 각 행이 같은 값을 가지고 있다. 각 행에 대해서, 즉 각 모든 데이터에 대해서 똑같은 벡터값을 더해주는 것이다.
이 $\mathbf{X, W, b}$ 의 선형 결합으로 이루어져 있는 모델을 선형모델로 기본적으로 사용하게 된다.
각각의 행벡터로 이루어져 있는 행렬 $\mathbf{X}$ 의 데이터들을 $\mathbf{W}$ 라는 가중치 행렬과 행렬곱을 하고, $\mathbf{b}$ 라는 절편 벡터의 합을 통해서 $\mathbf{O}$ 라는 출력을 내는 것이 기본적인 선형모델의 수식적인 표현이 된다.
당연히 데이터($\mathbf{x}_i$)가 바뀌면 결과값($\mathbf{o}_i$)도 바뀐다.
중요한 점은, 출력 벡터의 차원이 원래 데이터들이 모여있는 $d$ 차원에서 $p$ 차원으로 바뀌게 된다.
$\mathbf{X}$ 행렬은 데이터가 $n$ 개가 있으니까 $n \times d$ 행렬이 되지만, 여기에 $\mathbf{W}$ 라는 $d \times p$ 행렬을 곱했기 때문에, 두 행렬의 결과값인 $n \times p$ 행렬이 출력에 해당하는 $\mathbf{O}$ 행렬의 차원이 된다.
이렇게 출력 행렬에서 열에 해당하는 차원의 개수가 바뀐다는 것을 잘 기억해야 한다.
이를 도식으로 표현하면 아래와 같다.

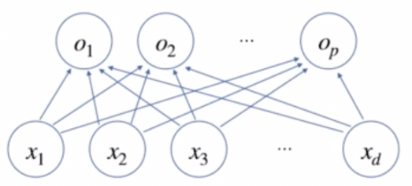
$image.png$
그림에 있는 $x_1$ 부터 $x_d$ 까지는 $\mathbf{X}$ 행렬의 행벡터에 있는 각 $d$ 개의 변수들이다. 즉 $\mathbf{x}$ 라는 벡터는 $d$ 개의 변수로 이루어져 있는 것이다.
$x_1, \ldots, x_d$ 에 $p$ 개의 선형 모델을 거쳐 $p$ 개의 잠재변수를 생성하는 것이 수식으로 쓴 $\mathbf{O} = \mathbf{XW} + \mathbf{b}$ 가 된다.
위 그림을 잘 보면 $x_1$ 부터 $x_d$ 까지의 변수들이 $o_1$ 부터 $o_p$ 까지의 출력으로 화살표로 연결되어 있다. 이 화살표에 해당하는 것이 가중치 행렬 $\mathbf{W}$ 의 $w_{ij}$ 들의 역할이라고 볼 수 있다.
즉 $\mathbf{x}$ 라는 행벡터를 $\mathbf{o}$ 라는 행벡터로 연결할 때, 즉 $x$ 변수들을 $o$ 변수들로 각각 선형결합으로 연결하게 될 때, $p$ 개의 선형모델을 만들어야 한다.
왜냐면 $x_1$ 에서 $o_1, \ldots, o_p$ 까지 연결되는 화살표는 $p$ 개가 만들어지기 때문이다. $x_2$ 도 마찬가지로 $p$ 개가 필요하다. 그러면 전체 $p \times d$ 개 만큼의 화살표가 필요하게 된다.
이 $p \times d$ 개의 화살표와 똑같은 값을 가지는 행렬이 $\mathbf{W}$ 가중치 행렬이 된다. 즉, 가중치 행렬의 원소의 개수인 $d \times p$ 에 해당하는 $w_{ij}$ 들이 바로 위 그림에서 화살표들의 값을 의미한다고 해석할 수 있다.
따라서 위와 같은 딥러닝 신경망의 그림에서 화살표들은 가중치 행렬 $\mathbf{W}$ 의 원소들이며, 선형모델로 표현되는 가중치 행렬의 $w_{ij}$ 가 각각 화살표들의 의미를 결정짓는다.

softmax

딥러닝을 가지고 여러가지 문제들을 풀어볼 수 있다. 선형회귀 같은 regression 문제 뿐만 아니라 주어진 데이터가 특정 class 에 해당하는지 예측하는 문제에도 사용할 수 있다.
이런 문제들을 분류 문제라고 부른다. 분류 문제들을 풀 때 모델을 학습시키기 위해 특별히 필요한 연산자가 있다. 바로 softmax 라는 연산자다.
softmax 연산은 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산이다. 즉 출력 벡터 $\mathbf{o}$ 에 softmax 함수를 합성하면 확률 벡터가 되어 특정 클래스 $k$ 에 속할 확률로 해석할 수 있다.
\[\text{softmax}(\mathbf{o}) = \left(\frac{\text{exp}(o_1)}{\sum^p_{k=1}\text{exp}(o_k)}, \cdots, \frac{\text{exp}(o_p)}{\sum^p_{k=1}\text{exp}(o_k)}\right)\]
분류 문제를 풀 때 선형결합과 softmax 함수를 결합해서 예측할 수 있다. 선형 모델의 결과값이 $\mathbf{Wx+b}$ 라는 출력이고, 여기에 softmax 를 씌우면 이를 통해서 특정 벡터가 어떤 클래스에 속할 확률을 계산할 수 있다.
즉 softmax 함수를 통해 $\mathbb{R}^p$ 에 있는 벡터를 확률벡터로 변환할 수 있다. (ex. [1, 2, 0] → [0.24, 0.67, 0.09])
softmax 함수는 exp, 즉 지수함수를 통해서 계산하게 된다. 선형모델의 결과물인 $\mathbf{o}$ 벡터를 softmax 안에 집어넣으면 확률 벡터로 변환시킬 수 있는 것이다.
이렇게 확률 벡터로 변환시키게 되면 주어진 데이터가 특정 클래스에 속할 확률이 얼마인지를 계산할 수 있다. 이를 통해서 현재 주어진 모델에 분류 문제를 학습시킬 때 특정 클래스에 속할 확률을 계산한 softmax 의 출력값을 사용할 수 있다.

softmax 함수를 구현할 때는 위 수식을 그대로 구현한다.

  import numpy as np
    
  def softmax(vec):
      denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
      numerator = np.sum(denumerator, axis=-1, keepdims=True)
      val = denumerator / numerator
      return val

분모(numerator)에 해당하는 것은 각 출력 벡터들의 값에 exp, 즉 지수함수를 씌운 것을 전부다 더해주는 것이다. 분자(denumerator)는 출력 벡터의 성분에 해당하는 값에 지수함수를 씌운다.
그러나 위 코드를 보면 한 가지 차이점이 있다. 이는 softmax 연산이 지수함수를 사용하다 보니 너무 큰 벡터가 들어오면 overflow 현상이 발생할 수 있기 때문에, 이 현상을 방지하기 위해서 np.max 함수의 값을 벡터에서 빼준 뒤 exp 를 씌운다.
이렇게 해주면 overflow 를 방지할 수 있으면서 동시에 원래 softmax 함수와 똑같이 계산할 수 있게 된다. 이런 트릭을 이용해서 softmax 함수를 이용하여 확률 벡터로 변환시킬 수 있다.
보통의 선형 모델로 출력된 값은 확률벡터가 아닌 경우가 많다. 왜냐면 보통 선형 결합이 모든 실수값에 해당하는 값들을 구성 성분으로 가질 수가 있기 때문에 그냥 계산하게 되면 확률로 해석할 수 없다. 따라서 softmax 함수를 이용해서 확률 벡터로 변환하고 이를 이용해 해석하고 실제 학습 때 사용하게 된다.
그러나 추론을 할 때는 one-hot 벡터로 출력값에서 최대값을 가진 주소만 1로 출력하는 연산을 사용하기 때문에, 학습이 아니라 추론하는 경우에는 굳이 softmax 를 사용하지는 않는다.
따라서 학습을 하는 경우에는 softmax 가 필요하지만 추론을 하는 경우에는 softmax 가 굳이 필요하지 않고 one-hot 벡터로 만드는 함수만 필요하게 된다.
보통 딥러닝 코드에서도 학습을 하는 경우에는 softmax 를 쓰지만 추론을 하는 경우에는 softmax 를 쓰지 않는다.
regression 문제가 아니라 분류 문제를 푸는 경우, 이와 같이 softmax 를 이용해서 어떤 선형 모델로 나온 출력값에 softmax 를 씌워줌으로써 분류 문제를 풀 수 있게끔 활용할 수 있다.
이처럼 softmax 를 씌워주게 되면 원래 선형 모델의 결과물을 원하는 의도로 바꿔서 해석할 수 있게 된다.
이것이 바로 활성화함수(activation function)를 사용하는 이유이다. 목적에 따라 softmax 를 포함한 다른 activation 함수들을 비선형 함수로 사용하여 신경망을 모델링하는 것이다.
즉 신경망은 선형모델과 활성화함수(activation function)를 합성한 함수다.
\[\mathbf{H} = (\sigma(\mathbf{z}_1), \cdots, \sigma(\mathbf{z}_n)) \quad \sigma(\mathbf{z}) = \sigma(\mathbf{Wx+b})\]
활성화함수는 선형모델이나 행렬곱을 사용하지 않고 비선형 함수로서 선형 모델로 나오게 된 출력물 각각의 원소에 적용된다.
즉 활성화함수 $\sigma$ 는 비선형함수로 잠재벡터 $\mathbf{z} = (z_1, \cdots, z_q)$ 의 각 노드에 개별적으로 적용하여 새로운 잠재벡터 $\mathbf{H} = (\sigma(\mathbf{z}_1), \cdots, \sigma(\mathbf{z}_n))$ 를 만드는 것이다.

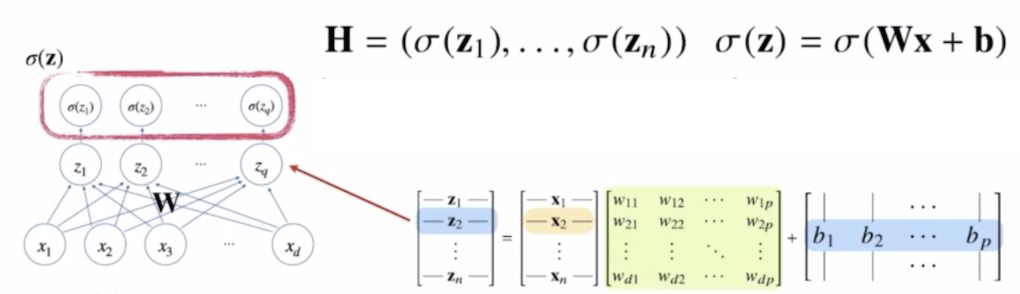
$image.png$
softmax 와 다른 활성화함수에 차이가 있다면, softmax 는 출력물의 모든 값을 다 고려해서 출력한다면 활성화함수는 다른 주소에 있는 출력값을 고려하지는 않고 오로지 해당 주소의 출력값만 가지고 계산한다.
따라서 softmax 는 주로 분류 문제의 출력층에서 사용되지만, Sigmoid 나 ReLU 와 같은 활성화함수는 벡터를 입력으로 받지 않고 하나의 실수값으로 입력을 받게 된다.
딥러닝에서는 이 활성화 함수를 이용해서 선형 모델로 나온 출력물을 비선형 모델로 변환시킬 수 있고 이렇게 변형을 시킨 벡터를 잠재벡터 또는 hidden vector 라고 부르게 된다. 이러한 벡터의 각 요소를 보통 뉴런이라고 부른다. 그리고 뉴런으로 이루어진 모델을 신경망(neural network)이라 부른다.
선형모델로 나온 출력물에 활성화함수를 씌우게 된 이 기본적인 뉴럴 네트워크를 역사적으로는 퍼셉트론이라 불렀다.

활성화함수

신경망에 대해 좀 더 알기 위해서는 활성화함수에 대해 자세히 알아야 한다.
활성화함수(activation function)는 실수값을 입력으로 받아서 출력을 실수값으로 뱉는, 즉 $\mathbb{R}$ 위에 정의된 비선형(nonlinear)함수로서 딥러닝에서 매우 중요한 개념이다.
만약 활성화함수를 쓰지 않고 딥러닝 모델을 구현하면 그 모델은 선형 모델과 전혀 차이가 없다.
그렇다면 딥러닝에서는 어떤 활성화함수를 많이 사용할까?

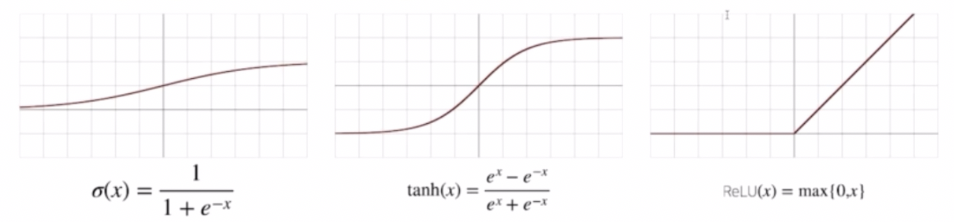
$image.png$
전통적으로 많이 사용했던 활성화함수는 시그모이드(Sigmoid) 함수나** 하이퍼볼릭 탄젠트(tanh)** 함수이다. 위 그림에서 첫번째가 sigmoid, 두번째 tanh 에 해당한다.
이 두 함수는 신경망의 역사와 퍼셉트론의 발전 역사에서 많이 사용됐던 함수다. 그러나 오늘날 가장 많이 쓰이는 활성화함수는 맨 오른쪽의 ReLU 이다.
활성화함수는 선형이 아니라 비선형 함수이고 sigmoid 와 tanh 는 딱 봐도 비선형 함수이다. 그러나 ReLU 를 잘 보면 $x < 0$ 일 때는 0 이고 $x > 0$ 일 때는 $x$ 로 표현되는 함수다. 선형함수와 별 차이 없는 것으로 보이지만, 이 함수는 아주 전형적인 비선형 함수로서 활성화함수로서 많은 좋은 성질들을 가지고 있다.
오늘날 딥러닝 연산에서 가장 많이 쓰이는 이 ReLU 에 대해서는 다른 포스트에서 더 알아보자.

신경망(Neural Network)

신경망은 선형모델과 활성화함수의 결합으로 표현하게 되는 함수다.
$\mathbf{x}$ 를 input 으로 받아서 선형모델을 통해 $\mathbf{z}$ 라는 출력을 얻으면, $\mathbf{z}$ 라는 출력물에 활성화함수를 씌워 새로운 잠재벡터인 $\mathbf{H}$ 를 만든다.
이 때 잠재벡터 $\mathbf{H}$ 를 다시 출력으로 연결시키는 선형모델을 생각해 볼 수 있다. 이렇게 선형모델이 두 개 쓰이면 2-layer 신경망이라고 부르게 된다.
이처럼 선형 모델과 활성화함수를 반복적으로 사용하는 것이 바로 오늘날 사용되는 딥러닝의 가장 기본적인 모형이다.

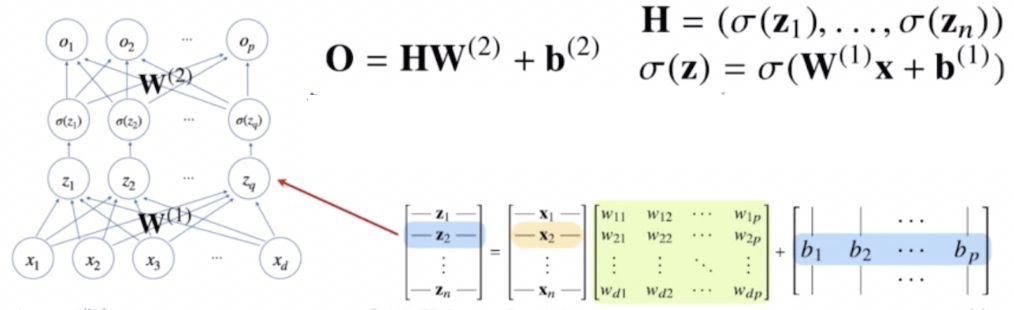
$image.png$
$\mathbf{x}$ 는 입력으로 받는 데이터 포인트다. 이를 입력으로 받아서 중간에 선형 모델을 거쳐 $\mathbf{z}$ 라는 변수들을 만들고, $\mathbf{z}$ 변수들에 활성화함수를 씌우는 은닉벡터를 연결시켜서 최종 출력물까지 연결한다. 이 때 중간에 여러 개의 층이 존재할 수 있다.
이렇게 선형 모델을 반복적으로 사용할 때 그 중간에는 활성화함수를 반드시 사용해야 한다. 그것이 신경망 구현의 가장 중요한 핵심 포인트다.
2-layer 신경망으로 부르는 이유는 가중치 행렬이 2개가 등장하기 때문이다.
잠재벡터 $\mathbf{H}$ 에 가중치 행렬 $\mathbf{W}^{(2)}$ 와 $\mathbf{b}^{(2)}$ 를 통해 다시 한 번 선형변환 해서 출력하게 되면 $(\mathbf{W}^{(2)}, \mathbf{W}^{(1)})$ 를 파라미터로 가진 2-layer 신경망이 된다.
즉 $\mathbf{x}$ 를 $\mathbf{z}$ 로 연결하는 $\mathbf{W}^{(1)}$ 행렬과 $\mathbf{H}$ 라는 벡터를 $\mathbf{O}$ 라는 출력 벡터로 연결하게 되는 $\mathbf{W}^{(2)}$ 행렬까지 가중치 행렬 2개를 사용하기 때문에 이 신경망을 2-layer 신경망으로 부르는 것이다.

MLP

위와 같이 선형 모델과 활성화함수를 반복적으로 적용하게 되면 multi-layer 퍼셉트론, 즉 MLP 라고 부르게 된다. MLP 는 오늘날 사용하는 딥러닝의 가장 기본적인 모형이며, 신경망이 여러 층 합성된 함수이다.

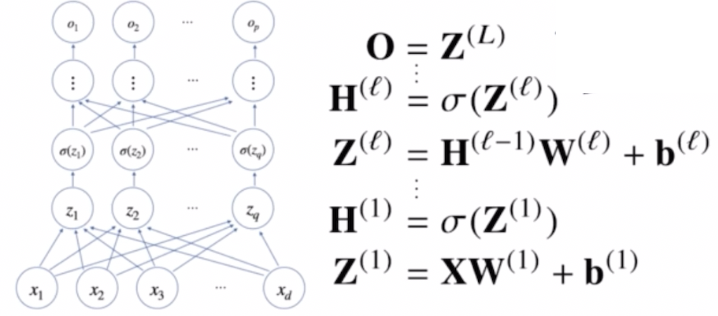
$image.png$
먼저 $\mathbf{x}$ 를 입력으로 받아서 $\mathbf{W}^{(1)}$ 가중치 행렬을 통해 $\mathbf{z}$ 로 보내고, 이 $\mathbf{z}$ 에 활성화함수를 씌워서 $\mathbf{H}$ 라는 잠재벡터로 보내게 된다.
활성화함수($\sigma$) 를 씌울 때, 활성화함수는 실수값을 입력으로 받는 것이기 때문에 각 벡터에 적용할 때도 각 벡터에 들어있는 요소들에 개별적으로 적용된다.
즉, $\sigma(\mathbf{Z})$ 는 수학적인 기호로 $\mathbf{Z}$ 에 해당하는 모든 변수들에 $\sigma$ 를 씌운 행렬이다. $\mathbf{Z}$ 라는 행렬이 들어왔을 때 그 행렬의 구성원소에 활성화함수를 씌운 행렬로 해석하면 된다.
따라서 $\mathbf{H}$ 라는 행렬은 $\mathbf{Z}$ 라는 행렬과 기본적으로 모양은 똑같고, 단지 $\mathbf{H}$ 에 있는 모든 구성성분들은 $\mathbf{Z}$ 의 구성성분에 활성화함수를 씌운 차이만 있다.
이 매커니즘을 반복적으로 적용해서 선형 모델과 활성화함수의 합성을 여러 층으로 이루게 되는 것이 바로 딥러닝의 기본적인 수식적 표현이 되는 것이다.
이러한 MLP 의 파라미터는 $\mathcal{L}$ 개의 가중치 행렬 $\mathbf{W}^{(\mathcal{L})}, \cdots, \mathbf{W}^{(1)}$ 로 이루어져 있고, 여기에 y 절편에 해당하는 $\mathbf{b}^{(\mathcal{L})}, \cdots, \mathbf{b}^{(1)}$ 절편 파라미터도 포함된다.
이렇게 총 $\mathcal{L}$ 개의 순차적인 신경망 계산을 통해서 최종 출력물로 $\mathbf{O}$ 라는 출력 행렬이 나온다. 이렇게 계산하는 순차적인 신경망 계산을 forward propagation, 즉 순전파라고 부른다.
따라서 순전파는 학습이 아니라 주어진 입력이 왔을 때, 출력물을 내뱉는 과정을 표현하는 연산이다.

왜 층을 여러개 쌓을까?

왜 딥러닝, 신경망에서는 층을 여러개 쌓을까?
이론적으로는 2-layer 신경망으로도 임의의 연속함수를 근사할 수 있다. 이를 universal approximation theorem 이라 부른다.
그러나 이론적으로는 보장을 해주지만 실제로 학습을 돌릴 때는 2-layer 신경망으로는 무리가 있다.
universal approximation theorem 에서 얘기하는 것은 2-layer 신경망이라 하더라도 굉장히 많은 뉴런이 필요할 수도 있다.
층이 깊을수록 목적함수를 근사하는데 있어서 필요한 뉴런(노드)의 숫자가 훨씬 빠르게 줄어들어 좀 더 효율적으로 학습이 가능하다.
따라서 층이 깊어질수록 적은 파라미터로도 훨씬 더 복잡한 함수를 표현할 수 있다.
만약에 층이 얇으면 필요한 뉴런의 숫자가 기하급수적으로 늘어나서 많은 뉴런이 담기게 된 넓은(wide) 신경망이 되어야 한다.
그렇기 때문에 복잡한 패턴을 배우기 위해서 많은 층을 쌓은 딥러닝 모델을 사용하게 되면 효율적으로 근사가 가능하다.
여기서 주의할 점은, 층이 깊다고 해서 좀 더 복잡한 함수를 근사를 할 수는 있지만, 그렇다고 해서 최적화가 더 쉽다는 얘기는 할 수 없다.
다시 말해, 좀 더 복잡한 함수를 표현하면 할수록 최적화는 훨씬 더 많은 노력을 기울여야 한다. 층이 깊어질수록 딥러닝 모델은 학습하기 어려워진다는 것이다.
이러한 맥락은 합성곱 신경망(CNN)의 residual block의 등장과정에서 잘 드러난다.
정리하면, 딥러닝에서 층을 여러개 쌓는 이유는 좀 더 적은 뉴런과 노드를 가지고도 복잡한 패턴을 표현할 수 있기 때문이다.

딥러닝 학습원리 : 역전파 알고리즘

이제부터 딥러닝 학습 원리인 역전파(back propagation) 알고리즘을 보자.
앞서 본 순전파(forward propagation) 의 경우 $\mathbf{x}$ 라는 입력을 받아서 최종 출력까지 보낼 때 선형모델과 활성화함수를 반복적으로 적용하는 연산이었다.
즉 순전파는 딥러닝의 학습이 아니라 주어진 입력이 왔을 때 출력물을 내뱉는 과정을 표현하는 연산이었다.
역전파는 경사하강법을 적용해서 각각의 가중치 행렬들을 학습시킨다. 이 때 각각의 가중치 행렬에 대한 그레디언트 벡터를 계산해야 경사하강법을 적용할 수 있다.
잠시 떠올려보면, 선형회귀분석에서 경사하강법을 적용할 때 선형모델의 계수에 해당하는 $\beta$ 에 해당하는 그레디언트 벡터를 계산해서 파라미터를 업데이트 했었다.
딥러닝에서도 똑같다. 다만 각 층에 존재하는 파라미터들에 대한 미분을 계산해서 그 미분들을 가지고 파라미터를 업데이트한다. 따라서 경사하강법으로 가중치를 업데이트를 할 때, 가중치 행렬들의 모든 원소와 y 절편을 포함한 모든 원소 개수만큼 경사하강법이 적용된다.
다시 말해 그냥 선형모델에서 경사하강법을 적용하는 것보다 훨씬 더 많은 파라미터들에 대해서 경사하강법이 적용된다.
문제는 선형모델의 경우 경사하강법을 한 층에서만 계산하는 원리이기 때문에 그레디언트 벡터를 동시에 계산할 수 있지만, 딥러닝에서는 순차적으로 각 층별로 쌓아서 계산하기 때문에 그레디언트 벡터를 계산할 때 한번에 계산할 수는 없다.
따라서 역전파 알고리즘을 통해서 역순으로, 순차적으로 한번씩 계산을 해주게 된다.
forward propagation 과 비슷하게 역전파도 미분을 계산할 때 순차적으로 계산해야 한다. 따라서 딥러닝은 역전파 알고리즘을 이용하여 각 층에서 사용된 파라미터 ${ \mathbf{W}^{(\ell)}, \mathbf{b}^{(\ell)} }^L_{\ell=1}$ 를 학습한다.
손실함수를 $\mathscr{L}$ 이라 했을 때, 역전파는 $\partial\mathscr{L} / \partial\mathbf{W}^{(\ell)}$ 정보를 계산할 때 사용된다. 즉, 역전파 알고리즘은 각각의 가중치 행렬 $\mathbf{W}^{(\ell)}$ 에 대해서 손실함수에 대한 미분을 계산할 때 사용하는 것이다.

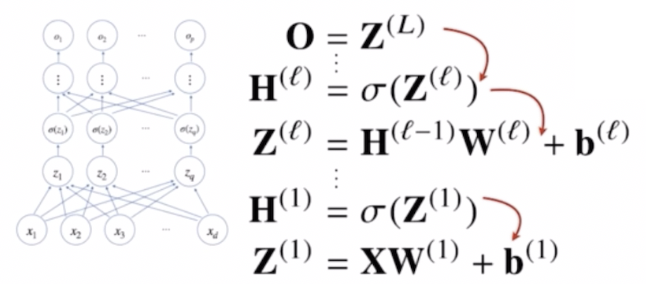
$image.png$
이 때 아래로 전달되는 것이 각 층에서 계산된 그레디언트이다.
아래 층으로 그레디언트가 전달되어야 하는 이유는 밑층의 그레디언트 벡터를 계산할 때, 즉 저층(1층, 2층)에 있는 그레디언트 벡터를 계산할 때는 위층의 그레디언트 벡터가 필요하기 때문이다.
다시 말해 역전파 알고리즘은 먼저 위층에 있는 그레디언트 벡터를 계산한 다음에 점점 밑층으로 가면서 그레디언트 벡터를 계산하고 업데이트하는 방식이라고 이해할 수 있다.
따라서 역전파 알고리즘의 원리는 각 층 파라미터의 그레디언트 벡터를 윗층부터 역순으로 계산하면서 역순으로 그레디언트 벡터를 전달하는 원리다.
이 때 합성함수의 미분법인 연쇄법칙을 사용해서 그레디언트 벡터를 전달하게 된다.

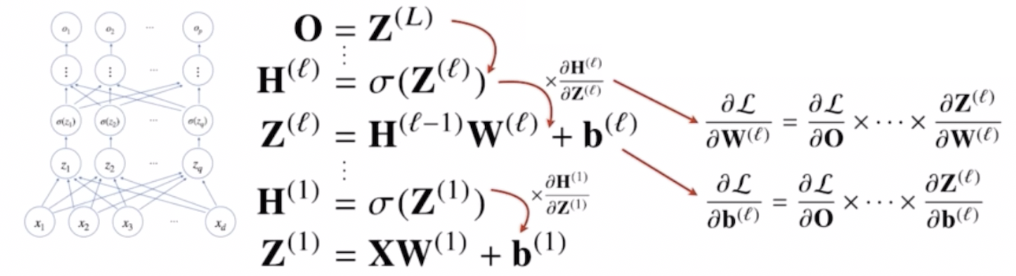
$image.png$
위 그림에서 수식을 보면, $\ell$ 번째 층에 있는 가중치행렬과 절편 벡터에 해당하는 $\mathbf{b}^{(\ell)}$ 의 그레디언트 벡터를 계산하기 위해 연쇄법칙을 이용해 식을 전개했음을 알 수 있다.
식을 보면 출력($\mathbf{O}$)에서부터 시작해서 $\mathbf{W}^{(\ell)}$ 보다 위층에 존재하는 모든 그레디언트 벡터들을 전부 계산해야만 $\ell$ 번째 가중치 행렬과 $\ell$ 번째 절편 벡터에 해당하는 그레디언트 벡터를 계산할 수 있다.
딥러닝은 이렇게 연쇄법칙을 통해서 그레디언트를 점점 밑 층으로 전달하면서 가중치들을 업데이트 한다. 이 알고리즘을 back propagation, 역전파 알고리즘이라 부르게 된다.

역전파 알고리즘 원리

역전파 알고리즘은 합성함수 미분법인 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation, autograd)을 사용한다. 이것이 오늘날 딥러닝 프레임워크에서 딥러닝을 학습시키는 방법이다.
$z = (x+y)^2$ 이라는 함수가 있다고 했을 때, $z$ 를 $x$ 에 대해서 미분하는 원리가 뭘까?
$z$ 함수를 둘로 쪼갤 수 있다. $x+y$ 를 $w$ 로 표현하게 되면 $z = w^2$ 으로 표현할 수 있다. 이렇게 $z = (x+y)^2$ 을 두 함수의 결합, 즉 $z = w^2, w = x+y$ 의 결합으로 표현할 수 있다는 것이다.
합성함수로 표현된 $z, w, x, y$ 의 관계를 이용해서 미분을 계산할 수 있다. $x$ 에 대한 $z$ 의 미분은 아래와 같이 계산된다.
\[\frac{\partial z}{\partial x} = \frac{\partial z}{\partial w} \frac{\partial w}{\partial x}\]
즉 연쇄법칙을 이용해서 원래 계산하고 했던 $z$ 에 대한 $x$ 의 미분을 $z$ 에 대한 $w$ 의 미분과 $w$ 에 대한 $x$ 의 미분, 두 미분의 곱으로 계산할 수 있다.
$z$ 를 $w$ 로 미분하게 되면 $2w$ 가 나오게 되고, $w$ 를 $x$ 로 미분하게 되면 1 이 나오게 된다. 따라서 아래 식이 구해진다.
\[\frac{\partial z}{\partial x} = \frac{\partial z}{\partial w} \frac{\partial w}{\partial x} = 2w \; \cdot \; 1 = 2(x+y)\]
결과적으로 $z$ 를 $x$ 로 미분하게 되면 $2(x+y)$ 로 표현되게 되는데, 이 결과값을 연쇄법칙을 통해서 구한 것이다.
이 연쇄법칙의 작동원리가 그대로 동작하는 것이 바로 딥러닝에서 사용되는 back propagation 알고리즘이다.
주의할 점은, 딥러닝에서 각 뉴런에 해당하는 값을 텐서라고 표현하는데, 각각의 텐서값을 컴퓨터의 메모리로 저장해줘야만 back propagation 알고리즘이 동작하게 된다.
즉 $z$ 를 $x$ 로 미분했을 때 $2x + 2y$ 라는 결과값이 나왔는데, $x$ 에 대한 미분을 계산하고 싶으면 같이 사용된 $x$ 와 $y$ 라는 값을 알고 있어야만 미분을 계산할 수 있다는 것이다.
따라서 각 뉴런 또는 노드에 해당하는 텐서값을 컴퓨터 메모리에 저장을 해둬야만 미분 계산이 가능하기 때문에, back propagation 알고리즘은 forward propagation 보다 좀 더 메모리를 많이 사용하게 된다.
다시 말해 순전파는 굳이 미분값을 저장할 필요 없지만, 역전파는 값을 계산하기 위해서 미분을 저장해야 하기 때문에 이런 메모리 사용 측면에서 차이가 있다.

역전파 예제 : 2-layer 신경망

2-layer 신경망은 $\mathbf{W}^{(1)}$ 과 $\mathbf{W}^{(2)}$ 두 개의 가중치 행렬을 파라미터로 가지고 있다.
두 가중치 행렬 중간에 히든(잠재)벡터 $\mathbf{h}$ 는 입력 $\mathbf{x}$ 로부터 선형모델로 변환된 $\mathbf{z}$ 에다가 활성화함수($\sigma$)를 씌운 형식으로 정의가 되어있다. 이 잠재벡터를 다시 출력으로 연결시키는 선형모델을 한 번 더 써서 2-layer 신경망을 구현한다.
이 때 첫번째 층에 해당하는 $\mathbf{W}^{(1)}$ 행렬에 대해서 경사하강법을 쓰고 싶다면, 그레디언트 벡터($\nabla_{\mathbf{W}^{(1)}}\mathcal{L}$)를 계산하기 위해 손실함수($\mathcal{L}$) 에 대해 $\mathbf{W}^{(1)}$ 로 편미분을 취해주어야 한다.
이 때 $\mathbf{W}^{(1)}$ 은 행렬이기 때문에 각 성분($W^{(1)}_{ij}$)에 대한 편미분을 구해주어야 한다.

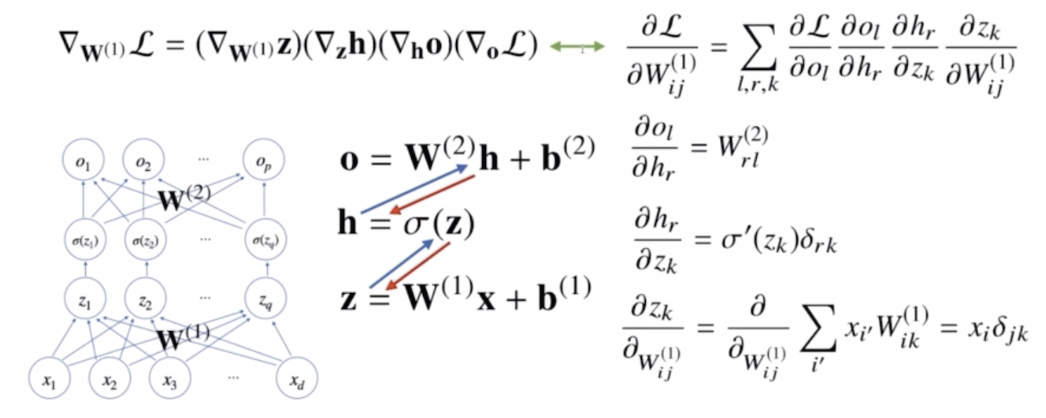
$image.png$
$\mathbf{W}^{(1)}$ 로 손실함수 $\mathcal{L}$ 에 대한 미분을 계산하는 것은 연쇄법칙을 순서대로 적용하게 되는 원리다.
먼저 손실함수 $\mathcal{L}$ 을 출력 $o$ 로 미분한 다음, 출력 $o$ 를 다시 $h$ 로 미분하고, 그 $h$ 를 다시 잠재변수인 $z$ 로 미분하고, 그 $z$ 를 $W^{(1)}_{ij}$ 로 미분한 것을 순차적으로 곱한 형태로 역전파 알고리즘이 동작하게 된다.
위 그림에서 화살표로 볼 때, 각각의 수식들 $\mathbf{o, h, z}$ 가 파란색 화살표로 연결되어 있는 것이 순전파, 빨간색 화살표가 역전파에서 미분이 전달되는 원리가 된다.
이처럼 손실함수를 첫번째 가중치 행렬에 대한 편미분으로 계산하면 복잡한 수식들이 계산된다. 총 4번의 연쇄법칙이 적용되어 최종 그레디언트 벡터를 계산할 수 있다.
각각의 연쇄법칙이 적용될 때, 미분값이 각 층마다 계산되고 이를 이용해서 실제 가중치 행렬 $\mathbf{W}^{(1)}$ 에 대한 경사하강법을 적용하기 위한 그레디언트 벡터를 계산할 수 있다.
최종적으로 계산된 값을 이용해서 경사하강법으로 실제 딥러닝을 학습하는데 사용하게 된다.

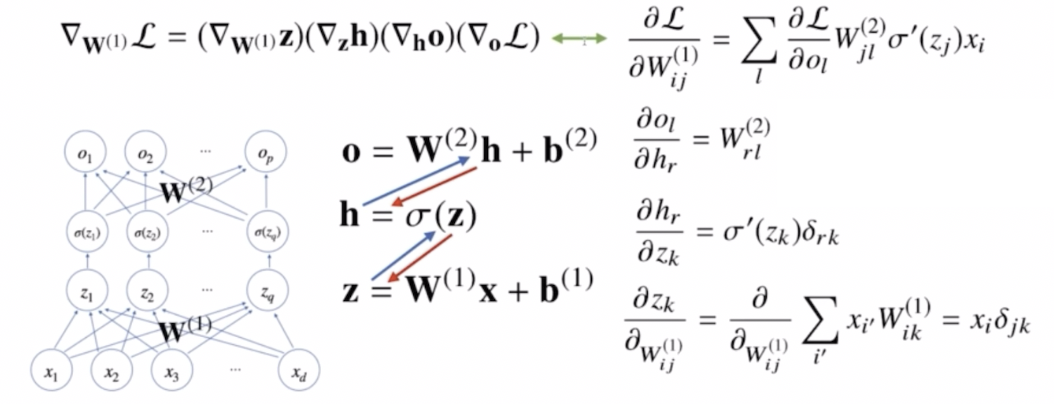
$image.png$
여기서 최종식을 보면 아래와 같다.
\[\begin{aligned} \frac{\partial \mathcal{L}}{W^{(1)}_{ij}}&= \sum_l \frac{\partial\mathcal{L}}{\partial o_l}W^{(2)}_{rl}\sigma^\prime(z_k)\delta_{rk}x_i\delta_{jk} \\ &= \sum_l \frac{\partial\mathcal{L}}{\partial o_l}W^{(2)}_{jl}\sigma^\prime(z_j)x_i \end{aligned}\]
이 때 $\delta_{rk}$ 와 $\delta_{jk}$ 는 각각 $h_r$ 에 대한 $z_k$ 의 편미분과 $z_k$ 에 대한 $W^{(1)}_{ij}$ 의 편미분에서 나오는 크로네커 델타를 뜻한다.
- 크로네커 델타는 두 개의 인덱스가 동일할 때 1이 되고, 그렇지 않을 때는 0이 되는 함수다.
  \[\delta_{ij} = \begin{cases} 1 \quad \text{if} \; i=j \\ 0 \quad \text{if} \; i\neq j \end{cases}\]
- 위 수식에서 $\delta_{rk}\delta_{jk}$ 때문에 $r=k=j$ 인 경우의 항만 남게 된다.
- 이처럼 역전파 과정에서 크로네커 델타가 등장하는 이유는, 역전파 과정에서 특정 행렬의 미분을 계산할 때 행렬의 원소들이 특정 조건에서만 영향을 주기 때문이다.
- 예를 들어 위 그림에서 보면 알 수 있듯 $\sigma(z_1)$ 은 $z_1$ 에만 의존적이고, $r \neq k$ 인 입력 $z_k$ 는 $h_r$ 에 영향을 주지 않는다.
- 따라서 $r = k$ 인 경우에만 활성화함수의 미분 값 $\sigma^{\prime}(z_k)$ 이 결과로 남고, 그렇지 않은 경우에는 0 이 되어버린다. 크로네커 델타는 이런 상황에서 특정 뉴런 간의 관계를 수학적으로 명확하게 나타내는 도구로 사용된다.
- $z_k$ 에 대한 $w^{(1)}_{ij}$ 의 편미분도 마찬가지다. $z_k=\sum_{i}x_iW_{ik}$ 이므로 $k=j$ 인 경우에만 $z_k$ 에 영향을 미치고 편미분으로 $x_i$ 가 남는다. 그렇지 않은 경우에는 0 이 되어버린다.
- 따라서 $r=k=j$ 인 경우 $\delta_{rk}\delta_{jk}$ 가 1 이 되어 수학적으로 명확한 관계가 나타나게 된다.
딥러닝을 학습시킬 때는 이렇게 계산한 각각의 가중치 행렬의 그레디언트 벡터를 SGD 를 이용해서 학습한다. 이 때 각각의 파라미터들을 미니배치로 번갈아가며 학습을 하게 된다.
이렇게 되어 주어진 목적식을 최소화하는 파라미터들을 찾을 수가 있고 이 원리가 오늘날 사용하게 되는 딥러닝의 학습 원리다.
최종적으로 정리하면, 딥러닝은 선형모델과 활성화함수들의 여러층에 대한 합성함수이고, 합성함수이기 때문에 그레디언트를 계산하려면 연쇄법칙이 필요한 것이다. 이 연쇄법칙을 적용한 학습방법 알고리즘으로 역전파를 쓴다.
수학적으로 좀 복잡했지만, 오늘날의 딥러닝 프레임워크는 이 모든 과정들을 자동화해서 계산할 수 있다. 따라서 원리적으로 이해하는데 초점을 두고, 실제 구현할 때는 편하게 구현할 수 있으니 걱정하지 말자!

맨 위로 이동 ↑

Bkkhyunn

[AI Math] 3. Deep Learning 학습방법

딥러닝

선형 모델

softmax

활성화함수

신경망(Neural Network)

MLP

왜 층을 여러개 쌓을까?

딥러닝 학습원리 : 역전파 알고리즘

역전파 알고리즘 원리

역전파 예제 : 2-layer 신경망

댓글 남기기

관련 게시글

[AI Math, Optimization] Gradient, Jacobian 및 Hessian

[Loss, AI Math] Variational Inference

[AI Math] 12. RNN 연산

[AI Math] 11. CNN 연산