[AI Math] 12. RNN 연산

RNN 연산

• RNN(Recurrent Neural Network)은 지금까지 배웠던 CNN 과 다르게 시계열 데이터 또는 sequence 데이터에 많이 적용되는 네트워크다.
• 주로 i.i.d. 라고 말하는 독립/동등 분포로 들어오는 데이터와 달리 시계열 데이터의 경우 독립적으로 들어오지 않는 경우가 상당히 많다.
• 그런 데이터에서 어떻게 모델을 설계하고, 설계한 후 어떻게 학습을 하는지 보자.
• RNN 은 모델 자체의 설계는 어렵지 않지만, 왜 이렇게 설계해야 하는지에 대한 이해가 필요하다.

시퀀스 데이터

• 시퀀스 데이터는 순차적으로 들어오는 데이터를 말한다. 소리, 문자열, 주가 등의 데이터를 시퀀스(sequence) 데이터로 분류한다.

  

• 음성은 소리 데이터다. 문자열 데이터의 경우 문자를 임의적으로 나열하는 것이 아니고 문법, 문맥, 단어의 사용, 문장을 쓸 때 앞에서의 의도 등이 반영되어 텍스트들이 시퀀스로 기록된다.

• 주가의 경우 시계열(time-series)데이터로서, 독립된 정보들이 주가에 반영되는 것이 아니라 시간 순서대로 시장의 상황, 불규칙적인 사건의 발생 등이 종합되어 시점별로 나타난다. 즉 시계열(time-series)데이터는 시간 순서에 따라 나열된 데이터로 시퀀스 데이터에 속한다.

  \[X_1, \ldots, X_t, \dots\]
• 이러한 시퀀스 데이터의 경우 이벤트의 발생 순서가 중요한 요소 중 하나로 동작하게 된다.
• 시퀀스 데이터는 독립동등분포(i.i.d. - independent and identical distribution) 가정을 위배하기 쉽다.
• 예를 들어 “개가 사람을 물었다” 와 “사람이 개를 물었다” 라는 두 개의 문장이 있을 때, 개가 사람을 문 경우는 발생할 수 있는 일이지만 사람이 개를 물었다는 것은 문법적으로는 맞지만 위치를 바꾸게 됨으로써 의미도 바뀌게 된다. 또한 데이터에서 관측되는 빈도도 바뀌게 된다.
• 이렇게 순서를 바꿨을 때 데이터의 확률분포가 바뀌거나 또는 과거의 정보를 가지고 미래를 예측할 때 과거의 정보에 손실이 발생해서 과거의 정보 일부를 쓸 수 없고 한정된 정보만 쓸 수 있는 경우에, 시퀀스 데이터는 예측 분포의 성격이 달라질 수 있다.
• 즉 시퀀스 데이터는 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 된다.
• 따라서 과거의 정보 또는 앞뒤 맥락 없이 미래를 예측하는 것은 어렵고 함부로 데이터의 순서를 바꿈으로써 인위적으로 조작해서 예측하게 되면 원하고자 하는 모델링이 잘 되지 않을 확률이 높게 된다.
• 이처럼 시퀀스 데이터는 독립동등분포 가정이 깨지기 쉽기 때문에 텍스트라던지 주가, 음성 데이터들에 대해서 위치를 바꿀 때 굉장히 조심해야 한다.
• 이런 특성을 반영해서, 시퀀스 데이터에서 학습을 진행할 때는 순차적으로 들어오게 되는 정보들을 어떻게 반영할지를 고민해야 한다.

시퀀스 데이터 다루기

• 시퀀스 데이터를 다룰 때, 즉 과거의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해서 조건부확률을 이용한다.

• $X_1$ 부터 $X_t$ 까지의 결합확률 분포 $P(X_1, \ldots, X_t)$ 까지를 조건부확률 법칙을 통해서 쪼갤 수 있다.

  \[P(X_1, \ldots, X_t) = P(X_t \vert X_1, \ldots, X_{t-1})P(X_1, \ldots, X_{t-1})\]
• $X_1$ 부터 $X_{t-1}$ 까지의 정보가 주어졌을 때 $X_t$ 에 대한 조건부확률분포와 $X_1, \dots, X_{t-1}$ 까지의 결합확률을 곱해주게 되면 원래 모델링하고자 했던 결합확률 분포 $P(X_1, \ldots, X_t)$ 를 모델링할 수 있다.

• 이런 식으로 조건부확률로 분해하는 것을 반복적으로 적용하게 되면 아래의 수식처럼 $X_1$ 부터 $X_{s-1}$ 까지를 조건부로 하여 $X_s$ 를 추론하는 것을 $X_1, \ldots, X_t$ 까지 곱해주는 형태로 표현할 수 있다.

  \[\small\begin{aligned} P(X_1, \ldots, X_t) &= P(X_t\vert X_1, \ldots X_{t-1})P(X_1, \ldots, X_{t-1}) \\ &= P(X_t\vert X_1, \ldots X_{t-1})P(X_{t-1}\vert X_1, \ldots, X_{t-2})P(X_1, \ldots, X_{t-2}) \\ & \quad \quad \vdots \\ &= \prod^t_{s=1}P(X_s\vert X_{s-1},\ldots,X_1) \end{aligned}\]
• $\prod^t_{s=1}$ 은 $s = 1, \ldots, t$ 까지 모두 곱하라는 기호다. 급수는 더하는 기호인데, 이 기호는 모두 곱하라는 기호다.
• 조건부확률을 모델링할 때는 위 식처럼 곱셈으로 조건부확률을 전개하기 때문에, 위와 같은 방식으로 결합확률분포를 조건부확률로 모델링하는 것이 가능하다.
• 정리하면, 맨 초기 시점인 $X_1$ 부터 $X_s$ 바로 직전의 과거 정보인 $X_{s-1}$ 시점 까지의 정보를 사용해서 현재 시점인 $X_s$ 를 모델링하는 이 조건부확률분포를 반복적으로 곱해주는 형태로 모델링할 때 사용하는 것이다. 이것이 시퀀스 데이터를 다룰 때 많이 사용하는 방법이다.

• 따라서 $X_1$ 부터 $X_{t-1}$ 까지의 정보가 조건부로 주어진 상황에서 현재 정보인 $X_t$ 를 모델링하는 이 조건부확률분포가 결국 시퀀스데이터를 다루는 가장 기본적인 방법론에 속한다.

  \[X_t \sim P(X_t \vert X_{t-1}, \ldots, X_1)\]
• 유의할 것은 위 조건부확률을 다룰 때 과거의 모든 정보를 사용하는 것처럼 기재했지만, 사실 시퀀스데이터를 분석할 때 모든 과거의 정보들이 필요한 것은 아니다.
  • 가령 어떤 기업의 주가를 가지고 모델링할 때, 기업이 20 ~ 30년된 오래된 기업이라고 할 때, 이 기업의 창설시점부터의 데이터가 필요한 것은 아니다. 보통 주가를 예측하는 경우 기업이 5 년정도 지속하고 있던 사업의 정보나 최근의 정보를 주로 다뤄 예측한다.
  • 즉 과거의 데이터를 가지고 현재 정보를 예측할 때 반드시 꼭 모든 정보를 가지고 예측해야만 하는 것은 아니라는 것이다.
  • 일부 데이터 분석 결과에서는 몇 개의 과거 정보들은 truncation 하는 것을 테크닉으로 이용할 수 있다.
  • 이처럼 조건부확률 모델링에서 과거의 정보 모두를 활용할 필요는 없다. 주가, 텍스트, 음성에서도 똑같다.
• 시퀀스 데이터를 다룰 때는 과거의 어떤 시점에서의 정보는 필요하지 않을 때가 있고, 아주 먼 과거의 정보가 필요할 때도 있지만, 어떤 경우에 필요하고 어떤 경우에 필요하지 않을 때가 있다.
• 이러한 필요성에 따라서 과거의 정보를 어떻게 활용할 지 시퀀스 데이터를 다룰 때 모델링의 방법에 따라 달라진다.
• 조건부확률분포를 반복적으로 사용하여 미래 예측에 대한 분포로 모델링할 수 있다.

• 문제는 시퀀스 데이터를 다루기 위해서는 길이가 가변적인 데이터를 다룰 수 있는 모델이 필요하게 된다.

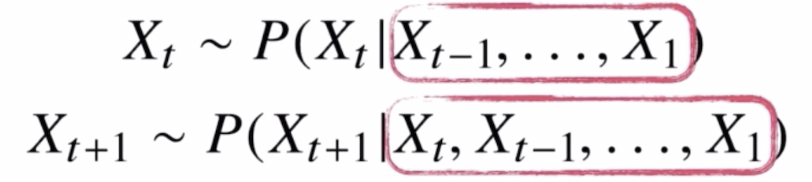  조건부의 길이가 가변적이다.

• $X_t$ 의 경우 $X_1$ 부터 $X_{t-1}$ 까지 $t-1$ 개의 정보가 필요하지만, $X_{t+1}$ 의 경우 $X_1$ 부터 $X_t$ 까지 $t$ 개의 데이터를 다룰 수 있는 모델이 필요하다. 즉 조건부에 들어가는 데이터 길이가 가변적이다.
• 이런 식으로 각각의 시퀀스 시점에서 다뤄야 할 데이터의 길이가 달라지기 때문에 조건부확률분포로서 시퀀스 데이터를 다룰 때에는 이런 가변적인 길이의 데이터를 다룰 수 있는 모델과 방법론이 필요하다.

• 과거의 모든 정보를 가지고 예측을 할 필요는 없기 때문에, 만약 현재 시점에서 봤을 때 최근 몇 년간의 데이터 또는 앞서 몇 개의 문장만 보고서도 충분히 모델링이 가능한 문제 같은 경우, 가변적으로 초기 시점부터의 모든 정보를 다 사용할 필요 없이 고정된 길이 $\tau$ 만큼의 시퀀스만 사용해서 예측을 할 때 이용할 수 있다.

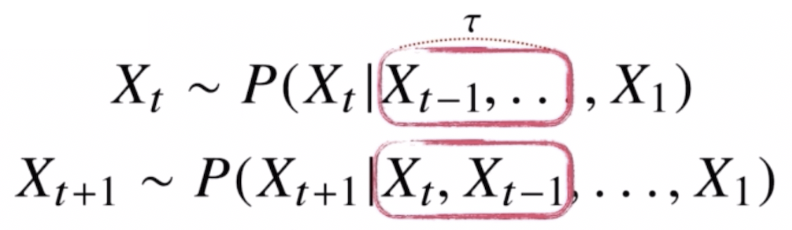  AR model. 고정된 길이만큼만 사용한다.

• 이런 경우에는 가변적인 길이가 아니라 $\tau$ 라는 고정된 길이를 사용하는 모델이 된다.
• 가령 $X_t$ 의 분포를 계산할 때 $t-1$ 부터 시작해서 $t-\tau$ 까지 $\tau$ 개의 정보를 활용하고, $t+1$ 시점의 미래 예측을 위해서는 $X_t$ 부터 $t-\tau+1$ 까지 $\tau$ 개의 정보를 활용할 수 있다.
• 이처럼 고정된 길이 $\tau$ 만큼의 시퀀스만 사용하는 경우 AR($\tau$) 자기회귀모델(Autoregressive Model)이라 부른다. 즉 Autoregressive Model 중에서 period 가 $\tau$ 인 경우에 해당하는 것이다.
• 이런 형태의 모델링을 통해서 시퀀스 데이터를 다룰 수 있다. 문제는 이런 $\tau$ 는 하이퍼 파라미터, 즉 모델링을 하기 전에 사전에 정해줘야 하는 변수가 된다. 이 $\tau$ 를 결정하는 것에 사전지식이 필요할 때가 있다. 문제에 따라서는 $\tau$ 가 바뀔 수도 있다.

• 어떤 경우에는 짧은 $\tau$ 만 있어도 되지만, 어떤 경우에는 먼 과거의 정보들도 필요할 때가 있다. 이런 경우에 사용하는 모델링 방법이 RNN 의 기본 모형인 latent autoregressive model 이 된다. 즉 잠재자기회귀 모델이다.

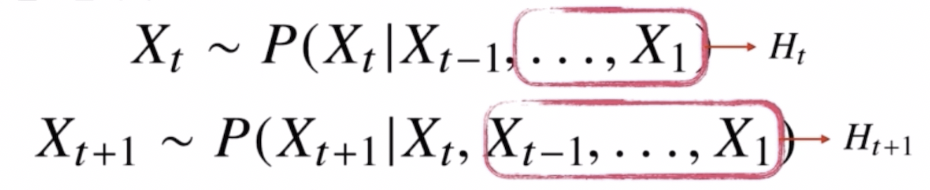  잠재AR model

• 바로 이전 과거의 정보와 훨씬 이전의 정보들을 묶어서, 즉 직전 정보와 직전 정보가 아닌 다른 과거의 정보들을 따로 모아서, 이전 직전의 정보는 $X_{t-1}$ 로 묶고, $X_{t-1}$ 이전의 다른 정보들은 $H_t$ 라는 잠재변수로 인코딩하게 된다.
• 그러면 $X_t$ 를 예측을 할 때는 $X_1, \dots, X_{t-2}$ 까지의 정보를 가지고 $H_t$ 라는 잠재변수를 만들게 되는 것이다. $X_{t+1}$ 을 예측할 때는 $X_1, \dots, X_{t-1}$ 까지의 정보를 가지고 $H_{t+1}$ 이라는 잠재변수를 만들게 되는 것이다.
• 이렇게 되는 경우, 바로 직전의 정보와 잠재변수 이 두 가지 데이터만 가지고 현재 시점, 미래 시점을 예측할 수 있기 때문에 이제부터는 길이가 가변적이지 않고 고정된 길이의 데이터를 가지고 모델링할 수 있다.
• 이처럼 잠재자기회귀 모델의 장점은 과거의 모든 데이터를 다 활용해서 예측할 수 있고, 가변적인 데이터 문제를 고정된 길이의 문제로 바꿀 수 있다.
• 잠재AR 모델의 문제는 과거의 정보들을 잠재변수로 어떻게 인코딩 할 것인지가 선택의 문제가 된다.

• 이 문제를 해결하기 위해 등장한 것이 RNN 순환신경망이 된다.

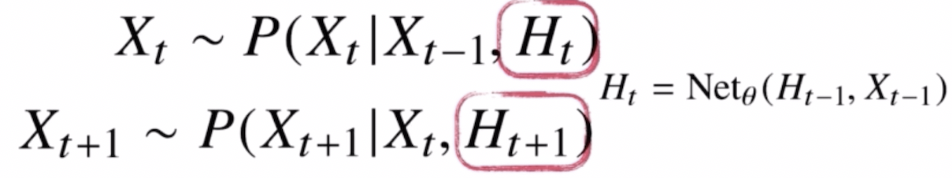  RNN

• $H_t$ 를 뉴럴네트워크에 과거 바로 이전의 정보와 이전 잠재변수를 넣어 예측한다. 이 모델이 바로 시퀀스 데이터의 패턴을 학습할 수 있게 설계된 RNN 이 된다.

RNN(Recurrent Neural Network)

• RNN 을 좀 더 이해해보자. 가장 기본적인 RNN 모형은 MLP 와 유사한 모양이다.

  \[\begin{aligned} \mathbf{O} &= \mathbf{HW}^{(2)} + \mathbf{b}^{(2)} \\ \mathbf{H} &= \sigma(\mathbf{XW}^{(1)} + \mathbf{b}^{(1)}) \end{aligned}\]
• MLP 는 입력 행렬에 해당하는 $\mathbf{X}$ 로부터 가중치 행렬 $\mathbf{W}$ 을 곱해주고 bias term 을 더해준 후에 활성화 함수 $\sigma$ 를 합성해서 잠재변수 $\mathbf{H}$ 를 만든다.
• 이 잠재변수 $\mathbf{H}$ 에 다시 선형모델을 결합시켜서 출력 행렬인 $\mathbf{O}$ 를 얻는다.

• 이 때 가중치 행렬 $\mathbf{W}^{(1)}$ 와 $\mathbf{W}^{(2)}$ 는 각각 첫번째, 두번째 layer 의 가중치 행렬이고, 시퀀스와 상관없이 불변인, 똑같이 share 하게 되는 가중치 행렬이다.

  \[\begin{aligned} \mathbf{O}_t &= \mathbf{H_tW}^{(2)} + \mathbf{b}^{(2)} \\ \mathbf{H}_t &= \sigma(\mathbf{X_tW}^{(1)} + \mathbf{b}^{(1)}) \end{aligned}\]
• 이 MLP 모델에 시퀀스 데이터를 입력으로 집어넣어서 모델링하게 되면, 위 모델로는 과거의 정보를 다룰 수 없다.
• 입력 행렬이 $t$ 번째 데이터, 즉 $\mathbf{X}_t$ 가 들어오기 때문에 현재 시점의 데이터만 가지고 예측을 해야 하는 모델이 된다. 이러한 기본적인 MLP 의 모형은 과거의 정보를 잠재변수에 다룰 수 없다.

• 그러면 여기서 어떻게 하면 과거의 정보를 $\mathbf{H}_t$ 안에 담을 수 있을까?

  

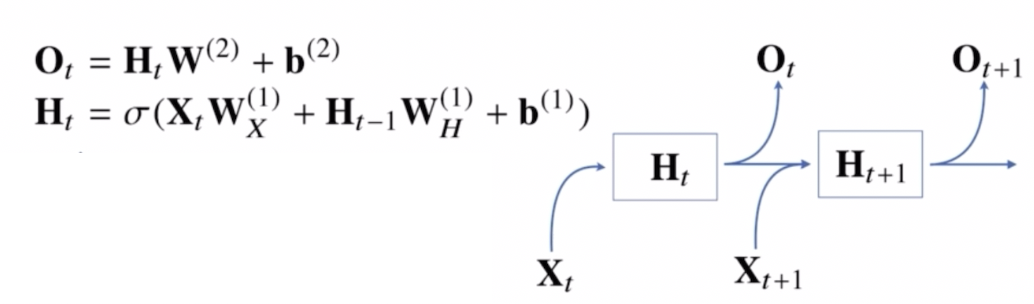
• 위와 같은 모양으로 과거의 정보를 다룰 수 있다.
• 앞의 MLP 와 차이점이 있다면,
  • $\mathbf{H}_t$ 를 표현할 때 중간에 등장하는 새로운 가중치 행렬이 등장한다.
  • 입력으로부터 전달하게 되는 $\mathbf{W}_X$ 가중치 행렬과 이전 잠재변수로부터 정보를 전달받게 되는 $\mathbf{W}_H$ 라는 새로운 가중치 행렬을 만들게 된다.
  • 그러면 $t$ 번째 잠재변수는 현재 들어온 입력벡터 \(\mathbf{X}_t\), 이전 시점의 잠재변수 $\mathbf{H}_{t-1}$ 을 받아서 현재 시점의 잠재변수 $\mathbf{H}_t$ 를 만들어낸다.
  • 이 $\mathbf{H}_t$ 를 이용해서 현재 시점의 출력인 $\mathbf{O}_t$ 를 만들어내게 된다.
  • 이 때 잠재변수 \(\mathbf{H}_t\) 를 다음 시점, 즉 \(\mathbf{H}_{t+1}\) 에 다시 사용하게 됨으로써 잠재변수 \(\mathbf{H}_t\) 를 복제한다.
  • 즉 잠재변수 \(\mathbf{H}_t\) 를 복제해서 다음 순서인 \(\mathbf{H}_{t+1}\) 잠재변수를 인코딩 하기 위해 사용하게 된다.
• 유의해서 볼 점은 가중치 행렬이 3개가 나오게 된다.
  • 먼저 첫번째 레이어의 $\mathbf{W}^{(1)}_X$ 는 선형모델로 입력 데이터를 통과시켜서 잠재변수로 인코딩하게 된다.
  • 이전 시점의 잠재변수로부터 정보를 받아서 현재 시점의 잠재변수로 인코딩해주는 $\mathbf{W}^{(1)}_H$ 를 사용한다.
  • 이렇게 만든 잠재변수를 통해서 출력으로 만들어주는 $\mathbf{W}^{(2)}$ 가 존재한다.
  • 이렇게 총 3개의 가중치 행렬이 있게 된다.
• $\mathbf{W}^{(2)}$ 와 $\mathbf{W}^{(1)}_X$, $\mathbf{W}^{(1)}_H$ 이 3개의 가중치 행렬은 $t$ 에 따라서, 즉 시점에 따라서 변하지 않는 가중치 행렬이다.
• $t$ 에 따라서 변하는 것은 오로지 잠재변수와 입력 데이터만 해당한다. RNN 에서 사용되는 가중치 행렬 $\mathbf{W}^{(1)}_X$, $\mathbf{W}^{(1)}_H$, $\mathbf{W}^{(2)}$ 는 $t$ 에 따라서 변하지 않는 행렬들이다.
• 이 가중치 행렬들은 동일하게 각각의 $t$ 시점에서 활용되어 모델링을 한다.
• 여기까지 RNN 의 forward propagation 에 해당한다.

• RNN 의 역전파는 계산그래프(computational graph)에 따라 거꾸로 그레디언트가 흐른다.

  

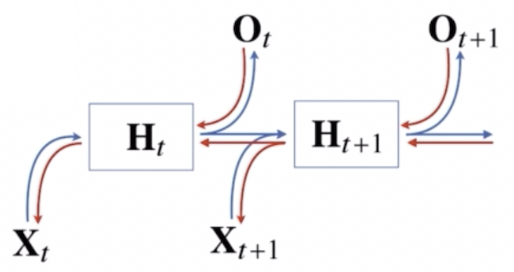
• $X_1$ 부터 $X_t$ 까지 RNN 의 모든 시점에서 예측이 전부 다 이뤄진 다음에, 맨 마지막 시점에서의 그레디언트가 점점 타고 타고 흘러가서 과거까지 그레디언트가 흐르는 방법이다.
• 이는 Back Propagation Through Time (BPTT) 라고 부르는 RNN 의 역전파 방법이다.
• 위 그림에서 보듯, 빨간색 선으로 이루어진 것이 역전파에서 그레디언트의 전달 경로다.
• 잠재변수에 들어오는 그레디언트는 2개다.
  • 다음 시점에서의 잠재변수에서 들어오는 그레디언트 벡터와, 출력에서 들어오는 그레디언트 벡터다.
• 이 잠재변수에 들어오는 그레디언트 벡터를 입력과 그 이전 시점의 잠재변수로 전달하게 되고, 이를 반복해서 RNN 의 학습이 이뤄지게 된다.

BPTT

• BPTT 를 통해 RNN 가중치 행렬의 미분을 계산해볼 수 있다.

• 모든 $t$ 시점에서의 손실함수를 계산한 다음 그레디언트를 계산하는 형태인데, 이를 계산해보면 아래와 같다.

  

• BPTT 를 통해서 각 가중치 행렬의 미분을 계산했을 때 최종적으로 나오게 되는 product term 을 보면, $i+1$ 부터 $t$ 시점까지의 모든 잠재변수에 대한 미분이 곱해지고 더해지게 된다.
• 즉 BPTT 를 통해 RNN 의 가중치 행렬의 미분을 계산해보면 미분의 곱으로 이루어진 항이 계산된다.
• 시퀀스 길이가 길어질수록 곱해지는 term 들이 불안정해지기 쉽다.
  • product term 안의 값이 1 보다 크게 되면 굉장히 커지게 되고, 1 보다 작게 되면 굉장히 작은 값으로 떨어지기 때문이다.
  • 즉 미분값이 엄청 커지거나 엄청 작아지게 될 확률이 높다.
• 따라서 일반적인 BPTT 를 모든 $t$ 시점에서 적용하게 되면 RNN 의 학습이 굉장히 불안정해지기 쉽다.

기울기 소실

• 이와 같이 BPTT 를 모든 $t$ 시점에 대해서, 즉 모든 관찰되는 예측 순간에 대해서 다 적용하게 되면 그레디언트를 전부다 곱해주는 형태이기 때문에, 그레디언트 계산이 불안정해질 확률이 높다.
• 특히 가장 주의해야할 문제는 그레디언트가 0 으로 줄어드는, 그레디언트가 vanishing 하는 기울기 소실 문제다.
• 그레디언트가 0 으로 줄어드는 것이 큰 문제가 된다.
  • 미래 시점에 가까울수록 그레디언트가 살아있고, 과거 시점에 갈수록 그레디언트가 점점 0 으로 가게 되면, 과거 시점에 대한 반영이 쉽지 않다.
  • 즉 그레디언트가 0 에 가까워지면, 과거 시점의 입력이나 상태가 모델의 학습에 영향을 미치지 않게 된다.
  • 이는 모델이 먼 과거의 정보를 기억하거나 반영하는 것이 매우 어렵다는 것을 의미한다. 이로 인해 RNN 은 멀리 떨어진 시점의 정보를 학습하기 어려워지며, 가까운 시점의 정보에만 의존하게 될 수 있다.
• 만약 문맥적으로 이전 시점의 정보가 필요한 텍스트 분석 또는 긴 시퀀스를 분석해야 하는 문제들의 경우 BPTT 를 가지고 역전파 알고리즘을 통해 그레디언트를 계산해서 학습을 진행할 때, 그레디언트가 0 으로 죽기 때문에 과거의 정보를 잃어버리는 문제가 발생하기 쉽다.
• 이 문제를 해결하기 위해서 사용하는 방법이 truncated BPTT 다.

• truncated BPTT 는 시간 단계(time step)를 일정한 길이로 잘라내어(truncation) 그 구간 내에서만 역전파를 수행하는 것이다.

  

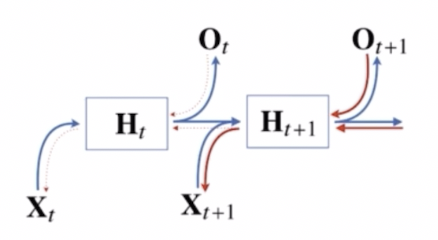
• 잠재변수에 들어오는 그레디언트 받을 때 미래 시점에서부터 $t+1$ 시점까지 들어오게 되는 그레디언트는 받다가, 여기서 부터 그레디언트를 $H_t$ 에 전달하지 않고, $H_t$ 는 오로지 출력에서 들어오는 그레디언트인 $O_t$ 에서만 그레디언트를 받아서 $H_t$ 에 전달하는 것이다.
• 이런 식으로 그레디언트를 전달할 때, 모든 $t$ 시점에서 전달하지 않고 특정 블록에서 끊고 그레디언트를 나눠서 전달하는 방식이 truncated BPTT 다.
• 예를 들어, 100 개의 시간 단계가 있다면, 그 중 10 개의 시간 단계씩 나누어 역전파를 수행할 수 있다.
• 이렇게 하면 긴 시퀀스 전체에 대해 역전파하는 것이 아니라, 작은 구간에 대해 역전파하므로 계산 효율이 높아지고, 기울기 소실 문제도 일부 완화된다.
• 즉 이 방법을 통해서 그레디언트 vanishing 을 어느정도 해결할 수 있지만, 완전한 해결책은 아니다.
  • 장기 의존성 문제: truncated BPTT 는 긴 시퀀스에서 멀리 떨어진 과거 정보를 학습하는 데 여전히 한계가 있다. 아주 긴 시퀀스에서 중요한 정보가 있다면, truncation 으로 인해 그 정보를 충분히 반영하지 못할 수 있기 때문이다.
  • 타임 스텝의 선택: 얼마나 많은 시간 단계를 잘라내어 역전파 할지를 선택하는 것도 중요하다. 너무 짧게 자르면, 모델이 장기 의존성을 잘 학습하지 못할 수 있고, 너무 길게 자르면 기울기 소실 문제를 여전히 겪을 수 있다.
• 따라서 이러한 그레디언트 vanishing 문제 때문에 오늘날에는 기본적인 RNN 모형을 사용하지 않는다.

• 길이가 굉장히 긴 시퀀스를 처리하는데 있어서는 LSTM 이나 GRU 라는 다른 advanced RNN 을 사용한다.

  

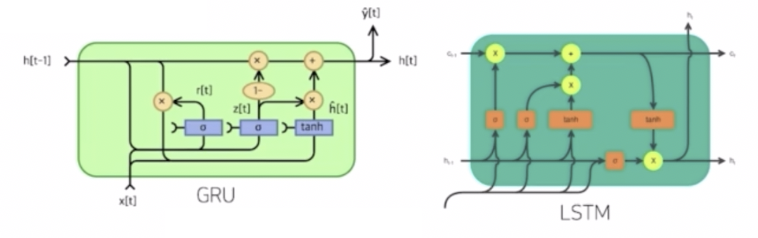
• 정리하면, 시퀀스 길이가 길어지는 경우 RNN 의 BPTT 를 통한 역전파 알고리즘의 계산이 불안정해지므로 길이를 끊는 truncated BPTT 이 어느정도 완화해줄 수 있다.
• 그러나 완전한 해결은 어렵기 때문에 일반적인 Vanilla RNN 은 길이가 긴 시퀀스를 처리하는데 문제가 있고, 이를 해결하기 위해 등장한 RNN 네트워크가 LSTM 과 GRU 다.
• LSTM 과 GRU 는 다른 포스트에서 다뤄보겠다.

맨 위로 이동 ↑