[AI Math] 11. CNN 연산

CNN 연산

• MLP 는 각 뉴런들이 선형모델과 활성함수로 모두 연결된 fully connected 구조로 만들어졌다.

• 주어진 입력 벡터($\mathbf{x}$)에 대해서 가중치 행렬 $\mathbf{W}$ 의 $\mathbf{W}_i$ 에 해당하는 행과 입력 벡터의 내적(행렬곱, $\odot$)을 통해서 잠재변수($h$)의 $i$ 번째 컴포넌트를 계산할 수 있다.

  

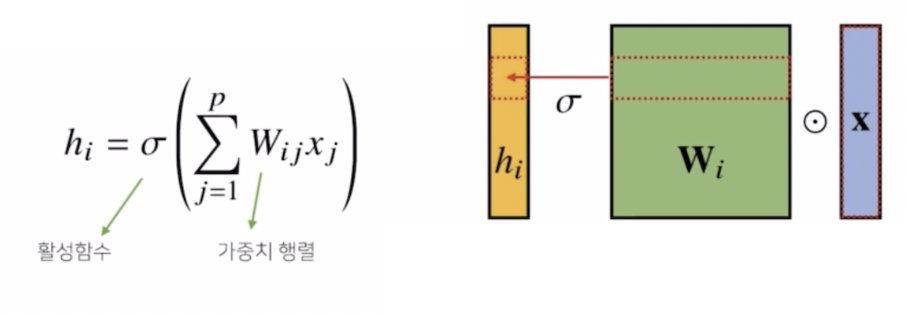
• MLP 에서 사용되는 fully connected 의 구조는 이렇게 각 성분 $h_i$ 에 대응하는 가중치 행($\mathbf{W}_i$) 이 $i$ 번째 위치마다 필요하다.
• 문제는 $h_i$ 를 계산할 때 $\mathbf{W}_i$ 를 필요로 하고, $i$ 가 바뀌게 되면 가중치 행렬의 행도 바뀌기 때문에 가중치 행렬의 사이즈가 커지게 된다. 즉 실제로 학습을 시켜야 하는 파라미터의 숫자가 커지게 된다.

• 그러나 Convolution 연산은 MLP 과 달리 커널(kernel)이라는 어떤 고정된 가중치 행렬을 사용한다. 고정된 커널을 입력벡터 상에서 움직여가면서 선형모델과 활성함수가 적용되는 구조다.

  

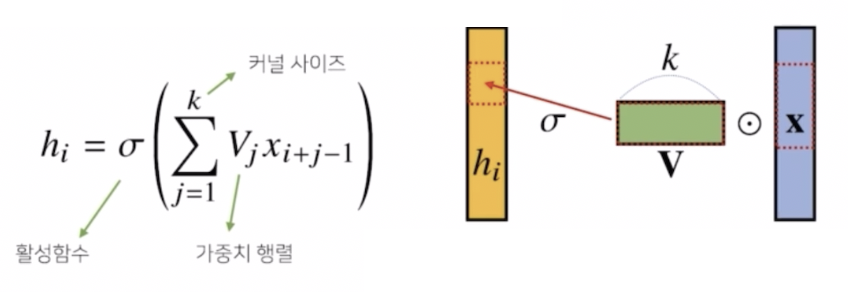
• 위 그림을 보면, $V$ 에 해당하는 것이 커널이다. $k$ 는 커널의 사이즈를 의미한다. 앞에서 사용된 가중치 행렬과는 다른 사이즈를 가진다.
• 중요한 것은 입력벡터 $\mathbf{x}$ 를 모두 다 활용하는 것이 아니라 커널 사이즈 $k$ 에 대응되는 사이즈 만큼 입력벡터에서도 추출하게 된다.
• 그래서 $i$ 번째 해당하는 $h_i$ 의 값을 계산할 때, 커널은 그대로 유지하고 입력벡터 $\mathbf{x}$ 상에서 커널 사이즈 만큼 움직여가면서 계산하는 방식이 Convolution 연산의 특징이다.
• 따라서 $i$ 가 바뀌게 되면 활성화함수와 커널을 제외하고 컨볼루션 연산이 입력벡터 위에서 움직여가면서 적용된다는 사실이 MLP 에서의 일반적인 선형모델과는 조금 다른 형태다.
  • 활성화함수를 제외한 커널을 사용해서 계산하는 컨볼루션 연산도 선형변환의 한 종류에 속한다.
  • 즉 컨볼루션 연산도 선형변환의 한 종류인 것은 변함없는 대신, 중요한 것은 앞에서 사용했던 가중치 행렬이 $i$ 에 따라서 바뀌는 것이 아니라 고정된 커널을 입력 벡터 상에서 움직여 가면서 계산을 적용한다는 사실이다.
• 이것이 컨볼루션 연산의 기본적인 특징이다.
• 공통된 커널을 사용해서 연산에 활용하는 것이 특징이기 때문에 가중치 행렬이 $i$ 번째 위치에 따라서 가중치 행이 따로 존재하지 않고, 커널은 그대로 즉 $i$ 의 개수에 상관없이 커널 사이즈는 고정된 형태로 커널이 공통적으로 적용된다. 따라서 파라미터 사이즈를 굉장히 많이 줄일 수 있다.

컨볼루션 연산의 의미

• 컨볼루션 연산의 수학적인 의미를 보자.
• 컨볼루션 연산은 두 가지 방식으로 정의할 수 있다.
  • 정의역이 연속인 공간에서 적분을 사용해서 정의할 수가 있.

  • 공간이 이산공간이라면 적분을 할 수 없기 때문에 급수로 표현하게 된다.

    

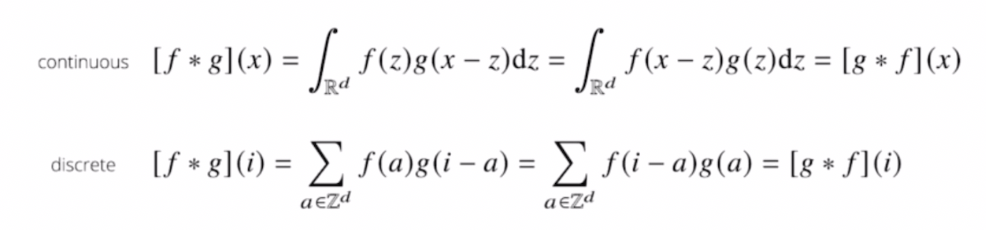
• 이처럼 적분이냐 급수냐 차이가 있을 뿐 적용되는 방식은 똑같다.
• 두 개의 함수 $f, g$ 가 있을 때 $x$ 라는 입력에 대해서 값을 계산할 때는 전체 정의역에서 $z$ 를 움직여가면서 두 함수를 곱해주고, 적분을 하거나 더해주는 형태로 컨볼루션 연산이 실행된다.
• $x-z$ term 이 들어가 있거나 $i-a$ term 이 들어가 있는 경우를 보통 신호(signal) term 이라고 한다.
• 따라서 신호에 해당하는 $g$ 와 커널에 해당하는 $f$ 가 있다. 위 수식과 같이 신호와 커널은 바뀔 수 있다.
• 컨볼루션 연산의 수학적인 의미는 신호(signal)를 커널을 이용해서 국소적으로 증폭 또는 감소시키는 것을 통해서 정보를 추출 또는 필터링하는 것이다.

• 이렇게 수식으로만 보면 이해하기 어렵다.

  

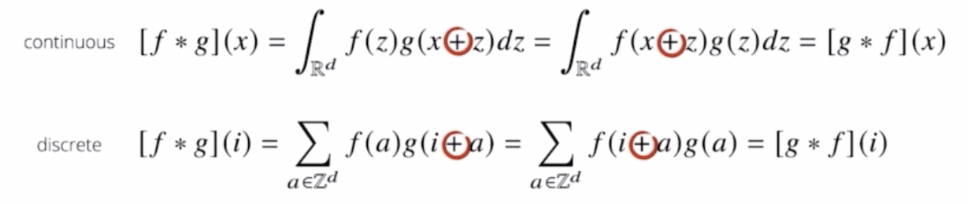
• 사실 일반적으로 딥러닝 프레임워크에서 CNN 에 사용하는 연산은 엄밀히 말하면 - 를 사용하지 않고 + 를 사용한 cross-correlation 을 사용한다. 따라서 엄밀히 말하면 정확한 용어는 convolution 연산이 아니라 cross-correlation 연산이다.
• 그러나 관용적으로 convolution 으로 불렀던 이유가 전체 공간에서는 +, - 가 중요하지 않기 때문이다.
  • 즉 필터를 반전하는 것을 제외하고는 convolution 과 완전 동일한 연산인 cross-correlation 을 통해 convolution 연산을 구현한다.
  • 어차피 필터의 값을 학습하려는 것이 목적이기 때문에 뒤집어서 convolution 을 하나 cross-correlation 으로 하나 동일하다.
  • 그러나 필터를 뒤집는 연산이 필요하지 않고 가중치 커널이 그대로 입력을 훑는 모습을 상상할 수 있기 때문에 직관적 적용이 가능하다.
  • 학습과 추론 시에 필터만 일정하면 된다. 따라서 딥러닝 프레임워크들은 convolution 이 아니고 그냥 cross-correlation 으로 구현되어 있다.
  • 따라서 엄밀히 말하면 cross-correlation 연산인데 역사적으로 convolution 연산이라고 계속 불렀기 때문에 이렇게 부른다.

• 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용한다.

  

  https://en.wikipedia.org/wiki/Convolution

• 파란색에 해당하는 것이 신호, 빨간색이 커널, 컨볼루션 연산의 결과물이 검은색이다.
• 커널은 정의역 내에서 계속 움직이지만 변하지 않는다. 즉 커널은 공통적으로 사용하기 때문에 변하지 않는 성질이 있어서 translation invariant 하다.
• 또한 주어진 파란색 signal 에 대해서 국소적으로 계산을 한 결과이기 때문에 이를 locality 가 있다고 얘기한다.
• 커널을 움직여가면서 파란 신호에 연산이 적용될 때 노란색에 해당하는 것이 국소적으로 적용되는 연산이다. 그 결과물이 검은색으로 나온다.
• 파란색의 원래 시그널에 해당했던 함수를 검은색으로 변환시켜서 정보를 확산시키거나 추출하거나 감소시키는 역할을 컨볼루션 연산이 수행하는 것이다.

영상처리에서 Convolution

• 다양한 종류의 컨볼루션 커널에 따라서 영상(이미지)에 적용했을 때 다양한 종류의 영상처리가 된다.
• 경계선, 주변선의 모양, 노이즈 제거, 블러처리 등 여러가지 효과를 컨볼루션을 통해서 영상에서 쓸 수 있다.
• 컨볼루션 연산을 영상처리에서 굉장히 많이 사용한다.
• 왜 컨볼루션을 활용한 CNN 이 영상(이미지)처리에 좋은 성능을 가져오는지는 이 글을 읽어보자.

다양한 차원에서의 convolution

• convolution 연산은 1차원 뿐 아니라 다양한 차원에서 계산이 가능하다.

  

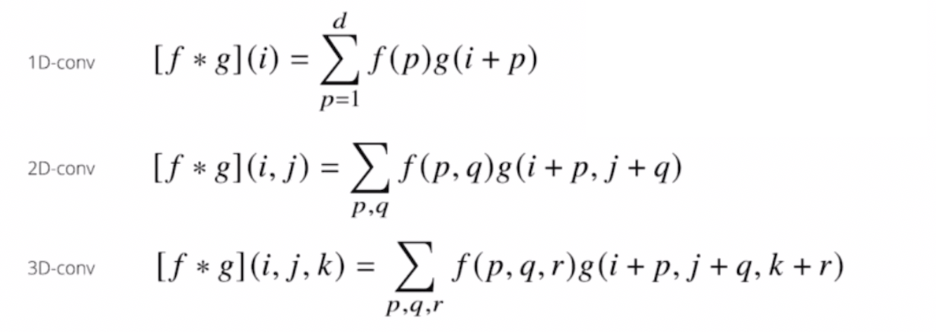
• 1차원 컨볼루션은 한 변수에 대해 움직이는 것이었다면, 2차원 컨볼루션 연산은 두 개의 위치($i, j$) 에 대해서 두 개의 좌표계에 동시에 움직이면서 적용되는 것이다. 3차원은 3개의 좌표계에서 움직이는 것이다.
• 각각의 데이터의 성격에 따라서 사용되는 커널의 종류가 달라지게 된다. 따라서 2d-conv, 3d-conv 는 데이터의 종류에 따라서 사용방법이 달라진다.
• 만약 음성, 텍스트와 같은 1d 데이터의 경우는 1d-conv 를 사용한다.
• 만약 흑백 영상(이미지) 같은 2d 데이터나 컬러 영상(이미지) 같은 3d 데이터 같은 경우는 각각에 사용되는 컨볼루션 연산의 종류가 달라지게 된다.
• 중요한 점은 차원이 높아진다 하더라도, $i, j, k$ 의 위치가 바뀌었을 때 커널 $f$ 의 값은 바뀌지 않는다는 사실이다.
• 따라서 컨볼루션 연산의 핵심은 커널이 위치에 따라서 바뀌지 않는다는 것이다.

2차원 Convolution 연산 이해하기

• 2d conv 연산은 영상(이미지)에서 사용하는 CNN 의 근간이 된다.

• 2d conv 에서는 커널을 2차원, 행렬 모양에 해당하는 커널을 사용하게 된다.

  

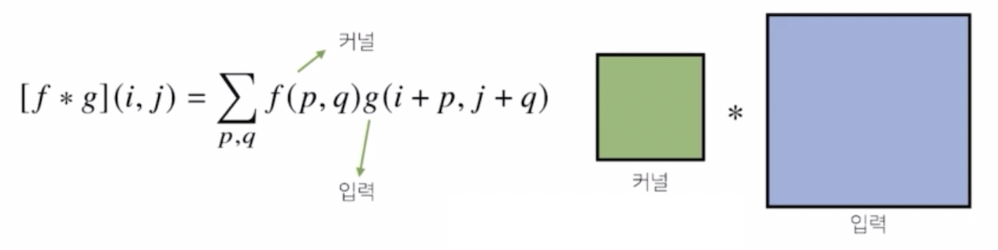
• 1차원에서의 커널을 입력벡터에서 한칸씩 움직이면서 계산하는 것과 달리 2차원 커널의 경우는 입력 행렬에 해당하는 데이터에서 커널을 $x, y$ 방향으로 한칸씩 움직여가면서 적용한다.

• 컨볼루션의 위치에 해당하는 $p, q$ 에 따라서, 즉 $i, j$ 가 고정된 상황에서 $p, q$ 를 움직여가면서 계산되는 방식이다.

  

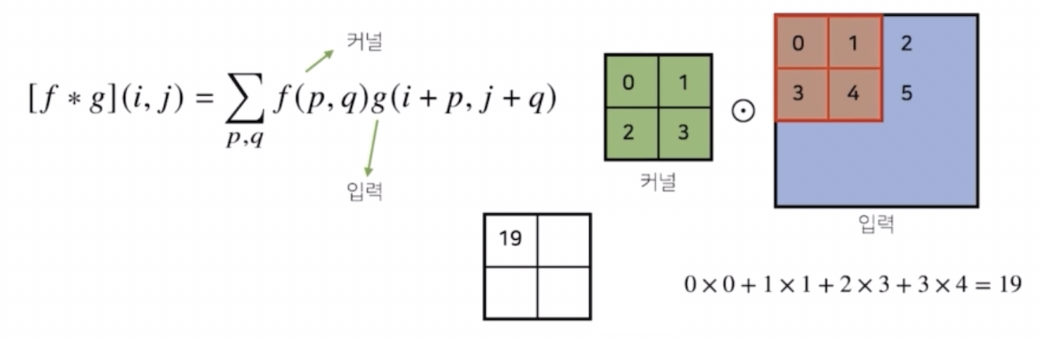
• 입력에 주어진 데이터에 커널의 크기만큼 적용해서 계산하는 것은 1차원 컨볼루션 연산과 똑같다.
• 위 예제를 보자.
  • 커널에 들어간 값이 0, 1, 2, 3으로 주어져있다. 이것이 $f(p,q)$ 와 같다. 이 때 $p, q$ 는 각각 0 과 1의 값을 가질 수 있다. 즉 커널의 위치좌표를 뜻한다.
  • 이 $p, q$ 의 변화에 따라서 입력 좌표의 $i, j$ 를 넣어주게 되면 컨볼루션 연산에 해당한다.
• 입력에서는 커널 사이즈에 맞춰서 계산하게 된다. 이 때 행렬 연산을 하는 것이 아니라 각각의 위치에 따라서 element-wise multiplication, 즉 성분곱을 해서 더해주는 연산을 한다.
• 이 커널을 한 칸씩 움직여 가면서 계산한다. 커널의 모양은 똑같이 유지한 상태에서 입력 행렬에서는 한 칸 우측으로 이동해서 똑같은 연산을 처리한다.

• 이 때 커널의 값은 바뀌지 않고 오로지 입력에서 사용되는 값만 바뀐다.

  

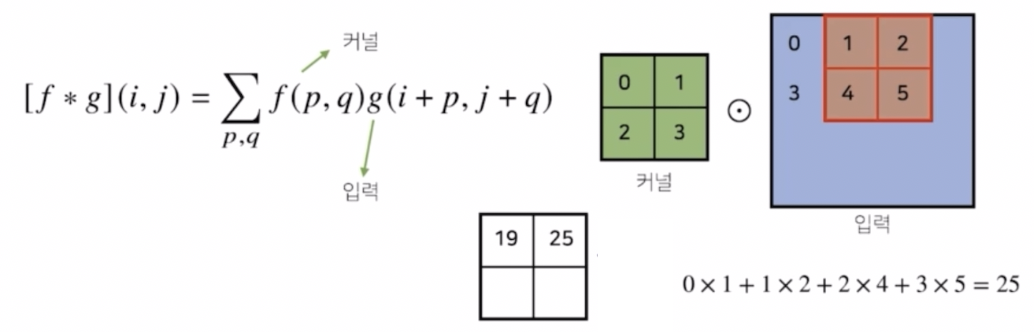
• 이와 같은 방식으로 커널을 가로로, 세로로 1칸씩 움직여가면서 계산하는 것이 2차원 컨볼루션 연산의 방식이 된다.
• 그러면 입력 크기와 커널 크기에 따라서 계산되는 컨볼루션 연산의 출력의 크기를 미리 예상해 볼 수 있다.

• 입력 크기를 $(H,W)$, 커널 크기를 $(K_H, K_W)$, 출력 크기를 $(O_H, O_W)$ 라고 하면 출력 크기는 아래와 같이 계산한다.

  \[\begin{aligned} O_H &= H-K_H+1 \\ O_W &= W-K_W +1 \end{aligned}\]
• 만약 입력이 28 x 28 이고 3x3 커널로 2d-conv 연산을 하면 그 결과물은 26x26 이 된다.
• 이런 식으로 입력의 사이즈가 있고 커널의 사이즈가 있을 때 출력의 크기를 미리 계산해 볼 수 있다. 이를 통해서 다음 컨볼루션 연산에서 활용하여 최종적인 결과물이 어떻게 나올지 미리 예측이 가능하다.
• 실제로 이미지 분석을 하는 경우, 채널이 여러개인 3차원 입력데이터를 다루는 경우가 많다.
• 흔히 RGB 데이터를 다루면, 2차원 영상(이미지)이지만, 3개의 채널이 존재하거나 투명도에 따라 4개의 채널이 존재할 수도 있다.

• 이렇게 채널이 여러 개인 2차원 입력의 경우에도 2차원 convolution 을 사용하게 되는데, 이 때 채널 개수 만큼 커널을 만들어서 적용한다고 생각할 수 있다.

  

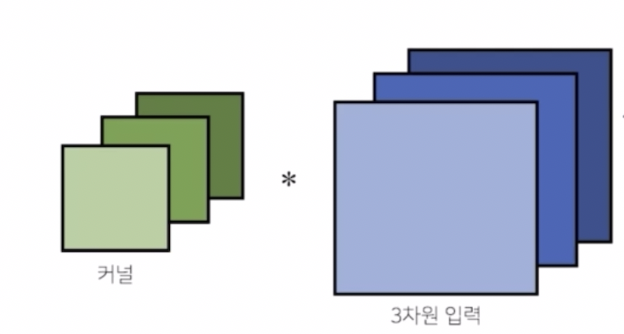
• 3차원 부터는 행렬이 아니라 텐서라고 부른다.

• 채널이 여러 개인 2차원 convolution 의 경우 각각의 채널 개수 만큼 2차원 입력들을 분리한 상태에서 각각의 채널 개수 만큼 커널을 만든 다음, 커널들을 각각의 2차원 입력에 컨볼루션 연산을 적용한 후에 그 결과물들을 더해줘서 2차원 컨볼루션을 수행한다.

  

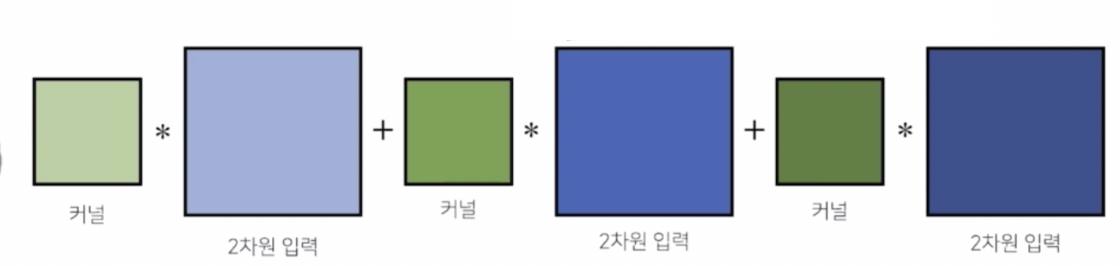
• 유의할 점은 입력의 채널이 여러 개인 경우 존재하는 입력 채널의 개수만큼 커널도 그 만큼 같은 개수로 있어야만 2차원 컨볼루션 연산이 수행된다.

• 텐서를 직육면체 블록으로 생각해서 이해할 수 있다. 2차원 입력에서 채널이 여러 개, 즉 3차원 입력을 가지고 2차원 컨볼루션을 계산할 때 커널도 채널이 여러 개인 형태의 텐서다.

  

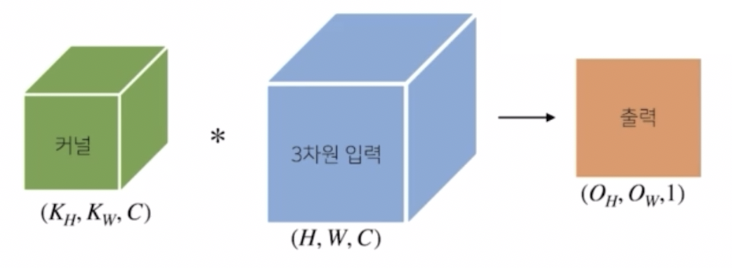
• 이 때 이 커널들과 채널이 여러 개인 3차원 입력 텐서를 컨볼루션 연산을 수행하게 되면 출력이 채널이 1개인 출력으로 도출된다.
• 커널의 채널 개수와 입력의 채널 개수를 같도록 설정했고, 각 2차원 입력이 컨볼루션 연산을 수행한 후 다 더해지기 때문에 출력에 해당하는 텐서의 채널에 1이 된다. 그리고 $O_H, O_W$ 는 출력의 사이즈 계산법이 그대로 적용되어 결과물을 얻게 된다.
• 이처럼 텐서를 직육면체 블록처럼 생각해서 컨볼루션 연산을 이해하면, 영상(이미지)에서의 컨볼루션 절차를 쉽게 이해할 수 있다.

• 만약 출력이 여러 개의 채널을 가지도록 하려면 어떻게 해야할까?

  

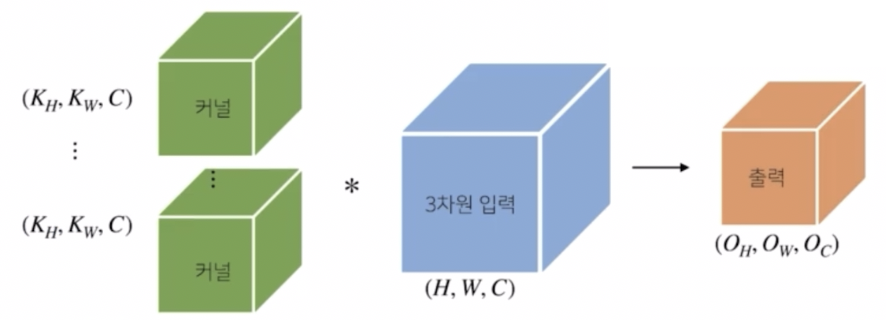
• 커널의 개수를 여러 개 만들면 된다. 커널을 $O_C$ 개 사용하면 출력의 채널이 $O_C$ 개가 되어 텐서가 된다.
• 즉 커널의 개수를 조절하여 출력의 채널을 조절하게 된다. 각각의 커널마다 컨볼루션 연산을 적용해서 $O_C$ 개의 채널을 가진 출력 텐서를 만들 수 있다.
• 이것이 바로 오늘날 2d 이미지 CNN 에서 사용되는 컨볼루션 연산의 기본적인 형태다. 오늘날에는 depthwise convolution, deformable convolution 등 이를 변형한 다양한 종류의 컨볼루션 연산이 있다.

Convolution 연산의 역전파

• 컨볼루션 연산도 선형변환인 것은 마찬가지다. 따라서 MLP 에서의 역전파 계산 방식과 동일하게 계산할 수 있다. 그러나 재밌는 특징이 있다.
• 컨볼루션 연산은 커널이 모든 입력 데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 똑같이 컨볼루션 연산이 나오게 된다.

• 수식적으로 살펴보자.

  \[\begin{aligned} \frac{\partial}{\partial x}[f \ast g](x) &= \frac{\partial}{\partial x}\int_{\mathbb{R}^d}f(y)g(x-y)\text{d}y \\ &= \int_{\mathbb{R}^d}f(y)\frac{\partial g}{\partial x}(x-y)\text{d}y \\ &= [f \ast g^\prime](x) \end{aligned}\]
• 컨볼루션 연산에 해당하는 변수 $x$ 에 대하여 미분을 하면, 적분이든 급수든 미분 기호가 안에 들어가면 signal 에 해당하는 부분에 미분이 적용되어 $g$ 의 도함수와 $f$ 가 컨볼루션 연산을 수행하는 형태로 컨볼루션 연산이 똑같이 나온다.
• 즉 컨볼루션 연산에 미분을 해도 똑같이 컨볼루션 연산이 나온다는 것이다. 이는 Continuous 나 Discrete 나 똑같이 성립한다.
• 그림으로 이해해보자.
• 5개의 값을 가지는 입력벡터가 있고 커널이 $w_1, w_2, w_3$ 이렇게 3개의 커널로 이루어진 1d 컨볼루션을 생각해보자.

• 입력 차원이 5개고 커널 차원이 3개기 때문에 출력차원은 5-3+1 로 3개가 된다.

  

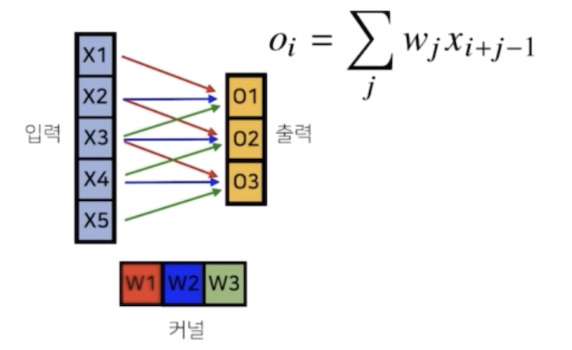
• 이 상황에서 컨볼루션 연산을 수행해보자.
• 색깔별로 빨간색 화살표는 $w_1$ 연산을 적용하는 것이고 파란색은 $w_2$, 초록색은 $w_3$ 를 적용해서 연산하게 된다.
• 그랬을 때 각각의 출력 위치 $i$ 에 따라 커널을 입력벡터 위에서 움직여가면서 컨볼루션 연산을 수행하게 된다.
• 이후 역전파 단계에서, 컨볼루션 연산을 수행한 후에 손실함수(loss function)에서 손실값을 계산한 후, 역전파가 뒤에서부터 오게 된다.

• 출력벡터에서는 $\delta_1, \delta_2, \delta_3$ 라는 미분값이 각각 출력벡터의 위치에 전달이 된다.

  

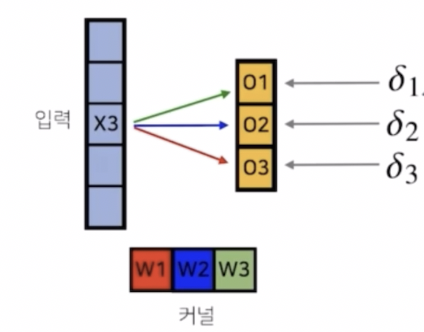
• 그러면 역전파 과정에서 $\delta_1, \delta_2, \delta_3$ 라는 그레디언트 벡터들이 어떤 식으로 $x_3$ 와 커널에 전달되는지 보자.

  

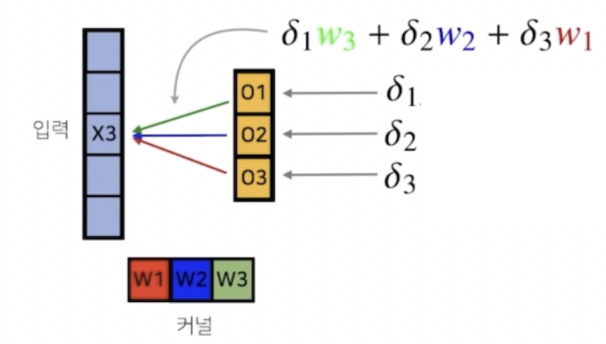
• 앞서 순전파 과정에서 $x_3$ 가 각각 $w_1, w_2, w_3$ 에 적용될 때 $o_1$ 에는 $w_3$ 가 적용됐고, $o_2$ 에는 $w_2$, $o_3$ 에는 $w_1$ 이 적용됐다.
• 역전파 과정에서는 각 출력에 적용된 $x_3$ 와 대응되는 가중치에 따라서 이 그레디언트 벡터가 연결된다.
• 다시 말해, 첫번째 $o_1$ 에서는 $x_3$ 가 $w_3$ 와 곱해지게 된다. 그렇기 때문에 그레디언트 벡터도 똑같이 $\delta_1$ 과 $w_3$ 이 곱해져서 $x_3$ 로 전달된다. 즉 순전파에서 적용된 가중치가 대응된다는 것이다.
• 이처럼 역전파 단계에서, 입력 벡터에는 각각 곱해졌던 커널 가중치들을 통해서 그레디언트가 전달되게 된다.

• 그러면 각각의 커널들은 어떻게 그레디언트가 전달될까?

  

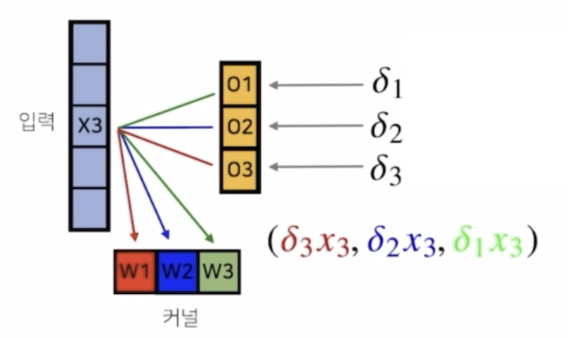
• 각각의 커널들도 똑같이 $o_3$ 가 $x_3$ 에 대해서 $w_1$ 을 통해서 그레디언트 벡터를 전달했기 때문에, $w_1$ 을 통해서 전달되었던 그레디언트 벡터인 $\delta_3$ 는 $w_1$ 로 흐른다.
• 이 때 $w_1$ 대신 $x_3$ 를 곱해서, 즉 $\delta_3x_3$ 가 $w_1$ 의 그레디언트가 된다. $w_2, w_3$ 도 마찬가지 방식으로 그레디언트가 구해진다.
• 즉 커널에는 $\delta$ 에 입력값 $x_3$ 을 곱해서 전달한다.

• 각각의 커널들은 $x_3$ 뿐 아니라 다른 입력에서도 적용되었기 때문에, 다른 입력들에 적용됐던 그레디언트도 똑같이 전달된다.

  

  \[\frac{\partial\mathcal{L}}{\partial w_i} = \sum_j\delta_jx_{i+j-1}\]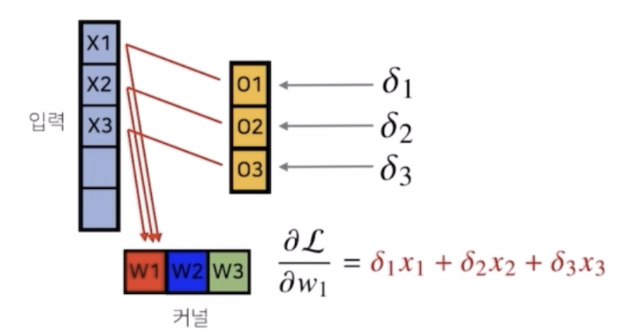
• 이렇게 각 커널에 들어오는 모든 그레디언트를 더하면 결국 그레디언트에 대한 컨볼루션 연산과 같다.

맨 위로 이동 ↑