Bkkhyunn

Bkkhyunn

배움과 경험을 기록하고,
세상과 사람을 매개하는
AI 개발자가 되기까지

[AI Math] 10. KL divergence 와 JSD

KL-div 와 JSD

  • 기계학습에서는 특정 dataset 의 분포를 추정하기 위해 그 집단을 대표하는 sample 을 뽑아 관찰하는 기법을 사용한다.
  • 예를 들어 연어와 농어가 서식하는 바다에서 10 마리의 물고기를 잡았을 때 연어 1마리와 농어 9마리가 잡혔다면, 우리는 이 바다에 살고 있는 물고기가 대략 연어 10%와 농어 90%로 이루어져 있다고 짐작할 수 있다.
  • 그렇다면 우리가 데이터의 분포를 추정했을 때 얼마나 잘 추정한 것인지 측정하는 방법이 뭘까?
  • Kullback-Leibler Divergence(KL-div) 와 Jensen-Shannon Divergence(JSD)는 서로 다른 확률 분포의 차이를 측정하는 척도다.
  • 우리가 추정한 확률 분포와 실제 확률 분포 사이의 차이가 작다면 좋은 추정이라고 할 수 있다.
  • 또한 기계학습에서는 복잡한 함수나 분포를 단순화 하여 하나의 간단한 함수로 나타내려는 노력을 많이 한다.
  • 예를 들어 실제 측정 결과 얻은 복잡한 확률 분포를 비교적 적은 파라미터를 갖는 Gaussian Distribution 등으로 근사한다면 약간의 오차는 있겠지만 정보를 저장하는 데 드는 비용을 크게 절감할 수 있을 것이다.
  • 이 때도 역시 가장 오차가 적은 Model 로 근사하기 위해 위와 같은 척도들을 이용한다.
  • 두 확률 분포 간의 차이를 나타내는 척도인 Kullback-Leibler Divergence 와 Jensen-Shannon Divergence 에 대해 잘 설명해 준 글을 참고해서 두 개념을 이해해보자.

알파벳 맞추기 게임

  • 다섯 개의 알파벳이 쓰인 카드들 중에서 하나를 골라야 한다. 이 때 각 알파벳이 뽑힐 확률은 다음과 같다고 하자.

    image.png

  • 이 확률 분포를 그래프로 나타내면 다음과 같다.

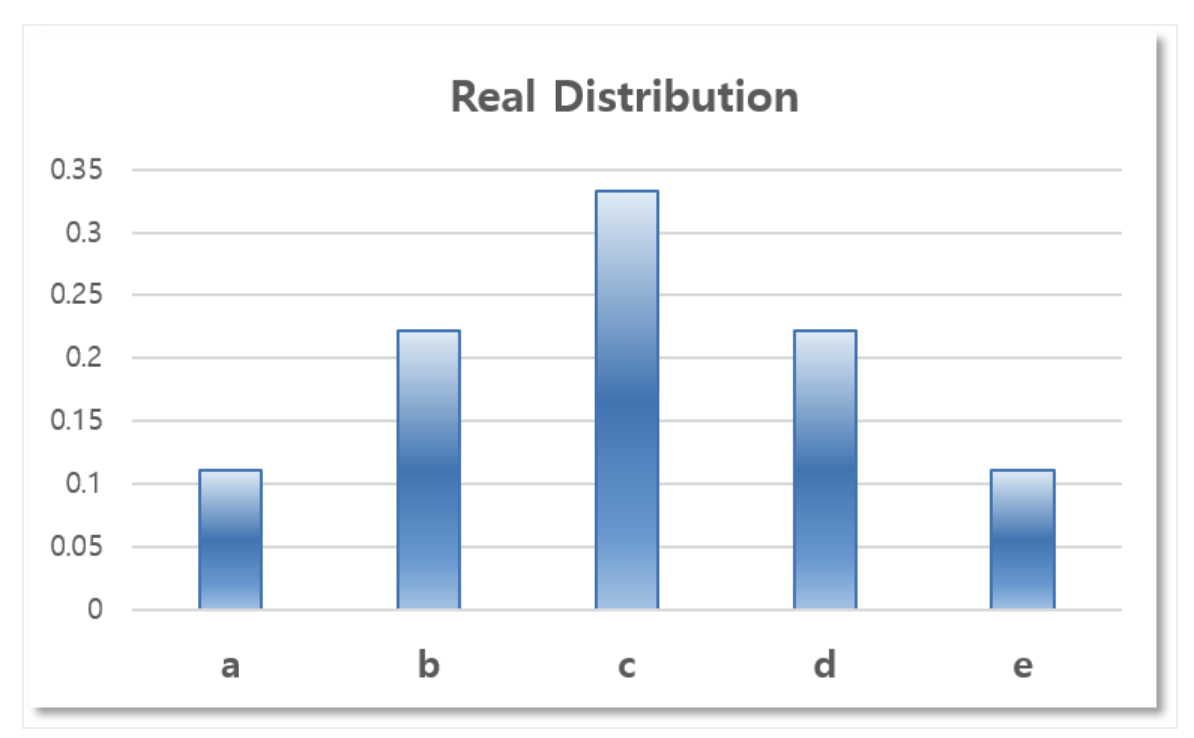
    image.png

  • 위와 같이 확률을 표로 나타내는 것은 정보를 저장하는데 많은 용량이 필요하며 수학적으로 다루기가 까다롭다. 따라서 위 확률 분포를 많이 쓰이는 확률 분포 모델로 근사하기로 하자.

확률 분포 근사

  • 모든 알파벳이 뽑힐 확률이 근사적으로 같다고 해보자.

    \[P_i = \frac{1}{5}, \quad i \in \{0,1,2,3,4\}\]

  • 즉 이는 Uniform Distribution, 균등분포로 근사한 것이다. 이를 통해 아래의 확률 분포를 얻을 수 있다.

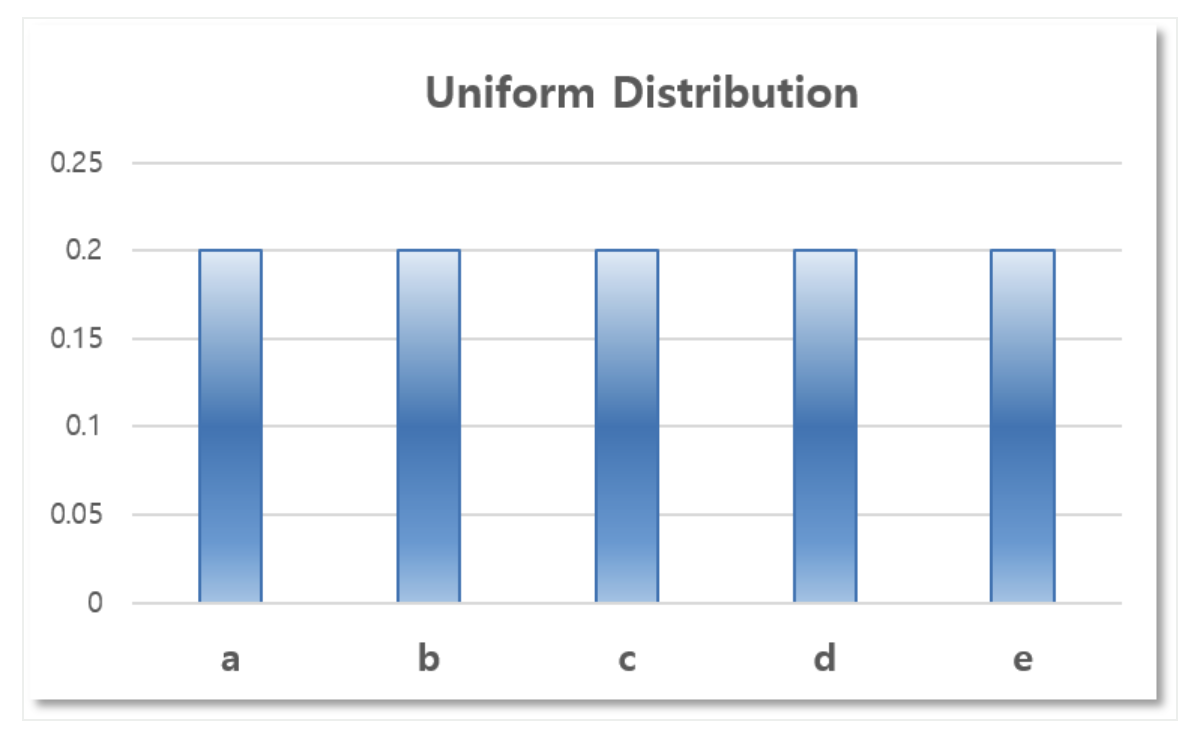
    image.png

    image.png

  • 이는 Real Distribution 과 비교했을 때 잘 근사한 느낌은 들지 않는다.

  • 그렇다면 Binomial Distribution 을 이용해서 근사해볼 수 있다.

    \[P_i = \binom{4}{i} \left(\frac{1}{2}\right)^i \left(\frac{1}{2}\right)^{4-i}, \quad i \in \{0,1,2,3,4\}\]

  • 마찬가지로 아래의 확률 분포를 얻을 수 있다.

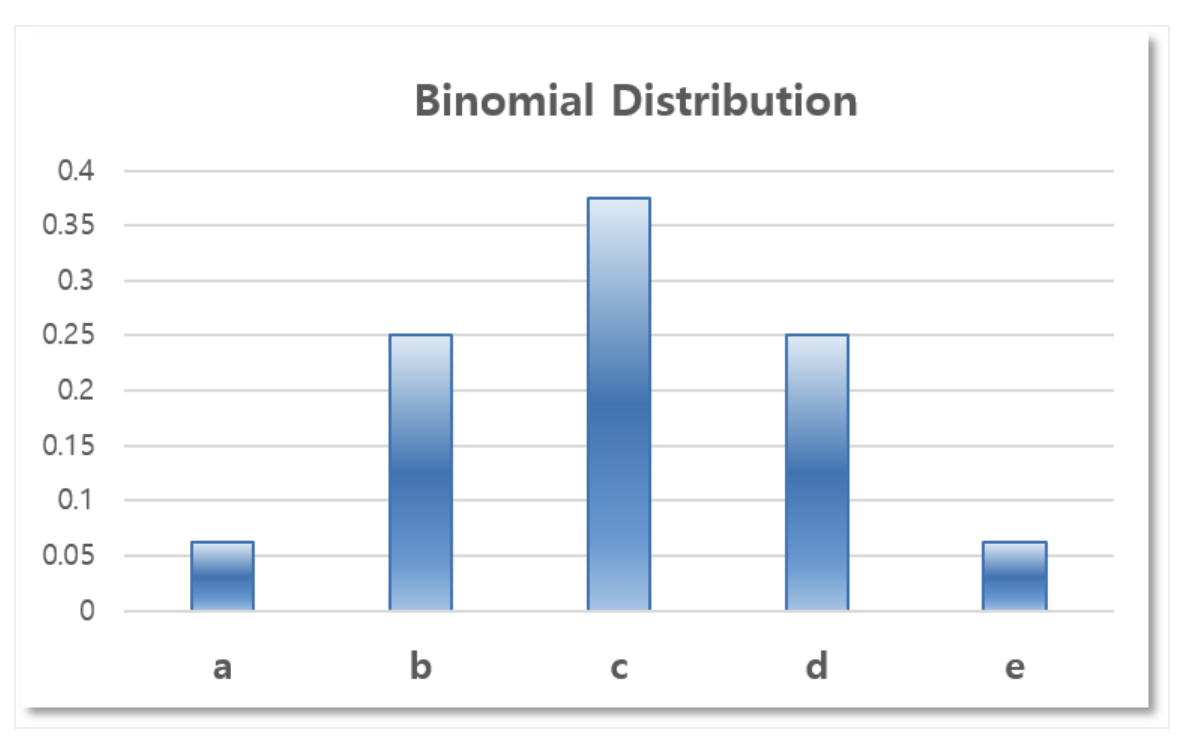
    image.png

    image.png

  • 여기까지 카드가 나올 확률을 표현할 두 가지 모델을 만든 것이다.
  • 그렇다면 어떤 모델이 실제 확률 분포를 더 잘 표현할까? 즉, 어떤 모델이 실제 확률 분포와 더 닮았을까?
  • 우리는 해당 모델이 실제 모델과 얼마나 닮았는지 알기 위한 정량적인 척도가 필요하다. 이러한 척도 중 하나가 바로 Kullback-Leibler Divergence(KL-div)다.

Kullback-Leibler Divergence

  • Kullback-Leibler Divergence 는 두 모델이 얼마나 비슷하게 생겼는지를 알기 위한 척도로써, 제시한 모델이 실제 모델의 각 item 들의 정보량을 얼마나 잘 보존하는지를 측정한다.
  • 즉, 원본 데이터가 가지고 있는 정보량을 잘 보존할수록 원본 데이터와 비슷한 모델이라는 것이다.

  • 먼저 item $s_i$ 가 갖는 정보량은 다음과 같이 계산할 수 있다.

    \[I_i = -\log(p_i)\]

  • 그리고 원본 확률 분포 $P$ 와 근사된 분포 $Q$ 에 대하여 $i$ 번째 item 이 가진 정보량의 차이(정보 손실량)는 다음과 같다.

    \[\Delta I_i = \log(p_i) - \log(q_i)\]

  • $P$ 에 대하여 이러한 정보 손실량의 기대값을 구한 것이 바로 KL-div 다.

    \[\mathbb{KL}(P \Vert Q) = \mathbb{E}[\log(p_i) - \log(q_i)] = \sum_i p_i \log \frac{p_i}{q_i}\]
  • 즉, KL-div 는 근사시 발생하는 정보 손실량의 기대값이라고 할 수 있고, 이 값이 작을 수록 더 가깝게 근사한 것이라고 할 수 있다.

  • 그러면 이제 위 두 모델중에 어떤 모델이 원본과 더 가까운지 측정해보자.

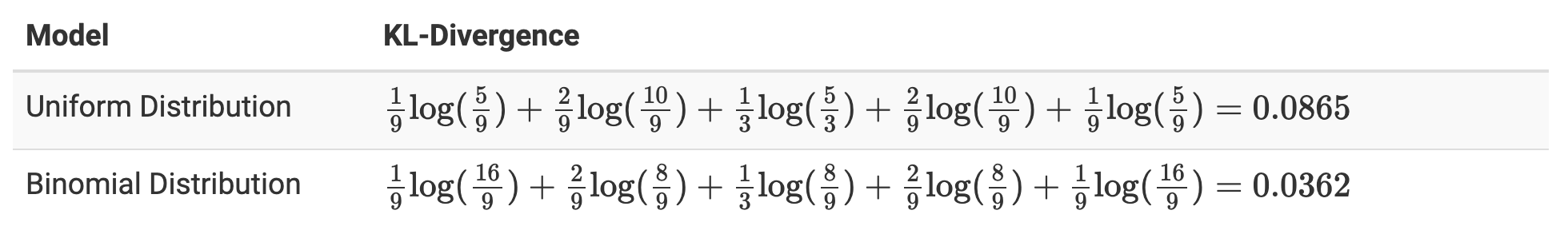
    image.png

  • 계산 결과, Binomial Distribution 으로 근사하는 것이 더 효과적이라는 결론을 얻을 수 있다.

Jensen-Shannon Divergence

  • KL-div 는 근사된 확률 분포가 얼마나 원본과 비슷한지를 측정하는 척도 이외에도, 단순히 두 대등한 확률 분포가 얼마나 닮았는지를 측정하는 척도로도 쓰일 수 있다.
  • 그러나 KL-div 는 Symmetric(대칭적)하지 않다. 즉 $\mathbb{KL}(P \Vert Q) \neq \mathbb{KL}(Q \Vert P)$ 이다.

  • 그렇기 때문에 KL-div 를 Symmetric 하게끔 개량한 Jensen-Shannon Divergence 를 쓴다.

    \[\mathbb{JSD}(P, Q) = \frac{1}{2}\mathbb{KL}(P \Vert \frac{P + Q}{2}) + \frac{1}{2} \mathbb{KL}(Q \Vert \frac{P + Q}{2})\]
  • 그러면 $\mathbb{JSD}(P, Q) = \mathbb{JSD}(Q, P)$ 가 되어 두 확률분포 사이의 거리(distance)로서의 역할을 할 수 있게 된다.

KL-div 와 크로스 엔트로피

  • 앞선 포스트에서는 KL-div 의 식이 크로스 엔트로피와 엔트로피로 분리할 수 있음을 봤다.

  • 사실 크로스 엔트로피에서 정보 손실량인 KL-div 를 구할 수 있다.

    \[\begin{aligned} H(P, Q) &= -\sum_i p_i \log q_i \\ &= -\sum_i p_i \log q_i + (-\sum_i p_i \log p_i + \sum_i p_i \log p_i) \\ &= H(P) + \sum_i p_i \log p_i -\sum_i p_i \log q_i \\ &= H(P) + \sum_i p_i \log\frac{p_i}{q_i} \end{aligned}\]
  • 즉 엔트로피($H(P)$) 에 $\sum_i p_i \log\frac{p_i}{q_i}$ 만큼 더해진 것이 크로스 엔트로피($H(P,Q)$)다.
  • 그 더해지는 것이 바로 KL-div 이다. 바로 분포 $P$ 와 분포 $Q$ 의 정보량 차이인 것이다.
  • 딥러닝에서 크로스 엔트로피를 loss fuction 으로 최소화하는 것은, 어차피 $H(P)$ 는 고정된 상수값이자 주어진 데이터이기 때문에, 결과적으로 KL-div 를 최소화하는 것과 같다.

Reference

맨 위로 이동 ↑

댓글 남기기

관련 게시글