Bkkhyunn

Bkkhyunn

배움과 경험을 기록하고,
세상과 사람을 매개하는
ML Engineer 가 되기까지

[Machine Learning] PCA

Dimensionality Reduction

  • Machine learning process는 크게 Pre-Processing -> Learning-> Error Analysis 로 구성이 되어있다.
  • 이 중 가장 첫 번째 단계인 Preprocessing 단계에서는 효율적인 Dataset 구성을 위해 Normalization, Image processing 등과 더불어 dimensionality reduction 을 수행한다.
  • 그렇다면 dimensionality reduction, 즉 차원 축소는 왜 해야 하는 걸까?
  • 우선 일반적으로 우리가 가지고 있는, 다뤄야 할 실제 세계의 데이터는 대부분 고차원 데이터다. 예를 들어 Documentation classification 을 진행할 때는 한 문서를 표현하기 위한 차원의 수가 그 언어가 가지고 있는 Token 또는 단어의 개수만큼 커진다. Recommendation systems 에서는 사용자 수 X item 수의 matrix 를 다루는데, 사용자 수와 영화와 같은 콘텐츠 개수를 곱한 값이 곧 matrix 의 차원이 된다. 뿐만 아니라 의료 분야에서의 활용을 위해 gene expression data 를 가지고 Clustering (군집분석)을 진행한다면, 해당하는 gene 들의 모든 condition 을 고려해야 하기 때문에 genes x conditions 만큼의 데이터가 필요하게 된다.

Curse of Dimensionality

  • “The number of instances increases exponentially to achieve the same explanation ability when the number of variables increases.”
  • 변수의 개수가 선형적으로 늘어날 때, 동일한 정보를 설명하기 위해서 필요한 객체 또는 샘플의 개수는 지수적으로 증가한다.

  • 즉 두 점 사이의 거리가 1 인 정보를 보전한다고 하면, 1차원에서 표현할 때는 점 두 개만 있으면 되지만, 2차원에서는 정사각형이 있어야 해당 정보를 보전할 수 있기 때문에 점 4개가 필요하다. 3차원에서는 정육면체가 있어야 하기 때문에 점이 8개가 필요하다. 이걸 일반화시켜보면, $d$ 차원의 개수에서는 $2^d$ 만큼의 점이 있어야 각 인접한 이웃 간의 거리가 1이라는 정보를 보전할 수 있게 된다.

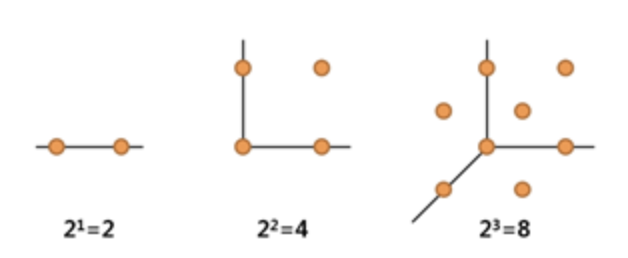
    Untitled

  • 데이터마이닝이나 머신러닝 관점에서 Occam’s Razor 의 ‘가장 단순한 게 가장 좋은 방법이다’ 라는 말이 의미하는 바는, 예를 들어 공정의 수율 예측 정확도가 90% 인데, 각각 sensor 를 10 개를 쓴 모형과 100 개를 쓴 모형이 있다면, 10개 를 쓴 모형을 선택하는 것이 더 낫다는 뜻이다.
  • 객체의 본질적인 정보를 보전하는 내재적인 차원(intrinsic dimension)의 수는 실제 original dimension 보다 훨씬 적은 경우가 많다.

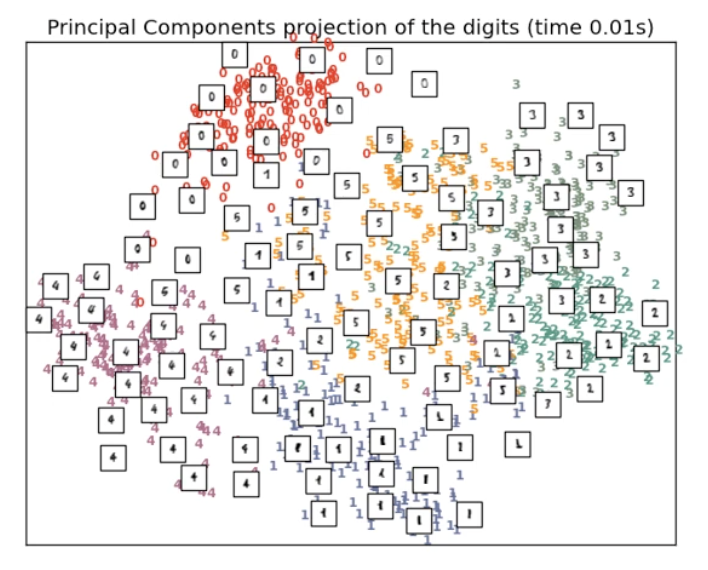
  • 실제로 MNIST Dataset 을 살펴보면, 기존에 16 by 16 pixel 로 256 dimension 이었던 데이터가 차원 축소 방법론인 PCA 를 통해 2 차원으로 축소해보면, 차원이 축소되었음에도 불구하고 각 숫자의 class 는 어느정도 정확하게 구분할 수 있는 예측 능력이 있음을 알 수 있다.

    Untitled

  • 현실 문제에서 차원이 커질수록, 즉 변수의 개수가 많아질수록 아래와 같은 문제점(차원의 저주)이 발생할 수 있다.
    • 개별적인 데이터에 대해서 변수가 많아질수록, 변수에 포함된 noise 가 발생할 확률이 증가한다.
    • 계산 복잡도가 높아진다.
    • 동일한 일반화 성능을 얻기 위해서 더 많은 객체 수가 필요하다.
    • 차원이 증가할수록 데이터 간의 거리가 기하급수적으로 증가하기 때문에 희소 구조를 가지게 되고 모델의 예측 신뢰도가 떨어지게 된다.
  • 이러한 차원의 저주를 극복하기 위해서 아래와 같은 방법을 사용할 수 있다.
    • domain knowledge 가 풍부한 연구자라면 일차적으로 이를 활용해서 feature 를 선택할 수 있다.
    • Ridge, Lasso, ElasticNet 과 같은 회귀분석 기법들은 목적함수 자체에 regularization term 을 두어서 되도록이면 적은 수의 변수를 선호하도록 설계되어 있기 때문에, 이를 통해 변수를 선택할 수 있다.
    • 정량적인 차원축소 technique 을 사용할 수 있다.
  • 정리하면, 차원축소의 목적은 모델에 대해서 가장 적합한 변수의 부분집합을 찾고자 하는 것이다.
  • 그리고 차원 축소를 통해 변수 간의 상관 관계가 없어짐으로 상관관계가 없어야 한다는 가정을 요구하는 여러 통계적인 모델을 그대로 사용할 수 있게 되고, 사후 post-processing 을 좀 더 단순화할 수 있게 되는 부분들도 있으며, 중복되거나 불필요한 변수들을 제거할 수 있게 됨과 동시에, 시각화에 용이하다.

Feature Selection & Feature Extraction

  • 일반적으로 차원 축소는 feature selection 과 feature extraction 으로 나눌 수 있다.

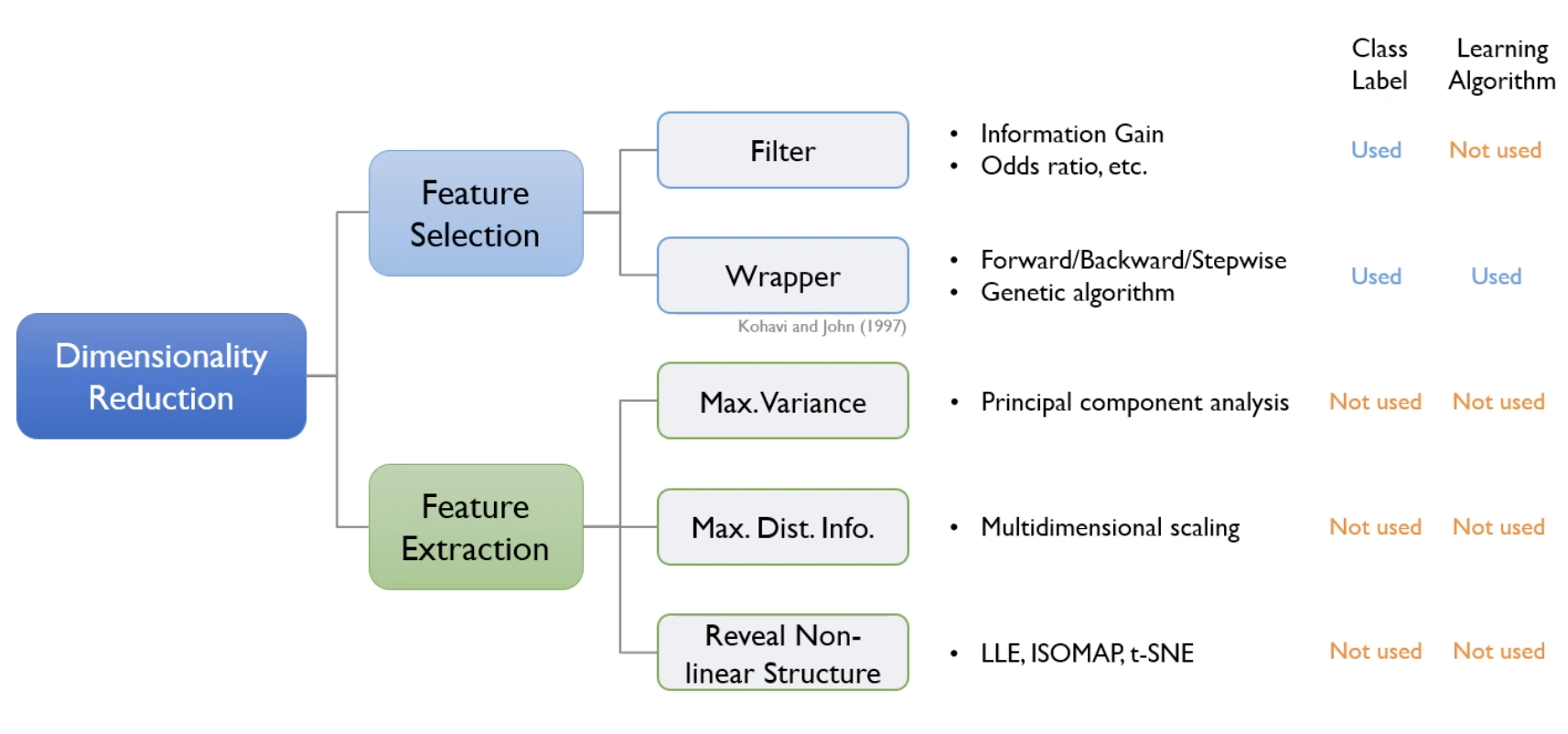
    Untitled

  • feature selection 은 말 그대로 특정 feature 에 종속성이 강한 불필요한 feature 는 아예 제거하는 것이다. 즉 원래 변수들 중 유의미할 것으로 판단되는 부분집합을 명시적으로 선택하는 방법이다.
    • 크게 Filter 방식과 Wrapper 방식이 있는데, Filter 방식은 알고리즘을 사용하지 않고 특정한 메커니즘에서 한 차례 변수를 선택하기 때문에 unsupervised 방식에 가깝다.
    • 반면 Wrapper 방식은 feedback loop 가 있는 supervised dimensionality reduction 방식에 해당되며, Forward/Backward/Stepwise/Genetic algorithm 이 Wrapper 방식에 해당된다.
  • Feature Extraction 은 class label 이라는 정보를 전부 사용하지 않고, learning algorithm 또한 사용하지 않는다. 어떻게 차원을 축소할 수 있냐면, 데이터가 가지고 있는 본질적인 정보를 가장 최대한으로 보존하는 방식으로 변수를 줄여 나간다. 결국 핵심은 데이터가 가지고 있는 본질적인 정보가 무엇이냐는 질문으로 귀결될 수 있다.
    • 우선 첫번째는 variance(분산)을 최대화하는 주성분분석(PCA)이 있다.
    • 객체 간의 거리 정보를 최대화하는 다차원 척도법(Multidimensional scaling)이 있다.
    • 위 방법들은 모두 선형 변환인데, 선형이 아닌 비선형 변환(hidden structure)을 찾아내는 방식이 non-linear structure 다. LLE, ISOMAP, t-SNE 가 비선형 변환에 해당된다.

PCA

  • PCA 는 데이터의 분산을 데이터의 특성으로 정의하고 이를 최대한 보존하기 위한 방법론이다.
  • PCA 의 목적 자체는 set of basis(기저)를 찾는 것인데, 이 기저들은 분산을 보존하는 역할을 한다. 이 때의 분산은 특정 기저에 모든 데이터가 사영(projection)된 이후에, 사영된 데이터의 퍼진 정도(분산)를 말한다. 즉 이러한 분산이 최대화되는 기저를 찾는 것이다.
  • 어떤 주성분에 데이터가 사영되었을 때 얼마만큼의 분산이 보존되었는지를 계산할 수 있다. 특정 기저(주성분)에 의해서 보존되는 분산의 양을 계산하는 방법을 통해 PCA 는 유의미한 변수들을 extraction 한다고 볼 수 있다.

  • 이러한 PCA 을 이해하기 위해서 아래와 같은 개념이 필요하다.

    1. Covariance
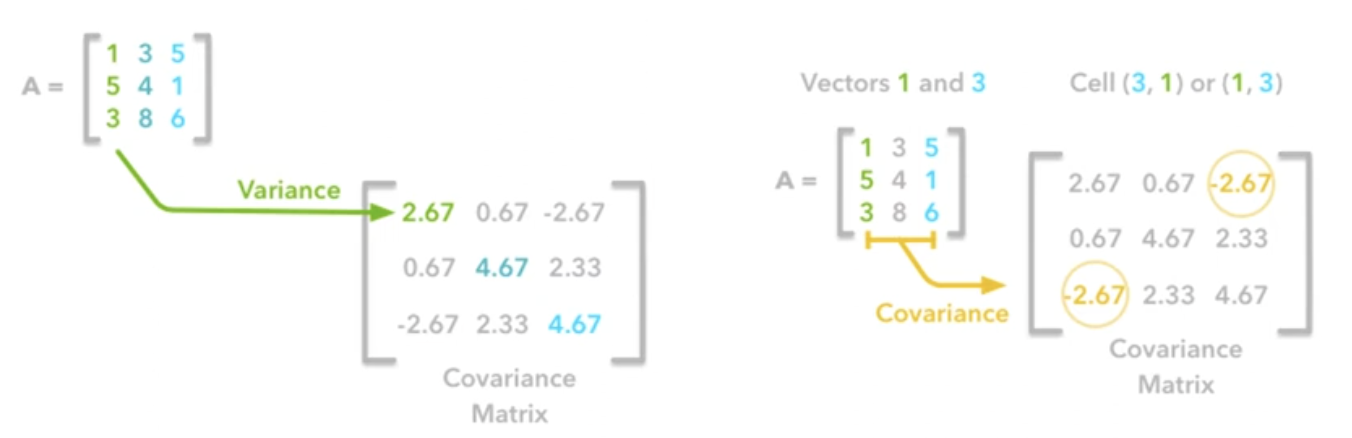
      • $\mathbf{X}$ 가 데이터셋일 때, 공분산 행렬 $Cov(\mathbf{X})$ 는 아래와 같이 구할 수 있다.
      \[Cov(\mathbf{X}) = \frac{1}{n}(\mathbf{X} - \bar{\mathbf{X}})(\mathbf{X} - \bar{\mathbf{X}})^T\]
      • $\mathbf{X}$ 는 $d \times n$ 의 크기를 가지고 있다. $d$ 는 변수의 개수이고, $n$ 은 데이터 레코드의 개수이다.
      • 공분산 행렬은 대칭을 이루고, 변수별 분산은 공분산 행렬의 대각 원소에 위치하기 때문에, 전체 데이터셋이 가지고 있는 분산의 합은 공분산 행렬의 대각합 trace 와 같다.
      \[\begin{aligned} Cov(\mathbf{X})_{ij} &= Cov(\mathbf{X})_{ji} \\ tr[Cov(\mathbf{X})] &= Cov(\mathbf{X})_{11} + Cov(\mathbf{X})_{22} + Cov(\mathbf{X})_{33} + \ldots + Cov(\mathbf{X})_{dd} \end{aligned}\]

      Untitled

    2. Projection onto a basis
      • 사영(Projection)한다는 것은, $b$ 라는 벡터를 $a$ 라는 기저에 사영시키게 되었을 때, 아래 그림과 같이 사영된 벡터($\vec{x}$)는 $a$ 의 방향을 가지고 있으면서 $p$ 라는 가중치를 가지는 벡터가 된다.

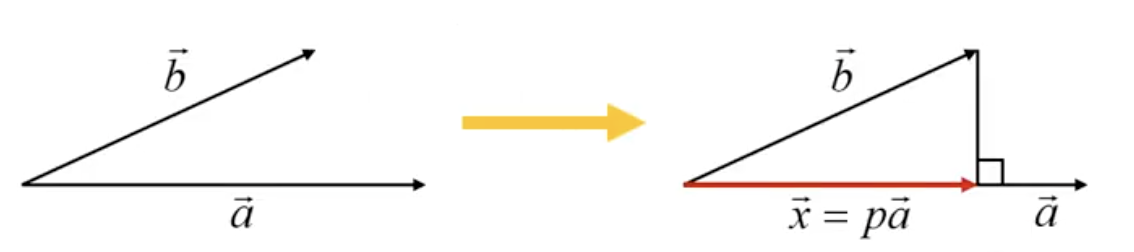
      Untitled

      • 그렇다면 사영을 시켰을 때 $a$ 에 직교하는 벡터를 $\vec{b} - p\vec{a}$ 라고 할 수 있고, 직교하기 때문에 아래와 같이 식을 나타낼 수 있다.
      \[(\vec{b} - p\vec{a})^T\vec{a} = 0 \; \Rightarrow \; \vec{b}^T\vec{a} - p\vec{a}^T\vec{a} = 0 \; \Rightarrow \; p = \frac{\vec{b}^T\vec{a}}{\vec{a}^T\vec{a}}\]
      • 따라서 사영된 벡터 $\vec{x}$ 는 아래와 같이 나타낼 수 있고, 만약 기저 벡터 $\vec{a}$ 가 단위 벡터(unit vector)라면, $\vec{x}$ 는 간단히 구할 수 있다.
      \[\vec{x} = p\vec{a} = \frac{\vec{b}^T\vec{a}}{\vec{a}^T\vec{a}}\vec{a} = (\vec{b}^T\vec{a})\vec{a}\]
      • 여기서 $\vec{a}$ 가 주성분(PC)가 되며, $\vec{b}$ 는 원데이터이고, $p$ 는 스칼라값이 된다.
    3. Eigenvalue and Eigenvector
      • 어떤 matrix $\mathbf{A}$ 가 있을 때, 아래 식을 만족하는 scalar value $\lambda$ 와 거기에 대응하는 벡터 $\mathbf{x}$ 를 쌍으로 가진다.
      \[\mathbf{A}\mathbf{x} = \lambda\mathbf{x} \quad \rightarrow \quad (\mathbf{A} - \lambda\mathbf{I})\mathbf{x} = 0\]
      • 즉 특정 matrix 에 특정 벡터를 연산했을 때, 그 특정 벡터의 scalar 배수 만큼 동일하게 되는 쌍이 있다. 이 때 각각의 scalar value 는 고윳값(eigenvalue)이고, 벡터는 고유벡터(Eigenvector)이다.
      • matrix 를 곱해준다는 것은, 특정 벡터를 linear transformation 해주는 것과 같다.

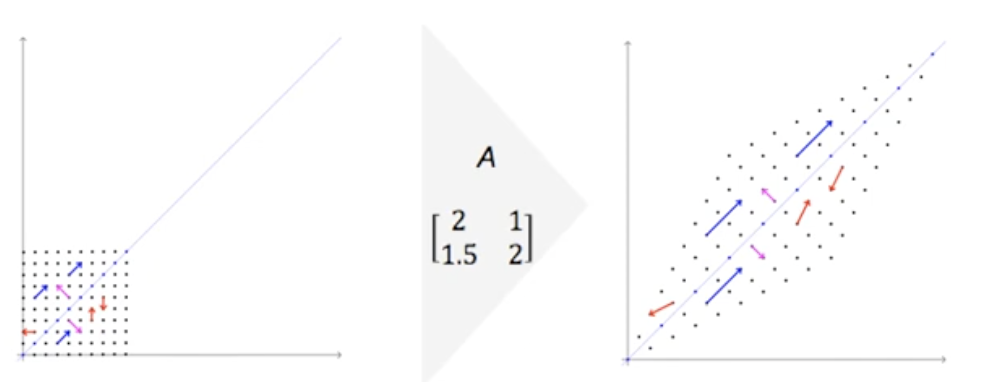
      Untitled

      • 위 그림을 보면, 선형 변환 이후에 빨간색 벡터는 방향이 바뀐다. 그러나 파란색, 분홍색 벡터는 벡터의 방향은 안 바뀌고 크기만 달라진다.
      • 결국 $\mathbf{A}$ matrix 에 대해서 크기만 바뀌고 방향이 바뀌지 않는 벡터가 두 개가 존재하게 된다. 그 벡터가 고유벡터가 되고, 크기가 변했을 때 그 변화한 양이 고윳값이 되는 것이다.
      • 또한 $\mathbf{A}$ matrix 가 역행렬이 존재(non-singular)하는 $d \times d$ matrix 일 때, 이 matrix 는 $d$ 개의 고유벡터와 고윳값 쌍을 가진다. 즉 랭크 개수만큼의 쌍을 가진다.
      • 고유벡터들은 서로 직교한다. 위 그림에서 파란색 벡터와 분홍색 벡터가 직교하는 것처럼, 어떤 고유벡터들이라도 항상 직교하여 $i\neq j$ 일 때 $e_i^Te_j =0$ 이다.
      • 마지막으로 해당하는 matrix 의 trace 값은 이 matrix 의 고윳값의 합과 같다.
      \[tr(\mathbf{A}) = \sum^d_{i=1} \lambda_i\]

PCA Procedure

  • PCA 의 실제 절차를 보도록 하자.

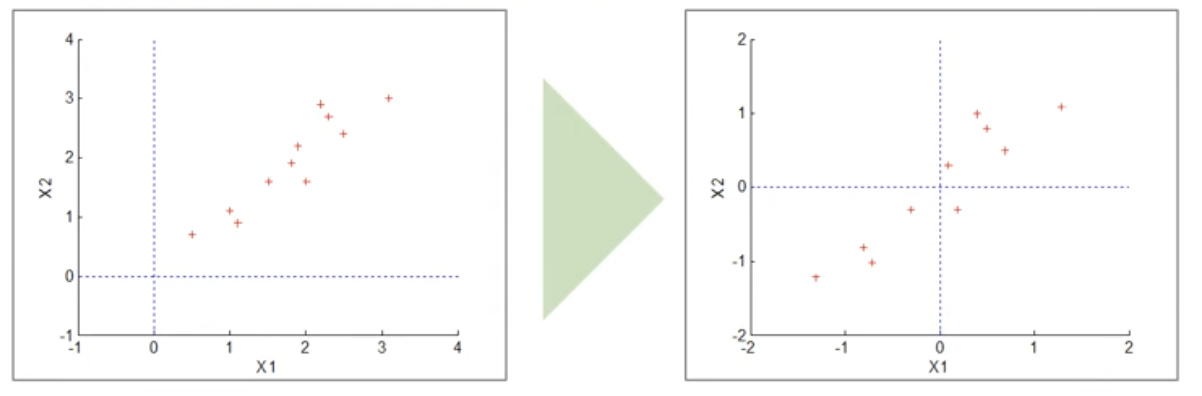
    1. Data Centering
      • 데이터에 대해서 평균을 0 으로 맞춰준다. 이는 데이터 평균이 0 이 아니면, 주성분이 실제 분산이 큰 방향보다 평균 방향으로 치우칠 수도 있기 때문이다. 또한 평균을 0 으로 맞춰 기준점을 잡아주면 회전이나 사영에서 왜곡이 생기지 않고 공분산을 간단히 표현 가능하다.
      • 각각의 변수들의 평균값을 빼줌으로써 각 변수들의 평균값이 0 인 matrix 를 구할 수 있다.

      Untitled

    2. Optimization Problem
      • 위와 같이 Data Centering 이 끝나면, 우리는 PCA 의 제약식과 목적식을 구해볼 수 있다.
      • Data Centering 이후 하나의 벡터 $\mathbf{x}$ 가 $\mathbf{w}$ 라는 basis 에 사영되었을 때, 분산은 아래와 같이 구할 수 있다.
      • 단 아래 식에서는 벡터들이 모인 행렬로 구한다. 즉 위에서 봤듯 모든 벡터들을 $\mathbf{w}$ 에 사영시킨 것이고, 분산의 정의에 따라 아래와 같이 구할 수 있다.
      \[V = \frac{1}{n}(\mathbf{w}^T\mathbf{X})(\mathbf{w}^T\mathbf{X})^T = \frac{1}{n}\mathbf{w}^T\mathbf{X}\mathbf{X}^T\mathbf{w} = \mathbf{w}^T\mathbf{S}\mathbf{w}\]
      • 위 식에서 두번째 식은 centering 에 의해 평균이 0 인 공분산행렬($\mathbf{XX^T}$)이라고 볼 수 있다. 따라서 이를 sample covariance matrix $\mathbf{S}$ 로 나타낸 것이다. 이는 $\mathbf{w}^T\Sigma\mathbf{w}$ 로 나타내기도 한다.
      • 그렇다면 목적은 이제 아래와 같다. $V$ 를 최대화하는 것이다. 즉 $\mathbf{w}$ 에 사영이 된 이후의 분산인 $\mathbf{w}^T\mathbf{S}\mathbf{w}$ 를 최대화하는 것이다.
      • 그러면서 기저의 크기를 전부 1 로 맞추는 normalization 을 하기 위해서 아래와 같은 제약식을 준다. 그 이유는 기저($\mathbf{w}$)의 크기를 제한하지 않으면 분산은 계속 커지게 되어 최적화의 의미가 없고, 이 제약식을 주어 아래에서 볼 Lagrangian multiplier 를 사용할 수 있다.
      \[\text{max}\; \mathbf{w}^T \mathbf{S}\mathbf{w}, \qquad \text{s.t.} \; \mathbf{w}^T\mathbf{w}=1\]
    3. Obtain Solution
      • 라그랑주 승수법은 제약이 있는 최적화 문제를 푸는 방법 중 하나로, 모든 제약식에 라그랑주 승수(Lagrange Multiplier) $\lambda$ 를 곱하고 등식 제약이 있는 문제를 제약이 없는 문제로 바꾸어 문제를 해결하는 방법이다. 이를 이용하여 최적화해보자.
      \[L = \mathbf{w}^T \mathbf{S}\mathbf{w} - \lambda(\mathbf{w}^T\mathbf{w} - 1)\]
      • 위 식은 기저에 대한 2차 함수이면서, 최대화해야 하는 함수이기 때문에, 1차 도함수의 값이 0 이면 된다.
      \[\frac{\partial L}{\partial \mathbf{w}} = 0 \quad \Rightarrow \quad \mathbf{Sw} - \lambda\mathbf{w} = 0 \quad \Rightarrow \quad (\mathbf{S} - \lambda\mathbf{I})\mathbf{w} = 0\]
      • 결국, $\mathbf{w}$ 는 $\mathbf{S}$ 의 고유벡터가 되고 $\lambda$ 는 고윳값이 된다.
    4. Find the base set of bases
      • 따라서 고유값과 고유벡터를 구할 수 있는데, 여기서 구한 고유벡터에 우리가 가진 원래 데이터를 사영해볼 수 있다. 그러면 사영이 된 이후의 분산이 얼마인지를 아래와 같이 구할 수 있다.
      \[\begin{aligned} &\mathbf{v} = (\mathbf{w}^T_1\mathbf{X})(\mathbf{w}^T_1\mathbf{X})^T = \mathbf{w}^T_1\mathbf{X}\mathbf{X}^T\mathbf{w}_1 = \mathbf{w}^T_1 \mathbf{S}\mathbf{w}_1 \\ &\text{Since} \; \mathbf{Sw}_1 = \lambda_1\mathbf{w}_1, \quad \mathbf{w}^T_1 \mathbf{S}\mathbf{w}_1 = \mathbf{w}^T_1\lambda _1\mathbf{w}_1 = \lambda _1\mathbf{w}^T_1\mathbf{w}_1 = \lambda _1 \end{aligned}\]
      • 따라서 $\mathbf{w}_1$ 이라는 기저에 사영을 시켰을 때 보존되는 분산의 양은 $\lambda_1$ 이라는 뜻이다.
      • 그러면 결국 고유벡터는 공분산 행렬의 랭크만큼 있기 때문에, 각 고유벡터(기저)에 사영시켰을 때의 분산 $\lambda _d$ 을 구할 수 있고 이 총합이 원 데이터의 분산이라고 할 수 있다.
      • 예를 들어 고유벡터(기저) $\mathbf{w}_1$ 에 사영시켰을 때 구한 분산(고유값) $\lambda _1$ 을 구하고 이를 전체 분산의 합에서 비율 $x$ 을 구하면, “2차원 데이터를 첫번째 주성분에 사영시키면 해당하는 데이터는 원 데이터 분산의 $x$% 를 보존한다.” 라고 할 수 있다.
    5. Extract new features
      • 몇 개의 기저(주성분, 고유벡터)를 사용할 것인지에 관해서 정성적 방법과 정량적 방법으로 나눌 수 있다.
      • 정성적 방법은 도메인 전문가의 개입으로 구하는 것이고, 정량적 방법으로는 주성분이 증가할수록 원 데이터의 보존되는 분산이 감소되는 때가 있는데 이 때 급격하게 감소되는 시점을 Elbow point 라고 한다. 이 Elbow point 를 기준으로 주성분의 수를 결정할 수 있다.
      • 또한 각 PC 에서 보존하는 분산을 누적합해서 최대 90% 의 분산을 보존해야 한다는 기준을 세울 수도 있다.

PCA Limitation

  • PCA 는 통계에서 출발한 방법론이기 때문에, 데이터의 분포가 Gaussian 분포를 가지고 있다는 것이 기본 가정이다. 따라서 Gaussian 분포가 아니거나 multimodal Gaussian 인 경우에는 PCA 의 결과물이 유용하지 않을 수 있다.
  • 또한 PCA 는 데이터가 가지고 있는 분산량을 최대한 보존하기 위한 방법론이지, 범주 정보가 주어졌을 때 분류 성능을 향싱시키는 방법론은 아니다.
  • 이는 단점이라기 보다 PCA 가 가진 특징이고, 아래 그림과 같이 PCA 는 사영시켰을 때 데이터의 분포가 가장 넓게 퍼져서 보존한다. 그러나 두 범주 간의 구분을 잘 할 수 있는 기저를 찾으려고 하면, Fisher-LDA(Linear Discriminant Analysis) 로 가능하다.

  • 따라서 비지도학습 관점에서 label 이 없을 때는 PCA 로 데이터를 축약해도 괜찮고, 데이터의 label 이 있으면 LDA 를 써서 분류를 해도 된다.

    Untitled

Reference

맨 위로 이동 ↑

댓글 남기기