[Loss] Visualizing the Loss Landscape of Neural Nets

해당 논문 Li et al.,(2018) “Visualizing the Loss Landscape of Neural Nets” @ NeurIPS 2018 은 network 의 구조, optimizer 의 선택, batch size 를 포함하는 neural network practitioner 의 다양한 선택의 결과에 대한 통찰력을 제공하는 시각화(visualization) technique 을 제안했다.

해당 논문을 파헤쳐보자. 시각화하는 방법도 중요하지만, 하이퍼 파라미터나 모델의 구조가 loss surface 에 미치는 영향을 중점적으로 보자. 이 논문을 잘 번역해놓은 블로그를 주로 참고했다.

Abstract

• Neural network 의 학습은 highly non-convex loss function 에서의 좋은 minimizer 를 찾는 능력에 의해 성능이 결정된다.
• ResNet 의 Skip Connection 과 같은 구조에서는 loss function 이 더 쉽게 학습될 수 있다. 이처럼 학습에 유리한 네트워크 구조로 알려진 특정한 네트워크 구조가 몇몇 있다.
• 또한 학습 과정에서 하이퍼 parameter(batch size, learning rate, optimizer)를 잘 설정하면 일반화(generalization) 성능이 좋은 minimizer 를 찾을 수 있는 것도 알려져 있다.
• 그러나 특정 하이퍼 parameter에서 일반화 성능이 좋다거나 특정 네트워크 구조가 학습이 쉬운 것과 같은 그러한 차이의 이유와 근본적인 loss landscape 에 대한 영향은 잘 알려져 있지 않다.
• 이 논문에선 다양한 시각화(visualization) 방법을 이용하여 neural loss function 의 구조와 generalization 측면에서의 loss landscape 의 효과에 대해서 탐구한다.
• 우선, loss function curvature(곡률)의 시각화를 돕는 filter normalization 이라는 방법을 제안하고, 각 loss function 간 비교를 실시한다.
• 다음으로, 다양한 시각화 방법을 이용하여 어떻게 network 의 구조가 loss landscape 에 영향을 주는지, 하이퍼 parameter가 minimizer 의 shape 에 어떻게 영향을 주는지 탐구한다.

Introduction

• Neural network 의 학습은 high-dimensional non-convex loss function 을 최소화 시키는 것이 필요하다.
• 일반적인 neural loss function 을 학습시키는 것은 NP-hard 문제라고 알려져 있다.
• 그러나 data 와 label 들이 학습 전에 randomized 되어있는 경우에도, gradient descent 와 같은 방법을 이용해 training loss 가 0 이거나 0 에 가까운 global minimizer 를 찾을 수 있다. 하지만 일반적인 경우는 아니다.
• neural net 의 학습 능력은 network 의 구조, optimizer 의 종류, 초기화(initialization) 방법 등등 다양한 고려사항에 의해 결정된다. 이는 하이퍼 parameter로 나타나는데, 어떤 선택이 loss surface 에 어떤 영향을 미치는지 불명확하다.

• 왜냐하면 loss function 의 평가 비용은 학습 데이터셋에서 모든 data point 들에 대하여 looping 이 필요하므로 비용이 많이 들어 불가능하기 때문에 이론적으로만 존재했다.

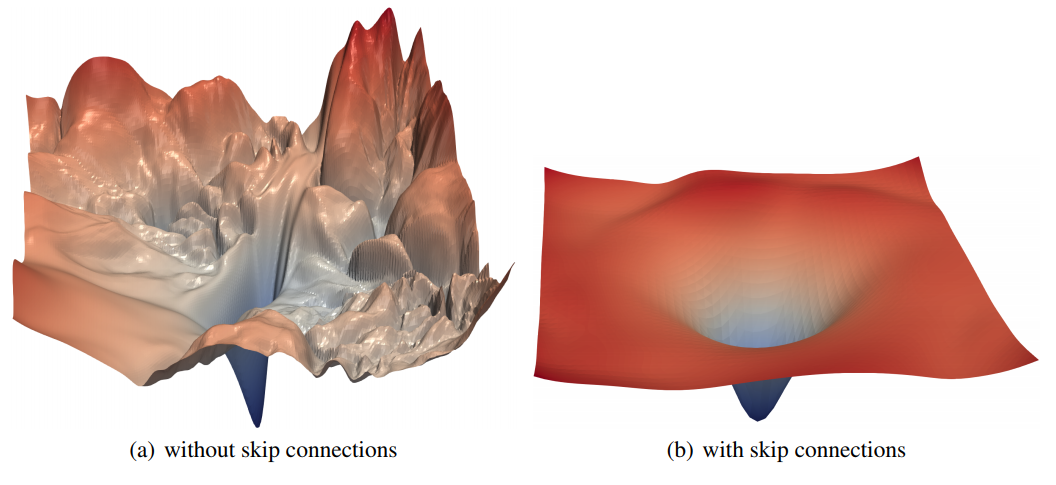  Figure 1. ResNet-56 에 대해 skip connection 의 유무에 따른 loss surface plot. 논문에서 제안하는
  filter normalization scheme 에 의해 shrpness, flatness 의 비교가 가능하다.

• 시각화는 neural network 가 왜 동작하는지에 대한 답변에 도움이 된다.
• 특히, 왜 우리가 highly non-convex neural loss function 을 최소화 시킬 수 있는지와 그 결과로 나타난 minima 들이 어떻게 일반화되는가에 대한 답변에 도움이 된다.
• 논문에서는 neural loss function 의 실증적 묘사를 위해 고해상도 시각화 방법을 사용하고, 어떻게 서로 다른 네트워크 구조가 loss landscape 에 영향을 끼치는지를 탐구한다.
• 또한 neural loss function 의 non-convex 구조가 그 네트워크의 학습 가능성과 연결되어있는지 탐구하고, 어떻게 neural minimizer 의 기하학적 특성(sharpness, flatness, surrounding land scape)이 일반화(generalization) 특성에 영향을 미치는지 살펴본다.
• 이러한 연구를 위해 training 과정 중 발견되는 서로 다른 minima 간의 비교를 위해 simple 한 “filter normalization” 방식을 제안한다.
• 다음으로 서로 다른 방법에 의해 찾아지는 minimizer 들의 sharpness/flatness 를 탐구하기 위해 시각화를 사용하고, 네트워크 구조의 차이(skip connection 이 있는지, filter 의 개수, 네트워크 깊이 등)가 loss landscape 에 어떤 영향을 끼치는가에 대한 연구를 수행한다.
• 본 논문의 목표는 어떻게 loss function 의 기하학적 특성이 neural net 의 일반화(generalization)에 영향을 미치는지에 대한 이해다.

Contributions

• 논문에선 의미있는 loss function 의 시각화에 대한 방법과 이러한 시각화 방법을 이용하여 loss landscape 의 기하학적 특성이 어떻게 학습 가능성과 generalization error 에 영향을 주는지에 대해 탐구한다.
• 아래에서 본 논문에서 다루는 더 자세한 issue 에 대해 설명한다.
  • 논문에서는 다양한 loss function 의 시각화 방법들의 단점을 드러내고, 그 시각화 방법들이 loss function minimizer 의 local geometry(sharpness or flatness) 를 정확하게 capture 하는데 실패하는 것을 보여준다.
  • 논문에서는 “filter normalization” 에 기반한 시각화 방법을 제안한다. 이 normalization 기법이 사용될 때 minimizer 들의 sharpness 가 generalization error 와 얼마나 관계가 있는지를 보이고, 서로 다른 네트워크 구조와 학습 방법에 대한 비교를 수행한다.
  • 논문에서는 네트워크가 충분히 깊을 때 neural loss landscape 가 거의 convex 상태에서 매우 복잡한(chaotic)상태로 빠르게 전환되는 것을 관찰한다. Convex 에서 chaotic 으로 가는 변환은 generalization error 의 급격한 하락과 함께 발생하며 학습가능성을 매우 낮추게 된다.
  • 논문에서는 skip connection 이 어떻게 minimizer 를 flat 하게 만들고, chaotic 하게 되는 것을 방지하는지에 대해 관찰한다. 그래고 매우 깊은 네트워크의 학습에는 skip connection 이 필수로 필요하게 되는지에 대한 설명한다.
  • 논문에서는 local minima 주변의 Hessian 의 smallest(most negative) 고유값을 계산하여 non-convexity 를 양적으로 측정한다. 그리고 이를 heat map 으로 시각화한다.
  • 논문에서는 SGD optimization 의 궤적(trajectory) 시각화에 대한 연구를 한다. 이러한 궤적 시각화에서 발생하는 어려움을 설명하고, extremely low dimensional space 에 있는 optimization trajectory 들을 보여준다. 이러한 low dimensionality 는 논문의 2-dimensional visualization 에서 관찰된 것처럼, loss landscape 에 large 하고 nearly convex 한 region 이 존재함으로 설명 가능하다.

The Basics of Loss Function Visualization

• Neural network 는 학습에 이미지 ${x_{i}}$ 와 그에 맞는 label ${y_{i}}$ 같은 feature vector 뭉치(corpus)가 필요하며 아래와 같은 형태의 loss function 을 최소화하는 과정이 포함된다. $\theta$ 는 neural network 의 weights parameter 다.

  \[L(\theta)=\frac{1}{m} \sum_{i=1}^{m}l(x_{i}, y_{i}\; ;\theta)\]
• 함수 $l$ 은 parameter $\theta$ 를 가진 neural network 가 얼마나 $m$ 개의 데이터 샘플들의 label 을 잘 예측하는지를 측정한다.
• Neural net 은 많은 parameter 를 포함하기 때문에 loss function 은 very high-dimensional space 에 존재하게 된다.
• 하지만 시각화는 1D(line) 나 2D(surface) plot 등 low-dimension 에서만 가능하며, dimensionality gap 을 줄이기 위한 몇 가지 방법들이 존재한다.

1-Dimensional Linear Interpolation

• Loss function 을 plot 하기 위한 간단하고 가벼운 방법이다.
• 두 개의 parameter vector 인 $\theta$ 와 $\theta’$ 를 선택하고, 이 두 점을 연결하는 선을 따라 loss function 의 값들을 plot 한다.

• scalar parameter $\alpha$ 를 고르고, 아래의 식을 통해 가중 평균을 정의하여 두 점을 이은 이 선을 parameterize 한다.

  \[\theta(\alpha) = (1 - \alpha)\theta + \alpha \theta'\]
• 그리고 $f(\alpha) = L(\theta(\alpha))$ 를 plot 한다.
• 이 방법은 Goodfellow 등에 의해 사용되었으며, 그들은 random initial guess 와 SGD 로 얻은 minima 사이의 선을 따라 loss surface 를 연구했다.
• 또한 이 방법은 다양한 minima 에서의 sharpness 와 flatness 에 대한 연구에 폭넓게 사용되었으며, batch size 에 의한 sharpness 의 dependence 의 연구에도 사용되었다.
• 그러나 1D linear interpolation 방법은 몇 가지 약점이 있다. 우선 1D plot 으로는 non-convexities(비볼록성) 의 시각화가 매우 어렵다.
  • 실제로 Goodfellow 등은 최소화 경로를 따라 loss function 이 local minima 를 거의 가지지 않음을 발견했는데, 2D model 을 활용해보니 어떤 loss function 은 극단적인 non-convexities 를 가지고 있으며 이러한 비볼록성이 서로 다른 네트워크 아키텍처 간의 일반화 차이와 상관관계가 있다.
• 다음으로, 이 방법은 네트워크의 batch normalization 이나 invariance symmetries 를 고려하지 않는다.
• 이러한 이유들로 인해 1D interpolation plot 으로 생성된 visual sharpness 비교는 잘못된 오해를 불러일으킬 수도 있다.

Contour Plots & Random Directions

• 이 방법을 이용하기 위해서는, 하나의 center point $\theta^{\ast}$ 를 그래프에서 선택하고, 두 개의 direction vector $\delta$ 와 $\eta$ 를 정한다.
• 그러면 $f(\alpha)=L(\theta^{\ast}+\alpha \delta)$ 형태의 function 으로 1D line 을 시각화할 수 있다.

• 또는 아래의 식을 이용하여 2D surface 로 plot 할 수 있다.

  \[f(\alpha , \beta)=L(\theta^{\ast}+\alpha \delta +\beta \eta) \qquad \cdots \qquad (1)\]
• 이 접근법도 다른 minimization 방법의 궤적을 탐구하는데 사용된다. 또한 2D 로 투영된 공간 안에서 local minima 를 찾는 다양한 optimization 알고리즘들을 시각화할 때도 사용한다.
• 그러나 2D plotting 은 연산량이 매우 많기 때문에, 이러한 방법들은 loss surface 의 복잡한 non-convexity 를 capture 하지 못하는 small region 을 저해상도(low-resolution)로 plot 한다.
• 이러한 이유로 본 논문에서는 neural network design 이 non-convex structure 에 어떻게 영향을 미치는지, weight space 의 large slice 에 대해 고해상도로 시각화한다.

Proposed Visualization: Filter-Wise Normalization

• 여기서는 적절하게 scaling 이 적용된 random Gaussian distribution 에서 sampled 한 random direction vector $\delta$ 와 $\eta$ 를 사용하는 식 (1) 의 plot 방식이 적용된다.
• Random directions 로 접근하는 것이 plotting 을 간단하게 만들지만, loss surface 의 본질적인 지형(geometry)을 capture 하는 것은 실패한다. 그리고 서로 다른 두 minimizer 나 네트워크의 geometry 를 비교하는 데에도 사용 할 수 없다.
• 이는 네트워크 weight parameter 들의 scale invariance 라는 특성 때문이다.
• 예를 들어 네트워크에 활성화함수로 ReLU non-linearities 가 사용될 경우, 네트워크의 어떤 레이어에서 얻어지는 weight 값들에 10 을 곱한 후 다음 레이어에서 10 으로 나누더라도 ReLU 에 의해 그 차이는 존재하지 않게 된다.
  • ReLU 는 $x > 0$ 일 때 그대로 사용되기 때문이다.
• 이러한 불변성(invariance)은 batch normalization 이 사용될 경우 더 중요하게 작용한다. 왜냐하면 각 레이어의 출력이 batch normalization 에 의해 re-scaled 되므로 필터의 사이즈(norm)가 무관해지기 때문이다.
• 따라서 네트워크의 동작은 결국 weight 를 re-scale 하더라도 바뀌지 않게 된다. 단, scale invariance 는 ReLU 가 사용된 rectified network 에서만 적용된다.
• Scale invariance 는 이를 방지하는 특별한 방법을 적용함에도 불구하고 plot 들을 비교할 때 의미있는 결과를 만드는 것을 방해한다.
• Large weights 를 갖는 neural network 는 smooth 하고 slowly 하게 변하는 loss function 을 갖는 것처럼 보일 수 있다. 왜냐하면 다른 것보다 scale 이 훨씬 큰 하나의 weight(one unit) 가 교란(perturbing)시키는 것은 네트워크의 성능에 매우 적은 영향을 미칠 것이기 때문이다.
• 그러나 만약 특정 weight 가 다른 weight 보다 매우 작다면, 같은 unit perturbation 이더라도 catastrophic effect 를 만들어 낼 것이며, loss function 을 weight perturbation 에 대해 꽤 민감하게 만들 것이다.
• Neural net 들은 scale invariant 하다는 점을 기억하자. 만약 small-parameter 와 large-parameter 네트워크가 존재하더라도 두 모델은 동일한 모델이 되며, loss function 에 대한 어떠한 차이도 단지 인공적인 scale invariance 에 의한 것들이다.
• 이러한 scaling effect 를 제거하기 위해 논문에서는 loss function 을 filter-wise normalized directions 를 이용하여 plot 한다.
• parameter $\theta$ 를 포함하는 네트워크의 direction 을 얻기 위해 $\theta$ 와 호환 가능한 dimension 을 가진 random Gaussian driection vector $d$ 만들어낸다.
• 그 다음에 $\theta$ 와 같은 norm 을 얻기 위해 각각의 $d$ 에 존재하는 filter 를 normalize 했다. 즉, $d_{i,j}\leftarrow \frac{d_{i,j}}{\parallel d_{i,j} \parallel}\parallel \theta_{i,j}\parallel$ 로 대체한다.
  • $d_{i,j}$ 는 $d$ 의 $i$ 번째 layer 에서 $j$ 번째 필터를 의미한다. $j$ 번째 weight 를 나타내는 것이 아니다.
  • $\parallel \; \dot \; \parallel$ 은 Frobenius norm 으로, Euclidian 거리다.
• 이러한 filter normalization 은 convolution layer 말고도 fc layer 에서도 적용된다. 왜냐하면 fc layer 는 $1\times 1$ conv layer 와 동일한 원리로 동작하기 때문이다.

The Sharp vs Flat Dilemma

• 위에서 시각화를 위한 filter normalization 의 컨셉에 대해 알아봤다.
• 이번 섹션에선 flat minimizer 보다 sharp minimizer 가 일반화(generalize)를 더 잘 시키는지 아닌지에 대한 것을 다룬다.
• 이를 통해 filter normalization 이 사용될 때 minimizer 의 sharpness 가 generalization error 와의 연관성이 크다는 것을 알 수 있다. 이는 plot 간의 side-by-side 비교를 가능하게 한다.
• 반면에 non-normailzed plot 들의 sharpness 는 왜곡되거나(distorted) 예측 불가능한(unpredictable)한 것처럼 보일 것이다.
• Large batch size 는 일반화(generalize)를 잘 시키지 못하는 sharp minima 를 만들어내는 반면, Small batch size 의 SGD 는 일반화를 잘 시키는 flat 한 minimizer 를 만들어낸다고 알려져 있다.
• 하지만 이에 대한 것은 아직 논의중으로, Dinh 나 Kawaguchi 등은 일반화가 loss surface 의 curvature(곡률) 와 직접적으로 연관되어 있지 않다고 주장한다. 또한 large batch size 로도 좋은 성능을 내는 학습 방법들이 제안되기도 한다.
• 이 섹션에선 sharp minimizer 와 flat minimizer 의 차이에 대해 탐구한다.
• 먼저 이러한 시각화(visualization)를 수행함에 있어 생기는 문제점들에 대해 짚어보고, 적절한 normalization 이 어떻게 plot 에서 왜곡된 결과(distorted result)를 만드는 것을 방지하는지에 대해 논한다.
• 논문에서는 CIFAR-10 데이터셋을 VGG-9(layer) 를 이용하여 학습시키고, batch normalization 를 일정한 epoch 마다 규칙적으로 수행한다.
• 또한 2 개의 batch size 를 사용했다.
  • large batch size 로 8192(16.4% of training data of CIFAR-10) 를 사용한다.
  • small batch size 로 128 을 사용한다.
• $\theta^{s}$ 와 $\theta^{l}$ 은 각각 small batch size 와 large batch size 를 사용하여 SGD 를 동작시켰을 때 얻어지는 결과를 나타낸다.

• linear interpolation approach 를 이용하여, 논문에서는 $f(\alpha)=L(\theta^{s}+\alpha (\theta^{l}-\theta^{s}))$ 와 같이 두 결과물을 포함한 방향을 따라 CIFAR-10 의 학습/테스트 데이터셋에서의 loss 값들을 plot 한다. 아래 그림을 보자.

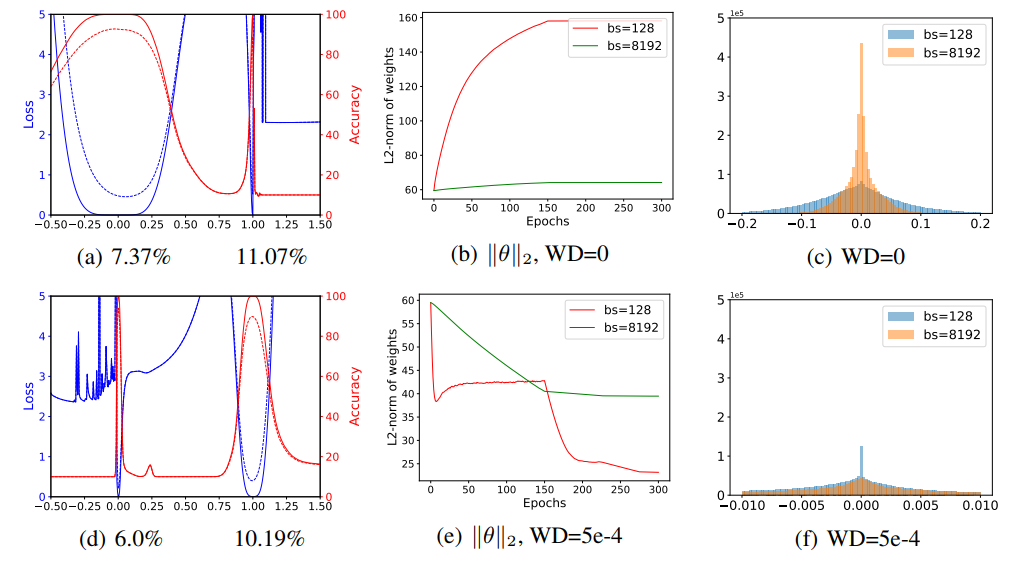  Figure 2. (a) 와 (d) 는 VGG-9 에서 small/large batch size 각각의 학습 결과를 1D linear interpolation 한 결과다. 파란선은 loss value, 빨간선은 accuracy 이며 실선은 training curve, 점선은 testing curve 다. Small batch 에서의 실험결과는 (a)에서 x 축 0, large batch 는 x 축 1 이다. 각 실험에 대한 test error 는 Figure 3 에서 확인할 수 있다.
  (b) 와 (e) 는 training 에서의 weight norm $\parallel \theta \parallel_{2}$ 의 변화를 나타낸다. Weight decay(WD) 가 비활성화 되는 경우(WD=0) weight norm 이 training 동안 제약 없이 서서히 계속 증가한다. (c) 와 (f) 는 weight histogram 으로, small batch size 를 사용하는 방법이 weight decay 가 비활성화일 때 더 큰 weights 를 생성하고, weight decay 가 활성화 되어 있을 때 더 작은 weight 를 생성한다는 것을 확인할 수 있다.

• Figure 2 에서 (a) 는 linear interpolation plot 으로, $x$ 축 0 은 small batch size 를 나타내는 $\theta^{s}$, $x$ 축 1 은 large batch size 를 나타내는 $\theta^{l}$ 를 의미한다.
• 우리는 small batch solution 이 더 넓고, large batch solution 은 좁고 sharp 함을 확인할 수 있다.
• 그러나 이러한 sharpness 양상은 weight decay 를 적용함으로써 확 바뀔 수 있다.
• Figure 2 의 (d) 는 같은 실험인데 weight decay 가 활성화되어 있는 결과다. 이 때는 large batch minimizer 가 sharp batch minimizer 보다 더 flat 함을 확인할 수 있다.
• 그러나 Figure 3 을 볼 때 모든 실험에서 small batch 를 사용했을 때 일반화 성능이 더 좋다. 즉 sharpness 와 generalization 사이에 명확한 상관관계가 없다는 뜻이다.
• 뒤에서 보겠지만, linear interpolation plot 으로 sharpness 를 비교했을 때 오해가 있다는 것이고 minima 의 특성을 잘 잡지 못했다는 것이다.
• Sharpness 의 분명한 차이들은 각 minimizer 에서의 weight 들에 대한 검토를 통해 설명이 가능하다.
• Network weight histogram 은 Figure 2 의 (c) 와 (f) 에서 보여진다. weight decay 를 비활성화 했을 때 Large batch 는 small batch 를 사용한 경우보다 더 작은 weight 값들을 갖는 경향을 보인다. 즉, weight 값의 분포가 0 에 더 몰려 있다.
• weight decay 를 활성화하면 large batch minimizer 는 small batch minimizer 보다 더 큰 weight 를 가지게 된다.
• 이러한 scale 의 차이는 간단한 이유로 인해 발생한다.
  • 더 작은 batch size 는 더 큰 batch size 보다 한 epoch 당 더 많은 weight update 를 한다. 따라서 weight norm 에 penalty 를 부과하는 weight decay 의 효과가 더 두드러지게 된다.
• 학습 중 weight norm 에 대한 변화는 Figure 2의 (b) 와 (e) 에서 볼 수 있다.
• Figure 2 는 minimizer 들의 내부의 sharpness 를 시각화하지 않고 오히려 무관한 weight scaling 에 대한 것만을 시각화한다.
• network 의 weight 를 scaling 하는 것은, Batch normalization 은 unit variance(단위 분산, 즉 분산값이 1)를 갖기 위해 output 을 re-scaling 하기 때문에 의미가 없다.

• 그러나 작은 weight 들은 여전히 변화에 민감하며, 더 sharp 하게 보이는 minimizer 들을 만들어낸다.

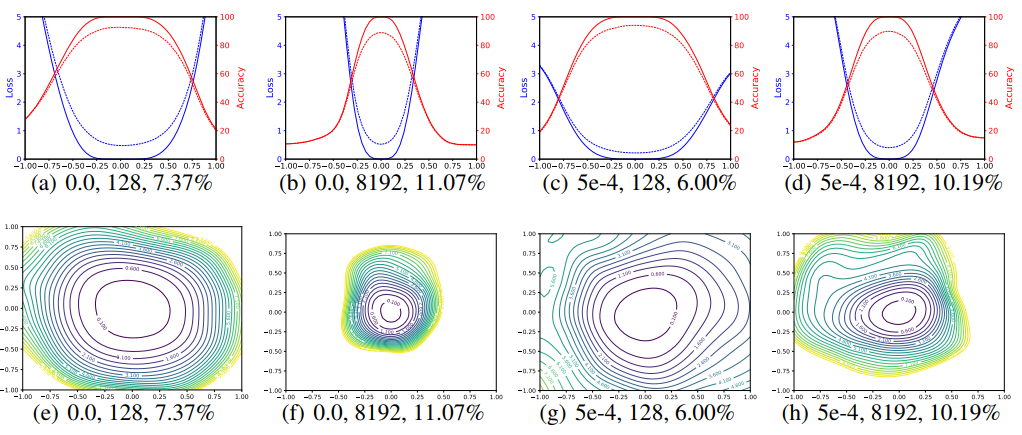  Figure 3. 서로 다른 weight decay 와 batch size 에서 SGD 를 이용하여 얻은 결과를 1D 와 2D 시각화한 것이다. 각 subfigure 의 각주는 weight decay, batch size, test error 를 나타낸다.

Filter Normalizaed Plots

• Figure 2 의 실험을 다시 반복한다. 하지만 이번엔 random filter-normalized directions 를 사용하여 각 minimizer 근처에서의 loss function 을 개별적으로 plot 한다.
• 이로 인해 Figure 2 의 (c) 와 (f) 에서 보여지는 scaling 에 의해 발생되는 지형(geometry)의 차이가 사라진다.
• Figure 3 의 실험 결과는 마찬가지로 small batch minima 와 large batch minima 사이의 sharpness 차이를 보여주지만, 여기서는 un-normalized plot 에서 보이는 것보다 훨씬 미묘한 것을 알 수 있다.
• 또한 논문에서는 두 개의 random directions 와 contour plot 들을 이용한 실험 결과를 시각화했다.
• 실험 결과, small batch size 와 non-zero weight decay 를 사용했을 때 large batch minimzer 보다 더 넓은 contour 를 갖는 결과를 얻었다.
• Figure 3 에서 filter-normalizeed plot 을 이용하면서 minimizer 간의 side-by-side(나란한) 비교가 가능했으며 이로부터 sharpness 가 generalization error 와 밀접한 연관이 있음을 볼 수 있었다.
• 즉 Large batch size 는 시각적으로 더 sharp 한 minima(다이나믹하진 않지만)를 만들어내고 더 높은 test error를 보였다.
  • Figure 3 의 각 plot title 을 보자.

What Makes Neural Networks Trainable? Insights on the (Non)Convexity Structure of Loss Surfaces

• Neural loss function 의 global minimizer 를 찾는 능력은 쉬운 일이 아니다. local minimizer 를 찾아도 적당한 성능이 나온다고도 알려져 있다.
• 그러나 어떤 모델 구조에서는 다른 것보다 loss function 의 minimizer 를 찾는 것이 더 쉬운 case 가 있다.
• 예를 들어, skip connection 을 쓰는 경우 매우 깊은 구조(architecture)의 모델들을 학습시킬 수 있고 skip connection 없이 그와 비슷한 깊이의 네트워크들은 학습이 불가능했다.
• 더욱이 이러한 네트워크를 학습시키는 능력은 학습을 시작할 때 초기 parameter 와 큰 관련이 있다.
• 시각화 방법을 이용하여, 해당 논문에서는 neural architecture 에 대한 실증적인 연구를 수행하여 왜 loss function 의 non-convexity 가 어떤 상황에서는 문제가 되고, 어떤 상황에서는 아닌지에 대한 탐구한다.
• 논문에선 다음 질문들에 대한 insight 를 제공한다.
  • Loss function 은 중요한 non-convexity 를 모두 가지고 있는가?
  • 만약 눈에 띄는 non-convexity 가 있는 경우, 왜 그러한 non-convexity 들이 항상 문제가 되지 않는가?
  • 왜 일부 모델 디자인은 쉽게 훈련할 수 있는 것인가?
  • 결과가 학습 초기 initialization 하는 것에 민감한 이유는 무엇인가?

• 논문에선 이러한 질문에 답하기 위해서 non-convexity 구조에서 극단적인(extreme) 차이를 가지는 아키텍쳐에 대해 살펴보고, 이러한 차이점들이 generalization error 와 연관이 있음을 살펴본다.

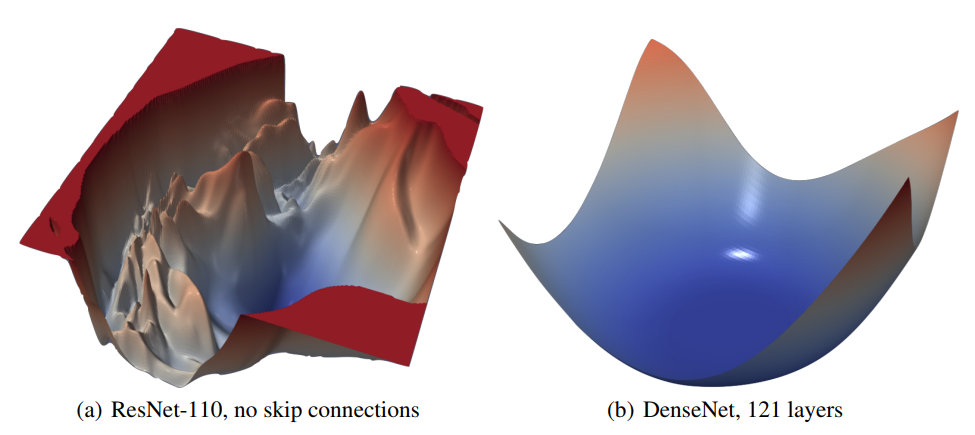  Figure 4. ResNet-110-noshort 와 DenseNet 의 CIFAR-10 에 대한 loss surface

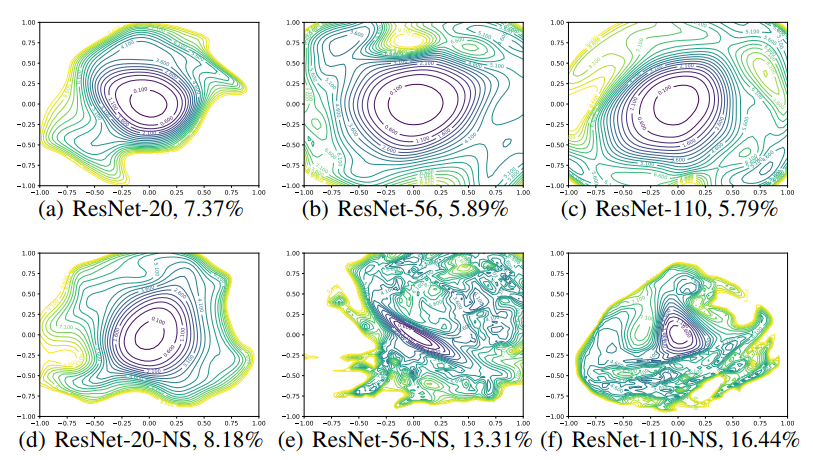  Figure 5. 서로 다른 depth 에서의 ResNet 과 ResNet-noshort 의 2D loss surface visuzlization

Experimental Setup

• Non-convexity 가 network architecture 에 어떤 효과를 미치는지 이해하기 위해 논문에서는 다양한 네트워크를 학습하고 filter-normalized random direction method 를 사용하여 얻은 minimizer 주변의 landscape 를 plot 한다.
• 실험에서는 neural network 들에 대해 3 가지 class 를 고려한다.
  • 1) CIFAR-10 대상으로 optimize 된 ResNets. 실험에서는 ResNet-20/56/110 을 사용했고, 각 숫자는 layer 의 숫자를 의미한다.
  • 2) Shortcut 이나 skip connection 을 포함하지 않는 ‘VGG-like’ 네트워크 사용. 즉 ResNet 에서 shortcut connection 을 제거한 것이다. ResNet-20/56/110-noshort 라고 표기한다.
  • 3) 첫번째의 CIFAR-10 optimized network 보다 레이어당 더 많은 필터 개수를 가지는 ‘Wide’ ResNets 사용.
• 모든 모델들은 CIFAR-10 데이터셋에 대해 Nesterov momentum 을 이용한 SGD 를 이용하며, batch-size 는 128, 300 epoch 마다 0.0005 의 weight decay 를 적용한다. Learning rate 는 0.1 로 초기화되었으며 150, 225, 275 epoch 마다 10 배씩 감소한다.
• 밑에서 기술되는 ResNet-56-noshort 같은 VGG-like 실험에서는 0.01 의 더 작은 learning rate 를 적용한다.
• 각각 다른 neural network 의 minimizer 에 대한 고해상도 2D plot 은 Figure 5 와 Figure 6 에서 확인 가능하다.
• 결과는 surface plot 이 아닌 convour plot 으로 보여지는데, 이는 non-convex structures 를 쉽게 확인할 수 있고 sharpness 를 쉽게 평가할 수 있게 해주기 때문이다.
• ResNet-56 에 대한 surface plot 은 Figure 1 에서 참고 가능하다.
• 각 plot 의 중심은 minimizer(minima) 이며, 두 축은 (1) 과 같이 filter-wise normalization 를 통해 두 개의 random direction 을 parameterize 한 결과다.
• 아래부터는 모델의 architecture 가 어떻게 loss landscape 에 영향을 미치는지에 대해 제시한다.

The Effect of Network Depth

• Figure 5 를 보면, skip connection 이 없을 때 network depth 가 neural network 의 loss surface 에 많은 영향을 미치는 것을 볼 수 있다.
• ResNet-20-noshort 네트워크에 대한 실험 결과(d)를 볼 때, 극단적인 non-convex 가 없고 중앙에 상당히 부드러운(benign) 지역으로 convex contour 를 보인다.
  • 이는 네트워크가 얕기 때문에 shortcut 에 의한 영향력이 적기 때문이다.
  • 또한 ImageNet 에 대한 original VGG 를 보면 19 개의 레이어를 갖고 효율적으로 학습이 가능했다는 점에서 그다지 놀랍지 않다.
• 그러나 네트워크의 깊이가 깊어질수록 VGG-like 네트워크(NS 가 붙은)의 loss surface 가 거의 convex 한 형태에서 chaotic 으로 변하게 된다.
  • 이는 네트워크가 깊어질수록 loss landscape 가 복잡해진다는 의미로 해석할 수 있다.
  • ResNet-56-NS 는 극단적인 non-convexity 를 가지며 넓은 지역에서 gradient direction 이 중앙의 minimizer 를 가리키지 않게 되는 것을 확인할 수 있다.
  • surface 가 복잡하므로 확률적으로 당연히 중양의 minima 로 optimization 되기 힘들다.
  • 또한 어떤 방향으로 움직일 때 loss function 이 극단적으로 커지게 된다.
• ResNet-110-NS 는 더 dramatic 한 non-comvexity 를 보인다.
  • 그리고 plot 에서 보여지는 모든 방향으로 움직일 때 extremely 하게 가파른 양상을 보인다.
• 거기에 더해서, 깊은 VGG-like 네트워크들의 plot 중앙에 위치한 minimizer 들은 상당히(fairly) sharp 한 모습을 보인다.
• ResNet-56-NS 의 경우 minimizer 가 꽤 ill-conditioned(불량 조건) 상태이고 minimizer 주변의 contour 들을 볼 때 상당히 기이한(eccentricity) 형태다.

Shortcut Connections to the Rescue

• Shortcut connection 들은 loss function 의 지형(geometry)에 대해 dramatic 한 효과를 가져온다.
• Figure 5 를 보면 상단의 residual connection 이 있는 네트워크가 깊이가 깊어지더라도 loss surface 의 chaotic 한 변화를 방지하는 것을 확인할 수 있다.
• 또한 0.1-level contour (중앙에 위치한) 의 width 와 shape 가 20-layer 와 110-layer 가 거의 동일한 것을 알 수 있다.
• 흥미롭게도 skip connection 의 효과는 deep network 에서 가장 중요한 것처럼 보인다.
• ResNet-20 이나 ResNet-20-NS 같은 shallow network 에 대해서는 skip connection 의 효과가 별로 없다(unnoticeable).
• 그러나 네트워크가 깊어질수록 residual connection(=shortcut, skip connection) 이 non-convexity 의 폭발적 증가(explosion)를 막아준다.

• 이 효과는 다른 종류의 skip connection 에서도 존재한다. Figure 4 에서 볼 수 있듯 DenseNet 의 loss landscape 를 통해 다른 종류의 skip connection 을 포함하는 깊은 구조임에도 non-convexity 를 보이지 않는 것을 확인할 수 있다.

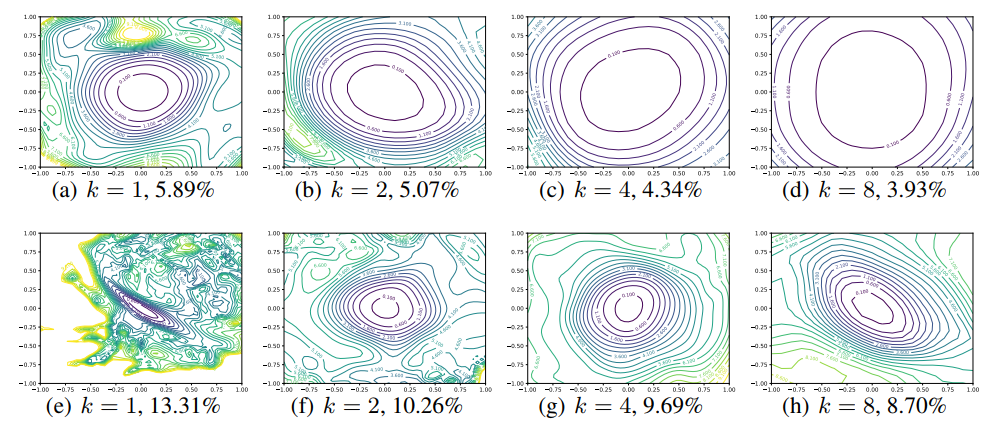  Figure 6. CIFAR-10 에 대한 Wide-ResNet-56 실험 결과. 위는 shortcut connection 이 있고 아래는 W/O shortcut connection 의 결과다.
  label $k=2$ 는 레이어당 2 배의 많은 filter 들이 존재하는 것을 뜻한다. test error 는 각 figure 밑에 표기되어 있다.

Wide Models vs Thin Models

• 레이어 당 convolutional filter 개수의 효과에 대해 보기 위해서, narrow CIFAR-optimized ResNets(ResNet-56) 과 $k$ 에 따라 레이어 당 filter 의 개수를 $k$ 배수 만큼 넓게 한 Wide-ResNets 을 비교한다.
• Figure 6 를 보면, 모델이 wider 할수록 ($k$ 가 큰 모델) 덜 chaotic 한 loss landscape 를 확인할 수 있다.
• 즉 네트워크의 넓이(width)를 넓게 할수록 flat 한 minima 와 넓은 convexity(볼록) 영역이 나타난다.
• 그리고 Figure 6 에서 상단의 결과를 보면 skip connection 이 minimizer 를 드라마틱하게 넓히는 것을 볼 수 있다.
• 또한 plot 별 아래 title 을 보면 sharpness 는 test error 와 매우 연관이 있음을 알 수 있다.

Implications for Network Initialization

• Figure 5 에서 볼 수 있는 하나의 재미있는 특성은 모든 네트워크에서 loss landscape 들이 low loss value 를 가진 convex 한 영역과 그 주변에 high loss value 를 가진 non-convex contour 들로 둘러쌓인 영역으로 구분할 수 있다.
• 이처럼 chaotic 과 convex 지역(region)의 분리(partitioning)는 좋은 initialization strategies 의 중요성에 대해 설명한다. 또한 좋은 네트워크 구조가 학습이 쉽게 되는 것도 설명 가능하다.
• Xavier initialization 과 같은 normalized random initialization strategy 를 초기화 방법으로 쓸 때, 전형적인 neural network 들은 initial loss value 를 2.5 보다 적게 얻는다.
• Figure 5 에서 상단의 ResNets 나 얕은 VGG-like 네트워크와 같이 잘 동작하는 네트워크의 loss landscape 는 loss value 를 4 또는 그 이상의 loss value 를 가지는 large, flat, nearly convex 가 대부분이다.
• 이러한 landscape 들에 대해, random initialization 은 well-behaved loss region 에 놓이게 될 것이다.
• 이는 landscape 가 좋으면 random 하게 weight 를 초기화 하더라도 좋은 지역에 놓이게 될 것이라는 의미다.
• 그리고 여기서 optimizer 알고리즘들은 high-loss 를 발생시키는 chaotic 한 고원(plateau)과 같은 non-convexity 들을 볼 수 없을 것이다. 즉, 쉽게 optimization 이 될 것이다.
• 반면에 ResNet-56/110-NS 의 chaotic 한 loss landscape 들은 더 낮은 loss 값을 얻을 수 있는 convexity 영역이 더 좁은 지역에서 관찰된다. 즉, loss 값이 낮아지는 방향으로 흘러갈 수 있는 확률이 낮아질 수 밖에 없다.
• 이처럼 Shallow enough attractor 를 가진 충분히 깊은 네트워크의 경우, 초기 epoch 는 gradient 정보가 쓸모 없는(uniformative) chaotic region 에 놓이게 된다. 이러한 경우 gradient 들은 흩어지게 되며(statter) 학습이 불가능하게 된다.
• skip connection 이 없는 156-layer 네트워크가 매우 작은 learning rate 로도 SGD 로 학습이 불가능하다는 것은 이러한 가설에 힘을 실어준다.

Landscape Geometry Affects Generalization

• Figure 5 와 6 은 landscape 의 지형이 일반화(generalization)에 미치는 dramatic 한 효과에 대해 보여준다.
• 우선, 시각적으로 더 평평한(flat) minimizer 들은 계속 낮은 test error 를 가진다. 이는 논문에서 제안하는 filter normalization 이 loss function 의 geometry 를 시각화하는 자연스러운 방법임에 더 큰 힘을 실어준다.
• 다음으로, skip connection 이 없는 deep network 의 chaotic landscape 결과들은 더 어려운 학습과 높은 test error 를 보인다. 반면에 더 convex 한 landscape 일수록 낮은 error를 보인다.
• 사실 Figure 6 의 윗줄에서 볼 수 있는 Wide-ResNets 과 같은 가장 convex 한 landscape 들은 가장 일반화(generalize)를 잘 시키며 chaotic 한 landscape 모습을 거의 찾아볼 수 없다.

Are we really seeing convexity?

• 우리는 여기서 dramatic 한 dimensionality 감소를 통해 loss surface 를 보고 있으므로 이러한 plot 을 해석함에 있어서 주의를 기울여야 한다.
• loss function 의 convexity level 을 정량화하기 위해서 principle curvatures(주곡률, 주곡선) 를 계산하는 방법이 있다. 이것은 간단하게 Hessian 의 고유값들을 뜻한다.
• Convex function 은 non-negative curvature 를 가진다. loss fucntion 이 convex 한지를 증명할 때 Hessian 행렬을 자주 사용하는데, 이 때 등장하는 positive semi-definite Hessian 이다. 반면에 non-convex function 은 negative curvature 를 가진다.
• 위에서 Figure 들로 본 dimensionality reduced plot(with random Gaussian directions) 의 prinicple curvatures 은 full-dimensional surface(where the weights are Chi-square random variables) 의 principle curvature 를 가중평균한 것이다.
• 이것은 몇가지 결과를 보여준다.
• 우선, 만약 non-convexity 가 dimensionality reduced plot 에 존재한다면, non-convexity 는 full-dimensional surface 에도 무조건 존재하게 된다.
• 그러나 low-dimensional surface 에 분명한 convexity 가 존재하더라도 high-dimensional function 이 truly convex 하다는 것을 의미하지는 않는다.

• 오히려 positive curvature 들이 dominant, 즉 mean curvature 또는 average eigenvalue가 양수임을 의미한다.

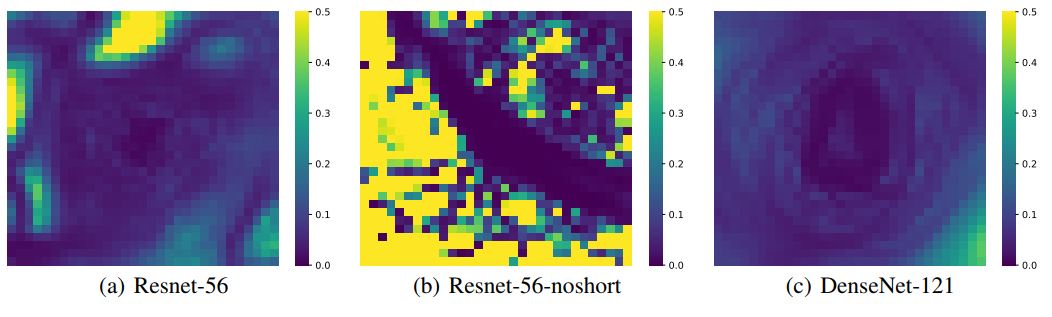  Figure 7. filter-normalized surface plot 각각의 point 에 대해 Hessian 의 maximum 과 minimum eigenvalue 를 계산하고, 이 두 eigenvalue 에 대한 비율을 heat map 으로 나타냈다.

• 우리는 여전히 이러한 시각화(visualization)가 포착(capture)하지 못하는 중요한 “숨겨진” non-convexity 가 존재할 수 있는지 궁금할 수 있다.
• 이에 답하기 위해서 Hessian 의 minimum eigenvalue $\lambda_{\text{min}}$ 과 maximum eigenvalue $\lambda_{\text{max}}$ 를 계산한다.
• 위 Figure 7 의 map 들은 위에서 봤던 loss surface 들(같은 minimizer 와 같은 random direction 사용)에 대한 $\vert \lambda_{\text{min}} / \lambda_{\text{max}} \vert$ 비율이다.
• 파란색은 양의 eigenvalue 에 비해 0 에 가까운 음의 eigenvalue 로, 더 convex 한 지역을 의미한다. 반면 노란색은 상당한 수준의 negative curvature 를 의미한다.
• 그러면 논문에서 그린 surface plot 에서의 convex-looking region 들은 실제로 negative eigenvalue 들이 미미한 영역과 일치한다는 것을 확인할 수 있다. 즉, plot 이 놓친 중요한 non-convex feature 는 없다는 의미다. 반면에 chaotic region 은 large negative curvature 들을 포함한다.
• DenseNet 과 같은 convex-looking surface 의 경우에는 plot 의 넓은 지역을 걸쳐 negative eigenvalue 들이 positive curvatures 크기의 1% 미만으로 매우 작게 유지되고 있음을 확인 할 수 있다.
• 정리해보자.
  • Figure 7 에서 파란 부분은 아래로 볼록한 부분이며 노란 부분은 위로 볼록한 것을 의미한다.
  • 따라서 파란색이 넓게 분포할수록 더 loss surface 에 chaotic 한 부분이 덜 존재하는 것을 의미하며, 이는 해당 모델이 Generalization 이 더 잘 되어 있음을 의미한다.(negative curvature가 더 좁게 존재)
  • 또한 고차원의 loss surface 를 저차원으로 plot 하면 고차원에 숨겨진 non-convexity 가 저차원으로 plot 되지 못한다고 생각 할 수 있다.
  • 이는 고차원의 데이터에 대한 hessian matrix 를 구한 후 계산되는 hessian eigenvector 의 최솟값과 최댓값의 비율 plotting 을 볼 때(Figure 7의 그림), chaotic 한 부분은 large negative curvature(노란부분)으로 eigenvalue plotting 에서 나타나게 되므로 고차원의 정보까지 plotting 이 가능한 것을 알 수 있다.
  • 즉 $N$ 차원의 loss surface 정보들을 taylor expansion 으로 근사화 한 후 해당 eigenvalue 들에 대한 최솟값/최댓값의 절댓값을 plotting 한 결과가 Figure 7 이다.
  • 따라서 전체 차원에 대한 곡률정보를 담고 있으므로 고차원에 숨겨진 non-convexity 또한 저차원인 2D plot 에 표현될 것이다.
  • 참고로 Hessian matrix 계산 시 필요한 Taylor expansion 의 eigenvalue 의 모든 값이 양수면 함수는 극소, 모든 값이 음수면 함수는 극대, 음과 양의 고유값을 모두 가지면 saddle point 로 판단한다.

Visualizing Optimization Paths

• 마지막으로, 서로 다른 optimizer 의 궤적(trajectory)들을 시각화하는 방법에 대해 탐구한다.
• 여기서는 random direction 이 효과적이지 못하다. 왜 random direction 이 효과적이지 못한지에 대한 이론적인 설명과 함께 효과적으로 loss function contour 위에 궤적(trajectory)을 효과적으로 plotting 하는 방법에 대해 연구한다.
• 몇몇의 저자들이 왜 random direction 이 optimization 궤적의 변화를 capture 하는 것이 실패하는지 연구했다. Figure 8 에는 실패한 시각화에 대한 예시가 담겨있다.
• Figure 8 의 (a) 에서는 SGD 가 두 random direction 으로 정의되는 평면에 반복적으로 영사한(나타낸) 궤적을 보인다. 실제로 움직임(motion)이 거의 capture 되지 않았다(참고로 축방향으로 엄청나게 확대 되어있으며 random하게 움직이는듯 함).
• 이에 대한 보완으로 one random direction 을 이용하여 initialization 부터 optimizer 의 궤적을 시각화 한다. 이 접근법이 Figure 8 의 (b) 다.

• 그러나 Figure 8 의 (c) 에서 볼 수 있듯, random axis 가 거의 변화가 없으므로 직선 경로로 잘못된 optimization path 를 보인다.

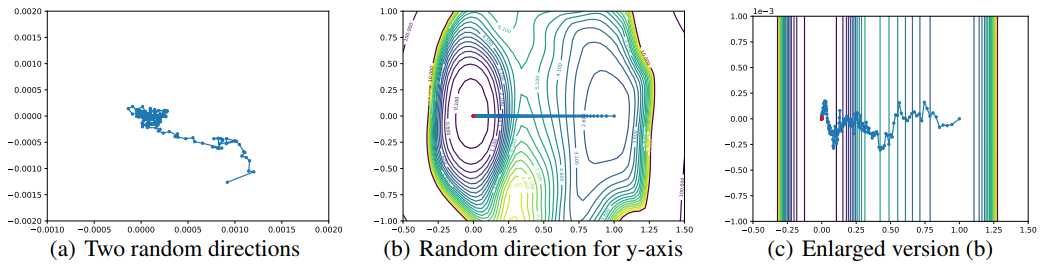  Figure 8. Optimizer 궤적의 효과적이지 못한 시각화 예시. 이러한 시각화 방법들은
  고차원에서의 random direction 의 직교성(orthogonality)으로 인해 제대로 동작하기 힘들다.

Why Random Directions Fail: Low-Dimensional Optimization Trajectories

• 고차원의 공간에 존재하는 두 random vector 들은 높은 확률로 직교한다는 것이 잘 알려져있다.
• $n$ 차원의 Gaussian random vector 들 사이의 cosine similarity 는 대략적으로 $\sqrt{2/(\pi n)}$ 다.
• 이는 저차원 공간에 optimization 궤적이 존재할 때 문제가 된다. 이런 경우 random 하게 선택된 vector 가 optimization path 를 포함하는 low-rank 공간에 orthogonal 하게 존재하게 되며, random direction 의 projection 은 변화가 거의 없게 된다.
• Figure 8 의 (b) 는 optimization 궤적이 저차원이라는 것을 보여준다. 이는 random direction 이 optimization path 를 따라 가는 벡터보다 적은 크기의 변화를 포착(capture)하기 때문이다.
• 아래에서는 PCA directions 를 이용하여 직접적으로 이러한 low dimensionality 를 증명하고, 동시에 효과적인 시각화 자료를 생성한다.

Effective Trajectory Plotting using PCA Directions

• 궤적의 변화를 포착하기 위해서, 논문에서는 non-random(and carefully chosen) direction 이 필요하다.
• 여기서 저자들은 얼마나 변화가 포작되었는가를 감지할 수 있는 PCA 를 기반으로 접근하고, 이를 이용해 loss surface 의 contour 를 따라 이러한 궤적(trajectory)들을 plot 한다.
• $\theta_{i}$ 를 $i$ 번째 epoch 의 model parameter 라고 해보자. 그러면 $n$ epoch 가 끝난 뒤의 parameter 들은 $\theta_{n}$ 이 된다.
• 주어진 $n$ epoch 학습에서, matrix $M=\begin{bmatrix}\theta_{0}-\theta_{n} ; \cdots ; \theta_{n-1}-\theta_{n}\end{bmatrix}$ 에 PCA 를 적용하고, 두 개의 explanatory(설명하기 위한) direction 을 선택한다.
• Figure 9 는 optimizer 의 궤적(파란점)과 loss surface 가 PCA direction 을 따라 그린 것이다. Learning rate 가 감소되는 epoch 에 대한 결과는 빨간점으로 나타난다.

• 또한 각각의 축에 대해 PCA direction 에 의해 포착된 하강(descent) path 의 변화가 측정되어 있다.

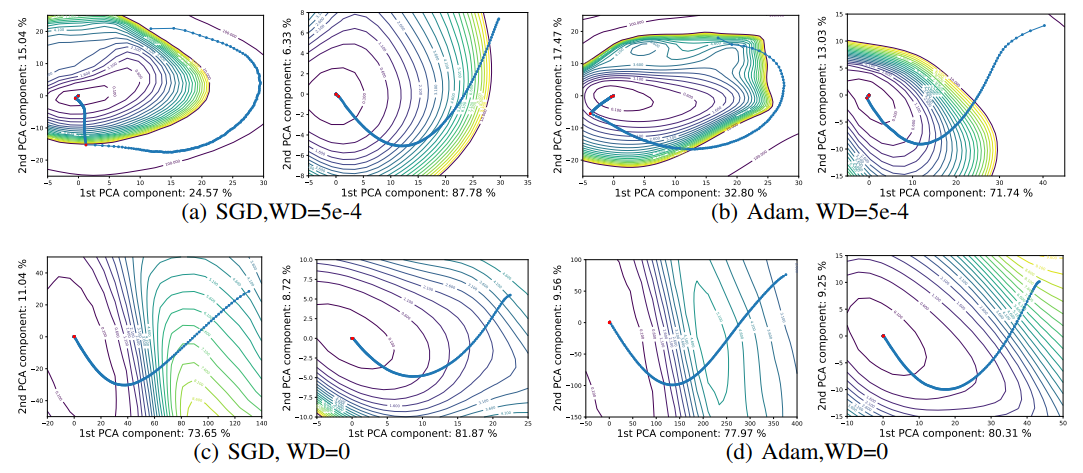  Figure 9. VGG-9 의 nurmalized PCA direction 을 이용하여 영사된 learning trajectories.
  각 subfigure 의 왼쪽이 batch size 128 이고 우측이 batch size 8192 이다.

• 학습 초반 stage 에서는 loss surface 의 contour 로 수직하게(perpendicular) path 가 움직이는 경향이 있다. 즉 비 확률적(non-stochastic) gradient descent 에서 기대할 수 있는 것처럼 gradient 방향을 따르게 된다. 이는 gradient 가 큰 방향으로 loss 가 감소하게 된다는 것을 의미한다.
• 확률성(stochasticity)은 training 의 뒤 stage 로 갈수록(학습의 후반부에 갈수록) 점점 여러 plot 들에서 뚜렷해진다. 이러한 현상은 weight decay 와 small batch 를 사용하는 경우 더 도드라진다. 갑자기 궤적이 꺾이는 지점이다.
• small batch 는 gradient noise 가 많아지고, 결정론적(deterministic) gradient direction 로부터 더 급진적(radical)으로 출발(departure)하게 되기 때문이다.
• 즉, batch 가 작아질수록 noise 성분이 많아져 더 빠르게 minima 에 도달 할 수 있게 된다는 의미다.
• Weight decay 와 small batch 가 함께 사용된 경우, contour 와 거의 평행한 방향으로 path 가 변하는 것을 볼 수 있으며, stepsize(lr rate) 가 클수록 solution 을 orbit(궤도에 진입)시킬 수 있게 된다.
• 빨간점을 지나 Stepsize 가 떨어지게 될 경우(10배씩 감소), system 의 효과적인 noise 는 감소하게 되며 path 가 가장 가까운 local minimizer 에 빠지면 구부러지기(kink) 시작하는 것을 확인할 수 있다.
• 마지막으로, optimizer 의 descent path 를 매우 낮은 차원에서 관찰했는데, descent path 의 변화(variation)의 40 ~ 90% 가 오직 2차원의 공간에 존재한다는 것을 알 수 있다.
• Figure 9 의 optimization trajectories 은 가까운 attractor direction 으로의 움직임(movement)이 지배적인 것(dominated by)으로 보인다.
• 이러한 low dimensionality 는 non-chaotic landscape 들이 wide, nearly convex minimizer 들에 의해 지배적이게 되는 것을 관찰한 것과 잘 맞아 떨어진다.

Conclusion

• 해당 논문에서는 network 구조, optimizer 선택, batch size 를 포함하는 neural network practitioner 의 다양한 선택의 결과에 대한 통찰력을 제공하는 시각화(visualization) technique 을 제안했다.
• Neural network 들은 복잡한 가정(assumption)을 가진 입증되지 않은(anecdotal) 지식(knowledge)과 이론적인 결과를 바탕으로 최근 극적으로(dramatically) 발전하고 있다.
• (연구의)진척(progress)이 계속되기 위해서는 neural network 의 구조에 대한 일반적인 이해가 더 필요하다.
• 효과적인 시각화(visualization)가 이론의 지속적인 발전과 결합되면 보다 빠른 training, 단순한 모델구조, 그리고 더 나은 일반화(generalization)가 가능해 질 것으로 기대된다.

맨 위로 이동 ↑