[Loss] Wasserstein distance

앞선 포스트에서 KL-divergence 와 JSD 에 대해 다루었다.

KL-div 는 MLE 와 밀접하게 관련이 있고, 이를 통해 VAE 에서 사용되는 Variational Inference 까지 살펴봤다. 또한 KL-div 가 충족하지 못하는 거리함수의 성질인 대칭성을 보완한 JSD 는 GAN 에서 loss function 으로 귀결됨을 확인했다.

아직 다루지 않은 loss function 과 관계가 깊은 거리함수는 Wasserstein Distance 가 있다. 이는 WGAN 논문에서 KL-div 와 JSD 의 한계를 짚으면서 사용한 Metric 이다.

수학적으로 매우 복잡한 개념이 들어가 있기 때문에 완벽한 이해는 어렵지만, Wasserstein Distance 를 왜 사용했고, 이를 활용하여 어떤 loss function 을 어떻게 유도했는지 확인해보자.

문제 상황

• Generative Model 에서 학습하는 $p(x)$ 는 확률분포다. 그리고 확률분포를 학습한다는 것은 고전적인 정답으로 확률밀도를 학습한다는 것이다.
• 이를 위해 parametric family $P_\theta$ 를 정의함으로써 데이터에 대한 likelihood $P_\theta(x)$ 를 최대화하는 parameter $\theta$ 를 찾게 된다. 그리고 이 때 계산의 효율성을 위해 $\log$ 를 사용한다.

• 따라서 우리가 실제 데이터 $\lbrace x^{(i)}\rbrace^m_{i=1}$ 를 가지고 있을 때 아래의 문제를 해결하는 것이다. 즉 maximum likelihood 다.

  \[\underset{\theta \in \mathbb{R}^d}{\text{max}}\frac{1}{m}\sum^m_{i=1}\log P_\theta(x^{(i)})\]
• 만약 실제 데이터 분포 \(\mathbb{P}_r\), parameterized density \(\mathbb{P}_\theta\) 가 있을 때, maximum likelihood 는 \(\mathbb{KL}(\mathbb{P}_r \Vert \mathbb{P}_\theta)\) 를 최소화하는 것과 동일하다.
  • 이에 관해서는 이 포스트에 잘 정리했다.
  • 이는 discriminative model 이나 generative model 이나 동일하다.
• 그러면 이를 계산하기 위해서 model density $P_\theta$ 가 존재해야 한다.
  • 이는 모델 분포 $P_\theta$ 가 실제 데이터 분포 $P_r$ 이 놓인 공간 내에서 정의되어야 함을 의미한다.
  • 모델 분포 $P_\theta$ 가 존재하지 않으면 KL-div 를 계산할 수 없으므로, 모델이 실제 데이터 분포와 얼마나 유사한지 측정할 수 없다.
• 그러나 manifold hypothesis 를 다루는 일반적인 상황에서 model manifold 와 실제 분포의 support 사이에 교차점을 가질 가능성은 거의 없다.
  • 실제 데이터 분포는 저차원 manifold 가정에 의해 지지되는 경우가 흔하다. 예를 들어, 고차원 데이터가 실질적으로는 저차원 구조 위에 존재하는 경우로 특히 이미지나 영상 데이터에서 자주 나타나는 현상이다.
  • 모델의 layer 를 늘려가면서 feature map 을 input image 의 spatial dimension 보다 작게 만들어내는 것과 같다.
  • 여기서 model manifold 와 실제 데이터 분포의 support 사이에 교차점이 거의 없다는 것은 실제 데이터가 있는 공간과 모델이 정의된 공간이 겹치는 영역이 거의 없다는 뜻이다.
  • 따라서 모델이 실제 데이터를 제대로 설명하지 못하는 상황이 발생할 가능성이 높다.
  • 해당 문제의 경우 아래 섹션에서 더욱 구체적으로 다룬다.
• 이러한 경우 KL-div 를 계산할 때 문제가 발생한다. 즉 KL-div 가 정의되지 않는다는 것을 의미한다.
  • 두 분포의 support 가 겹치는 영역이 거의 없다면, KL-div 는 무한대가 되거나 계산이 불가능할 수 있다.
  • 이는 maximum likelihood 그 자체를 추정하는 것이 KL-div 가 fail 하면 어려워질 수 있다는 것을 의미하기도 한다.
  • 따라서 이와 같은 경우에는 KL-div 를 최소화하는 접근이 적절하지 않을 수 있다.
• 위에서 얘기하는 support 라는 개념은 지지집합으로, 원래 함수의 정의역을 유효한 범위로 축소하는 역할을 한다. 즉 실수 범위의 정의역에서 함수값(확률)이 0 이 아닌 영역으로 정의역을 축소하는 것이다.
  • 이러한 support 는 “0 이 아닌 점 들의 집합” 이라고 이해하면 편하다.

• 전형적인 해결책은 model distribution 에 noise term 을 추가하는 것이다.

  

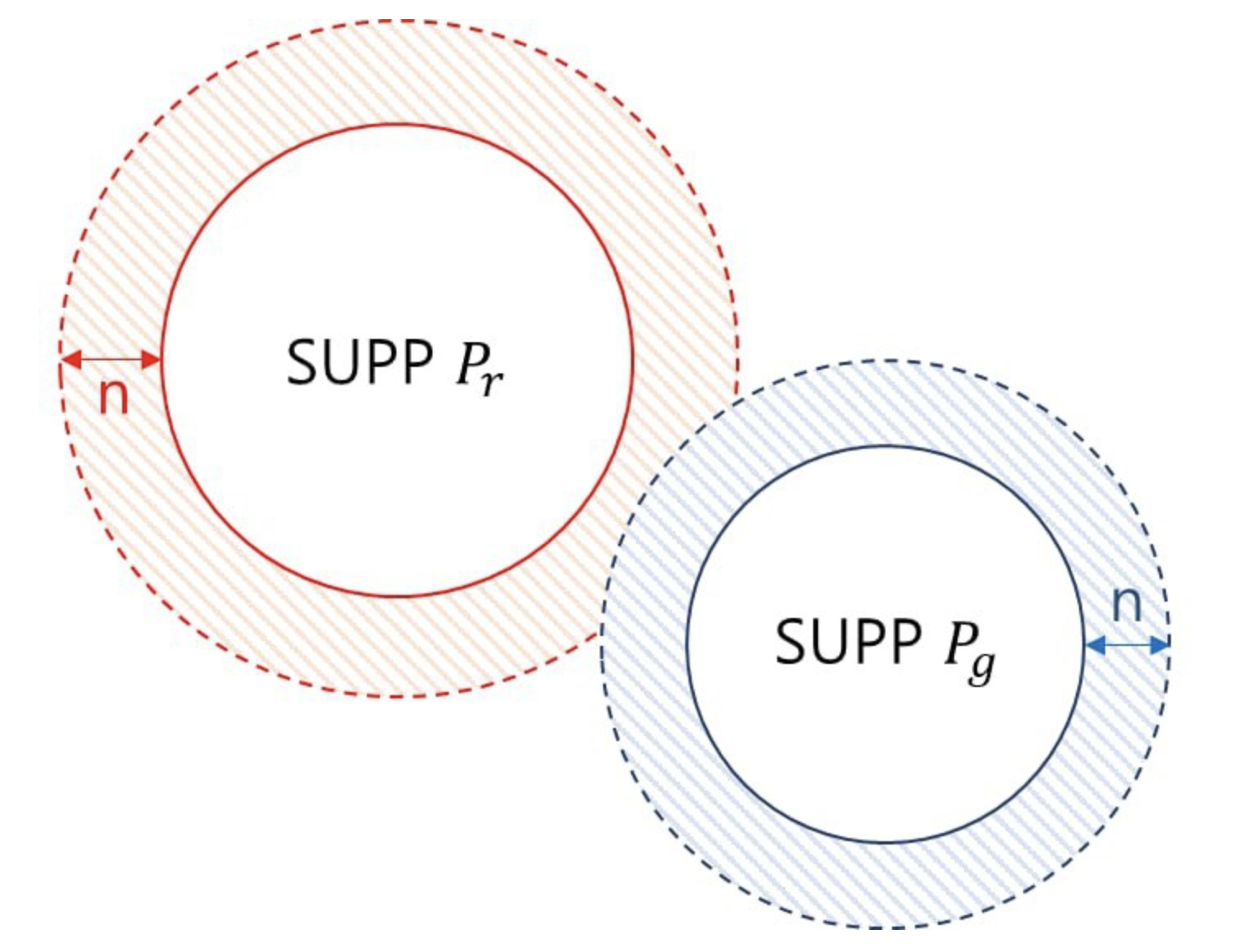
  • 즉 위 그림처럼 noise $n$ 을 추가해주면서 위 그림처럼 두 분포의 support 영역을 넓혀 겹칠 수 있도록 만들어 주는 것이다.
  • 가장 간단한 경우에, 모든 예시들을 커버하기 위해 상대적으로 높은 대역폭을 가지는 Gaussian noise 를 가정한다.
  • 그러나 이미지 생성 모델에서 이러한 noise는 샘플의 품질을 저하시키고 뿌옇게 만든다는 사실이 잘 알려져 있다.
• 또 가능한 방법은 $\mathbb{P}_r$ 을 추정하는 것 대신에 fixed distribution $p(z)$ 를 가지는 random variable $z$ 를 정의할 수 있다.
  • $z$ 를 parametric function $g_\theta: \mathcal{Z} \rightarrow \mathcal{X}$ 에 통과시켜 어떤 분포 $\mathbb{P}_\theta$ 를 따르는 샘플을 만들어 낼 수 있다.
  • 이 때 $\theta$ 를 다르게 하면서 이 분포를 변화시킬 수 있고 실제 데이터 분포 $\mathbb{P}_r$ 에 가깝게 만든다.
  • 즉, latent space 를 사용하는 이 접근법은 저차원의 manifold 에 정의된 분포를 표현할 수 있다.
  • VAE 와 GAN 은 이러한 접근법을 취한다.
  • 단 VAE 는 ELBO 를 통해 explicit 하게 density estimation 을 하고, GAN 은 경쟁적으로 implicit 하게 학습한다.

GAN 의 어려운 학습

• GAN 이 가장 해결해야 할 문제는 학습이 잘 안된다는 문제다.
• DCGAN 이 나옴으로써 이미지에서는 어느 정도 해결된 문제지만 여전히 mode collpase 라는 문제를 가지고 있다.
  • mode collapse 는 비슷한 이미지만 계속 만드는 현상이라고 할 수 있다.
  • MNIST 데이터셋을 예로 들면, Generator 가 만약 6 이라는 숫자만 잘 만들어 낸다면 Discriminator 의 입장에서는 6 만 가짜라고 생각하고 나머지 숫자들은 모두 진짜라고 생각해 버릴 수 있다는 것이다.
  • 그렇게 되는 순간 Discriminator 는 진짜/가짜를 판별하는 것이 아니라 6 인가 6 이 아닌가를 판별하는 Discriminator 로 변해 버리는 것이다.
  • 그러한 Generator 는 다시 어떻게든 Discriminator 를 속여야 할 테니까 6 이 아닌 다른 숫자를 만들어내기 시작할 것이다.
  • 그렇게 해서 다시 예를 들어 8 이라는 숫자를 만들어내기 시작하고 Discriminator 는 Generator 한테 속지 않기 위해 다시 8 인지 아닌지를 판별하는 Discriminator 로 바뀐다.

• 이런 현상은 반복되게 되고, 이를 mode collapse 문제라고 한다. 아래의 그림은 Improved Training of Generative Adversarial Networks using Representative Features 라는 논문에 실린 그림인데, GAN 의 mode collapse 문제를 보여준다.

  

• WGAN 은 이를 loss function 의 distance measure 로 인한 것으로 본다. 즉 WGAN 에서는 GAN 이라는 distance measure 가 적합하지 않을 수 있다고 이야기한다.

• 그 이유는 위에서 본 것처럼, KL-div 뿐만 아니라 JSD 는 비교하는 두 개의 분포가 support 의 교차점을 가지지 않으면 정의가 되지 않기 때문이다.

  \[\mathbb{KL}(P_A \Vert P_B) = \int \log\frac{P_A(x)}{P_B(x)}P_A(x)dx\]
• 위 KL-div 의 정의를 보면, $P_A(x) = 0$ 인 점이면 확률밀도가 0 이 되니 그렇다쳐도, $P_A(x) > 0$ 인 어떤 점 $x$ 에서 확률밀도 함수의 비율이 정의되려면 $P_A(x)$ 가 0 이 아닌 점에서 $P_B(x)$ 가 0 이 되어서는 안된다.
• manifold hypothesis 관점에서 보면 데이터 공간에 비해 데이터를 잘 표현하는 의미있는 manifold 는 극히 작은 공간에 몰려있다.
• 따라서 데이터의 분포와 생성된 결과의 분포의 support 가 겹치지 않을 확률이 아주 높다고 볼 수 있다.
• 만약 그런 경우, loss function 이 실제 데이터 분포와 생성된 데이터 분포 간의 거리를 제대로 표현하지 못하게 되고, 결국 gradient 가 parameter 를 제대로 업데이트 하지 못하게 된다. 그래서 수렴이 어려울 수 있다고 WGAN 의 저자들은 주장한다.
• 결국 GAN 에서 JSD 보다 더 정의가 되기 쉽고 JSD 보다 수렴도 더 잘 되는 거리를 찾고자 한다.
• 정리해보자.
  • 데이터의 분포와 비슷한 분포를 만들려고 하면, parameter $\theta$ 가 정의하는 분포와 실제 데이터의 분포가 얼마나 비슷한지를 측정해야 한다.
  • GAN 에서는 그 측도로 JSD 를 쓴다.
  • 그러나 JSD 가 분포 간의 거리를 제대로 설명해주는 metric 이 아닐 수도 있다는 것이 WGAN 의 주장이다.

• WGAN 논문에서는 2차원 공간에서 정의된 다음과 같은 2개의 분포를 예로 들어 TV, KL-div, JSD 의 한계를 짚었다. 논문에서는 example 1 이다.

  \[\mathbb{P}_0 = (0, Z), \; \mathbb{P}_\theta = (\theta, Z), \quad \text{where}\; Z \sim U(0, 1), \; \theta \in \mathbb{R}_{[0, \infty)}\]

Total Variation

• Total Variation Distance 는 두 확률분포의 차이를 나타내는 값으로, 주어진 사건 집합에서 두 분포가 가장 크게 다를 수 있는 차이의 최대값(supremum)을 나타낸다이다.

  \[\delta(\mathbb{P}_r, \mathbb{P}_g) = \underset{A \in \Sigma}{\text{sup}}\vert \mathbb{P}_r(A) - \mathbb{P}_g(A) \vert\]

• 위에서 $\mathbb{P}_r$ 은 데이터의 분포이고 $\mathbb{P}_g$ 은 모델의 분포를 의미한다.

  

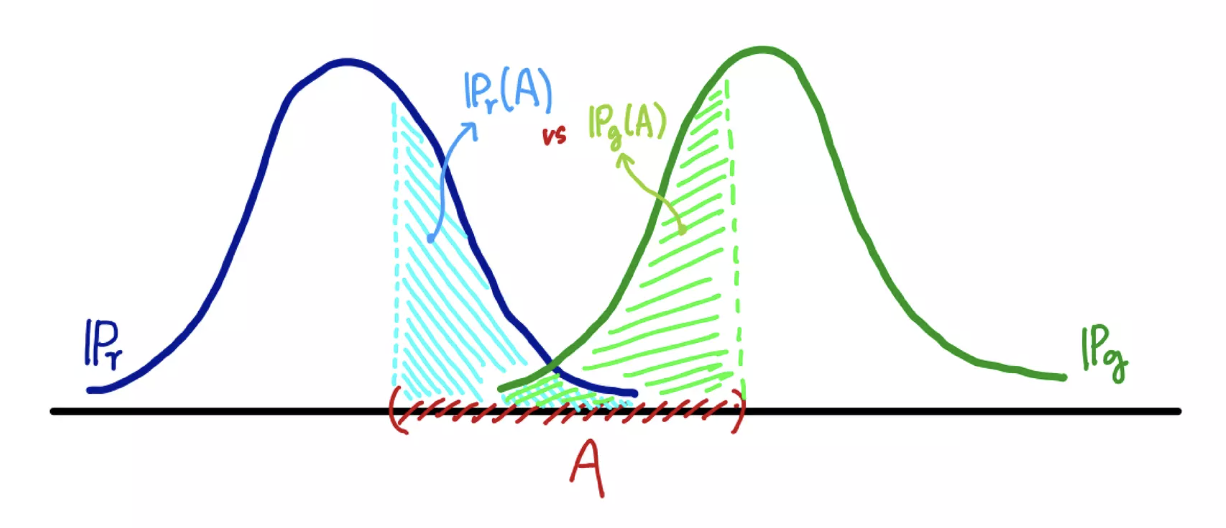
• 같은 집합 $A$ 라고 하더라도 두 확률분포가 측정하는 값은 다를 수 있다. 이 때 TV 는 모든 $A \in \Sigma$ 에 대해 가장 큰 값을 거리로 정의한 것이다.

• 만약 두 확률분포의 확률밀도함수가 서로 겹치지 않는다면, 즉 두 확률분포의 support 의 교집합이 공집합이라면 TV 는 무조건 1 이다.

  \[\delta(\mathbb{P}_r, \mathbb{P}_g) = \vert 0 - 1 \vert = 1\]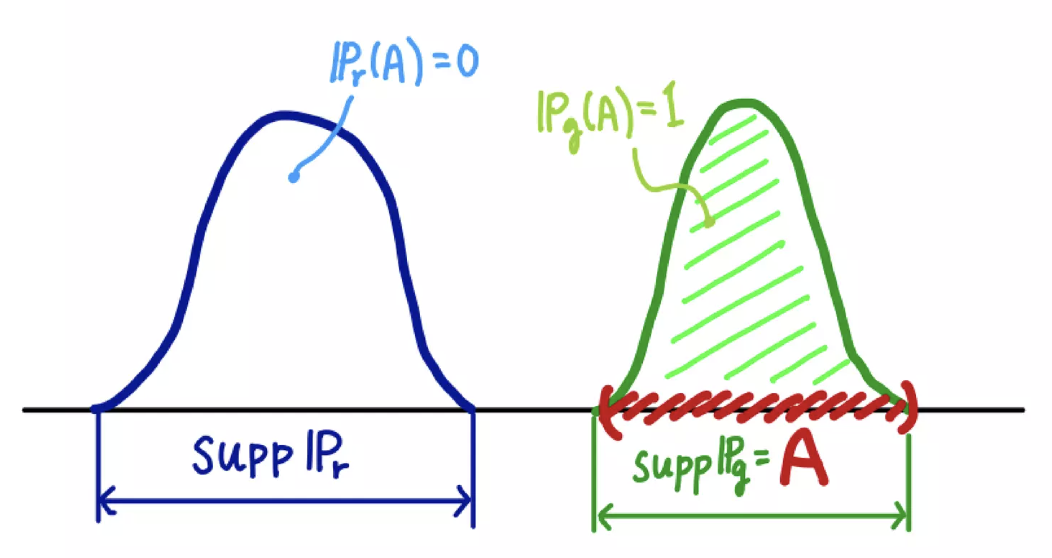

  

• 따라서 아래 그림을 보면 두 분포 사이의 거리인 $\theta$ 가 0 이 아니면($\theta \neq 0$), 두 분포 \(\mathbb{P}_0\) 와 \(\mathbb{P}_\theta\) 는 서로 겹치지 않는 확률분포가 되므로 TV 가 1 이 된다.

  

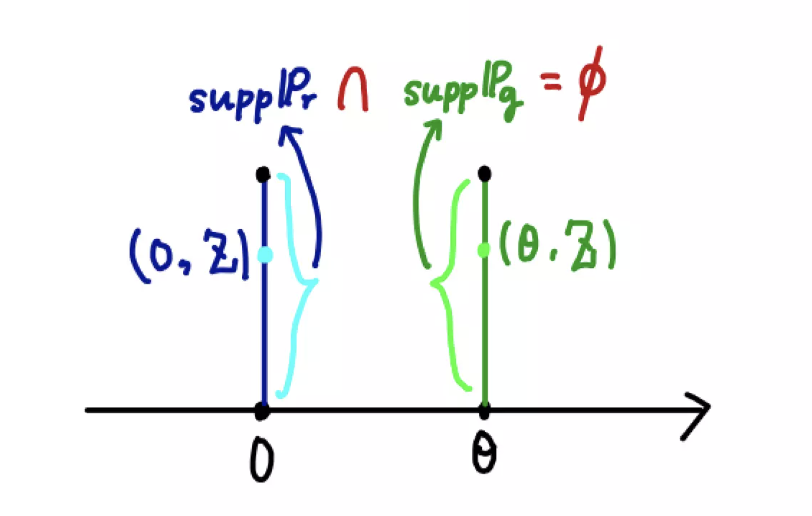
• 즉 아래와 같이 나타낼 수 있다.

  \[\delta(\mathbb{P}_0, \mathbb{P}_\theta) = \begin{cases} 1 & \text{if} \; \theta \neq 0 \\ 0 & \text{if} \; \theta = 0 \end{cases}\]

KL-div, JSD

• KL-div 의 식과 JSD 의 식을 다시 보자.

  \[\begin{aligned} \mathbb{KL}(\mathbb{P}_r \Vert \mathbb{P}_g) &= \int \log \left( \frac{P_r(x)}{P_g(x)}\right)P_r(x)dx\\ \mathbb{JSD}(\mathbb{P}_r \Vert \mathbb{P}_g) &= \frac{1}{2}\mathbb{KL}\left( \mathbb{P}_r \Vert \frac{\mathbb{P}_r + \mathbb{P}_g}{2}\right) + \frac{1}{2}\mathbb{KL}\left( \mathbb{P}_g \Vert \frac{\mathbb{P}_r + \mathbb{P}_g}{2}\right) \end{aligned}\]

• JSD 는 KL-div 의 대칭성을 보완한 distance 다.

  

• 위 그림을 다시 보면, $\theta = 0$ 인 경우를 제외한 어떤 경우에도 두 분포가 겹칠 수 없다.

• 따라서 두 분포 중 하나가 0 이 아닌 값을 가지면 다른 분포에서는 0 인 값을 가지게 된다. 따라서 $\theta \neq 0$ 인 경우 아래와 같다.

  \[\begin{cases} P_0(x) \neq 0 & \Rightarrow \quad P_\theta(x) = 0\\ P_\theta(x) \neq 0 & \Rightarrow \quad P_0(x) = 0 \end{cases}\]

• 그렇다면 $P_\theta > 0$ 인 곳에서 $\log$ 값은 $\infty$ 가 된다.

  \[\log \left(\frac{P_\theta(x)}{P_0(x)} \right) = \infty\]
• 따라서 KL-div 는 $\theta = 0$ 이 되지 않는 한 $\infty$ 가 된다. 정의가 되지 않는 것이다.

• 이 상황은 JSD 에서도 똑같다. 그러나 KL-div 처럼 $\infty$ 가 되지는 않는다.

  \[P_m = \frac{P_\theta + P_0}{2} \\ \begin{cases} P_0(x) \neq 0 & \Rightarrow \quad P_\theta(x) = 0 \quad \Rightarrow \quad P_m = \frac{P_0}{2}\\ \\ P_\theta(x) \neq 0 & \Rightarrow \quad P_0(x) = 0 \quad \Rightarrow \quad P_m = \frac{P_\theta}{2} \end{cases}\]

• 위 식을 JSD 에 대입해보자.

  \[\mathbb{KL}(\mathbb{P}_0 \Vert \mathbb{P}_m) = \int_{P_0 \neq 0} \log \left( \frac{P_0(x)}{P_0(x)/2}\right)P_0(x)dx = \log 2 \\ \mathbb{KL}(\mathbb{P}_\theta \Vert \mathbb{P}_m) = \int_{P_\theta \neq 0} \log \left( \frac{P_\theta(x)}{P_\theta(x)/2}\right)P_\theta(x)dx = \log 2\]

• 따라서 $\theta \neq 0$ 이면 JSD 는 $\log 2$ 가 된다.

  \[\mathbb{JSD}(\mathbb{P}_\theta \Vert \mathbb{P}_0) = \begin{cases} \log 2 & \text{if} \; \theta \neq 0 \\ 0 & \text{if} \; \theta = 0 \end{cases}\]
• 이런 상황에서 TV, KL-div, JSD 를 사용하더라도 두 분포 간의 거리는 $\theta$ 에 대한 적절한 정보를 주지 못한다.
• 즉 Neural Network 에서 gradient 는 $\theta$ 를 얼만큼 움직이면 두 분포의 거리가 얼마가 변할 거라는 정보를 담고 있어야 하는데, $\theta$ 가 0 이 되는 순간 분포의 거리가 0 이라는 사실만 알려준다.
• 그리고 $\theta$ 가 0 이 아니라면 TV 의 경우 1, JSD 의 경우 $\log 2$ 라는 일정한 값만 뱉는 것이다. 물론 KL-div 는 $\infty$ 다.
• 이런 일이 일어나는 이유는, TV, KL-div, JSD 는 두 확률분포가 서로 다른 영역에서 측정된 경우 완전히 다르다고 판단을 내리게끔 metric 이 계산되기 때문이다. 즉 두 확률분포의 차이를 깐깐하게(harsh) 본다는 것이다.
• 이것이 상황에 따라 유리할 수도 있겠지만, GAN 의 경우 Discriminator 의 학습이 잘 죽는 원인이 된다.
  • Loss Function 은 가까우면 가깝다고, 멀면 멀다고 명확히 말을 해주어야 이에 따른 gradient 를 계산할 수 있다.
  • 그러나 두 분포의 support 가 겹치지 않는다면 ‘두 분포가 완전히 다르다.’ 라는 정보만 줄 뿐 어떻게 가깝게 만들지에 대한 정보, 즉 gradient 를 계산할 수 없다.
  • 높은 dimension 의 문제를 푸는 이미지 생성과 같은 GAN 에서는 이렇게 분포가 겹치지 않는 문제가 더 심하게 발생할 것이기 때문에 GAN 의 학습 성능이 떨어지는 크리티컬한 문제로 다가온다.
• 그래서 GAN 의 학습에 맞게 조금 유연하면서도 수렴에 포커스를 맞춘 다른 metric 이 필요한 것이고, 그것이 Wasserstein distance 다.

Wasserstein distance

• 위와 같은 상황에서 Wasserstein Distance(W-거리) 를 사용하면 아래의 결과를 얻을 수 있다.

  \[W(\mathbb{P}_0, \mathbb{P}_\theta) = \vert \theta \vert\]

• 즉, W-거리를 사용하면 아래 두 분포를 일치시키기 위해 $\theta$ 를 0 방향으로 움직여야 함을 알 수 있는 것이다.

  

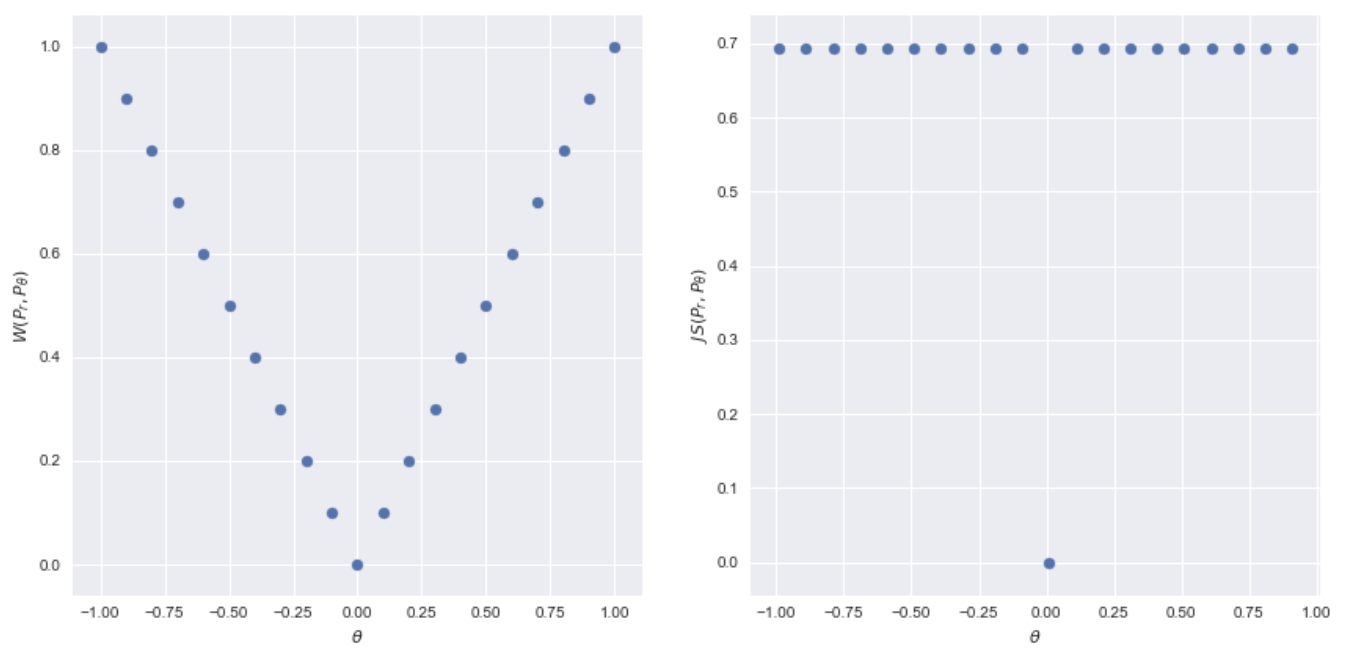  좌: Wasserstein, 우: JSD, 출처: https://kionkim.github.io/2018/06/01/WGAN_1/

• 그러면 Wasserstein distance 의 정의를 살펴보고 어떻게 이런 결과를 낼 수 있는지 파헤쳐보자.

• 분포 간의 거리를 재는 W-거리의 정의는 아래와 같다.

  \[W_p(\mathbb{P}_r, \mathbb{P}_\theta) = \underset{\gamma \in \prod(\mathbb{P}_r, \mathbb{P}_\theta)}{\text{inf}}\mathbb{E}_{(x,y) \sim \gamma(x, y)}(\vert x - y \vert^p)\]
• 여기서 \(\prod(\mathbb{P}_r, \mathbb{P}_\theta)\) 는 두 확률분포 \(\mathbb{P}_r, \mathbb{P}_\theta\) 의 결합확률분포(joint distribution)들을 모은 집합이다. $\gamma$ 는 그 중 하나다.
• 즉 위 정의는 모든 결합확률분포 중에서 $\vert x - y \vert^p$ 의 기대값을 가장 작게 추정한 값을 의미한다.
• $\vert x - y \vert^p$ 는 두 점 간의 거리로 $p$ 차 norm 을 뜻한다. 일반적으로 $p=2$ 인 Fabuluous Norm, 즉 $L2$ norm 을 쓴다.
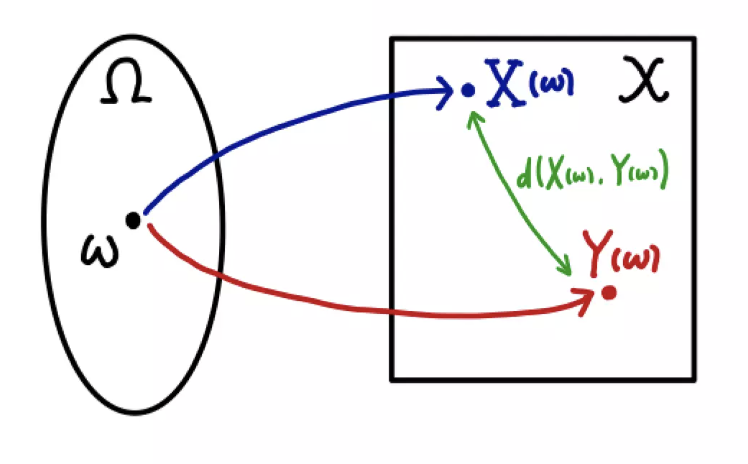
• 그림으로 이해해보자. 두 확률변수 $(X, Y)$ 가 각각 \(X \sim \mathbb{P}_r, \; Y \sim \mathbb{P}_\theta\) 라고 해보자.

• $w$ 를 하나 샘플링하면 $X(w)$ 와 $Y(w)$ 를 뽑을 수 있다. 이 때 두 점 간의 거리 $d(X(w), Y(w))$ 역시 계산할 수 있다.

  

• 샘플링을 계속할수록 $(X, Y)$ 의 결합확률분포 $\gamma$ 의 윤곽이 나오게 된다. 더불어 \((\mathbb{P}_r, \mathbb{P}_\theta)\) 는 $\gamma$ 의 주변확률분포(marginal distribution)가 된다.

  

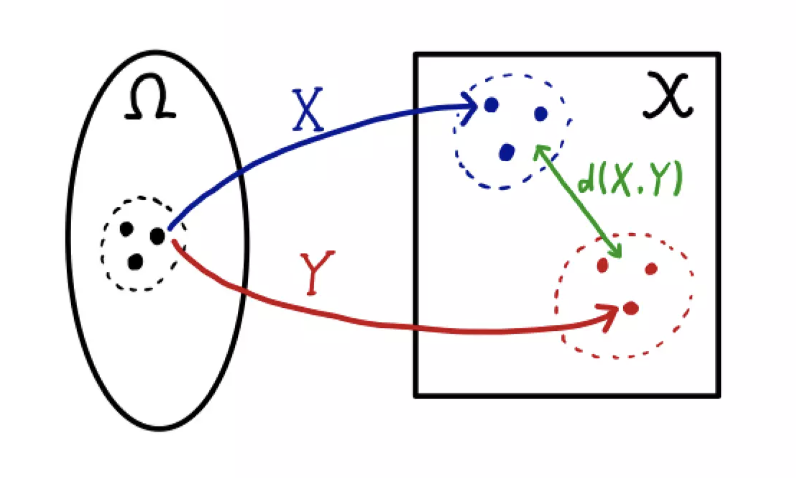
• 이 때 $\gamma$ 가 두 확률변수 $X, Y$ 의 연관성(dependency)을 어떻게 측정하느냐에 따라 $d(X, Y)$ 의 분포가 달라지게 된다.

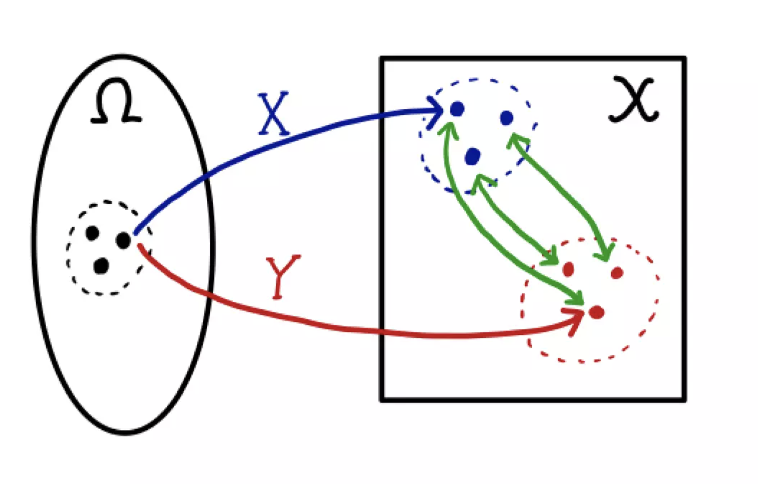
• 주의할 점은 \(\mathbb{P}_r, \mathbb{P}_\theta\) 는 바뀌지 않기 때문에 각 $X, Y$ 가 분포하는 모양은 변하지 않는다. 다만 $w$ 에 따라 뽑히는 경향이 달라질 뿐이다.

  

• W-거리는 이렇게 여러가지 $\gamma$ 중에서 $d(X, Y)$ 의 기대값이 가장 적게 나오는 확률분포를 취한다.

  

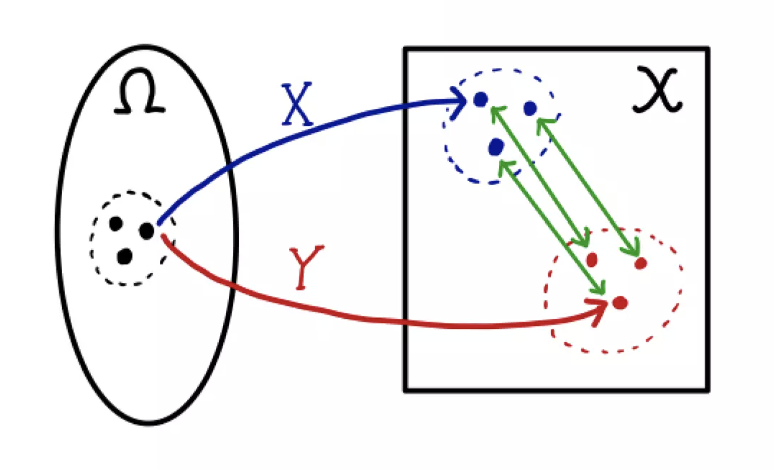
• 이제 논문의 example 1 을 보자.

• 두 확률변수 $(X, Y)$ 가 각각 \(X \sim \mathbb{P}_0, \; Y \sim \mathbb{P}_\theta\) 라고 한다면, $w$ 에 대해서 $X, Y$ 는 다음과 같이 2차원 공간에서 매핑된다.

  \[X(w) = (0, Z_1(w)), \quad Y(w) = (\theta, Z_2(w))\]

• 그러면 두 점 사이의 거리는 아래와 같이 계산된다.

  \[d(X, Y) = (\vert \theta - 0 \vert^2 + \vert Z_1(w) - Z_2(w) \vert ^2)^{\frac{1}{2}} \geq \vert \theta \vert\]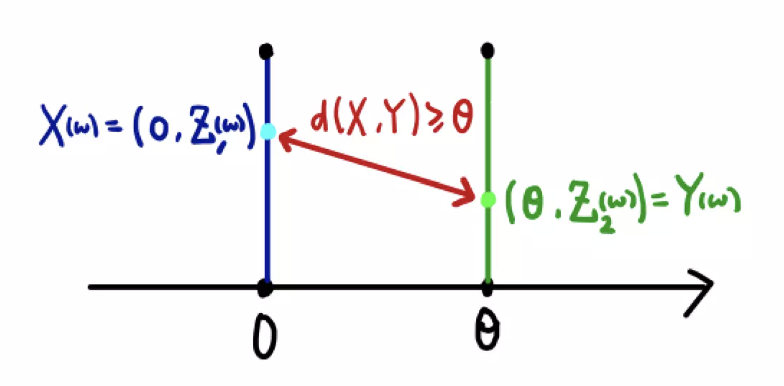

  

• 즉 $d(X, Y)$ 의 기대값은 어떤 결합확률분포 $\gamma$ 를 사용하든 항상 $\vert \theta \vert$ 보다 크거나 같다.

  \[\mathbb{E}^\gamma[d(X, Y)] \geq \mathbb{E}^\gamma[\vert \theta \vert] = \vert \theta \vert\]

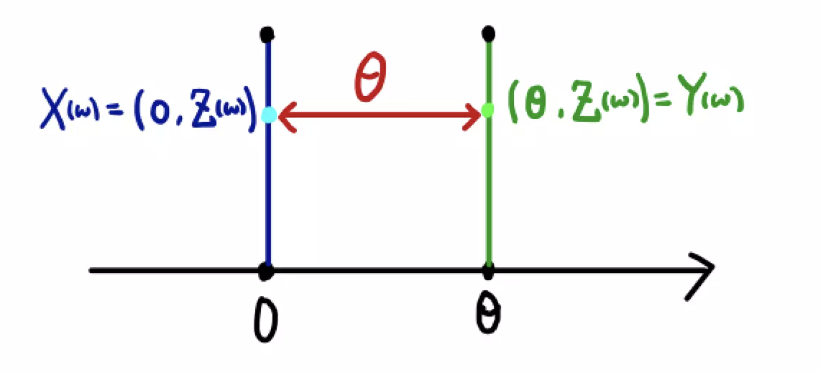
• 기대값이 $\vert \theta \vert$ 인 상황은 항상 $Z_1 = Z_2$ 인 분포를 따른다면 가능하다.

  

• 그러면 우리가 위에서 봤던 결론을 얻을 수 있다.

  \[W(\mathbb{P}_0, \mathbb{P}_\theta) = \vert \theta \vert\]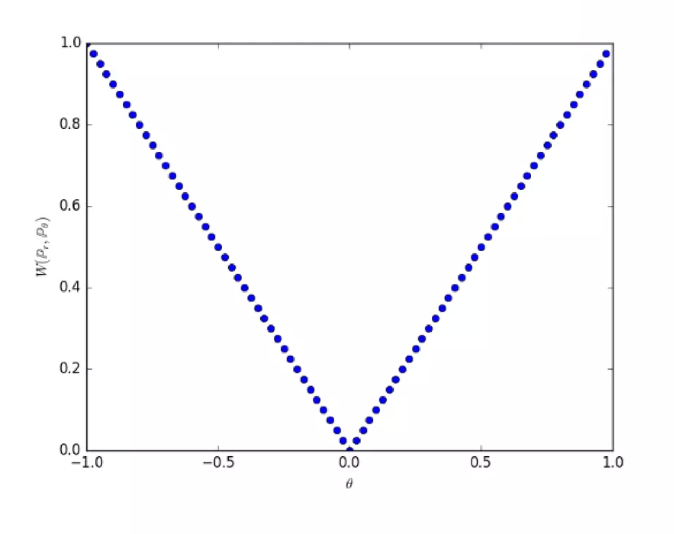

  

• 참고로 W-거리는 두 개의 주변확률분포를 일치시키기 위해 하나의 분포를 다른 분포로 변화시키기 위해 mass 를 옮기는 과정인 transportation plan 을 상상한다. 머신러닝/딥러닝 분야에서 이 거리를 Earth Moving Distance, EM 이라고 한다.
  • W-거리는 수많은 transportation plan 중에서 cost 를 가장 작게하는 방법을 바탕으로 두 분포의 거리를 정의한다.
  • 이에 관해서는 해당 블로그를 참고하자.
  • 기억해야 할 것은, W-거리는 두 개의 분포를 주변분포로 하는 결합분포 중에서 cost 인 \(\mathbb{E}(\vert x - y \vert^p)\) 를 가장 작게 하는 분포를 골랐을 때 $\vert x-y \vert^p$ 의 기대값이다.
• 그러나 모든 가능한 결합확률분포 중에 cost 를 가장 작게 하는 결합확률분포를 찾아내고, 그 결합확률분포에 대한 기대값을 찾아내는 일은 매우 어렵다.
• 따라서 논문에서는 정의 그대로 W-거리를 계산하기 보다는 이 W-거리를 좀 더 쉽게 구할 수 있는 현실적인 대안을 제시한다.
• 바로 W-거리(EM distance, EMD) 를 계산할 때 Kantorovich-Rubinstein duality 를 이용해 식을 도출한다. 이를 통해 loss function 을 1-Lipschitz 인 $f$ 를 이용해 표현 가능해진다.
  • 자세한 증명은 해당 블로그 를 참고하자. 정말 어려운 내용이다 ㅜㅠ

  • Lipschitz Function 는 두 점 사이의 거리를 일정 비 이상으로 증가시키지 않는 함수다.

    \[\frac{\vert f(x_1) - f(x_2) \vert}{\vert x_1 - x_2 \vert} \leq K\]
  • 위와 같은 Lipschitz 조건이 성립하면 균등연속함수이므로 해당 범위에서 미분이 가능하며, 미분 계수는 정해진 $K$ 값을 넘을 수 없게 된다.
  • 쉽게 해석해보면 Lipschitz 함수일때 기울기가 $K$ 를 넘지 않으므로 gradient exploding 과 같은 문제를 예방할 수 있다.
• 요약해보자.
  • EMD 를 구하기 위해 모든 가능한 결합확률분포의 집합에서 cost 를 가장 작게하는 분포를 고르고 그 분포에 대해 기대값을 구하는 작업을 해야한다.
  • 이를 가능하게 할 수 있도록, Lipschitz 조건을 만족하는 함수족 중 \(\mathbb{E}_{P_\theta}(f) - \mathbb{E}_{P_r}(f)\) 를 가장 크게하는 함수를 찾고 그 함수에 대한 기대값을 구하는 문제로 전환한 것이다.

• 따라서 Kantorovich-Rubinstein duality 에 의한 W-거리는 아래와 같이 된다.

  \[W(\mathbb{P}_r, \mathbb{P}_\theta) = \underset{\Vert f \Vert \leq 1}{\text{sup}}\; \mathbb{E}_{X \sim \mathbb{P}_r}(f(X)) -\mathbb{E}_{X \sim \mathbb{P}_\theta}(f(X))\]
• 만약 $K$-Lipschitz 함수족으로 거리를 정의한다면 W-거리의 $K$ 배로 정의된다.

WGAN loss function

• 위에서 W-거리를 구하기 위한 식까지 도출했는데, 그럼에도 여전히 Lipschitz 조건을 만족하는 함수의 집합은 크다.
• 따라서 모든 Lipschitz 조건을 만족하는 함수보다는 특정 parameter $w$ 로 표현할 수 있는 함수만을 고려한다.

• 이 함수가 $\vert f_w \vert \leq 1$ 을 만족하면 아래의 식을 생각할 수 있다. $\mathcal{W}$ 는 parameter $w$ 의 공간이다.

  \[\underset{w \in \mathcal{W}}{\text{sup}}\; \mathbb{E}_{\mathbb{P}_r}(f_w(X)) -\mathbb{E}_{\mathbb{P}_\theta}(f_w(X)) \leq \underset{\Vert f \Vert \leq K}{\text{sup}}\; \mathbb{E}_{X \sim \mathbb{P}_r}(f(X)) -\mathbb{E}_{X \sim \mathbb{P}_\theta}(f(X))\]
• $f_w$ 중에 우측 term 의 값을 극대화하는 경우 정확한 W-거리를 찾을 수 있겠지만, 이는 현실적으로 불가능하기 때문에 적절한 근사값을 찾는다고 볼 수 있다.

• 즉 우리는 1-Lipschitz 로 함수를 제약하여 아래의 loss function 을 도출해낼 수 있다. 이를 GAN 에서의 loss function 과 비교해서 보자.

  \[\begin{aligned} \text{GAN} \; &\Rightarrow \; 2 \text{JSD}(\mathbb{P}_r \Vert \mathbb{P}_g) - 2\log 2 \\ & \Rightarrow \; \underset{G}{\text{min}}\underset{D}{\text{max}} \; \mathbb{E}_{x \sim P_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim P_z(z)}[\log(1 - D(G(z)))] \\ &\\ \text{WGAN} \; &\Rightarrow \; \underset{\gamma \in \prod(\mathbb{P}_r,\mathbb{P}_g)}{\text{inf}} \mathbb{E}_{(x,y) \sim \gamma}[\Vert x - y \Vert] \\ & \Rightarrow \; \underset{w \in \mathcal{W}}{\text{max}} \; \mathbb{E}_{x \sim P_{\text{data}}(x)}[f_w(x)] - \mathbb{E}_{z \sim P_z(z)}[f_w(g_\theta(x))] \end{aligned}\]
• 이러한 W-거리가 연속이고 미분 가능한지에 대해 자세한 증명은 해당 자료의 8p 부터 참고하자.

• $f_w$ 가 W-거리를 잘 measure 했다면 이를 바탕으로 $\theta$ 에 대해 편미분하여 gradient 를 구할 수 있다. 첫번째 term 은 $\theta$ 와 상관없으므로 사라지고 두번째 term 만 남는다.

  \[\nabla_\theta W(\mathbb{P}_r, \mathbb{P_\theta}) = - \mathbb{E}_{z \sim P_z(z)}[\nabla_\theta f(g_\theta(z))]\]
• 위 식에 근거해서 parameter $\theta$ 를 학습하게 된다.
• 기존의 GAN 에서는 discrimator 가 있어서, fake 와 real 의 분포를 보고 생성된 데이터가 real 인지 fake 인지 판단한다.
• 하지만, WGAN 에서는 이분법적으로 판단하는 것이 아니라, 얼마나 실제와 유사한지를 W-거리를 재어 그 거리를 줄여주는 방향으로 generator 를 업데이트 한다.
• 따라서 학습에서 아래의 순서를 따른다.
  • $\theta$ 가 고정된 상태에서 \(W(\mathbb{P}_r, \mathbb{P_\theta})\) 를 구한다. 거리를 가장 잘 구하기 위해서 \(\mathbb{E}_{x \sim P_{\text{data}}(x)}[f_w(x)] - \mathbb{E}_{z \sim P_z(z)}[f_w(g_\theta(x))]\) 의 supremum(=max) 를 구해야 하므로 목적함수를 증가시키는 방향으로 $f_w$ 의 파라미터인 $w$ 를 학습시킨다. 이는 정확한 거리를 재기 위한 단계다.
  • $f_w$ 가 어느정도 수렴하는, 즉 나름 정확한 W-거리를 찾고 나면 이 함수를 이용해서 목적함수의 gradient 인 \(- \mathbb{E}_{z \sim P_z(z)}[\nabla_\theta f(g_\theta(z))]\) 를 추정한다. 이 때는 거리를 최소화해야 하므로 목적함수를 줄이는 방향으로 $\theta$ 를 학습한다.

• 즉 아래의 그림과 같이 학습하게 된다.

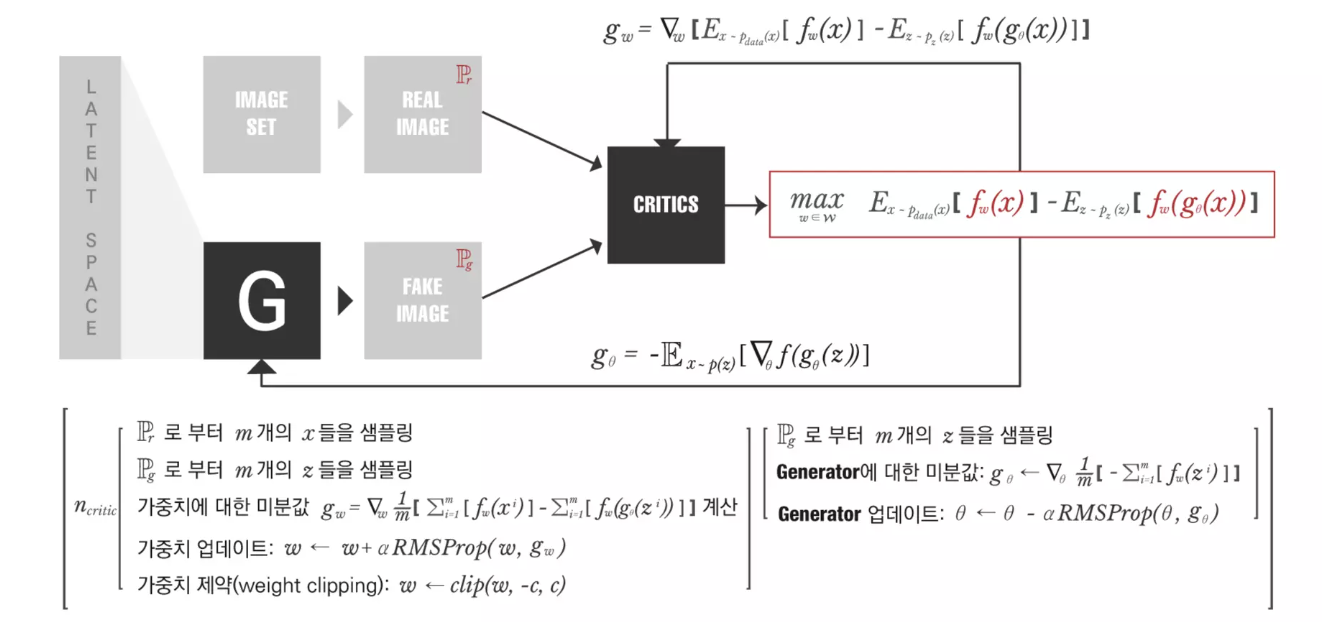  출처 : https://www.slideshare.net/slideshow/16wgan-wasserstein-gans/128394646

정리

• 정리하면 TV, KL-div, JSD 는 support 를 공유해야만 잘 정의되는 거리다. 그러나 manifold hypothesis 에 따르면 support 를 공유하지 않을 확률이 아주 높다.
  • support 를 공유한다는 것은 absolute continuity 가정을 충족한다는 것이다.
• 따라서 안정적으로 정의되고 분포 간의 거리를 재는 metric 이 필요한데, W-거리가 이 성질을 만족한다.
  • W-거리는 비교하는 두 분포 간의 absolute continuity 를 요구하지 않는 거리다.
  • 즉 기존의 조건보다 많이 완화된 조건을 가지고 있다.
• 또한 KL-div, JSD 가 0 으로 수렴하지 않더라도 W-거리는 0 으로 수렴할 수 있고, W 거리가 수렴하면 KL-div, JSD 는 수렴해야만 한다.
• 따라서 W-거리를 0 으로 만드는 작업이 KL-div, JSD 를 0 으로 만드는 작업보다 훨씬 안정적으로 정의되는 것이다.
• 여기까지 Wasserstein Distance 를 알아보았다. 이해하기 매우 어려웠지만, 안정적으로 정의되는 distance 임을 기억하고 적재적소에 활용해보자.

Reference

• https://www.slideshare.net/slideshow/wasserstein-gan-i/75554346
• https://kionkim.github.io/2018/06/01/WGAN_1/
• https://kionkim.github.io/2018/06/08/WGAN_2/
• https://www.slideshare.net/slideshow/16wgan-wasserstein-gans/128394646

맨 위로 이동 ↑