[Loss] KL-divergence, JSD

거리함수와 기계학습

• 기계학습에서 사용되는 손실함수들은 사실 아무렇게나 사용되는 손실함수들이 아니다.
• 기계학습에서 사용되는 손실함수들은 기계학습 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도할 수 있다.
• 또한 통계학에서 MLE 로 추정하게 되는 많은 모델 학습방법론이 확률분포의 거리를 최적화하는 것과 밀접하게 관련이 있다.
• 데이터 공간에 두 개의 확률분포 $P(\mathbf{x}), Q(\mathbf{x})$ 가 있을 경우, 두 확률분포 사이의 거리(distance) 를 계산하는 방법에는 여러가지 방법이 있다.
  • 총변동 거리(Total Variation Distance, TV)
  • 쿨백-라이블러 발산(Kullback-Leibler Divergence, KL)
  • 바슈타인 거리(Wasserstein Distance)
• 이 포스트에서는 이러한 두 확률분포 사이의 거리를 구하는 방법이 어떻게 손실함수를 유도하는지를 알아보자.

Discriminative vs. Generative

• 딥러닝 모델은 Dicscriminative model 과 Generative model 로도 구분할 수 있다.
  • Discriminative vs. Generative 의 구분은 모델의 학습 방식과 데이터를 처리하는 방법에 관한 것이고, Frequentist vs. Bayesian 의 구분은 확률, 모델 parameter 에 대한 해석과 불확실성 처리 방식에 관한 것이다. 두 구분은 다른 관점에서 접근하지만, 일부 겹치는 개념도 있다.
  • Frequentist vs. Bayesian 구분에 대해서는 이 포스트에 정리했다.
  • Bayesian 딥러닝이 항상 generative model 을 모델링하지는 않는다. Bayesian 딥러닝은 모델의 가중치와 예측값에 확률분포를 할당하여, 모델 불확실성(epistemic uncertainty)과 데이터 불확실성(aleatoric uncertainty)을 측정한다.
  • 즉 Bayesian 딥러닝은 불확실성 관리를 위한 확률적 추론 방법을 딥러닝 모델에 결합한 것으로 주된 목적은 모델의 불확실성 정량화다.
  • Generative Model 은 데이터 분포를 학습하고 그 분포에서 새로운 데이터를 생성하는 것이 목적이다.
  • Bayesian 딥러닝이 항상 Generative model 인 것은 아니지만, 일부 생성모델(VAE 등)은 Bayesian 접근을 사용해 데이터의 분포를 학습하고 새로운 데이터를 생성한다.
  • VAE 는 잠재변수 $z$ 에 대한 분포를 추정할 때 Variational Inference 라는 Bayesian 접근을 활용한다. 이 포스트를 참고하자.

• 머신러닝/딥러닝 중 Supervised Learning 은 대부분 Discriminative model 이다. 즉 구별하는 모델인데, 결국 아래를 알아내는 것이다.

  \[p(y \vert x)\]
• 즉 어떤 input $x$ 가 들어갔을 때 label 혹은 class 인 $y$ 인 확률을 알아낸다. 여기서 확률은 “판단의 근거”가 된다.
• 그렇다면 확률분포는 어떠한 parameter 에 따라서 확률이 변하는 일종의 함수로써, 결국 확률분포를 추정한다는 것은 확률을 추정하는 것이고 이것이 판단의 근거가 되는 것이다.
• 따라서 Discriminative model 의 경우 $p(y \vert x)$ 를 추정함으로써 주어진 input 으로부터 lable or class 판단의 근거를 삼겠다는 것이다.
• 이제 딥러닝은 parameter 를 기반으로 추정하기 때문에 $p(y \vert x)$ 에 모델의 parameter $w$ 를 추가하면 아래와 같이 된다.

• 우리가 구하고자 하는 것은 모델의 parameter 다. 이를 통해 “내 모델($w$)에 따르면 $x$ 일 때 $y$ 일 확률이 가장 높다” 를 말할 수 있다.

  \[p(w \vert x, y) = \frac{p(y \vert x, w)p(w)}{p(y \vert x)}\]
• 여기서 $x$ 일 때 $y$ 일 확률이 가장 높은 모델을 만들려면, 학습 과정에서 주어진 데이터를 가장 잘 설명할 수 있도록 $p(y \vert x, w)$ 가 최대가 되는 $w$ 를 찾는다. 이를 Maximum Likelihood Estimation(MLE) 라고 한다.
• 반면에 Generative model 의 경우는 data 를 생성해내는 모델이다. 이는 보통 Unsupervised Learning 의 형태로 이뤄진다.

• input data 를 생성해내기 위해서 결국 필요한 것은 다음과 같은 joint probability 를 알아내는 것이다.

  \[p(x, z) = p(x \vert z)p(z)\]
• 여기서 $z$ 는 latent vector 로 잠재변수라고 한다. 데이터 $x$ 가 형성되는 숨겨진 원인을 모델링하는 데 사용된다.
• 위 joint probability 를 알아내기 위해서 우리는 샘플링하는 $p(x \vert z)$ 외에 $z$ 의 분포 $p(z)$ 도 가정해야 한다. 결국에는 위 식을 $z$ 로 marginalization 하여 $p(x)$ 를 알아내는 것이 Generative model 의 최종 목표다.

• 즉 Generative model 에서 우리의 최종 목표는 아래의 식을 추정해야 하며, 이러한 확률분포로부터 “데이터 생성”의 판단 근거인 확률을 알아내는 것이다.

  \[p(x)\]
• 여기서 Discriminative model 과 같이 parameter 를 변화시켜 가며 $p(x \vert w)$ 확률분포의 MLE 를 하면 된다.
• 그러나 $p(x)$ 를 알아내는 것은 불가능하기 때문에, Generative model 의 학습은 위와 같이 $z$ 와 그것으로부터 data 를 생성해내는 $p(x \vert z)$ distribution 을 학습한다고 볼 수 있다.
• 그리고 $z$ 를 학습하기 위해 AutoEncoder 계열에서는 $p(z \vert x)$ 를 학습하는 방법이 존재하고, 아니면 GAN 계열과 같이 간접적으로 $p(x)$ 를 학습하게 하는 방법도 존재한다.
• 그러나 핵심은 데이터를 생성하는 $p(x \vert z)$ 를 학습하고 $z$ 를 단순하게 가정하는 것이다.
• 이렇게 Generative 모델은 학습한 잠재변수 분포에서 샘플링한 후 이를 기반으로 데이터를 생성한다.

MLE 와 거리함수

• Discriminative model 과 Generative model 은 결국 $w$ 혹은 $\theta$ 로 결정되는 확률모델 하나를 가정하고 가장 확률적으로 높고 그럴듯한 확률모델을 찾는 것이다. 그리고 이를 위해서 확률모델을 결정지을 수 있는 모델 parameter $w$ 혹은 $\theta$ 를 추정하는 것이다. 그리고 전자는 decision boundary 를 찾고, 후자는 데이터를 생성한다.
• 위 과정을 MLE 라고 하며, MLE 는 두 분포 사이의 거리, 즉 실제 분포 $P$ 와 내가 모델링한 분포 $Q$ 사이의 KL-divergence 를 최소화하는 것과 동일하다. 자세한 것은 아래 섹션에서 다룰 것이다.
• 이렇게 MLE 를 통해 loss function 을 유도했으니 학습을 진행하면 되는데, 이 때 우리는 실제 데이터 분포를 절대 알 수 없기 때문에 수집한 데이터셋을 가지고 학습을 진행한다.

• 즉 $N$ 개의 학습 데이터셋 $\mathcal{D}$ 가 실제 데이터의 분포 $P_{\text{data}}$ 에서 나왔다고 가정하고, 데이터셋 $\mathcal{D}$ 로부터 empirical distribution 을 아래와 같이 나타낼 수 있다.

  \[\tilde{p}(x) = \frac{1}{N}\sum^N_{i=1}\delta(x - x_i)\]

• 여기서 $\delta$ 는 Dirac-delta function 으로, 보통 좌표계 상에서 point 를 정의하고자 사용한다.

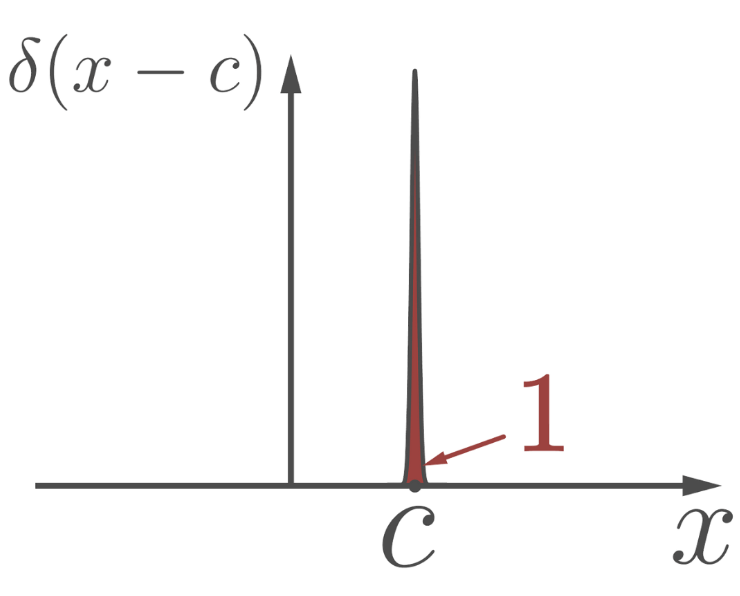  Dirac-delta Function

  • 이 함수는 극한으로 정의되며 $\delta(x)$ 에서 $x$ 가 0 일 때 값이 무한이 되고 0 이 아니면 값이 0 이 된다. 위 식에서 $\delta(x-x_i)$ 는 $x$ 를 $x_i$ 로 평행이동 한 것이다. 따라서 데이터 point 에서만 값이 솟은 함수다.
  • 또한 위 그림처럼 적분값이 1 이 된다.
  • 내가 가진 데이터셋에서 각각의 데이터 포인트가 나올 확률은 모두 동일하므로 위 식에서 $N$ 으로 나눠준 것을 확인할 수 있다.
• 따라서 우리는 실제 데이터 분포를 알 수 없으니 우리가 수집한 데이터셋으로 Empricial Distribution 을 얻고, 이와 우리가 모델링하는 모델의 분포 사이의 거리를 최소화 하는 것이다. 이를 Empirical Risk Minization(ERM) 이라고 한다.

• 그러면 우리는 아래와 같이 증명 가능하다.

  \[\mathbb{KL}(P_{\text{data}} \Vert P_{\theta}) = \color{blue}{\mathbb{E}_{x \sim P_{\text{data}}}[\log P_{\text{data}}(x)]} \color{red}{- \mathbb{E}_{x \sim P_{\text{data}}}[\log P_{\theta}(x)]}\]
  • 위 식에서 파란색 term 은 $\theta$ 와 상관없기 때문에 최적화 과정에서 무시할 수 있다. 우리는 빨간색 term 을 최소화하여 두 확률분포 사이의 거리를 줄일 수 있다.

  • 그러면 위 빨간색 term 을 부호를 바꿔 maximize 로 바꿔주고, 이를 Empirical Distribution 으로 표현해보자.

    \[\begin{aligned} \mathbb{E}_{x \sim P_{\text{data}}}[\log P_{\theta}(x)] \; \approx \; \mathbb{E}_{x \sim \tilde{P}}[\log P_{\theta}(x)] &= \int \tilde{P}(x)\log P_{\theta}(x)dx \\ &= \frac{1}{N}\int \sum^N_{i=1}\delta(x - x_i)\log P_{\theta}(x)dx \\ &= \frac{1}{N}\sum^N_{i=1}\log P_{\theta}(x_i) \end{aligned} \\ \\ \therefore \quad \underset{\theta}{\text{argmax}} \; \frac{1}{N}\sum^N_{i=1}\log P_{\theta}(x_i) = \hat{\theta}_{\text{MLE}}\]
  • 위 두번째 등호에서는 Dirac-delta function 의 성질 중 하나인 선별(Sifitng) 특성이 이용된다. $x=x_i$ 일 때만 값이 0 이 아니라 적분에서 의미가 있으므로 $\log P_\theta(x)$ 가 $\log P_\theta(x_i)$ 로 변하게 된다. 그리고 Empirical Distribution 의 적분은 1 이므로 세번째 등호와 같은 식이 나온다.
• 따라서 우리는 위와 같은 식으로 Likelihood 를 최대화시키는 $\theta$ 를 학습 과정에서 찾는다.
• Empirical Distribution 에서 데이터 수 $N$ 이 커지면 모집단의 parameter 로 수렴한다는 대수의 법칙(Law of Large Number)과 Glivenko-Cantelli theorem 에 의해 실제 데이터 분포에 수렴한다.
• 이러한 수렴 성질은 우리가 Empirical Distribution 에 기반해 학습을 진행해도 궁극적으로 실제 분포에 가까운 모델을 학습하게 됨을 보장한다.
  • 자세한 것은 잘 정리해둔 이 블로그를 참고하자.
  • 주의할 것은 딥러닝과 같이 parameter 가 많은 모델을 학습할 경우, empirical distribution 을 전부 외워버리는 over fitting 문제가 발생할 수 있다. 이를 위해 Regularization 기법을 잘 알아둬야 한다.
• 거리함수와 손실함수에 대해 정리할 이 포스트에서 해당 부분을 짚고 넘어가는 이유는 MLE 와 거리함수 두 개념이 모델 학습방법론(loss function)에 있어서 밀접하게 관련되어 있음을 보기 위해서다.
• 또한 Generative model 의 대표적인 VAE, GAN 등은 지금껏 본 MSE 나 Cross Entropy 말고도 loss function 에 거리함수를 명시적으로 사용한다.
• 아래부터는 KL-divergence 를 포함한 거리함수가 어떤 방식으로 특정 모델의 loss function 을 유도하는데 사용되는지를 알아보자.

Metric(Distance)

• 아래 내용은 WGAN 논문과 임성빈 교수님의 자료에서 대부분의 내용을 참고했다.
• Metric 은 위상수학에서 나오는 용어로, distance 라고도 불린다. 거리함수 $d$ 는 아래의 성질들을 만족한다.
  • non-negativity(양의 성질) : $d(x, y) \geq 0$
  • symmetry(대칭성) : $d(x, y) = d(y, x)$
  • self-identity axiom(동일성) : $d(x, y) = 0 \; \text{if and only} \; x=y$
  • 삼각부등식 성립 : $d(x, y) \leq d(x, z) + d(z, y)$

• 실수 공간 $\mathbb{R}$ 에서 거리함수는 절대값이다.

  \[d(x, y) = \vert x - y \vert\]

• 유클리드 공간 $\mathbb{R}^2$ 에서는 유클리드 거리, 맨해튼 거리 등이 대표적인 metric 이다.

  

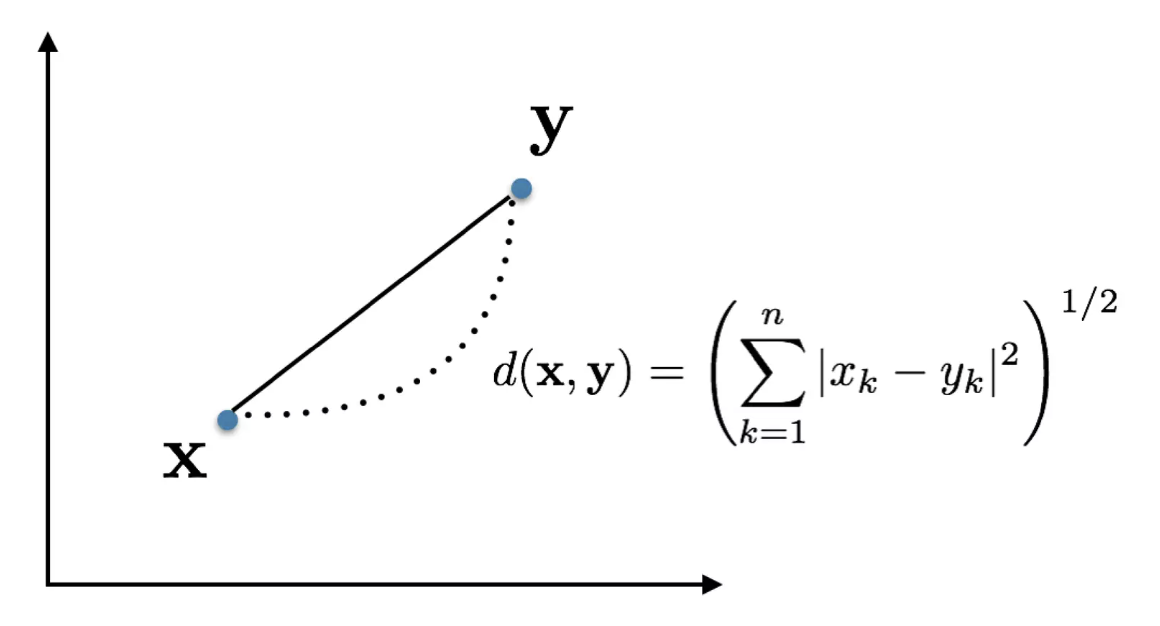
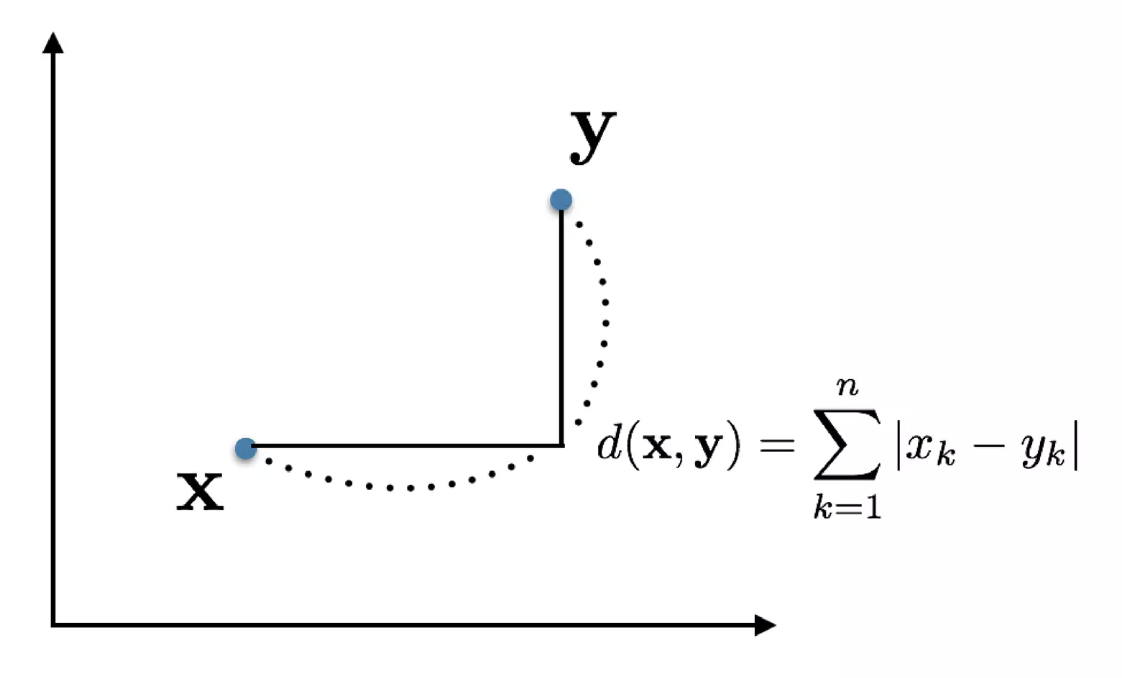
  • 위 그림에서 왼쪽이 유클리드 거리, 오른쪽이 맨해튼 거리다.

• 힐베르트 공간(Hilbert space)에서는 내적(inner product) 으로 metric 을 정의한다.

  \[d(\mathbf{u, v}) = ((\mathbf{u}-\mathbf{v})\; \cdot \;(\mathbf{u}-\mathbf{v}))^{\frac{1}{2}}\]
  • 힐베르트 공간은 유클리드 공간에서 성립하는 개념인 원소의 크기, 두 원소 사이의 거리와 직교성 등의 개념을 무한차원으로 일반화한 것이다.

  • 함수들의 집합인 함수 공간도 여기에 속한다. 대표적으로 $L1$ 거리, $L2$ 거리가 있다.

    \[\begin{aligned} L_1 \quad &\rightarrow \quad d_1(f, g) = \Vert f-g \Vert_1 = \int_{\mathcal{X}}\vert f(x) - g(x) \vert dx \\ L_2 \quad &\rightarrow \quad d_2(f, g) = \Vert f-g \Vert_2 = \left(\int_{\mathcal{X}}\vert f(x) - g(x) \vert^2 dx \right)^{\frac{1}{2}} \end{aligned}\]
• 즉 한 공간에 정의내릴 수 있는 metric 은 한 가지만 있는 것이 아니다.
• 또한 어떤 공간에 metric 개념이 중요한 이유는 수렴(convergence)이란 개념을 정의내릴 수 있기 때문이다. 수학에서는 위상(topology)을 유도하다(induce)라는 어려운 표현을 쓴다.
• 그리고 거리함수가 바뀌면 수렴의 방식이 바뀔 수 있다. 자세한 것은 아래 reference 의 임성빈 교수님의 WGAN 설명을 참고하자.
• 우리는 위에서 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포 사이의 거리를 통해 손실함수를 유도할 수 있다고 했다. 따라서 metric 이 확률분포들의 공간에서 정의되는 것이다.
• 확률측도(probability measure)란 우리가 확률분포(probability distribution)이라 불러온 $\mathbb{P}$ 와 같다. 즉 확률측도와 확률분포는 정의는 다르지만 실상 같은 용어다.

  • 확률측도 $\mathbb{P}$ 는 표본공간(sample space) $\Omega$ 위에 정의된 측도다.

    

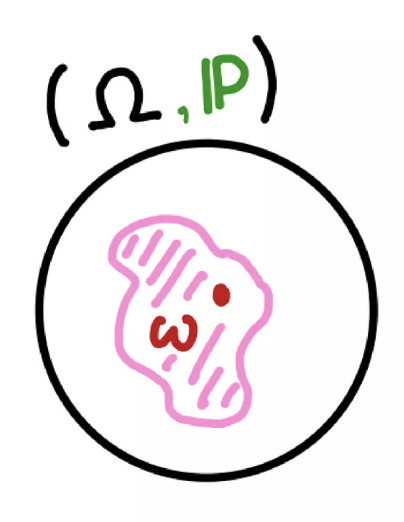
  • 확률변수 $X$ 는 표본공간 상의 $w$ 를 $\mathcal{X}$ 상의 원소 $x$ 로 사상(mapping)하는 함수다.

    

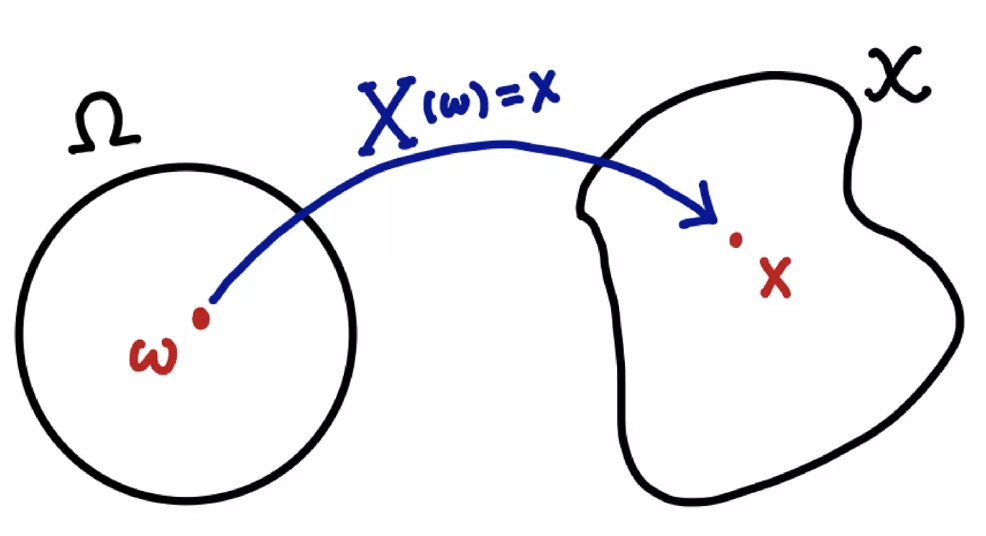
  • 확률분포는 $X$ 가 어떻게 mapping 되는지 보여주는 $\mathcal{X}$ 상의 측도다.

    

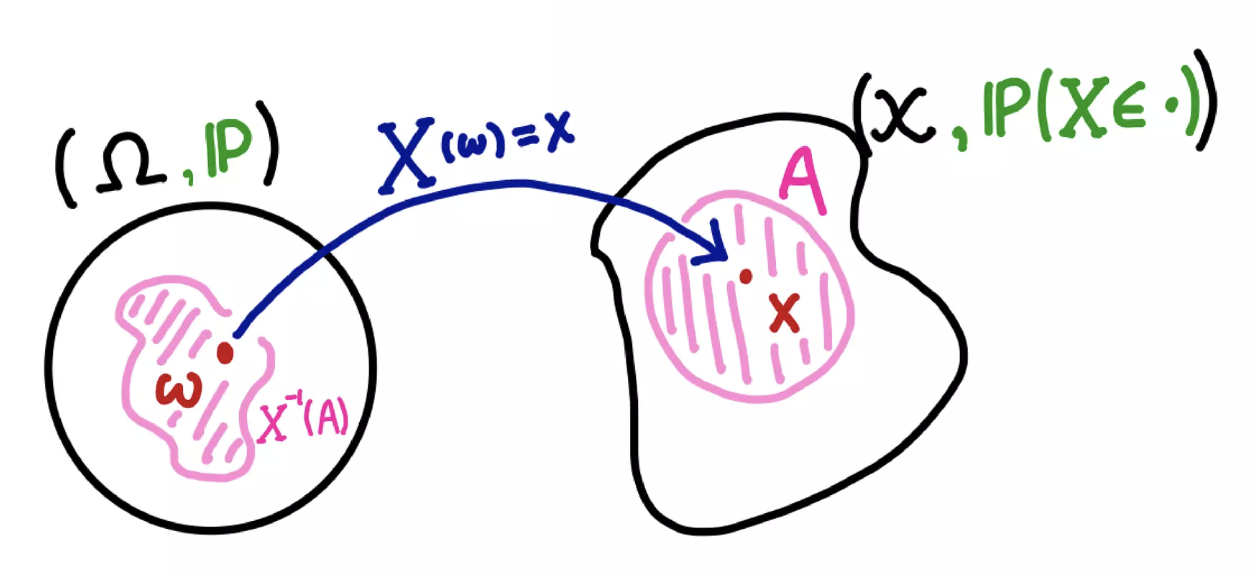
  • 즉 아래와 같은 식으로 표현된다. 역행렬이 등장하는 것은 이 포스트를 참고하자. 행렬을 벡터공간에서 사용되는 연산자(operator)로 이해한 것이다.

    \[\mathbb{P}(X^{-1}(A)) = \mathbb{P}(X \in A)\]
• 예를 들어 동전 던지기를 가정해보자.

  • 앞이 나오는 경우가 $H$, 뒤가 나오는 경우를 $T$ 라고 해보자. 그렇다면 표본공간은 아래와 같다.

    \[\Omega = \{ \color{red}{H}, \color{blue}{T} \}\]

  • 이 경우 확률측도 $\mathbb{P}$ 는 $\Omega$ 위에서 아래와 같이 베르누이 분포로 정의된다.

    \[\mathbb{P}(\color{red}{H}) = p, \quad \mathbb{P}(\color{blue}{T}) = 1-p\]

  • 그리고 확률변수 $X$ 는 $H$ 와 $T$ 를 각각 1 과 0 으로 보내는 것으로 정의한다.

    \[X(\color{red}{H}) = 1, \quad X(\color{blue}{T}) = 0\]

  • 이 때 확률분포는 다음과 같이 \(\mathcal{X} = \{ 0, 1 \}\) 위에 똑같이 정의된다.

    \[\mathbb{P}(X = \color{red}{1}) = p, \quad \mathbb{P}(X = \color{blue}{0}) = 1-p\]

  • 따라서 확률측도는 확률분포와 전혀 다르지 않다.

    \[\mathbb{P}(\color{red}{H}) = \mathbb{P}(X = \color{red}{1}), \quad \mathbb{P}(\color{blue}{T}) = \mathbb{P}(X = \color{blue}{0})\]

• 우리가 numpy 에서 seed 함수로 샘플링을 고정하는 것은 $w \in \Omega$ 를 하나 뽑는 것이고, numpy.random 의 특정분포로 값을 추출하는 것은 $X(w)$ 를 뽑는 것이다.

    import numpy as np
  
    np.random.seed(10)            # w 를 고정
    np.random.normal(mu, sigma)   # X(w) 를 샘플링
  

• 마지막으로 추가적인 용어를 정리해보자. 자세한 개념은 마찬가지로 임성빈 교수님의 자료를 참고하면 된다.
  • $\mathcal{X}$ 는 compact metric set 이다. compact 하다는 것은 경계가 있고(bounded) 동시에 경계를 포함한다(closed)는 집합을 뜻한다.
  • $\Sigma$ 는 $\mathcal{X}$ 내에서 측정가능(measurable)한 부분들로 Borel 집합이라 한다.
  • 여기서 측정가능의 의미는 확률분포로 확률값이 계산될 수 있는 집합을 말하고, 이는 연속함수의 기대값을 계산하기 위한 수학적인 최소조건이 된다.
  • support 라는 개념은 지지집합으로, 원래 함수의 정의역을 유효한 범위로 축소하는 역할을 한다. 즉 실수 범위의 정의역에서 함수값(확률)이 0 이 아닌 영역으로 정의역을 축소하는 것이다.
• 그리고 몇몇 논문을 읽다보면, $\text{inf}$ 와 $\text{sup}$ 이라는 용어들이 나온다.

  • Infimum 은 the greatest lower bound 라고 부른다. 즉 하한(lower bound) 중 가장 큰 값(maximum)이다.

    \[\text{inf} \; A = \color{red}{\text{max}}\{\color{blue}{\text{lower bound}} \; \text{of} \; A \}\]

  • Supremum 은 the least upper bound 라고 부른다. 즉 상한(upper bound) 중 가장 작은 값(minimum)이다.

    \[\text{sup} \; A = \color{red}{\text{min}}\{\color{blue}{\text{upper bound}} \; \text{of} \; A \}\]

  • 이 개념들이 필요한 이유는 모든 집합이 최대값 혹은 최소값을 가지지 않지만 $\text{sup}$ 과 $\text{inf}$ 는 항상 존재하기 때문이다.

Total Variation Distance(TV)

• Total Variation Distance 는 두 확률분포의 차이를 나타내는 값으로, 주어진 사건 집합에서 두 분포가 가장 크게 다를 수 있는 차이의 최대값(supremum)을 나타낸다이다.

  \[\delta(\mathbb{P}_r, \mathbb{P}_g) = \underset{A \in \Sigma}{\text{sup}}\vert \mathbb{P}_r(A) - \mathbb{P}_g(A) \vert\]

• 위에서 $\mathbb{P}_r$ 은 데이터의 분포이고 $\mathbb{P}_g$ 은 모델의 분포를 의미한다.

  

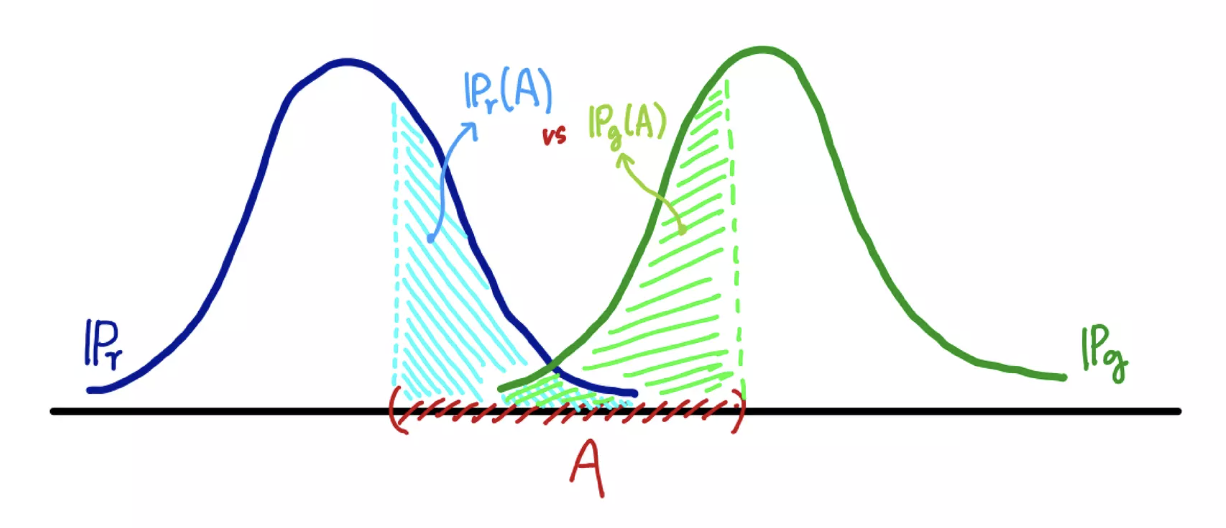
• 같은 집합 $A$ 라고 하더라도 두 확률분포가 측정하는 값은 다를 수 있다. 이 때 TV 는 모든 $A \in \Sigma$ 에 대해 가장 큰 값을 거리로 정의한 것이다.

• Total Variation Distance 는 KL divergence 와 아래와 같이 관련이 있다.

  \[\delta(\mathbb{P}_r, \mathbb{P}_g) \leq \sqrt{\frac{1}{2}\mathbb{KL}(\mathbb{P}_r \Vert \mathbb{P}_g)}\]
  • 자세한 증명은 wiki 를 참고하자.

• 또한 Total Variation Distance 는 $L1$ distance 의 절반에 해당한다. 이는 이산확률과 연속확률로 아래와 같이 표현할 수 있다.

  \[\begin{aligned} \delta(\mathbb{P}_r, \mathbb{P}_g) &= \frac{1}{2}\sum_{x \in \mathcal{X}}\vert \mathbb{P}_r(x) - \mathbb{P}_g(x) \vert \\ \delta(\mathbb{P}_r, \mathbb{P}_g) &= \frac{1}{2}\int_{x \in \mathcal{X}}\vert \mathbb{P}_r(x) - \mathbb{P}_g(x) \vert dx \end{aligned}\]
  • 즉, TVD 는 두 분포의 차이를 절대값으로 측정한 후 그 총합을 구하는 방식인 $L_1$ 거리를 절반으로 나눈 값으로 해석될 수 있다.
  • 해당 증명은 이 자료에서 Proposition 4.2 를 보면 알 수 있다.
• 이처럼 Total Variation Distance(TVD) 는 두 확률분포 사이의 차이를 측정하는 지표로 두 분포가 얼마나 다른지 나타낸다. 이 거리를 최소화하는 방식으로 모델을 학습시킬 수 있다. 따라서 이미지 처리에서 noise 를 제거하는 Total Variation Denoising 과는 다른 개념이다.
• TVD 는 Adversarial Training 나 Domain Adaptation, VAE 의 변형 등에서 사용된다. 그러나 고차원 공간 상에서 TVD 를 계산하는 것은 비효율적이라 다른 거리 함수(KL-divergence, Wasserstein distance 등)를 자주 사용한다.

Kullback-Leibler Divergence

• Kullback-Leibler Divergence 는 두 확률분포의 차이를 계산할 때 사용하는 함수로, 어떤 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링 할 때 발생할 수 있는 정보 엔트로피 차이를 계산한다.
  • 즉 KL-div 는 두 분포의 상대적인 차이를 측정하며, 특히 한 분포를 다른 분포로 근사할 때 발생하는 정보 손실을 나타낸다.
  • 따라서 KL-div 를 상대 엔트로피, 정보 획득량(information gain), information divergence 라고 부르기도 한다.

• KL-div 는 아래와 같이 정의한다.

  \[\small{\mathbb{KL}(P\Vert Q) = \sum_{\mathbf{x} \in \mathcal{X}}P(\mathbf{x})\log\left(\frac{P(\mathbf{x})}{Q(\mathbf{x})}\right) \quad \mathbb{KL}(P\Vert Q) = \int_{ \mathbf{x} \in \mathcal{X}}P(\mathbf{x})\log\left(\frac{P(\mathbf{x})}{Q(\mathbf{x})}\right)}\text{d}\mathbf{x}\]
• 이산확률변수의 경우 두 개의 확률변수 $P(\mathbf{x}), Q(\mathbf{x})$ 에 대해 먼저 뒷자리에 들어가게 되는 $Q(\mathbf{x})$ 를 로그의 분모에 집어넣게 되고, 앞자리에 들어가는 $P(\mathbf{x})$ 를 로그의 분자와 로그값으로 계산되는 것에 곱한다. 연속확률변수의 경우도 같은 함수를 적분하는 형태로 정의한다.

• 이 때 KL-div 는 기대값의 정의에 따라 아래와 같이 두 개의 항으로 분해할 수 있다. 정보이론에서는 앞의 term 이 크로스 엔트로피, 뒤의 term 이 negative 엔트로피가 된다.

  \[\mathbb{KL}(P\Vert Q) = -\mathbb{E}_{\mathbf{x}\sim P(\mathbf{x})}[\log Q(\mathbf{x})] + \mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[\log P(\mathbf{x})]\]

• $P$ 는 데이터의 분포이고, $Q$ 는 우리가 모델링하는 분포이다. 이를 위에서 살펴본 notation 으로 다시 쓰면 아래와 같다.

  \[\mathbb{KL}(P_{\text{data}} \Vert P_{\theta}) = \color{blue}{\mathbb{E}_{x \sim P_{\text{data}}}[\log P_{\text{data}}(x)]} \color{red}{- \mathbb{E}_{x \sim P_{\text{data}}}[\log P_{\theta}(x)]}\]
• 파란색 term 은 최적화와 상관없기 때문에 빨간색 term 을 최소화해야 KL-div 가 작아진다. 부호를 바꾸어 최소화 문제를 최대화 하도록 한다.
• 또한 위에서 증명했듯 우리는 $P_{\text{data}}$ 는 알 수 없기 때문에 우리가 가지고 있는 학습 데이터셋 $\mathcal{D}$ 의 Empirical Distribution 을 근사하도록 한다.
• 이는 대수의 법칙(Law of Large Number)과 Glivenko-Cantelli theorem 에 의해 실제 데이터 분포에 수렴함을 보장한다.

• 그러면 아래와 같이 KL-div 를 최소화하는 문제는 Likelihood 를 최대화하는 MLE 와 동일함을 알 수 있다.

  \[\underset{\theta}{\text{argmax}} \; \frac{1}{N}\sum^N_{i=1}\log P_{\theta}(x_i) = \hat{\theta}_{\text{MLE}}\]
• 또한 위 빨간색 term 은 크로스 엔트로피기 때문에 KL-div 를 최소화하는 문제는 크로스 엔트로피를 최소화하는 것과 동일함을 알 수 있다.

KL-div 성질

• KL-div 의 성질을 알아보자.

1. $\mathbb{KL}(P\Vert Q) = 0 \; \text{if} \; P=Q$
   • 정보이론에서 크로스 엔트로피($H(P, Q)$)는 엔토로피($H(P)$) 보다 항상 크거나 같다. 이를 Gibbs’ Inequality 라고 한다.
   • $P(X)$ 와 $P(Q)$ 가 같으면 KL-div 가 0 이 된다. 정보량의 차이는 두 분포가 같으면 0 이 될 수밖에 없기 때문이다.
2. $\mathbb{KL}(P\Vert Q) \geq 0$
   • KL-div 는 크로스 엔트로피에서 엔트로피를 빼준 것과 같다. 여기에 위 성질을 이용하면 크로스 엔트로피는 엔트로피 보다 항상 크거나 같기 때문에, KL-div 는 0 보다 크거나 같다.

   • 이는 젠센 부등식(Jensen’s Inequality)을 통해 증명할 수 있다.

     

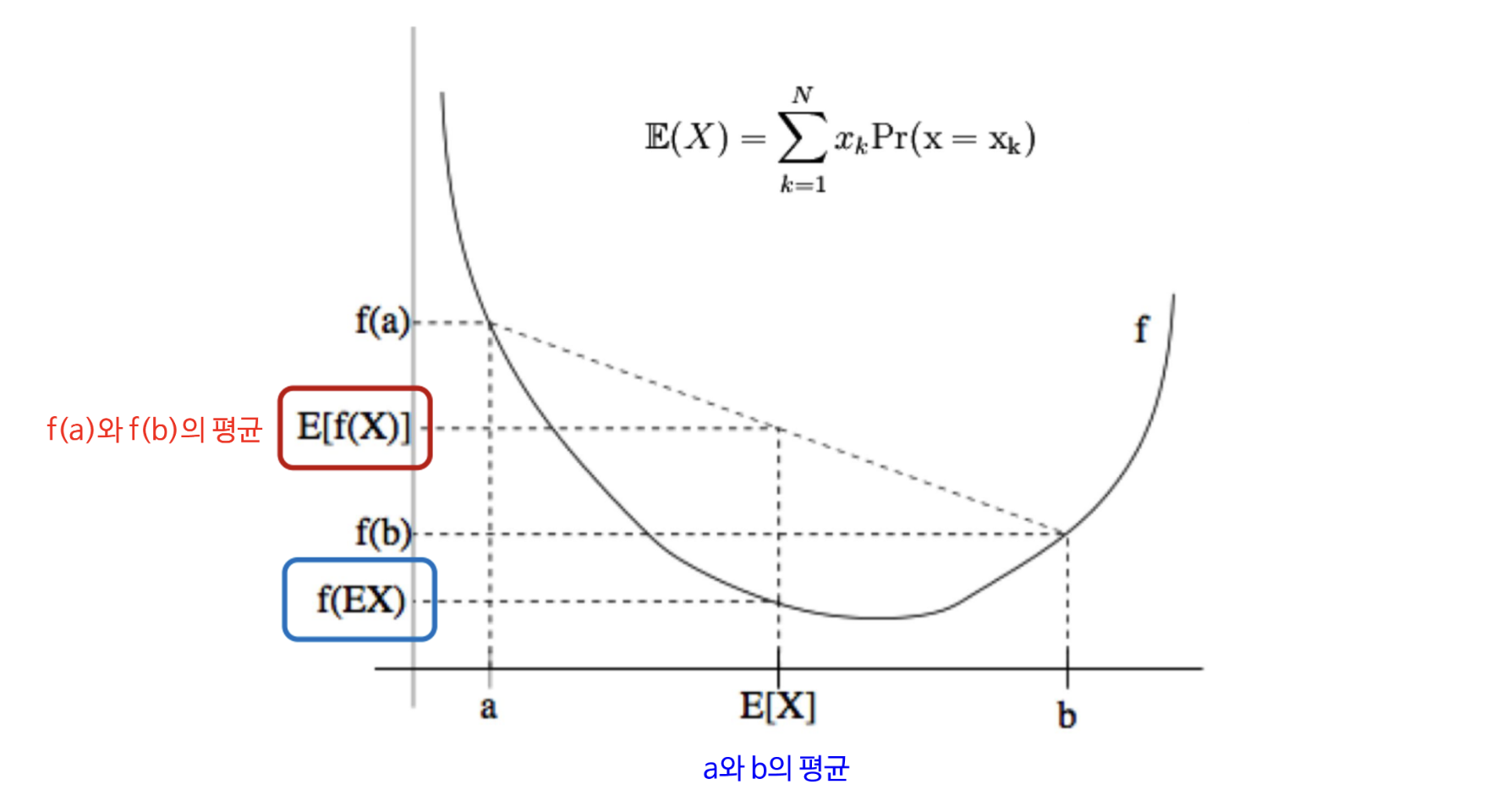
   • 젠센 부등식은 위 그래프와 같이 아래로 볼록(convex)한 그래프에서 함수값의 평균이 평균의 함수값 보다 크다는 것을 의미한다.

     \[\mathbb{E}[f(x)] \geq f(\mathbb{E}[x])\]
   • $\log$ 함수는 정의역이 양수일 때 항상 두 점을 잇는 선분 위의 점이 함수보다 아래에 있거나 같다. 우리가 딥러닝에서 사용하는 확률변수 값들은 양수이기 때문에 convex 함을 알 수 있다.

   • 따라서 아래와 같이 증명 가능하다. $f$ 가 $-\log$ 가 되는 것이다.

     \[\begin{aligned} \mathbb{KL}(P \Vert Q) &= H(P, Q) - H(P) \\ &= \sum P(X) \log \frac{P(X)}{Q(X)} \\ &= \sum P(X) - \log \frac{Q(X)}{P(X)} \\ &\geq -\log \sum P(X)\frac{Q(X)}{P(X)} \\ &= -\log \sum Q(X) \\ &= 0 \end{aligned}\]
3. $\mathbb{KL}(P\Vert Q) \neq \mathbb{KL}(Q\Vert P)$
   • KL-div 는 위와 같이 교환법칙이 성립하지 않는다. 즉 거리함수의 성질인 대칭성(symmetry)을 만족하지 않는다.
   • 따라서 KL-div 는 정확히는 거리함수라고 말할 수 없다.
   • 그러나 두 분포가 다를수록 큰 값을 가지며 두 분포가 일치할 때에만 0 이 된다는 성질을 이용하여 거리함수와 비슷한 용도로 사용할 수 있다. 그렇게 많이 사용되고 있다.
4. $P$ 를 고정하고 $Q$ 를 움직일 때, $\mathbb{KL}(P\Vert Q)$ 의 변화는 $H(P, Q)$ 의 변화와 같다.
   • 이 성질의 경우 우리는 근사할 때 사용하는 모델링 분포 $Q$ 를 학습시키며 업데이트 한다. 또한 위 식에서 보듯 $P$ 에 대한 term 은 최적화와 관계없다.
   • 따라서 크로스 엔트로피의 변화가 KL-div 의 변화가 되고, 우리가 크로스 엔트로피를 loss function 으로 사용해서 값을 줄이는 것이 KL-div 를 줄이는 것과 같다. 그리고 이것이 Likelihood 를 최대화 하는 것과 같다.

Variational Inference

• Generative Model 은 모르지만 존재한다고 가정하는 어떤 분포($P_{\text{data}}$)와 우리가 모델링하고 학습할 수 있는 probably density($P_{\theta}$)가 있을 때, 그 두 분포 사이의 거리를 최소화하는 방향으로 학습하여 density 를 최적화시킨다.
• 그리고 위에서 살펴본 것처럼 $P_{\text{data}}$ 와 $P_{\theta}$ 사이의 거리(KL-div)를 최소화하는 것은 log likelihood 인 $\log P_\theta(x)$ 를 최대화하는 것과 의미가 같다.
• Generative Model 의 중요한 모델 중 하나인 VAE 뿐만 아니라 여러 모델들이 loss function 을 유도할 때 여기서부터 출발한다.
• 그러나 복잡한 실제 분포 $P_{\text{data}}$ 를 근사하는데 상대적으로 간단한 parametric 분포 $P_\theta$ 를 사용하기 때문에 기대하는 만큼의 생성을 이루어낼 수 없다. 즉 복잡한 실제 분포를 근사하기도 어렵고, 해당 $P_\theta(x)$ 에서 데이터를 생성한다고 해도 성능이 좋지 않다는 것이다.
• 따라서 모델이 실제 분포보다 차원이 작으면서 중요한 정보를 포함하여 데이터를 잘 설명할 수 있는 latent space 를 가지도록 할 수 있다. 복잡한 데이터 분포를 잠재공간에서 저차원으로 변환하고 이 잠재공간에서 샘플링하여 데이터를 생성하는 것이다.

• 그러면 우리는 $P_\theta$ 를 $x$ 와 $z$ 의 joint distribution 으로 아래와 같이 표현할 수 있다.

  \[\underset{\theta}{\text{argmax}} \left[ P_\theta(x) = \int_z P_\theta(x, z) = \int_z P_\theta(x \vert z)P_\theta(z) \right]\]
• 여기서 적분으로 나타내는 것 즉, 결합확률을 marginalize 하는 이유는 데이터 $x$ 의 관찰 확률을 구할 때 잠재변수 $z$ 를 고려하지만, $z$ 는 관찰되지 않기 때문에 이를 적분하여 없애는 것이다.
• 그러나 위와 같은 적분은 계산할 수 없다. $z$ 를 만들기 위해 수많은 parameter 가 들어가기 때문에 매우 높은 차원을 가지기 때문이다.
• 우리가 한 가지 떠올려볼 것은, Generative Model 은 샘플링된 $z$ 를 통해 $x$ 와 유의미하게 유사한 데이터를 생성($P_\theta(x \vert z)$)해야 한다는 점이다. 바로 Decoder 에 해당하는 부분이다.

• 따라서 $z$ 를 샘플링할 때 $x$ 와 유의미하게 유사한 샘플이 나올 수 있는 $p_\theta(z \vert x)$ 에서 샘플링하는 해법을 취해볼 수 있다. 즉 Encoder 를 최적화하는 것이다.

  \[p_\theta(z \vert x) = \frac{p_\theta(x \vert z)p_\theta(z)}{p_\theta(x)}\]
• 그러나 위 식에서 볼 수 있듯 사후확률 $p_\theta(z \vert x)$를 구하기 위해서는 분모의 $p_\theta(x)$ 를 계산할 수 없기 때문에, 이 때 Bayesian 추론의 한 방법인 Variational Inference 를 이용한다.
  • VI 는 데이터 $x$ 가 들어왔을 때 latent vector $z$ 에 대한 사후확률 $P_\theta(z \vert x)$ 를 구하고자 한다.
  • 사후분포 $P_\theta(z \vert x)$ 는 계산이 불가능(intractable)하므로, 이를 최적화 문제로 바꾸어서 variational dist $q_{\phi}(z\vert x)$ 를 활용하여 근사한다.
  • 근사할 때는 KL-div 를 이용한다.
  • 따라서 VI 는 데이터 $x$ 가 주어졌을 때, 잠재변수 $z$ 에 대한 posterior 분포를 직접적으로 구하기 어려운 상황에서 사용할 수 있는 접근법이다.
• 이 VI 를 통해 식을 전개하면 우리는 Maximum Likelihood & Minimum KL-div 라는 목적을 이룰 수 있으면서 샘플링 함수를 잘 근사하는 목적도 이룰 수 있는 ELBO 를 유도할 수 있다.

ELBO(Evidence Lower Bound)

• 기억해야 할 것은 우리의 목표는 $\log P_\theta(x)$ 를 최대화하는 것이고, 여기에 잠재변수 $z$ 를 추가하면 나오는 적분식이 계산할 수 없었다는 것이다.
• 그리고 Variational Inference 는 variational distribution($q_{\phi}(z \vert x)$) 과 posterior distribution($p_{\theta}(z\vert x)$) 사이의 거리가 KL-div 관점에서 최소화하도록 최적화하는 것이다.

• 그러면 이제 Variational Inferecne 를 통해 어떻게 Maximum Likelihood 가 ELBO 를 기준으로 이루어질 수 있는지 유도해보자.

  

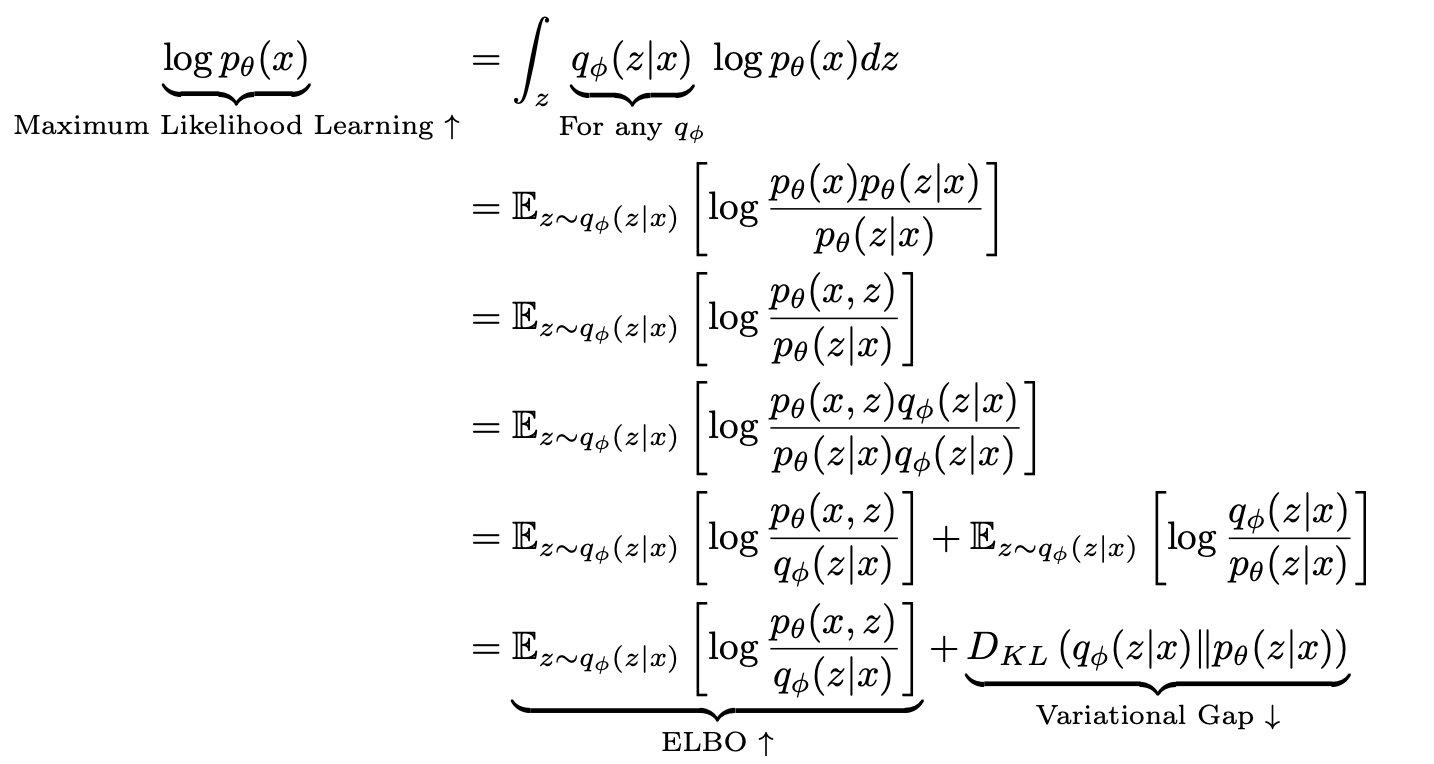
  • 첫번째 식에서 $\int_{z}q_{\phi}(z \vert x)$ 는 1 이므로 $\log p_\theta(x)$ 와 같이 쓸 수 있다.
  • 두번째 식은 연속확률변수에서의 기대값의 정의에 따라 $q_{\phi}(z \vert x)$ 로 정리하고, $\log p_\theta(x)$ 의 분모와 분자에 $\log p_\theta(z \vert x)$ 를 곱한 것이다.
  • 세번째 식은 조건부확률 정의에 따라 분자를 다시 나타내고, 네번째 식에서 분모와 분자에 $\log q_\phi(z \vert x)$ 를 곱해준다.
  • 이를 $\log$ 함수의 정의에 따라 전개하면 맨 아래의 식이 나온다.
• 자세히 보면, 두번째 term 은 Variational Inference 의 목표와 같고 이를 최소화해야 한다. 그러나 $p_\theta(z \vert x)$ 는 구할 수 없다.
• 따라서 counter part 에 해당하는 첫번째 term 인 ELBO 를 최대화함으로써 Variational Gap 을 줄이는 것이다. 이를 통해 내가 원하는 variational dist 를 posterior 와 최대한 근사시키는 것이다.
• 또한 KL-divergence 는 항상 0 보다 크거나 같기 때문에 $\log P_\theta(x)$ 는 ELBO 보다 크거나 같다.
  • 이처럼 Maximum Likelihood 의 하한선(Lower Bound)을 잡아주면서 $P_\theta(x)$ 가 Evidence 에 해당하기 때문에 ELBO 라고 불리는 것이다.
• 즉 ELBO 를 최대화하는 것은 원래의 문제인 log likelihood 를 최대화하는 것과 동일하며, 동시에 Variational Inference 의 목표인 posterior 와 variational dist 사이의 거리를 최소화시키는 것이다.
• 따라서 maximum likelihood 라는 목표는 maximum ELBO 로 바뀌게 된다. 이제 최적화할 때 이 ELBO 를 최적화하는 것이다.

• 이제 이 ELBO 를 다시 한번 전개하면 아래와 같이 나타낼 수 있다.

  \[\begin{aligned} \underbrace{\mathbb{E}_{z \sim q_{\phi}(z\vert x)}\left[\log \frac{p_\theta(x, z)}{q_\phi (z \vert x)}\right]}_{\color{red}{\text{ELBO} \; \uparrow}} &= \int q_\phi(z\vert x)\log \frac{p_\theta(x \vert z)p(z)}{q_\phi(z\vert x)} \text{d}z \\ &= \int q_\phi(z\vert x)\log p_\theta(x\vert z) - \int q_\phi(z \vert x) \frac{q_\phi(z \vert x)}{p(z)} \\ &= \underbrace{\mathbb{E}_{q_\phi(z \vert x)}[\log p_\theta(x \vert z)]}_{\color{blue}{\text{Reconstruction Term}}} - \underbrace{\mathbb{KL}(q_\phi(z \vert x) \Vert p(z))}_{\color{blue}{\text{Prior Fitting Term}}} \\ \end{aligned}\]
• 기대값을 전개하고 결합확률을 chain rule 로 펼친 뒤 정리한 것이다.
• VAE 에서 $q_{\phi}$ 는 Encoder 를 뜻한다. 그렇다면 첫번째 Reconstruction Term 은 Encoder 를 통과한 latent vector $z$ 를 가지고 $x$ 를 만들어내는 Decoder 가 모두 식에 있으므로, Encoder 와 Decoder 를 모두 통과한 것이 된다.
  • 이 term 을 높이는 것이 reconstruction 을 잘하는 것이다. 이것만 있으면 AE(AutoEncoder) 와 동일하다.
  • 사실 이 term 을 보면 negative cross entropy 와 같다. 또한 log likelihood 와도 같기 때문에 MSE 도 될 수 있다. 즉 $x$ 에 대한 복원 오차를 나타낸다.
• 두번째 term 인 prior fitting term 은 - 가 붙어있기 때문에 ELBO 를 높일 때 이 term 은 낮추게 된다.
  • $p(z)$ 는 prior 다.
  • Gaussian Distriution 과 같은 내가 미리 정해놓은 $z$ 에 대한 prior distribution 과 Encoder 를 통과해서 나오는 $z$ 들의 분포를 KL-div 로 계산하는 것이다.
  • prior fitting term 을 낮추는 것은 두 분포를 비슷하게 만드는 것이다. 즉 term 속에 prior 가 들어가기 때문에 latent vector $z$ 가 그냥 존재하는게 아니라 내가 미리 정해놓은 prior 와 최대한 비슷하게 만드려는 것이다.
  • 이는 $q_\phi(z \vert x)$ 가 prior $p(z)$ 와 유사했으면 좋겠다는 생각을 반영한 term 이다. 마치 MAP 와 유사하게 Regularization 의 역할을 한다고 볼 수 있다.
  • 따라서 VAE 에서 모델이 잠재공간을 구조화하는 데 중요한 역할을 하는 Regularization Term 이라고도 부른다.
• 정리해보자.
  • Maximum Likelihood 에서 부호를 뒤집어 경사하강법을 사용할 수 있는 loss function 을 유도하고 이를 최적화한다.
  • 따라서 여기서는 ELBO 를 최소화해야 한다.
  • 그러면 Encoder 와 Decoder 를 통과해서 나오는 reconstruction loss 를 최소화해야 한다.
  • 동시에 데이터 $x$ 들을 Encoder 에 통과시켰을 때 얻는 $z$ 들을 미리 정해놓은 prior dist 와 비슷하게 만드는 prior fitting term 를 loss function 에 더해주어 Regularization 으로 같이 최적화한다.

Jensen-Shannon Divergence

• 위에서 봤듯 KL-div 는 근사된 확률 분포가 얼마나 원본과 비슷한지를 측정하는 척도이며 두 대등한 확률 분포가 얼마나 닮았는지를 측정하는 척도로 쓰일 수 있다.
• 그러나 KL-div 의 성질에서 살펴본 것처럼 KL-div 는 Symmetric(대칭적)하지 않다. 따라서 엄밀한 의미의 거리함수가 아니다.
  • 이는 KL-div 가 데이터의 분포인 $P$ 를 기준으로 계산하기 때문이다.
  • 데이터의 분포 $P$ 에 우리가 모델링한 분포 $Q$ 를 근사하기 위해 KL-div 를 사용하는 것은 문제가 없지만, 두 분포 간의 명확한 차이를 알기 위해서 대칭적이지 못한 것은 문제가 된다.
  • 예를 들어 정답 분포는 없고 두 분포 간의 거리만 알고 싶을 때가 그렇다.

• 이러한 단점을 보완하여 KL-div 를 Symmetric 하게끔 개량한 것이 Jensen-Shannon Divergence 다.

  \[\mathbb{JSD}(P, Q) = \frac{1}{2}\mathbb{KL}(P \Vert \frac{P + Q}{2}) + \frac{1}{2} \mathbb{KL}(Q \Vert \frac{P + Q}{2})\]
  • 이는 단순하게 KL-div 식을 두 번 사용하여 symmetric 하게 만든 것이다.
  • 이를 통해 $\mathbb{JSD}(P, Q) = \mathbb{JSD}(Q, P)$ 가 되어 두 확률분포 사이의 거리(distance)로서의 역할을 할 수 있게 된다.
  • 또한 $P=Q$ 일 때 $\mathbb{JSD}(P, Q)$ 는 0 이 된다.
• 이 JSD 는 GAN 에서 loss function 으로 사용된다.

GAN

• GAN 은 주어진 데이터의 분포를 파악하고, 이렇게 파악한 결과로 학습한 데이터들과 유사한 데이터를 만들어낼 수 있게끔 하는 학습 알고리즘이다. 여기서 데이터의 분포는 데이터의 확률분포다.
• 결국 GAN 은 주어진 데이터의 확률분포를 예측하는 모델이다. 즉 주어진 데이터의 실제 확률분포와 GAN 이 예측한 확률분포 사이의 Jensen-Shannon Divergence 를 최소화 하는 알고리즘이다.
• GAN 은 아주 중요한 모델로, 따로 Generative Model 카테고리에서 포스트를 만들어서 정리한다. 여기서는 GAN 에 대해 간단하게만 보고, JSD 가 어떻게 loss function 이 되는지를 중점적으로 보자.
• GAN 은 Generative Model 인 Generator(G)와 Discriminative Model 인 Discriminator(D) 이렇게 두 Neural Network 로 이루어져 있다.
  • D 의 목적은 ‘진짜 Data 와 G 가 만들어낸 Data 를 완벽하게 구별해 내는 것’이고, G 의 목적은 ‘그럴듯한 가짜 Data 를 만들어내서 D 가 진짜와 가짜를 구별하지 못하게 하는 것’이다. 이렇듯 D 와 G 는 서로 경쟁적으로(Adversarially) 학습한다.
  • D 와 G 가 경쟁하면서도 실제로는 서로에게 학습의 방향성을 제시해주게 되어, Unsupervised Learning 이 가능하게 된다.

• GAN 의 objective funtion 은 Min-Max Problem 이다.

  \[\underset{G}{\text{min}}\;\underset{D}{\text{max}}\{\log(D(x)) + \log(1 -D(G(z)))\}\]

• 위 식은 $x$ 와 $z$ 에 대한 식이다. $x$ 는 우리가 가진 Dataset 으로부터 sampling 되고 $z$ 또한 random 한 방식으로 sampling 된다. sampling 에 따른 불확실성을 반영하기 위해 위 식에 기대값을 적용시켜보자.

  \[\underset{G}{\text{min}}\;\underset{D}{\text{max}}[V(G, D)] \\ V(G, D) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]\]

JSD

• 위 식을 바탕으로 먼저, $G$ 가 고정되었다고 가정하고 $D$ 를 최적화시켜보자.

• 이 때 $\mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]$ 에서 우리가 실제 sampling 을 통해 관찰하는 것은 $z$ 가 아니라 $G(z)$ 이므로 $y=G(z)$ 에 대하여 아래와 같이 쓸 수 있다.

  \[\mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))] = \mathbb{E}_{y \sim p_g(y)}[\log(1 - D(y))] \\ \downarrow \\ V(G, D) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{y \sim p_g(y)}[\log(1 - D(y))]\]

• 그러면 기대값의 정의에 따라 아래와 같이 계산 가능하다.

  \[\begin{aligned} V(G, D) &= \int_x p_{\text{data}}(x)\log D(x)dx + \int_y p_g(y)\log(1-D(y))dy \\ &=\int_x p_{\text{data}}(x)\log D(x) +p_g(x)\log(1-D(x))dx \end{aligned}\]
• $y$ 는 잠재공간 $z$ 에서 sampling 되어 $G$ 를 통과한 데이터이지만, 데이터 공간에서는 실제 데이터 $x$ 와 생성된 데이터 $y$ 가 동일한 공간에 존재한다.
• 즉, 생성된 데이터 $y$ 는 $x$ 와 동일한 차원의 데이터 공간에 대응되므로, 실제 데이터를 다루는 수식과 동일한 적분 범위를 가진다. 이는 모델이 학습하는 과정에서 실제 데이터 분포와 생성된 데이터 분포가 같은 차원의 공간에서 정의되기 때문이다.

• 위 식은 $a = p_{\text{data}}(x)$ , $b=p_g(x)$ 로 두면 아래와 같은 꼴이다.

  \[f(x) = a\log x + b\log(1-x)\]
• 이 함수를 그래프로 그려보면 위로 볼록한 모양이 되고, 0 과 1 사이에서 미분 가능하다.

• GAN 에서 $D$ 를 최적화할 때는 최대값을 구하므로 미분했을 때 0 이 되는 점을 구해보자.

  \[\begin{aligned} \frac{f(x)}{dx} &= \frac{a}{x} - \frac{b}{1-x} \\ &= a(x-1) + bx\\ &= (b+a)x -a = 0 \\ \end{aligned} \\ \therefore x=\frac{a}{a+b}\]

• 위 식에 $a = p_{\text{data}}(x)$ , $b=p_g(x)$ 를 다시 대입하면 Optimal $D^\ast$ 가 나온다.

  \[D^\ast = \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)}\]
• 이제 $V(G, D)$ 에서 $D$ 를 $D^\ast$ 로 고정하고 Generator 를 최적화해보자.

• 그러면 아래와 같이 식을 전개할 수 있다.

  \[\small{ \begin{aligned} V(G, D^\ast) &= \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D^\ast(x)] + \mathbb{E}_{x \sim p_g(x)}[\log(1 - D^\ast(x))] \\ &= \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)}] + \mathbb{E}_{x \sim p_g(x)}[\log \frac{p_{\text{g}}(x)}{p_{\text{data}}(x) + p_g(x)}] \\ &= \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log \frac{1}{2}\frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)/2}] + \mathbb{E}_{x \sim p_g(x)}[\log \frac{1}{2}\frac{p_{\text{g}}(x)}{p_{\text{data}}(x) + p_g(x)/2}] \\ &= -2\log2 + \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log p_{\text{data}}(x) - \log \frac{p_{\text{data}}(x) + p_g(x)}{2}] \\ &\qquad + \mathbb{E}_{x \sim p_g(x)}[\log p_g(x) - \log \frac{p_{\text{data}}(x) + p_g(x)}{2}] \\ &= -2\log2 + \mathbb{KL}(p_{\text{data}}\Vert \frac{p_{\text{data}} + p_g}{2}) + \mathbb{KL}(p_g\Vert \frac{p_{\text{data}} + p_g}{2}) \\ &= -2 \log 2 + 2 \times \mathbb{JSD}(p_{\text{data}}\Vert p_g) \end{aligned} }\]
• 결국, $D$ 가 최적화 되어있는 상황에서 $G$ 를 최적화시키는 일은 $\mathbb{JSD}(p_{\text{data}}\Vert p_g)$ 를 최소화 시키는 일과 같음을 알 수 있다.
• 이는 $p_{\text{data}}$ 와 $p_g$ 사이의 Jensen-Shannon Divergence 를 최소화시키는 것으로, Generated data 의 distribution 이 Real data 의 distribution 에 가까워지도록 하는 일이라는 뜻이 된다.
• 이처럼 GAN 은 실제 주어진 data 와 동일한 형태의 distribution 을 구해나가는 알고리즘이며, 우리는 이로써 GAN 이 주어진 dataset 의 distribution 을 알아내는 알고리즘이라는 결론을 얻을 수 있다.

BCE

• GAN 을 구현할 할 때 실질적인 loss function 은 Binary Cross Entropy(BCE)를 사용한다.

• 즉 $D$ 는 Real Image 를 받았을 때 1 을 출력하고 Fake Image 를 받았을 때 0 을 출력하기를 원한다. 따라서 아래의 식을 최소화한다.

  \[\text{Loss}_D = \text{Error}(D(x), 1) + \text{Error}(D(G(z)), 0)\]

• 또한 $G$ 는 자신이 만든 Fake Image 를 $D$ 가 받았을 때 1 을 출력하기를 원한다. 따라서 다음 식을 최소화한다.

  \[\text{Loss}_G = \text{Error}(D(G(z)), 1)\]

• 여기서 $\text{Error}$ 가 Binary Cross Entropy 다.

  \[\text{Error}(p, t) = -t \log (p) - (1-t) \log (1-p)\]

• 따라서 두 Loss 를 다시 쓰면 아래와 같다.

  \[\begin{aligned} \text{Loss}_D &= -\log(D(x)) -\log(1 - D(G(z))) \\ \text{Loss}_G &= -\log(D(G(z))) \end{aligned}\]

• 여기서 $G$ 는 사실 $D$ 가 maximize 하고 싶은 것을 minimize 하고 싶어하기 때문에 위에서 본 것처럼 Min-Max Problem 으로 표현할 수 있다.

  \[\underset{G}{\text{min}}\;\underset{D}{\text{max}}\{\log(D(x)) + \log(1 -D(G(z)))\}\]
• 여기서 $G$ 가 $\log(1-D(G(z)))$ 를 minimize 하느냐, $\log(D(G(z)))$ maximize 하느냐에 차이가 있는데, 수식적으로 차이는 있어도 $D(G(z))$ 가 0 이 아닌 1 에 가까워지는 방향을 지향한다는 점에서 결과적으로 같다.
• 그러나 우리가 실제 구현에서 $\log(D(G(z)))$ 를 maximize 하는 방법을 쓴다.
• 그 이유는 $G$ 는 처음에 아무런 학습이 되지 않은 상태에서 Fake Image 를 생성하기 때문에 $D$ 가 유리한 상태로 시작한다. 따라서 $G$ 가 초반에 더 빠르게 학습할 수 있도록 도와주어야 하고, $\log(D(G(z)))$ 를 maximize 하는 것이 0 지점에서 기울기가 급격하기 때문에 초반에 더 급격한 변화를 이끌어낼 수 있다.

• 따라서 실제 구현에서는 2 step 으로 나누어서 아래의 loss function 2 개를 쓴다.

  \[\begin{aligned} \text{Loss}_D &= -\log(D(x)) -\log(1 - D(G(z))) \\ \text{Loss}_G &= -\log(D(G(z))) \end{aligned}\]
• 학습할 때는 먼저 $G$ 를 고정시키고 $D$ 를 업데이트하고, 그 다음에 $D$ 를 고정시키고 $G$ 를 업데이트한다.
• 그러면 이는 $D$ 가 최적화 되면서 $G$ 를 학습시키는 것이 위에서 본 것처럼 $p_{\text{data}}$ 와 $p_g$ 사이의 거리인 JSD 를 최소화 시키는 것이다.

Reference

• https://gaussian37.github.io/ml-concept-basic_information_theory/
• https://hyeongminlee.github.io/post/gan002_gan_math/
• https://www.slideshare.net/slideshow/wasserstein-gan-i/75554346

맨 위로 이동 ↑