[Loss] Cross Entropy

정보이론 관점에서의 Cross Entropy

• 크로스 엔트로피에서 엔트로피는 정보이론에서 정의되는 용어다. 이 크로스 엔트로피를 정보이론 관점에서 해석해보자.

Entropy 란?

• 정보 이론(information theory)은 확률분포 $P(X)$ 의 불확실 정도를 평가하는 방법이다.
• 이 포스트에서 공부했듯, 정보량(information)은 불확실성을 해소하기 위해서 필요한 질문(정보)의 수 또는 어떤 Event 가 발생하기 까지 필요한 시행의 수를 뜻한다.
  • 1 ~ 16 사이의 숫자 중 상대방이 선택한 하나의 숫자를 맞추는 게임을 진행한다고 했을 때, binary search 를 이용하여 $\log_2 16 = 4 $ 만큼의 질문을 통해 답을 찾을 수 있다.
  • 여기서 $\log$ 의 밑인 2 는 Yes/No 의 경우의 수를 의미한다. 그리고 4 가 정보량이 된다.
• 위 게임에서 처음에는 상대방이 생각한 숫자를 전혀 모르기 때문에 불확실성이 매우 큰 상황에서 질의를 통해 점점 불확실성을 줄여간다.
• 최종적으로 불확실성이 완전히 줄어들어서 정답을 찾을 때까지 4번의 질의가 필요한 것이고, 이 4 가 정보량이 된다.
• 사실 위 예제는 어떤 숫자를 선택할 지를 모두 동등한 확률($p$) 1/16 으로 가정한 것이다.

• 일반적으로 어떤 event 의 확률이 $p$ 라고 했을 때, 그 event 에 대한 정보량 $I$ 는 아래와 같이 계산한다.

  \[I = \log_2 (\frac{1}{p}) = - \log_2 (p)\]
• 이러한 정보량의 기대값을 엔트로피(Entropy)라고 한다. 엔트로피는 $H$ 로 나타낸다.

• 이산확률에서의 기대값은 아래와 같은 공식으로 구할 수 있다.

  \[\mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[f(\mathbf{x})] = \sum_{\mathbf{x} \in \mathcal{X}}f(\mathbf{x})P(\mathbf{x})\]

• 위 예제에서 16개의 수 각각에 대해서 정보량을 구하고, 위 공식을 활용하여 그 정보량의 평균(기대값)을 구한다면 아래와 같이 구할 수 있다.

  \[\begin{aligned} H(X) &= -\sum^{16}_{i=1}P(X=i)\log_2P(X=i) \\ &= \sum^{16}_{i=1}\frac{1}{16}\log_2(\frac{1}{16}) = 4 \end{aligned}\]
• 이는 불확실성을 해결하기 위해서 평균적으로 4번의 질의가 필요함을 뜻한다.

• 즉 확률분포 $P(X)$ 에 대한 정보량의 기대값을 의미하는 엔트로피는 아래와 같은 공식으로 구할 수 있다.

  \[H(X) = -\sum_X\color{blue}{P(X)}\color{red}{\log_2(P(X))}\]
  • 기대값의 공식에서 $f(\mathbf{x})$ 에 정보량이 들어간 것과 같다. 즉, 파란색 term 은 확률을 의미하고 빨간색 term 은 정보량을 의미한다.
• 위 예제는 각 event 가 발생할 확률이 모두 같은 uniform distribution 이었다.

• 이제 동전 던지기를 한다고 생각해보자. 앞(1), 뒤(0)의 확률에 따라 아래와 같이 엔트로피를 구할 수 있다.

  \[\begin{aligned} P(X=1) &= p \\ P(X=0) &= 1-p \end{aligned} \\ H(P) = -p\log_2p - (1-p)\log_2(1-p)\]
• 이 때 앞, 뒤의 발생확률이 각각 1/2 인 uniform distribution 에서는 엔트로피 값이 1 이 나온다. 그러나 동전이 구부러져 앞, 뒤 발생확률이 다른 non-uniform distribution 이면 엔트로피 값이 달라진다.

• 즉, 확률분포 $P(X)$ 에 따라 엔트로피 값이 달라진다는 것이다. $p$ 에 따른 엔트로피의 그래프를 그리면 아래 그림과 같다.

  

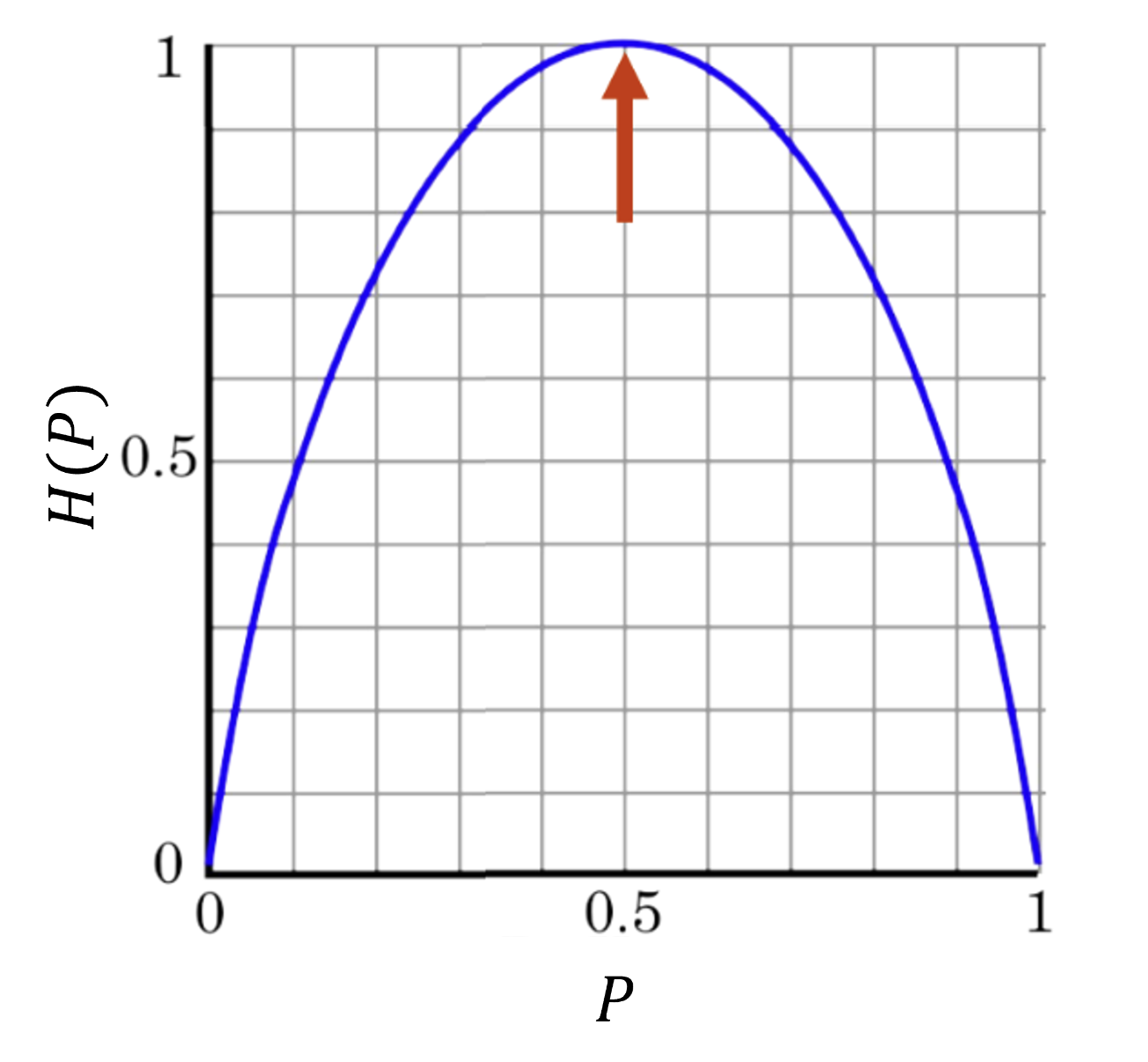
• 엔트로피의 의미를 생각해볼 때, $P(X)$ 가 불균형한 분포일 때 불확실성이 더 작다. 어느 하나의 확률이 크다면 최소 질문 횟수가 적어질 수 있기 때문이다.

  

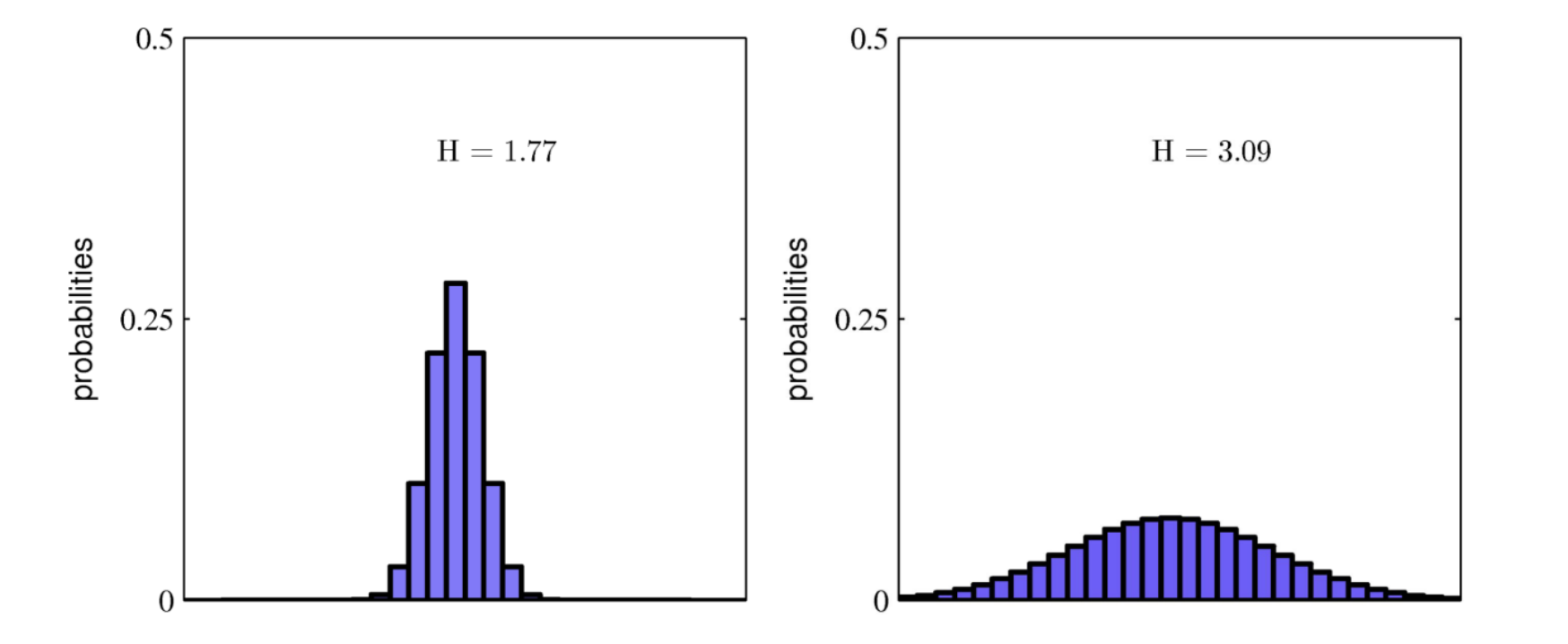
• 그러나 각 event 의 발생확률이 균등한 분포일 때는 불확실성이 높다. 앞면의 발생확률이 1/2 인 경우와 8/9 인 경우 어느 경우가 더 불확실한지를 생각해보면 그렇다.
• 텍스트를 예로 들어보면, 어떤 글에서 단어의 출현 빈도를 확률 분포라고 나타내었을 때 분포가 균등한 것은 특정 주제가 없는 글이라서 단어의 출현 빈도가 균등하다고 보면되고 분포가 편향되어 있는 것은 특정 주제가 있는 글이라서 특정 단어가 자주 나온다고 생각할 수 있다.
• 정리하면, 엔트로피는 확률분포 $P(X)$ 에서 일어날 수 있는 모든 사건들의 정보량의 기대값이다.
  • 엔트로피를 이용하여 $P(X)$ 의 불확실 정도를 평가한다.
  • 머신러닝/딥러닝에서 엔트로피를 사용할 때는 $\log$ 의 밑을 $e$ 로 사용하는 자연 로그를 이용한다. 이렇게 해도 엔트로피의 크기를 비교할 때는 문제가 없고 미분 등의 계산을 할 때 유리하다.
  • 엔트로피는 항상 양수다.

Cross Entropy

• 현재 가지고 있는 데이터의 분포가 $P(X)$ 일 때, 이 $P(X)$ 를 근사할 수 있는 새로운 분포 $Q(X)$ 를 이용해서 엔트로피를 구해볼 수 있다.

• 엔트로피의 정의에 따라, 정보량으로 $Q(X)$ 를 사용하고 이 때 사용되는 확률분포를 $P(X)$ 로 사용하면 아래와 같이 표현할 수 있다.

  \[H(P, Q) = \sum_X P(X)\log\frac{1}{Q(X)} = -\sum_X P(X)\log Q(X)\]
• 위의 식이 크로스 엔트로피가 된다.
• 크로스 엔트로피는 실제 데이터는 $P(X)$ 분포로부터 생성되지만 $Q(X)$ 분포에서 정보량을 측정하여 계산한 정보량의 기대값을 의미한다.
• 일반적으로 $H(P, Q) \geq H(P)$ 를 만족한다.
  • 우리가 A, B, C, D 중 한 글자를 맞춘다고 했을 때, 가장 최적의 전략이 반씩 쪼개서 물어보는 전략이다. 위에서 1~16 사이의 숫자를 맞추는 예제도 binary search 를 이용했다.
  • 사실 엔트로피 $H(P)$ 는 최적의 전략 하에서 필요한 질문 개수의 기대값이다.
  • 따라서 크로스 엔트로피 $H(P, Q)$ 는 최적의 전략일 수도 있고 아닐 수도 있는 특정 전략을 쓸 때 예상되는 질문 개수의 기대값이 된다.
  • 이 때문에 크로스 엔트로피는 엔트로피 보다 작을 수 없다. $Q(X)$ 가 $P(X)$ 와 같아지면 엔트로피와 같아진다.
• 또한 $H(P, Q) \geq H(P)$ 의 의미는 모델의 예측($Q(X)$)이 실제 분포($P(X)$)를 얼마나 잘 근사하느냐에 따라 크로스 엔트로피가 커지거나 같아질 수 있다는 점을 나타낸다.
• 모델이 실제 분포를 완벽하게 근사할 때 $H(P, Q) = H(P)$ 가 된다.

Kullback-Leibler Divergence(KL-div)

• 크로스 엔트로피는 엔트로피보다 항상 크고 $P(X) = Q(X)$ 일 때만 같으므로, 두 엔트로피의 차이를 분포 사이의 거리처럼 사용할 수 있다.

• 크로스 엔트로피 식을 아래와 같이 전개해보자.

  \[\begin{aligned} H(P, Q) &= -\sum_i p_i \log q_i \\ &= -\sum_i p_i \log q_i + (-\sum_i p_i \log p_i + \sum_i p_i \log p_i) \\ &= H(P) + \sum_i p_i \log p_i -\sum_i p_i \log q_i \\ &= H(P) + \color{red}{\sum_i p_i \log\frac{p_i}{q_i}} \end{aligned}\]
• 즉 크로스 엔트로피는 엔트로피에 무언가 더해진 형태다. 빨간색 term 으로 더해진 것이 정보량의 차이를 의미하는 KL-div 다.

• 위 식에서 위치만 바꿔줬을 때, KL-div 는 $H(P, Q)$ 에서 $H(P)$ 를 뺀 값이 된다. 결과적으로 두 분포의 차이를 나타내는 것이다.

  \[\mathbb{KL}(P \Vert Q) = \mathbb{E}[\log(p_i) - \log(q_i)] = \sum_i p_i \log \frac{p_i}{q_i}\]
• 즉 KL-div 는 두 확률분포의 차이를 계산할 때 사용하는 함수로, 어떤 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링 할 때 발생할 수 있는 정보 엔트로피 차이를 계산한다.
  • KL-div 를 상대 엔트로피, 정보 획득량(information gain), information divergence 라고 부르기도 한다.
• KL-div 의 성질은 아래와 같다.
  • $P(X)$ 와 $P(Q)$ 가 같으면 0 이 된다. 이는 정보량의 차이는 두 분포가 같으면 0 이 될 수밖에 없다.
  • $\mathbb{KL}(P \Vert Q) \geq 0 $ 이 성립한다. 젠센 부등식을 통해 증명 가능하다.
  • 교환법칙이 성립하지 않는다. 즉 $\mathbb{KL}(P \Vert Q) \neq \mathbb{KL}(Q \Vert P)$ 다.
  • $P(X)$ 를 고정하고 $Q(X)$ 를 움직일 때 $\mathbb{KL}(P \Vert Q)$ 의 변화는 $H(P, Q)$ 와 같다. 이 또한 식을 보면 알 수 있다.
• 두 확률분포의 차이를 계산하는 것은 두 확률분포의 거리를 계산하는 것과 같다. KL-div 는 엄밀하게 거리 함수로 정의되지는 않지만, 유사하게 사용되고 이를 보완한 JSD 라는 함수도 있다.
• 기계학습에서 사용되는 손실함수들은 기계학습 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도할 수 있다.
• MLE 로 추정하게 되는 많은 모델 학습방법론이 확률분포의 거리를 최적화하는 것과 밀접하게 관련이 있다.
• 따라서 KL-div 는 다음 포스트에서 위 성질들을 포함하여 자세하게 정리한다.

딥러닝과의 연결점

• 딥러닝에서 크로스 엔트로피는 분류 문제에서 손실함수로 많이 사용된다. 이는 binary(2-class) classification 이든 k-class classification 이든 마찬가지다.
• 우리가 가진 데이터가 $P(X)$ 분포를 따르고 모델의 예측이 $Q(X)$ 분포를 따를 때, $Q(X)$ 에서 정보량을 측정해서 정보량의 기대값을 낮추는 것은 불확실성을 낮추는 것과 같다.
• 정보량이 게임의 정답을 맞추기 위한 질문횟수를 나타낼 때, 질문의 횟수가 적다는 것은 불확실성이 해소되는 것이기 때문이다. 따라서 학습을 통해 $Q(X)$ 를 개선시켜 불확실성을 해소하는 것이다.
• 분류 문제에서 크로스 엔트로피는 softmax 함수와 함께 자주 사용된다.
  • softmax 함수는 모델의 출력값을 확률로 변환하는 역할을 하며, 크로스 엔트로피는 이 확률 분포 $Q(X)$ 와 실제 라벨 분포 $P(X)$ 간의 차이를 최소화한다.
  • 이를 통해 모델의 예측을 실제 라벨과 일치시키는 방향으로 학습을 진행한다.
• 이렇게 정보이론 관점에서 크로스 엔트로피를 해석할 수 있다.

확률 관점에서의 Cross Entropy

• 크로스 엔트로피는 MLE 와도 관계가 깊다. 주로 분류 문제에서 손실함수로 자주 사용되는 크로스 엔트로피를 확률 관점에서 명확하게 해석해보자.

• 다시 한 번 크로스 엔트로피를 수식으로 보자.

  \[H(P, Q) = -\sum_i P(X) \log Q(X)\]
• 이 때 $P(X)$ 는 특정 확률에 대한 참값 또는 목표 확률이고, $Q(X)$ 는 현재 학습한 확률값 즉 예측값이다. $Q(X)$ 가 학습하면서 $P(X)$ 에 가까워질수록 크로스 엔트로피 값이 작아지게 된다.

Bayes Theorem 과 Logistic Regression

• 우리는 분류를 하고자 할 때 아래와 같이 사후확률을 기준으로 삼는다.

  \[X : Y_1 \; \text{if} \; P(Y_1 \vert X) > P(Y_2 \vert X) \\ X : Y_2 \; \text{if} \; P(Y_1 \vert X) < P(Y_2 \vert X)\]

• 이처럼 두 개의 클래스가 있는 binary(2-class) classification 인 경우, 판별 기준인 사후확률(posterior)을 전개해보자.

  \[P(Y_1 | X) = \frac{P(X | Y_1) P(Y_1)}{P(X)} \\ P(Y_2 | X) = \frac{P(X | Y_2) P(Y_2)}{P(X)}\]

• 이 때 분모의 Evidence 는 아래와 같다.

  \[P(X) = P(X | Y_1)P(Y_1) + P(X | Y_2)P(Y_2)\]

• 그렇다면 사후확률은 Likelihood 와 Prior 의 곱으로 결정된다. 그러면 각 클래스($k$)별로 Likelihood 와 Prior 의 곱을 정의하는 것은 의미가 있다.

  \[a_k = \log(P(X|Y_k)P(Y_k))\]
• 여기서 $\log$ 를 쓰는 것은 $\log$ likelihood 를 쓰는 것과 같은 이유다.

• 따라서 클래스 1 의 사후확률은 아래처럼 나타낼 수 있다.

  \[P(Y_1 | X) = \frac{P(X | Y_1) P(Y_1)}{P(X | Y_1)P(Y_1) + P(X | Y_2)P(Y_2)} = \frac{e^{a_1}}{e^{a_1}+e^{a_2}}\]

• 이 식을 분자로 분모와 분자를 모두 나눠주면 아래와 같다.

  \[P(Y_1 | X) = \frac{1}{1+e^{a_2 - a_1}}\]

• 여기서 $a_2 - a_1$ 를 분모 분자를 뒤집으면 Log Odds 라고 부르는 식이 나온다.

  \[\begin{aligned} a_2 - a_1 &= \log( \frac{P(X | Y_2)P(Y_2)}{P(X | Y_1)P(Y_1)} ) \\ a = -(a_2 - a_1) &= \log(\frac{P(X | Y_1)P(Y_1)}{P(X | Y_2)P(Y_2)}) \end{aligned}\]
  • Odds 는 사건이 발생할 확률을 사건이 발생하지 않을 확률로 나눈 비율이다.
  • 즉 $P(Y_1 \vert X)$ 를 $1 - P(Y_1 \vert X)$ 로 나눈 값이다. 이 때 Odds 는 0 < Odds < $\infty$ 의 범위에 속하기 때문에 범위에 제약이 있다. 또한 확률값과 Odds 값은 비대칭성(Asymmetirc)을 띈다.

  • 이러한 한계를 극복하기 위해 Odds 에 $\log$ 를 씌울 수 있다. 이를 logit 이라 부르고, logit(Log Odds)은 범위가 실수 전체가 된다.

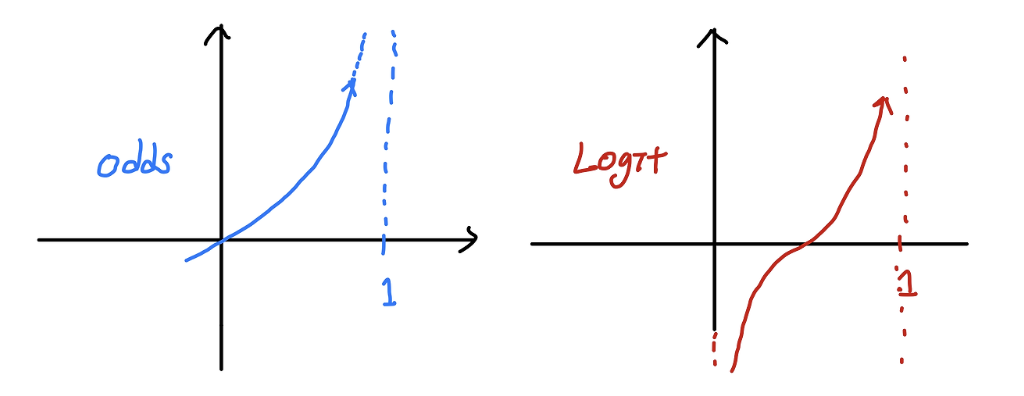    출처: https://csm-kr.tistory.com/43

  • binary classification 에서는 단순 선형함수 $\mathbf{y}=\mathbf{W}\mathbf{x} + \mathbf{b}$ 로는 풀기 힘들다. 따라서 최종 예측값이 0.5 보다 작으면 0 으로, 0.5 보다 크면 1 로 판단하는 확률로 해석하는 것이 용이하다.
  • 그러면 Odds 는 그 값이 1 보다 큰 지가 결정기준이 되고, logit 은 $\log$ 를 씌웠으므로 0 보다 큰 지가 결정기준이 된다.
  • 이를 이용하면 단순 선형함수로 풀기 힘든 binary classification 문제를 $\log(\text{Odds}(\mathbf{y})) = \mathbf{W}\mathbf{x} + \mathbf{b}$ 로 풀 수 있다.

• 이를 위 Log Odds 를 이용해서 다시 사후확률을 정의하면 아래와 같다.

  \[P(Y_1 | X) = \frac{1}{1+e^{-a}}\]
• 이를 $a$ 에 대한 함수로 그려보면 그 유명한 Sigmoid Function 이 나온다. 이를 $\mathbf{W}\mathbf{x} + \mathbf{b}$ 로 다시 정리해보자.

• 즉 실수 전체의 범위를 가지는 선형회귀의 식($\mathbf{W}\mathbf{x} + \mathbf{b}$)을 logit 으로 하여 위 식의 $a$ 대신에 넣어주면, 그 값을 0 에서 1 사이의 값으로 변환시켜주는 sigmoid(logistic) funtion 인 것이다.

  \[\begin{aligned} \log(\text{Odds}(\mathbf{y})) = \mathbf{W}\mathbf{x} + \mathbf{b} \; &\rightarrow \; \text{Odds}(\mathbf{y}) = e^{\mathbf{W}\mathbf{x} + \mathbf{b}} \\ \frac{P(Y | X)}{1 - P(Y | X)} = e^{\mathbf{W}\mathbf{x} + \mathbf{b}} \; &\rightarrow \; \frac{1- P(Y | X)}{P(Y | X)} = e^{-(\mathbf{W}\mathbf{x} + \mathbf{b})} \\ \frac{1}{P(Y | X)} &= e^{-(\mathbf{W}\mathbf{x} + \mathbf{b})} + 1 \\ \therefore \; P(Y | X) &= \frac{1}{1+e^{-(\mathbf{W}\mathbf{x} + \mathbf{b})}} \end{aligned}\]
• Naive Bayes 에서는 Likelihood 와 Prior 의 확률 분포를 구분하지만, 이를 구분하지 않고 위 함수에 Fitting 하는 문제가 된다면 Logistic Regression 이 된다.

• 2 개의 클래스인 Binary Classification 이 아닌 K-Class Classification 도 마찬가지로 Likelihood 와 Prior 의 곱으로 정의할 수 있다.

  \[P(Y_1 | X) = \frac{P(X|Y_1)P(Y_1)}{P(X|Y_1)P(Y_1) + P(X|Y_2)P(Y_2) + \ldots + P(X|Y_k)P(Y_k)}\]

• 위 식에서 우리가 사후확률의 분포로 판단을 하고, 그것은 Likelihood 와 Prior 의 곱에 비례했기 때문에 정의한 $a_k=\log(P(X \vert Y_k)P(Y_k))$ 를 이용하면 아래와 같다.

  \[P(Y_1 | X) = \frac{e^{a_1}}{e^{a_1}+e^{a_2}+ \ldots +e^{a_k}} = \frac{e^{a_1}}{\sum _{j}^{}{e^{a_j}}}\]
• 이는 결국 Softmax Function 이 된다.
• 따라서 베이즈 정리를 통해 분류 문제에서 결정 기준을 사후확률로 잡고, 이를 이용하여 binary 에서는 Sigmoid 를, k-class 에서는 Softmax 를 유도할 수 있었다.
• 또한 일반적인 선형함수로는 분류 문제에 접근하기 어렵기 때문에, 선형함수를 이용할 수 있도록 Odds 와 logit 같은 확률적 해석을 적용했고, 이를 이용해서도 Sigmoid 와 Softmax 를 유도했다.

MLE 와 Cross Entropy

• 위에서 Logistic Regression 을 정의했고, 이를 아래와 같이 나타낼 수 있다.

  \[P(Y \vert X) = \frac{1}{1+e^{-(\mathbf{W}\mathbf{x} + \mathbf{b})}} = \sigma(\mathbf{W}\mathbf{x} + \mathbf{b})\]
• 이제 위 식에서 parameter 인 $\mathbf{W}$ 를 추정해야 한다.
• 이 때 MLE 를 사용하여 주어진 Data 로부터 어떤 parameter 를 선택했을 경우 주어진 Data 가 가장 잘 설명이 될지, 즉 Likelihood $P(\text{Classes}\vert X, w)$ 가 최대가 될 지를 구한다.
• 따라서 MLE 를 통해 binary classification 에서 모델을 학습하기 위한 손실함수를 유도할 수 있다.

• Binary Classification 에서 $y$ 는 continuous 한 값이 아닌 discrete 한 값을 가지고, 0 과 1 중 하나이므로 Bernoulli Distribution 을 따른다고 볼 수 있다.

  \[\text{Bern}(x;\mu) = \mu^x(1-\mu)^{(1-x)}\]

• 그러면 아래와 같이 logistic regression 의 확률분포를 표현할 수 있다.

  \[P(Y_1 \vert X)^y(1-P(Y_1 \vert X))^{(1-y)}\]

• 여기서 예측값을 $y_n$ 으로 두고 $y_n = P(Y \vert X) = \sigma(w^Tx)$ 라고 한다면 아래와 같이 Bernoulli 분포로 표현할 수 있다.

  \[\text{Likelihood} = \prod^N_{n=1}y_n^{t_n}(1-y_n)^{(1-t_n)}\]

• 이를 Log likelihood 로 바꾸면, 결국 아래의 식을 Maximize 해야 한다.

  \[\text{Log Likelihood} = \sum_{n=1}^{N}{t_n \log(y_n) + (1-t_n) \log(1-y_n)}\]
• $t_n$ 은 결국 실제 Label 값이고, $y_n$ 은 Logistic function 으로서 예측값이 된다.
  • 참고로, 여기서 $t_n$ 은 Bernoulli 분포에서 0 또는 1 이기 때문에 우리가 Classification 에서 One-hot vector 를 쓰게 된다.
• 위 식을 잘 보자. $t_n$ 이 $P(X)$ 가 되고, $y_n$ 이 $Q(X)$ 가 되면 크로스 엔트로피 식을 부호만 바꾼 것과 같다.
• 따라서 위 식은 negative cross entropy 가 된다. 이러한 이유로 크로스 엔트로피는 negative log likelihood 라고 불리기도 한다.
• 결국 Logistic Regression 에서 Log Likelihood 를 최대화 하는 것이 크로스 엔트로피를 최소화 하는 것과 확률적 관점에서 완벽하게 같은 의미가 되는 것이다.

• 위와 같은 과정으로 binary classification 문제에서 손실함수를 유도할 수 있다. 여기서의 크로스 엔트로피는 binary cross entropy(BCE) 라고 불린다.

  \[\text{Loss} = - \sum _{n=1}^{N}{t_n \log(\sigma (w^T x)) + (1-t_n) \log(1 - \sigma (w^T x))}\]
• K-class classification 일 때는 사후확률을 softmax function 으로 구할 수 있었다.

• 이 때는 $y$ 가 3 개 이상의 discrete class 를 가지므로 Category Distribution 을 따른다고 볼 수 있다.

  \[\text{Cat}(x;\mu) = \mu^{x_1}_1\mu^{x_2}_2 \cdots \mu^{x_K}_K = \prod^N_{i=1}\prod^K_{k=1}\mu^{x_{i,k}}_k\]
• 이 식에서 $x$ 는 $k$ 개의 원소를 가지는 One-hot vector 이고, $N$ 번의 반복시행을 했다.

• 이 또한 마찬가지로 MLE 를 취하여 log likelihood 를 최대화 한다면, 아래의 크로스 엔트로피에 - 를 취한 것과 동일한 식을 얻을 수 있다.

  \[\text{Log Likelihood} = \sum^d_{k=1}\left(\sum^n_{i=1}x_{i,k}\right)\log \mu_k = \sum^d_{k=1}n_k\log \mu_k\]
• 자세한 것은 이 포스트에 정리한 내용을 참고하자.

KL-div 와 log likelihood

• 만약 실제 데이터 분포 $P$ 와 우리가 설계하는 모델 $Q$ 를 가지고 $\mathbb{KL}(P \Vert Q)$ 를 최소화 하는 것은 log likelihood 를 최대화 하는 것과 같다.

  \[\begin{aligned} \mathbb{KL}(P \Vert Q) &= \mathbb{E}_{x \sim P(X)}\left[ \log\frac{P(X)}{Q(X)}\right] = \mathbb{E}_{x \sim P(X)}[\log P(X) - \log Q(X)] \\ &= \mathbb{E}_{x \sim P(X)}[\log P(X)] - \mathbb{E}_{x \sim P(X)}[\log Q(X)] \\ &= \color{blue}{-H[P(X)]} + \color{red}{H[P(X), Q(X)]} \end{aligned}\]
• 위 식에서 파란 부분은 엔트로피이고, 빨간 부분은 크로스 엔트로피다.
• 이 때 엔트로피는 $Q(X)$ 를 학습하는 것과는 무관하므로 고정값으로 두면, 실제 모델을 학습 할 때 영향을 끼치는 것은 크로스 엔트로피다.

• 위 크로스 엔트로피에 대수의 법칙(Law of Large Numbers) 를 적용하면 아래와 같이 적을 수 있다.

  \[\text{Cross Entropy} \; : \; - \mathbb{E}_{x \sim P(X)}[\log Q(X)] = \color{red}{-\frac{1}{N}\sum^N_i P(X) \log Q(X)}\]
• 위 크로스 엔트로피는 앞서 살펴본 negative log likelihood와 같다.
• 두 분포 사이의 거리를 최소화 하는 것은 결국, 크로스 엔트로피를 최소화 하여 $P(X)$ 와 $Q(X)$ 의 분포 차이를 최소화 하는 것이다. 따라서 크로스 엔트로피를 minimize 하는 것이 log likelihood 를 maximize 하는 것과 같다.
• 또한 확률분포 $P, Q$ 에 대한 크로스 엔트로피는 $H(P) + \mathbb{KL}(P \Vert Q)$ 이고, $H(P)$ 는 True Distribution 으로 모델의 parameter 값에 대해 변화가 없는 상수다.
• 따라서 크로스 엔트로피를 minimize 하는 것은 KL-div 를 minimize 하는 것이고, KL-div 를 minimize 하는 것 또한 결국 log likelihood 를 maximize 하는 것과 같다.
• 즉, 모델의 예측 분포($Q$)를 실제 분포($P$)에 근사시켜 두 분포 사이의 거리(KL-div)를 줄이는 것은 크로스 엔트로피를 손실함수로 최소화하면서 가능하고, 이는 Classification 문제에서 MLE 를 취해 주어진 데이터를 모델이 가장 잘 설명할 수 있는 parameter 를 찾는 것과 같다.

convex

• 그렇다면 이제 손실함수가 convex 하다는 것을 증명해보자.
• 손실함수가 convex 하게 되면, unique 한 solution 이 존재하게 되고, 경사하강법을 통해 쉽게 해를 구할 수 있기 때문이다.
• 우리는 구하고자 하는 parameter $w$ 에 대해 손실함수를 미분하므로, 손실함수가 convex 한지 non-convex 한지 알기 위해서는 Hessian 행렬을 통해 알 수 있다.
• Hessian 이 Positive Definite 하게 되면 일반적인 2차 함수($ax^2 + bx + c$)에서 $a > 0$ 과 같은 의미가 되어 convex 함이 보장된다고 한다.

• 그리고 Hessian 이 Positive Definite 한 것은 아래와 같을 때이다.

  \[x^THx > 0\]

• 우리가 위에서 구한 logistic regression 의 손실함수를 다시 보자.

  \[Loss = - \sum _{n=1}^{N}{t_n log(\sigma (w^T x)) + (1-t_n) log(1 - \sigma (w^T x))}\]

• 위 손실함수의 Hessian 을 구하면 다음과 같다.

  \[\sum _{n=1}^{N}{y_n (1-y_n) x_n {x_n}^T}\]
• 위 식에서 $x$ 는 vector 이고, $y$ 는 Logistic Function 의 Output 으로서 0 과 1 사이의 값을 가지므로, Positive Definite 가 되어 Convex 를 보장하게 된다.
• 즉 Cross Entropy 가 손실함수로서 손색이 없다는 뜻이다!

MSE 와 Cross Entropy

• 마지막으로 왜 분류 문제에서는 손실함수로 MSE 가 아니라 크로스 엔트로피를 사용하는지 알아보자.
• logistic regression 은 위에서 살펴봤듯 linear regression 에 단순히 Sigmoid 를 취한 것인데 왜 손실함수가 달라질까?
• 구체적으로, MSE 를 분류 문제에 적용하면 gradient vanishing 문제를 야기할 수 있고, 이는 학습을 방해한다.

  • Sigmoid 의 미분은 아래와 같다.

    \[\sigma^\prime(x) = \sigma(x)(1-\sigma(x))\]
  • Simgoid 는 0 에서 1 사이의 값이고, 위와 같이 역전파 과정에서 미분하면 Sigmoid 가 또 나오게 된다. 이러한 특성 때문에 학습 과정에서 gradient vanishing 이 발생할 수 있다.

  • 이는 Sigmoid 의 그래프를 떠올려보면 알 수 있다. 입력값이 매우 크거나 작아 Sigmoid 의 출력이 0 이나 1 에 가까워지면 미분값(기울기)은 거의 0 에 수렴하게 된다.

    

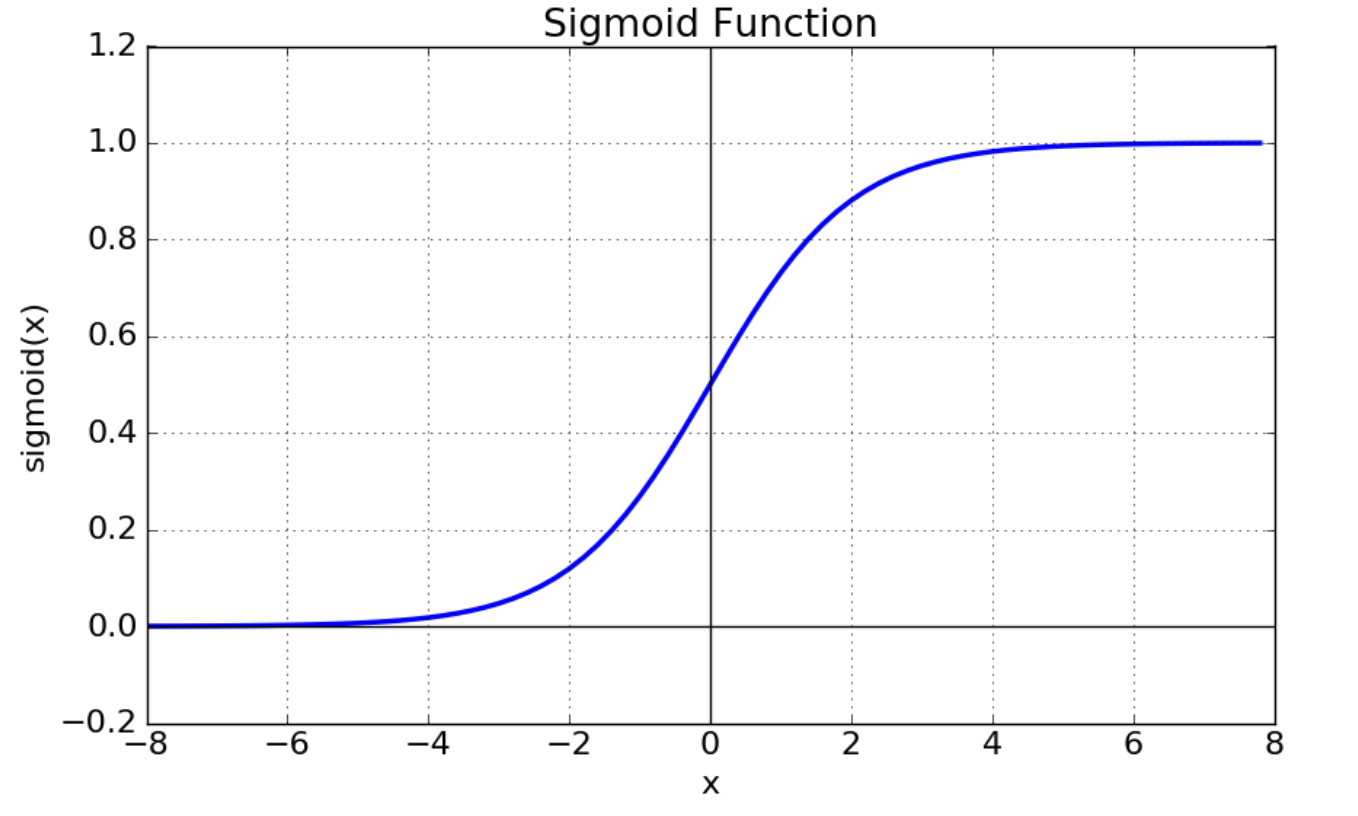
  • 손실함수로 Simgoid 와 MSE 를 함께 사용했을 때, 연쇄법칙을 사용하여 기울기를 구해보면 아래와 같다. $z$ 는 선형변환을 거친 후의 결과값($\mathbf{W}\mathbf{x} + \mathbf{b}$)을 뜻한다.

    \[\frac{1}{n}\sum_i -2(y_i - \sigma(z_i))\sigma^\prime(z_i)\]
  • 이처럼 손실함수의 미분이 Sigmoid 의 특성에 영향을 많이 받는다.
  • 즉 예측값 $\sigma(z)$ 가 0 또는 1 에 가까운 경우 기울기가 매우 작아지기 때문에 gradient vanishing 문제가 발생할 수 있다.

  • 그러나 크로스 엔트로피와 Sigmoid 를 함께 썼을 때는 아래와 같이 기울기가 구해진다.

    \[\frac{1}{n}\sum_i (\sigma(z) - y_i)\]
  • 즉 크로스 엔트로피와 Sigmoid 를 함께 사용하면 미분 결과에 Sigmoid 의 미분값이 곱해지지 않는다.
  • 따라서 Sigmoid 가 특정 범위에서 기울기가 0 에 수렴하는 특징을 가졌음에도 불구하고 전 범위에서 gradient vanishing 현상을 방지할 수 있게 된다.
• 정리하면, Sigmoid 와 함께 쓰였을 때 MSE 가 제공하는 gradient 는 충분한 학습을 이끌어내지 못한다. 이 문제는 특히 예측값이 0 또는 1 에 가까울 때 더 두드러진다.
• 또한 크로스 엔트로피는 확률적 해석을 기반으로 하여 모델이 예측한 확률 분포와 실제 확률 분포 간의 차이를 직접적으로 측정하며, Sigmoid 와 결합할 때 convex 한 손실함수를 만들어낸다.
• 그러나 logistic regression 에서 Sigmoid 를 사용하게 되면 MSE loss 가 non-convex 해진다.
  • 여기서 증명은 하지 않지만, 실제로 손실함수를 편미분 해보면 Hessian 행렬이 굉장히 복잡해지고, positive definite 하지 않다는 것이 증명된다.
• 즉, MSE 는 logistic regression 에서는 비효율적이며, 크로스 엔트로피가 더 적합한 손실함수다. 이는 Softmax regression 에서도 마찬가지다.

정리

• MLE, 크로스 엔트로피, KL-div 에 대해 최종적으로 정리해보자.
• MSE 와 크로스 엔트로피는 사실 가정한 분포가 달라서 다르게 보이는 수식이다.
• MSE 는 Gaussian 분포에서, 크로스 엔트로피는 Bernoulli 분포에서 MLE 를 풀 경우 자연스레 나오는 수식들이다.
• 이 두 수식 모두 고정된 관측치에서 Likelihood 를 최대화하는 parameter 를 찾는 과정(MLE)으로 loss function 이 된다.
• MLE 를 하는 것은 KL-div 를 최소화하는 것과 동일하다.
• 분류 문제에서 크로스 엔트로피가 loss function 으로 특히 많이 사용하는데 그 이유는 다음과 같다.
  • MSE 는 Sigmoid 나 Softmax 를 썼을 때 non convex 해진다.
  • 크로스 엔트로피는 Sigmoid 나 Softmax 와 잘 작동하며, convex 한 손실 함수가 되기 때문에 최적화에 유리하다.
  • 분류 문제의 경우 정답 label 을 one-hot encoding 방식으로 사용하여 정답만 1 이고 나머지는 0 이 된다. 이는 정보량 관점에서 엔트로피가 0 이 된다.
  • 따라서 KL-div 식에서 엔트로피가 사라지고 크로스 엔트로피만 남아, 분류 문제에서 KL-div 와 크로스 엔트로피가 동일한 식이 될 수 있는 특수한 해석이 가능하다.

Reference

• https://gaussian37.github.io/ml-concept-basic_information_theory/
• https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html
• https://www.postype.com/@theeluwin/post/6080524

맨 위로 이동 ↑