[Loss] MSE, MAE, Huber

오차 최소화 관점

• 여기서 손실함수 $J(\theta)$ 는 오차 $\epsilon$ 의 크기를 나타내는 함수로 정의된다.
• 어떤 함수로 오차의 크기를 표현하느냐에 따라 성질이 달라진다.

Norm

• Norm 은 벡터의 크기(magnitude) 또는 길이(length)를 측정하는 방법을 의미한다.
• Norm 은 거리 함수(distance function)로도 사용 가능하다. 두 점 사이의 거리를 계산할 때 두 점의 차이 벡터를 구한 후 Norm 을 계산할 수 있다.
• 벡터의 길이를 구하는 Norm 으로는 $L_1$ Norm, $L_2$ Norm, $p$ Norm 등이 있다.
• $p$ Norm 의 식으로 정의된다. 아래의 공식은 원점과 $x$ 벡터 상의 거리를 구하는 공식이다.

  • $p$ 의 값에 따라 Norm 의 종류가 달라진다.

    \[\Vert x \Vert_p = \left( \sum^n_{i=0} \vert x_i \vert^p \right)^{\frac{1}{p}}, \quad p \leq 1\]

  • $p$ 가 1 일 때 $L1$ Norm 이 되며, 벡터 $x$ 의 각 요소에 절대값을 취해서 합산한 값이다.

    \[\Vert x \Vert_1 = \sum^n_{i=0} \vert x_i \vert\]

  • $p$ 가 2 일 때 $L2$ Norm 이 되며, 벡터 $x$ 의 각 요소를 제곱한 후 합산하여 제곱근을 취한 값이다.

    \[\Vert x \Vert_2 = \left( \sum^n_{i=0} \vert x_i \vert^2 \right)^{\frac{1}{2}}\]
• 거리 척도의 관점에서 $L1$ Norm 은 Manhattan 거리에 해당한다. 두 데이터 간 절대값 거리다.
• $L2$ Nrom 은 Euclidean 거리에 해당한다. 두 데이터 간 직선거리이자 가장 짧은 거리다.
• $p$ Norm 은 Minkowski 거리라고 하며 Euclidiean 거리와 Manhattan 거리를 일반화한 거리다.
  • $p$ 가 1 일 경우 Manhattan, 2 일 경우 Euclidiean, $\infty$ 일 경우 두 벡터값 간 가장 큰 차이를 나타내는 Chebyshev 거리와 동일하게 된다.

• $L1$ Norm 과 $L2$ Norm 의 차이는 다음과 같다.

  출처 : https://hwanii-with.tistory.com/58

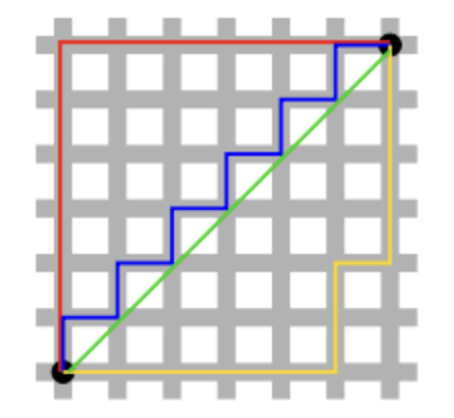
  • 검정색 두 점 사이의 $L1$ Norm 은 빨간색, 파란색, 노란색 선으로 표현될 수 있고, $L2$ Norm 은 오직 초록색 선으로만 표현될 수 있다.
  • 즉 $L1$ Norm 은 여러 가지 path 를 가지지만 $L2$ Norm 은 Unique shortest path 를 가진다.

  • 또한 공간상에 표현되는 기하학적 성질이 달라진다.

    

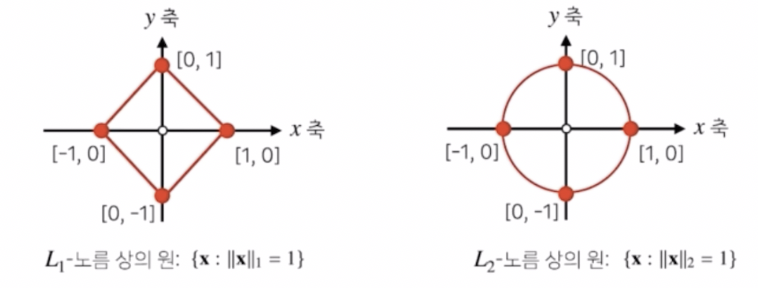
  • 성질이 달라진 기하세계에서 학습을 진행하게 되면 다른 성질들이 성립하게 된다. 이렇게 다른 성질들을 이용해서 기계학습에서 다양한 종류의 학습 방법이나 정규화 방법들을 사용할 때 응용할 수 있다.
  • 예를 들어 $L1$ Norm 은 Robust 한 학습과 Lasso 회귀에서 사용되고, $L2$ Norm 은 Laplace 근사, Ridge 회귀에서 사용된다.
• 또한 두 Norm 모두 Regularization 으로 모델 학습에서 패널티를 줄 수 있다. 자세한 것은 Optimization 카테고리 내 Regularization 포스트에서 정리할 예정이니 간단하게만 정리해보자.
  • 손실함수에 $L1$ Norm 을 더해 패널티를 주면, $w$ 가 양수인지 음수인지에 따라 미분했을 때 일정한 값 1 또는 -1 이 나온다. 이를 경사하강법(GD)에 따라 $w$ 에 빼주면 큰 $w$ 지속적으로 감소하고 작은 $w$ 는 지속적으로 증가하여 $w$ 가 0 이 되는 지점이 생기게 된다. 이를 통해 feature selection 의 효과를 얻을 수 있다.
  • $L2$ Norm 으로 패널티를 주면, $w$ 값이 클수록 더 큰 패널티를 주고, 작을수록 더 작은 패널티를 준다. $w$ 의 값이 0 이 되지는 않으나 $w$ 를 커지지 않게 강제하고 모델이 만드는 함수를 최대한 부드러운 함수로 만드는 효과를 얻을 수 있다.
• 이제 딥러닝 모델 관점에서 보면, 모델의 예측과 실제값의 차이를 오차 $\epsilon$ 으로 둘 수 있다. 두 값의 차이를 $L1$ Norm 으로 하는지 $L2$ Norm 으로 하는지에 따라 MAE(Mean Absolute error), MSE(Mean Squared Error) 라고 부른다.

MAE

• MAE 는 $N$ 개의 데이터에 대해 오차의 $L1$ Norm 의 평균으로 정의한다.

• 즉 각각의 실제값($y_i$)과 예측값($\hat{y_i}$) 간 차이의 절대값을 구한 후 평균을 구한 것이다.

  \[\text{MAE} = \frac{1}{n}\sum^n_{i=1}\vert y_i - \hat{y_i} \vert\]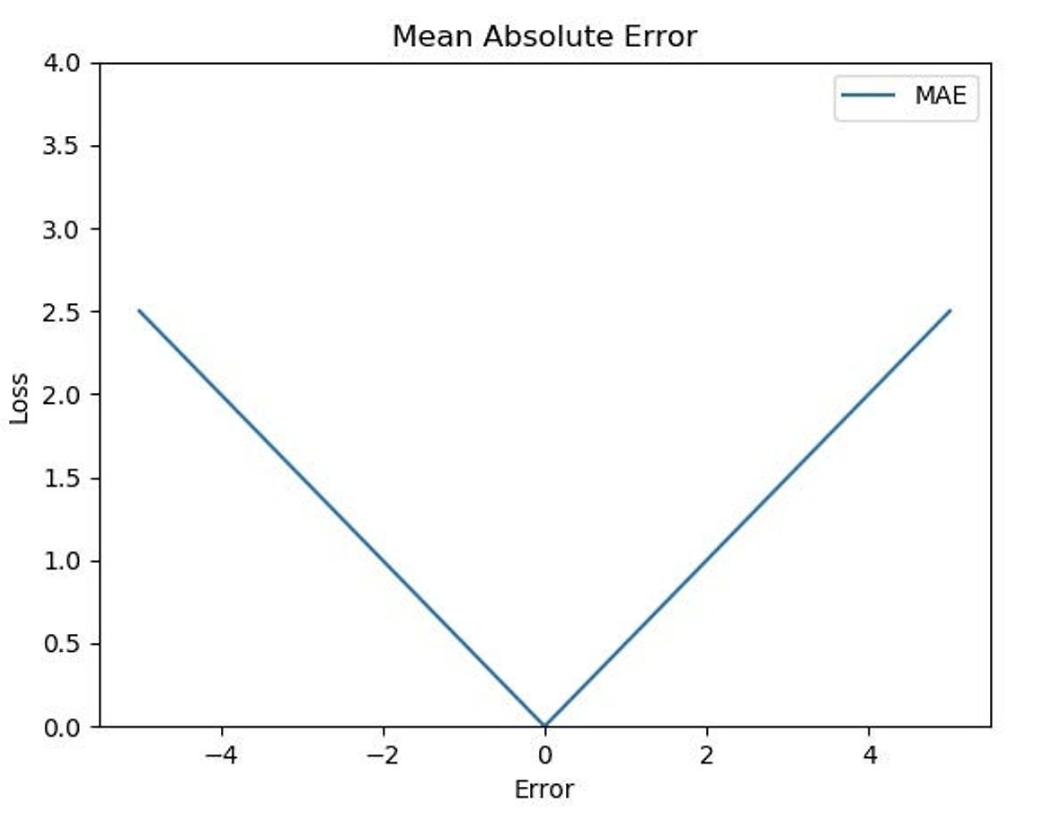

  출처: https://excelsior-cjh.tistory.com/198

• MAE 는 $L1$ Norm 을 기반으로 한 손실함수며, $L1$ loss 라고도 불린다.
• 오차를 절대값으로 계산하기 때문에, 모델이 예측을 타깃 데이터의 중앙값으로 끌어가는 방향으로 학습된다.
• 즉, MAE 는 예측값이 중앙값에 가까워질수록 낮아지기 때문에, MAE 를 최소화하는 방향으로 학습하는 과정에서 모델이 타깃 데이터의 중앙값을 예측하는 경향이 있다.
• 또한 MAE 는 Loss 를 계산하기 간단한 구조로 계산 비용이 높지 않고, 오차가 커지더라도 손실이 선형적으로 증가하기 때문에 이상치에 덜 민감하다.
• 하지만 절대값을 쓰기 때문에 절대값 특성상 미분이 불가능한 지점이 존재한다. 따라서 구간별로 미분을 처리해야 한다.
  • 이러한 미분 불가능한 지점은 Sub-gradient 와 같은 개념을 사용하여 목적함수를 최소화할 수 있다.
  • Sub-gradient 와 관련된 정리는 이 글을 참고하자.
  • 실제로 예측값이 정확히 실제값과 일치하는 경우는 드물기 때문에 자주 발생하지는 않는다.
• 위 그래프를 보면 학습에서 역전파 시 미분값이 일정하다. 즉 이동거리가 일정하여 가중치 업데이트가 일정하게 이루어지기 때문에, 최적값으로 수렴하는 데 오래 걸릴 수 있다.

MSE

• MSE 는 $N$ 개의 데이터에 대해 오차의 $L2$ Norm 의 제곱의 평균으로 정의된다.

• 즉 각각의 실제값($y_i$)과 예측값($\hat{y_i}$) 간 차이에 대해 제곱을 한 후 평균을 구한 것이다.

  \[\text{MAE} = \frac{1}{n}\sum^n_{i=1}(y_i - \hat{y_i})^2\]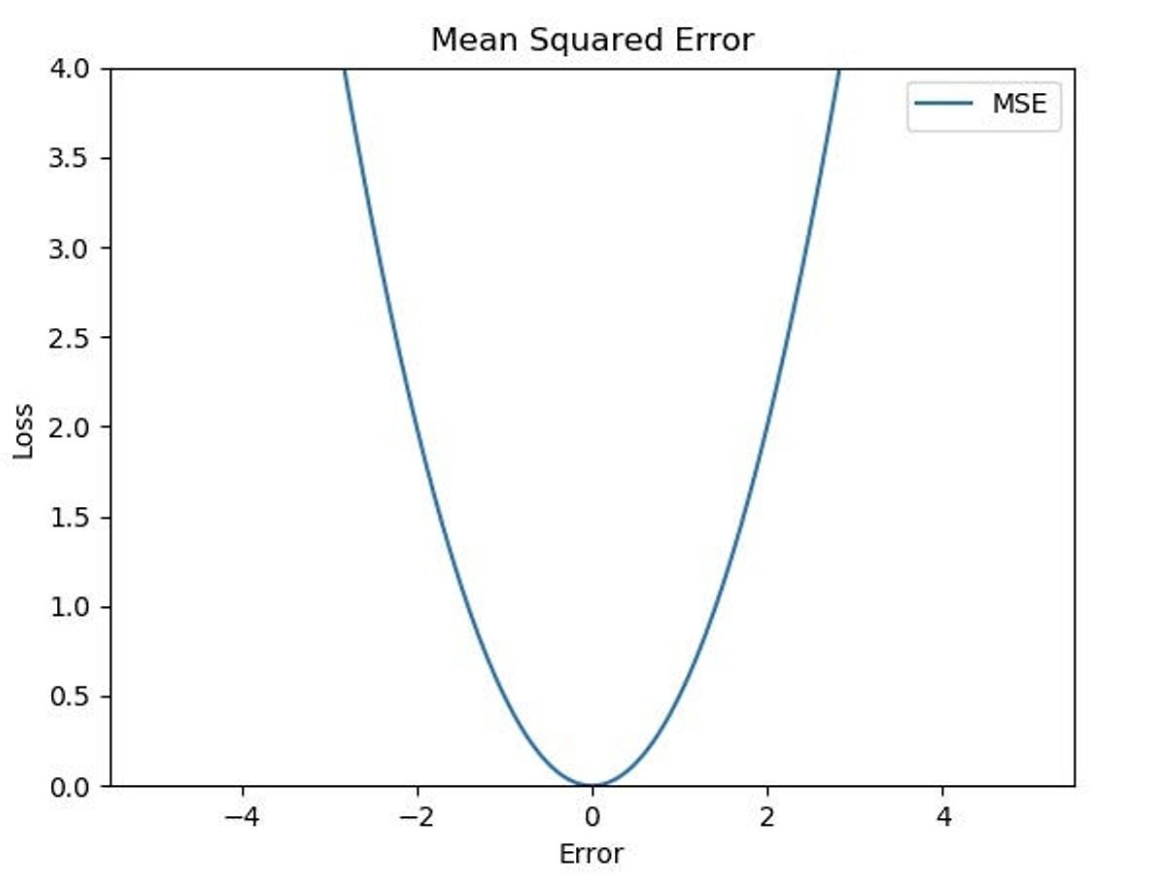

  출처: https://excelsior-cjh.tistory.com/198

• MSE 는 $L2$ Norm 을 기반으로 한 손실함수며, $L2$ loss 라고도 불린다.
• MSE 는 모델이 타깃 값의 평균을 예측하도록 유도하는 경향이 있다. 이는 MSE 를 최소화하는 예측값이 실제 데이터의 평균값과 일치하기 때문이다.
  • MSE 를 미분해서 최소화하는 점, 즉 0 이 되는 점을 찾으면 예측값이 실제값의 평균인 경우 MSE 가 최소화된다는 것을 알 수 있다.
• 또한 MSE 가 분산과 동일한 구조를 가지는 것을 확인할 수 있다.

  • 분산은 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 통계치로서, 아래와 같이 데이터 포인트와 평균의 차이를 제곱한 후 형균을 계산한다.

    \[\text{Var}(y) = \frac{1}{n}\sum^n_{i=1}(y_i - \bar{y})^2\]

  • 즉 MSE 는 예측값이 실제값으로부터 얼마나 퍼져있는지를 나타내는 지표라고 할 수 있다.

• 제곱항을 통해서 오차의 평균이 0 이 되는 것을 방지한다. 또한 작은 오차의 경우 MSE 의 기울기가 감소하므로, 최소값에 효율적으로 수렴할 수 있다.
• 위 식에서 알 수 있듯이 MSE 는 오차의 제곱에 비례하기 때문에 오차가 큰 값에 대해 상대적으로 더 높은 패널티를 부여한다.
  • 즉 오차를 제곱하기 때문에, 오차의 절대값이 큰 경우 값이 기하급수적으로 커지게 된다.
  • 이로 인해 학습과정에서 역전파 시 exploding gradient 가 발생할 수 있다.
  • exploding gradient 현상은 네트워크의 특정 층에서 기울기(gradient)의 값이 매우 커지면서, 역전파(backpropagation) 과정에서 이 기울기가 계속해서 곱해져 다음 층으로 전파될 때 기울기가 기하급수적으로 증가하는 상황이다.
  • 경사하강법(GD)에서는 손실함수의 기울기를 따라 가중치를 업데이트 하는데, exploding gradient 가 발생하면 가중치의 업데이트 폭이 과도하게 커지면서 최적화 과정이 불안정해진다.
• 또한 이상치(Outlier)에 민감하게 반응하여 학습에 큰 영향을 미칠 수 있다. 즉 이상치로 인한 큰 오차는 제곱에 의해 더 커지게 되므로 학습이 왜곡될 수 있다.

확률 관점에서의 MSE

• 이 포스트에서 정리했듯, 최대우도추정법(MLE)으로 딥러닝에서 사용하는 대부분의 손실함수를 유도할 수 있다.
• 딥러닝에서 구하고자 하는 모델의 파라미터는 학습과정 동안 지속적으로 업데이트 된다. 이 때 파라미터가 주어진 데이터를 얼마나 잘 설명하는지를 따져 업데이트 할 정도를 정하게 된다.
• 우리는 “실제값($y_i$)이 예측값($\hat{y_i}$)을 평균으로 하고 특정값 $\sigma$ 를 표준편차로 하는 gaussian distribution 을 따른다.” 고 가정해볼 수 있다. 왜냐하면 정규분포는 평균에서 가장 값이 높기 때문이다.
  • 전통적인 머신러닝에서의 선형회귀 함수 $y_i = w^Tx_i + \epsilon_i$ 에서 $\epsilon$ 은 평균이 0 인 정규분포를 따른다고 가정한다.
  • 참고로 Gaussian 분포에서 $\sigma$ 는 데이터의 분산을 나타낸다. 만약 $\sigma$ 를 학습 가능한 파라미터로 설정한다면, 모델은 데이터의 불확실성까지 학습하게 된다. 이는 베이지안 딥러닝에서 자주 사용하는 방법으로, 데이터의 불확실성까지 고려한 예측을 가능하게 한다.
• 그러면 모델은 “파라미터($w$)가 주어졌을 때 데이터에 대한 예측값($wx + b$)이 실제값일 확률이 가장 높은 모델” 이어야 한다. 즉 $P(\mathcal{D}\vert w)$ 가 최대가 되는 모델이다.
  • 이렇게 보면, MSE 가 타깃 값의 평균을 예측하도록 유도하는 경향이 있는 것을 이해할 수 있다.
• $P(\mathcal{D}\vert w)$ 는 주어진 데이터가 모델에 의해 생성될 확률을 나타내는 Likelihood 다. Likelihood 는 특정한 파라미터로 정의된 모델의 분포가 데이터에 대해 얼마나 잘 들어맞는지에 대한 통계적인 정의다.
• 이 Likelihood 가 최대화가 되는 지점이 주어진 데이터를 가장 잘 설명하는 지점일 것이고, 우리는 경사하강법을 이용해서 최적화를 진행하기 때문에 부호를 반대로 해서 minimize 하도록 한다. 이 때 계산의 효율성과 편리함을 위해 log 를 취한 negative log likelihood(NLL) 를 사용한다.

• 즉 아래의 수식을 전개할 수 있다.

  \[\begin{aligned} \text{likelihood} &= p(D \vert w) = \prod^N_{i=1}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(t_i-y(x_i \vert w))^2}{2\sigma^2}} \\ \log \; \text{likelihood} &= \log(p(D \vert w)) = \sum^N_{i=1}\{-\log(\sqrt{2\pi} \sigma)- \frac{(t_i - y(x_i \vert w))^2}{2 \sigma^2}\} \end{aligned}\]

• 위 식에서 $\sigma$ 와 $\pi$ 는 상수 값이다. 그렇기 때문에 log likelihood 를 최대화시키는 $w$ 에 영향을 주지 않는다. 그래서 관련된 term 들을 전부 제거한 다음, 앞의 부호를 바꿔주어 maximize 대신 minimize 하기로 하면 다음 식이 남게 된다.

  \[\sum^N_{i=1}(t_i - y(x_i \vert w))^2\]
• 많이 본 식이다! 예측값($y(x_i \vert w)$)과 실제값($t_i$)의 차이의 제곱, 즉 $L2$ Loss 다.
• 딥러닝에서 regression 시에 일반적으로 가장 많이 쓰는 Loss 함수가 튀어나왔다. 이렇게 MLE 를 이용하면 regression 에서 $L2$ Loss 를 쓰는 이유를 증명해 낼 수 있다.
• 반대로, 우리가 딥러닝에서 $L2$ Loss 를 이용한다는 것은 주어진 데이터로부터 얻은 Likelihood 를 최대화시키겠다는 뜻으로 해석할 수 있다. $L2$ Loss 를 최소화 시키는 일은 Likelihood 를 최대화 시키는 일인 것이다.

• 만약 실제값이 Laplace distribution 을 따른다고 가정하면, MLE 를 통해 $L1$ loss 를 유도할 수 있다. 이는 $L1$ loss 가 이상치에 더 강건한 특성을 가지게 하는 이유를 설명해준다.

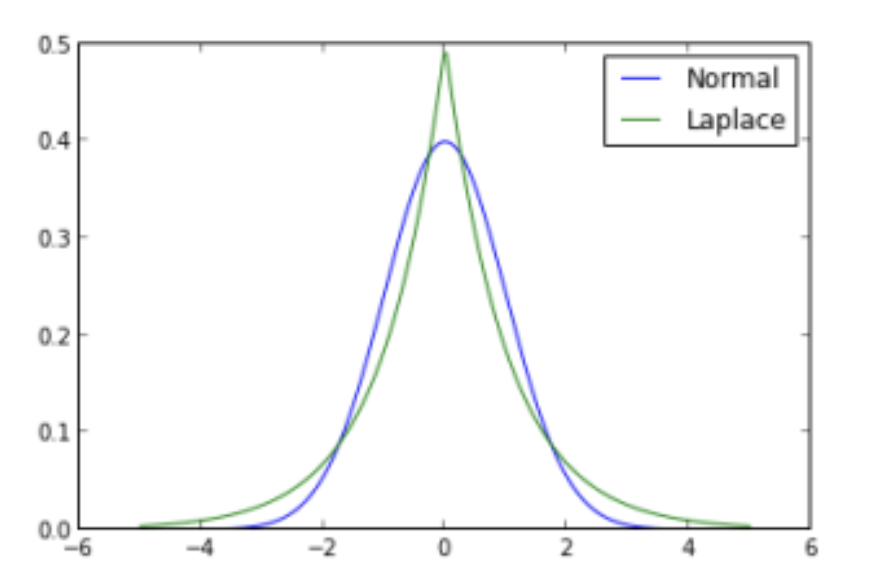  출처: https://hongl.tistory.com/228

  • 위 그림과 같이 정규분포는 평균으로부터 멀어지면 확률이 급격히 작아지는 light tail 분포이고 Laplace 분포는 평균으로부터 멀어도 확률이 어느 정도 높은 ‘heavy tail’ 분포를 띄게 된다.
  • 즉 Gaussian 분포는 평균으로부터 멀어질수록 확률이 급격히 줄어드는 반면, Laplace 분포는 평균에서 멀어져도 확률이 급격하게 줄어들지 않아 이상치에 대한 영향을 덜 받는다.
  • 이상치가 존재할 경우 Gaussian 분포로부터 유도된 $L2$ loss 는 오차의 제곱만큼 페널티를 가하기 때문에 이상치에 대해 영향을 많이 받는다. 이에 반해 Laplace 분포나 Student-t 분포 같은 heavy tail 분포는 이상치에 대해서 이미 어느정도 높은 likelihood 를 부여하기 때문에 이상치의 영향력이 적어진다.

• 참고로 분류 문제에서는 bernoulli distribution 을 이용하면 비슷한 방법으로 Cross Entropy Error 를 유도할 수 있다.

  \[\text{Cross Entropy Loss} = -\sum^N_{i=1} [t_i \log(\hat{y_i}) + (1 - t_i) \log(1 - \hat{y_i})]\]
• 즉 Likelihood 함수를 어떻게 정의하느냐에 따라 목적함수가 달라진다.

Huber Loss & Smooth L1 Loss

• 일반적인 regression 은 예측값과 실제값 차이의 절댓값인 $L1$ loss 나 예측값과 실제값 차이의 제곱인 $L2$ loss 를 목적함수로 사용한다.
  • $L2$ loss 는 모든 구간에서 안정적으로 미분이 가능하지만 제곱항으로 인해 이상치에 민감하게 반응한다.
  • $L1$ loss 는 $L2$ loss 대비 이상치에 강건한 대신 미분이 불가능한 지점이 존재하고 평균 대신 중앙값(median)을 추정하는 만큼 부정확한 요소가 존재한다.
  • 따라서 $L1, L2$ loss 를 합친 Huber loss 와 Smooth L1 loss 가 제안되었다.
• 두 Loss 모두 특정 하이퍼파라미터를 두고, 그 하이퍼파라미터가 커지거나 작아질 때 손실함수가 $L1$ loss 와 $L2$ loss 사이에서 부드럽게 전환(smooth transition)된다. 즉 미분 가능한 방식으로 전환된다.

Huber Loss

• Huber Loss 는 MSE 와 MAE 를 반영한 손실함수다.
• 즉 $L1$ loss 와 $L2$ loss 의 장점을 취해 모든 지점에서 미분 가능하면서 outlier 에 영향을 덜 받는(robust) 형태를 가진다.

• 오차(예측값과 실제값의 차이)가 $\delta$ 보다 작으면 $L2$ loss, 클 경우에는 $L1$ loss 처럼 동작하게 된다.

  \[\text{Huber Loss} = \sum^N_{i=1} l_i \\ \text{Where} \; \; l_i = \begin{cases} \frac{1}{2}(y_i - \hat{y_i})^2, & \text{if} \; \vert y_i - \hat{y_i} \vert < \delta \\ \delta(\vert y_i - \hat{y_i} \vert - \frac{1}{2}\delta), & \text{otherwise} \end{cases}\]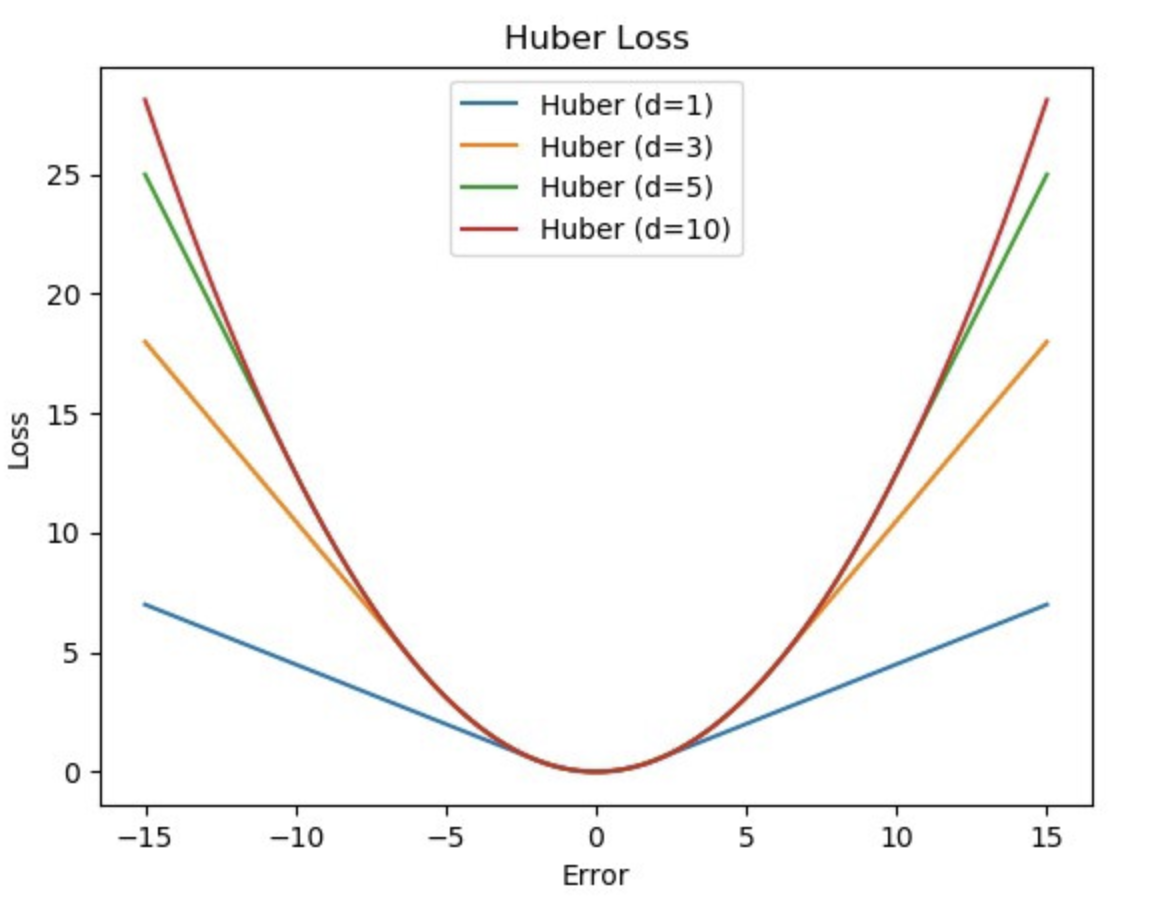

  출처: https://excelsior-cjh.tistory.com/198

• 위 수식을 직관적으로 해석해보면, 오차가 $\delta$ 보다 작을 때는 $L2$ loss 의 제곱항이 더 세밀하게 작은 오차를 반영하고, 오차가 $\delta$ 보다 커지면 $L1$ loss 로 전환되면서 큰 오차에 대해 덜 민감해진다고 볼 수 있다.
• 위 그림을 보면, 오차가 $-\delta$ 와 $\delta$ 사이에서는 $L2$ loss 와 유사하며 그 외 영역에서는 $L1$ loss 와 유사한 형태를 보인다.
• Huber Loss 는 하이퍼파라미터인 $\delta$ 를 통해서 loss 를 조절할 수 있다.
  • $\delta$ 는 $L2$ loss 에서 $L1$ loss 로 전환되는 임계점을 조절한다.
  • $\delta$ 값이 크면, 오차가 어느 정도 커질 때까지 $L2$ loss 처럼 동작하게 되어 이상치에 민감해진다.
  • $\delta$ 값이 작으면, 작은 오차에도 금방 $L1$ loss 로 전환되어 동작하기 때문에 이상치에 강건해진다.
• 또한 위 식을 보면 알 수 있듯 Huber Loss 에서 $\delta$ 는 오차가 클 때 적용되어 $L1$ loss 부분에 들어가 있다.
  • 즉 $\delta$ 는 오차로 미분하게 되었을 때 $L1$ loss 의 기울기를 조절하는 역할을 한다. 따라서 $L1$ loss 부분의 기울기가 $\delta$ 에 비례한다.
• $\delta$ 가 1 인 경우, Smooth $L1$ Loss 와 동일하다.

Smooth L1 Loss

• Smooth L1 Loss 또한 MSE 와 MAE 를 반영한 손실함수다.
• 이 또한 Huber Loss 처럼 $L1$ loss 와 $L2$ loss 의 장점을 취해 모든 지점에서 미분 가능하면서 outlier 에 영향을 덜 받는(robust) 형태를 가진다.
• 여기서는 하이퍼파라미터인 $\beta$ 를 가지고 loss 를 조절한다.

  • 마찬가지로 예측값과 실제값의 차이가 $\beta$ 보다 작으면 $L2$ loss, 클 경우에는 $L1$ loss 처럼 동작하게 된다.

    \[\text{Smooth L1 Loss} = \sum^N_{i=1} l_i \\ \text{Where} \; \; l_i = \begin{cases} \frac{1}{2}(y_i - \hat{y_i})^2 / \beta, & \text{if} \; \vert y_i - \hat{y_i} \vert < \beta \\ \vert y_i - \hat{y_i} \vert - \frac{1}{2}\beta, & \text{otherwise} \end{cases}\]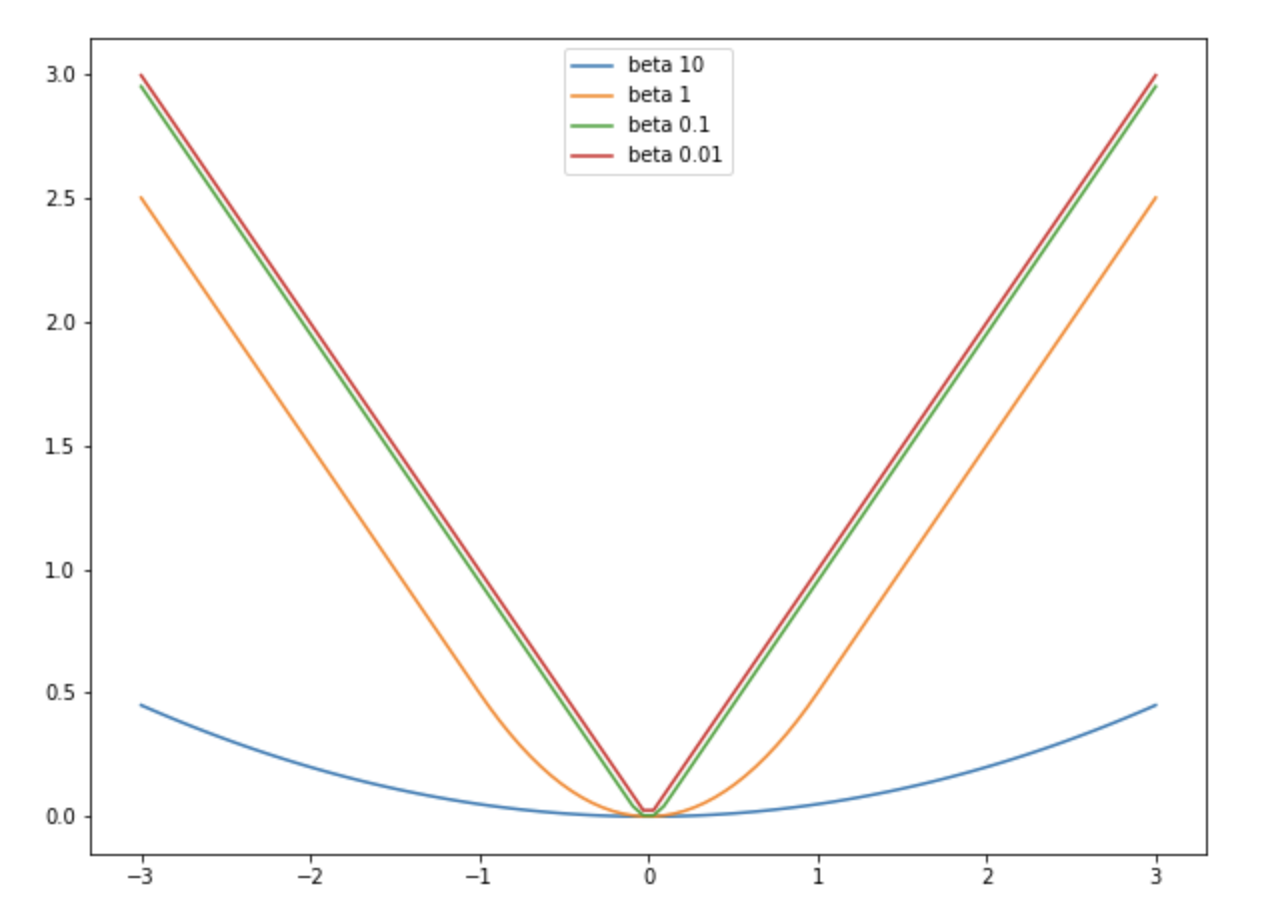

    출처: https://hongl.tistory.com/345

• $\beta$ 값이 커질수록 $L2$ loss 와 유사해지고, $\beta$ 값이 작아질수록 $L1$ loss 와 유사하게 동작한다.
  • 즉 $\beta$ 보다 작은 오차에서는 $L2$ loss 처럼, 큰 오차에서는 $L1$ loss 처럼 동작하는 것이다.
• 또한 $\beta$ 값에 상관없이 $L1$ loss 부분의 기울기가 1 로 일정하다. 즉 $\beta$ 는 $L1$ loss 의 기울기에 영향을 주지 않는다.
• 그러나 Huber loss 와 다르게 $\beta$ 가 $L2$ loss 부분에 붙어있다. 따라서 Smooth L1 loss 에서의 하이퍼파라미터 $\beta$ 는 $L2$ loss 부분에만 영향을 미친다.
  • 이는 Smooth L1 Loss 가 본질적으로 $L1$ loss 를 기반으로 하며, 오차가 작을 때만 $L2$ loss 로 부드럽게 전환되도록 설계되었기 때문이다.
• $\beta$ 가 0 이 되면 Smooth L1 loss 는 $L1$ loss 와 동일해진다.
  • 이는 Smooth L1 loss 의 이름이 뜻하는 것처럼 기본적으로는 $L1$ loss 이고 예측값과 실제값 차이가 매우 작은 부분에 대해서만 $L2$ loss 처럼 부드럽게 치환된 것이라 볼 수 있다.
• 마찬가지로 $\beta$ 가 1 인 경우, Huber Loss 와 동일하다.
  • Pytorch 의 F.smooth_l1_loss() 는 Huber Loss 를 이용하여 Loss 를 계산한다.

Reference

• https://excelsior-cjh.tistory.com/198
• https://hongl.tistory.com/228
• https://hongl.tistory.com/345

맨 위로 이동 ↑