[Loss] MLE, MAP

우리는 현실 세계의 문제를 풀 때 데이터로부터 decision policy 를 얻는다. 정해지지 않은 여러 개의 parameter 로 이루어진 함수를 모델링 한 후에, 이 모델이 주어진 데이터를 가장 잘 설명하도록 parameter 들을 구해낼 수 있다면 어떨까? (간단하지는 않지만)주어진 데이터가 현실 세계를 잘 대표할 수 있다면 모델링한 함수를 이용하여 새로운 데이터에 대한 예측의 성능이 매우 좋을 것이다. 이러한 방식을 이용하는 대표적인 알고리즘이 바로 딥러닝이다.

그러나 풀고자 하는 현실의 문제를 나타내는 함수(혹은 확률분포)를 명시적으로 알 수 없기 때문에, 딥러닝에서는 데이터를 가지고 학습을 통해 데이터를 가장 잘 설명할 수 있는 parameter 를 찾아 현실의 함수나 분포를 근사한다. 이 때 모델이 데이터에 대해 현재 예측을 얼마나 잘하고 있는지 알아야 학습 방향을 어느 방향으로, 얼마나 개선할지 판단할 수 있다. 이렇게 예측 값과 데이터 값의 차이에 대한 함수를 loss function 이라고 한다. 이 loss function 을 최소화함으로써 모델을 적절한 표현력을 갖추도록 학습시킬 수 있다.

딥러닝의 기본적인 loss function 들은 대부분 Maximum Likelihood Estimation(MLE) 과 Maximum A Posterior(MAP) 를 통해 유도된다. 또한 확률을 기반으로 하기 때문에 이 두 이론을 공부하고 나면 확률과 딥러닝 사이의 연결고리를 파악하는 데 큰 도움이 된다.

문제 정의

• regression 문제를 생각하자. regression 은 continuous 한 input $x$ 를 넣었을 때 나오는 output $y$ 가 실제 정답 $t$ 와 같도록 만드는 문제다. 즉 실제 output 이 어떻게 될 지 예측하는 모델이다.

• 예를 들면 키를 보고 몸무게를 예측하는 모델이 있다. 이 모델을 학습시키기 위해 $N$ 명의 사람들에 대하여 실제 키($x_i$)와 동일 인물의 실제 몸무게($t_i$)를 조사한 결과인 Dataset $D$ 를 가지고 있다.

  \[D = \{(x_1,t_1), (x_2, t_2), (x_3, t_3), \ldots, (x_N, t_N)\}\]
• 이제 parameter $w$ 를 갖고 키($x$)를 넣으면 예측된 몸무게($y$)가 나오는 함수 $y(x\vert w)$ 를 정의하여, 가능한 모든 키($x$)에 대하여 예측된 몸무게($y(x\vert w)$)가 실제 몸무게($t$)에 최대한 가깝게 나오도록 $w$ 를 정해줘야 한다.
• 여기서 $w$ 는 함수 $y(x\vert w)$ 가 갖는 parameter 로, 일차함수 $y = ax + b$ 의 예를 들면 $a$ 와 $b$ 같은 계수를 의미한다.
• parameter 는 하나의 값일 수도 있고 여러 개의 값일 수도 있으며, 벡터일 수도 있고 행렬일 수도 있다. 이러한 역할을 하는 parameter를 싸잡아서 $w$ 로 표현한 것이다.

• 이렇게 parameter 들을 잘 학습하여 완벽한 모델 $y(x\vert w)$ 를 얻었다고 해보자. 그렇다면 모든 가능한 키($x$)에 대하여 실제 몸무게($t$)를 알고 싶을 때 다음 식을 이용하면 된다.

  \[t = y(x\vert w)\]
• 그러나 항상 $t = y(x\vert w)$ 라고 말할 수는 없다. 즉 “실제 몸무게($t$)는 내가 예측한 몸무게($y$)와 정확히 일치한다.” 와 같이 언제나 정확한 값을 예측하는 것은 불가능하다. “실제 몸무게($t$)는 내가 예측한 몸무게($y$)일 확률이 가장 높지만, 아닐 수도 있다.” 라고 말하는 것이 현명할 것이다.
• 여기서 “아닐 수도 있다.” 의 의미는 예측 성능 때문이 아니라 데이터의 형태 때문이다.
• 예를 들어, 키가 175cm 인 사람 중에는 몸무게가 70kg 인 사람도 있지만, 몸무게가 69kg 인 사람도, 71kg 인 사람도 충분히 존재한다. 애초에 $x=175$ 라는 input 에 대해서 실제 몸무게($t$)를 100% 완벽하게 예측할 수 없다.
• 즉 우리가 예측하는 능력이 부족해서가 아니라, 근본적으로 발생하는 불확실성이라고 볼 수 있다.
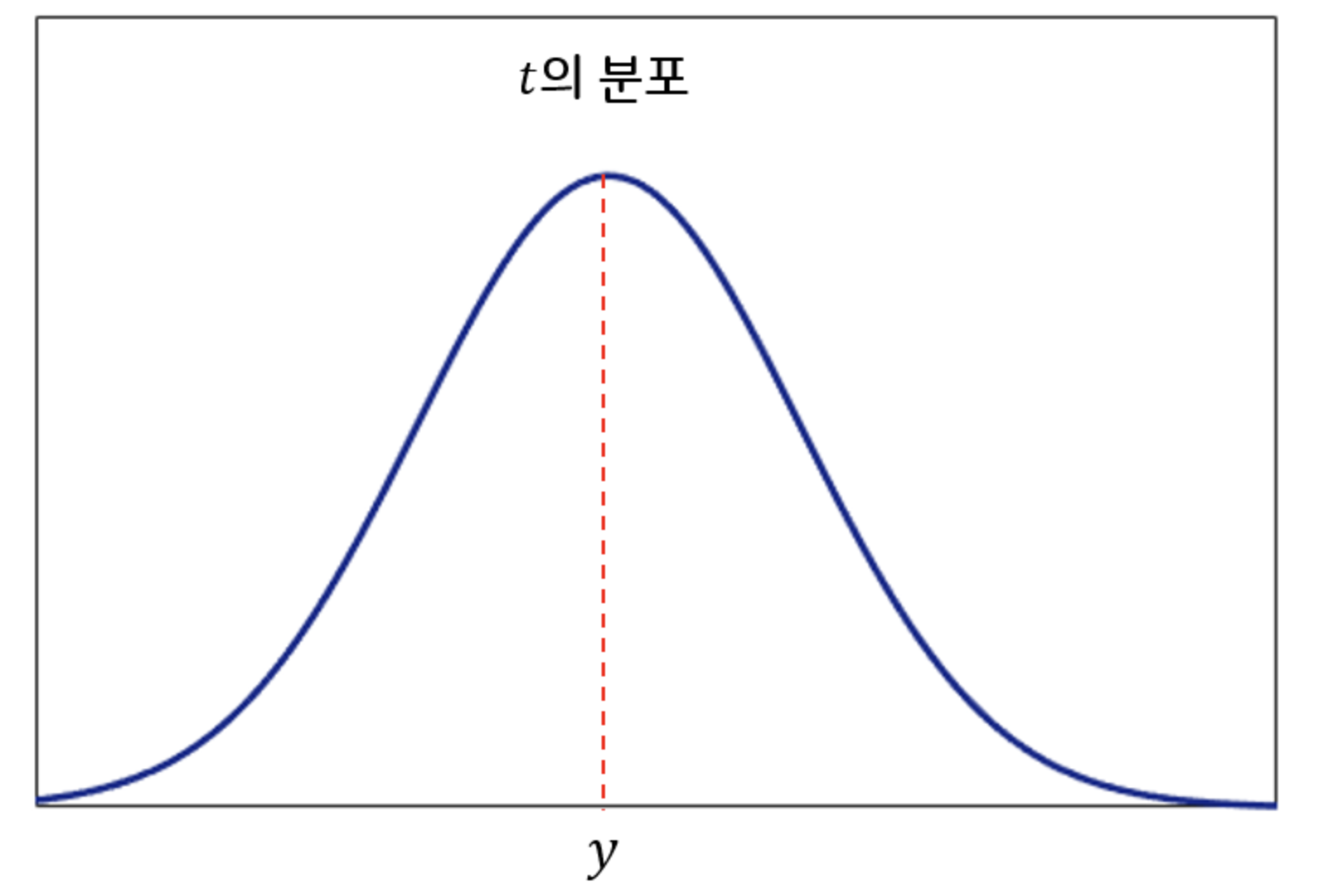
• 이 말을 조금 더 수학적인 표현을 섞어 하면 “실제 몸무게는($t$)는 우리가 모르기 때문에 random variable 인데, 아래 그림과 같이 내가 예측한 몸무게($y$)를 평균으로 하는 Gaussian 분포(정규분포)를 따른다고 볼 수 있다.” 이렇게 말하면 앞에서 한 말과 비슷한 의미를 전달할 수 있게 된다.

• Gaussian 분포는 평균에서 확률 밀도가 가장 높기 때문이다.

  

• 이를 조금 더 수학적인 표현을 이용해서 말하면 “실제 몸무게($t$)는 내가 예측한 몸무게($y$)를 평균으로 하고 특정 값 $\sigma$ 를 표준편차로 하는 gaussian distribution 을 따른다.” 고 할 수 있고, 다음과 같이 쓸 수 있다.

  \[t \sim N(y(x \vert w), \sigma^2) \\ \\ p(t\vert x, w, \sigma) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(t-y(x \vert w))^2}{2\sigma^2}}\]
• 여기서 $\sigma$ 는 무엇을 의미할까?
• 우리가 gaussian distribution 을 이용하는 이유는 예측을 100% 확신할 수 없기 때문이라고 했다. 그래서 위 그림과 같은 형태로 대답하게 된 것인데, 그림에서 distribution 의 폭이 작다는 것($\sigma$ 가 작다는 것)은 무엇을 의미할까?
• 바로 우리가 예측한 값에 더 확신한다는 뜻이다. 반대로 폭이 크다는 것($\sigma$ 가 크다는 것)은 그 만큼 우리가 예측한 값에 자신이 없다는 뜻이다.
• 즉 $\sigma$ 는 우리가 한 예측이 얼마나 불확실한지의 정도를 나타낸다. 하지만 앞에서도 말했듯이 $\sigma$ 는 우리의 예측 능력에 따른 변수가 아니다. 우리가 풀려는 문제의 특성에 따라 설정되는 값이다.
• 우리가 풀려는 문제가 각 $x$ 에 대해서 $t$ 값이 대부분 하나로 일정하게 나오는 문제라면 $\sigma$ 는 작을 것이고, 위에서 설명한 몸무게 예측 문제처럼 $x$ 가 같더라도 다양한 $t$ 가 나올 수 있는 문제라면 $\sigma$ 는 클 것이다.
• 따라서 $\sigma$ 는 우리가 문제의 특성을 파악하고 설정해주는 상수 값이다. 참고로 여기서는 이렇게 우리가 임의로 정해주게 되지만, 이후 중요하게 작용할 때가 오니 잘 기억해두자.

Maximum Likelihood Estimation

• 위 수식에서 $\sigma$ 와 $w$ 는 parameter 이므로 좌변의 notation 에서 생략할 수 있다. 그렇다면 $p(t\vert x)$ 가 의미하는 바가 무엇일까?

  \[p(t\vert x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(t-y(x \vert w))^2}{2\sigma^2}}\]
• 바로 input 인 키가 $x$ 일 때 실제 몸무게가 $t$ 일 확률(밀도)이다. 변수가 continuous 하기 때문에 확률 밀도라고 부르는 것이므로 편의상 확률이라고 하자.

• 이제 앞에서 학습을 위해 가지고 있던 데이터를 다시 보자.

  \[D = \{(x_1,t_1), (x_2, t_2), (x_3, t_3), \ldots, (x_N, t_N)\}\]
• $p(t\vert x)$ 의 의미는 키가 $x$ 일 때 실제 몸무게가 $t$ 일 확률이라고 했다. 그렇다면 데이터가 위와 같이 구성될 확률($p(D)$)은 어떻게 구할 수 있을까?
• 데이터가 위와 같이 구성될 확률은 다시 말하면 “키가 $x_1$ 일 때 실제 몸무게가 $t_1$ 이고, 키가 $x_2$ 일 때 실제 몸무게가 $t_2$ 이고, $\cdots$ , 키가 $x_N$ 일 때 실제 몸무게가 $t_N$ 일 확률”을 구하고 싶은 것이다.

• 이는 각 데이터가 독립이라고 할 때, 곱의 법칙을 통해 다음과 같이 구할 수 있다.

  \[p(D) = \prod^N_{i=1}p(t_i \vert x_i) = \prod^N_{i=1}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(t_i-y(x_i \vert w))^2}{2\sigma^2}}\]
• 그러나 $p(D)$ 값은 $w$ 에 따라 다르게 구해진다. 즉 “키가 $x_1$ 일 때 실제 몸무게가 $t_1$ 이고, 키가 $x_2$ 일 때 실제 몸무게가 $t_2$ 이고, $\cdots$ , 키가 $x_N$ 일 때 실제 몸무게가 $t_N$ 일 확률” 은 $w$ 에 따라 바뀔 수 있다.
• 그래서 $p(D)$ 보다는 $p(D \vert w)$ 라고 할 수 있다. 이 상황에서 어떤 $w$ 를 구해야 가장 잘 예측하는 모델이 될까? 몸무게를 가장 잘 예측하는 모델은 다음과 같아야 할 것이다.
  • “키가 $x_1$ 일 때는 실제 몸무게가 $t_1$ 일 확률이 가장 높다고 말하고, 키가 $x_2$ 일 때는 실제 몸무게가 $t_2$ 일 확률이 가장 높다고 말하고, $\cdots$ , 키가 $x_N$ 일 때는 실제 몸무게가 $t_N$ 일 확률이 가장 높다고 말하는 모델”
• 다시 말하면 $p(D \vert w)$ 가 가장 높다고 대답하는 모델, 즉 $p(D \vert w)$ 가 최대가 되는 모델이어야 한다.
• 결국 우리가 해야 할 일은 $p(D \vert w)$ 가 최대가 되는 $w$ 를 찾는 것이고, 여기서 $p(D \vert w)$ 가 바로 likelihood 기 때문에 이 방식의 이름이 Maximum Likelihood Estimation, MLE 다.

Prior, Likelihood, Posterior

• 베이즈 정리를 구성하는 3가지 확률이다.
• 이 Prior, Likelihood, Posterior 를 구분하기 위해서는 확률 또는 확률분포를 구하고자 하는 대상을 선택해야 한다.
• 베이즈 정리에 대해 정리했던 포스트에서는 그 대상이 농어($w_1$)인지 연어($w_2$)인지의 여부였다.
• 일반적인 MLE, MAP 를 포함하여 딥러닝까지 대부분의 머신러닝 알고리즘들이 구하고자 하는 대상은 바로 모델의 parameter인 $w$ 다.
• 구하고자 하는 대상 다음으로 중요한 것이 바로 주어진 대상이다. 이전에는 농어와 연어의 피부 밝기($x$)에 대한 정보가 주어졌다.
• 대부분의 머신러닝/딥러닝 알고리즘에서 주어진 대상은 당연히 데이터셋, 즉 $D$ 가 된다.
• 이 두 개념을 이용하여 Prior, Likelihood, Posterior 의 일반적인 의미를 파악해 보면 다음과 같다.
  • Posterior
    • $p(w \vert D)$
    • 데이터가 주어졌을 경우, 구하고자 하는 parameter 의 확률 분포다.
  • Likelihood
    • $p(D \vert w)$
    • 구하고자 하는 parameter 의 분포를 모르지만 안다고 가정하고, parameter 가 주어졌을 경우 데이터의 분포다.
    • $w$ 를 모르기 때문에 $w$ 에 대한 함수 형태로 나올 것이다.
  • Prior
    • $p(w)$
    • 주어진 대상들과 무관하게, 즉 데이터와 무관하게 상식을 통해 우리가 구하고자 하는 대상에 대해 이미 알고 있는 사전 정보다.
    • 연구자의 경험을 통해 정해주어야 한다.
• 이 사실들을 통해 Maximum Likelihood Estimation 과 Maximum A Posterior 의 이름의 뜻을 파악해볼 수 있을 것이다.

MLE 계산

• 이제 다시 Maximum Likelihood Estimation 으로 돌아가서 수식 전개를 해보자.

• Maximum Likelihood Estimation 에서 우리가 해야 할 일은 바로 다음 식을 최대로 하는 $w$ 를 찾는 일이다.

  \[\text{likelihood} = p(D \vert w) = \prod^N_{i=1}p(t_i \vert x_i) = \prod^N_{i=1}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(t_i-y(x_i \vert w))^2}{2\sigma^2}}\]
• 이런 문제에서 우리는 주로 $\log$ 를 취해 준다. 많은 이유가 있지만 대표적으로는 아래의 이유 때문이다.
  • log 함수의 경우 단조증가함수이기 때문에, likelihood 가 최대면 likelihood 의 $\log$ 값도 최대다. 따라서 $\log$ 를 취해줘도 문제가 발생하지 않는다.
  • Gaussian 이나 Bernoulli 같은 지수함수 형태로 표현되는 지수족(expoentail family) 확률분포의 경우 log 를 취하면 지수 항이 상쇄되어 다항식으로 변환되기 때문에 다루기 쉬워진다.
  • 복잡한 곱셈 연산을 덧셈 연산으로 바꿔주기 때문에 수식의 전개가 용이하다.

  • $N$ 개의 샘플에 대한 곱셈을 돗셈으로 바꾸면 underflow 를 방지할 수도 있다. 확률은 항상 1보다 작기 때문에 이를 $N$ 번 곱하면 underflow 가 심해진다. 이를 log 를 사용하여 합산 형태로 바꿔주어 방지할 수 있다.

    \[\log \; \text{likelihood} = \log(p(D \vert w)) = \sum^N_{i=1}\{-\log(\sqrt{2\pi} \sigma)- \frac{(t_i - y(x_i \vert w))^2}{2 \sigma^2}\}\]
• 이제 이 log likelihood 를 최대가 되게 하는 $w$ 를 찾아주면 된다.

• 위 식에서 $\sigma$ 와 $\pi$ 는 상수 값이다. 그렇기 때문에 log likelihood 를 최대화시키는 $w$ 에 영향을 주지 않는다. 그래서 관련된 term 들을 전부 제거한 다음, 앞의 부호를 바꿔주어 maximize 대신 minimize 하기로 하면 다음 식이 남게 된다.

  \[\sum^N_{i=1}(t_i - y(x_i \vert w))^2\]
• 많이 본 식이다! 예측값($y(x_i \vert w)$)과 실제값($t_i$)의 차이의 제곱, 즉 L2 Loss 다.
• 딥러닝에서 regression 시에 일반적으로 가장 많이 쓰는 Loss 함수가 튀어나왔다. 이렇게 MLE 를 이용하면 regression 에서 L2 Loss 를 쓰는 이유를 증명해 낼 수 있다.
• 반대로, 우리가 딥러닝에서 L2 Loss 를 이용한다는 것은 주어진 데이터로부터 얻은 Likelihood 를 최대화시키겠다는 뜻으로 해석할 수 있다.
• 이렇게 L2 Loss 를 최소화 시키는 일은 Likelihood 를 최대화 시키는 일인 것이다.
• 참고로 분류 문제에서는 bernoulli distribution 을 이용하면 비슷한 방법으로 Cross Entropy Error 를 유도할 수 있다.
• 이는 이 포스트에서 확률 관점에서의 Cross Entropy 에 정리한다.

Maximum A Posterior

• Maximum Likelihood Estimation 가 Likelihood 를 최대화시키는 작업이었다면, Maximum A Posterior 는 이름 그대로 Posterior 를 최대화시키는 작업이다.
• Likelihood 와 Posterior 의 차이는 Prior 의 유무다. Posterior 는 Likelihood 와 다르게 사전 지식인 Prior 가 포함되어 있다.
• 즉 구하고자 하는 대상을 철저히 데이터만을 이용해서 구하고 싶다면 MLE 를 이용하는 것이고, 데이터와 더불어 우리가 갖고 있는 사전 지식까지 반영하고 싶다면 MAP 를 이용하는 것이다.
• 그렇다면 Prior 를 반영해서 좋은 점은 무엇일까?
• 물론 우리가 매우 강력한 사전 지식을 갖고 있다면 $w$ 값을 구하는 데 있어서 매우 큰 도움이 될 것이다. 하지만 우리에게 별다른 사전 지식이 없더라도 Prior 를 반영하는 것은 좋은 경우가 많다.
• 대표적으로 output 을 우리가 원하는 대로 제어할 수 있다.
  • 예를 들어 모델링한 함수 $y(x \vert w)$ 가 키($x$)를 줬을 때 몸무게($t$)를 잘 맞추게만 하고 싶으면 MLE 를 써도 상관없다.
  • 그러나 잘 맞춤과 동시에 함수 $y(x \vert w)$ 의 parameter $w$ 의 절댓값이 작기를 원한다면, 즉 0 주변에 분포해 있기를 원한다면 $w$ 가 0 주변에 분포한다는 Prior 를 넣어 주어야 한다.
  • 이렇게 output 에 대한 특정 제약조건을 걸고 싶은 경우에 MAP 를 쓰는 것이 좋다.
• Posterior 를 Maximize 해야 하는 이유는 Likelihood 의 경우보다 단순하다. Posterior는 애초에 $w$ 의 확률 분포이기 때문에 $w$ 가 될 확률이 가장 높은 값으로 정해주는 것이다.

• 그렇다면 본격적으로 Posterior 를 구해서 Maximize 해보자. Posterior 는 데이터가 주어졌을 경우 구하고자 하는 parameter 의 확률 분포로, 다음과 같이 구할 수 있다.

  \[p(w \vert D) = \frac{p(D \vert w)p(w)}{\int p(D\vert w)p(w)\text{d}w}\]
• 분모가 $\int$ 로 주어진 이유는 $w$ 가 continuous 하기 때문이다.
• 이 때 $w$ 에 대해서 적분을 하고 있고 $D$ 는 주어진 값이기 때문에 결국 $\int p(D\vert w)p(w)\text{d}w$ 는 상수가 되어 $\eta$ 로 치환 가능하다.

• 위 식에서 $\eta = \frac{1}{\int p(D\vert w)p(w)\text{d}w}$ 로 치환하면 아래와 같은 식을 얻을 수 있다.

  \[p(w\vert D) = \eta p(D\vert w)p(w)\]
• 그러면 이제 $w$ 의 Prior $p(w)$ 를 정해줘야 하는데, $w$ 에 대한 특별한 사전지식은 갖고 있지 않은 상황이다.
• 따라서 나름대로의 제약조건을 걸어주도록 하자. 딥러닝에서 오버피팅을 방지하기 위해 사용하는 방법들 중에 Weight Decay(Regularization)라는 방식이 있다.
• Loss 에 $w^2$ 또는 $\vert w \vert$ 등을 추가하여 $w$ 자체의 크기를 줄여 네트워크의 표현력을 감소시키는 방식이다. 이 방식을 MAP 를 이용해 유도할 수 있다.
• 즉 우리의 목표는 “오버피팅을 방지하기 위해서는 네트워크의 표현력을 감소시켜야 하는데, 그러기 위해서는 $w$ 의 절댓값이 작아야 한다. 즉 $w$ 가 0 주변에 분포해야 한다.” 이다.

• $w$ 의 크기를 줄이는 방식에는 여러 가지가 있겠지만, 우리는 $w$ 에 Prior 를 걸어 줄 것이다. $w$ 에 0 을 평균으로 하는 정규분포를 Prior 로 걸어주게 되면, $w$ 는 자연스럽게 0 주변에 배치 될 것이다.

  \[w \sim N(0, \sigma^2_w) \\ \\ p(w) = \frac{1}{\sqrt{2\pi}\sigma_w}e^{-\frac{w^2}{2\sigma^2_w}}\]

• 이제 Maximum A Posterior 의 이름에서 알 수 있듯, likelihood 에서와 같이 Posterior 에 log 를 취해준다. 그리고 그 값을 최대로 하는 $w$ 를 찾는 것이 우리의 목표이다.

  \[\begin{aligned} w^\ast &= \text{argmax}_w \{\log p(w\vert D)\} \\ &= \text{argmax}_w \{\log \eta + \log p(D\vert w) + \log p(w)\} \end{aligned}\]
• 위 식에서 $\log p(D \vert w)$ 는 likelihood 이므로 이 값을 maximize 하는 것은 $\sum^N_{i=1}(t_i - y(x_i \vert w))^2$ 를 minimize 하는 것과 같다.

• $\sum^N_{i=1}(t_i - y(x_i \vert w))^2$ 를 $L(w)$ 라고 치환하여 대입하면 아래와 같다.

  \[w^\ast = \text{argmax}_w \{\log \eta - L(w) + \log p(w)\}\]

• 이제 $\log p(w)$ 식을 대입하면 아래와 같다.

  \[w^\ast = \text{argmax}_w \{\log \eta - L(w) - \log (\sqrt{2\pi}\sigma_w) - \frac{w^2}{2\sigma^2_w}\}\]

• 여기서 $\eta, \pi, \sigma_w$ 는 전부 상수이므로 관련 term 들을 제거해주면 다음 식을 minimize 하는 문제가 된다.

  \[L(w) + \frac{w^2}{2\sigma^2_w} = \sum^N_{i=1}(t_i - y(x_i \vert w))^2 + \frac{w^2}{2\sigma^2_w}\]
• $1/2\sigma^2_w$ 는 상수이므로 $\alpha$ 등으로 치환할 수 있다. 그렇게 되면 Weight Decay(L2 Regularization) 방식을 적용한 딥러닝의 Loss 함수가 된다.
• 즉 정규분포를 Prior 로 준 문제의 MAP 로부터 Weight Decay 식을 유도해 낸 것이다.
• 또한 앞으로 머신러닝/딥러닝에서 Weight Decay, 그 중에서도 L2 Regularization 을 쓴다는 것은 주어진 데이터를 적용함과 동시에 $w$ 에 정규분포라는 Prior 를 걸어 주어 MAP 를 통해 $w$ 를 구하겠다는 것으로 해석할 수 있다.
• L2 Regularization 을 적용하는 일은 $w$ 에 Gaussian Distribution 을 Prior 로 걸어 주는 일인 것이다.
• 참고로 Laplacian Distribution 을 Prior 로 걸어 주면 L1 Regularization 을 얻을 수 있다.

Reference

• https://hyeongminlee.github.io/post/bnn002_mle_map/

맨 위로 이동 ↑