[Loss] Loss function

Objective Function & Loss Function

• 머신러닝/딥러닝에서 “러닝” 이란 다양한 환경에서 나오는 데이터로부터 목적에 따라 배우는 것이다.
• 여기서 배우는 것은 학습을 뜻하며, 시간이 지남에 따라 어떤 작업에 대해 더 나아지고 개선되는 것을 의미한다.
• 그러나 무엇을 보고 개선되는 것을 판단할까? 예를 들어, 우리가 모델을 업데이트할 때, 모델이 개선된 것인지 아닌지에 어떻게 판단할 수 있을까?
• 이를 위해 모델의 좋고 나쁨을 평가할 수 있는 공식적인 측정 기준이 필요하다.
• 머신러닝/딥러닝 그리고 최적화(Optimization)에서는 이러한 기준을 목적함수(objective function)라고 부른다.
• 관례적으로 우리는 목적 함수를 정의할 때, 값이 낮을수록 더 좋다고 설정한다.
  • 값이 높을수록 좋은 함수를 목적 함수로 쓴다면, 함수의 부호를 뒤집어 값이 낮을수록 좋은 함수로 바꿀 수 있다.
  • 값이 낮을수록 좋은 함수로 정의하기 때문에, 이러한 함수들을 손실함수(loss function)라고 부르기도 한다.
• 최적화 과정에서 손실함수를 모델의 파라미터(parameter)에 대한 함수로 생각하고, 학습 데이터셋(training dataset)을 상수로 간주한다.
• 학습 데이터셋에서 발생한 손실을 최소화함으로써 모델이 최적의 파라미터 값을 학습한다. 그러나 학습 데이터에서 좋은 성능을 보인다고 해서 학습 과정에서 보지 못한 데이터에서도 잘 작동할 것이라는 보장은 없다.
• 따라서 일반적으로 사용 가능한 데이터를 두 개의 파티션으로 나누어 사용한다.
  • 모델 파라미터를 학습하기 위한 학습 데이터셋(training set)
  • 평가를 위해 학습에 사용하지 않는 테스트 데이터셋(test set)
• 학습에서의 성능은 실제 시험을 준비하기 위해 사용된 모의 시험에서 학생이 얻은 점수와 유사하다. 모의 시험 결과가 좋더라도, 그것이 실제 시험의 성공을 보장하지는 않는다. 학습 과정에서 학생이 모의 질문을 암기할 수도 있고, 주제를 잘 마스터한 것처럼 보이지만, 실제 시험에서 처음 보는 질문들에 직면하면 실패할 수 있다는 것이다.
• 이처럼 모델이 학습에서는 잘 작동하지만 보지 못한 데이터에 일반화되지 않는 경우, 이를 학습 데이터에 과적합(overfitting)되었다고 말한다.
• 따라서 모델의 최적의 학습을 유도하고, 평가의 기준이 되는 손실함수는 머신러닝/딥러닝에서 필수적이다.

손실함수의 역할

• 손실함수를 사용하는 이유는 각 테스크나 문제의 특성에 맞는 최적의 학습을 유도하기 위해서이다.
• 손실함수는 모델이 학습 과정에서 최적화해야 할 목표(혹은 대상의 특성)를 정의하므로, 문제(대상 또는 환경)의 특성을 잘 반영하는 손실 함수를 사용하면 더 효과적이고 효율적인 학습이 가능하다.
• 문제의 유형
  • 회귀, 분류, Ranking, 생성 모델 등 다양한 유형의 문제가 있다.
  • 각 문제 유형에 따라 예측값과 실제값 간의 차이를 측정하는 방식이 다르므로, 이에 맞는 손실 함수를 선택해야 한다.
• 테스크의 목표
  • 같은 유형의 문제라도 테스크의 목표에 따라 최적의 손실 함수가 달라질 수 있다.
  • 예를 들어, Object Detection 에서는 bounding box 의 정확한 위치를 예측하는 것이 중요하므로 Smooth L1 Loss 를 사용하는 반면, Segmentation 에서는 픽셀 단위의 정확도가 중요하므로 Dice Loss 나 Tversky Loss 를 사용할 수 있다.
• 데이터의 특성을 반영
  • 데이터의 분포, 이상치 존재 여부, 클래스 불균형 등 데이터의 특성에 따라 적절한 손실 함수를 사용해야 한다.
  • 예를 들어, 이상치에 강건한 Huber Loss 나 클래스 불균형을 다루기 위한 Focal Loss 등이 있다.
• 손실함수의 형태에 따라 최적화 과정에서의 수렴 속도와 안정성이 달라질 수 있다. 적절한 손실 함수를 선택하면 학습 과정을 가속화하고 안정적인 수렴을 유도할 수 있다.
• 손실함수는 특정 범위의 데이터를 어느 정도 만큼 모델에 반영할 것인지 결정하는 역할을 한다.
  • 데이터의 정답과 예측값의 차이가 얼마인지에 따라 모델의 parameter(가중치)를 어느 정도 크기 만큼 변경할 것인지 정할 수 있다.
  • 정답과 차이가 얼마 나지 않는다면 손실함수의 값을 작게 설정한다. 손실함수 값이 작다면 모델의 현재 상태에서 작은 양 만큼 변경한다.
  • 반대로 정답과 차이가 많이 난다면 정답에서 벗어나는 만큼, 큰 손실 함수 값으로 모델을 크게 변경한다.

손실함수의 설계 시 고려할 점

• 0 이상의 값
  • 손실함수는 모든 가능한 예측에 대해 0 또는 양의 값이어야 한다.
  • 손실이나 오차가 없는 이상적인 경우를 0 으로 표현하고, 오차가 클수록 그 값이 증가하는 구조를 가지도록 해야 한다.
  • 이로 인해 모델의 예측이 얼마나 잘못되었는지를 직관적으로 반영할 수 있다.
• 미분 가능성
  • 많은 최적화 기법들이 손실함수의 기울기(미분값)를 사용하기 때문에, 손실함수는 모든 매개변수에 대해 미분 가능해야 한다.
  • 이를 통해 경사 하강법과 같은 알고리즘을 사용하여 최적의 매개변수를 찾을 수 있다.
  • 따라서 딥러닝 모델의 손실함수는 주로 연속적이고 미분 가능한 함수로 설계된다.
• 오차의 크기 반영
  • 손실함수는 실제값과 예측값 사이의 오차를 정량적으로 측정해야 한다.
  • 즉, 모델이 잘못된 예측을 할 때 더 높은 손실 값을 부여하여, 모델이 더 정확한 예측을 하도록 유도해야 한다.
• Convexity
  • 이상적인 손실 함수는 최소한 모델의 출력에 대해서는 볼록(Convex)한 성질을 갖는 것이 바람직하다.

  • 함수 $f(\mathbf{w})$ 가 볼록하다는 것은 함수의 그래프가 아래로 굽어져 있다는 것이다. 수식적으로 나타내면 아래와 같다.

    \[f((1-\alpha)x_1 + \alpha x_2) \leq (1-\alpha)f(x_1) + \alpha f(x_2)\]
  • 즉 함수의 임의의 두 점을 잡고 그것을 연결한 선분 $(1-\alpha)f(x_1) + \alpha f(x_2)$ 보다 함수가 아래에 있을 때 그 함수는 convex function 이다.
  • 그러나 많은 딥러닝 문제에서는 Non-Convex 손실함수를 자주 사용한다. 비선형 활성화함수와 복잡한 네트워크 구조로 인해 모든 매개변수에 Convex 한 손실함수가 거의 존재하기 힘들기 때문이다.
  • Convex 하지 않은 손실함수를 사용하면 경사하강법을 적용할 때, 제대로 된 방향성을 찾지 못해 학습이 제대로 이루어지지 않게 될 수 있다. local minima 와 안장점(saddle points) 문제를 동반하기 때문이다.
  • 이 경우에는 하이퍼파라미터 튜닝이나, 다양한 모델 학습 스킬, Optimizer 등을 이용하여 최대한 최솟값에 가깝게 도달하도록 해야 한다.
  • 따라서 딥러닝은 non-convex function 이지만 convex optimization 을 사용하는 것이다. 사용하는 손실함수에 convexity, smoothness, strong-convexity 등의 가정을 추가하고 최적화의 효율성을 가져오는 것이다.
  • 대표적으로 convex optimization 에는 Adam 이나 SGD 가 있다.
  • 이와 관련해서는 Optimization 카테고리에서 자세하게 정리할 것이다.
• 목적 적합성
  • 손실함수는 모델이 해결하려는 문제에 적합해야 한다.
  • 예를 들어, 분류 문제에서는 크로스 엔트로피가 적합하며, 회귀 문제에서는 MSE 가 적합하다.
• 정규화와 과적합 방지
  • 손실함수에 정규화 항을 추가하면 과적합(overfitting)을 방지하는 데 도움이 된다.
  • 정규화는 모델의 복잡성을 제어하고, 더 일반화된 모델을 학습하도록 유도한다.
  • L1 정규화(라쏘)와 L2 정규화(릿지) 등이 있다.

손실함수 정의 기준

• 모델이 정확하게 예측하려면, 모델은 관측 데이터를 잘 설명하는 함수를 표현해야 한다. 이 때 모델이 표현하는 함수의 형태를 결정하는 것이 바로 손실함수다.

  

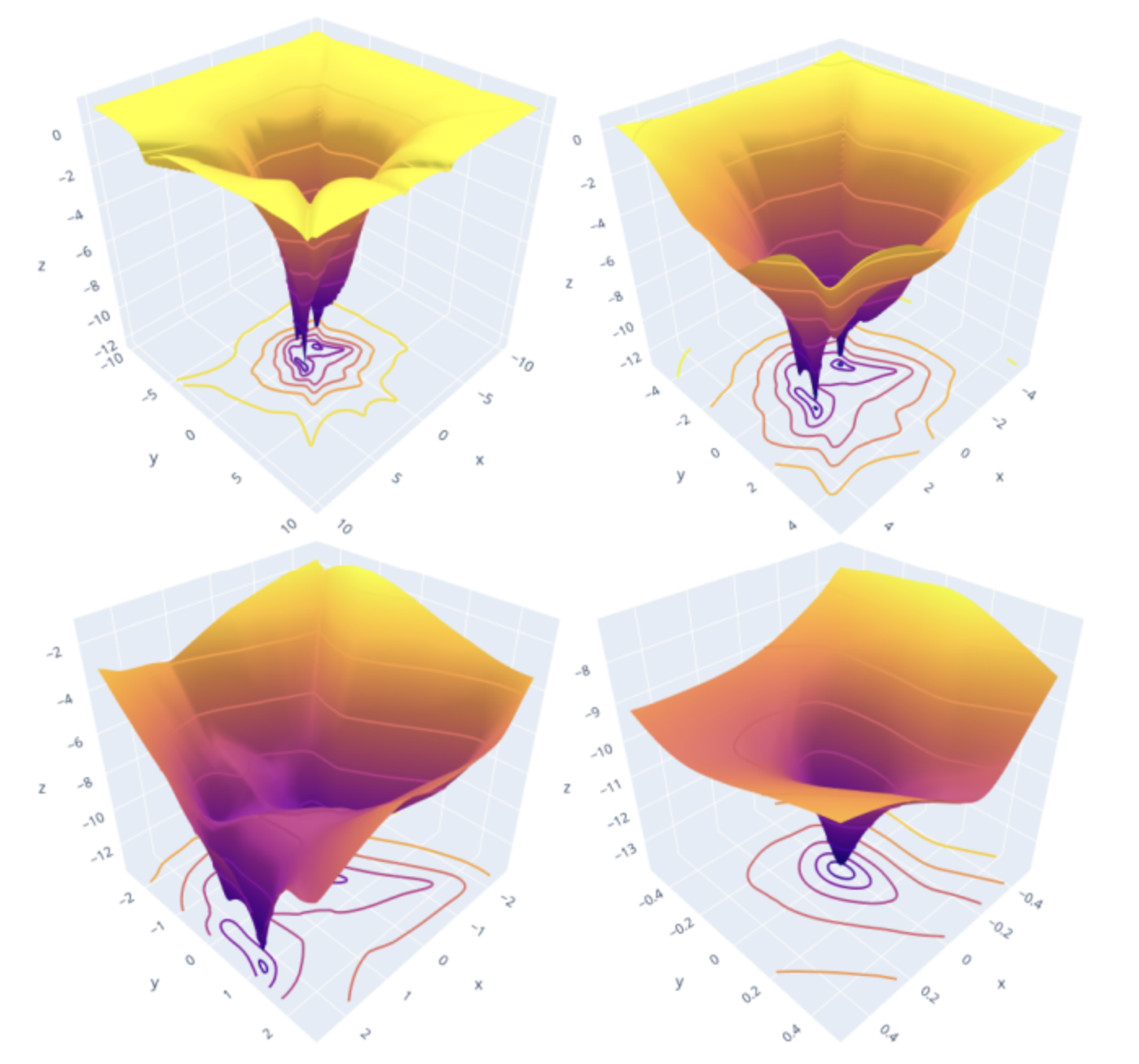
• 손실함수가 위 그림과 같을 때, 가장 아래로 볼록하게 내려간 부분의 파라미터값이 손실함수의 최적해가 된다. 그리고 모델은 그 손실함수의 최적해를 파라미터로 가지는 함수를 표현한다.
• 만약 손실함수가 달라지면 최적해도 바뀌게 된다.
• 따라서 관측 데이터를 잘 설명하는 함수(모델)를 표현하려면, 손실함수는 최적해가 모델의 파라미터 값이 되도록 정의되어야 한다.
• 손실함수를 정의하는 기준은 두가지 관점이 있다.
  • 오차 최소화(error minimization)
  • 최대우도추정(maximum likelihood estimation)
• 이 두가지 관점은 서로 배타적이지 않다.

• 예를 들어, 오차 최소화 관점에서의 MSE 는 정규분포를 가지고 MLE 한 것과 동일한 최적해를 갖는다. 또한 베르누이 분포를 가지고 MLE 하여 유도된 크로스 엔트로피는 실제 분포와 모델이 예측한 분포 간의 차이를 측정하는 함수이기도 하다.

  오차 최소화

  • 모델의 오차는 모델의 예측과 실제값의 차이다.

    \[\epsilon = y_i - \hat{y}\]
  • 손실함수의 목표가 모델의 오차를 최소화하는 것이므로 손실함수를 정의할 때 어떤 방식으로 오차의 크기를 측정할지를 결정한다.
  • 따라서 손실함수 $J(\theta)$ 는 오차 $\epsilon$ 의 크기를 나타내는 함수로 정의되며 오차의 크기를 어떻게 표현하냐에 따라 성질이 달라진다.
  • 이 때 Norm 의 개념이 이용되며, MSE loss 와 MAE loss 가 있다.

  MLE

  • 관측된 데이터를 가장 잘 설명하는 파라미터를 추정하는 방법이다. 이 때 가능도 함수를 최대화하는 파라미터 값을 찾는다.
  • 대부분의 딥러닝 모델은 확률 모델을 가정하기 때문에 MLE 방식으로 손실 함수를 유도할 수 있다.
  • 여기서는 손실함수가 무엇인지에 대해서만 정리하므로, MLE 에 대해서는 이 포스트에서 자세하게 정리한다.

Loss Surface

• loss surface 란 loss function 의 그래프다. 즉, 모델의 parameter(weight)와 loss 값 사이의 관계를 시각화한 것이다.
• loss surface 는 고차원 공간에서 매우 복잡한 지형을 나타낼 수 있으며, 이는 여러 local minima 와 안장점(saddle points) 등을 포함한다.
• 경사하강법은 loss surface 의 local minimum 에 해당하는 weight 를 찾는 것을 목적으로 한다.
• 딥러닝에서 알려진 중요한 사실 중 하나는, 적당히 깊은 local minima 도 매우 좋은 성능을 나타낼 수 있다는 점이다. 반드시 최적점에 해당하는 global minimum(optimal point) 을 찾지 않더라도, 성능 차이가 크게 나지 않는 경우가 많다.
• 따라서 적당한 local minima 도 충분히 만족스러운 결과를 제공할 수 있다.
• 이처럼 딥러닝은 1) 적당한 곳에서 optimal point 라고 여겨도 된다고 알려져 있고, 2) 실험적으로 flat 한 옵티마와 sharp 한 옵티마 중에는 flat 한 optimal point 가 훨씬 안정적인 값을 가질 확률이 높다.

• 결국 딥러닝은 loss surface 에서 flat 한 local minima 를 찾는 것이라고 볼 수 있다.

  

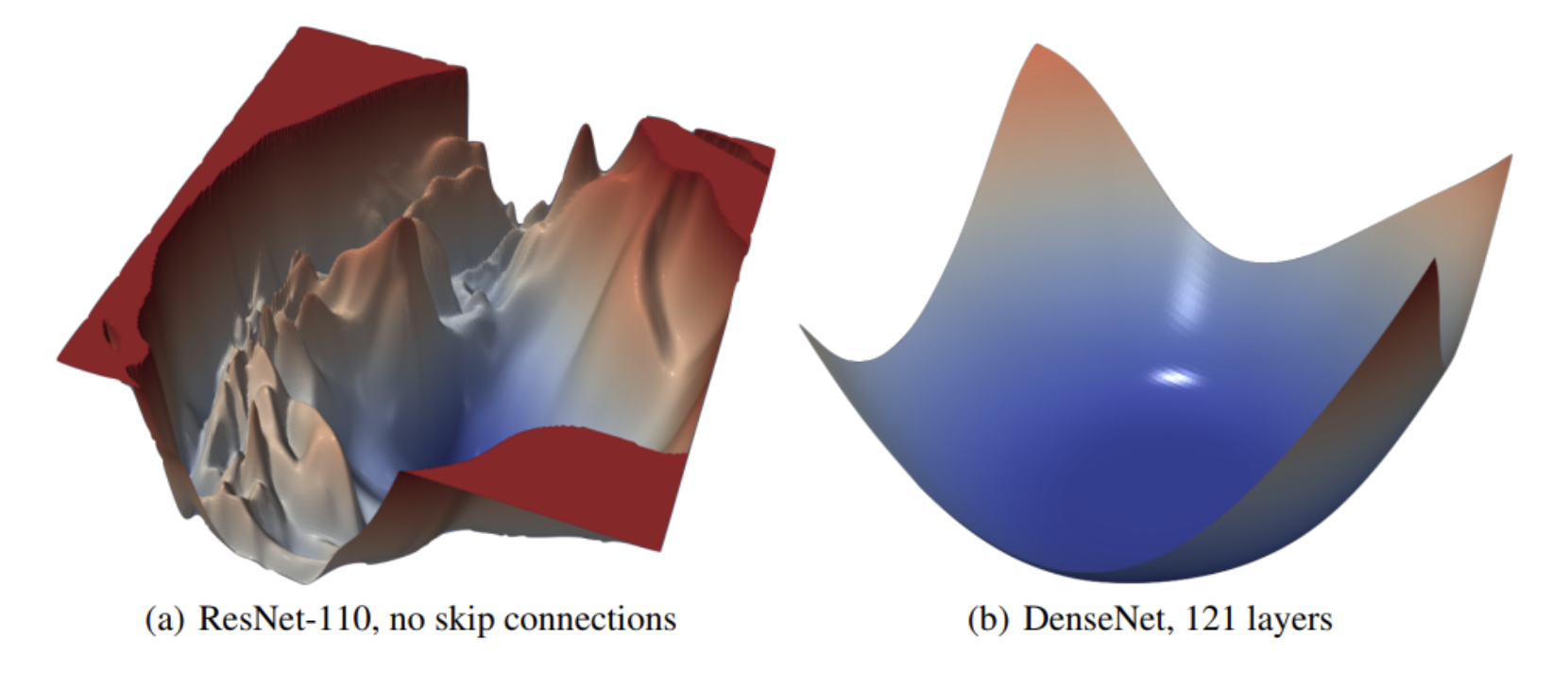
• 위 그림처럼 loss surface 는 모델의 parameter 값에 따라 loss 의 변화를 시각화하는 표현방법이다. 이를 통해 gradient descent 방법으로 오차의 gradient 를 최소화하는 방향으로 모델을 업데이트되는 경로를 쉽게 시각화할 수 있다.
• 이 때 loss surface 의 z 축은 loss function 의 값이다. 반면 x 축과 y 축을 정하는 것은 복잡하다.
• 딥러닝에서 paremeter(=가중치)의 갯수는 적어도 수만 개이고, 대규모 모델은 천억 개가 넘는 parameter 를 가지고 있다.
• 따라서 시각화를 위해 1개(2D visualization) 내지는 2개(3D visualization)의 변수를 선정해야 한다.
• 이를 위해 Li et al.,(2018) “Visualizing the Loss Landscape of Neural Nets” @ NeurIPS 2018 에서 제안한 방법을 활용할 수 있다.
  • 하나의 center point $\theta^\ast$ 를 그래프에서 정의하고, 두 개의 direction vector $\delta$ 와 $\eta$ 를 정한다.
  • 이를 통해 손실함수를 $f(\alpha) = L(\theta^\ast + \alpha\delta)$ 의 1D Line 이나 $f(\alpha, \beta) = L(\theta^\ast + \alpha\delta + \beta\eta)$ 의 2D Surface 로 시각화한다.
  • 이 때 적절한 scaling 이 적용된 random Gaussian distribution 에서 sampled 된 random direction vector $\delta , \eta$ 를 사용한다.
  • 그렇게 되면 $x=\alpha, y=\beta, z=f(\alpha, \beta)$ 로 3차원에 투영할 수 있다.
• 해당 논문은 loss surface 를 시각화하여 loss surface 가 어떻게 학습 가능성과 generalization error 에 영향을 주는지에 대해 탐구했다. 따로 포스트를 만들어 정리해보자.

다양한 손실함수

• 숫자 값을 예측할 때(회귀) 가장 흔히 사용되는 손실함수는 제곱 오차(squared error)다. 이는 예측값과 실제값의 차이를 제곱한 것이다.
• 분류 문제에서는 가장 흔한 목적이 오류율(error rate)을 최소화하는 것이며, 이는 예측값이 실제값과 일치하지 않는 비율을 나타낸다.
  • 제곱 오차와 같은 목적함수는 최적화하기 쉽지만, 오류율과 같은 목적함수는 미분이 불가능하기 때문에 최적화하기 어려울 수 있다. 이러한 경우, 대체 목적함수(surrogate objective)를 최적화하는 것이 일반적이다.
• 이처럼 다양한 문제에 따라 손실함수가 존재하는데, 간략하게 보자. 각각의 손실함수에 대해서는 시간이 허락하는대로 이 블로그에 정리할 것이다.
• 회귀(Regression) 문제
  • Mean Squared Error (MSE): 예측값과 실제값 차이의 제곱 평균. 가장 일반적으로 사용되는 회귀 손실 함수다.
  • Mean Absolute Error (MAE): 예측값과 실제값 차이의 절댓값 평균. 이상치에 덜 민감하다.
  • Huber Loss: MSE 와 MAE 의 장점을 결합한 손실 함수로 이상치에 강건하다.
• 이진 분류(Binary Classification) 문제
  • Binary Cross-Entropy: 로지스틱 회귀에서 주로 사용. 실제 클래스와 예측 확률 분포 간의 차이를 계산한다.
  • Hinge Loss: 서포트 벡터 머신(SVM)에서 사용. 마진을 최대화하도록 유도한다.
• 다중 클래스 분류(Multi-class Classification) 문제
  • Categorical Cross-Entropy: 실제 클래스와 예측 확률 분포 간의 차이를 계산한다.
  • Sparse Categorical Cross-Entropy: 정수로 인코딩된 실제 클래스를 사용할 때 적용한다.
• 시퀀스(Sequence) 관련 문제
  • Connectionist Temporal Classification (CTC) Loss: 시퀀스 레이블링, 음성 인식 등에 사용된다.
• 생성 모델(Generative Models)
  • Reconstruction Loss: 오토인코더의 입력 복원 오차를 측정한다. L1 Loss, L2 Loss 등이 사용된다.
  • Adversarial Loss: GAN 에서 생성자와 판별자의 경쟁을 통해 학습한다.
• 이 외에도 Triplet Loss, Contrastive Loss 등 특정 태스크에 특화된 손실함수들도 있다.
• 문제의 특성과 데이터의 형태에 따라 적절한 손실 함수를 선택하는 것이 중요하다. 또한 경우에 따라 여러 손실함수를 조합하여 사용하기도 한다.
  • Object Detection
    • Focal Loss: 클래스 불균형이 심한 상황에서 효과적인 loss function. 잘 분류된 샘플의 손실 기여도를 줄이고, 잘못 분류된 샘플에 더 집중한다.
    • Smooth L1 Loss: Bounding Box Regression 에 사용되며, 이상치에 덜 민감하다.
  • Segmentation
    • Dice Loss: 의료 관련 segmentation 에 자주 사용되며, 두 segmentation 마스크 간의 중첩 정도를 측정한다.
    • Tversky Loss: Dice Loss 의 일반화된 버전으로, False Positives 와 False Negatives 에 대한 가중치를 조정할 수 있다.
    • Focal Tversky Loss: Tversky Loss 에 Focal Loss 의 개념을 적용하여 어려운 픽셀에 더 집중한다.
  • 3D 비전
    • Chamfer Distance Loss: 3D 객체 재구성 등의 테스크에서 두 점군(Point Cloud) 간의 대응 관계를 측정한다.
    • Earth Mover’s Distance (EMD) Loss: 두 점군 간의 최적 운송 문제를 기반으로 한 손실 함수
  • 메트릭 학습(Metric Learning)
    • Contrastive Loss: 유사한 샘플 간 거리는 가깝게, 다른 샘플 간 거리는 멀도록 학습한다.
    • Angular Loss: 샘플 간의 각도 기반 유사도를 학습하여 더 효과적인 임베딩을 생성한다.
  • 강화 학습(Reinforcement Learning)
    • Policy Gradient Loss: 에이전트의 행동 정책을 최적화하기 위한 손실 함수
    • Q-Learning Loss: 최적의 행동 가치 함수를 학습하기 위한 손실 함수
  • Pairwise Ranking
    • Margin Ranking Loss: 랭킹 문제에서 두 입력 간의 상대적인 순위를 학습한다.
    • Triplet Loss: 얼굴 인식, 이미지 검색 등에 사용되며, Anchor, Positive, Negative 샘플 간의 거리를 최적화한다.

Reference

• https://modulabs.co.kr/blog/machine_learning_loss_function/

맨 위로 이동 ↑