[Generative] Generative Model Part 2

Maximum Likelihood Learning

• Likelihood 는 우도(가능도)를 뜻한다. 이를 가지고 어떤 parameter 가 주어졌을 때 이 데이터가 얼마나 likely 한 지, 이 데이터를 얼마나 잘 설명하는지를 판단한다.
• 이러한 Likelihood 를 최대화 하는 방향으로 parameter 를 학습시키는 것을 Maximum Likelihood Learning 이라고 한다.
• 이 컨셉은 VAE 를 설명하는 Latent Variable Models 로 자연스럽게 이어진다.

• MLE 자체는 이전 포스트에서 잘 정리했다.

  

• Generative Model(생성모델)은 모르지만 존재한다고 가정하는 어떤 분포($P_{\text{data}}$)와 우리가 모델링하고 학습할 수 있는 probably density($P_{\theta}$)가 있을 때, 그 두 분포 사이의 거리를 최소화하는 방향으로 학습하여 density 를 최적화시킨다. 이것을 best-approximating density 라고 한다.
• 그리고 우리가 학습할 수 있는 분포(probably density)들의 경우의 수를 model family 라고 부른다.
• 가장 먼저 정의해야 할 것은 어떤 기준으로 좋음을 판단할지, 즉 근사할 때 어떤 기준으로 근사가 잘되는지를 정의하는 것이 중요하다. 내가 무언가를 학습 또는 최적화할 때 그 기준을 명확히 정의하지 않으면 어떤 결론을 명확히 설득할 수 없다.

• 따라서 “어떤 기준으로 분포 사이의 거리가 가까워진다” 라는 것을 정의해야 한다. 이 때 대표적으로 KL-divergence 를 사용할 수 있다.

  

• KL-div 는 근사적으로 어떤 두 확률분포 사이의 거리를 말한다.
• 그러나 정확히는 거리가 아닌데, 어떤 것을 거리라고 표현하기 위해서는 거리를 측정했을 때 $(a,\;b) =( b,\;a)$ 가 같다. 즉 대칭성이 있다는 것이다.
• KL-div 는 대칭성을 만족하지 않지만, 근사적으로 두 분포 사이의 거리를 의미한다고 볼 수 있고 많이 사용된다.
• $P_{\text{data}}$ 는 데이터를 생성해내는 분포이고, $P_{\theta}$ 는 parameter 화 된 $\theta$ 를 가지고 모델링하여 학습하는 분포다. 이제 $\theta$ 를 최적화 해서 $P_{\theta}$ 를 $P_{data}$ 에 근사시킨다.

• 우리는 KL-div 를 아래처럼 간단하게 표현할 수 있다.

  \[\mathbb{KL}(P_{\text{data}} \Vert P_{\theta}) = \color{blue}{\mathbb{E}_{x \sim P_{\text{data}}}[\log P_{\text{data}}(x)]} \color{red}{- \mathbb{E}_{x \sim P_{\text{data}}}[\log P_{\theta}(x)]}\]
• 파란색의 첫번째 term 은 $\theta$ 와 상관없기 때문에 무시할 수 있다. 즉 최적화와 상관 없는 term 이다.
• 따라서 KL-div 를 최소화하기 위해 빨간색의 두번째 term 을 최소화하면 된다. 이 때 부호 - 를 뒤집어서 최대화하는 것으로 보면, log likelihood($P(x\vert\theta)$) 를 최대화하는 것이 된다.
• 즉 KL-div 를 최소화하는 것이 함의적으로 likelihood 를 최대화하는 것과 동일한 효과를 가져온다는 것이다.
• 정리하면, 내가 모델링하는 $P_{\theta}$ 와 내가 모르지만 존재한다고 가정하는 $P_{\text{data}}$ 사이의 KL-div 를 최소화 한다는 것은:
  • input 들이 내가 찾고자 하는 $P_{\text{data}}$ 에서 주어지고,
  • 그 input 들을 내가 최적화하려고 하는 $P_{\theta}$ 에 집어넣었을 때,
  • 그 likelihood 가 최대화 되는 방향으로 $\theta$ 를 최적화하는 것이 KL-div 를 최소화 하는 것과 같다는 것이다.
  • 즉 두 개의 확률 분포의 거리를 최소화한다는 개념과 주어진 데이터를 통해서 목적으로 하는 확률분포의 최적화된 모수(parameter)를 구하는 것은 동일한 개념이다.
• 따라서 “앞으로는 likelihood 를 최대화하는 방법으로 생성모델을 학습시키겠다!” 라고 말할 수 있어, 전체 스코프를 Maximum Likelihood Learning(MLL) 이라고 하는 것이다.
• 여기서 꼭 유념해야 할 것은, Maximum Likelihood Learning 이 Generative Model 의 것은 아니다. Maximum Likelihood Learning 은 생성모델을 풀 수 있는 쉬운 방법 중 하나인 것으로 이해하자.

• 또한 우리는 $P_{\text{data}}$ 를 모른다. 따라서 존재한다고 가정은 하지만 그 $P_{\text{data}}$ 에 접근할 수 없다.

  

• 따라서 empirical log-likelihood 로 근사한다.
  • 원래라면 $P_{\text{data}}$ 의 모든 가능한 $x$ 에 대해서 log-likelihood 를 계산하여 최대화하는 방향으로 $\theta$ 를 최적화해야 하지만,

  • 그렇게 할 수 없기 때문에 $\mathcal{D}$ 개의 데이터셋을 만들어 놓고, $\mathcal{D}$ 가 $P_{data}$ 에서 나왔다고 가정하고서, 그 $\mathcal{D}$ 를 이용하여 $P_{\theta}$ 인 우리의 parameter 분포를 학습하겠다는 것이다.

    \[\max_{P_\theta} \frac{1}{\vert \mathcal{D} \vert}\sum_{x \in \mathcal{D}} \log P_\theta(x)\]
• 이처럼 전체를 보는 게 아니라 모아진 데이터만 가지고 학습하려는 기계학습 방법론을 empirical ML 이라 부른다. 따라서 데이터의 숫자가 많지 않을 때는 정확하지 않을 수 있다.
• 또한 이렇게 empirical log likelihood 를 이용하는 것을 empirical risk minimization(ERM) 이라고 부른다.
• 즉 ERM 은 MLL 에서 자주 사용되는 방법이다. 그러나 ERM 은 한정된 데이터로 최적화를 하기 때문에 over fitting 위험이 있다.
• over fitting 을 막기 위해서 hypothesis space 에 제약을 주어 model space 를 줄일 수 있다.
  • 모든 분포의 공간에서 문제를 푸는 것이 아니라, 생성모델을 모델링 할 수 있는 hypothesis space 를 줄이는 것이다.
  • 물론 모델링 공간에 제약을 주게 되면 각각의 모델의 성능 자체에 한계를 주는 것이기 때문에, trade-off 가 있다.
  • MAP (Maximum A Posterior) 에서 Prior 로 정규분포를 주어 weight decay 하는 방식과 비슷하다.
• 또한 MLL 은 under fitting 에 취약하다. 모든 가능한 확률분포를 사용할 수 없기 때문이다.
  • 다시 한번 MLL 은 주어진 데이터에 대해 모델의 parameter 를 최적화하는 방법으로, 모델이 관측된 데이터를 가장 잘 설명할 수 있도록 likelihood 를 최대화하는 방식이다.
  • under fitting 은 모델이 너무 단순해서 데이터의 복잡한 패턴을 제대로 학습하지 못하는 경우를 나타낸다. 이렇게 모델이 데이터에 적합하지 않으면, 예측 성능이 떨어지고 일반화 능력이 부족해진다.
  • MLL 은 종종 spherical Gaussian 과 같은 간단한 parametric 분포를 사용한다. spherical Gaussian 분포란 모든 차원에서 동일한 분산을 가지는 Gaussian 분포를 의미한다.
  • 최적화를 위해서 경사하강법을 사용하고, 그러려면 미분 가능한 log-likelihood 를 써야한다. 이 때 만만한 것이 Gaussian 이기 때문에 spherical Gaussian 분포를 사용했고, GAN 이 나오기 전까지 유의미한 분포를 모델링할 수 없었다.
  • 이처럼 너무 단순한 분포를 사용하면, 실제 데이터의 복잡한 구조를 충분히 표현할 수 없다. 그 결과 모델이 데이터의 패턴을 제대로 학습하지 못하고 under fitting 이 발생할 수 있다.
  • 즉, MLL 이 under fitting 에 취약한 이유는 데이터가 복잡한 구조를 가지고 있는데도 불구하고 접근할 수 없기 때문에, 단순한 분포로 모델링하려 하기 때문이다.

• 지금까지 살펴본 것처럼 KL-div 를 metric 으로 사용하게 되면 maximum likelihood learning 으로 귀결된다.

  

• KL-divergence 는 MLL 로 이어지고, MLL 을 좀 더 근사하면 VAE 가 된다. 아래에서 자세히 보자.
• Jensen-Shannon divergence(JSD) 는 KL-div 가 교환법칙이 성립하지 않아 대칭성을 가지고 있지 않기 때문에, 거리함수로 사용할 수 있도록 두 개의 KL-div 를 더해서 2 로 나눠준 값이다. 이 JSD 는 GAN 에서 사용된다.
• Wasserstein distance 도 확률분포 사이의 거리를 의미하는데, 이것을 이용하면 WAE, AAE 를 도출할 수 있다.
• 즉 새로운 확률분포 사이에 evaluation metric 을 정의할 때마다 서로 다른 생성모델 방법론이 튀어나온다,

Latent Variable Models

• VAE 는 label 에 해당하는 점들을 제한된 공간(Gaussian distribution, latent space)에 모으고, 그 공간 내에서 결과값을 뽑아낸다(sampling, decoder).
• 이러한 VAE 를 좀 더 이해해보자.

Auto Encoder

• Auto Encoder(AE) 는 어떤 입력이 들어왔을 때 Encoder 를 거쳐 latent 벡터(잠재벡터)를 만들고 Decoder 를 거쳐서 다시 원래 입력으로 복원하는 네트워크다.
• 그러면 Auto Encoder 는 Generative Model 일까?
  • 결론은 아니다. Auto Encoder 자체는 그냥 모델인 반면 VAE 는 Generative Model 이다.
  • VAE 와 AE 는 목적이 전혀 다르다.
  • AE 의 목적은 어떤 데이터를 잘 압축하는것, 어떤 데이터의 특징을 잘 뽑는 것, 어떤 데이터의 차원을 잘 줄이는 것이다.
    • AE 는 학습을 진행하고 나중에 Decoder 부분을 떼어 버린다.
    • 이후 input data 의 중요한 정보만 담고 있는 $z$ 로 input data 를 예측하면 원래보다는 결과가 나아진다.
  • 반면 VAE 의 목적은 Generative Model 로서 어떤 그럴듯한 새로운 데이터를 만들어내는 것이다. 즉 Decoder 가 중요하다.
• 어떤 부분이 달라서 VAE 가 Generative Model 이 되는지 보자.

Variational Auto Encoder

• VAE 는 내가 모르지만 샘플링할 수 있는 분포에서 input 이 나왔다고 가정하고, 이 input 에 대해서 $P_{\theta}$ 를 최대화하는 MLL 을 수행한다.
• 그러나 $P_{\theta}$ 로 많은 것을 사용할 수 없다. 앞에서 봤듯 표현력이 높지 않은 분포가 사용하기 유리했기 때문에 under fitting 에 취약했다. 즉 원하는 만큼의 퀄리티가 나오지 않았다.
• 또한 Generative Model 은 보통 Unsupervised Learning 으로 학습된다.
  • Unsupervised Learning(비지도학습)은 데이터의 label(정답)이 주어지지 않더라도 input 이 주어졌을 때 해당 데이터가 어떠한 label 에 속하는지를 알아낼 수 있도록 하는 방법이다.
  • 꼭 label 이 아니어도 feature 값으로 생각할 수도 있는데, 어떤 데이터의 정답 feature 값이 주어지지 않더라도 해당 데이터가 어떠한 feature 값을 가져야 하는지 알아낼 수 있는 것이다.
  • 그러나 일반적으로 딥러닝 모델은 loss function 을 줄이는 방향으로 학습시켜야 하는데, 정답 데이터가 주어지지 않으면 실제 정답과 예측에 대한 loss function 을 구할 수 없다.

• 이를 해결하고자 하는 방법이 Variational Auto Encoder 다.

  

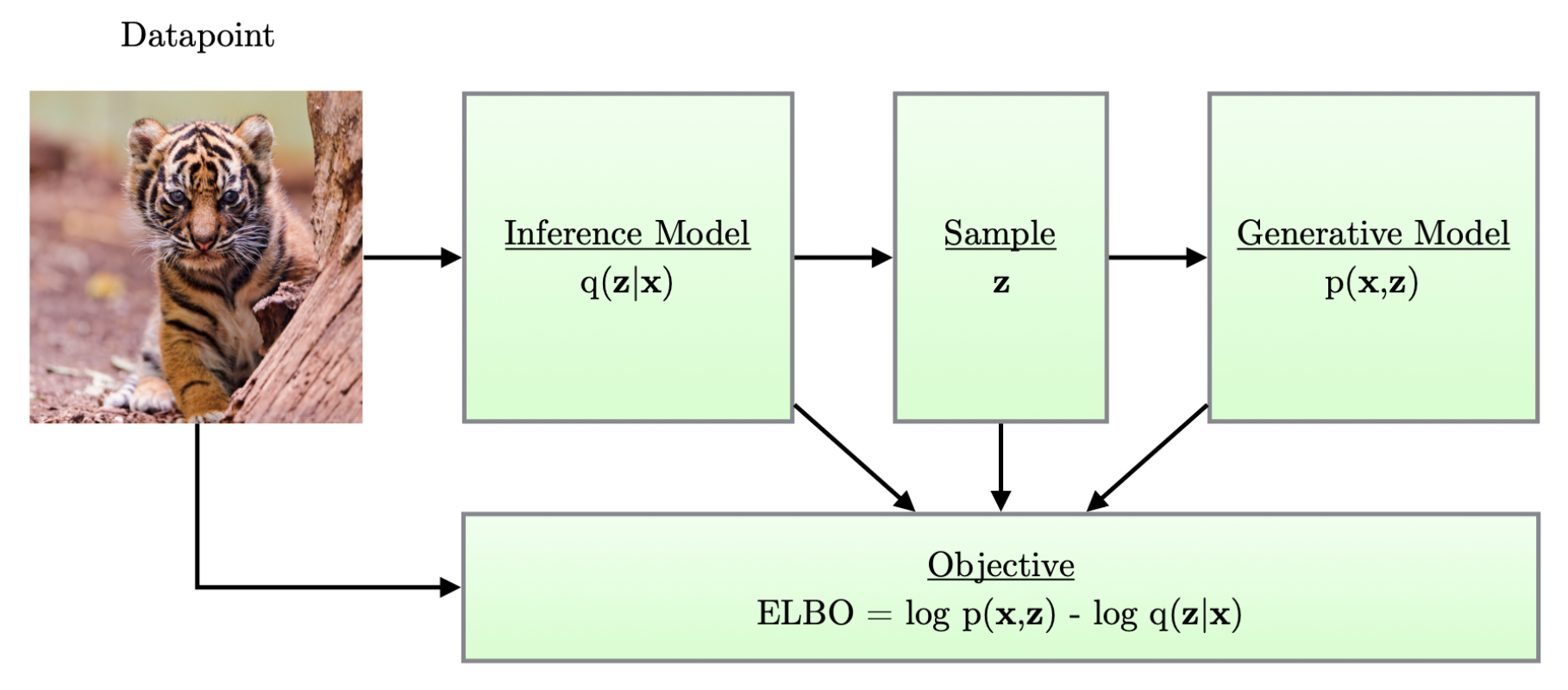
• 예를 들어 이미지를 학습시킨다고 해보자.
• Variational AutoEncoder 에서는 이미지 $\mathbf{x}$ 를 Encoder 에 넣어서 $\mathbf{x}$ 보다 차원이 작은 $\mathbf{z}$ 라는 결과를 구하고, 이 $\mathbf{z}$ 를 바탕으로 Decoder 를 통해 새로운 이미지를 reconstruction 한다.
• 여기서 $\mathbf{z}$ 의 차원이 $\mathbf{x}$ 보다 적다는 것은, $\mathbf{z}$ 는 $\mathbf{x}$ 에 대한 중요한 정보만을 담고 있어야 한다는 의미이고, 이로 인해 $\mathbf{z}$ 를 가지고 $\mathbf{x}$ 와 유사한 새로운 input data 인 $\hat{\mathbf{x}}$ 를 만들어 낼 수 있는 것이다.
• 그러면 $\Vert \mathbf{x} - \hat{\mathbf{x}} \Vert^2$ 와 같은 의미를 가진 loss function 을 설정하여 이를 최소화하는 방향으로 모델을 학습시키면, $\mathbf{z}$ 에는 결국 reconstruction 하기 위한 중요한 정보를 담게 할 수 있다.
• 이러한 VAE 는 완전히 input 과 똑같은 이미지를 생성하고 싶은 것이 아니라, 유사하지만 조금은 다른 조정된(controlled) 이미지를 생성하고 싶은 것이므로 확률분포를 이용한다.
• 이 때 위에서 언급한 것처럼 MLL 만으로는 생성에서 원하는 퀄리티가 나오지 않기 때문에, Variational Inference 를 사용한다.

Latent Variable

• Variational Inference 에서는 $z$ 라는 latent vector 가 등장한다. 이는 무엇을 뜻할까?
• Generative Model 은 그럴듯한 데이터 생성을 위해 데이터의 상세한 부분까지 모두 파악해야 한다. 따라서, 사람이 수동으로 라벨링한 정보를 주로 활용하는 분류나 인식 모델을 넘어서는 다양한 기술이 요구된다.
• 예를 들어, 그럴듯한 얼굴 이미지가 되기 위해서는 얼굴 생김새 뿐만 아니라 일관성도 중요하다. 눈 색깔과 크기, 고개 돌림 각도, 조명 강도 및 방향, 바람의 세기와 방향 등 여러 요인이 얼굴 이미지 생성에 관여하지만, 그 모든 것을 수동으로 라벨링 하기는 불가능에 가깝다.
• Generative Model 에서는 이와 같은 독립 변수들을 사람이 직접 라벨링하지 않고, 모델 스스로 찾아가게 하는 전략을 사용한다. 따라서 Generative Model 은 기본적으로 Supervised Learning 형태를 취하지 않는다.
• 학습에 사용되는 이미지는 실제로 존재하는 사물과 상황에 대한 포착이라고 보고 실제로 존재하는 사물과 상황의 모습을 결정하는, 즉 데이터의 분포를 설명하는데 중요한 조건들을 ‘잠재변수(latent variable)’로 모델링 한다.
• 이러한 잠재변수를 사용하면 관찰 데이터의 분포를 효과적으로 설명하고 복잡한 패턴을 파악하는데 유용하다.
• 또한 잠재변수로 이루어진 latent space 는 실제 data 의 space 보다 더 작은 차원을 가지면서 잘 설명할 수 있는 공간이다.
• 이와 관련해서 Manifold hypothesis 가 깊게 관련되어 있다.
  • 데이터의 차원이 증가할수록, 데이터의 밀도는 희박해지기 때문에 학습이나 예측 등이 정상적으로 모델링 될 수 없다. 일명 차원의 저주다.
  • Manifold hypothesis 는 고차원 데이터가 사실은 더 저차원인 manifold 에 존재한다는 가정이다. 즉, 우리가 관측하는 데이터는 고차원 공간에 분포하지만, 그 데이터는 더 낮은 차원의 구조를 따르고 있다고 보는 것이다.
  • 예를 들어, 자연 이미지나 음성 데이터는 매우 고차원 공간(수천 또는 수백만 차원)에서 나타나지만, 실제로는 그 모든 차원을 독립적으로 사용하는 것이 아니라 저차원적인 manifold 위에 데이터를 표현할 수 있다는 가정이다.
  • 즉 사람 얼굴 이미지의 경우 눈, 귀, 코 등이 각각 저차원에서 몰려있다고 보는 것이다.
  • 그 데이터의 Manifold 공간을 찾는 것이 Generative Model 의 목표이기도 하다.
• 결국 저차원 manifold 를 잘 찾아낸다는 것은, 데이터를 잘 아우르는 저차원 manifold 의 분포를 토대로 sampling 을 할 수 있다는 것이고, 이로부터 새로운 data sample 을 생성할 수 있게 돈다.
• 또한 manifold 를 잘 찾는다는 것은, 의미 있는 feature(representation) 를 찾는다는 것과 같다. 따라서 저차원 manifold 가 이미지의 의미있는 feature 를 잘 담고 있다면, 저차원 공간에서 가까운 것이 고차원 공간에서 보다 의미있는 distance metric 이 될 수 있다. 고차원 공간에서는 차원의 저주 때문에 유의미한 거리 측정 방식을 찾기 어렵기 때문이다.
• VAE 는 데이터를 latent space 로 매핑하여, 잠재 변수 $z$ 를 통해 고차원 데이터 $x$ 를 생성하는 구조를 갖고 있다.
• 즉 VAE 는 잠재 공간에서 샘플링된 잠재 벡터 $z$ 를 decoder 를 통해 고차원 데이터 $x$ 로 변환한다.
• 이 변환 과정은 잠재 공간에서 특정 구조를 따르는 저차원적인 정보가 고차원 데이터로 변환될 수 있다는 가정을 따른다.
• 이를 통해 좀 더 다채롭고 그럴듯한 이미지를 생성 가능한 것이다.
• 그렇다면 이제 Variational Inference 에 대해 살펴보자.

Variational Inference(VI)

• Variational Inference(VI) 는 bayesian inference 에서 일반적으로 사용되는 방법론이다.

• VI 는 내가 찾고자 하는 분포가 있는데 그 분포가 너무 복잡해서 모델링할 수 없을 때, 그 분포를 내가 찾을 수 있는 간단한 분포로 근사하는 것이다.

  

• 일반적으로 bayesian 에서는 사후분포(posterior, 데이터가 주어졌을 때 parameter 의 확률분포)를 찾고자 한다.
  • 사후분포는 observation 이 주어졌을 때, 관심있는 random variable 의 확률분포다.
  • 일반적으로 딥러닝에서 관심있는 random variable 은 모델의 parameter 이며, observation 은 data 다.
  • 그러면 여기서는 어떻게 사후분포를 설정할까?
• VI 에서는 $z$ 라는 latent vector 를 도입하여 사후분포 $p_\theta(z \vert x)$ 를 찾고자 한다.
• 따라서 latent space 를 통해 어떤 데이터가 어떤 feature 를 가지는지를 표현하고, 이 latent space 의 분포인 $p_\theta(z \vert x)$ 는 사후분포가 된다.
• 그러나 이러한 사후분포($p_\theta(z \vert x)$)는 계산할 수 없기 때문에 찾는 것이 불가능하다. 베이즈 정리에 따라 식을 전개하면 분모에 위치하는 Evidence 때문인데, 이에 관한 자세한 이유는 이 포스트에서 알아볼 것이다.

• 따라서 상대적으로 간단하지만 최적화할 수 있는 분포($q_{\phi}(z \vert x)$)를 만들어서 사후분포에 근사시킨다. 이것이 VI 다.

  

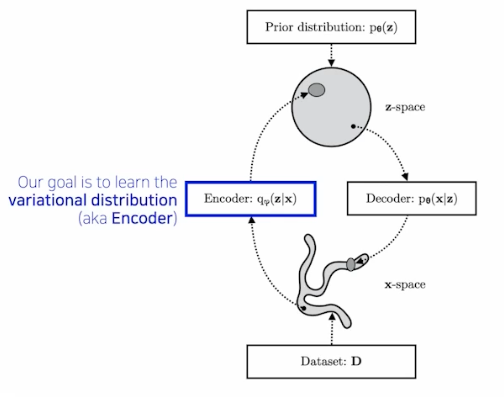
• 구체적으로 우리가 최적화하여 근사시키는 분포인 variational distribution($q_{\phi}(z \vert x)$)가 posterior distribution($p_{\theta}(z\vert x)$) 와 KL-div 관점에서 최소화하도록 최적화하는 것이다.
  • 여기서 $z$ 는 latent vector 이고, $x$ 는 input 이다.
  • 사후분포(posterior dist, $p_{\theta}(z \vert x)$)는 우리가 건드릴 수 없고 계산할 수 없는 분포이고, variational dist($q_{\phi}(z\vert x)$) 는 계산할 수 있지만 상대적으로 표현력이 떨어지는 분포다.

MLL 과 VI

• 위의 개념들이 어떻게 연결되는지 좀 더 이해해보자.
• 다시 한번, Generative Model(생성모델)은 모르지만 존재한다고 가정하는 어떤 분포($P_{\text{data}}$)와 우리가 모델링하고 학습할 수 있는 probably density($P_{\theta}$)가 있을 때, 그 두 분포 사이의 거리를 최소화하는 방향으로 학습하여 density 를 최적화시킨다.
• 그리고 위에서 살펴본 것처럼 $P_{\text{data}}$ 와 $P_{\theta}$ 사이의 거리를 최소화하는 것은 log likelihood 인 $\log P(x\vert\theta)$ 혹은 $\log P_\theta(x)$ 를 최대화하는 것과 의미가 같다. 따라서 MLL 을 하는 것이다.
• 즉 VAE 의 목표도 결국 Likelihood 를 Maximize 하는 것이다.
• 그러면 우리의 목표는 $\log P_\theta(x)$ 를 최대화해야 하는데, 복잡한 실제 분포를 근사하는데 상대적으로 간단한 parametric 분포를 사용하기 때문에 기대하는 만큼의 생성을 이루어낼 수 없다.
• 복잡한 실제 분포를 근사하기에도 어렵고, 해당 $P_\theta(x)$ 에서 데이터를 생성한다고 해도 성능이 좋지 않다는 것이다.
• 따라서 모델이 실제 분포보다 차원이 작으면서 중요한 정보를 포함하여 데이터를 잘 설명할 수 있는 latent space 를 가지도록 할 수 있다.
• 즉 복잡한 데이터 분포를 잠재공간에서 저차원으로 변환하고 이 잠재공간에서 샘플링하여 데이터를 생성하는 것이다.

• 그러면 우리는 $P_\theta$ 를 $x$ 와 $z$ 의 joint distribution 으로 아래와 같이 표현할 수 있다.

  \[\underset{\theta}{\text{argmax}} \left[ P_\theta(x) = \int_z P_\theta(x, z) = \int_z P_\theta(x \vert z)P_\theta(z) \right]\]
  • 여기서 $P_\theta(x)$ 를 $z$ 에 대한 marginal likelihood function 이라고도 부른다. 또한 bayesian 통계학 관점에서 Evidence 로 바라보기도 한다. $P_\theta(z \vert x)$ 를 계산할 때 분모의 Evidence 와 같기 때문이다.
  • 이를 적분으로 나타내는 것 즉, 결합확률을 marginalize 하는 이유는 데이터 $x$ 의 관찰 확률을 구할 때 잠재변수 $z$ 를 고려하지만, $z$ 는 관찰되지 않기 때문에 이를 적분하여 없애는 것이다.
• 그러나 위와 같은 적분은 계산할 수 없다. $z$ 를 만들기 위해 수많은 parameter 가 들어가기 때문에 매우 높은 차원을 가지기 때문이다.
• 만약 $P_\theta(z)$ 를 다루기 쉬운 Gaussian Distribution 으로 가정하고, 단순하게 $z$ 를 $P_\theta(z)$ 에서 뽑아 maximum 이 되도록 학습을 진행하면 성능이 좋지 않다. 해당 포스트를 참고하자.
• 여기서 우리가 한 가지 떠올려볼 것은, 샘플링된 $z$ 를 통해 우리는 $x$ 와 유의미하게 유사한 데이터를 생성해야 한다는 점이다. 이 부분은 Decoder 에 해당하는 부분이다. 그런데 위에서 $z$ 를 다루기 쉬운 분포를 가정한 $p_\theta(z)$ 에서 샘플링하면 성능이 그리 좋지 않았다.

• 따라서 $z$ 를 샘플링할 때 $x$ 와 유의미하게 유사한 샘플이 나올 수 있는 $p_\theta(z \vert x)$ 에서 샘플링하는 해법을 취해볼 수 있다. 즉 Encoder 를 최적화하는 것이다.

  \[p_\theta(z \vert x) = \frac{p_\theta(x \vert z)p_\theta(z)}{p_\theta(x)}\]
• 그러나 위 식에서 볼 수 있듯 사후확률 $p_\theta(z \vert x)$를 구하기 위해서는 분모의 $p_\theta(x)$ 를 계산할 수 없기 때문에, 이 때 Bayesian 추론의 한 방법인 Variational Inference 를 이용한다.
  • VI 는 데이터 $x$ 가 들어왔을 때 latent vector $z$ 에 대한 사후확률 $P_\theta(z \vert x)$ 를 구하고자 한다.
  • 사후분포 $P_\theta(z \vert x)$ 는 계산이 불가능(intractable)하므로 최적화 문제로 바꾸어서 variational dist $q_{\phi}(z\vert x)$ 를 활용해서 근사한다.
• 이제 이 VI 를 통해 식을 전개하면 우리는 Maximum Likelihood 라는 목적을 이룰 수 있으면서 샘플링 함수를 잘 근사하는 목적도 이룰 수 있는 ELBO 를 유도할 수 있다.

ELBO(Evidence Lower Bound)

• 기억해야 할 것은 우리의 목표는 $\log P_\theta(x)$ 를 최대화하는 것이고, 여기에 잠재변수 $z$ 를 추가하면 나오는 적분식이 계산할 수 없었다는 것이다.
• 그리고 Variational Inference 는 variational distribution($q_{\phi}(z \vert x)$) 과 posterior distribution($p_{\theta}(z\vert x)$) 사이의 거리가 KL-div 관점에서 최소화하도록 최적화하는 것이다.

• 그러면 이제 Variational Inferecne 를 통해 어떻게 Maximum Likelihood 가 ELBO 를 기준으로 이루어질 수 있는지 유도해보자.

  

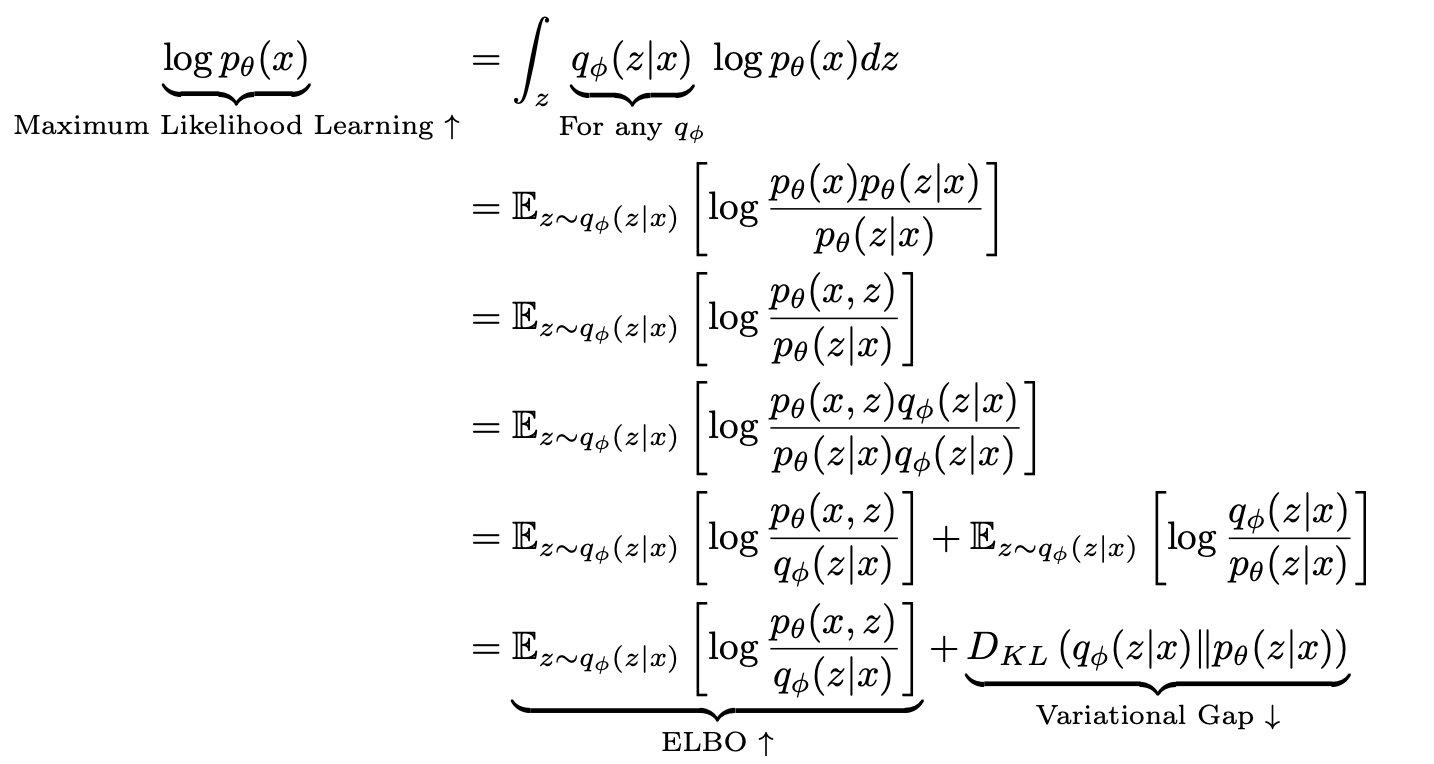
  • 첫번째 식에서 $\int_{z}q_{\phi}(z \vert x)$ 는 1 이므로 $\log p_\theta(x)$ 와 같이 쓸 수 있다.
  • 두번째 식은 연속확률변수에서의 기대값의 정의에 따라 $q_{\phi}(z \vert x)$ 로 정리하고, $\log p_\theta(x)$ 의 분모와 분자에 $\log p_\theta(z \vert x)$ 를 곱한 것이다.
  • 세번째 식은 조건부확률 정의에 따라 분자를 다시 나타내고, 네번째 식에서 분모와 분자에 $\log q_\phi(z \vert x)$ 를 곱해준다.
  • 이를 $\log$ 함수의 정의에 따라 전개하면 맨 아래의 식이 나온다.

• 자세히 보면, 두번째 term 은 Variational Inference 의 목표와 같고 이를 최소화해야 한다. 그러나 $p_\theta(z \vert x)$ 는 구할 수 없다.

  

• 따라서 counter part 에 해당하는 첫번째 term 인 ELBO 를 최대화함으로써 Variational Gap 을 줄이는 것이다. 이를 통해 내가 원하는 variational dist 를 posterior 와 최대한 근사시키는 것이다.
• 또한 KL-divergence 는 항상 0 보다 크거나 같기 때문에 $\log P_\theta(x)$ 는 ELBO 보다 크거나 같다.
• 그렇게 보면 $\log P_\theta(x)$ 에서 $P_\theta(x)$ 는 Evidence 에 해당하고 하한선 Lower Bound 를 잡아주기 때문에 ELBO 라고 불리는 것이다.
• 즉 ELBO 를 최대화하는 것은 원래의 문제인 log likelihood 를 최대화하는 것과 동일하며, 동시에 Variational Inference 의 목표인 posterior 와 variational dist 사이의 거리를 최소화시키는 것이다.
• 따라서 maximum likelihood 라는 목표는 maximum ELBO 로 바뀌게 된다. 이제 최적화할 때 이 ELBO 를 최적화하는 것이다.

• 이제 이 ELBO 를 다시 한번 전개하면 아래와 같이 나타낼 수 있다.

  \[\begin{aligned} \underbrace{\mathbb{E}_{z \sim q_{\phi}(z\vert x)}\left[\log \frac{p_\theta(x, z)}{q_\phi (z \vert x)}\right]}_{\color{red}{\text{ELBO} \; \uparrow}} &= \int q_\phi(z\vert x)\log \frac{p_\theta(x \vert z)p(z)}{q_\phi(z\vert x)} \text{d}z \\ &= \int q_\phi(z\vert x)\log p_\theta(x\vert z) - \int q_\phi(z \vert x) \frac{q_\phi(z \vert x)}{p(z)} \\ &= \underbrace{\mathbb{E}_{q_\phi(z \vert x)}[\log p_\theta(x \vert z)]}_{\color{blue}{\text{Reconstruction Term}}} - \underbrace{\mathbb{KL}(q_\phi(z \vert x) \Vert p(z))}_{\color{blue}{\text{Prior Fitting Term}}} \\ \end{aligned}\]
• 기대값을 전개하고 결합확률을 chain rule 로 펼친 뒤 정리한 것이다.
• VAE 에서 $q_{\phi}$ 는 Encoder 를 뜻한다. 그렇다면 첫번째 Reconstruction Term 은 Encoder 를 통과한 latent vector $z$ 를 가지고 $x$ 를 만들어내는 Decoder 가 모두 식에 있으므로, Encoder 와 Decoder 를 모두 통과한 것이 된다.
  • 이 term 을 높이는 것이 reconstruction 을 잘하는 것이다. 이것만 있으면 AE(AutoEncoder) 와 동일하다.
  • 사실 이 term 을 보면 negative cross entropy 와 같다. 또한 log likelihood 와도 같기 때문에 MSE 도 될 수 있다. 즉 $x$ 에 대한 복원 오차를 나타낸다.
• 두번째 term 인 prior fitting term 은 - 가 붙어있기 때문에 ELBO 를 높일 때 이 term 은 낮추게 된다.
  • $p(z)$ 는 prior 다.
  • Gaussian Distriution 과 같은 내가 미리 정해놓은 $z$ 에 대한 prior distribution 과 Encoder 를 통과해서 나오는 $z$ 들의 분포를 KL-div 로 계산하는 것이다.
  • prior fitting term 을 낮추는 것은 두 분포를 비슷하게 만드는 것이다. 즉 term 속에 prior 가 들어가기 때문에 latent vector $z$ 가 그냥 존재하는게 아니라 내가 미리 정해놓은 prior 와 최대한 비슷하게 만드려는 것이다.
  • 이는 $q_\phi(z \vert x)$ 가 prior $p(z)$ 와 유사했으면 좋겠다는 생각을 반영한 term 이다. 마치 MAP 와 유사하게 Regularization 의 역할을 한다고 볼 수 있다.
  • 따라서 Regularization Term 이라고도 부른다.
• 정리하면, 우리는 Maximum Likelihood 를 부호를 뒤집어 loss function 으로 만들고 이를 최적화하기 때문에 ELBO 를 최소화해야 한다. 그러면 Encoder 와 Decoder 를 통과해서 나오는 reconstruction loss 를 최소화함과 동시에, 데이터 $x$ 들을 Encoder 에 통과시켰을 때 얻는 $z$ 들을 미리 정해놓은 prior dist 와 비슷하게 만드는 prior fitting term 을 같이 최적화 시키면 된다.

• 단점도 몇가지 있다!

  

  • 근사를 통해 최적화하기 때문에 여기서 나오는 Encoder 와 Decoder 를 모두 확률분포라고 보기 어렵다.
  • prior fitting term 도 미분이 가능해야 한다. 그럴려면 KL-div 가 미분 가능해야 하는데, 많은 경우에 해당하는 continous 공간에서 KL-div 는 적분으로 이루어져 있기 때문에 미분하려면 적분이 풀려야 한다.
  • 따라서 다양한 latent prior distribution 을 사용할 수 없고, 많은 경우에 Gaussian 을 활용한다.
  • 더욱이 prior dist 를 isotropic Gaussian 으로 가정을 했을 때만 prior fitting term 이 미분 가능해진다.
  • 따라서 VAE 에서 Gaussian 을 쓰는 이유는 prior fitting term 을 최적화하기 위해서이다. 자세한 것은 VAE 를 정리하는 포스트에서 알아보자.
  • 이런 제약조건들을 풀어나갔던 논문들이 AVB, AAE, WAE 다. 이것들은 non-Gaussian dist 를 prior 로 활용하는 알고리즘이다.
• 최종적으로,
  • Variational Autoencoder(VAE)는 latent variable 모델로, 데이터를 압축된 표현(latent space)으로 변환한 후 다시 원본과 유사한 출력을 생성한다.
  • 이 latent space 에서의 샘플링을 통해 새로운 데이터나 예측이 생성될 수 있게 되는 것이 VAE 의 주요 특징 중 하나이다.
  • 사실 VAE 로 생성된 결과들이 그렇게 좋지는 않다. 밑에서 다룰 GAN 이나 diffusion 이 훨씬 잘 된다.

Generative Adversarial Networks

• GAN 에 대해 간략하게 알아보자. 아래 그림은 GAN 의 학습방법을 나타낸다.

  

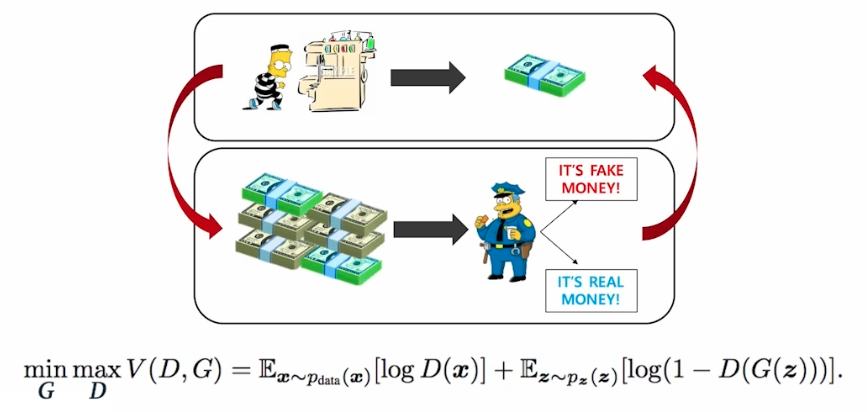
• 판별자($D$)는 내가 들고 있는 실제 데이터인지, 생성자($G$)가 만든 가짜 데이터인지를 구분한다.
  • 즉 판별자 Discriminator 는 가짜와 진짜 샘플을 구별하는 모델로, 진짜 샘플에 대한 확률을 최대화하려고 한다.
• 생성자($G$)는 판별자($D$)를 속이는 역할을 한다.
  • 즉 생성자 Generator 는 실제 데이터 분포와 유사한 샘플을 생성하는 모델로, Discriminator 가 가짜 샘플을 진짜로 잘못 분류하게 만드는 것을 목표로 한다.
• GAN 의 이름에 포함되어 있는 Adversarial 는 적대시한다는 것인데, 이는 두 개의 네트워크($D, G$)가 서로가 서로를 속이려고 하기 때문이다.
• GAN 의 학습은 JSD 를 최소화한다고 말하는 경우가 많다. 왜 그럴까?

  • 앞에서 봤듯 GAN 에는 두 개의 네트워크 $D, G$ 가 존재한다.

    

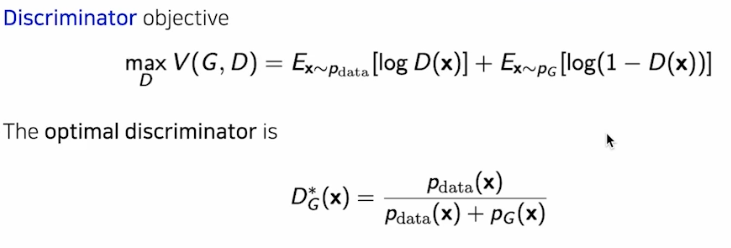
  • 이 때 $G$ 를 고정한 상태에서 $D$ 를 최적화 하면 optimal 포인트($D^{\ast}_G(X)$)가 존재한다.

  • 이를 GAN 의 objective function 에 대입하면 아래와 같다.

    

  • 결과로 JSD 가 튀어 나온다. 이 포스트에서 정리했듯 JSD 는 KL-div 를 조금 바꾸어 대칭성을 만족시켜 사용하는 것이다.
  • 위 식에서 볼 수 있듯 GAN objective 의 lower bound 는 항상 $-\log 4$ 다.
• GAN 의 전체 목적함수는 Discriminator 의 log likelihood 를 최소화하고, Generator 의 log likelihood 를 최대화하는 것을 포함한다.
• 이 때 이 목적함수는 뭔지 모르지만 존재하는 $P_{\text{data}}$와 최적화하려고 하는 Generator $P_G$ 사이의 JSD 를 최소화하는 objective 라고 해석 할 수 있다.
• 많은 GAN 의 아류들은 이 objective 를 조금씩 치환해서 학습을 잘 시키도록 발전했다.
• GAN 은 학습이 굉장히 어렵다. 판별자 $D$ 만 삐끗해도 생성자 $G$ 가 망가지기 때문이다. 즉 서로가 서로에게 적대시하지만 의존하고, 두 개의 모델 사이의 밸런스를 맞추는 것이 어렵다.
• 실제로 GAN 학습 중 Discriminator 가 완벽하게 학습되면 Generator 는 학습이 어려워지는 vanishing gradient 문제에 직면하게 될 수 있다.

• DCGAN 등 엄청나게 많은 GAN 방법론들이 나왔다. 이러한 것들은 시간이 되는대로 하나씩 정리해볼 예정이다.

  

Diffusion Models

• 요즘 생성모델은 Diffusion model 을 빼놓을 수 없다.
• 이 Diffusion Model 에는 수식이 굉장히 많이 들어간다. 종이로만 정리해도 3장이 넘어간다.
• 간단하게만 말하면, Diffusion Model 은 노이즈로부터 이미지를 만드는 것이다.
  • 예를 들어 VAE 를 생각해보면, 노이즈 벡터로부터 이미지를 만든다고 볼 수 있다. latent space 가 Gaussian 분포이고, 샘플링된 Gaussian 벡터가 이미지로 만들어지기 때문이다.
  • GAN 도 마찬가지다. 어떤 latent vector $z$ 혹은 노이즈 벡터 $z$ 로부터 $G$ 를 통과하면 이미지가 나온다. 노이즈로부터 이미지를 생성한다는 것은 비슷한 것이다.

• 큰 차이점은, Difussion Model 들은 이미지들 혹은 노이즈들을 조금씩 변경시켜 가면서 이미지를 만든다.

  

• Diffusion 논문은 노이즈 벡터로부터 1000번의 연산을 반복해서 이미지를 얻는다. 그러나 성능이 엄청 좋다. 잘 구현했을 때 생성되는 이미지의 퀄리티는 GAN, VAE 비해 월등히 좋다.
• 데이터가 고정되어 있고, 모델의 parameter 숫자가 거의 동일하다면 이미지 생성 입장에서 Diffusion Model 이 성능이 가장 좋다고 알려져 있음.

• 여기서는 2가지 key concept 을 이해해야 한다.

  

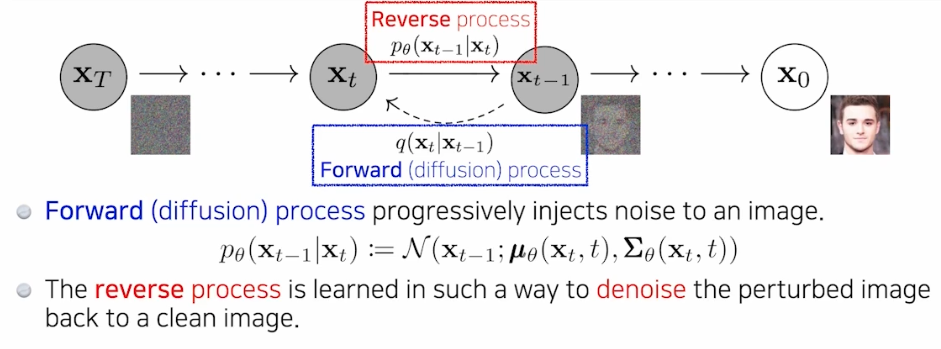
  • 첫번째는 diffusion process 다.
    • 이것 때문에 모델의 이름이 Diffusion 이다.
    • Diffusion Model 은 정확히 말하면 이미지를 만드는 과정이 아니라 오히려 반대다.
    • 즉 이미지에 노이즈를 집어 넣어서 이미지를 점점 노이즈화 시키는 것이다.
    • 이 forward process 즉 diffusion process 는 미리 정해져 있다.
  • 두번째는 reverse process 다.
    • 실제 학습하는 부분으로 diffusion process 의 역과정이다.
    • 즉 우리가 미리 정해진 방법으로 노이즈를 집어넣는 diffusion process 에서 노이즈를 없애고 오리지널 이미지를 복원하는 것을 학습하는 것이다.
• 이 두 가지 concept 에 대해서는 따로 포스트를 만들어 이해할 것이다.
• 이러한 Diffusion Model 은 굉장히 오랜 스텝을 거쳐서 노이즈 벡터를 오리지널 이미지로 조금씩 복원하는 과정이다.
• DALL-E2
  • 이 모델로 Diffusion Model 이 유명해졌다고 생각한다.
  • CLIP 이라고 불리는 모델과 Diffusion 모델을 섞어서 할 수 있다.

  • CLIP 은 이미지와 텍스트 사이의 유사도를 계산하는 모델이다.

    

• Diffusion 모델의 정말 큰 장점은 위 그림처럼 editing 이 가능하다는 것이다. 즉 어떤 특정 영역에 대해서만 내가 이미지를 바꿀 수 있다.

Reference

• 네이버 부스트캠프 AI Tech
• https://glanceyes.com/entry/Deep-Learning-Generative-Model

맨 위로 이동 ↑