[Generative] Generative Model Part 1

Generative Model

• 일반적으로 머신러닝/딥러닝에서 모델을 크게 두 범주로 분류하자면 Discriminative Model 과 Generative Model 로 구분할 수 있다.
• Discriminative model 은 데이터의 레이블을 예측하는 것처럼 decision boundary 를 잘 결정하는 것이 목표인 모델이다.
  • 우리가 일반적으로 잘 아는 classficiation, segmentation, object detection 과 같은 task 를 잘 수행하는 모델로 볼 수 있다.
• 그에 반해 Generative model 은 기본적으로 어떠한 input 이 주어졌을 때 이를 모델에 통과하여 output 을 내는데, 그 결과가 기존 input 과 비교했을 때 핵심적인 내용은 유사하지만 noise 또는 stochastic variation 이 추가될 수 있는 모델이다.
  • 더 정확한 표현으로 정리하자면, 우리가 설명하려는 학습 데이터의 분포를 따르면서 그 분포에서 샘플을 샘플링하여 새로운 데이터를 생성하는 모델이다.

  • 그러면 학습 데이터의 분포를 아는 게 중요한데, 일반적으로 학습 데이터가 주어졌을 때 이 데이터들이 어떠한 분포에서 나왔을 확률이 높은지를 구하는 maximum likelihood estimation(MLE) 으로 구한다.

    

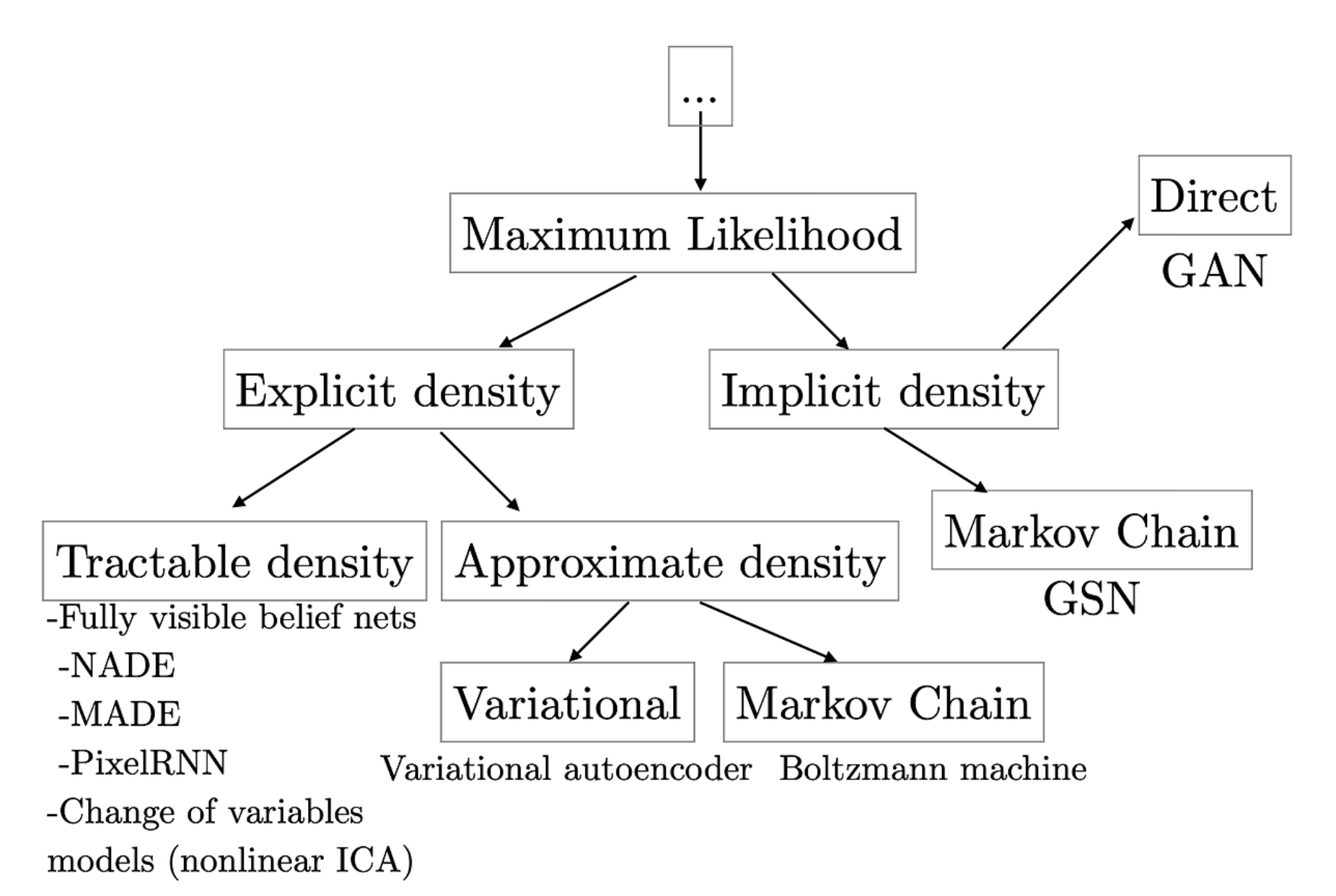
• 이처럼 Generative model 은 설명하려는 학습 데이터의 분포가 어떠한 분포에서 왔을 가능성이 높은지를 maximum likelihood 로 구한다고 했는데, 모델링하려는 확률분포를 명백한 수학적인 모델로 구하는 방법이 explicit density, 그러한 분포를 명백하게 구하지 않는 방법이 implicit density 다.
• Explicit density 방식에서도 두 가지로 분류할 수 있는데, tractable density 방법과 approximate density 방법으로 나눌 수 있다.
• Implicit density 에서는 학습하려는 분포를 직접 구하기보다는 어떻게 그러한 분포를 잘 따르도록 샘플링할지에 관한 방법에 주목한다.
• 일반적으로 Generative model 이라면 자주 언급되는 모델은 아래와 같다.
  • 학습 데이터의 분포에 근사하는 분포를 구하는 VAE(Variational AutoEncoder)
  • 직접적인 분포를 구하지 않고 그러한 분포를 따르는 샘플링을 그럴 듯하게 수행하는 GAN(Generative Adversarial Network)
• 위의 그림을 보면 VAE 는 explicit density 의 approximate density 방법에 속하고, GAN 은 implicit density 에서 direct sampling 을 수행하는 방법으로 분류되어 있다.

• Generative Model 을 학습하는 것은 input 에 대한 distribution $P(X)$ 를 학습하는 것으로 볼 수 있다.

  

Generation

• Generative Model 은 ‘그럴 듯한 가짜’ 또는 ‘실제 데이터 셋에서 볼 수 있을 법한 input’ 을 만들어내는 모델이라고 볼 수 있다.
• 여기서 ’그럴 듯하다’라는 것은 수학적으로 실제 데이터의 분포와 비슷한 분포에서 나온 데이터라는 것을 의미한다.
• 수학적으로 Generative Model 의 목적은 실제 데이터 분포에 근사하는 것이며, 실제 데이터 분포로 근사하는 분포에서 샘플링된 값으로 새로운 데이터를 생성하는 것이다.
• 단순히 generation 만 할 수 있는 모델은 Implicit generative model 이라고 한다. 즉 확률 분포를 직접 모델링하지 않고, 단지 데이터를 생성하는 방법을 학습하는 모델이다. 대표적으로 GAN 이 있다.

Density Estimation

• Density estimation 은 Generative Model 의 중요한 토픽이다.
• 확률분포를 직접 모델링할 수 있는 Generative Model 은 Explicit model 이다.
• 이 모델들은 데이터 생성뿐만이 아니라 확률값(probability denstiy)을 명시적으로 추정할 수 있다.
• 대표적으로 VAE 가 있다.

Distributions

• Generative Model 이 input 에 대한 distribution 을 학습하는 것이라면, 학습 데이터의 distribution 을 어떻게 나타낼 수 있을까?

• 어떤 random distribution 을 정의할 때는 나올 수 있는 경우의 수와 분포를 정의하는 모수(parameter)의 숫자를 체크하는 습관을 들이는 것이 중요하다.

  

• Categorical distribution 을 정의할 때 필요한 parameter 수는 $m-1$ 개다. 모두 다 더하면 1 이 나오기 때문에 $m-1$ 개를 알면 나머지 하나는 자동으로 정해지게 된다.

• RGB 이미지의 하나의 픽셀을 모델링하는 예시를 들어보자. 즉 RGB joint distribution 을 모델링하려는 것이다.

  

• 하나의 픽셀은 RGB 각각의 값으로 이루어져 있기 때문에 경우의 수는 각 채널이 가질 수 있는 경우의 수를 모두 곱해준 것과 같다. ($256 \times 256 \times 256$)
• 이 distribution 을 표현하는 데 필요한 parameter 수는 $256 \times 256 \times 256 - 1$ 과 같다.

Independence

• 위 예시를 보면, 모든 경우의 수를 고려해서 확률분포를 정확하게 표현하기 위한 parameter 수가 엄청 많음을 알 수 있다.
• 이를 간략화하는 방법으로 기계학습 방법론이 발전해왔다. 이 때 가장 기본이 되는 성질 중 하나가 Independence 다.

• 예시를 보자.

  

• binary image(gray scale) 의 모든 가능한 경우의 수를 고려한 확률분포를 모델링 하는 것은 불가능에 가깝다.
• MNIST Dataset 조차 28 x 28 의 크기로 가능한 경우의 수가 ${2}^{784}$ 다. 하나의 픽셀은 0 또는 1 을 가지고 총 784 개의 픽셀이 있기 때문이다.
• 이처럼 데이터의 숫자가 내가 학습하고자 하는 parameter 의 숫자보다 적으면 학습이 어렵다. 즉 간단한 이미지를 모델링 하려고 하더라도, 전체 경우의 수를 고려한다면 수많은 데이터가 필요하다.
• 그렇다면 Independence 는 무엇을 뜻할까?
  • random variable(확률변수)들이 independent 하다는 것은 joint distribution(결합확률)이 각각의 개별적인 확률분포로 쪼개질 수 있음을 의미한다.
  • 위 예시로 따진다면 서로의 픽셀이 옆의 픽셀에 아무런 영향을 주지 않는 것이다.
  • independence structure 를 설정(independence assumption)하는 것은 random variable 을 대상으로 하기 때문에 경우의 수는 아무런 차이가 없다. 즉 binary image 예시에서 independence 를 주나 안주나 경우의 수는 $2^n$ 이다.
  • 그러나 independence 를 통해 이 분포를 표현할 수 있는 parameter 의 숫자가 엄청나게 줄어든다.
  • 총 경우의 수가 $n$ 개일 때 이 경우의 수를 표현할 수 있는 parameter 수는 $n-1$ 이었다. 즉, 위 예시에서 $2^{784}$ 개의 경우의 수가 있기 때문에 $2^{784}-1$ 개의 parameter 가 있으면 이미지를 표현할 수 있다.
  • independence structure 를 설정하더라도 우리가 가지는 이미지는 여전히 동일하고 그 이미지의 경우의 수도 여전히 동일하지만, 이 확률분포를 표현하기 위한 parameter 의 숫자는 $2^{n}-1$ 에서 $n$ 으로 줄어든다.
  • 이것을 exponential reduction 이라고 한다.
• 이러한 independence assumption 은 굉장히 많은 기계학습 분야에서 사용해왔다. 대부분의 경우 latent variable(잠재변수) 사이에는 independence assumption 이 가해진다.
• independence assumption 을 한다는 것의 의미는 우리가 표현할 수 있는 표현력을 줄여버리는 것을 의미한다.
  • independence assumption 을 걸어줄 경우, 두 변수 사이의 상관관계를 완전히 무시하기 때문에, 변수 간의 관계를 모델링할 수 없게 된다.
  • 위 예시에서 우리가 independence assumption 를 갖고 binary image 를 모델링한다면 의미있는 이미지를 얻어낼 수 없을 것이다. 왜냐하면 모든 각각의 픽셀들이 서로 독립적이기 때문에 우리가 원하는 모양을 절대로 생성할 수 없다.
  • 각 이미지의 픽셀들이 서로 독립적이라고 가정하는 것은 비현실적이다. 실제로, 이미지 내의 픽셀들은 서로 연관이 있으며 이러한 상관관계가 이미지의 중요한 특성을 형성한다. 만약 모든 픽셀을 독립적이라고 가정하면, 이미지에 대한 중요한 정보를 놓치게 되고 모델의 예측력이 크게 떨어진다.
  • 즉 independence assumption 은 우리가 어떤 현상을 모델링할 때 parameter 의 숫자를 줄여 계산을 단순하게 만드는 효과는 있지만, 유의미한 분포를 모델링하는데 있어서는 좋지 않다.
• 이를 보완하기 위해 conditional independence 가정을 사용한다.

Conditional Independence

• 이 가정은 모델의 복잡도를 줄이면서도 표현력을 어느정도 유지하는 데 중요한 역할을 한다.
• joint distribution 이 있고 independence assumption 이 걸려 있다면 그 중간 어딘가에 우리가 원하는 좋은 공간이 있을 것이다.
• 즉 결합확률을 각각의 개별확률의 곱으로 표현하여 한 변수가 다른 변수에 아무런 영향을 미치지 않는 것보다, 두 변수 간의 상관관계를 완전히 무시하지 않고 조건이 주어졌을 때만 독립적인 관계로 취급할 수 있다.

• 그런 것들을 표현하기 위해서 Conditional Independence 라는 말을 하고, 확률론을 배우면 알 수 있는 내용인 3가지 중요한 규칙을 이해해야 한다.

  

  1. Chain rule 은 결합확률을 조건부확률로 분해하는 규칙이다. Independent 조건 없이도 항상 만족하는 규칙이다.
  2. Bayes rule 은 기본적으로 conditional distribution 사이의 관계를 의미한다.
  3. Conditional Independence 는 조건이 있다.
     • $\text{if} \; x \bot y \; \vert \; z$ 의 의미는 $z$ 라는 random variable 이 주어졌을 때 $x$ 와 $y$ 가 independent 하다는 것이다. 즉 항상이 아니라 $z$ 라는 조건이 주어졌을 때만 독립이다.
     • 이 Conditional Independence 조건은 $z$ 가 주어졌을 때 $x$ 에 대한 conditional distribution($x\vert y$) 이 $y$ 를 때낼 수 있게 된다.
     • 즉 conditional part 를 떼어내기 위해 Conditional Independence 를 쓸 수 있다.
• Independence 가정은 모든 변수를 독립적이라고 가정함으로써 파라미터 수를 크게 줄일 수 있지만, 그 대가로 모델의 표현력을 잃게 된다. 반면, Conditional Independence 가정은 특정 조건이 주어졌을 때만 변수가 독립적이라고 가정하여 파라미터 수를 감소시키면서도 어느정도 모델의 표현력을 유지할 수 있다.
• 예시를 통해 좀 더 이해해보자.

  • Chain rule 은 거의 무조건 만족한다. 그러면 위 binary image 예시에서 Chain rule 을 이용하면 몇 개의 parameter 가 필요할까?

    

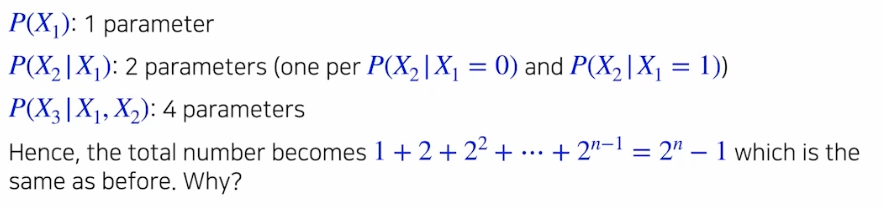
  • 전체 분포를 한번에 보는 것이 아니라 각각의 conditional distribution 으로 쪼개고 parameter 숫자를 모아서 더하는 것이다.
  • 결론부터 보면, 앞에서 본 $2^n -1$ 과 동일하다.
  • 즉 아무런 조건이 주어지지 않았기 때문에 parameter 수는 여전히 같다. 새로운 조건이 생긴 것이 아니라 항상 만족하는 chain rule 을 가지고 원래 우리가 가지고 있던 joint distribution 을 쪼갠 것에 불과하기 때문이다.
  • 위에서 $P(X_2 \vert X_1)$ 는 2 개의 parameter 를 가진다. 이는 $P(X_2)$ 는 1 개의 parameter를 가지고, $X_1$ 은 0 또는 1 인 2 개의 경우의 수를 가지기 때문이다.
  • 즉 등비수열의 합이 된다. 그리고 이는 앞에서 본 joint dist 에서 필요한 parameter 숫자와 정확히 일치한다.

  • 여기에 Conditional Independence 조건을 가하면 어떻게 더 쪼개지는지 보자. 구체적으로 아래와 같이 Markov assumption 을 가하는 것이다.

    

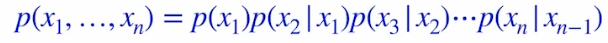
  • Chain rule 에서 길게 붙은 조건부가 다 쪼개지고 하나의 조건부만 붙는 것이다.
  • 이렇게 Markov assumption 을 가한 parameter 수는 $2n -1$ 이 된다. 즉 $1 + 2 + 2 + \ldots + 2$ 가 된다.
  • 이는 앞에서 본 fully independence 조건 하에서의 parameter 수($n$) 보다는 크고, independence 조건이 없는 parameter 수($2^n-1$) 보다는 작다.
• 위 예시를 통해 Conditional Independence assumption 을 주고 중간 어딘가에 있는 좋은 공간을 가져온 것을 알 수 있다.
• 이렇게 Conditional Independence assumption 은 실용적이면서 사용할 여지가 있다.
  • 불필요하고 복잡한 상관관계를 모두 모델링하지 않으면서, 필요한 관계만을 유지할 수 있다. 이를 통해 모델은 적은 파라미터로 데이터의 중요한 구조를 학습할 수 있다.
  • 실제 데이터에서는 모든 변수가 독립적이지 않으며, 특정 조건 하에서만 독립적일 수 있다. Conditional Independence 가정은 이러한 현실적인 상황을 반영하여 변수 간 상관관계를 모델링할 수 있다.
  • Conditional Independence 을 이용하면 모델의 계산 복잡도를 줄일 수 있어 더 빠르게 학습할 수 있다.
• 이것을 가장 잘 활용하는 모델이 AR(AutoRegressive)모델이다.

Autoregressive Models

• Autoregressive Model 은 주어진 과거 값들에 조건을 둔 현재 값의 확률을 모델링하는 것이다. 다시 말해, AR 모델은 과거의 데이터 포인트들을 바탕으로 현재 값의 조건부 확률을 계산하려고 시도한다.

• 아래 예시를 통해 이해해보자. 우리는 아래와 같은 28 x 28 binary image 를 가지고 있다.

  

• AR 모델에서도 학습 데이터의 확률분포 $P(X)$ 를 모델링 하는 것이 목적이다. 여기서 $P(X)$ 는 아래와 같다.

  \[P(X) = P(X_1, \ldots, X_{784}), \quad X \in \{ 0, 1 \}^{784}\]

• 이 $P(X)$ 를 모델링하기 위해서 Chain rule 과 conditional independence(Markov assuption) 구조를 활용하여 joint distribution 을 쪼갠다.

  \[P(X_{1:784}) = P(X_1)P(X_2\vert X_1)P(X_3 \vert X_2)\cdots\]
• 위처럼 $X_1$ 은 그 자체로 존재하고, 두번째 픽셀($X_2$)은 첫번째 픽셀에 dependent, 세번째 픽셀은 두번째 픽셀에 dependent 하는 식으로 순차적으로 정의되는 모델을 AR 모델이라고 한다.
• 이 때 ordering 이라고 하는 중요한 limitation 이 존재한다.
  • AR 은 1 차원의 시퀀스가 필요하다. 이미지를 row-wise 하게 한 줄로 순서를 매기는 것을 raster scan order 라고 부른다.
  • 우리가 임의의 방법으로 2, 3 차원에 존재하는 이미지를 한 줄로 피는 ordering 작업이 AR 에서는 꼭 필요하다.

NADE(Neural Autoregressive Density Estimator)

• AR 을 딥러닝에 가장 먼저 활용한 논문이 NADE(Neural Autoregressive Density Estimator) 다.
• NADE 는 데이터의 결합확률 분포를 모델링하는 데 사용되는 신경망 기반의 방법론이다.

• 데이터의 각 차원에 대한 조건부확률을 학습하여 전체 데이터의 확률 분포를 추정한다. 이러한 접근법은 복잡한 밀도 추정 문제에 효과적으로 사용될 수 있다.

  

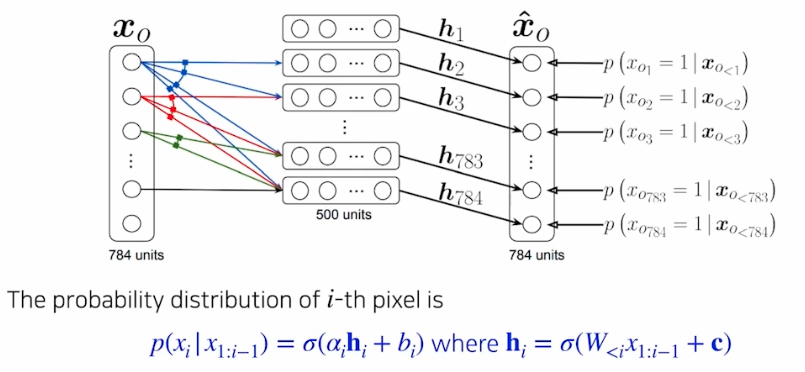
• 위와 같은 conditional dist 를 NN 를 이용해서 모델링한다.

• NADE 는 explicit 모델이다. 즉 단순히 무언가를 생성할 수 있을 뿐 아니라 어떤 새로운 input 이 주어졌을 때, 그 input 혹은 그 이미지가 우리가 모델링 하는 분포에 얼마나 likely 한지 density 를 구할 수 있는 모델이다.

  

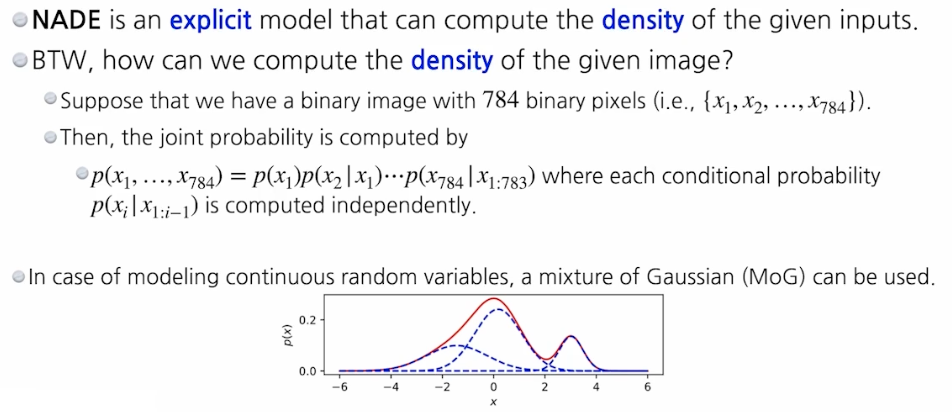
• 그렇다면 어떻게 density(probably density)를 구할 수 있을까?
• joint dist 는 각각의 conditional dist 의 곱으로 표현할 수 있다.
• NADE 가 모델링 하는 것은 각각의 conditional dist 를 모두 구할 수 있는 방법으로 모델링 된다.
• 각각의 이미지가 주어졌을 때 모든 항들을 다 구하고, 이 항들을 다 곱하는 방법으로 전체 이미지에 대한 joint dist 를 구하는 것이다.
• continuous random variable 에서도 가능하다. 이 경우에는 Mixture of Gaussian(MoG) 방법론을 이용해서 conditional dist 를 모델링 할 수 있다.

Pixel RNN

• RNN 을 사용하여 AR model 을 정의할 수도 있다.

• $n \times n$ 의 RGB 이미지인 경우에 모델링하는 $P(X)$ 는 다음과 같다.

  \[P(X) = \prod^{n^2}_{i=1}P(X_{i,R}\vert X_{<i})P(X_{i, G}\vert X_{<i}, X_{i, R})P(X_{i, B}\vert X_{<i}, X_{i, R}, X_{i, G})\]
• $i$ 번째 픽셀은 1 부터 $i-1$ 까지의 픽셀 뿐만 아니라 $i$ 번째 픽셀의 RGB 값도 고려한다.

• Pixel RNN 은 ordering 을 어떻게 하느냐에 따라 두 가지로 나눌 수 있다.

  

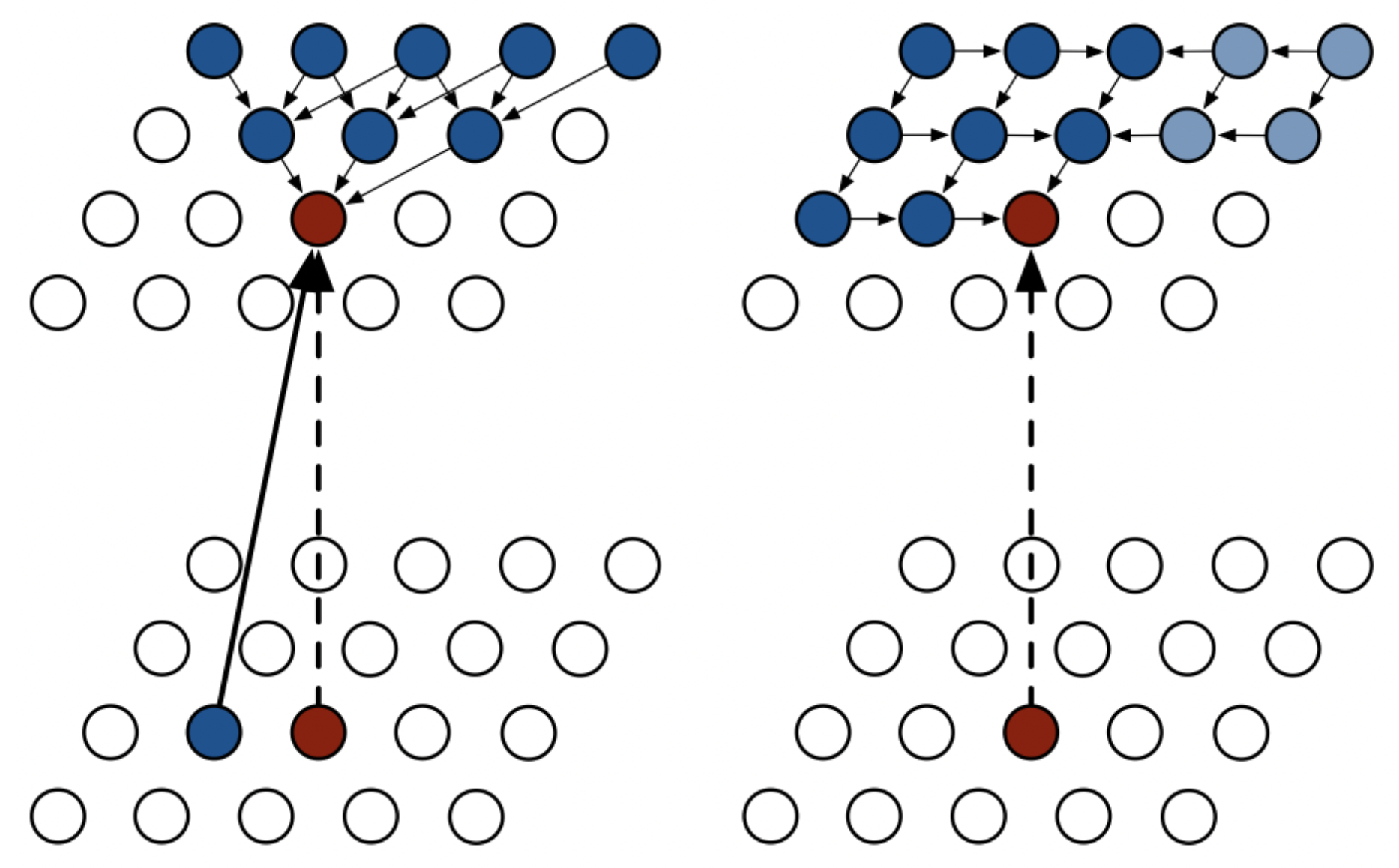
• 위 그림에서 왼쪽이 Row LSTM, 오른쪽이 Diagonal LSTM 방식을 도식화한 것이다.

AR 의 장점과 단점

• 첫번째 장점은 샘플링이 굉장히 쉽다는 점이다.
  • 전체 이미지 혹은 데이터를 한번에 모델링 하기 위해서는 꽤 큰 네트워크가 필요하다.
  • AR 은 기본적으로 전체 input 을 dim 별로 쪼개서 모델링 하기 때문에 샘플링 하기 쉽다.
  • 첫번째 값을 샘플링하고, 그것을 고정한 상태에서 conditional dist 의 다음 것을 샘플링 한다. 즉 sequential 하게 샘플링하는 것이다.
• 두번째 장점은 explicit 한 모델이라는 것이다.
  • implicit 모델은 생성을 할 수 있지만 새로운 이미지가 주어졌을 때 이것에 대한 probably density(밀도 추정)를 구할 수 없는 경우가 많다. GAN 이 대표적인 implicit 모델이다.
  • 그러나 AR 은 새로운 입력이 주어졌을 때 이것에 대한 joint dist 혹은 dist 를 꽤 쉽게 구할 수 있다.
• 세번째로 joint dist 를 구하는 것의 장점 중 하나는 각각의 dim 별로 쪼개서 구할 때 병렬화를 할 수 있어 확률을 계산하는 것(density estimation)이 빠르다는 점이다.
• 마지막으로 descrete random variable 에서 continuous random variable 로 확장하기 꽤 쉽다.
  • 다른 생성 모델들은 둘 다 고려하는 게 쉽지 않다. 하지만 AR 은 꽤 잘할 수 있다.
  • AR Model 은 여러 변수 간의 시간적인 의존성을 모델링하는데 효과적이다. 연속 변수로의 확장성이 좋으며, Gaussian Model 과 같은 확률 모델을 사용하여 예측을 수행할 수 있다.
• 단점으로 샘플링은 $n$ 번의 NN 을 sequential 하게 통과해야 한다는 점이다.
  • 즉 병렬화할 수 없다. 왜냐하면 $i$ 번째 입력을 만들기 위해서는 $i-1$ 번째 입력이 필요하기 때문이다. 이러한 이유로 Generation 이 느리다.

Reference

• 네이버 부스트캠프 AI Tech
• https://glanceyes.com/entry/Deep-Learning-Generative-Model

맨 위로 이동 ↑