[Deep Learning, Pytorch] Autograd
기울기를 자동으로 계산하는 기능은 딥러닝 알고리즘 구현을 매우 간단하게 해준다. 이 포스트에서 다룰 자동 미분(automatic differentiation)이 나오기 전에는 복잡한 모델에 작은 변화를 주더라도 복잡한 도함수를 일일이 손으로 다시 계산해야 했다.
이러한 자동 미분은 대부분의 딥러닝 라이브러리들의 고유한 기능이다. 딥러닝 라이브러리는 기본적으로 행렬 연산을 하는 라이브러리지만, 기존의 행렬 연산 라이브러리와 달리 딥러닝 라이브러리에는 Autograd 기능이 있다. Autograd 는 forward 와 backward pass 가 편리하게 가능하도록 만들어준다.
계산그래프와 자동 미분 덕분에 딥러닝을 사용하려는 유저의 난이도를 낮춰놨고, 다양한 사람들이 쉽게 딥러닝에 접할 수 있게 됐다. 이번 글에서는 Pytorch 에서 수행하는 자동 미분에 대해 알아보자. 간단한 미분 예제와 그에 대응하는 코드를 통하여 Pytorch 에서 미분이 어떻게 계산되는지 살펴볼 것이다.
Autograd 기본
- 우리가 딥러닝에서 하나의 값을 계산하기 위해서 다양한 프로세스를 거쳐 계산을 진행하는데, 그 속의 많은 변수들을 가지고 있다.
- 그리고 이 연산을 반대로하여 gradient 를 계산할 수 있도록 쉽게 만들어주는 것이 Autograd 다.
- 위에서 언급한 것처럼 과거에는 forward 를 일일이 손으로 계산하고 backward 를 일일이 구현했다. 그러나 이제는 computational graph(계산그래프) 라는 편리한 데이터 구조를 사용해서 automatic differentiation(자동 미분) 을 진행한다.
- 어떤 tensor 가 학습에 필요한 tensor 라면 back propagation 을 통하여 gradient 를 구해야 한다. 즉 미분을 해야 한다.
- tensor 의 gradient 를 구할 때는 아래의 조건들이 만족되어야 한다.
- 1) tensor 의 옵션이
requires_grad = True로 설정되어 있어야 한다. 기본적으로 tensor 를 생성할 때 기본값은requires_grad = False다. - 2) back paropagation 을 시작할 지점의 output 은
scalar형태여야 한다.
- 1) tensor 의 옵션이
- tensor 의 gradient 를 구하는 방법은 back propagation 을 시작할 지점의 tensor 에서
.backward()함수를 호출하면 된다. - gradient 값을 확인하려면
requires_grad = True로 생성한 tensor 에서.grad를 통해 값을 확인할 수 있다.
Autograd 예제
- Pytorch 의
Autograd는자동 미분 (Auto differentitation)을 이용하여기울기(Gradient)계산을 한다는 것을 뜻한다.
import torch
x1 = torch.ones(2, 2)
print(x1)
# tensor([[1., 1.],
# [1., 1.]])
x2 = torch.ones(2, 2, requires_grad = True)
print(x2)
# tensor([[1., 1.],
# [1., 1.]], requires_grad=True)
- 위 예제에서
x1은torch.ones를 이용하여(2, 2)크기의 tensor 를 생성한 것이고,x2는requires_grad=True옵션을 주고 생성한 것이다. x2의 경우 출력 결과에requires_grad=True가 나타난다. 이는 이후 역전파 과정을 수행 후 해당 tensor 의 gradient 를 구할 수 있도록 한다.- 이제 위에서 사용한
x1과x2를 이용하여 추가적인 산술 연산을 하면 어떻게 되는지 살펴보자.
import torch
x1 = torch.ones(2, 2)
print(x1)
# tensor([[1., 1.],
# [1., 1.]])
y1 = x1 + 2
print(y1)
# tensor([[3., 3.],
# [3., 3.]])
x2 = torch.ones(2, 2, requires_grad=True)
print(x2)
# tensor([[1., 1.],
# [1., 1.]], requires_grad=True)
y2 = x2 + 2
print(y2)
# tensor([[3., 3.],
# [3., 3.]], grad_fn=<AddBackward0>)
- 각
x1과x2에 덧셈 연산을 수행하여y1,y2를 만든다. 코드 결과를 보면,requires_grad=True를 준 tensor 인y2의 연산 수행 결과에grad_fn=<AddBackward0>가 있는 것을 확인할 수 있다. grad_fn에는 tensor 가 어떤 연산을 했는지 연산 정보를 담고 있고, 이 정보는 역전파 과정에 사용된다.
import torch
x = torch.ones(2, 2, requires_grad=True)
y1 = x + 2
print(y1)
# tensor([[3., 3.],
# [3., 3.]], grad_fn=<AddBackward0>)
y2 = x - 2
print(y2)
# tensor([[-1., -1.],
# [-1., -1.]], grad_fn=<SubBackward0>)
y3 = x * 2
print(y3)
# tensor([[2., 2.],
# [2., 2.]], grad_fn=<MulBackward0>)
y4 = x / 2
print(y4)
# tensor([[0.5000, 0.5000],
# [0.5000, 0.5000]], grad_fn=<DivBackward0>)
- 행렬의 대부분의 연산은 위 식에서 나타나는 사칙연산(덧셈, 뺄셈, 곱셈, 나눗셈)을 이용한다.
- 이 때, 각 tensor 에서 나중에 이루어지는 역전파를 위해 기록되는
grad_fn에는 각각AddBackward0,SubBackward0,MulBackward0,DivBackward0와 같이 저장되어 있다.
x = torch.ones(2, 2)
y = x + 2
print(x)
# tensor([[1., 1.],
# [1., 1.]])
print(y)
# tensor([[3., 3.],
# [3., 3.]])
y.requires_grad_(True)
print(x)
# tensor([[1., 1.],
# [1., 1.]])
print(y)
# tensor([[3., 3.],
# [3., 3.]], requires_grad=True)
- 만약
requires_grad가 없는 tensor 에서 속성을 추가할 때에는y.requires_grad_(True)와 같은 방식으로 속성값을 추가해준다. - 다만, 이렇게 별도로
requires_grad를 추가한 경우 앞에서 연산한 이력이grad_fn으로 자동으로 저장되지는 않는다.
derivative
-
Pytorch 에서 실제 미분은 어떻게 연산 되는지 살펴보자. 먼저 아래의 식을 $x$ 에 대하여 미분하자.
\[f(x) = 9x^{4} + 2x^{3} + 3x^{2} + 6x + 1\] -
도함수 $df(x) / dx$ 를 구하면 $x = a$ 지점의 gradient 를 구할 수 있다.
\[\frac{df(x)}{dx} = \frac{d(9x^{4} + 2x^{3} + 3x^{2} + 6x + 1)}{dx} = 36x^{3} + 6x^{2} + 6x + 6\] - 만약 $x = 2$ 라고 하면 gradient 는 $36 \times 2^{3} + 6 \times 2^{2} + 6 \times 2 + 6 = 330 $ 이다.
- 이 과정을 코드로 보자.
x = torch.tensor(2.0, requires_grad=True)
y = 9*x**4 + 2*x**3 + 3*x**2 + 6*x + 1
y.backward()
print(x.grad)
# tensor(330.)
- 여기서 유의할 점은 output 인
y가 scalar 라는 점이다. 앞에서 언급한 바와 같이 output 이 scalar 여야backward연산이 된다. - 만약 output 이 scalar 가 아니면
backwrard연산이 되지 않는다.
x = torch.randn(2, 2, requires_grad=True)
y = x + 2
z = (y * y)
z.backward()
# RuntimeError: grad can be implicitly created only for scalar outputs
- 위 예제는
z가 scalar 값이 아니라2, 2크기의 matrix 이기 때문에 에러가 발생한다. - 따라서 다음과 같은 방식으로 고쳐서 사용해야 정상적으로 사용 가능하다.
x = torch.randn(2, 2, requires_grad=True)
y = x + 2
z = (y * y).sum()
z.backward()
print(x)
# tensor([[ 2.5455, 1.3913],
# [-0.4362, -0.5303]], requires_grad=True)
print(y)
# tensor([[4.5455, 3.3913],
# [1.5638, 1.4697]], grad_fn=<AddBackward0>)
print(z)
# tensor(36.7684, grad_fn=<SumBackward0>)
print(x.grad)
# tensor([[9.0910, 6.7827],
# [3.1276, 2.9394]])
print(y.grad)
# None
print(z.grad)
# None
- 위 예제에서 실제 값이 할당된 tensor 인
x의 경우backward를 통해 계산된grad가 저장된 것을 볼 수 있다. - 반면 중간 과정인
y,z의 경우 실제grad가 저장되지는 않고backward연산에만 참여된 것으로 볼 수 있다. 그 결과y.grad, z.grad는None이 된다. - 만약
backward를scalar가 아닌 matrix 에서 진행하려면 다음과 같이 사용할 수 있다.
x = torch.randn(2, 2, requires_grad=True)
y = x + 2
z = (y * y)
y.backward(z)
print(x.grad)
# tensor([[2.2796, 3.2123],
# [5.1224, 0.6321]])
- 위의
y.backward(z)처럼z를tensor.backward()의 인자로 넣어주면 연산이 가능해진다. -
그러면 이번에는 위 예제를 응용하여 input 인
\[f(X) = \overline{3(X_{ij} + 2)^{2}} = \frac{1}{4}\sum_{i = 0}^{1}\sum_{j=0}^{1} 3(X_{ij} + 2)^{2}\]x가 scalar 가 아니라(2, 2)shape 의 matrix 형태로 사용해보자. -
위 식에 대한 도함수는 아래와 같다.
\[\frac{df(X)}{dX} = \frac{1}{4} \sum_{i=0}^{1}\sum_{j=0}^{1} (6X_{ij} + 12) = \sum_{i=0}^{1}\sum_{j=0}^{1} (1.5X_{ij} + 3) = 1.5(X_{00} + X_{01} + X_{10} + X_{11} ) + 3 \cdot 4\] -
matrix 에서 각 원소의 값에 대하여 (편)미분하면 다른 원소는 영향을 주지 않는다. 예를 들어 $X_{00}$ 에 대하여 미분하면 그 결과는 $1.5(X_{00}) + 3$ 이 된다. 따라서 2 x 2 matrix $X$ 의 미분 결과는 아래와 같다.
\[\frac{df(X)}{dX} = \begin{bmatrix} 1.5(X_{00}) + 3 & 1.5(X_{01}) + 3 \\ 1.5(X_{10}) + 3 & 1.5(X_{11}) + 3 \end{bmatrix}\] -
그러면 matrix $X$ 가 $X = \lbrace 1.0, 2.0, 3.0, 4.0 \rbrace$ 일 때, 다음과 같이 gradient 값을 구할 수 있다.
\[\frac{df(X)}{dX} = \begin{bmatrix} 1.5(X_{00}) + 3 & 1.5(X_{01}) + 3 \\ 1.5(X_{10}) + 3 & 1.5(X_{11}) + 3 \end{bmatrix} = \begin{bmatrix} 4.5 & 6.0 \\ 7.5 & 9.0 \end{bmatrix}\] - 위 예제를 코드를 통해 살펴보자.
x = torch.tensor([[1.0, 2.0],[3.0, 4.0]], requires_grad = True)
# tensor([[1., 2.],
# [3., 4.]], requires_grad=True)
y = x + 2
# tensor([[3., 4.],
# [5., 6.]], grad_fn=<AddBackward0>)
z = y * y * 3
# tensor([[ 27., 48.],
# [ 75., 108.]], grad_fn=<MulBackward0>)
out = z.mean()
# tensor(64.5000, grad_fn=<MeanBackward0>)
out.backward()
print(x.grad)
# tensor([[4.5000, 6.0000],
# [7.5000, 9.0000]])
- 수식으로 푼 것과 일치하는 것을 확인할 수 있다. 만약 tensor 에서
requires_grad = True를 입력하지 않으면 오류가 발생한다.
partial derivative
-
이번에는 편미분 예제를 다뤄보자. 식 $y = x^{2} + z^{3}$ 이 있다. 이를 변수 $x$ 에 대하여 편미분 해보자.
\[\frac{\partial}{\partial x}(x^{2} + z^{3}) = 2x\] -
다음으로 변수 $z$ 에 대하여 편미분 해보자.
\[\frac{\partial}{\partial z}(x^{2} + z^{3}) = 3z^{2}\] -
이제 $f’(x, z) = f’(1, 2)$ 연산을 해보자. 먼저 $x$ 에 대해 연산하면 아래와 같다.
\[\frac{\partial(f(x) = x^{2})}{\partial x} \quad \text{where } x=1\] \[y'(1) = 2\] -
다음으로 $z$ 에 대해 연산하면 다음과 같다.
\[\frac{\partial(f(z) = z^{3})}{\partial z} \quad \text{where } z=2\] \[y'(2) = 12\] -
위 예제를 코드로 살펴보자.
x = torch.tensor(1.0, requires_grad=True)
z = torch.tensor(2.0, requires_grad=True)
y = x**2 + z**3
y.backward()
print(x.grad, z.grad)
## tensor(2.) tensor(12.)
details
- 역전파 알고리즘의 가장 기본은 chain rule이다. chain rule 은 연쇄를 따라가는 것인데, 여기서 연쇄를 그래프로 나타낸 것이 계산그래프라고 볼 수 있다.
- 그 연쇄, history 를 따라갈 수 있어서 backward 를 구현하기 쉽게 만드는 computational graph 를 항상 유지하고 있는 것이 Autograd 의 핵심 데이터 구조다.
-
예제를 보자.

- $y$ 에 대한
backward를 호출하면, forward 과정에서 $y$ 를 계산하며 저장해 온 computational graph 를 가지고 거꾸로 역전파를 진행한다. - 즉 computational graph 덕분에 역전파를 한 번에 할 수 있고, $\partial y / \partial (?)$ 에서 $?$ 에 들어갈 수 있는 모든 변수에 대해 계산해 놓고 있다.
x.grad는 $\partial y / \partial x$ 를 출력하는 것이다. 이것은 결국 $y$ 함수를 $x$ 에 대해서 미분한 것인데, 위 예제에서는 3 이 나와야 한다.- 그러나 결과값을 보면 300 과 0.3(
tensor([300.0000, 0.3000])) 이 나왔다. 그 이유는backward함수 내에서gradients라는 argument 가 들어갔기 때문이다. gradientsargument 는backward함수의 인자로서 $\partial y / \partial (?)$ 를 계산하는 것이 아니라gradients와 $\partial y / \partial (?)$ 의 곱을 계산해준 것이다.backward함수의 API 는 이런 식으로 설계되어 있다. 그 이유는 스칼라 값에 대해서 미분을 해가면서 위쪽에서 역전파를 통해서 gradient 가 넘어오면, 아래쪽과 chain rule 을 완성시키기 위해 이런 backward API 를 만든 것이다.- 즉 윗단의 gradient 가
backward()안에 들어가게 되는 것이다. 그러면 윗단으로부터 전달되어backward안에 들어가는 argument 와backward함수를 호출한 것이 곱해지면서 chain rule 이 성립되는 것이다. - 이것을 잘 모듈화해서 앞단의 gradient 를 구한 뒤 그 다음 단에 넘겨주는 것을 반복하는 것이다. 그러면 chain rule 이 성립해서 역전파가 된다.
- 위 예제는
.backward()에 gradient vector 를 넣어줬는데, 위에서 본 것처럼 scalar 를 미분할 때는 gradient 를 안 넣어줘도 된다.- 즉 loss 와 같은 스칼라 값이 아니라 vector 로부터
backward가 시작될 때는 해당 vector 와 같은 모양인 gradient 를 argument 로 전달해야 한다. - 아래 예제에서 gradient argument
external_grad는Q자기 자신에 대한 gradient 를 나타낸다. 일반적으로 scalar 값에backward를 진행할 때도 자기 자신에 대한 gradient 인1.0이 default 다.
- 즉 loss 와 같은 스칼라 값이 아니라 vector 로부터
import torch
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
Q = 3*a**3 - b**2
external_grad = torch.tensor([1., 1.]) # Q 자기 자신에 대한 gradient
Q.backward(gradient=external_grad) # gradient 전달
print(9*a**2 == a.grad) # tensor([True, True])
print(-2*b == b.grad) # tensor([True, True])
- 따라서 그림 예제에서
y.backward()에gradient인자를 넣어준 이유는 $y$ 가 2 dim vector 이기 때문이다. 이와 관련한 개념이 있는데, output 인 $y$ 가 vector 인 경우 $x$ 에 대한 $y$ 의 gradient 는 자코비안 행렬이 된다.-
자코비안 행렬(Jacobian Matrix) $J$ 는 vector 함수의 입력 vector 에 대한 출력 vector 의 변화율을 표현한 행렬이다. 이를 통해 다변수 함수에서 입력 변화에 따른 출력 변화의 관계를 나타낼 수 있다. 즉 각 원소별 편미분을 모아놓은 행렬이다.
\[J = \frac{\partial \vec{y}}{\partial \vec{x}} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix}\] - 위처럼 자코비안 행렬 $J$ 는 $x$ 의 각 성분 $\lbrace x_1, x_2, \ldots, x_n \rbrace$ 에 대해 $y$ 의 각 성분 $\lbrace y_1, y_2, \ldots, y_m \rbrace$ 의 편미분을 모아놓은 행렬이다.
- $\frac{\partial y_i}{\partial x_j}$ 은 $y_i$ 를 $x_j$ 로 편미분한 값이다. 따라서 $J$ 의 크기는 $m \times n$ 이다.
-
- Pytorch 의 autograd 는 네트워크의 출력에 대한 입력 변수의 gradient 를 계산하는데, 내부적으로 자코비안-vector 곱(Jacobian-vector product, JVP)이라는 효율적인 방식을 사용한다.
-
만약 출력 $y$ 가 스칼라 값이라면 자코비안 행렬 $J$ 는 열벡터 즉, gradient 벡터 $\nabla y$ 로 축소된다.
\[\vec{g} = \frac{\partial y}{\partial \vec{x}} = \begin{bmatrix} \frac{\partial y}{\partial x_1} & \frac{\partial y}{\partial x_2} & \cdots & \frac{\partial y}{\partial x_n} \end{bmatrix}\] -
그러나 출력 $y$ 가 vector $\vec{y}$ 라면 위처럼 자코비안 행렬을 계산해야 하는데, Pytorch 에서는 자코비안 행렬 전체를 계산하지 않고 특정한 벡터 $v$ 와의 곱 $J^\top v$ 만 계산한다. 이를 자코비안-vector 곱(Jacobian-vector product, JVP)이라고 부른다.
-
import torch
from torch.autograd.functional import jacobian
# scalar 에 대한 gradient 계산
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = x.pow(2).sum() # y = x_1^2 + x_2^2 + x_3^2
y.backward()
print(x.grad) # [2*x_1₁, 2*x_2, 2*x_3] tensor([2., 4., 6.]) -> gradient 벡터
# 자코비안 행렬 계산
def func(x):
return torch.stack([x[0]**2, x[1]**2, x[2]**2])
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
J = jacobian(func, x)
print(J)
# tensor([[ 2., 0., 0.],
# [ 0., 4., 0.],
# [ 0., 0., 6.]])
# 자코비안-벡터 곱
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = torch.stack([x[0]**2, x[1]**2, x[2]**2])
v = torch.tensor([1.0, 1.0, 1.0]) # 자기 자신에 대한 gradient
y.backward(v)
print(x.grad) # J^T * v
# tensor([ 2., 4., 6.])
-
이를 종합해보면
\[\vec{v} = \frac{\partial \ell}{\partial \mathbb{y}} = \left( \frac{\partial \ell}{\partial y_1}, \cdots, \frac{\partial \ell}{\partial y_m} \right)\]torch.autograd는 자코비안-벡터 곱을 계산하는 엔진이다. 만약 vector $\vec{v}$ 가 스칼라 함수(loss function) $\ell=g(\vec{y})$ 의 gradient 인 경우 위에서 본 것처럼 아래 식으로 나타낼 수 있다. -
그리면 연쇄 법칙에 따라 vector $\vec{v}$ 와 자코비안 행렬 $J$ 의 곱이 나오게 되고, 이는 $\vec{x}$ 에 대한 $\ell$ 의 gradient 가 된다.
\[\frac{\partial \ell}{\partial \mathbb{y}} \cdot \frac{\partial \mathbb{y}}{\partial \vec{x}} = J^\top \cdot \vec{v} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_1} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_1}{\partial x_n} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \begin{bmatrix} \frac{\partial \ell}{\partial y_1} \\ \vdots \\ \frac{\partial \ell}{\partial y_m} \end{bmatrix} = \begin{bmatrix} \frac{\partial \ell}{\partial x_1} \\ \vdots \\ \frac{\partial \ell}{\partial x_n} \end{bmatrix} = \frac{\partial \ell}{\partial \vec{x}}\] - 이를 통해 vector 와 자코비안 행렬이 곱해져서 gradient vector 가 나오도록 유도해주는 형태로
backward가 구현이 되어있다고 이해할 수 있다. - 실제로 Pytorch 의 Loss function 을 구하는 함수나 클래스들은 일반적으로 데이터 batch 에 대한 평균(
mean) 또는 합산(sum)된 값으로 loss 를 정의한다. 즉reduction을 하게 되어 있다.- batch loss value 를 스칼라로 축약하지 않으면, 각 샘플마다 별도의 gradient 를 계산해야 하며, 이는 역전파 알고리즘의 설계 및 계산 효율성을 저해하기 때문이다.
- 따라서 scalar loss function 이 일반적이고, 이를 통해 실제 학습 과정에서는 gradient 인자를 건네줄 필요 없이
loss.backward()만 해주면 된다. -
이후 스칼라 값에 대해서 미분을 해가면서 역전파를 통해 gradient 가 넘어오면, 아래쪽과 chain rule 을 완성시키기 위해 이러한 자코비안-벡터 곱이 사용되는 것이다. 그리고
backward()에 위쪽에서부터 흘러온 gradient 가 argument 로 들어가게 되는 것이다.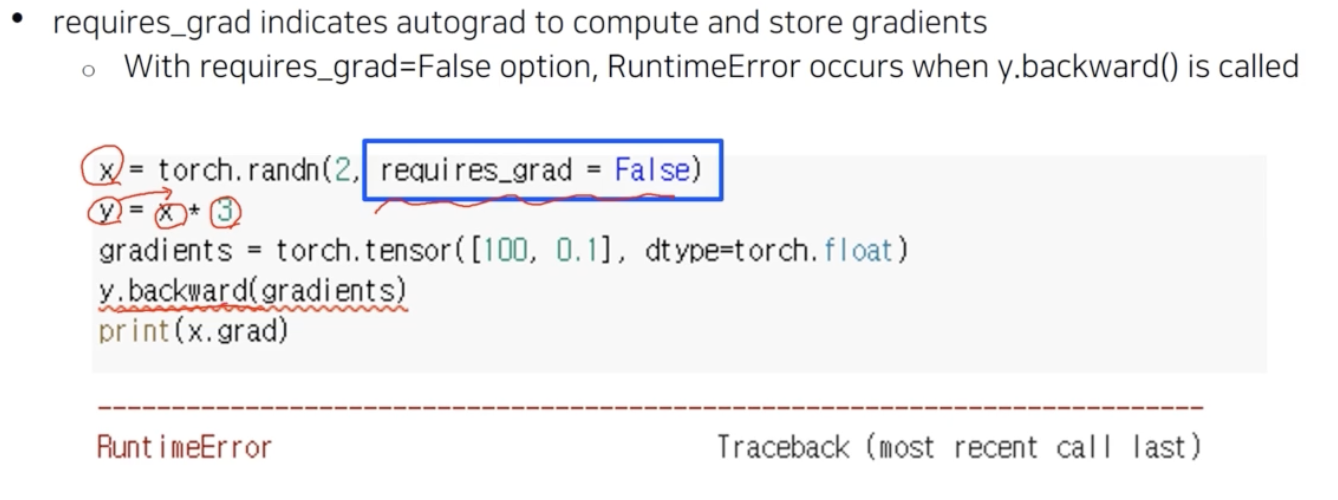
requires_grad = True가 뜻하는 것은 $x$ 가 gradient 를 저장할 수 있는 변수임을 선언하기 위함이다. 그래야지x.grad를 호출할 수 있다.- 만약 위 예제처럼
requires_grad = False를 줘서 $x$ 가 gradient 를 저장하지 못하게 만들면 backward 시 에러가 발생한다. -
즉
y.backward()를 통해 $y$ 에서부터 backward 가 흘러가는데, $y$ 에서 사용된 변수나 상수가 gradient 를 담을 수 있는 그릇이 없는 것이다. 그러면 backward 가 불가능한 함수가 된다.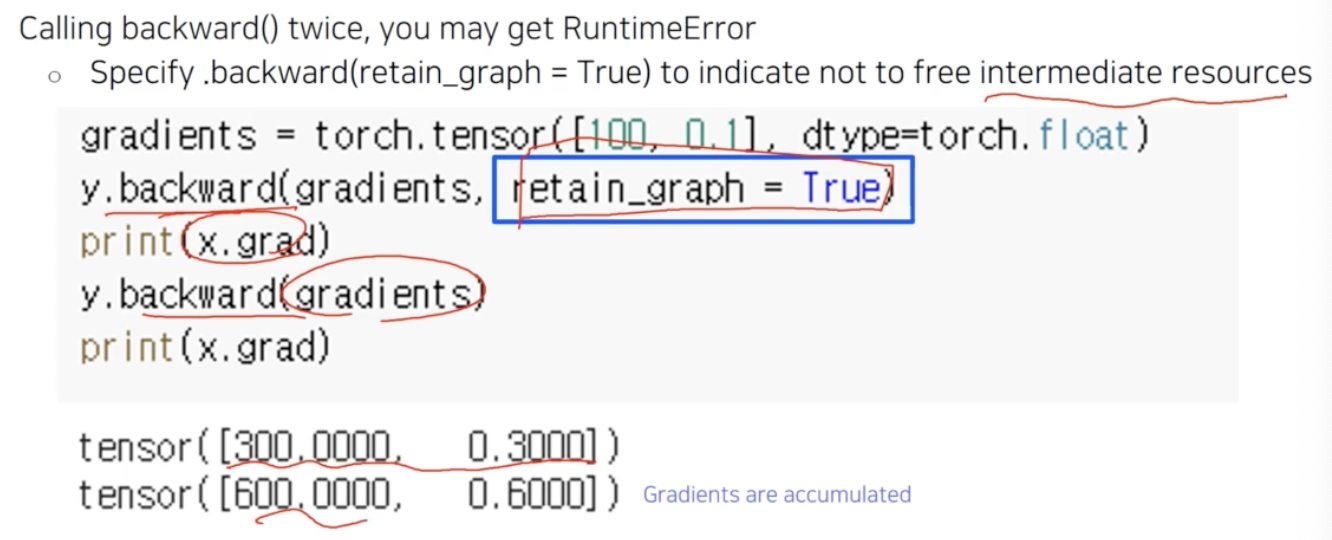
- 또 다른 주의점은 $y$ 에 대해서
backward를 한 번 호출하고 두 번 호출하게 되면, 기존에 있었던 미분값과 두번째 호출에서의 미분값이 더해진다. 즉 중첩(accumulation)이 된다. 그러나 일반적으로 두 번 호출하면 에러가 난다. 이는backward내부의 동작 때문이다. backward를 한 번 호출하면 그 중간에 계산했었던 계산 그래프를 계속 저장하고 있으면 너무 무거우니까 지워버린다. 중간의 intermediate resources 를 다 버려서 메모리를 조금 아낀다.- 역전파를 하면 중간에 계산 그래프를 다 날리더라도 맨 마지막의 gradient 인 leaf tensor 의 gradient 만 확보하면 된다. 따라서 계산 그래프를 날리는 게 default 로 설정되어 있다. 즉
backward를 한 번 호출하면 계산 그래프가 날라가 버리는 것이다. - 만약
backward를 여러 번 호출하고 싶다면retain_graph = True를backward()안에 걸어주면 된다. 이렇게 하면 계산그래프가 사라지지 않는다. - 위 예제를 보면, 처음
backward에retain_graph=True가 되어있고 2 번 실행하니 이전의 결과와 두번째 결과가 더해져 gradient 가 accumulation 되는 효과를 볼 수 있다. - 정리하면,
backward(retain_graph=True)로 설정하면 intermediate resources 를 free 하지 않도록 해서, gradient 를 두 번 계산했을 경우 이전 gradient 와 함께 새로 계산된 gradient 가 accumulated 된다. -
중요한 것은
retain_graph를 쓰던 안쓰던 backward 를 쓰고zero_grad()를 해주지 않으면 gradient 가 계속 누적되는 특성이 있다. 그리고 이러한zero_grad()는 학습과정에서 Optimizer 가 도와주게 된다.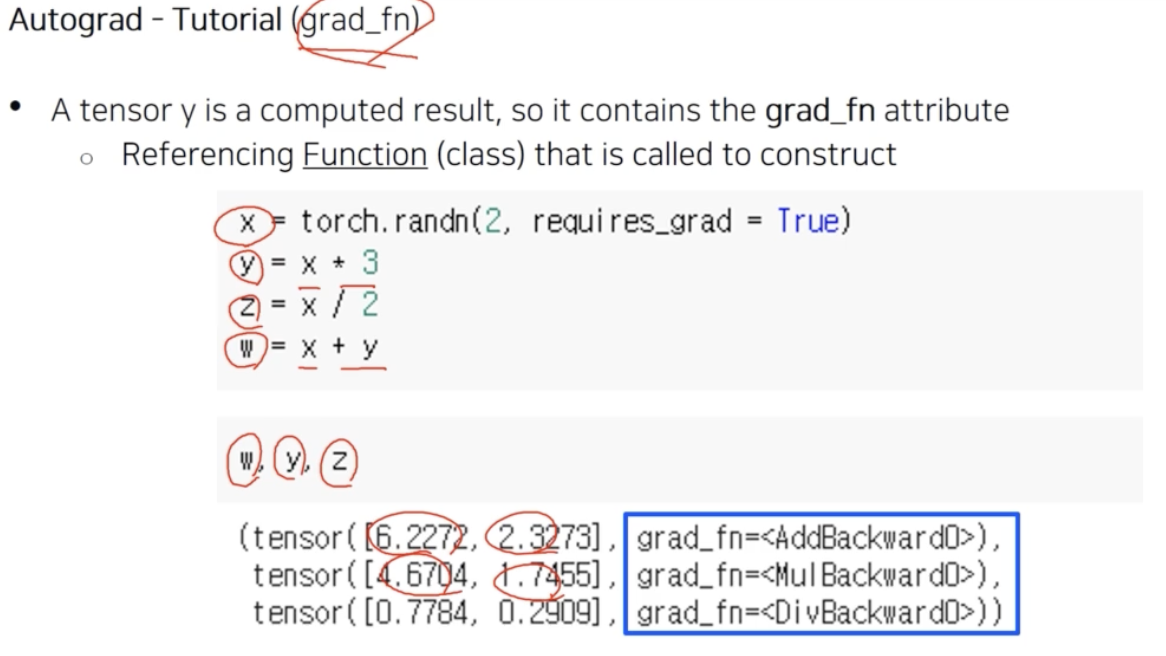
- 위 그림처럼 계산 그래프를 만들었다고 해보자. 위 예제는 $x$ 를 사용해서 $y, z, w$ 를 만들었다.
- $y, z, w$ 가 각각 계산 그래프를 가지고 있는 것이다. 이 계산 그래프를 실제로 역전파할 때 어떤 식으로 구현되느냐를 보면,
grad_fn attribute로 구현되어 있다. - 파란 박스를 보면 $w$ 출력 결과에
<AddBackward0>class 가 등록되어 있다. $w$ 바로 직전에 계산 그래프의 operation 은 더하기(w=x+y)다. 그 더하기에 $x$ 와 $y$ 변수가 걸려있다. - 그래서 $w$ 의 gradient 를 역전파 할 때, 이
grad_fn은 더하기를 통해서 이루어져 있고, 이 더하기의 backward 가 어떻게 구현이 되어야 하는지를 func class 로서 어떤 생성자로 등록되어 있는 것이다. - 즉 backward 를 호출하면
<AddBackward0>가 호출되고 역전파가 이뤄지게 되는 것이다. $y$ 와 $z$ 도 마찬가지다. - 이처럼 하나의 변수가 계산 그래프를 가지고 있는 원리는
grad_fn attribute를 기반으로 되어있다고 이해할 수 있다.
Autograd 관련 Tensor 메서드
- Autograd 기능 관련한
torch.Tensor가 가진 메서드를 알아보자. torch.backward(gradient, retain_graph, create_graph=False)- 인수(기본적으로 1x1 tensor)를 루트 tensor 로 해서 추적 가능한 모든 leaf tensor 까지 backward graph 를 통해 gradient 를 전달하면서 실제로 계산한다.
torch.no_grad()- test 또는 inference 할 때 유용하다. autograd 작동을 비활성화하기 때문이다.
- 이를 통해 memory 사용량을 줄이고, 계산 속도를 빠르게 할 수 있다.
with구문이나@데코레이터와 함께 쓰이며, back propagation 을 할 수 없다. 이를 통해 test 혹은 inference 에서 원하지 않는 내용을 back propagation 하지 않는다.model.eval()은model.train()의 반대 개념으로 모델의 모든 layer 에 test 모드인 것을 알려 batch normalization 이나 dropout layer 가 training 대신 eval 모드로 작동하도록 한다.
import torch
x = torch.tensor(1.0, requires_grad = True)
y = x*2
print(y.requires_grad) # True
with torch.no_grad():
y = x*2
print(y.requires_grad) # False
detach()- loss 로부터 detach 된 지점을 넘어 back propagate 가 되지 않는다.
- GAN 에서 fake image generator 와 discriminator 라는 두 개의 네트워크가 있는데, discriminator 만 학습하고 싶을 때 detach 를 사용한다.
x = torch.tensor(1.0, requires_grad = True)
print(x.requires_grad) # True
y = x.detach()
print(y.requires_grad) # False
print(x.eq(y).all()) # Tensor(True) - tensor 의 모든 요소가 같지만 graph 에서 분리된다.
.grad()- 기본값은 None 이다.
backward()시 self 의 gradient 를 계산한 Tensor 가 된다.- 계산된 gradient 를 포함하여, 이후 호출에서
backward()에 대한 gradient 를 누적한다.
is_leafrequires_grad가 False 인 tensor 는 보통 leaf tensor 가 된다.reauires_grad가 True 고, 사용자가 직접 만든 경우 leaf Tensor 가 된다. 이 때는 연산의 결과가 아니므로 grad_fn 이 None 이 된다.- leaf tensor 만이
backward()시 grad 를 구성한다. leaf tensor 가 아닌 tensor 에 대해 grad 를 구성하려면,retain_grad를 사용한다. - 이 때 leaf tensor 는 Computational Graph 의 leaf node 라는 뜻이다. Computational Graph 에 포함되지 않는 node 역시 leaf node 가 된다.
retain_graph- mini-batch 처럼 한 iteration 에서 여러 번 back propagate 해야 할 때 유용하다.
- 기본적으로 back propagate 가 되면 내부적으로 computational graph 는 파괴된다. 리소스를 아끼기 위해서다. 따라서 back propagate 가 되면 맨 마지막의 gradient 만 확보하고 graph 를 날리는 것이 default 다.
- back propagate 를 여러 번 하려면 computational graph 를 유지해야 한다. 이러한 경우는 loss function 이 여러 개여서
backward를 여러 번 해야 하거나, 네트워크의 head 가 여러 개일 때에 해당한다. - input 과 output 사이에 모델이 두 개 있고, 각 모델을 지날 때마다 loss function 을 확인하는 구조의 network 라면, 첫 loss 에서
retain_graph=True하는 방법이 있고,total_loss = loss1 + loss2를 해서 total_loss 를backward하는 방법이 있다. - optimizaer 를 달리 쓰고 싶거나, step size(or learning rate)를 조정하고 싶을 때 사용할 수 있다.
requires_grad- 기본값은 False 다. tensor 에 대해 gradient 를 계산해야 하는 경우 True 로 해야 한다. 이 때 autograd 가 자동으로 계산해준다.
- tensor 에 대해 gradient 를 계산하더라도, grad 속성을 populate 하지는 않는다.
requires_grad와is_leaf가 동시에 True 인 경우에만 grad attribute 가 populate 된다. 즉tensor.grad로None이 나오지 않는다. requires_grad를 직접 설정할 때는 pre-trained 모델의 일부를 고정하고 일부 학습시킬 때 사용한다.requires_grad가 설정된 tensor 는 weight 와 같은 tensor 가 있고 연산의 결과로 생성되는 중간 tensor 가 있다. 이 때 중간 tensor 들은 gradient update 해 줄 필요가 없다.
- forward 과정에서 위 메서드들이 어떻게 사용되는지 코드로 살펴보자.
weight = torch.tensor(2.0, requires_grad = True)
# weight
# data = tensor(2.0)
# grad = None
# grad_fn = None
# is_leaf = True
# requires_grad = True
input = torch.tensor(3.0)
# input
# data = tensor(3.0)
# grad = None
# grad_fn = None
# is_leaf = True
# requires_grad = False
operation = a*b
# operation
# data = tensor(6.0)
# grad = None
# grad_fn = MulBackward
# is_leaf = False
# requires_grad = True
# Dynamically Created Computational Graph in PyTorch
W_x = torch.randn(20, 10, requires_grad = True)
W_h = torch.randn(20, 20, requires_grad = True)
x = torch.randn(1, 10) # input
prev_h = torch.randn(1, 20)
i2h = torch.mm(W_x, x.t())
h2h = torch.mm(W_h, prev_h.t())
next_h = h2h + i2h
next_h = next_h.tanh()
loss = next_h.sum()
loss.backward() # compute gradients
Autograd 깊게 이해하기
- Autograd 를 diagram 을 이용해서 깊게 이해해보자.
예제 1
-
아래의 diagram 에는 값이 2 인 tensor a 와 3 인 tensor b 가 있다. c 는 a 와 b 를 곱한 것이다.
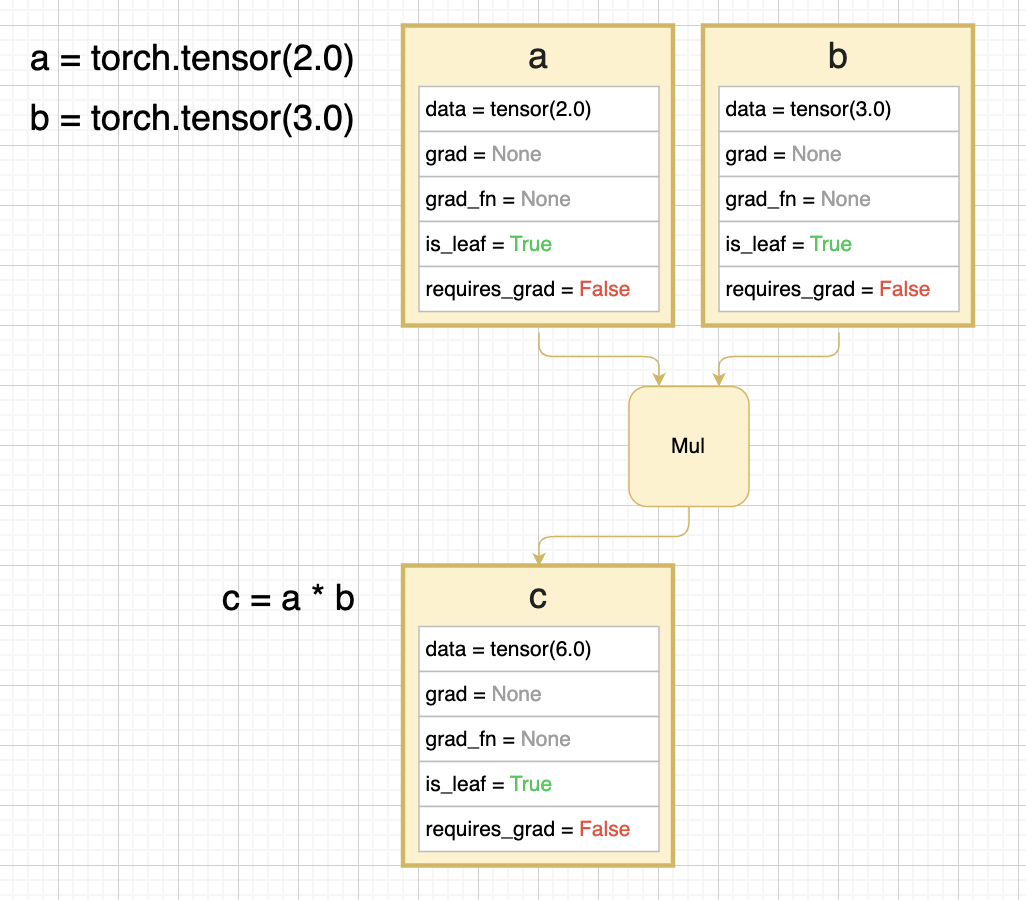
- 위 diagram 에서 각 tensor 를 나타내는 사각형은 tensor 가 가지고 있는 일부 attribute 를 나타낸다.
data: tensor 의 값을 나타낸다.grad: 계산된 gradient value 다.x.grad는 $\frac{\partial \text{out}}{\partial x}$ 다.grad_fn: gradient 를 계산하기 위한 backward function 이다. backward graph 에 있는 node 를 가리키고 있고, 해당 tensor 가 어떤 연산을 통해 forward 되었는지에 따라 결정된다.is_leaf: graph 의 leaf 에 해당하는 tensor 인지를 나타낸다. 즉 backward 기준으로 가장 마지막 tensor 인지를 나타낸다.-
requires_grad: 이 속성이False면 backward graph 가 만들어지지 않는다. 위 diagram 에서 a 와 b 모두False이기 때문에 c 도False다. 위 diagram 에서는 graph 가 만들어지지 않기 때문에 a, b, c 모두 leaf tensor 다.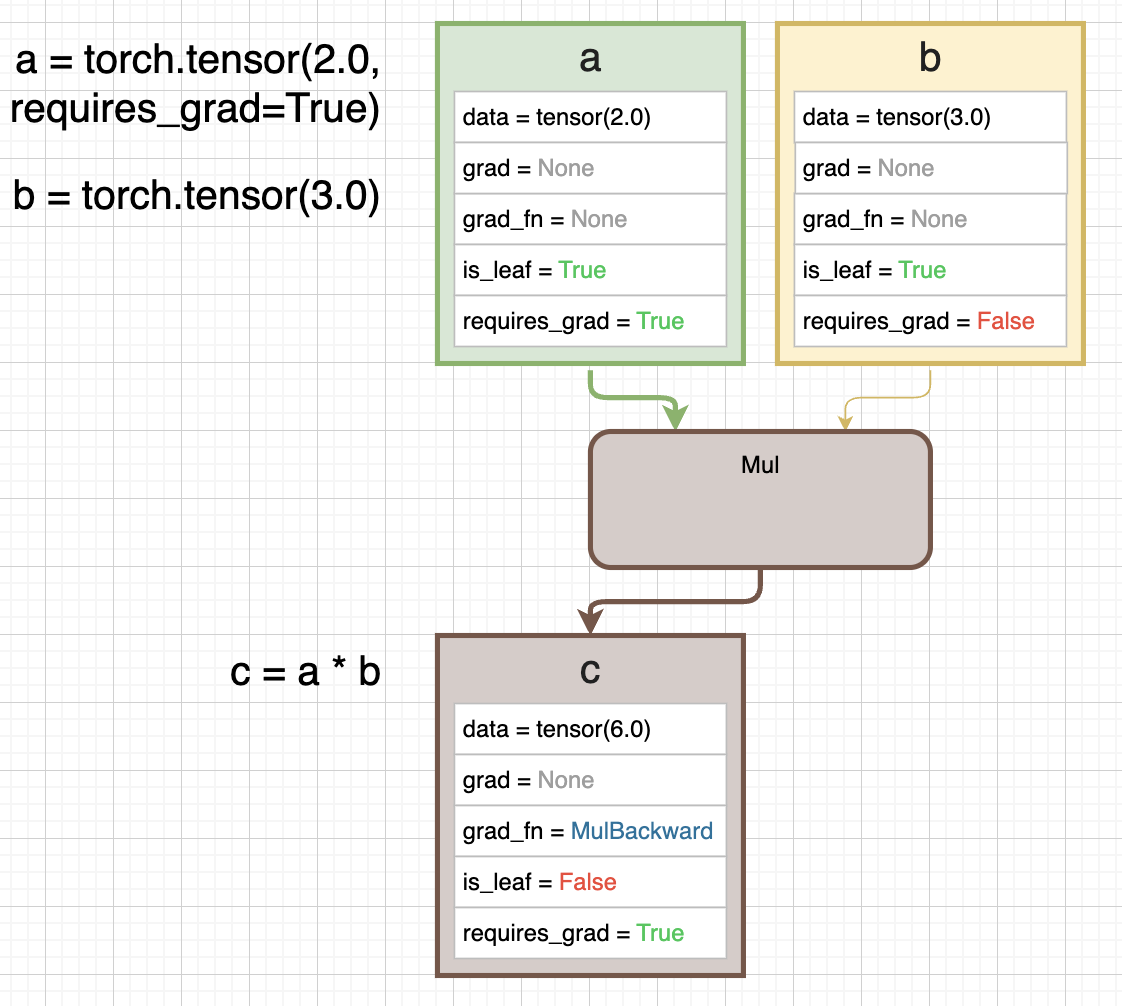
- 만약 위처럼 a tensor 를
requires_grad=True로 설정하고, a 를 곱하기와 같은 어떤 연산에 통과시키면 c 와 같은 output tensor 는 graph 의 일부분이 된다. - c tensor 또한
requires_grad=True가 되고is_leaf=False가 된다. 더 이 상 backward 기준 마지막 tensor 가 아니기 때문이다. - 또한
grad_fn=MulBackward로 설정된다. 이는 backward graph 의 node 를 가리키고 있다. -
즉
requires_grad=True로 backward graph 가 만들어지고,grad_fn은 이 graph 에서 특정MulBackwardnode 를 가리킨다.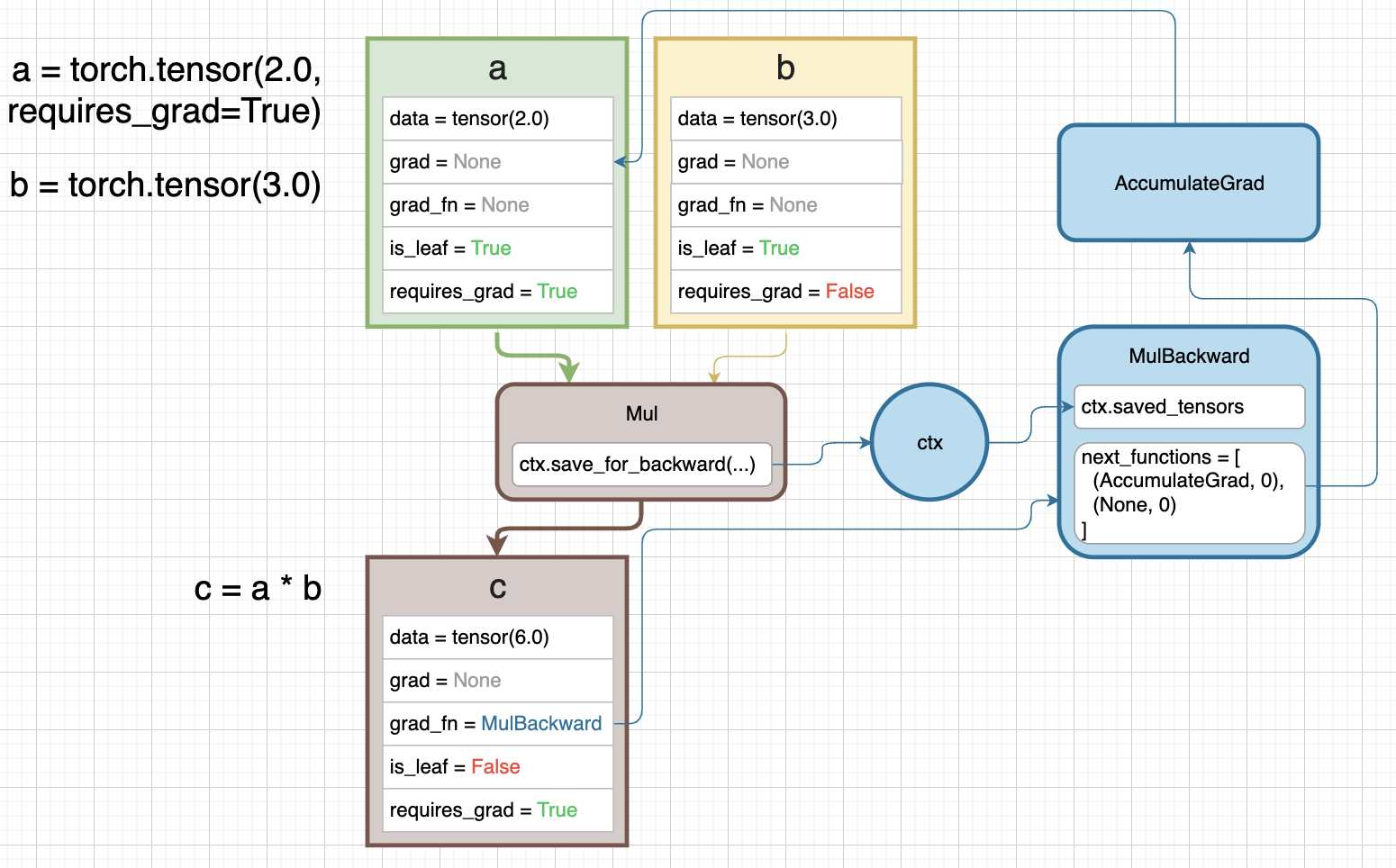
- 위 diagram 의 파란색 부분이 backward graph 다.
- 우리가
Mulfunction 을 호출하면 context variable 인ctx에 접근한다.ctx.save_for_backward(...)가 이를 나타낸다. - 즉
save_for_backward()메서드는 context variablectx가 backward pass 에 필요한 값을 저장하는 것을 의미한다. 이ctx가 backward pass 에서MulBackward연산에 통과된다. ctx.saved_tensorsproperty 는 forward 의ctx.save_for_backward()로부터 context variable 에 저장된 값을 의미한다. backward pass 에서 참조되는 input tensor 를 가지고 있다.- 계산 그래프에 포함되지 않는 in_place 연산 등으로 인해 tensor 값이 변경되는 경우를 대비하여 계산 당시의 tensor 값을 context 변수에 저장해 놓는 것이다.
- 만약
Add처럼 이전 tensor 값이 필요하지 않은 연산의 경우 context 변수가 값을 저장해 두지 않아도 된다.
- 곱하기와 같은 pytorch 의 built-in operator 는
C++로 실행되기 때문에save_for_backward()와saved_tensorsproperty 는 위 diagram 에 작성된 것처럼 code 에서 동작하지는 않는다. MulBackward의next_functions는 tuple 로 이루어진 list 다.- 각각은
Mulfunction 에 통과되는 서로 다른 input a, b 를 뜻한다. 여기서AccumulateGrad는 a 를 뜻하고None은 b 를 뜻한다. - b 가
None인 이유는requires_grad=False이기 때문이다. 따라서 b 에는 gradient 를 통과시키지 않아도 된다.AccumulatedGrad는 a tensor 에 gradient 를 accumulate 하기 위해 사용된다. - 즉
next_functions에 담긴 tuple 의 첫번째 값은 backward 기준으로 다음 tensor 의grad_fn이다. is_leaf=True이고requires_grad=True일 경우 a tensor 와 같이grad_fn은AccumulatedGrad가 된다. 이는 계산된 gradient 를self.grad에 저장하는 것이다.- b tensor 와 같이
is_leaf=True면서requires_grad=False일 경우None이 된다. - 여기서 tuple 의 두번째 값은 첫번째 값인
grad_fn의 몇 번째 input 으로 전달될 것인지를 뜻한다. -
보통은
grad_fn이 하나의 input 만 받지만 forward 연산의 output 이 여러 개인 경우grad_fn이 여러 개의 input 을 받을 수 있다.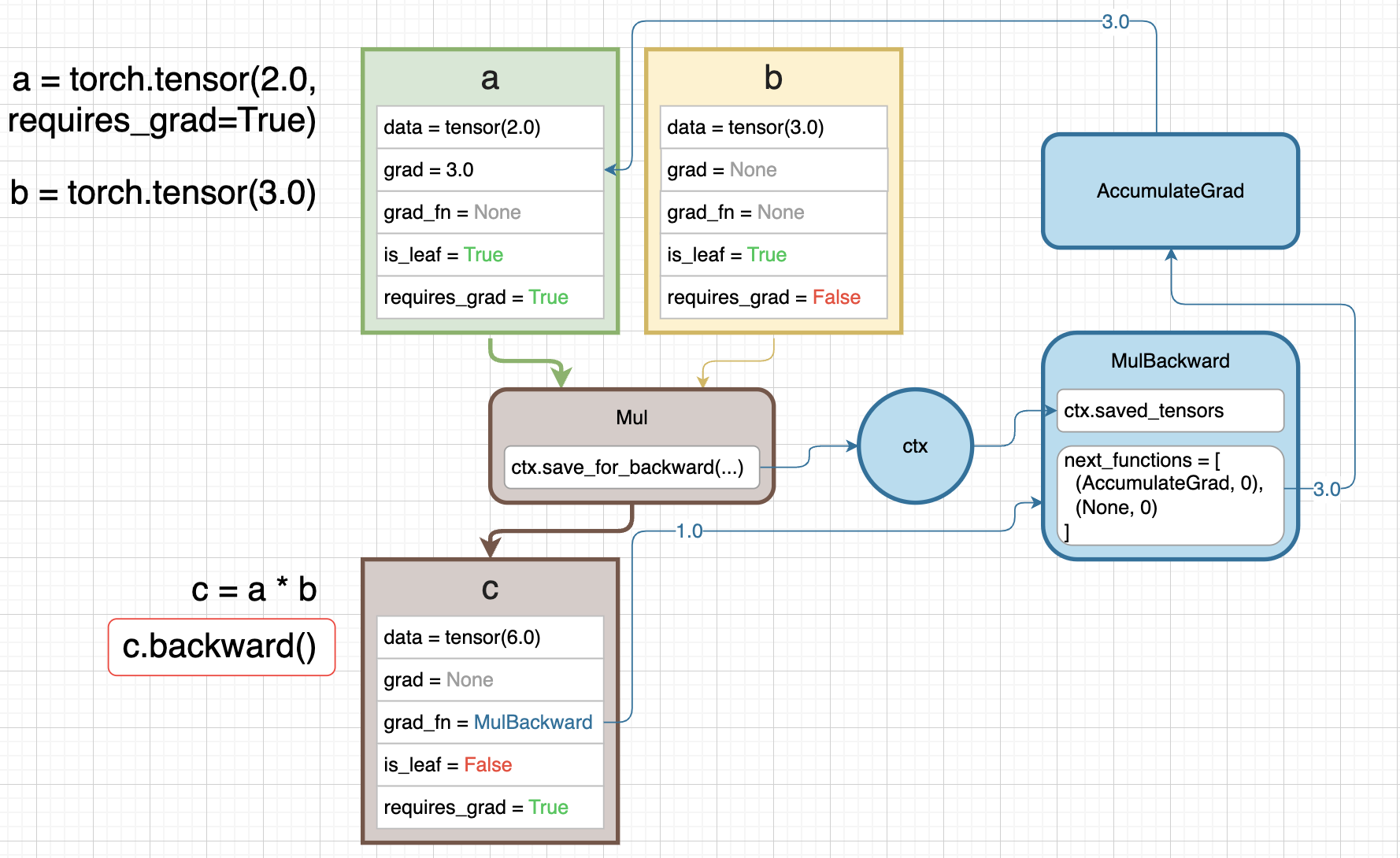
- 각각은
- 이제
c.backward()를 호출하면 gradient 의 backward pass 가 시작된다. 맨 처음c로부터 흐르는 gradient 는1.0으로 initializing 된다.- Scalar 의 경우
backward()를 호출할 때 gradient 를 특별히 설정하지 않으면 기본값인1.0($\frac{\partial z}{\partial z}$)로 설정된다.
- Scalar 의 경우
1.0은grad_fn을 타고 흘러가면서MulBackward에 흐르고, 들어오는 gradient1.0과 현재 연산에서의 gradient 가 chain rule 에 의해 곱해진다.- 즉 tensor 에
backward()가 호출되면, 해당 tensor 의 시작 gradient 인1.0이 해당 tensor 의grad_fn으로 흘러가고grad_fn의next_functions에 있는 다음grad_fn으로 계속해서 흘러가는 것이다. 이 때 들어오는 gradient 와 현재 연산에서의 gradient 가 chain rule 에 의해 곱해져서 다음으로 흘러간다. 만약grad_fn이None이면 흐르지 않는다. - 이후
AccumulateGrad를 만나면 이를 가진 tensor 의.grad에 gradient 를 저장한다. - 위에서 본 것처럼
is_leaf=True인 경우에만AccumulateGrad로 gradient 가 저장되고,is_leaf=False면 gradient 가 저장되지는 않고grad_fn을 따라 계속 흘러가기만 한다. - 만약 중간 tensor 에서도 gradient 를 저장하려면
tensor.retain_grad()메서드를 사용하면 된다.
예제 2
-
조금 더 복잡한 예제를 들어보자. 이번엔 a 와 b tensor 모두
requires_grad=True다. 또한 c 말고도 새로운 d 와 e tensor 가 등장한다.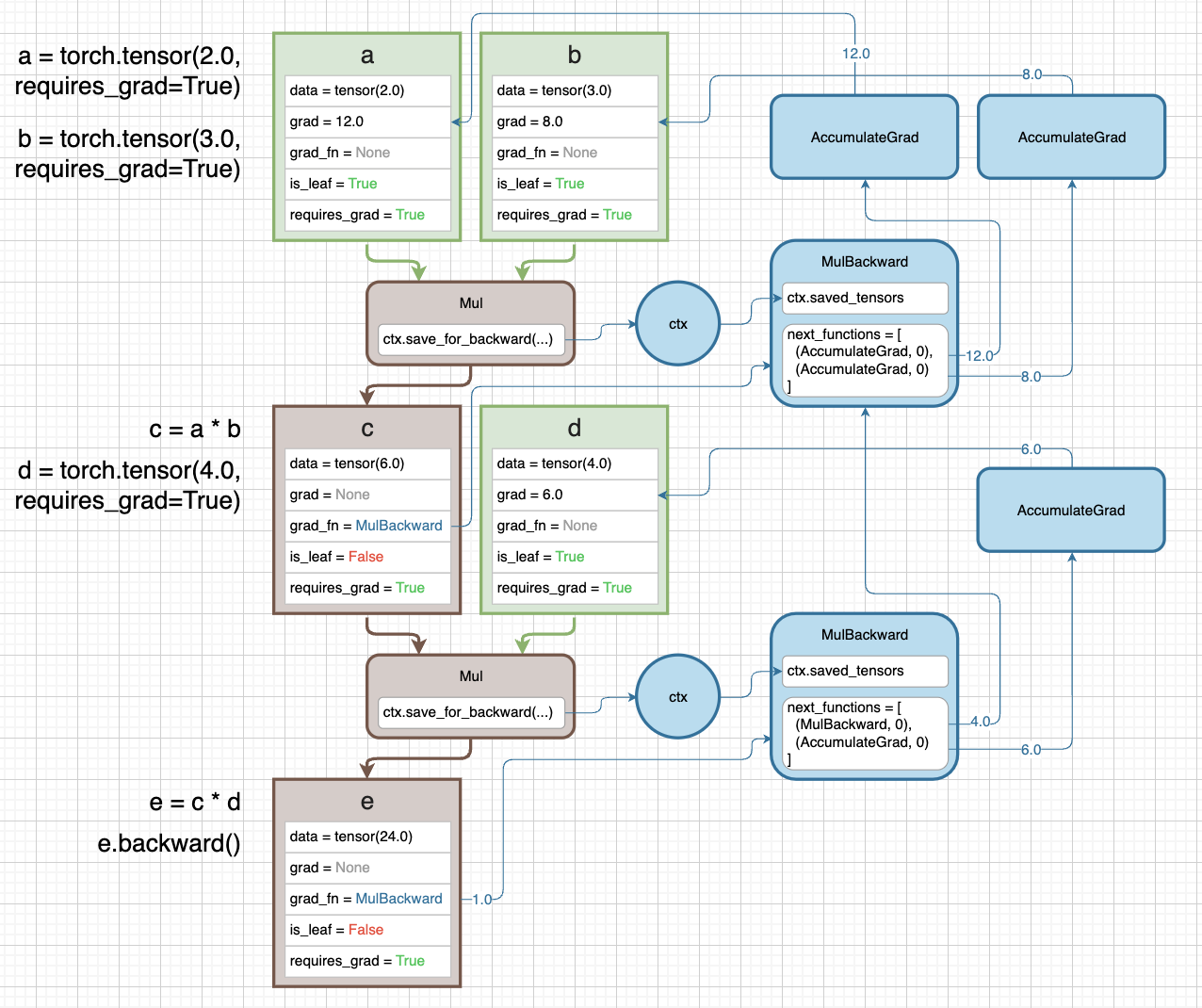
- 각 tensor 의 정보가 나타난 사각형에 있는
grad_fn속성을 따라가면 쉽다. 마찬가지로 파란색 박스와 그래프가 backward pass 를 나타내고 있다. 이러한grad_fn은 각 tensor 가 forward 에서 어떤 연산을 통해 만들어졌는지를 나타낸다. - 여기서 주의깊게 볼 점은 연산 중간에 있는 c 와 같은 중간 tensor 는
is_leaf=False로 gradient 가grad에 저장되지 않는다. e.backward()를 실행하면, 최초의 gradient1.0이e의grad_fn인MulBackward로 흐른다.- 여기서 c 와 d tensor 가 가진
grad_fn이next_functions에 담겨있다. d tensor 는grad_fn=None이지만is_leaf=True, requirs_grad=True이기 때문에AccumulateGrad가 된다. - 해당
Mul연산에서 구할 수 있는 input tensor 에 대한 gradient 가 incoming gradient 인1.0과 곱해져 다음grad_fn으로 향하는 것이다.
예제 3
- 위 예제에서, backward pass 과정에서
MulBackward가ctx.saved_tensors를 불러와 gradient 를 계산한다. - 이 때 forward 과정에서
saved_tensors에 저장된 tensor 는 값이 변하지 않는다. -
그러나 forward 과정에서 graph 의 context variable 에 저장된 tensor 가 값이 변하면 어떻게 될까?
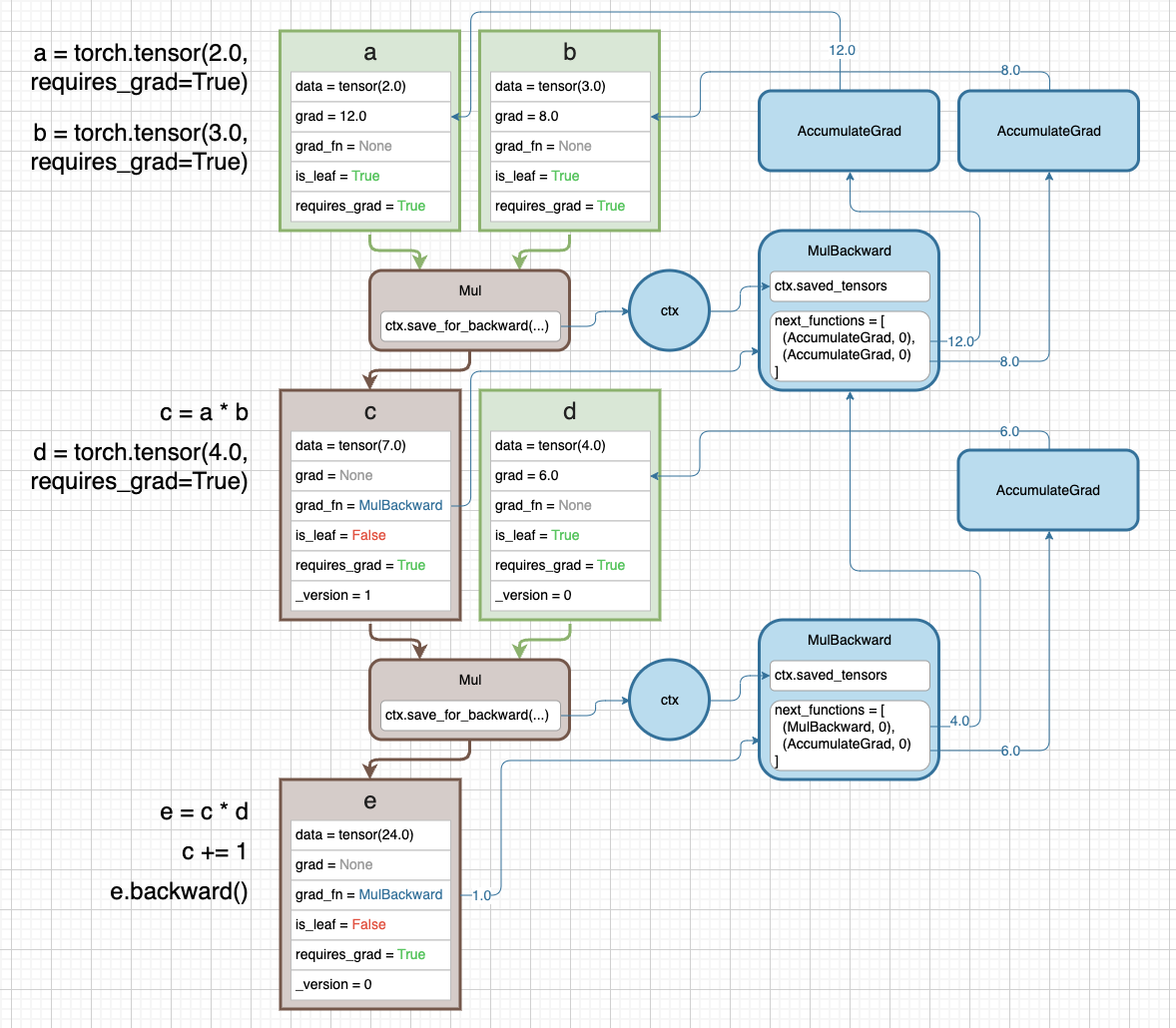
- 값의 변화를 추적하기 위해 diagram 에서 볼 수 있듯 tensor 를 생성할 때
_version을 함께 저장한다.c+=1과 같은 inplace 연산을 실행하면_version이 증가하게 된다. e.backward()를 실행하기 전에 inplace 연산을 실행하면,MulBackward에서saved_tensors에 저장된 c tensor 를 참조하면서_version을 확인한다.-
_version=1이지만 forward 에서Mul을 통과할 때는_version=0였기 때문에_version=0의 c tensor 를 사용하고 error 를 방지한다.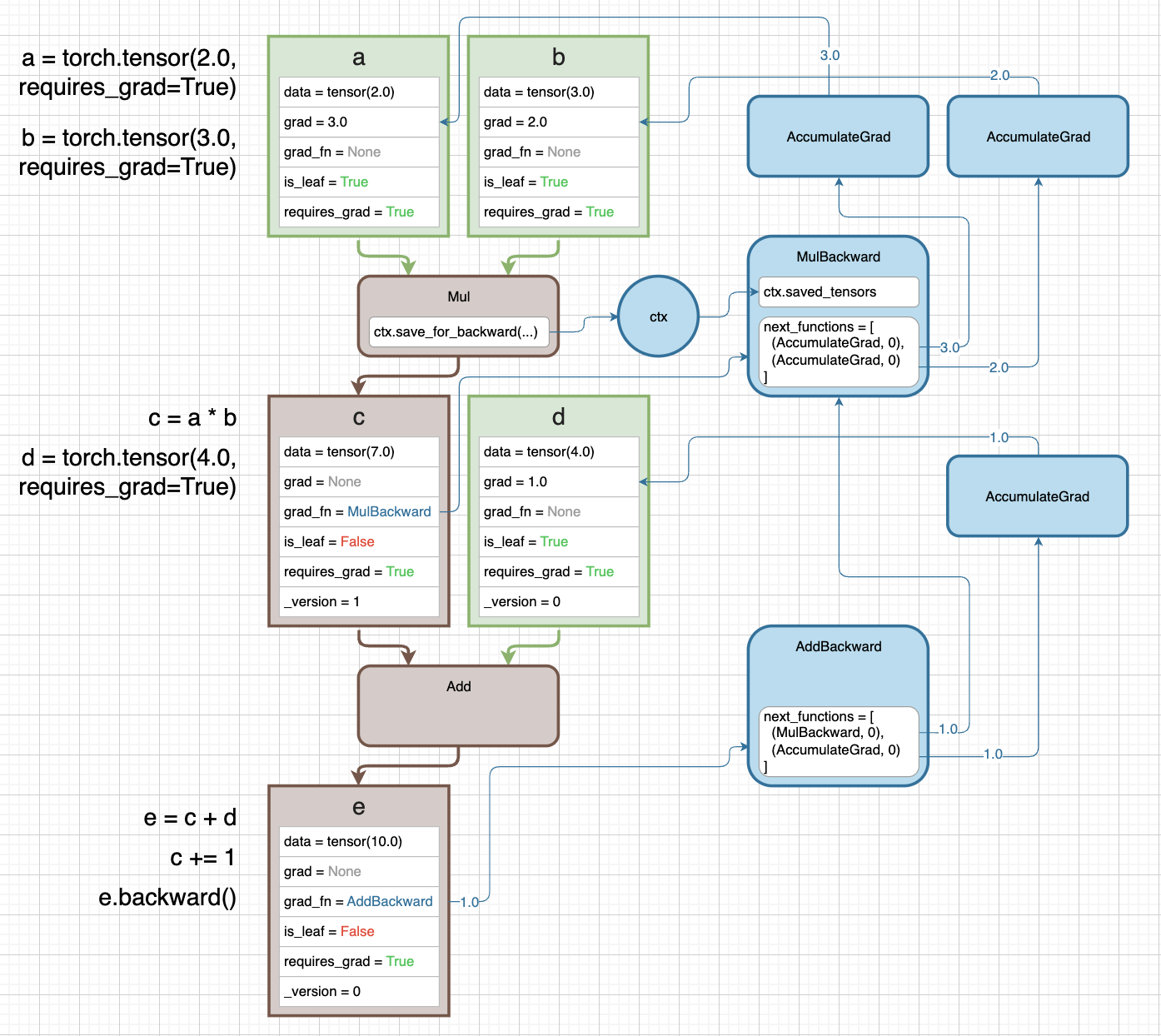
- 그러나 위
Addfunction 와 같은 경우는 backward pass 를 위한 어떤ctx.saved_tensors를 만들지 않는다. 왜냐하면 더하기 연산 특성상 gradient 가 그냥 다음grad_fnnode 로 흐르면 되기 때문이다. - 이 때
c+=1의 inplace 연산을 수행하고e.backward()를 수행하더라도 error 가 발생하지 않는다. 왜냐하면 해당AddBackward의 경우 c tensor 의 값에 의존하지 않기 때문이다. - 다만 주의할 점은
is_leaf=True인 tensor 에 대해서 inplace 연산을 진행하면 아래와 같은 오류를 발생시키게 된다.
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
Cell In[69], line 6
4 d = torch.tensor(4.0, requires_grad=True)
5 e = c + d
----> 6 a += 1
7 c.backward()
8 a.grad
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.
예제 4
-
vector 에 대한 Autograd 를 알아보자. 여기서는
grad_fnnode 의next_functions에 속한 tuple 의 두번째 값에 대해 알아볼 수 있다.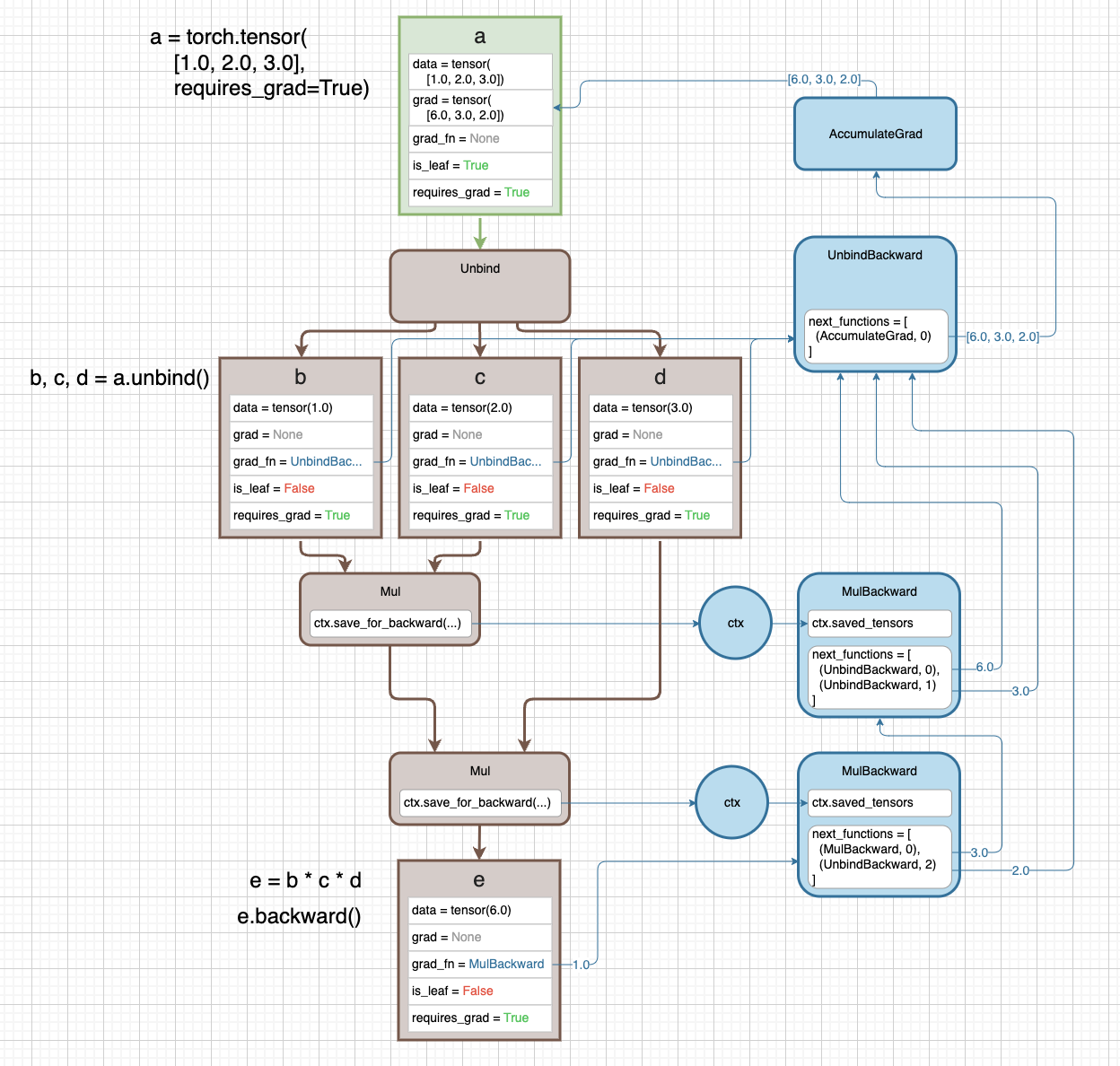
- a 는 1d tensor 다. 이를
Unbind연산을 취해 각각의 tensor b, c, d 로 만든다. 즉 unpack 하는 것이다. e=b*c*d지만 내부적으로 b 와 c 가 먼저 곱해지고, 해당 output 이 d 와 곱해진다. 따라서 2 개의MulBackward가 만들어진다.- 이 때
MulBackward의next_functions를 보면 tuple 의 두번째 값이 0 이 아닌 값이다. 이는 forward 의Unbindfunction 의 output index 를 뜻한다. - output index 를 알아야 하는 이유는,
UnbindBackward가 다음grad_fnnode 로 향하기 전에 gradient 가 어떤 output 인지를 알아야 하기 때문이다. - 따라서
MulBackward를 2 개 다 통과하면 gradient vector 의 해당 output index 에 gradient 값이 위치하게 된다. - 화살표를 보며 흐름을 이해하자.
예제 5
- 마지막 예제다. 좀 더 복잡한 graph 를 그려보고 이를 이해하면 Autograd 에 대해 깊은 이해를 했다고 볼 수 있다.
-
또한 여기서는 간단한 설명을 위해 scalar value 를 가진 tensor 를 썼지만 이후 vector 나 matrix 를 써도 기본 원리는 똑같다.
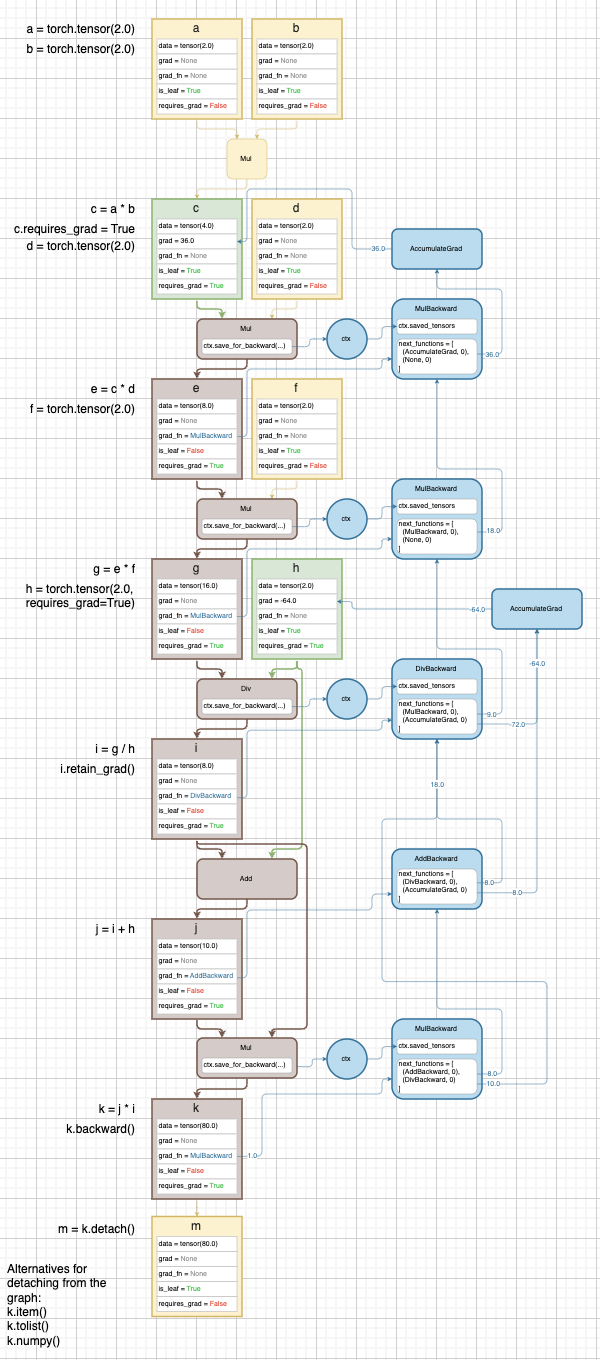
- 여기서
c.requires_grad=True를 주어is_leaf=True, requires_grad=True가 되었다. 따라서 c tensor 를 이용한 연산은 backward graph 를 만들게 된다. - h tensor 또한 leaf tensor 로 만들어 준 것이다. 특히 h tensor 는 두 가지의 연산
Div, Add에 사용되어 h 에 대한AccumulatGrad는 2 개의 input 을 가진다. - i tensor 도 마찬가지로
Add, Mul2 개의 forward 연산을 거친다. 이 때Addbackward에 보면 gradient 가 합쳐져DivBackward로 흘러가는 것을 볼 수 있다. - 그러나 i tensor 는
is_leaf=False이기 때문에AccumulateGrad가 아닌 해당 i tensor 를 만든 연산인Div연산의DivBackward로 흘러가게 된다. - 즉 forward graph 에서는 split 되는데, backward graph 에서는 convergence 된다.
k.backward()를 호출하면 모든 backward graph 상의 node 를 화살표에 따라 흘러가며 gradient 가 전달되고,AccumulateGrad를 만난 순간 leaf tensor 의grad에 gradient 를 accumulate 하게 된다.- default 로 gradient 는 leaf tensor 에만 저장된다. 그러나
i.retain_grad()를 호출하면 중간 tensor 인 i tensor 에도 gradient 가 저장되게 된다.retain_grad()은 hook 을 설정하고 backward pass 상에서 i tensor 의grad_fn에 들어왔을 때 hook 이 실행되어 gradient 가 i tensor 의grad에 저장되게 된다.
m=k.detach()를 실행하면 m 은 k 와 메모리를 공유하지만grad_fn=None이고requires_grad=False인 tensor 를 만들게 된다. graph 에서 떨어져 나왔기 때문에is_leaf=True가 된다.- 주의할 점은 메모리를 공유하기 때문에 m 의 값을 바꾸면 k 의 값도 바뀌게 된다.
detach를 사용하는 이유는 해당 tensor 가 training loop 에서 빠져나오도록 하는데 있다.- 위 예제 맨 아래에
detach대신numpy(), item(), tolist()를 써도 된다고 나와있지만, CPU 와 GPU 동기화를 막고 좀 더 효율적인 학습이 되기 위해서detach를 쓰는 것이 더 권장된다.
clone, detach
- 위에서
detach가 메모리를 공유하지만 backward graph 에서 떨어진is_leaf=True, requires_grad=False인 tensor 를 만드는 것을 확인했다. 이는 얕은 복사인데, 위에서 다룬 김에 Pytorch 에서의 깊은 복사인clone과 얕은 복사인detach를 정리해보자. - 먼저
clone메서드는 복사한 tensor 를 새로운 메모리에 할당한다. 즉 깊은 복사로서, 복사 대상 tensor 의 값이 변해도 복사한 tensor 의 값이 변하지 않는다. - 그러나
detach메서드는 tensor 를 복사하지만 복사 대상 tensor 와 메모리를 공유한다. 따라서 기존 tensor 의 값이 변하면 복사한 tensor 의 값도 따라서 변하게 된다. 다만, back propagation 을 위한 계산 그래프에서 제외된다. clone- 어떠한 tensor 를
clone메서드를 이용해 복사하게 되면 기존 계산 히스토리 이력은 그대로 유지하면서 새로운 메모리를 할당한다. - 따라서 gradient 계산도 그대로 적용되면서, inplace operation error 도 피할 수 있다.
- inplace operation 이란 위에서도 봤지만 새로운 변수에 할당하지 않고 기존 변수를 그대로 사용하면서 연산을 적용시키는 것이다. 예를 들어 tensor 의 특정 index 를 어떤 값으로 치환하거나 값에 연산을 취하는 것이다.
- Pytorch 에서는 gradient 가 계산(
requires_grad=True)되는 leaf node(tensor)에 대해서 inplace operation 이 금지되어 있다. - inplace operation 이 필요한 경우 원하는 tensor 에 대해
clone메서드로 복사한 이후 실행하면 error 가 발생하지 않는다. clone메서드를 써서 복사한 tensor 는 원본 tensor 의grad_fn을 가지게 되고 이는 backward graph 상에서 gradient 가 전파되도록 한다.- 그러나
grad_fn을 통해 gradient 는 전파시키지만 그 자체는grad값을 가지지 않는다. 왜냐하면 leaf tensor 가 아니기 때문이다.
- 어떠한 tensor 를
a = torch.tensor(2.0, requires_grad=True)
b = torch.tensor(2.0, requires_grad=True)
c = a * b
d = torch.tensor(4.0, requires_grad=True)
e = c + d
e.backward()
print(a.grad, a.requires_grad, a.is_leaf) # tensor(2.) True True
aa = a.clone()
print(aa.grad, aa.requires_grad, aa.is_leaf) # None True False
detach- backward graph 에서 아예 배제하고 싶다면
detach메서드를 사용한다. detach메서드로 tensor 를 복사하게 되면 원본 tensor 와 메모리는 공유하지만requires_grad=False인 tensor 를 만들게 되어 해당 tensor 에 대해서는 gradient 가 계산되지 않는다.- 주의할 점은 메모리를 공유하기 때문에 복사한 tensor 의 값을 바꾸면 원본 tensor 에도 동일하게 적용된다.
- 따라서
clone메서드와 달리detach메서드로 복사한 tensor 에 inplace operation 을 적용하게 되면 메모리를 공유하기 때문에 error 가 발생한다.
- backward graph 에서 아예 배제하고 싶다면
clone().detach()ordetach().clone()- 결국 tensor 의 복사는
clone과detach의 특성을 합쳐 사용하는 것이 제일 깔끔하다. clone().detach()와detach().clone()모두 computational graph(backward graph) 에서 제외된 tensor 를 새로운 메모리로 할당하는 동작은 같다.clone().detach()를 하게 되면 먼저 새로운 tensor 를 메모리에 할당하고 그것을 기존 graph 와 끊어버린다.detach().clone()을 하게 되면 먼저 gradient 가 계산되지 않는 graph 로부터 떨어진 tensor 를 만들고 새로운 메모리에 할당한다.-
두번째
detach().clone()이 먼저 graph 에서 떨어져 나왔으므로 이후의cloneoperation 이grad_fn등을 트래킹하지 않기 때문에 조금 더 빠르다.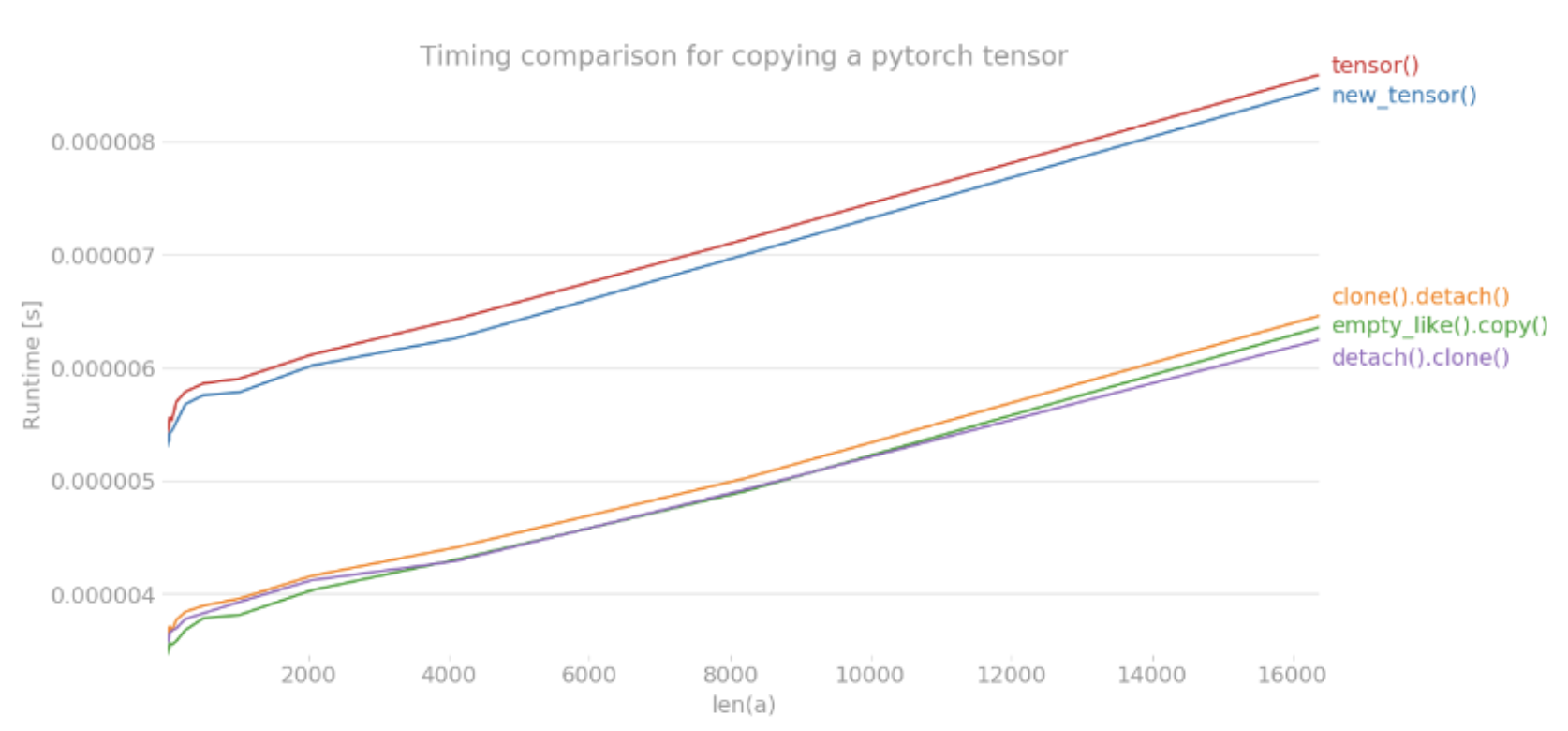 출처 : https://seducinghyeok.tistory.com/10
출처 : https://seducinghyeok.tistory.com/10
- 결국 tensor 의 복사는
train 모드와 eval 모드
- 앞에서 다룬 모든 예제는 gradient 를 구하기 위해서
tensor의 속성을requires_grad = True로 설정했다. - 여기서
requires_grad=True로 gradient 를 구한다는 것은 학습 대상이 되는 weight 임을 의미한다. - 반면 학습이 모두 끝나고 학습한 결과를 실행에 옮기는 inference 단계에서는 굳이 학습 모드로 사용할 필요가 없다.
- 이를 위해 사용하는 것이
torch.no_grad()다.torch.no_grad()가 적용된 tensor 는 비록 실제 속성은requires_grad = True더라도 gradient 를 업데이트 하지 않고, dropout 과 batch normalization 등이 적용되지 않는다.
x = torch.tensor(1.0, requires_grad = True)
print(x.requires_grad)
# True
with torch.no_grad():
print(x.requires_grad)
print((x**2).requires_grad)
# True
# False
print(x.requires_grad)
# True
- 위 예제를 살펴보면
with torch.no_grad():에서requires_grad = True인 tensorx에 어떤 연산이 적용되면requires_grad = False로 변경되는 것을 확인할 수 있다. - 그리고 with 문을 벗어나면 다시
requires_grad = True로 원복된다. 이러한 방식으로 gradient 를 업데이트 하는 모드와 그렇지 않은 모드를 구분할 수 있다.
Reference
- https://gaussian37.github.io/dl-pytorch-gradient/
- https://www.youtube.com/watch?v=MswxJw-8PvE&t=0s
- https://jay-chamber.tistory.com/entry/torchTensor%EC%97%90-%EB%8C%80%ED%95%98%EC%97%AC

댓글 남기기