[Deep Learning, Optimization] Bias 와 Variance

머신러닝/딥러닝에서 bias 와 variance 는 under-fitting, over-fitting 과 이어지는 개념이다. 이러한 bias 와 variance 가 trade-off 관계에 있다는 것은 유명한 사실이지만, 실제 모델링 과정에서 내 모델이 bias 와 variance 사이에서 어떤 상태에 있는지를 정확히 파악하는 것이 중요하다. 그래야 조치를 취할 수 있기 때문이다.

이를 위해서 bias 와 variance 에 대해 자세히 정리한 글을 참고하여 완벽히 이해해보자. 이를 통해 어렴풋이 알고 있었던 딥러닝에서의 법칙(?), 예를 들어 모델의 layer 가 깊으면 over-fitting 이 발생하기 쉽다거나, over-fitting 이 발생했을 때 training data 수를 늘리는 것이 해결방법 중 하나라는 것들이 왜 그런 것인지 이해할 수 있다. 참고한 글은 아래 Reference 에 기재해둔다.

Bias 와 Variance 의 정의

• 먼저 bias 와 variance 의 정의에 대하여 알아보기 전에 이 두 개념을 정의할 때 사용하는 notation 인 $f(x), \; \hat{f}(x), \; E[ \hat{f}(x) ]$ 의 뜻에 대해 알아보자.

  

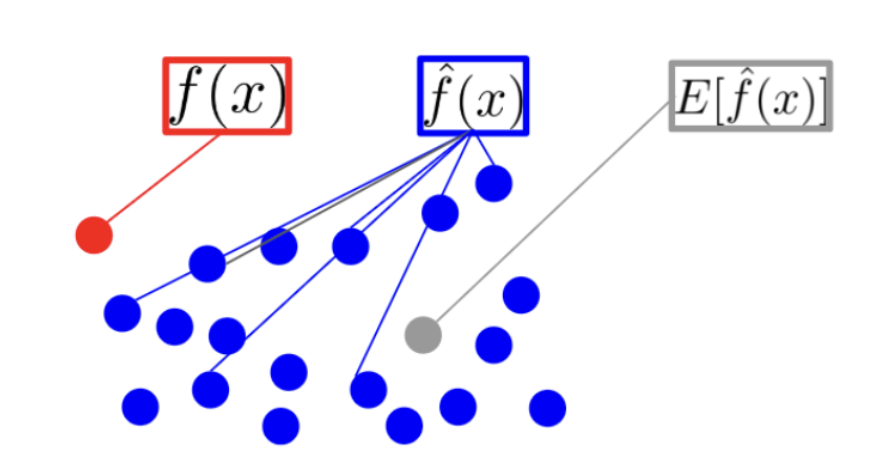
• $f(x)$ 는 입력 데이터 $x$ 에 대해 실제 정답에 해당하는 값이다. 정답은 하나만 존재하기 때문에, 위 그림에서도 정답 $f(x)$ 는 빨간색 점으로 하나만 존재한다.
• $\hat{f}(x)$ 는 모델에 입력 $x$ 를 넣었을 때 모델이 출력하는 예측값이다. 이 값은 parameter 와 같은 모델의 상태에 따라 다양한 값들을 출력할 수 있다. 따라서 위 그림에서 여러 개의 파란색 예측값들을 만들어 낼 수 있다.
• $E[ \hat{f}(x) ]$ 는 모델의 예측값($\hat{f}(x)$)들에 대한 기대값(평균)에 해당한다. 즉, 모델의 예측값을 대표하는 값이라고 생각할 수 있다.

Bias

• bias 는 모델을 가지고 real world function 을 근사할 때 만들어지는 Error 의 기대값(Expected Error)이다. 이는 학습 알고리즘에서 잘못된 가정을 했을 때 발생하는 오차인 것이다.
• 쉽게 말해, bias 는 모델을 통해 얻은 예측값과 실제 정답과의 차이의 기대값(평균)을 나타낸다. 즉, 예측값이 실제 정답값과 얼만큼 떨어져 있는지를 나타낸다.

• 이러한 예측값과 실제 정답과의 차이의 기대값(평균)을 수식으로 나타내면 다음과 같다.

  \[\text{Bias}[ \hat{f}(x) ] = E[ \hat{f}(x) - f(x) ]\]
• 따라서 bias 가 높은 경우, 그만큼 예측값과 정답값 간의 차이가 크다고 말할 수 있다. 또한 학습 알고리즘이 데이터의 특징과 결과물과의 적절한 관계를 놓치게 만드는 under-fitting 문제를 발생시킨다.

Variance

• variance 는 “다양한 학습 데이터셋에 대하여 모델의 예측값이 얼만큼 변화할 수 있는지에 대한 양(Quantity)” 의 개념이다. 즉 variance 는 학습 데이터셋에 내재된 작은 변동(fluctuation) 때문에 발생하는 오차다.

• variance 를 수식으로 나타내면 다음과 같다. 말 그대로 예측값과 그 평균의 편차를 제곱하여 나타낸 것이다. 자세한 증명은 wiki 를 참고하자.

  \[\text{Var}[ \hat{f}(x) ] = E[ (\hat{f}(x) - E[ \hat{f}(x)])^{2} ] = E[ \hat{f}(x)^{2} ] - E[ \hat{f}(x) ]^{2}\]
• variance 는 모델이 가지는 flexibility 를 의미하는 것으로 생각할 수 있으며, 분산(variance)의 본래 의미와 같이 얼마나 예측값이 퍼져서 다양하게 출력될 수 있는지에 대한 정도로 해석할 수 있다.
• variance 가 높은 경우, 큰 noise 까지 모델링에 포함시키는 over-fitting 문제를 발생시킨다.

모델과 Bias 및 Variance 의 관계

• bias 와 variance 는 머신러닝/딥러닝 모델의 학습 상태를 나타낼 수 있는 좋은 척도다. 아래 그림을 보자.

  

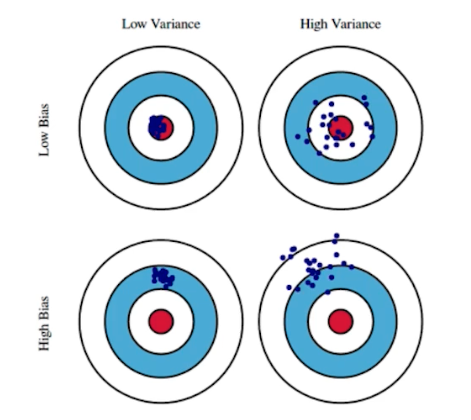
• 위 그림은 bias 와 variance 의 크고 작음에 따라서 4가지 경우로 분류하고 있다.
• 각 경우에 따라서 머신러닝/딥러닝 모델이 예측한 값들의 분포(파란 점)와 정답(과녁의 중앙 빨간 영역) 간의 관계를 한 번 살펴보자.
  • ① Low Bias & Low Variance : 예측값들이 정답 근방에 분포되어 있고(bias 가 낮음) 예측값들이 서로 몰려 있다(variance 가 낮음). 이는 Bias 와 Variance 가 모두 작아 에러율이 가장 낮은 모델이다.
  • ② Low Bias & High Variance : 예측값들이 정답 근방에 분포되어 있으나(bias 가 낮음) 예측값들이 서로 흩어져 있다(variance 가 높음). 학습 데이터셋에 매우 적합하지만 데이터의 noise 패턴도 같이 학습하기 때문에 테스트 데이터셋에 일반화하지 못하는 경우가 이에 해당한다.
  • ③ High Bias & Low Variance : 예측값들이 정답과 상대적으로 멀고(bias 가 높음) 예측값들이 서로 몰려 있다(variance 가 낮음). 단순한 모델일수록 학습 데이터에서 모든 패턴을 찾지 못해 Bias 가 크고 Variance 는 작다.
  • ④ High Bias & High Variance : 예측값들이 정답과 상대적으로 멀고(bias 가 높음) 예측값들이 서로 흩어져 있다(variance 가 높음).
• 머신러닝/딥러닝 모델과 bias, variance 의 관계에서 가장 적합한 것은 첫번째 경우에 해당하는 Low Bias & Low Variance 다.

Bias-Variance trade-off

• 통계학과 기계학습에서 오차(Error)는 bias, variance, 그리고 데이터 자체가 내재하고 있는 것이기 때문에 어떤 모델링으로도 줄일 수 없는 오류의 합으로 본다.
• 이 때 Bias-Variance trade-off(또는 dilemma) 는 지도학습 알고리즘이 학습 데이터셋의 범위를 넘어 지나치게 일반화하는 것을 예방하기 위해 두 종류의 오차(bias, variance)를 최소화 할 때 겪는 문제다.
• 이 Bias 와 Variance 의 trade-off 관계를 살펴보기 위해 loss function 중 하나인 Squared Error(즉, MSE) 를 분해해보자.
• 그 전에 우리의 목표는 실제 관계함수(real function)인 $y = f(x)$ 를 학습 알고리즘을 통해 최대한 잘 근사하는 함수 $\hat{f}(x)$ 를 찾는 것이다. 그리고 여기서 “최대한 잘 근사한다”는 것은 정량적으로 $y$ 와 $\hat{f}(x)$ 사이의 loss 를 최소화하는 것을 말한다.
• 그러나 위에서 언급한 것처럼 $y$ 에는 우리가 피할 수 없는 오차(noise) $\epsilon$ 이 포함된다. 따라서 우리가 데이터셋을 가지고 학습할 때 모델링하는 실제 관계함수는 $y_i = f(x_i) + \epsilon$ 이 된다.
• 그리고 우리는 MSE 를 분해하기 때문에, Regression 문제에서 그렇듯 이 $\epsilon$ 은 평균이 $0$ 이고 분산이 $\sigma^2$ 인 Gaussian Distribution 을 따른다.

• 이제 아래와 같은 Squared Error(MSE) 를 분해해보자.

  \[E\left[(y - \hat{f}(x))^2\right]\]

• 위에서 봤듯 bias 와 variance 는 각각 아래와 같은 식으로 나타낼 수 있었다.

  \[\begin{aligned} \text{Bias}[\hat{f}(x)] &= E[ \hat{f}(x) - f(x) ] \\ \text{Var}[\hat{f}(x)] &= E[ (\hat{f}(x) - E[ \hat{f}(x)])^{2} ] \end{aligned}\]

• 편의를 위해 $f = f(x)$, $\hat{f} = \hat{f}(x)$ 라고 두자. 그리고 Error 를 분해할 때 사용하기 위해서, 우리는 기대값의 정의를 활용하여 확률변수 $X$ 에 대해 아래와 같이 전개할 수 있다.

  \[\begin{aligned} E[X^2] &= E[X^2] \color{gray}{-E[2XE[X]] + E[E[X]^2] + E[2XE[X]] - E[E[X]^2]} \\ &= E[X^2 - 2XE[X] + E[X]^2] + 2E[X]^2 - E[X]^2 \\ &= E[(X - E[X])^2] + E[X]^2 \\ &= \text{Var}[X] + E[X]^2 \end{aligned}\]
  • 즉 확률변수의 제곱의 기대값은 variance 와 확률변수 기대값의 제곱으로 나타낼 수 있다.
• 그리고 우리가 모델링하는 $\hat{f}$ 은 학습 데이터에 따라 달라질 수 있는 확률적 모델이지만, 실제 함수 $f$ 는 고정되어 있어 변화하지 않는다. 즉, $f$ 의 값은 정답이기 때문에 학습 과정에서 영향을 받지 않고, 항상 동일하다는 것이다.

• 따라서 $f$ 는 결정되어 있으므로 분산의 성질에 의해 그 분산은 0 이 되고, 결과적으로 $\text{Var}[f] = 0$ 이 성립한다. 그러면 우리는 이 성질과 분산의 정의에 의해서 아래와 같은 식을 도출할 수 있다.

  \[\begin{aligned} 0=\mathrm {Var} [f]=\mathrm {E} [(f-\mathrm {E} [f])^{2}] \; \Rightarrow \; f-\mathrm {E} [f]=0\Rightarrow \mathrm {E} [f]=f \end{aligned}\]

• 그리고 $y = f + \epsilon$ 이고, $\epsilon \sim \mathcal{N}(0, \sigma^2)$ 에 따라 $E[\epsilon] = 0$ 이므로 위의 식을 이용하면 아래가 성립한다.

  \[E[y] = E[f + \epsilon] = E[f] = f\]

• 그리고 이제 위에서 정의한 것들과 $\text{Var}[\epsilon] = \sigma^2$ 임을 이용하면 아래와 같다.

  \[{\displaystyle {\begin{aligned}\mathrm {Var} [y]=\mathrm {E} [(y-\mathrm {E} [y])^{2}]=\mathrm {E} [(y-f)^{2}]=\mathrm {E} [(f+\epsilon -f)^{2}]=\mathrm {E} [\epsilon ^{2}]=\mathrm {Var} [\epsilon ]+\mathrm {E} [\epsilon ]^{2}=\sigma ^{2}\end{aligned}}}\]

• 최종적으로 우리는 아래와 같이 MSE 를 bias 와 variance 로 분해할 수 있다.

  \[{\displaystyle {\begin{aligned}\mathrm {E} {\big [}(y-{\hat {f}})^{2}{\big ]}&=\mathrm {E} [y^{2}+{\hat {f}}^{2}-2y{\hat {f}}]\\ &=\mathrm {E} [y^{2}]+\mathrm {E} [{\hat {f}}^{2}]-\mathrm {E} [2y{\hat {f}}]\\ &=\mathrm {Var} [y]+\mathrm {E} [y]^{2}+\mathrm {Var} [{\hat {f}}]+\mathrm {E} [{\hat {f}}]^{2}-2f\mathrm {E} [{\hat {f}}]\\ &=\mathrm {Var} [y]+\mathrm {Var} [{\hat {f}}]+(f-\mathrm {E} [{\hat {f}}])^{2}\\ &=\color{green}{\sigma ^{2}}+ \color{blue}{\mathrm {Var} [{\hat {f}}]} + \color{red}{\mathrm {Bias} [{\hat {f}}]^{2}}\end{aligned}}}\]
• 먼저 빨간색 term 은 bias 의 제곱이다.
  • 이는 정답($f$)과 대표 예측값($E[\hat{f}]$)이 얼만큼 다른지를 나타낸다.
  • bias 제곱 term 은 비선형인데 선형 모형을 세운 것처럼 모델에 대한 가정이 잘못되었을 때 나타나는 것이다.
  • 즉 bias 값이 존재하면 ${\displaystyle {\hat {f}}(x)}$ 를 세울 때 사용한 가정에 오류가 존재한다는 뜻이다.
• 파란색 term 은 variance 에 해당한다.
  • 예측값의 평균과 각 예측값들의 차이가 클수록 variance 가 높다.
  • 내 모델의 예측값 $\hat{f}$ 이 그 평균의 근처에서 얼만큼의 폭으로 변동하느냐를 나타낸다.
• 마지막 초록색 term 은 irreducible error 라고 한다.
  • 이는 근본적으로 줄일 수 없는 오차를 뜻한다. 위에서 언급한대로 bias 와 variance 를 0 으로 만든다고 하더라도 그 모델이 항상 완벽할 수는 없기 때문이다.
  • bias 는 제곱이 되어있고, variance 또한 식에서 제곱이 되어 있으므로 위 식에서 모든 항의 값은 0 이상이다. 따라서 이 항은 보이지 않는 표본들의 Expected Error 의 하한값의 역할을 한다.
• $\hat{f}(x)$ 가 복잡할수록 더 많은 데이터들을 포착할 수 있기 때문에 bias 값이 작아지지만, 모델이 각 점을 포착하기 위해 더 많이 움직여야 하므로 그만큼 variance 값은 커지게 된다.
• 모델을 선택할 때(model selection)는 모델이 학습 데이터의 규칙을 정확하게 포착하는 것 뿐만 아니라, 보이지 않는 범위에 대해서 일반화(generalization)되는 것이 이상적이다.
• 그러나 안타깝게도 이 둘을 동시에 성취하는 것은 사실상 불가능하다.
• high variance 학습 알고리즘은 학습 데이터셋을 잘 표현하기는 하지만, 지나치게 큰 noise 나 아예 부적절한 학습 데이터까지 over-fitting 할 위험이 있다.
• 반대로 high bias 학습 알고리즘은 over-fitting 문제가 거의 없는 단순한 모델을 제시하지만 학습 데이터로부터 중요한 규칙성을 제대로 포착하지 못하는 under-fitting 문제가 발생한다.
• bias 값이 낮은 모델은 더 높은 차수의 회귀 다항식처럼 일반적으로 더 복잡하기 때문에학습 데이터셋을 더 정확히 표현한다. 하지만 모델링 과정에서 커다란 noise 성분까지 반영할 가능성이 있고, 그런 경우에는 더 복잡함에도 불구하고 덜 정확한 추론을 하게 된다.
• 반대로 bias 값이 높은 모델의 경우 낮은 차수의 회귀 다항식처럼 더 간단한 경향이 있는데, 학습 데이터셋의 데이터를 모델에 충분히 포함하지 못해 variance 값이 낮게 나올 수가 있다.
• 이처럼 복잡한 모델일수록 bias 가 작고 variance 가 크며, 단순한 모델일수록 bias 가 크고 variance 가 작다.
• 따라서 bias 를 낮추기 위해 capacity 가 큰 복잡한 모델을 쓰면 variance 가 커지고, variance 를 낮추기 위해 간단한 모델을 쓰면 bias 가 커진다는 것이다. 이렇게 서로의 변화에 따라 상반되게 움직이는 관계를 trade-off 관계에 있다고 한다.
• 이제 모델과 bias, variance 가 어떤 관계를 가지는지 예제를 들어 살펴보자.

Regression example

• 먼저 regression 예제다. 아래 그래프에서 점선은 예측값이고 각 점은 정답값이다.

  

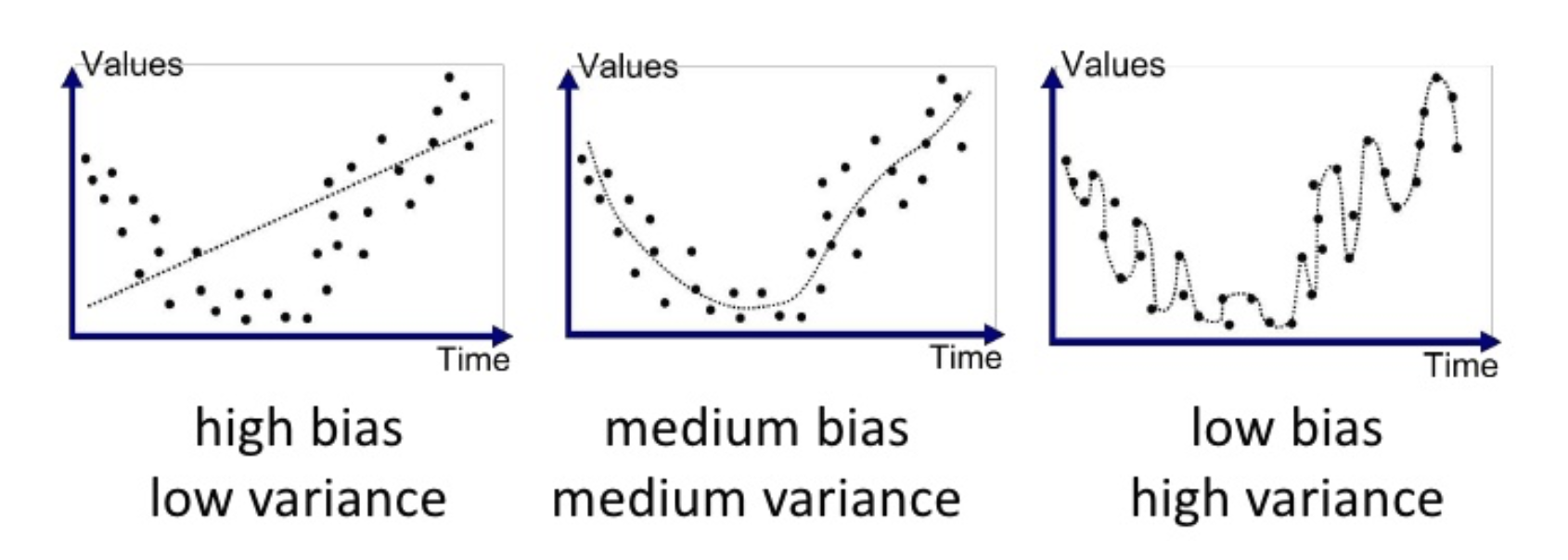
• 첫번째 그래프는 high bias & low variance 하다.
  • high bias 인 이유는 예측값이 실제 정답값과 많이 다르기 때문이고 low variance 한 이유는 예측값들의 편차가 작기 때문이다.
• 두번째 그래프는 medium bias & medium variance 하다.
  • 첫번째 그래프에 비해 예측값과 정답값이 상대적으로 유사하고, variance 측면에서는 첫번째 그래프에 비해서 예측값들의 편차가 상대적으로 커졌다.
• 세번재 그래프는 low bias & high variance 하다.
  • 예측값과 정답이 굉장히 유사하기 때문에 low bias 다.
  • 반면 모델의 예측값이 구불구불하여 편차가 매우 크기 때문에 high variance 하다.

Classification example

• 이번에는 classification 예제를 다뤄보자. regression 문제와 동일한 성격의 예제다.

  

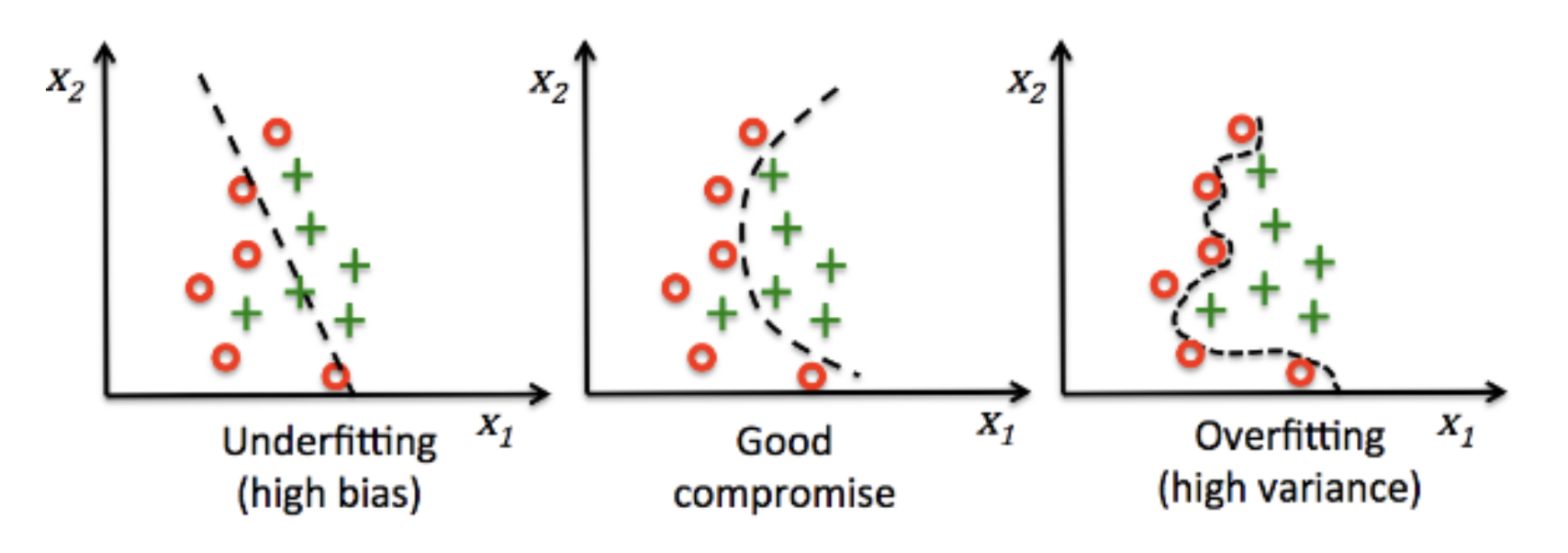
• 첫번째 그래프는 high bias & low variance 하다.
  • high bias 인 경우는 모델이 정답을 잘 예측하지 못하는 경우로 under-fitting 이 발생한 경우라고 볼 수 있다.
• 반면, 세번재 그래프는 low bias & high variance 하다.
  • 이는 모델이 필요 이상으로 복잡하여 예측값 간의 편차가 크게 발생하는 경우다. 이와 같은 경우를 over-fitting 이 발생한 경우라고 볼 수 있다.

Model Complexity

• 위에서 살펴본 것처럼 bias 와 variance 는 모델의 복잡도(complexity, capacity)와 관련이 있다. 또한 이 관계를 잘 살펴보면 bias 와 variance 는 서로 영향을 끼치고 있다.
• under-fitting 이 발생한 경우 이를 개선하기 위해 bias 를 낮추려고 할 것이다. bias 를 낮추려면 모델의 복잡도 높이게 될 것이고 이에 따라 variance 가 높아지게 된다. 그러면 over-fitting 이 발생할 위험이 생기는 것이다.
• 반대로 over-fitting 이 발생한 경우 이를 개선하기 위해 variance 를 낮추려고 할 것이고, 그렇게 모델의 복잡도를 낮추게 되면 bias 가 증가하여 under-fitting 이 발생할 위험이 높아지게 된다.

• 따라서 중요한 것은 적당한 수준의 bias 와 variance 를 만들기 위하여 적정한 수준에서 모델의 학습을 종료 시켜야 한다는 것이다.

  

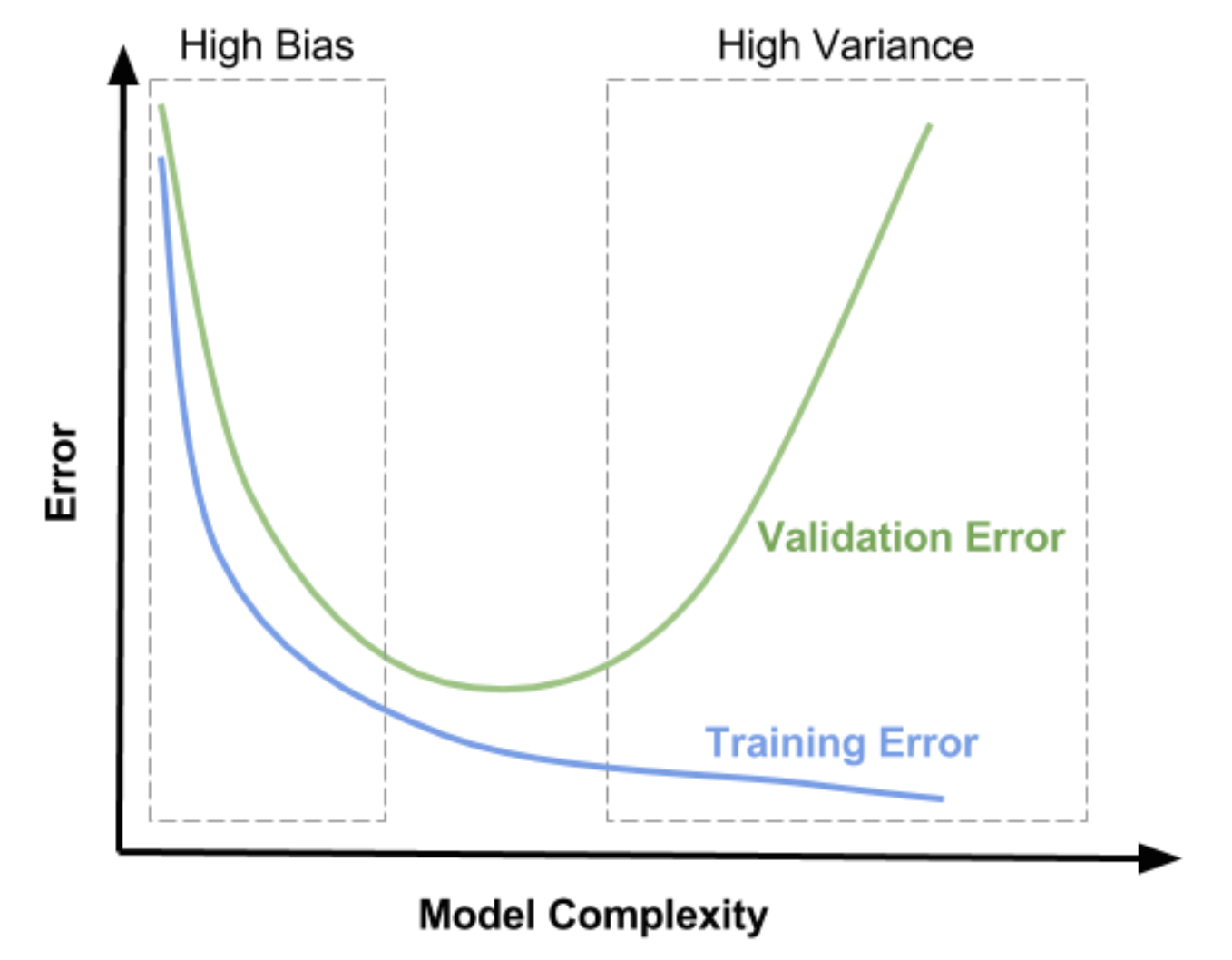
• 우리는 위 그림에서 그 적정 수준의 학습에 대한 단서를 찾을 수 있다. 위 그림과 같이 train 데이터셋과 validation 데이터셋을 이용하는 것이다.
• train 데이터를 통해 학습을 하면서 train error 를 줄여나가면 bias 는 점점 줄어들고 variance 는 점점 증가하게 된다.

• 이 때, validation 데이터도 동시에 error 를 계산하여 validation error 도 감소하는 것을 관측하다가 다시 증가하는 지점을 확인하여 low(medium) bias & low(medium) variance 를 찾는 것이다.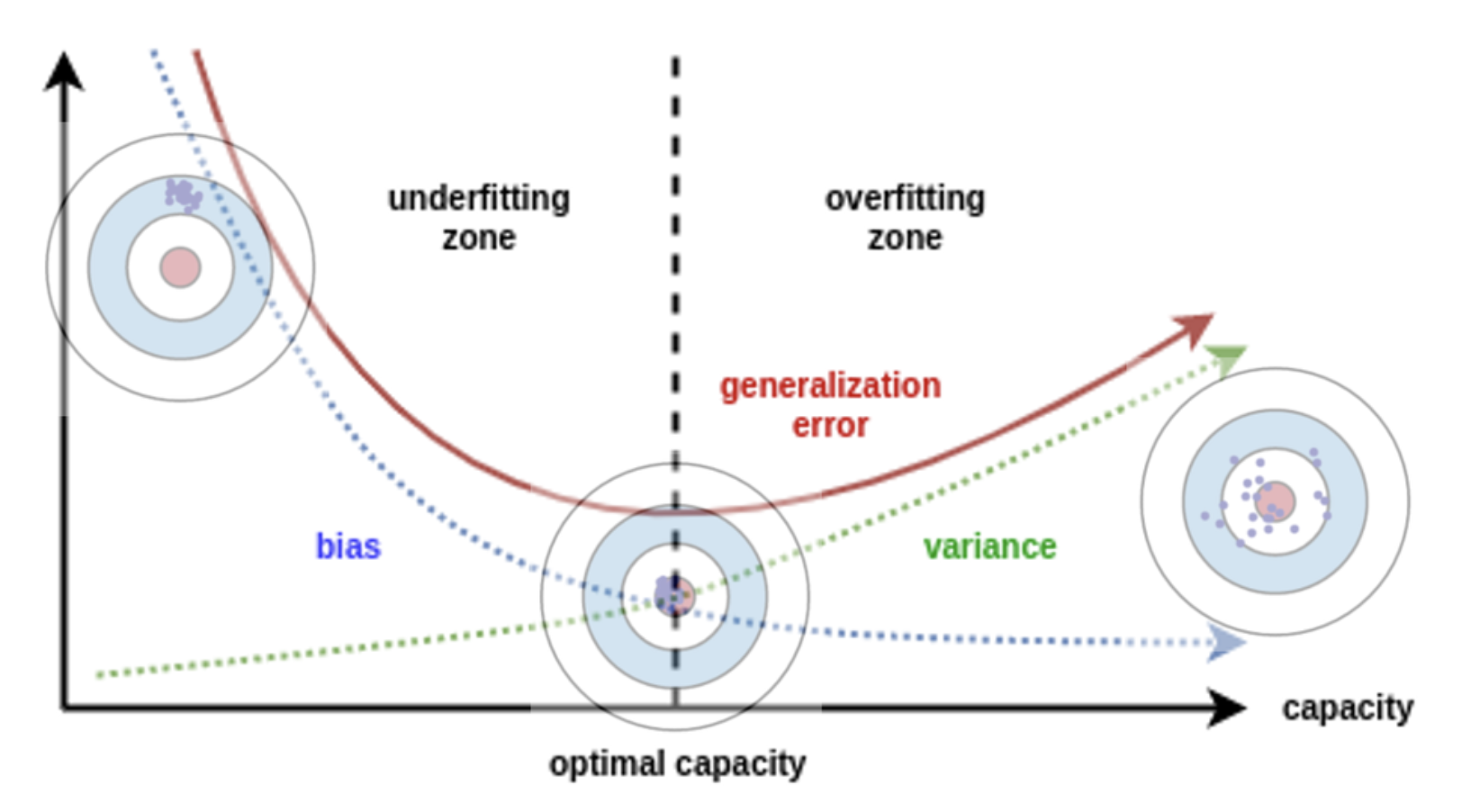

  

• 위 그래프를 보면 전형적인 학습 진행 상황을 under-fitting, over-fitting 구간으로 나누어서 볼 수 있다.
• 학습을 진행할 수록 generalization error 에 대한 곡선이 점점 줄어들다가 다시 증가하는 지점이 발생한다. 이 지점에서 모델은 low(medium) bias & low(medium) variance 를 만족하게 된다.

Over-fitting vs. Under-fitting

• 아래는 Andrew Ng 의 Machine Learning 강의에서 발췌한 Bias 와 Variance 에 대한 내용이다.

  

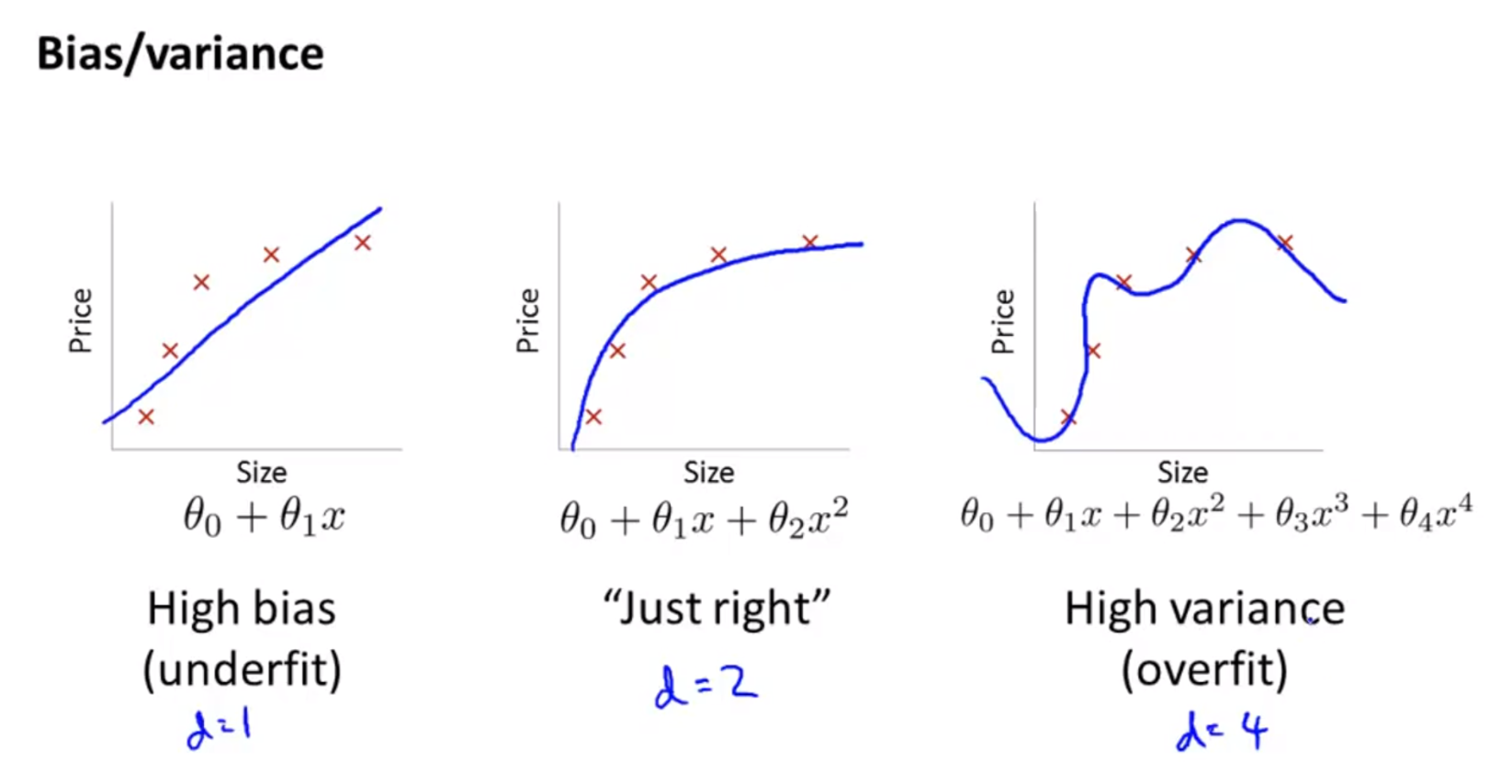
• high bias 문제는 데이터의 분포에 비해 모델이 너무 간단한 경우에 해당한다. 그림을 보면 모델의 차수(degree) $d$ 가 1 에 해당하는 간단한 모델이다. 이는 under-fitting 이 발생하게 된다.
• high variance 문제는 데이터 분포에 비해 모델이 복잡한 경우에 해당한다. 그림을 보면 모델의 차수 $d$ 가 4 에 해당하고, 모델이 만든 예측값이 데이터에 tight 하게 fitting 하여 over-fitting 이 발생하게 된다.
• 딥러닝에서 최적화의 목표는 loss 를 최소화하는 model parameter 를 찾는 것이고, 궁극적인 목표는 그러한 model 이 generalization error 를 최소화하여 학습 중 보지 못한 새로운 데이터에 대해서도 좋은 성능을 내는 것이다.

• 그러나 under-fitting 혹은 over-fitting 이 발생하면 generalization error 가 늘어나 성능이 안 좋을 수밖에 없다.

  

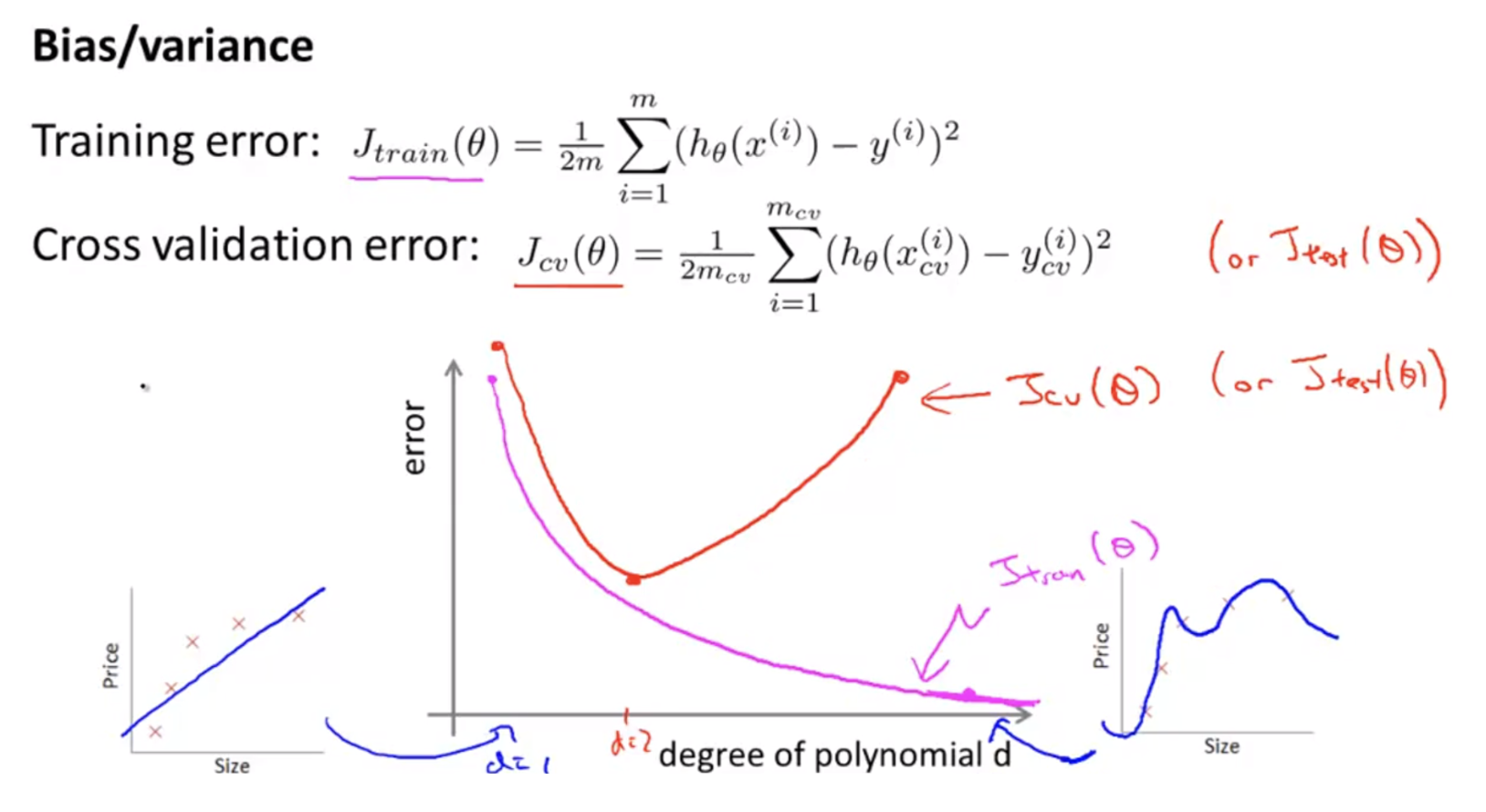
• 위 그림은 모델의 degree(degree of polynomial $d$) 에 따른 training error 와 (cross)validation error 를 그린 것이다.
• 우리는 위에서 $d$ 를 늘리면 모델(식)의 표현력이 더 증가해서 성능이 증가하지만 데이터 분포에 비하여 너무 표현력이 증가하여 over-fitting 이 발생할 수 있음을 확인했다.
• 위 그림을 보면 $d = 1$ 일 때, 식이 너무 단순해서 데이터를 잘 표현하지 못하는 under-fitting 문제가 발생한다. 이 때는 training error 와 validation error 가 둘 다 높다.
• degree 를 높이다 보면 training error 와 validation error 가 둘 다 감소하는 구간이 있다. 두 error 가 모두 감소하는 마지막 구간이 가장 적합한 degree 다.

• degree 를 계속 증가시키다 보면 training error 는 감소하지만 validation error 는 다시 증가하는 현상이 발생하는데 이 때가 over-fitting 이 발생한 구간이다.

  

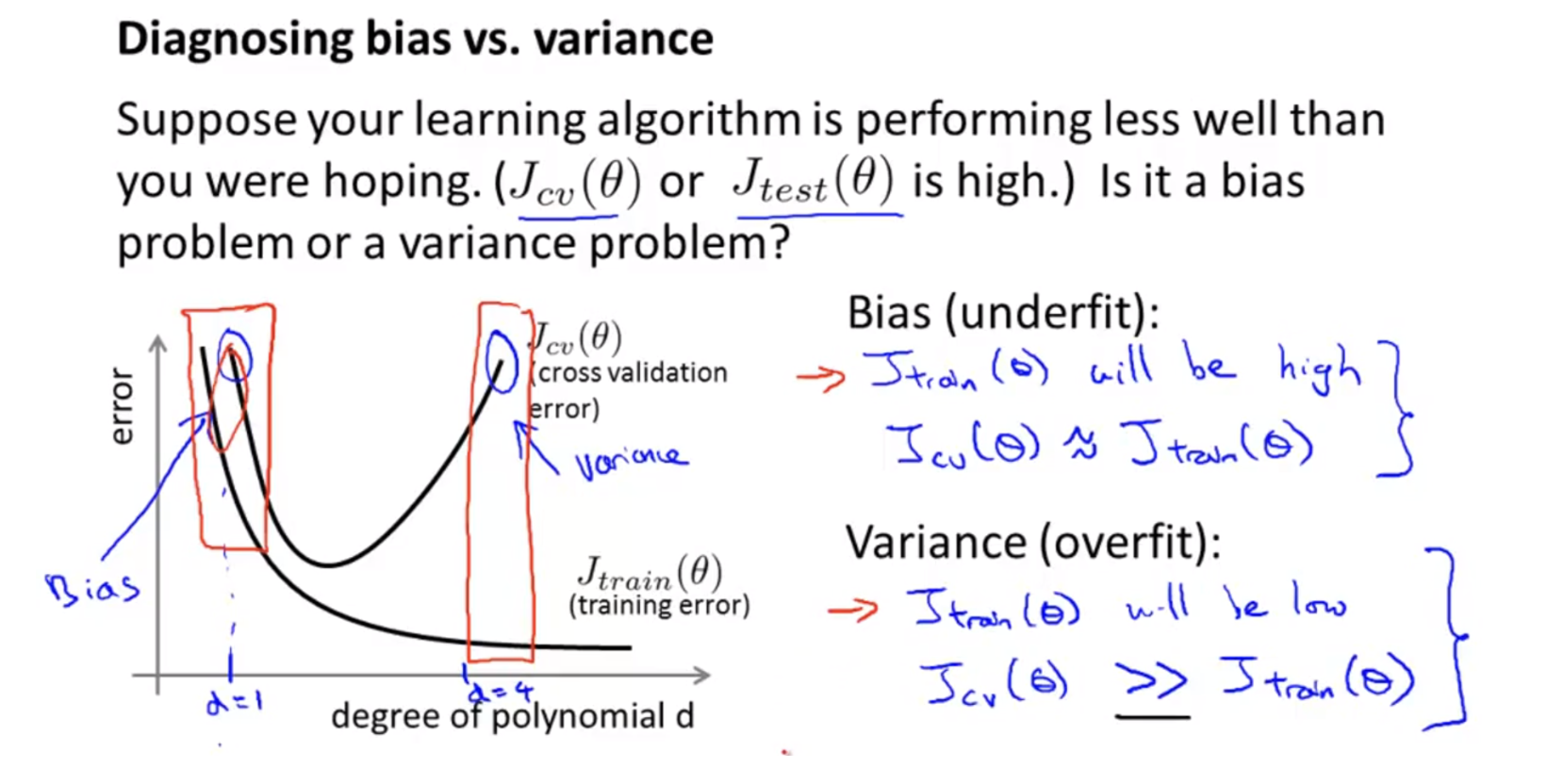
• 위 그림에서 bias problem 이 under-fitting 에 해당하고, variance problem 이 over-fitting 에 해당한다.
• $J_{\text{cv}}(\theta)$ 와 $J_{\text{test}}(\theta)$ 는 각각 validation 과 test 과정에서의 loss(error) 값이다.
• 만약 내 모델이 학습을 다 했는데도 $J_{\text{cv}}(\theta)$ 와 $J_{\text{test}}(\theta)$ 가 모두 높을 때 우리는 어떤 진단을 내릴 수 있을까?
  • 만약 $J_{\text{train}}(\theta)$ 이 높은데 $J_{\text{cv}}(\theta)$ 또한 높다면 이는 bias 가 높은 under-fitting 문제가 발생한 것이다. 이 경우 모델의 복잡도를 데이터의 분포를 잘 표현할 수 있도록 늘려야 한다.
  • 그러나 만약 $J_{\text{train}}(\theta)$ 이 낮은데 $J_{\text{cv}}(\theta)$ 가 높은 경우, 이는 variance 가 높은 over-fitting 문제가 발생한 것이다. 이 경우 모델의 복잡도가 너무 높아 학습 데이터를 “암기”해버린 것으로 모델의 복잡도를 낮추거나, 학습 과정에서 regularization 을 걸거나, 학습 데이터를 더 모아야 한다.
• 그러나 transformer 등 오늘날 사용되는 모델의 경우 충분히 복잡하다. 따라서 under-fitting 보다는 over-fitting 에 좀 더 유의해야 한다.
• 여기서 가져가야 할 것은 bias(underfit) 와 variance(overfit) problem 이 언제 발생하고 이 때의 train error 와 validation error 의 관계를 파악하는 것이다. 이를 통해 모델 개선의 방향성을 잡을 수 있다.

Regularization and Bias/Variance

• 이번에는 앞에서 알아본 bias/variance 과 regularization 의 관계를 알아보자.

• 이전 포스트 에서 다루었듯, weight decay 는 linear regression 문제에서 regularization 기법으로 많이 쓰인다.

  

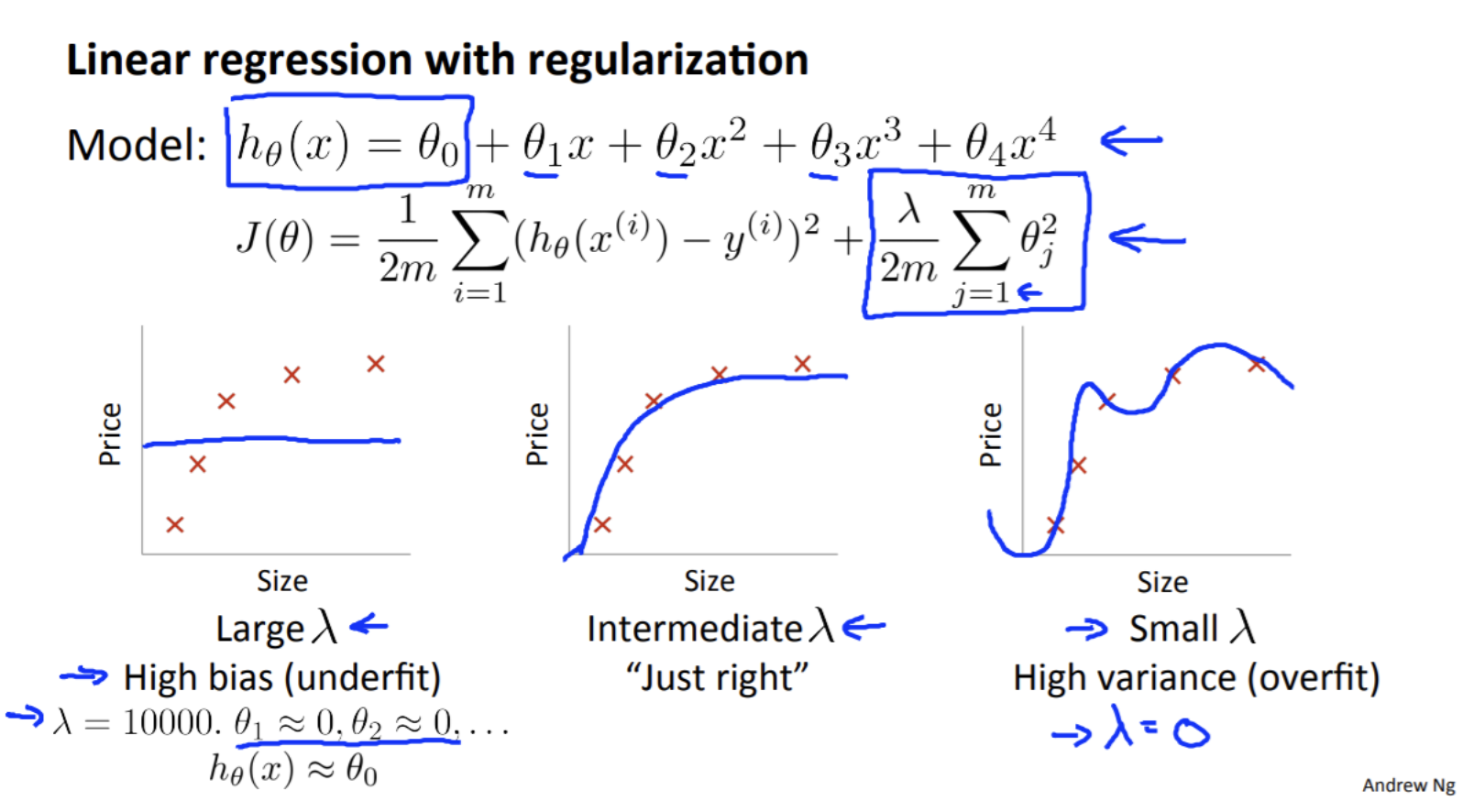
• 위 그림과 같이 polynomial 로 표현된 linear model 이 있고 weight decay regularization 을 적용했다고 가정해보자.
• 위 그림에서 linear model 은 $d = 4$ 로 regularization 이 없으면 over-fitting 이 발생했었다. 이 때, 하이퍼파라미터인 $\lambda$ 값에 따라서 bias/variance problem 의 양상이 변하게 된다.

• weight decay 가 적용되었을 때, SGD 를 사용하는 경우 weight update 는 아래의 방식으로 이루어진다.

  \[\mathbf{w}\; \leftarrow \; \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)\]
• 먼저 regularization term 을 보면 $j = 1, \ldots, m$ 의 범위를 가진다. 따라서 $\lambda$ 가 아주 큰 값을 가지게 되면 $\theta_{1}, \ldots, \theta_{m}$ 에 대해서는 학습이 진행될수록 0 에 수렴하여 학습이 안되게 된다.
• 그러나 $\theta_{0}$ 의 값은 남게 되어 High bias 의 그래프 처럼 수평선 그래프가 그려지게 된다.
• 반대로 High variance 의 상황을 보면 $\lambda = 0$ 인 경우로 생각할 수 있다. 이 상황은 regularization 을 사용하지 않은 것과 같기 때문에 over-fitting 이 발생하게 된다.

• 따라서 가운데 그래프처럼 적당한 bias 와 variance 를 가지도록 $\lambda$ 값을 설정할 필요가 있다.

  

• 따라서 위 그림과 같이 $\lambda$ 를 정할 때, $\lambda = 0$ 부터 시작해서 점점 더 크기를 올리면서 적용하는 것이 좋다.
• 위 그림은 각각의 $\lambda$ 후보값들을 이용하여 validation error($J_{\text{cv}}(\theta)^{(i)}$) 를 구하고 그 error 가 최소인 $\lambda$ 를 선택했다.

• regularization parameter $\lambda$ 의 변화에 따라 train error 와 validation error 를 그리면 아래 그래프와 같다.

  

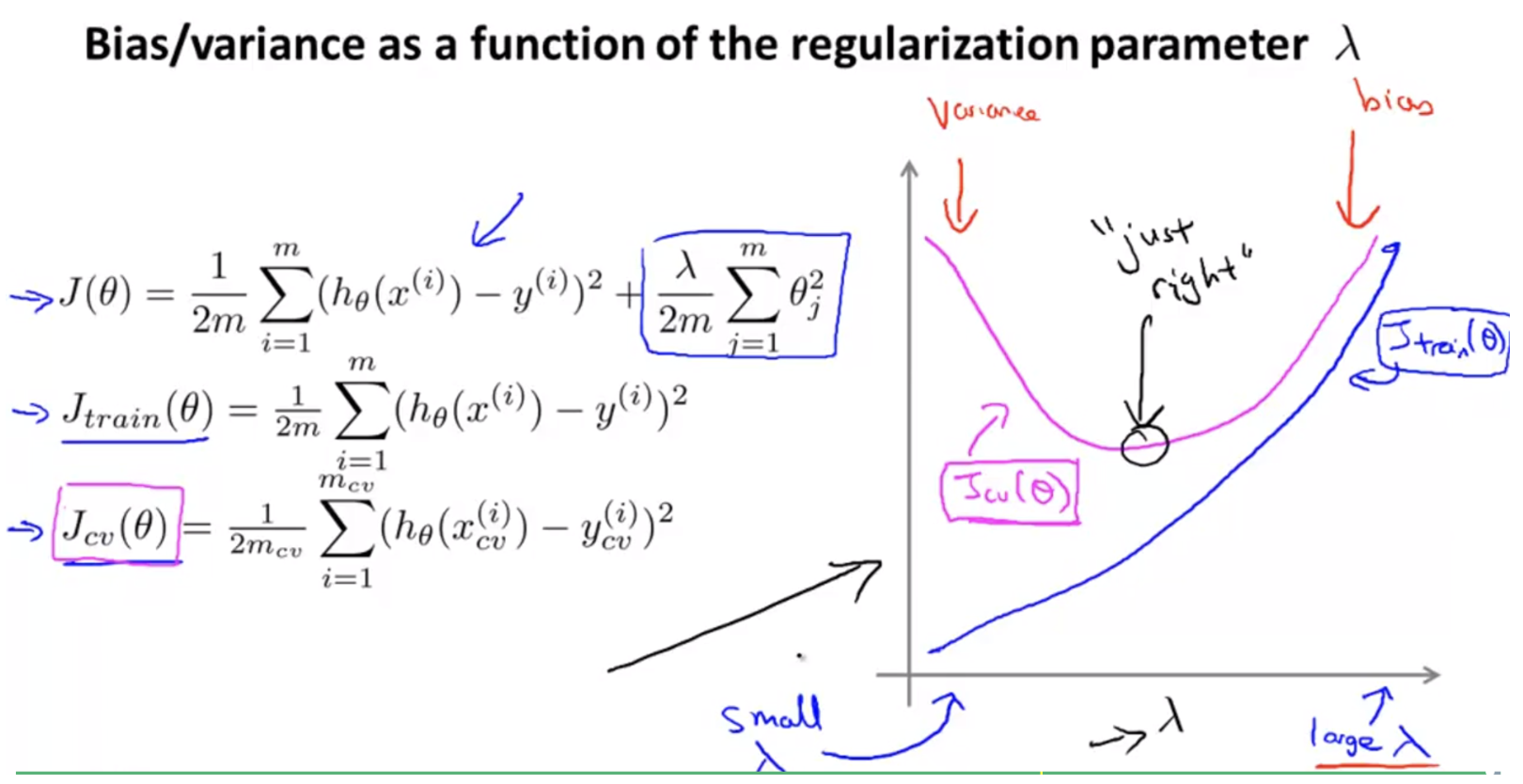
• train error 의 경우 $\lambda$ 의 크기가 커질수록 error 의 크기가 더 커지게 된다.
  • 이는 loss function 을 보면 알 수 있듯이 regularization term 은 항상 양수 값이 더해지기 때문이다.
• 반면 validation error 의 경우 $\lambda$ 가 점점 커질수록 error 가 줄다가 다시 커지게 된다.
  • 매우 작은 값(0)에서 적당한 값으로 커지게 되면 over-fitting 문제가 조금씩 해결되면서 validation error 가 줄어든다.
  • 그러나 적정 크기의 regularization parameter 보다 값이 커지게 되면 항상 error 에 양의 값이 더해지게 되므로 error 값이 증가하게 된다.
  • 이는 regularization parameter 가 적당한 값까지 증가할 때는, error 에 양수 값이 더해지는 것 보다 variance 문제가 해결되는 효과가 더 커서 error 가 줄어든다고 해석할 수 있다.
  • 반면 최적점을 지나 regularization parameter 값이 계속 커지게 되면 error 값에 더해지는 regularization 값도 계속 커지게 되어 error 가 증가하게 되고, bias problem(under-fitting)에 빠지게 된다.

Dataset size and bias/variance

• 이번에는 training dataset 의 크기에 따른 bias 와 variance 의 변화를 살펴보자.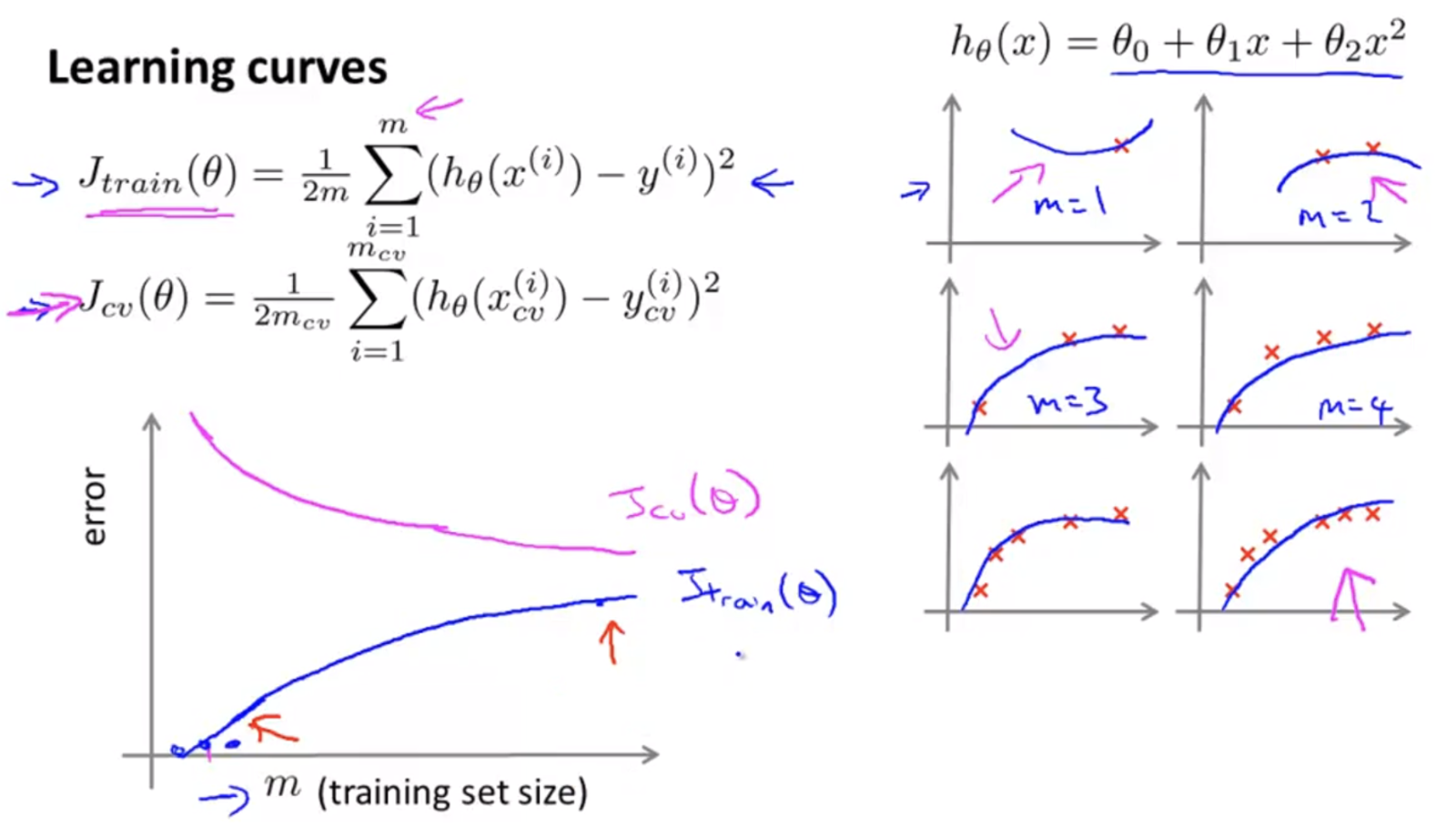

  

• 위 그림을 보면 training set 의 크기 $m$ 에 따라 $J_{\text{train}}(\theta)$ 와 $J_{\text{cv}}(\theta)$ 사이의 차이가 줄어들면서 모델의 generalization 성능이 상승되는 것을 확인할 수 있다.
• 그림의 오른쪽을 보면 데이터가 1 개 있을 때부터 점점 증가하여 데이터가 6 개 있을 때까지 그래프의 모양이 변형된다.
  • 이는 데이터의 수($m$)가 많아질수록 parameter 가 데이터에 맞춰 학습이 되기 때문에 점점 더 데이터의 모집단 분포에 가까워 지게 됩니다.
• 또한 $J_{\text{train}}(\theta)$ 와 $J_{\text{cv}}(\theta)$ 의 그래프를 보면 학습 데이터셋의 크기가 매우 작은 경우, $J_{\text{train}}(\theta)$ 는 상당히 작고 $J_{\text{cv}}(\theta)$ 는 상당히 큼을 알 수 있다.
  • 이는 데이터가 너무 없다는 것은 데이터의 분포가 매우 간단하는 것이고 이는 어느정도 복잡한 모델도 over-fitting 된다는 것을 뜻한다.
• 그러나 데이터 수($m$)가 점점 증가할수록 training error 는 점점 증가하다가 정체된다. 이 경향이 일반적인 training error 의 변화 과정이다.
• 반면에 validation error 는 학습 데이터의 수가 늘어날수록 training error 보단 크지만 유사한 수준으로 감소하는 것을 볼 수 있다.
• 이는 데이터의 수가 많을수록 over-fitting 을 방지할 수 있고, generalization 성능이 커지게 됨을 의미한다.

• 아래 그림을 통해 training set size 와 bias/variance 의 관계를 좀 더 자세히 알아보자.

  

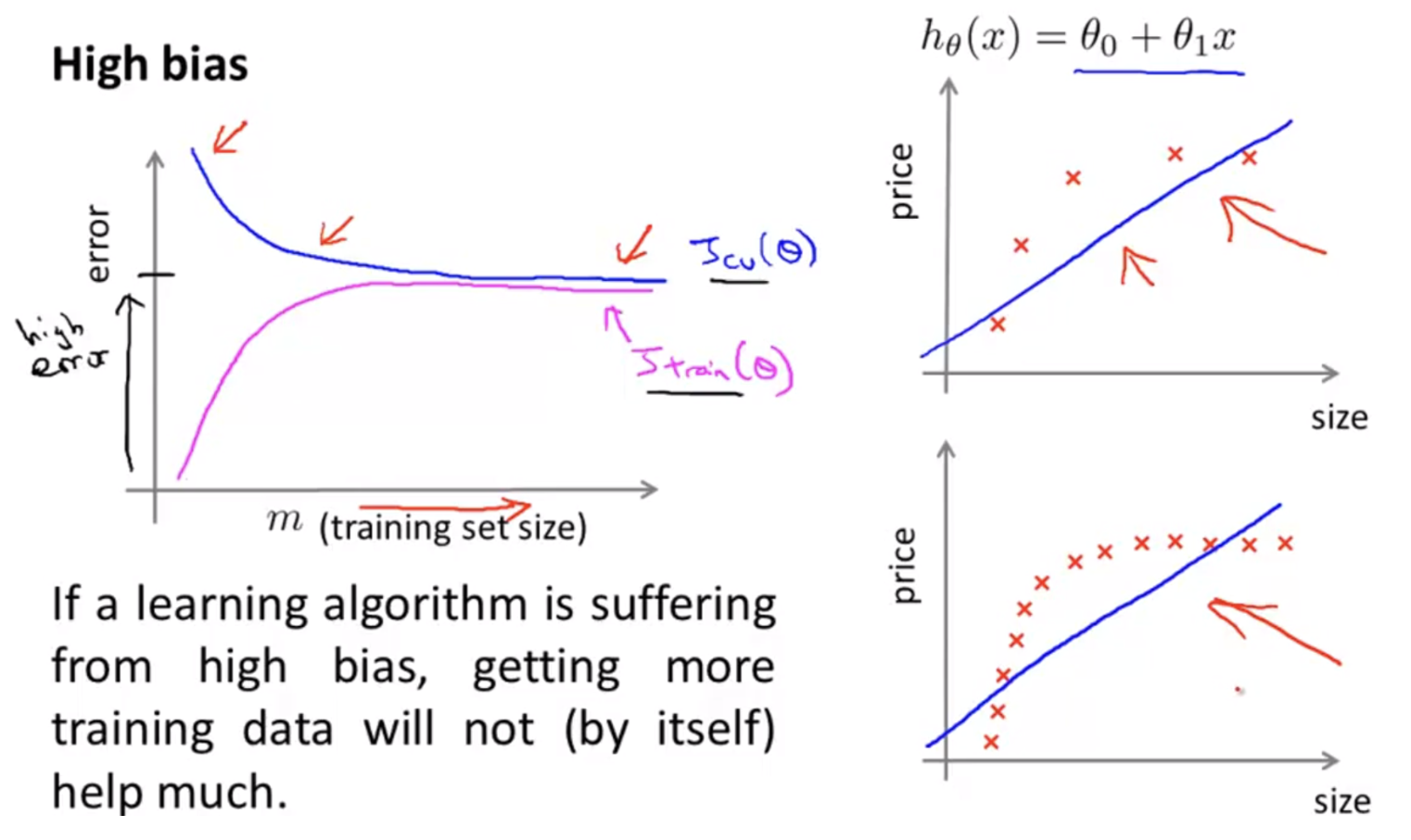
• high bias 의 경우, 기본적으로 모델의 복잡도가 낮아서 모델의 표현력이 데이터를 표현하기 부족하기 때문에 예측과 정답의 차이가 커 under-fitting 이 발생했다.
• 위 그림처럼 $d=1$ 인 간단한 linear model 의 경우 데이터의 수가 많든 적든 데이터 분포를 적합하게 표현할 수가 없다.

• 따라서 기본적으로 error 가 높고, training data size 를 늘리더라도 크게 도움되지 않는다.

  

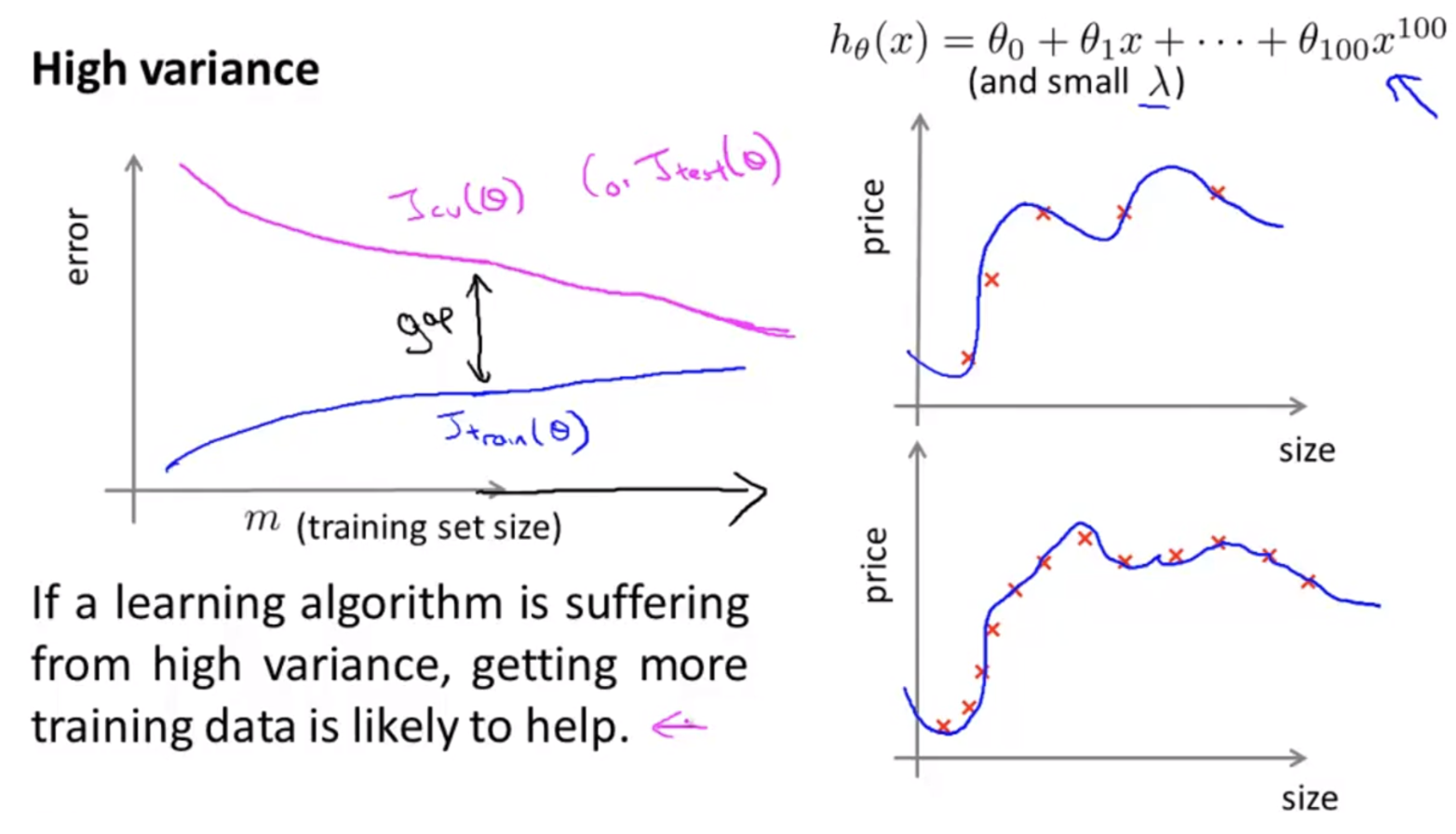
• 반면 high variance 의 경우, 기본적으로 학습 데이터에 비하여 모델의 복잡도가 너무 높아서 모델이 너무 과하게 학습한 over-fitting 문제가 발생한다.
• 위 그림을 보면 $d=100$ 이고, weight decay parameter $\lambda$ 또한 작은 경우다.
• 이 경우는 데이터의 분포를 모델이 너무 잘 표현한다는 것이기 때문에, 학습 데이터의 크기를 늘려서 validation/test error 를 줄이는 것이 상당히 적합하다.
• 따라서 표현력이 너무 좋아서 문제가 된 모델은 더 많은 학습 데이터를 통하여 데이터의 분포를 더 복잡하게 만들어주고, 복잡한 모델은 이를 표현할 능력을 가지고 있으므로 generalization 성능도 올라가게 된다. 즉 validation/test error 가 줄어들게 된다.

정리 및 딥러닝과의 관계

• 최종적으로 bias 와 variance 에 대해 기억해야 할 점을 정리해보자.

  

• 위 그림의 상황은 모델을 학습하고 나서 test 상황에 여전히 error 가 높은 경우 취할 수 있는 방법들을 정리했다.
• high variance 문제, 즉 over-fitting 을 개선하기 위해서는
  • training data 의 수를 늘린다.
  • feature 의 개수를 줄인다. 즉 모델의 복잡도를 낮춘다.
  • regularization 기법(e.g. weight decay)을 사용할 때는 regularization parameter $\lambda$ 의 크기를 증가시킨다.
• high bias 문제, 즉 under-fitting 을 개선하기 위해서는
  • feature 의 갯수를 늘린다. 즉 모델의 복잡도를 높인다.
  • linear model 의 경우 $x^2_1, x^2_2, x_1, x_2$ 와 같은 polynomial feature 를 추가한다. 이 또한 좀 더 복잡한 모델을 사용하는 것과 같다.
  • regularization parameter $\lambda$ 의 크기를 줄인다.

Deep Learning and over-fitting

• 앞서 언급했지만, 오늘날의 딥러닝 모델은 충분히 복잡하고 이름에 걸맞게 layer 가 deep 한 모델들이 많다.
• 딥러닝 모델들은 다양한 분야에서 매우 뛰어난 성능을 보이고 있지만, 학습 과정에서 당연하게 over-fitting 의 위험이 언제나 도사리고 있다.
• 왜냐하면 Neural Network 에서 layer 의 수는 parameter 의 수와 비례하기 때문이다.
• 개인적으로도 under-fitting 문제는 거의 드물고, over-fitting 을 프로젝트 단계에서 매우 많이 만났다.
• 이 때문에 다양한 Regularization 기법들이 발전하고 있고, 이 블로그에서도 따로 카테고리를 두어 다양한 regularization 기법들을 정리한다.

• 여기서는 over-fitting 에 대해 언제나 주의하는 것이 중요함을 잊지 말도록 하고, 모델 복잡도 측면에서 over-fitting 을 보도록 하자.

  

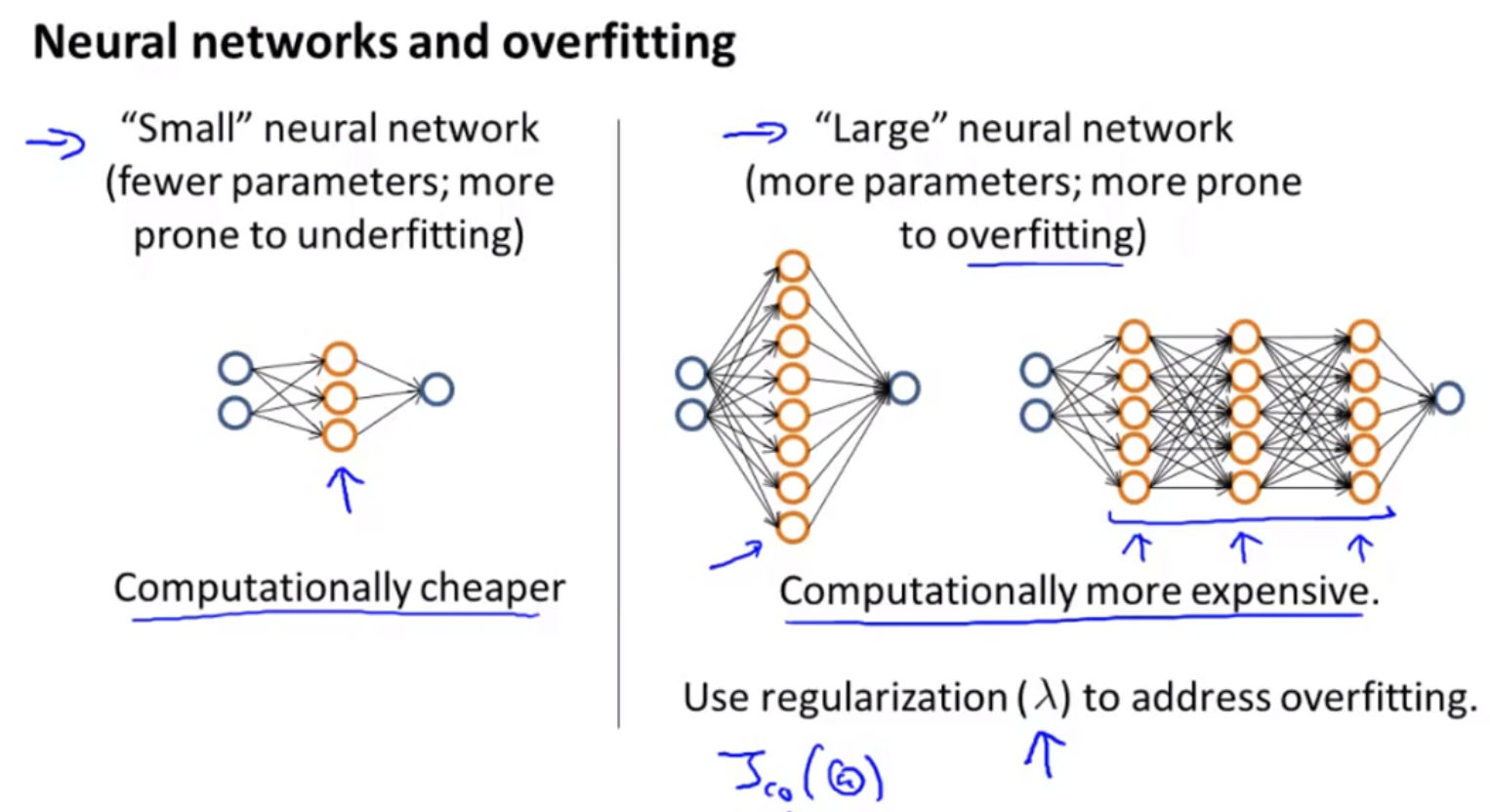
• 위 그림처럼 계산적으로 가볍고 작은 neural network 는 under-fitting 의 위험이 있다. 즉 layer 의 수가 작으면 계산 비용은 작지만 high bias 문제에 빠질 가능성이 있다. 이 때는 layer 를 추가하거나 더 복잡한 모델을 쓰는 것이 좋다.
• 반면에 layer 의 수가 너무 많은 복잡한 모델들은 parameter 수가 엄청 나며 계산 비용도 많이 들고 high variance 문제에 빠질 가능성이 높다.
• over-fitting 을 개선하기 위해서 1) 데이터의 수를 늘리거나, 2) regularization 을 추가하거나, 3) layer 의 수를 줄이는, 즉 좀 더 간단한 모델을 사용하는 것이 좋다.

Reference

• https://gaussian37.github.io/machine-learning-concept-bias_and_variance/

맨 위로 이동 ↑