[Deep Learning, d2l] MLP 구현 (2)

2024-10-25

앞선 포스트에서 Pytorch 의 nn.Module, nn.Sequential 을 사용하여 custom module 을 만들었다. 이제 module 안에서의 parameter 관리, parameter initialization, custom layer 제작 등을 알아보자. 이 다음 포스트는 공부한 것을 정리하여 MLP 로 이루어진 모델을 구현하고 학습할 예정이다.

Parameter Management

architecture 를 선택하고 하이퍼파라미터를 설정한 후, 우리는 loss function 을 최소화하는 parameter 값을 찾기 위해서 학습 loop 에 들어간다. 학습이 끝난 후에는 예측(inference)을 위해 이 parameter 들이 필요하다.
또한, parameter 를 추출하여 다른 코드에서 재사용하거나, 디스크에 모델을 저장해 다른 소프트웨어에서 실행하거나, 검토 목적으로 활용하기도 한다.
앞 포스트에서 언급한대로, 대부분의 경우 parameter 가 선언되고 조작되는 세부적인 사항은 Pytorch 와 같은 딥러닝 프레임워크가 수행하는 주요 작업에 의존할 수 있다.
그러나 일반적인 layer 로 구성된 architecture 에서 벗어나게 되면 parameter 의 선언과 조작에 대한 세부적인 작업이 필요할 때도 있다. 여기서는 아래의 내용을 다뤄보자.
- debugging, 검토, visualization 을 위한 parameter 접근
- 모델의 다른 구성 요소 간 parameter 공유
우선 하나의 hidden layer 를 가지는 MLP 에 초점을 맞추어 살펴보자.

import torch
from torch import nn

mlp = nn.Sequential(nn.LazyLinear(8),
                    nn.ReLU(),
                    nn.LazyLinear(1))

X = torch.rand(size=(2, 4))
mlp(X).shape  # torch.Size([2, 1])

Parameter Access

위 모델에서 parameter 에 접근하는 방법부터 보자. nn.Sequential 클래스를 통해 모델을 정의하면, 마치 모델이 list 인 것처럼 indexing 하여 각 layer 에 접근할 수 있다.
각 layer 의 parameter 는 indexing 으로 접근한 해당 layer 의 .state_dict() 으로 확인할 수 있다.

mlp[2].state_dict()
# OrderedDict([('weight',
#               tensor([[ 0.2833,  0.1916,  0.0866,  0.1649,  0.0927, -0.2409,  0.0981, -0.2389]])),
#              ('bias', tensor([0.2846]))])

이 fully connected layer nn.LazyLinear(1) 에는 weight 와 bias 에 해당하는 두 가지 parameter 가 포함되어 있음을 알 수 있다.

Targeted parameter

각 parameter 는 nn.parameter.Parameter 클래스의 인스턴스로 표현된다. 이러한 parameter 로 유용한 작업을 수행하려면 먼저 숫자 값에 접근해야 한다.
이를 위해 몇 가지 방법이 있다. 아래의 코드는 neural network 의 2번째 layer 의 bias 를 추출하여 nn.parameter.Parameter 클래스 인스턴스를 반환하고, 그 parameter 의 값에 접근한다.

print(mlp[2].bias)  # Parameter containing: tensor([0.2846], requires_grad=True)
print(type(mlp[2].bias)) # <class 'torch.nn.parameter.Parameter'>
print(mlp[2].bias.data)  # tensor([0.2846])

parameter 는 값과 gradient, 그리고 추가적인 정보들을 포함하는 복합 객체이므로, 위와 같이 값을 명시적으로 요청해야 한다.
값 외에도 각 parameter 는 gradient 에도 접근할 수 있다. 다만 아직 위 예제의 mlp 에 대해 back propagation 을 호출하지 않았기 때문에 초기 상태 None 으로 남아 있다.

print('grad' in dir(mlp[2].weight)) # True
mlp[2].weight.grad == None  # True

All parameters at once

만약 모든 parameter 에 대해 연산을 수행하는 등의 작업을 할 때, 위 방법처럼 parameter 에 하나씩 접근하는 것은 번거로울 수 있다.
특히 중첩된 모듈과 같이 더 복잡한 구조에서는 전체 트리를 통해 각 하위 모듈의 parameter 를 재귀적으로 추출해야 하므로 상황이 더욱 복잡해질 수 있다.
아래 예시는 모든 layer 의 parameter 에 접근하는 방법을 보여준다.

[(name, param.shape) for name, param in mlp.named_parameters()]
# [('0.weight', torch.Size([8, 4])),
#  ('0.bias', torch.Size([8])),
#  ('2.weight', torch.Size([1, 8])),
#  ('2.bias', torch.Size([1]))]

Tied Parameters

또한 딥러닝을 구현하다 보면, 여러 layer 에 걸쳐 parameter 를 공유하고 싶을 때가 종종 있다. 이를 우아하게 처리하는 방법을 살펴보자.
아래 예제에서는 fully connected layer 를 구현한 후, 해당 layer 의 parameter 를 사용해 다른 layer 의 parameter 를 설정하는 방법을 보여준다.
이 때 nn.LazyLinear 의 특성 상 net(X) 로 forward propagation 을 실행한 후에 parameter 에 접근해야 한다.

shared = nn.LazyLinear(8)
net = nn.Sequential(nn.LazyLinear(8), nn.ReLU(),
                    shared, nn.ReLU(),
                    shared, nn.ReLU(),
                    nn.LazyLinear(1))

net(X)
print(net[2].weight.data[0] == net[4].weight.data[0])
# tensor([True, True, True, True, True, True, True, True])

net[2].weight.data[0, 0] = 100
print(net[2].weight.data[0] == net[4].weight.data[0])
# tensor([True, True, True, True, True, True, True, True])

위 예제는 두번째와 세번째 layer 의 parameter 가 서로 연결되어 있음을 보여준다. 즉, 단순히 값이 같은 것이 아니라 동일한 tensor 로 표현된다. 따라서 이 경우 하나의 parameter 를 변경하면 다른 parameter 도 같이 변경된다.
이처럼 parameter 가 공유될 때 gradient 는 어떻게 될까?
각각의 모델 parameter 에는 gradient 가 포함되어 있기 때문에, back propagation 시 두번째 hidden layer 와 세번째 hidden layer 의 gradient 가 합산된다.

Parameter Initialization

이제 parameter 에 접근하는 방법을 알았으니, 이를 적절히 initialization 하는 방법에 대해 살펴보자.
적절한 initialization 의 필요성은 앞선 포스트에서 살펴봤다.
Pytorch 와 같은 딥러닝 프레임워크는 기본적으로 layer 에 random initialization 을 제공하지만, 다양한 방법으로 weight 를 초기화하고자 할 때가 많다.
Pytorch 는 자주 사용되는 parameter initialization 방식을 제공하며, 사용자가 custom 한 initialization 방식을 만들 수 있도록 허용하고 있다.
기본적으로 PyTorch 는 weight 와 bias matrix 를 입력과 출력 차원에 따라 계산된 범위 내에서 균등하게 무작위 추출해 초기화한다. 즉, Kaiming Uniform initialization 을 default 로 하고 있다.
PyTorch 의 nn.init 모듈을 통해 기본으로 제공하고 있는 다양한 초기화 방법을 사용할 수 있다. 여기를 클릭하면 확인 가능하다.

Built-in Initialization

built-in initialization 방법을 사용해보자. 아래 코드에서는 모든 weight parameter 를 표준편차(std)가 0.01 이고 평균(mean)이 0 인 Gaussian random variables 로 초기화하고, bias parameter 는 0 으로 초기화한다.

net = nn.Sequential(nn.LazyLinear(8), nn.ReLU(), nn.LazyLinear(1))
X = torch.rand(size=(2, 4))
print(net(X).shape)  # torch.Size([2, 1])

def init_normal(module):
    if type(module) == nn.Linear:
        nn.init.normal_(module.weight, mean=0, std=0.01)
        nn.init.zeros_(module.bias)

net.apply(init_normal)
net[0].weight.data[0], net[0].bias.data[0]
# (tensor([-0.0003, -0.0205,  0.0059, -0.0121]), tensor(0.))

위 예제에서는 torch.nn.Module.apply 를 사용했지만, class 로 모델을 정의할 때 init_noraml 함수를 정의하여 생성자 __init__ 안에서 호출할 수도 있다.

class Net(nn.Module):
    
    def __init__(self):
        super().__init__()
        
        self.layer1 = nn.Sequential(
            nn.Linear(4, 8),
            nn.ReLU()
        )
        self.layer2 = nn.Linear(8, 1)
        
        self.init_normal(self.layer1)
        self.init_normal(self.layer2)
        
    def init_normal(self, model):
        for module in model.modules():
            
            if isinstance(module, nn.Linear):
                nn.init.normal_(module.weight, mean=0, std=0.01)
                
                if module.bias is not None:
                    nn.init.zeros_(module.bias)
                    
    def forward(self, X):
        return self.layer2(self.layer1(X))
    
X = torch.rand(size=(2, 4))
net = Net()
print(net(X).shape) # torch.Size([2, 1])
net.layer1[0].weight.data[0], net.layer1[0].bias.data[0]
# (tensor([ 0.0140, -0.0071,  0.0040,  0.0047]), tensor(0.))

위 방법에서 주의해야 할 점은 nn.LazyLinear 는 입력 데이터의 크기를 기반으로 weight 와 bias 를 초기화하기 때문에, 모델이 처음 forward 메서드에서 입력 데이터를 받을 때까지는 weight 가 초기화되지 않는다. 따라서 nn.Linear 로 교체했다.
또한 모든 parameter 를 일정한 값(ex. 1)으로 초기화할 수도 있다.

def init_constant(module):
    if type(module) == nn.Linear:
        nn.init.constant_(module.weight, 1)
        nn.init.zeros_(module.bias)

net.apply(init_constant)
net[0].weight.data[0], net[0].bias.data[0]
# (tensor([1., 1., 1., 1.]), tensor(0.))

또한 특정 블록에 대해 다른 초기화 방법을 적용할 수도 있다. 예를 들어, 아래 예제에서는 첫번째 layer 는 Xavier 초기화 방식으로, 두번째 layer 는 상수값 42 로 초기화한다.

def init_xavier(module):
    if type(module) == nn.Linear:
        nn.init.xavier_uniform_(module.weight)

def init_42(module):
    if type(module) == nn.Linear:
        nn.init.constant_(module.weight, 42)

net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
# tensor([-0.0974,  0.1707,  0.5840, -0.5032])
print(net[2].weight.data)
# tensor([[42., 42., 42., 42., 42., 42., 42., 42.]])

Custom Initialization

가끔은 우리가 필요한 initialization 방법이 딥러닝 프레임워크에서 제공하지 않을 수도 있다. 예시를 들어보자.
아래와 같은 독특한 분포를 사용하여 weight parameter $w$ 를 초기화해보자.
\[\begin{aligned} w \sim \begin{cases} U(5, 10) & \textrm{ with probability } \frac{1}{4} \\ 0 & \textrm{ with probability } \frac{1}{2} \\ U(-10, -5) & \textrm{ with probability } \frac{1}{4} \end{cases} \end{aligned}\]
이를 위해 my_init 함수를 다시 구현한다.

def my_init(module):
    if type(module) == nn.Linear:
        print("Init", *[(name, param.shape)
                        for name, param in module.named_parameters()][0])
        nn.init.uniform_(module.weight, -10, 10)
        module.weight.data *= module.weight.data.abs() >= 5

net = nn.Sequential(nn.LazyLinear(8), nn.ReLU(), nn.LazyLinear(1))
X = torch.rand(size=(2, 4))
net(X)

net.apply(my_init)
# Init weight torch.Size([8, 4])
# Init weight torch.Size([1, 8])
net[0].weight
# Parameter containing:
# tensor([[ 0.0000, -8.5026,  8.8556,  7.1111],
#         [-0.0000,  0.0000,  9.9805, -0.0000],
#         [ 9.5080, -0.0000,  7.6434, -6.4125],
#         [ 9.5425, -9.9032, -0.0000,  0.0000],
#         [ 8.8614, -6.4974,  9.8048,  8.8713],
#         [ 9.5115,  0.0000,  0.0000,  0.0000],
#         [-6.4449, -0.0000,  0.0000,  0.0000],
#         [-0.0000,  0.0000, -7.6779, -6.5139]], requires_grad=True)

또한 parameter 를 아래와 같이 직접 설정할 수도 있다는 점을 기억하자.

net[0].weight.data[:] += 1
net[0].weight.data[0, 0] = 42
net[0].weight.data[0]
# tensor([42.0000, -7.5026,  9.8556,  8.1111])

Lazy Initialization

지금까지 d2l 의 예시는 모델의 설정에서 여러 세부사항을 간단히 넘어간 것처럼 보일 수 있다. 특히 다음과 같은 직관적이지 않은 설정을 사용했는데, 이는 제대로 동작하지 않을 것처럼 보일 수 있다.
- nn.LazyLinear 를 통해 입력 차원을 명시하지 않고 모델 아키텍처를 정의했다.
- 이전 layer 의 출력 차원을 명시하지 않고 layer 를 추가했다.
- 모델이 포함해야 할 parameter 개수를 결정하기 위한 충분한 정보를 제공하기 전에 parameter 를 초기화했다.
지금까지는 딥러닝 프레임워크가 모델의 입력 차원을 알 수 있는 방법이 없음에도 불구하고 코드가 실행됐다.
여기서 사용된 트릭은 딥러닝 프레임워크가 초기화를 미루고, 처음으로 데이터를 모델에 통과시킬 때(forward) 각 layer 의 크기를 실시간으로 유추한다는 것이다.
이 기술은 이후에 CNN 을 다룰 때 더욱 유용해진다. 예를 들어 입력 차원(ex. image resolution)이 각 layer 의 차원에 영향을 미칠 수 있다.
따라서 코드를 작성할 때 차원의 값을 몰라도 parameter 를 설정할 수 있는 기능은 모델을 지정하고 수정하는 작업을 크게 단순화한다.
아래에서 initialization 의 메커니즘을 더 깊이 파헤쳐 보자. 먼저, MLP 를 인스턴스화한다.

net = nn.Sequential(nn.LazyLinear(256), nn.ReLU(), nn.LazyLinear(10))

이 시점에서 모델은 input layer 의 weight 차원을 알 수 없기 때문에, 아직 어떤 parameter 도 초기화할 수 없다. 만약 parameter 에 접근하려고 시도하면 아래와 같이 출력된다.

net[0].weight
# <UninitializedParameter>

이제 데이터를 모델에 통과시켜 프레임워크가 parameter 를 초기화할 수 있도록 한다.

X = torch.rand(2, 20)
net(X)

net[0].weight.shape
# torch.Size([256, 20])

입력 차원이 20 으로 주어진 후, 프레임워크는 첫번째 layer 의 weight matrix 크기를 20 으로 설정할 수 있다.
첫번째 layer 의 shape 을 인식하면, 프레임워크는 두번째 layer 로 진행하며, 모든 layer 의 크기가 확인될 때까지 이 과정을 반복한다.
이 경우, 첫번째 layer 만 Lazy Initialization 이 필요하지만 프레임워크는 순차적으로 초기화를 수행한다.
그렇게 모든 parameter 의 크기가 확정되면, 프레임워크는 마침내 parameter 를 초기화할 수 있다. 위에서 봤듯 이름에 Lazy 가 들어간 nn.LazyLinear 의 효과다.
아래의 코드는 모델에 더미 데이터를 전달하여 모든 parameter 크기를 추론하고 이후 parameter 를 초기화하는 방식이다. 이러한 메서드 활용 방식은 default random initialization 을 원하지 않을 때 사용된다.

import torch
import torch.nn as nn

class Net(nn.Module):
    def __init__(self):
        super().__init__()
        
        self.layer = nn.Sequential(
            nn.LazyLinear(256),
            nn.ReLU(),
            nn.LazyLinear(10)
        )
        
        self._initialized = False

    def init_normal(self, input_shape):
        # 더미 데이터 생성하여 레이어 초기화
        dummy_input = torch.empty(*input_shape)
        self.layer(dummy_input)
        
        # 가중치 초기화
        for module in self.layer.modules():
            if isinstance(module, nn.Linear):
                nn.init.normal_(module.weight, mean=0, std=0.01)
                if module.bias is not None:
                    nn.init.zeros_(module.bias)
        
        self._initialized = True
        
    def forward(self, X):
        # 초기화가 되지 않았을 때만 init_normal 호출
        if not self._initialized:
            self.init_normal(X.shape)
        
        return self.layer(X)

net = Net()
print(net._initialized)  # False

X = torch.rand(size=(2, 4))
print(net(X).shape)  # torch.Size([2, 10])
print(net._initialized)  # True
print(net.layer[0].weight[:1], net.layer[0].bias[:1])
# tensor([[ 0.0088,  0.0024, -0.0093,  0.0072]], grad_fn=<SliceBackward0>), tensor([0.], grad_fn=<SliceBackward0>)

Custom Layer

딥러닝의 성공 요인 중 하나는 다양한 작업에 맞춘 모델 architecture 를 설계하기 위해 창의적으로 구성할 수 있는 광범위한 layer 의 존재다.
예를 들어, 연구자들은 image, text, sequential data 처리 및 동적 프로그래밍을 위한 특정 layer 를 구현해왔다.
언젠가는 딥러닝 프레임워크에 존재하지 않는 layer 가 필요할 수도 있다. 이러한 경우에는 custom layer 를 구축해야 한다. 여기서는 그 방법을 살펴보자.

Layers without Parameters

먼저, 자체 parameter 를 가지지 않는 layer 를 만들어보자. 이는 단순히 더하기 모듈이나 아래 예제 같은 모듈이다.
다음 CenteredLayer 클래스는 input 에서 mean 을 빼는 역할을 한다. 이를 구축하려면 기본 layer 클래스 nn.Module 을 상속하고 forward 함수를 구현하기만 하면 된다.

class CenteredLayer(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, X):
        return X - X.mean()

데이터를 입력해 layer 가 의도한 대로 작동하는지 확인하면 아래와 같다.

layer = CenteredLayer()
layer(torch.tensor([9, 6, 6, 10, 13], dtype=torch.float32))
# tensor([ 0.2000, -2.8000, -2.8000,  1.2000,  4.2000])

이제 이 layer 를 더 복잡한 모델을 구축하는 데 사용해보자.

net = nn.Sequential(nn.LazyLinear(128), CenteredLayer())

random 데이터를 모델에 전달하여 결과의 평균이 실제로 0 인지 확인할 수 있다.

Y = net(torch.rand(4, 8))
Y.mean() # tensor(6.5193e-09, grad_fn=<MeanBackward0>)

위 결과는 floating point 수를 다루기 때문에, 컴퓨터의 quantization 으로 인해 0 과 가까운 아주 작은 non-zero 값이 나타난다.

Layers with Parameters

이제 간단한 layer 를 정의하는 방법을 알았으니, 학습을 통해 조정 가능한 parameter 를 가지는 layer 를 정의해 보자.
우리는 built-in 함수를 사용해 parameter 를 생성할 수 있고, 이는 접근, 초기화, 공유, 저장 및 불러오기 등의 기본 기능을 제공한다.
이제 직접 fully connected layer 를 만들어보자. 이 layer 에는 weight 와 bias 를 나타내는 두 개의 parameter 가 필요하다.
아래 예제에서는 기본값으로 F.relu 활성화함수를 포함했다. 이 layer 는 인스턴스화 할 때 in_units 와 units 라는 두 개의 argument 가 필요하며, 이는 각각 입력과 출력의 개수를 나타낸다.

class MyLinear(nn.Module):
    def __init__(self, in_units, units):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(in_units, units))
        self.bias = nn.Parameter(torch.randn(units,))

    def forward(self, X):
        linear = torch.matmul(X, self.weight.data) + self.bias.data
        return F.relu(linear)

이제 MyLinear 클래스를 인스턴스화하고 모델 parameter 에 접근해보자.

linear = MyLinear(5, 3)
linear.weight
# Parameter containing:
# tensor([[ 2.0418, -0.1902,  1.0902],
#         [-0.2241,  0.0437,  0.9108],
#         [-0.1377,  0.4482,  1.2890],
#         [-0.0370,  0.1391,  1.2077],
#         [-2.3620, -0.1391, -0.3061]], requires_grad=True)

이러한 custom layer 를 사용하여 직접 forward 계산을 수행할 수 있다.

linear(torch.rand(2, 5))
# tensor([[0.0000, 0.9930, 2.6068],
#        [0.0000, 0.7905, 3.2713]])

또한 custom layer 를 사용해 모델을 구성할 수도 있다. 이렇게 하면 built-in fully connected layer 와 마찬가지로 사용할 수 있다.

net = nn.Sequential(MyLinear(64, 8), MyLinear(8, 1))
net(torch.rand(2, 64))
# tensor([[0.0000],
#         [0.3056]])

File I/O

우리는 학습시킨 모델을 나중에 다양한 상황에서 사용할 수 있도록 결과를 저장하고 싶을 것이다. 실제 deployment 환경에서 예측을 수행하기 위해 저장된 모델을 배포할 때 이러한 저장 결과가 필요하다.
또한 긴 학습을 진행할 때, checkpoint 와 같은 중간 결과를 주기적으로 저장하는 것은 좋은 습관이다. 이렇게 하면 서버가 우연히 다운되어도 지금까지 진행된 계산 결과를 잃지 않을 수 있다.
이제 개별 weight vector(tensor) 와 전체 모델을 불러오고 저장하는 방법을 배워보자.

Loading and Saving Tensors

개별 tensor 의 경우, 직접 load 및 save 함수를 호출하여 각각 읽고 쓸 수 있다. 두 함수 모두 파일 이름을 입력해줘야 하며, save 함수는 저장할 변수 또한 입력해줘야 한다.

x = torch.arange(4)
torch.save(x, 'x-file')

이제 저장된 파일에서 아래와 같이 데이터를 읽어 메모리에 다시 로드할 수 있다.

x2 = torch.load('x-file')
x2  # tensor([0, 1, 2, 3])

또한 여러 tensor 의 목록을 저장하고 다시 메모리에 불러올 수도 있다.

y = torch.zeros(4)
torch.save([x, y],'x-files')
x2, y2 = torch.load('x-files')
(x2, y2)  # (tensor([0, 1, 2, 3]), tensor([0., 0., 0., 0.]))

또한 문자열을 key 로 하고 tensor 를 값으로 가지는 dictionary 를 쓰고 읽을 수도 있다. 이는 모델 내의 모든 parameter 를 읽거나 쓸 때 유용하다.

mydict = {'x': x, 'y': y}
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')
mydict2  # {'x': tensor([0, 1, 2, 3]), 'y': tensor([0., 0., 0., 0.])}

Loading and Saving Model Parameters

개별 weight vector(tensor)를 저장하는 것은 유용하지만, 전체 모델을 저장하고 나중에 불러오고자 할 때 이 작업은 매우 번거로울 수 있다. 딥러닝 모델은 수백 개의 parameter 그룹이 여기저기 분산되어 있기 때문이다.
이러한 이유로 딥러닝 프레임워크는 전체 네트워크를 불러오고 저장하는 기본 기능을 제공한다. 여기서 중요한 세부 사항은 모델 전체가 아닌 모델의 parameter 를 저장한다는 점이다.
따라서 3-layer MLP 가 있다면, 모델의 architecture 는 별도로 지정해야 한다. 즉 아래 예제처럼 layer 별로 클래스 인스턴스가 되어야 한다.
그 이유는 모델 자체가 임의의 코드로 구성될 수 있어 serialization 이 자연스럽게 이루어질 수 없기 때문이다.
따라서 모델을 복원하려면 코드에서 architecture 를 생성하고 디스크에서 parameter 를 load 해야 한다. 익숙한 MLP 모델로 시작해보자.

class MLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.LazyLinear(256)
        self.output = nn.LazyLinear(10)

    def forward(self, x):
        return self.output(F.relu(self.hidden(x)))

net = MLP()
X = torch.randn(size=(2, 20))
Y = net(X)

다음으로, 모델의 parameter 를 “mlp.params” 라는 이름의 파일로 저장한다.

torch.save(net.state_dict(), 'mlp.params')

모델을 복원하기 위해 원래 MLP 모델의 복제본을 인스턴스화한다. 그리고 모델 parameter 를 무작위로 초기화하는 대신, 파일에 저장된 parameter 를 직접 읽어온다.
이 때 parameter 를 torch.load 로 읽고, 그 기존의 저장된 parameter 를 torch.nn.Module.load_state_dict 로 모델에 복사하여 적용한다.

clone = MLP()
clone.load_state_dict(torch.load('mlp.params'))
clone.eval()

아래 예제는 두 인스턴스 net 과 clone 이 동일한 모델 parameter 를 가지고 있으므로 동일한 입력 X 에 대한 계산 결과도 동일함을 보여준다.

Y_clone = clone(X)
Y_clone == Y
# tensor([[True, True, True, True, True, True, True, True, True, True],
#         [True, True, True, True, True, True, True, True, True, True]])

GPUs

2000 년 이래로 GPU 성능은 매 10 년마다 약 1000 배씩 증가해왔다. 이는 딥러닝에 있어 큰 기회가 되지만, 동시에 이러한 성능에 대한 수요가 상당했다는 것을 시사한다.
여기서는 이러한 컴퓨팅 성능(computational performance)을 모델링에 활용하는 방법을 다룬다. 먼저 single GPU 사용법을 설명하고, 이후 multiple GPU 와 multiple server(with multiple GPUs)를 사용하는 방법을 보자.
- 물론 나는 Macbook Pro M1 을 사용하고 있기 때문에 예시에서 gpu 와 함께 mps 를 다뤄보자.
- mps 에 대해서는 Pytorch 의 공식문서를 확인하자.
구체적으로, NVIDIA GPU 를 사용하여 계산하는 방법에 대해 다룬다. 그러기 위해서는 먼저 NVIDIA GPU 를 설치한 다음, NVIDIA 드라이버와 CUDA 를 다운로드하고 적절한 경로를 설정하는 안내를 따른다. 준비가 완료되면 nvidia-smi 명령어로 그래픽 카드 정보를 확인할 수 있다.
Pytorch 에서는 모든 배열이 device 를 가지며, 이를 보통 context 라고 한다.
지금까지는 기본적으로 모든 변수와 관련 계산이 CPU 에 할당되었다. 일반적으로 context 는 여러 GPU 가 될 수 있으며, 여러 서버에 작업을 배포할 경우 더 복잡해질 수 있다.
배열을 적절히 할당함으로써 장치 간 데이터 전송 시간을 최소화할 수 있다. 예를 들어, GPU 가 있는 서버에서 Neural Network 를 학습시킬 때 모델의 parameter 를 GPU 에 배치하는 것이 일반적이다.
d2l 에서 들은 예시들은 최소 두 개의 GPU 가 필요하다. 이는 대부분의 데스크탑에서는 부담스러울 수 있지만, AWS EC2 와 같은 클라우드에서는 다중 GPU 인스턴스를 통해 쉽게 사용할 수 있다. 여기에서는 장치 간 데이터 흐름을 설명하기 위해 이렇게 한다.

Computing Devices

우리는 저장 및 계산을 위해서 CPU 와 GPU 라는 device 를 지정할 수 있다. 기본적으로 tensor 는 메인 메모리에 생성되고 CPU 를 통해 계산된다.
Pytorch 에서는 CPU 와 GPU 를 각각 torch.device('cpu') 와 torch.device('cuda') 로 표시할 수 있다.
주의할 점은 cpu device 는 모든 물리적 CPU 와 메모리를 의미한다. 이는 Pytorch 의 계산이 모든 CPU 코어를 사용하려고 한다는 의미다.
그러나 gpu device 는 하나의 카드와 해당 메모리만을 나타낸다. 따라서 여러 GPU 가 있는 경우 torch.device(f'cuda:{i}') 로 $i$ 번째 GPU($i$ 는 0부터 시작) 를 나타낸다. gpu:0 과 gpu 는 동일하게 취급된다.

def cpu():
    """Get the CPU device."""
    return torch.device('cpu')

def gpu(i=0):
    """Get a GPU device."""
    return torch.device(f'cuda:{i}')

def mps():
    """Get a MPS device."""
    return torch.device('mps')

cpu(), gpu(), gpu(1), mps()
# (device(type='cpu'),
#  device(type='cuda', index=0),
#  device(type='cuda', index=1),
#  device(type='mps'))

아래처럼 사용 가능한 GPU 의 개수를 조회할 수 있다. 아래는 내 노트북 Macbook Pro M1 에서 실행한 결과다.

def num_gpus():
    return torch.cuda.device_count()

def num_mps():
    return torch.mps.device_count()

num_gpus(), num_mps() # (0, 1)

다음으로 요청한 GPU 가 존재하지 않더라도 코드를 실행할 수 있게 하는 두 개의 편리한 함수를 정의한다.

def try_gpu(i=0):
    """Return gpu(i) if exists, otherwise return cpu()."""
    if num_gpus() >= i + 1:
        return gpu(i)
    return cpu()

def try_all_gpus():
    """Return all available GPUs, or [cpu(),] if no GPU exists."""
    return [gpu(i) for i in range(num_gpus())]

def try_mps(i=0):
    """Return mps() if exists, otherwise return cpu()"""
    if num_mps() >= i + 1:
        return mps()
    return cpu()

try_gpu(), try_gpu(10), try_all_gpus(), try_mps()
# (device(type='cpu'), device(type='cpu'), [], device(type='mps'))

Tensors and GPUs

위에서 언급했지만 기본적으로 tensor 는 CPU 에 생성된다. 아래처럼 tensor 가 위치한 장치를 조회하여 확인할 수 있다.

x = torch.tensor([1, 2, 3])
x.device   # device(type='cpu')

앞으로 딥러닝을 할 때 주의해야 할 것은, 여러 term 에 대해 연산할 때 해당 term 들이 모두 동일한 장치에 있어야 한다는 점이다.
예를 들어 두 tensor 를 합산할 때 두 tensor 가 모두 동일한 장치에 있어야 한다. 그렇지 않으면 Pytorch 와 같은 딥러닝 프레임워크는 해당 연산이 수행될 위치와 연산의 결과를 저장할 위치에 대해 알 수 없게 되어 오류를 반환한다.

x = torch.tensor([1, 2, 3])
y = torch.tensor([1, 2, 3], device='mps')
print(x.device, y.device)  # cpu, mps:0

x + y
# RuntimeError: Expected all tensors to be on the same device, but found at least two devices, mps:0 and cpu!

Storage on the GPU

tensor 를 GPU 에 저장하는 여러 가지 방법이 있다. 예를 들어, tensor 를 생성할 때 저장 장치를 지정할 수 있다.

X = torch.ones(2, 3, device=try_gpu())
X
# tensor([[1., 1., 1.],
#         [1., 1., 1.]], device='cuda:0')

X = torch.ones(2, 3, device=try_mps())
X
# tensor([[1., 1., 1.],
#         [1., 1., 1.]], device='mps:0')

위 예제에서는 첫번째 GPU 에 tensor 변수 X 를 생성한다. 이렇게 GPU 에 생성된 tensor 는 해당 GPU 의 메모리만 사용한다. 즉 위에서는 cuda:0 의 메모리만 사용한다.
이 때 터미널에서 nvidia-smi 명령어를 사용하여 GPU 메모리 사용량을 확인할 수 있다. 이를 잘 활용하여 GPU 메모리 한도를 초과하는 데이터를 생성하지 않도록 주의해야 한다.

nvidia-smi 결과
이제 두 개 이상의 GPU 가 있다고 가정하면 아래 코드로 두번째 GPU 에 random tensor Y 를 생성할 수 있다.

Y = torch.rand(2, 3, device=try_gpu(1))
Y
# tensor([[0.0022, 0.5723, 0.2890],
#         [0.1456, 0.3537, 0.7359]], device='cuda:1')

Copying

위 예제에서 X + Y 연산을 수행하려면 연산의 위치를 결정해야 한다. 예를 들어 아래 그림에서 X 를 두번째 GPU 로 전송한 후 거기서 연산을 수행할 수 있다.
만약 tensor 가 생성된 device 가 다른 상황에서 단순히 X 와 Y 를 더하면 에러가 발생한다. Runtime 엔진이 동일한 장치에서 데이터를 찾을 수 없기 때문이다.
Y 가 두번째 GPU 에 있으므로, 두 tensor 를 더하기 전에 X 를 두번째 GPU 로 이동시켜야 한다.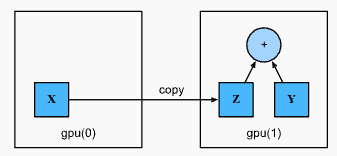
아래처럼 X 의 device 를 옮기면 두 데이터(Z 와 Y)가 동일한 GPU 에 있으므로 합산할 수 있다.

Z = X.cuda(1)
print(X)
# tensor([[1., 1., 1.],
#         [1., 1., 1.]], device='cuda:0')
print(Z)
# tensor([[1., 1., 1.],
#         [1., 1., 1.]], device='cuda:1')

Y + Z
# tensor([[1.0022, 1.5723, 1.2890],
#         [1.1456, 1.3537, 1.7359]], device='cuda:1')

만약 변수 Z 가 이미 두번째 GPU 에 있을 때 Z.cuda(1) 을 호출하면 어떻게 될까? 이 경우 복사하지 않고 원래의 Z 를 반환하며 새로운 메모리를 할당하지 않는다.

Z.cuda(1) is Z  # True

이제 이를 mps 로 수행하면 아래와 같다.

X = torch.ones(2, 3, device=try_mps())
Y = torch.ones(2, 3, device='cpu')

X + Y
# RuntimeError: Expected all tensors to be on the same device, but found at least two devices, mps:0 and cpu!

Z = X.cpu()
Z + Y
# tensor([[2., 2., 2.],
#         [2., 2., 2.]])

Side Notes

GPU 를 사용하는 이유는 속도 때문이다. 딥러닝 연산의 가장 근간인 행렬 연산은 CPU 보다 GPU 가 더 빠르기 때문이다.
- 이에 관한 내용은 해당 포스트에서 잘 정리했다.
그러나 장치 간 데이터 전송은 연산하는 것보다 훨씬 느리다. 이는 CPU 와 GPU 를 연결하는 PCI bus 의 속도가 느리기 때문이다. 따라서 이 작업이 느리다는 사실을 명확히 이해하는 것이 중요하다.
왜냐하면 딥러닝 프레임워크는 시키는대로 장치 간 데이터 전송을 수행하기 때문에 우리가 작성한 코드가 느린 코드라는 사실을 알아채지 못할 수도 있기 때문이다.
또한 중요한 것은 장치 간 데이터 전송은 느린 것 뿐만 아니라, 병렬화(parallelization)도 훨씬 어렵게 만든다. 전송이 완료될 때까지 기다려야 추가 작업을 수행할 수 있기 때문이다.
따라서 .cpu() 나 .cuda() 와 같은 Copying 작업은 주의 깊게 수행해야 한다.
일반적으로 여러 개의 작은 연산보다는 하나의 큰 연산이 훨씬 낫다. 또한 여러 연산을 한꺼번에 수행하는 것이 단일 연산을 코드 중간 중간에 분산시키는 것보다 낫다. 이러한 경우 장치 하나가 다른 장치가 완료될 때까지 기다려야 할 수 있기 때문이다.
마지막으로 tensor 를 출력(print)하거나 numpy 형식으로 변환할 때, 데이터가 메인 메모리에 없는 경우 프레임워크가 이를 메인 메모리로 먼저 복사하기 때문에, 추가적인 전송 오버헤드(transmission overhead)가 발생한다.
더 나쁜 것은 모든 GPU 가 Python 의 GIL(global interpreter lock)으로 인해 대기해야 하는 경우다.
- Python 의 GIL 은 해당 포스트에 잘 정리했다.

Neural Networks and GPUs

tensor 뿐 아니라 이를 활용하는 모델에도 device 를 지정할 수 있다. 아래의 코드는 모델 parameter 를 GPU 에 저장한다. 다만 여기서는 mps 를 이용해보자.

net = nn.Sequential(nn.LazyLinear(1))
net = net.to(device=try_mps())

앞으로 볼 계산이 복잡하고 더욱 깊은 모델들을 다룰 때는 거의 항상 GPU 에서 모델을 실행할 것이다. 이 때 입력이 GPU(mps) 에 있는 tensor 인 경우 모델은 동일한 GPU(mps) 에서 결과를 계산한다.

X = torch.rand((2, 3), device='mps')
net(X)
# tensor([[0.5120],
#         [0.5409]], device='mps:0', grad_fn=<LinearBackward0>)

만약 입력이 모델 parameter 와 동일한 GPU(mps)에 없다면 오류를 발생시킨다.

net = nn.Sequential(nn.LazyLinear(1))
net = net.to(device=try_mps())

X = torch.rand(2, 3)
net(X)
# RuntimeError: Tensor for argument input is on cpu but expected on mps

이제 모델 parameter 가 동일한 GPU(mps) 에 저장되어 있는지 확인하면 아래와 같다.

net[0].weight.data.device  # device(type='mps', index=0)

모델러들은 학습 과정에서 모든 데이터와 parameter 가 동일한 장치에 있도록 하여 모델 학습을 효율적으로 만들어야 한다.

Summary

모델 parameter 에 접근하고 공유하는 여러 방법이 있다.
built-in initializer 나 custom initializer 로 parameter initialization 을 할 수 있다.
lazy initialization 은 프레임워크가 parameter 크기를 자동으로 추론할 수 있어 편리하다. 이는 아키텍처를 쉽게 수정할 수 있게 해주며 일반적인 오류의 원인을 제거해 준다. 이를 사용할 때는 모델에 데이터를 전달하여 프레임워크가 최종적으로 parameter 를 초기화하도록 한다.
기본 layer 클래스인 nn.Module 이나 nn.Sequential 을 통해 custom layer 를 설계할 수 있다. 이는 라이브러리에 존재하는 layer 와는 다르게 동작하는 새로운 layer 를 정의할 수 있게 한다.
또한 한 번 정의된 custom layer 는 임의의 아키텍처에서 호출할 수 있다. layer 는 built-in 함수를 통해 local parameter 를 가질 수 있다.
save 와 load 함수는 tensor 객체의 파일 입/출력에 사용할 수 있다. 전체 네트워크의 parameter 세트를 parameter dictionary 를 통해 저장하고 불러올 수 있다. 중요한 것은 모델(아키텍처)의 저장은 parameter 각각이 아닌 코드로 수행해야 한다.
저장 및 계산을 위한 장치로 CPU 나 GPU 를 지정할 수 있다. 기본적으로 데이터는 메인 메모리에 생성되고 CPU 를 사용해 계산이 이루어진다.
딥러닝 프레임워크에서는 모든 입력 데이터를 동일한 장치(CPU 또는 동일한 GPU)에 두어야 한다. 그래야만 계산이 가능하다.
장치 간 데이터 이동(전송)을 함부로 사용하면 성능을 크게 잃을 수 있다. 대표적인 실수는 GPU 에서 mini-batch loss 를 계산하고 이를 모든 mini-batch 마다 CLI 에 나타나게 하거나, numpy.ndarray 로 logging 하는 것이다.
이는 모든 GPU 작업을 멈추게 하는 GIL(Global Interpreter Lock) 을 발생시킬 수 있다. 따라서 GPU 내부에 log 를 위한 메모리를 할당해두고, 더 큰 log 데이터만 한 번에 옮기는 것이 더 효과적이다.

맨 위로 이동 ↑

Bkkhyunn