[Deep Learning, d2l] MLP (Multi Layer Perceptron) (5)

우리가 좋은 예측 모델에 대해 기대하는 바를 잠깐 생각해보자. 우리는 모델이 학습 과정에서 보지 않은 데이터에서도 잘 작동하기를 원한다. 즉 일반화가 잘 되는 모델이다.

고전적인 일반화 이론에 따르면, 학습과 테스트 성능의 차이를 줄이기 위해서는 단순한 모델을 목표로 해야 한다. 단순성은 적은 차원의 수에서 나타날 수 있다. 여기서 차원은 변수 또는 특성(feature)의 수로 생각할 수 있는데, 차원이 적으면 모델이 간단해지고 해석하기도 쉽다. 우리는 linear model 의 monomial basis 함수에 대해 논의할 때 이를 탐구했다. linear model 의 경우 monomial basis 함수를 사용하여 다변량 데이터를 표현할 수 있다. Polynomial function 은 여러 monomial 들의 선형결합으로 이루어지며, 각 monomial 은 기저(basis) 역할을 한다. 이 때 monomial 의 차수(degree)가 이 함수의 복잡성을 결정하며 차수가 조금만 증가하더라도 모델이 급격하게 복잡해진다.

또한, weight decay($\ell_2$ regularization)를 다룰 때 봤던 것처럼, parameter 의 norm 도 유용한 단순성 척도가 될 수 있다. weight 가 클수록 모델이 데이터에 더 세밀하게 맞춰지는데, 이는 over-fitting 의 원인이 될 수 있다.

모델의 복잡성이 증가하면 학습 데이터에 대한 성능은 좋아지지만, 테스트 데이터에 대한 성능은 오히려 나빠질 수 있다. 이는 모델이 학습 데이터에 너무 맞춰져, 새로운 데이터에 대한 일반화 성능이 떨어지는 over-fitting 이 발생하기 때문이다. 반면에, 적절한 단순성을 유지한 모델은 새로운 데이터에 대한 예측 성능이 더 좋을 가능성이 크다.

또 다른 유용한 단순성의 개념은 매끄러움(smoothness)이다. 즉, 함수가 입력의 작은 변화에 민감하지 않아야 한다는 뜻이다. 예를 들어, 우리가 이미지를 분류할 때, 픽셀에 약간의 무작위 noise 를 추가하더라도 결과에 큰 영향을 미치지 않아야 한다. 매끄러운 모델은 일반적으로 더 좋은 일반화 성능을 보인다. 입력의 작은 변동에 의해 크게 변동하지 않으므로, 새로운 데이터에서도 안정적인 예측을 할 수 있기 때문이다. 이는 데이터의 작은 변동에 덜 민감하게 학습한 모델이 더 잘 일반화할 가능성이 크다는 아이디어와 일맥상통한다.

Bishop 은 입력에 noise 를 추가하여 학습하는 것이 Tikhonov regularization 과 동등하다는 것을 증명하면서 이 아이디어를 형식화했다. 이 연구는 함수가 매끄럽고(따라서 단순해야 하며) 입력의 변동에 대해 회복력이 있어야 한다는 요구 사이에 명확한 수학적 연결을 제시했다. 그 후 Srivastava, Hinton, Krizhevsky 등 은 Bishop 의 아이디어를 신경망의 내부 layer 에도 적용하는 기발한 아이디어를 개발했다. 그 아이디어가 바로 드롭아웃(dropout)이다.

Dropout

• Dropout 은 forward propagation 동안 각 내부 layer 를 계산할 때 noise 를 주입하는 방법이다. 이 기술은 neural network 학습의 표준 기법이 되었다.
• 이 방법이 dropout 이라 불리는 이유는 학습하는 동안 일부 뉴런을 문자 그대로 드롭(제거)하기 때문이다.
• 학습 과정 내내, 각 iteration 에서 표준 dropout 은 각 layer 에서 일부 노드를 제거(0 으로 만든다)한 뒤 다음 layer 를 계산하는 방식이다.
• 저자들은 neural network 의 over-fitting 이 각 layer 가 이전 layer 의 특정 활성화 패턴에 의존하는 상태라고 주장하며, 이를 공적응(co-adaptation)이라고 부른다.
• Dropout 은 공적응을 깨뜨리며 딥러닝 이전에도 Dropout 기법 자체는 오랜 시간 동안 유용하다는 것이 증명되었다.
• 대부분의 딥러닝 라이브러리에서 다양한 형태의 Dropout 이 구현되어 있다.
• 핵심 과제는 이러한 noise 를 어떻게 주입할 것인가이다. 한 가지 아이디어는 noise 가 없는 경우와 동일한 값을 유지하도록 각 layer 의 기대값을 편향되지 않게(unbiased) 주입하는 것이다.
• Bishop 의 연구에서는 linear model 의 입력에 Gaussian noise 를 추가했다.
• 각 학습 iteration 에서 평균이 0 인 분포에서 샘플링한 노이즈 $\epsilon \sim \mathcal{N}(0,\sigma^2)$ 를 입력 $\mathbf{x}$ 에 추가해, 노이즈가 섞인 점 $\mathbf{x}’ = \mathbf{x} + \epsilon$ 을 만들었다.
• 이 때 기대값에서는 $E[\mathbf{x}’] = \mathbf{x}$ 가 된다.
• 표준 dropout regularization 에서는 각 layer 에서 일부 노드를 0 으로 설정한 다음, 남아 있는(제거되지 않은) 노드의 비율로 각 layer 의 편향을 보정(debias)한다.

• 다시 말해, dropout 확률 $p$ 를 통해 각 중간 활성화 값 $h$ 는 다음과 같은 확률 변수 $h’$ 로 대체된다.

  \[\begin{aligned} h' = \begin{cases} 0 & \textrm{ with probability } p \\ \frac{h}{1-p} & \textrm{ otherwise} \end{cases} \end{aligned}\]
• 마찬가지로 설계상 기대값은 변하지 않는다, 즉 $E[h’] = h$ 다.

Dropout in Practice

• hidden layer 와 5개의 hidden unit 이 있는 MLP 구조를 떠올려 보자.
• hidden layer 에 dropout 을 적용하면, 각 hidden unit 을 확률 $p$ 로 0 으로 만든다. 그 결과, 원래 뉴런의 부분 집합만을 포함하는 네트워크를 볼 수 있다.
• 예를 들어, 아래 그림처럼 $h_2$ 와 $h_5$ 가 제거된다면 출력 계산은 더 이상 $h_2$ 나 $h_5$ 에 의존하지 않으며, 역전파(backpropagation) 과정에서 이 unit 들의 gradient 도 사라진다.

• 이렇게 하면 출력 layer 계산에서 $h_1, \ldots, h_5$ 중 어느 한 요소에 과도하게 의존할 수 없게 된다.

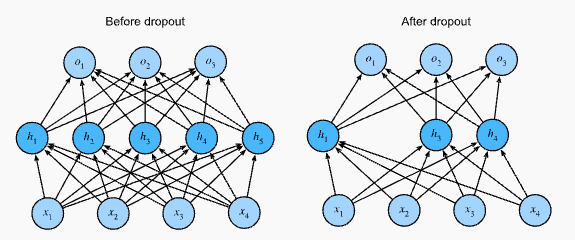  MLP before and after dropout

• 일반적으로 dropout 은 테스트 시에는 비활성화된다.
• 학습된 모델과 새로운 예시가 주어지면, 어떤 노드도 드롭하지 않으며 따라서 normalize 가 필요 없다.
• 하지만 몇 가지 예외가 있다. 일부 연구자들은 dropout 을 테스트 시에도 사용하여 neural network 예측의 불확실성(uncertainty)을 추정하는 휴리스틱으로 사용한다.
• 만약 여러 다른 dropout 출력에서 예측이 일치한다면, 해당 neural network 가 더 높은 확신을 가지고 있다고 말할 수 있다.

Concise Implementation

• 단일 layer 에 대한 dropout 기능을 구현하려면, 해당 layer 의 차원 수만큼 Bernoulli(이진) 확률 변수에서 샘플을 뽑아야 한다.
• 이 확률 변수는 확률 $1-p$ 로 값 $1$(유지)을, 확률 $p$ 로 값 $0$ (제거)을 가진다.
• 이를 간단하게 구현하는 방법 중 하나는 먼저 0 과 1 사이의 uniform distribution $U[0, 1]$ 에서 샘플을 뽑는 것이다.
• 그 후, 해당 샘플이 $p$ 보다 큰 노드를 유지하고 나머지를 제거하면 된다.

• 아래 코드에서는 텐서 입력 X 의 요소를 확률 dropout 으로 dropout 하는 dropout_layer 함수를 구현한 것이다. 이 때 살아남은 요소들을 1.0-dropout 으로 나눈다.

    def dropout_layer(X, dropout):
        assert 0 <= dropout <= 1
        if dropout == 1: return torch.zeros_like(X)
        mask = (torch.rand(X.shape) > dropout).float()
        return mask * X / (1.0 - dropout)
  

• 아래에서는 dropout 확률을 각각 0, 0.5, 1 로 설정한 후 입력 X 를 dropout 연산에 통과시켜 dropout_layer 함수를 테스트한 것이다.

    X = torch.arange(16, dtype = torch.float32).reshape((2, 8))
    print('dropout_p = 0:', dropout_layer(X, 0))
    print('dropout_p = 0.5:', dropout_layer(X, 0.5))
    print('dropout_p = 1:', dropout_layer(X, 1))
  

  dropout 확률 $p$ 에 따른 결과

• 모델링 할 때는 각 hidden layer 의 출력에 활성화 함수 이후 dropout 을 적용한다.
• 이 때 활성화 함수 이후에 dropout 을 적용하는 이유는 dropout-sigmoid 관계를 생각해보면 알 수 있다. dropout 을 하면 뉴런 값이 0 이 된다. 그리고 sigmoid 함수에 0 을 넣으면 0.5 가 된다.
• 그러면 dropout 으로 0 으로 없앤 뉴런인데 이를 sigmoid 를 취함으로써 다시 살아나는 것이다. 이는 dropout 을 쓰는 이유에 위배된다.
• 따라서 dropout 과 activation 의 순서는 dropout 이 activation 뒤에 오는 것을 지켜줘야 한다.
• 또한 각 층에 대해 dropout 확률을 별도로 설정할 수 있다. 일반적인 선택은 입력 층에 가까울수록 더 낮은 dropout 확률을 설정하는 것이다. 그리고 dropout 은 오직 학습 중에만 활성화된다.
• Pytorch 와 같은 고수준 API 를 사용하면, 각 fully connected layer 뒤에 dropout layer 를 추가하고, dropout 확률을 argument 로 전달하기만 하면 된다.
• 학습 중에는 Dropout layer 가 이전 layer 의 출력을 무작위로 dropout 하거나, 동등하게 다음 layer 의 입력을 dropout 확률에 따라 제거한다.
• 학습 모드가 아닐 때는, Dropout layer 는 테스트 시 데이터를 그대로 통과시킨다.

Summary

• 차원(dimension)의 수(model complexity)와 weight vector 의 크기를 제어(weight decay)하는 것 외에도, dropout 은 over-fitting 을 방지하기 위한 또 다른 도구이다. 또 동시에 generalization 성능을 개선하기 위한 도구다.
• 위와 같은 도구들은 하나만 쓰이는 게 아니라 종종 함께 사용된다.
• dropout 은 학습 중에만 사용된다는 점에 유의하자. 또한 dropout 은 activation 값 $h$ 를 기대값이 $h$ 인 확률변수로 대체한다.

맨 위로 이동 ↑