[Deep Learning, d2l] MLP (Multi Layer Perceptron) (4)

앞서 우리는 linear model 을 학습 데이터에 맞춰 regression 과 classification 문제를 다뤘다. 두 경우 모두 관측된 학습 label 의 maximum likelihood 를 찾기 위한 loss function 을 유도했다. 그리고 학습 데이터를 맞추는 것은 단지 중간 목표일 뿐이고, 우리의 진정한 목표는 동일한 데이터 분포에서 새로 추출된 예시에서도 정확한 예측을 할 수 있는 일반적인 패턴을 발견하는 것이다. 머신러닝/딥러닝 개발자는 최적화 알고리즘의 소비자이자 새로운 최적화 알고리즘을 개발하는 생산자다. 그러나 궁극적으로 최적화는 목적이 아닌 수단에 불과하다. 머신러닝/딥러닝의 핵심은 통계적 분야이며, 우리는 최종 모델이 우리가 수집한 데이터셋을 넘어 일반화할 수 있도록 어떤 통계적 원칙에 따라 training loss 를 최적화하고자 한다.

긍정적인 측면에서 보면, SGD 로 학습된 deep neural network 는 Computer Vision, NLP, 시계열 데이터, 추천 시스템 등 다양한 예측 문제에 대해 놀라울 정도로 잘 일반화된다. 그러나 최적화 관점에서 “왜 우리가 학습 데이터에 맞출 수 있는지” 와 일반화 관점에서 최종 모델이 보지 못한 예시에 대해 어떻게 일반화하는지” 에 대한 명확한 설명을 기대했다면 아직 부족하다. linear model 을 최적화하는 절차와 솔루션의 통계적 특성은 포괄적인 이론으로 잘 설명되지만, 딥러닝에 대한 이해는 아직 두 영역 모두에서 불완전한 상태다.

딥러닝의 이론과 실무는 빠르게 진화하고 있으며, 이론가들은 무슨 일이 일어나는지 설명하기 위해 새로운 전략을 채택하고 있고, 실무자들은 빠른 속도로 혁신을 계속하며 deep neural network 를 학습시키기 위한 경험적 방법들과 직관, 그리고 상황에 맞는 기술을 선택하는 데 도움을 주는 지식들을 구축하고 있다.

현재의 상황을 요약하자면, 딥러닝 이론은 유망한 연구 결과와 흥미로운 발견들을 내놓고 있지만,

• (1) 왜 우리가 neural network 를 최적화할 수 있을까?
• (2) gradient descent 로 학습된 모델이 왜 고차원(high-dimensional) 문제에서도 놀랍도록 잘 일반화할까?

위와 같은 질문들에 대한 포괄적인 설명을 제공하기에는 아직 미흡하다. 그러나 실무에서는 (1) 은 거의 문제가 되지 않는다. 왜냐하면 항상 모든 학습 데이터를 맞출 수 있는 매개변수를 찾기 때문이다. 따라서 (2) 와 같이 일반화 문제를 이해하는 것이 훨씬 더 중요한 문제로 남아 있다. 반면, 일관된 과학적 이론이 없는 상황에서도 실무자들은 실제로 잘 일반화되는 모델을 만들 수 있는 다양한 기법을 개발해왔다. 딥러닝에서의 일반화라는 방대한 주제를 간결하게 요약하는 것은 불가능하고, 연구의 전반적인 상태가 아직 해결되지 않았지만, 여기서는 연구와 실무의 현황에 대한 개괄적인 설명을 제공하고자 한다.

Revisiting Overfitting and Regularization

• Wolpert 와 Macready 의 “no free lunch” 정리에 따르면, 어떤 학습 알고리즘이 특정 데이터 분포에서는 더 잘 일반화하고 다른 분포에서는 더 나쁘게 일반화한다. 즉, 모든 최적화 문제에 대해 일관되게 우월한 알고리즘이 존재하지 않는다.
• 유한한 학습 데이터셋이 주어져 있을 때 모델은 특정 가정에 의존한다. 모델이 인간 수준의 성능을 달성하려면 인간이 세상을 생각하는 방식이 반영된 inductive bias 를 사용하는 것이 유용할 수 있다.
• inductive bias 는 특정한 속성을 가진 해결책을 선호하는 경향을 나타낸다.
  • 예를 들어, 깊은 MLP 는 간단한 함수의 합성(composition)으로 복잡한 함수를 구축하는 것에 대한 inductive bias 를 가지고 있다.
  • CNN 은 입력에서 각 픽셀간의 관계가 서로 가까운 요소들에 존재한다는 Locality 와 위치에 따라 값이 변하지 않는다는 translation invariance 라는 inductive bias 를 가지고 있다.
• 머신러닝/딥러닝 모델이 inductive bias 을 encoding 할 때, 이를 학습하는 방식은 일반적으로 두 단계로 나뉜다.
  • 학습 데이터를 맞춘다.
  • holdout(validation) 데이터로 모델을 평가하여 일반화 오류(모집단에 대한 실제 오류)를 추정한다.
• 학습 데이터에 대한 fit 과 테스트 데이터에 대한 fit 사이의 차이를 generalization gap 이라고 하며, 이 차이가 클 때, 모델이 학습 데이터에 over-fitting 되었다고 한다.
• over-fitting 이 극단적인 경우, 학습 데이터를 정확히 맞출 수 있지만 테스트 오류는 여전히 클 수 있다.
• 고전적인 관점에서, over-fitting 되었을 때 모델이 너무 복잡하다고 해석할 수 있으며, 이 경우 feature 의 수를 줄이거나, 학습된 0 이 아닌 parameter 의 수를 줄이거나, parameter 의 크기를 줄여야 한다.

• 이전에 보았던 모델 복잡도(model complexity)와 loss 를 비교한 그림을 다시 보자.

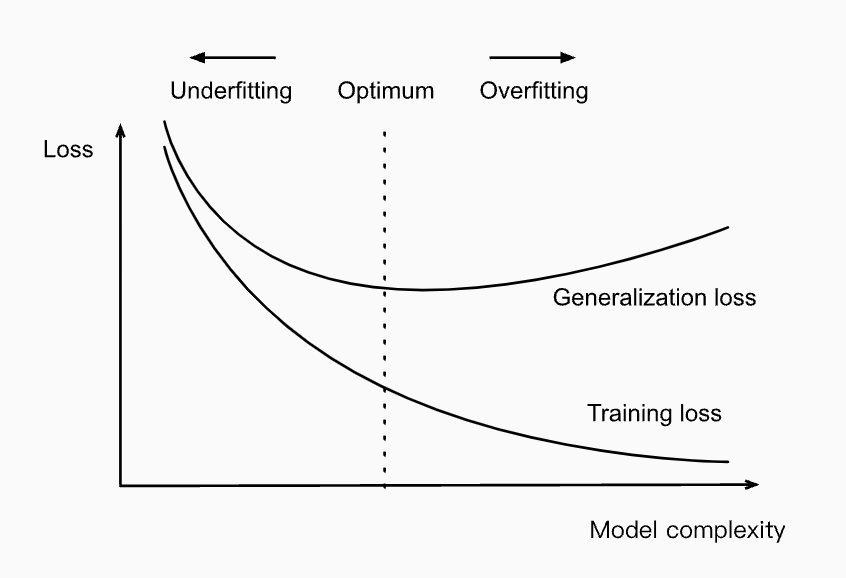  Influence of model complexity on under-fitting and over-fitting

• 그러나 딥러닝은 위 그림을 직관에 반하는 방식으로 복잡하게 만든다.
• 첫째, classification 문제의 경우, 우리의 모델은 보통 모든 학습 예제를 완벽하게 맞출 만큼 표현력이 충분하다. 심지어 수백만 개의 데이터셋으로 이루어진 데이터에서도 마찬가지다.
• 고전적인 관점에서 봤을 때 위 경우는 모델 복잡성 축의 가장 오른쪽 끝에 위치할 것이며, generalization error 의 개선을 위해서는 모델 클래스의 복잡성을 줄이거나, parameter 가 가질 수 있는 값의 범위를 제한하는 방식으로만 가능할 것이라고 생각할 수 있다. 하지만 바로 여기서부터 상황이 이상하게 돌아간다.
• 놀랍게도, 많은 딥러닝 작업(e.g. image recognition and text classification)에서 우리는 training loss 를 낮게 할 수 있는 모델 아키텍처 중 하나를 선택하게 된다. 즉 모델이 0 의 training error 를 달성하는지를 고려하여 선택한다.
• 따라서 추가적인 개선의 유일한 방법은 over-fitting 을 줄이는 것이다. 그러나 더 이상한 점은 학습 데이터를 완벽하게 맞춘 후에도, 모델의 표현력을 더 확장(e.g., layer 를 추가하거나, 노드를 추가하거나, 더 많은 epoch 동안 학습)하여 generalization error 를 실제로 더 줄일 수 있다는 점이다.
• 여기서 끝이 아니다. generalization gap 과 model complexity(네트워크의 깊이나 너비) 사이의 패턴이 비단조적일 수 있다. 즉 모델 복잡성이 처음에는 악영향을 미치다가 이후에 “이중 하강(double-descent)” 패턴에서 다시 개선될 수 있다.
• 따라서 딥러닝 실무자는 모델을 어떤 방식으로든 제한하는 것처럼 보이는 트릭들과, 모델을 더 표현력 있게 만드는 것처럼 보이는 트릭들을 가지고 있으며, 이 모든 트릭(bag of tricks)들은 over-fitting 을 완화하기 위해 적용된다.
• 복잡한 것은, 고전적인 학습 이론에서 보장하는 것들이 고전적인 모델에서는 보존되는 반면에 deep neural network 가 일반화하는 이유를 설명하는 데는 전혀 힘을 발휘하지 못한다는 것이다.
• deep neural network 는 $\ell_2$ regularization 을 사용하더라도 대규모 데이터셋에 대해서 임의의 label 을 맞출 수 있기 때문에, VC dimension 이나 가설 클래스의 Rademacher 복잡성과 같은 전통적인 복잡성 기반의 generalization bound 는 neural network 가 일반화하는 이유를 설명하지 못한다.

Inspiration from Nonparametrics

• 딥러닝을 공부할 때, 딥러닝을 모수적(parametric) 모델로 생각하는 것이 편할 수 있다. 딥러닝 모델들은 수백만 개의 parameter 를 가지고 있기 때문이다.
• 또한 우리가 모델을 업데이트할 때는 parameter 를 업데이트한다. 모델을 저장할 때는 parameter 를 디스크에 기록한다. 이처럼 neural network 가 분명히 parameter 를 가지고 있지만, 어떤 면에서는 이를 비모수(non-parametric) 모델처럼 생각하는 것이 더 유익할 수 있다.
• 그렇다면 정확히 무엇이 모델을 비모수적(non-parameteric)으로 만들까? 비모수적 방법들은 이용 가능한 데이터의 양이 증가함에 따라 복잡도가 증가하는 경향이 있다는 공통된 특징을 가진다.
• 비모수 모델의 가장 간단한 예는 $k$-nearest neighbor algorithm(kNN) 이다.
  • kNN 에서는 학습 시점에 학습자(learner)가 단순히 데이터셋을 기억한다. 그런 다음 예측 시점에, 새로운 점 $\mathbf{x}$ 을 마주했을 때 학습자는 $k$ 개의 가장 가까운 이웃들을 찾는다.
  • $k$ 개의 가장 가까운 이웃은 어떤 거리 $d(\mathbf{x}, \mathbf{x}_i’)$ 를 최소화하는 $k$ 개의 점 $\mathbf{x}_i’$ 다.
  • $k=1$ 일 때 $1$-nearest neighbors 알고리즘 이라고 불리며, 이 알고리즘은 항상 0 의 training error 를 달성한다.
  • 이것이 $1$-NN 이 일반화하지 못한다는 것을 의미하지는 않는다. 약간의 조건이 만족되면, $1$-NN 알고리즘은 일관적으로 결국 최적의 예측에 수렴한다.
• $1$-NN 은 어떤 거리 함수 $d$ 를 명시하거나, 동등하게 벡터 값의 basis function $\phi(\mathbf{x})$ 을 지정해야 한다.
• 어떤 distance metric 을 선택하든 0 의 학습 오류를 달성하고 결국 최적의 예측기에 도달할 수 있지만, 서로 다른 distance metric $d$ 는 서로 다른 inductive bias 를 encoding 하고, 이용 가능한 데이터가 유한할 때 서로 다른 예측기를 만들어낼 것이다.
• distance metric $d$ 의 선택은 기저 패턴에 대한 다른 가정을 나타내며, 이 때 예측기의 성능은 그 가정이 관찰된 데이터와 얼마나 잘 맞는지에 따라 달라질 것이다.

• neural network 는 학습 데이터를 맞추기 위해 필요한 것보다 훨씬 더 많은 parameter 를 가지고 있기 때문에, 학습 데이터를 interpolate 하는, 즉 완벽하게 맞추는 경향이 있다. 바로 이 점에서 비모수 모델처럼 작동하는 경향이 있다.

  

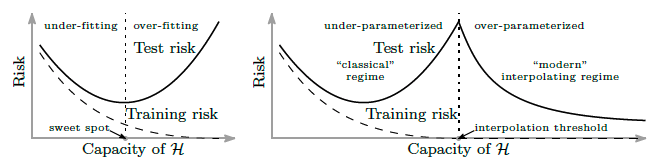
• 최근의 이론 연구는 대형 neural network 와 비모수적 방법, 특히 kernel method 사이에 깊은 연관성을 밝혀내고 있다.
• Jacot 등은 무작위로 초기화된 가중치를 가진 MLP 가 무한히 넓어질 때, 그 MLP 는 특정 kernel 함수(사실상 거리 함수)를 사용하는 (비모수적) kernel method 와 동등해진다고 증명했다. 그들은 이 kernel 함수를 neural tangent kernel 이라고 부른다.
• 현재 neural tangent kernel 모델이 현대의 딥러닝 neural network 의 동작을 완전히 설명하지는 못하지만, 분석 도구로서 많이 사용된다는 점은 over-parameterized 된 deep neural network 의 동작을 이해하는 데 비모수 모델링이 유용하다는 점을 강조한다.

Early Stopping

• deep neural network 는 잘못되거나 무작위로 label 이 할당된 경우에도 이를 잘 맞출 수 있는 능력(capabel of fitting)을 가지고 있다. 하지만 이런 능력은 학습의 많은 반복 과정을 통해서만 나타난다.
• 최근의 연구는 label 에 noise 가 있는 상황에서, neural network 가 먼저 깨끗하게 label 이 지정된 데이터를 학습하고 이후에 잘못 label 이 지정된 데이터를 맞추기 시작한다는 것을 밝혔다.
• 더 나아가, 위와 같은 현상은 generalization 에 직접적으로 이어진다는 것이 확인되었다. 즉, 모델이 깨끗한 label 이 지정된 데이터를 맞추고, 무작위로 label 이 지정된 데이터를 맞추지 않았다면 모델은 일반화에 성공한 것이다.
• 이러한 발견들은 early stopping 과 같이 deep neural network 를 규제하는 고전적인 기법을 더욱 촉진시킨다. early stopping 은 가중치의 값을 직접적으로 제한하는 대신에 학습 epoch 의 수를 제한한다.
• 가장 일반적인 종료 기준은 학습 중에 validation error 를 지속적으로 모니터링(일반적으로 1 epoch 당 1 번 확인)하면서 validation error 가 일정 수의 epoch 동안 작은 값 $\epsilon$ 보다 많이 감소하지 않으면 학습을 중단하는 것이다. 이 때 $\epsilon$ 을 patience criterion 이라고도 한다.
• label 에 noise 가 있는 상황에서 더 나은 일반화를 가능하게 한다는 점 외에도, early stopping 은 시간을 절약하는 또 다른 이점을 제공한다.
• patience criterion 을 충족하면 학습을 종료할 수 있기 때문에, 8 개 이상의 GPU 를 동시에 사용하면서 오랫동안 학습시켜야 하는 모델의 경우 잘 조정된 early stopping 은 연구자의 시간을 며칠씩 절약하고, 고용주에게 수천 달러를 절감할 수 있다.
• 특히 label noise 가 없고 데이터셋이 realizable 한 경우(class 가 실제로 구분 가능한 경우), early stopping 은 일반화에 큰 개선을 가져오지 않는다.
• 반면 label 에 noise 가 있거나 label 에 본질적인 변동성이 있는 경우(환자의 사망률 예측과 같은 경우), early stopping 은 매우 중요하다. noise 가 있는 데이터를 맞출 때까지 모델을 학습시키는 것은 일반적으로 좋지 않은 아이디어다.

Classical Regularization Methods for Deep Networks

• 우리는 앞서 모델의 complextiy 를 제한하기 위한 여러 고전적인 regularization 기법을 봤다. 특히 weight decay(가중치 감소) 방법을 주로 봤는데, 이는 loss function 에 regularization term 을 추가하여 가중치의 큰 값에 penalty 를 주는 기법이다.
• 어떤 가중치의 norm 으로 penalty 를 주는지에 따라 이 기법은 Ridge regularization($\ell_2$ penalty) 또는 Lasso regularization($\ell_1$ penalty) 으로 불린다.
• 이러한 고전적인 정규화 기법들은 가중치의 값을 충분히 제한하여 모델이 무작위 label 을 맞추지 못하게 하는 것으로 간주된다.
• 딥러닝 구현에서도 weight decay 는 여전히 인기 있는 도구다. 하지만 연구자들은 $\ell_2$ regularization 의 일반적인 강도는 딥러닝 네트워크가 데이터를 과하게 맞추는 것을 막기에 충분하지 않으며, 따라서 early stopping 기준과 함께 사용해야만 그 정규화의 이점이 의미가 있다고 지적했다.
• 만약 early stopping 이 없다면, 딥러닝에서 layer 수나 노드 수 또는 $1$-NN에서의 distance metric 과 마찬가지로, 이러한 방법들이 neural network 의 성능을 실질적으로 제한하는 것이 아니라 데이터셋에서 발견되는 패턴과 더 잘 맞는 inductive bias 를 encoding 하기 때문에 일반화를 이끌어낼 수 있다.
• 따라서 고전적인 정규화 기법은 딥러닝 구현에서 여전히 인기가 있지만, 그 이론적 효능에 대한 해석은 크게 다를 수 있다.
• 특히, 딥러닝 연구자들은 모델 입력에 noise 를 추가하는 고전적인 정규화 맥락에서 처음으로 인기를 끌었던 기법들을 발전시켰다.
• 다음 포스트에서는 딥러닝에서 매우 중요한 기법이 된 dropout 기술을 소개할 것이다. 이 기법은 이론적 근거가 여전히 미스터리한 상태임에도 불구하고 폭넓게 사용되고 있다.

Summary

• 학습 데이터보다 parameter 가 더 적은 경향이 있는 고전적인 linear model 과는 달리, deep neural network 는 대부분의 task 에서 과도하게 parameter 가 많고(over-parameterized), 학습 데이터를 완벽하게 맞출 수 있다.

  

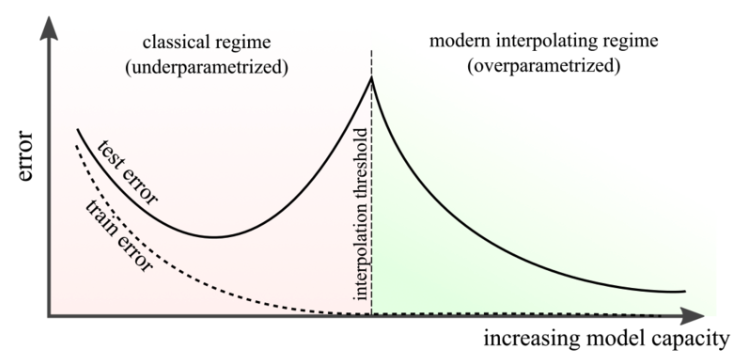
• 위 그림과 같이 deep neural network 가 위치한 interpolation regime 은 오랫동안 굳어져 온 많은 직관에 도전한다.
• 기능적으로 neural network 는 parametric 모델처럼 보이지만, 때로는 non-parametric 모델로 생각하는 것이 더 직관적인 경우가 있다.
• deep neural network 들은 학습 label 을 모두 맞출 수 있는 경우가 많기 때문에, 거의 모든 개선이 over-fitting 을 줄이는 방향(즉 generalization gap 을 좁히는 것)으로 이루어진다.
• 역설적으로, generalization gap 을 줄이기 위한 개입은 때로는 모델 복잡성을 증가시키고, 다른 때는 복잡성을 감소시키는 것처럼 보인다.
• 그러나 이러한 방법들은 전통적인 이론이 딥러닝 네트워크의 일반화를 설명할 수 있을 정도로 복잡도를 충분히 낮추지 못하는 경우가 많으며, 특정 선택이 왜 일반화를 개선하는지에 대한 이유는 많은 뛰어난 연구자들이 집중적으로 노력함에도 불구하고 여전히 대부분 해결되지 않은 거대한 질문으로 남아 있다.

맨 위로 이동 ↑