[Deep Learning, d2l] MLP (Multi Layer Perceptron) (3)

우리는 여기까지 initialization(초기화) 방식과 그 선택이 어떻게 이루어지는지에 대해 세부적으로 다루지 않았다. 어쩌면 이러한 선택이 그다지 중요하지 않다고 생각했을 수도 있다.

그러나 실제로는 initialization 방식을 어떻게 선택하느냐가 neural network 학습에서 중요한 역할을 하며, 수치적 안정성을 유지하는 데 필수적일 수 있다. 또한, 이러한 initialization 에 대한 선택은 비선형 활성화함수의 선택과 흥미롭게도 얽혀 있을 수 있다.

어떤 함수를 선택하느냐와 parameter 를 어떻게 초기화하느냐는 최적화 알고리즘이 얼마나 빨리 수렴하는지를 결정할 수 있다. 여기서 잘못된 선택을 하면 학습 중 기울기가 폭발(exploding)하거나 사라지는(vanishing) 문제에 직면할 수 있다. 여기서는 이러한 주제들을 더 깊이 탐구하고, 딥러닝에서 유용하게 사용할 수 있는 유용한 경험적 방법들을 다뤄보자.

Vanishing and Exploding Gradients

• 어떤 깊은 네트워크에서 $L$ 개의 layer 와 입력 $\mathbf{x}$, 출력 $\mathbf{o}$ 가 있다고 가정하자.

• 각 layer $l$ 은 가중치 $\mathbf{W}^{(l)}$ 로 parameterized 된 선형변환 $f_l$ 로 정의되며, 해당 layer 의 hidden layer 출력은 $\mathbf{h}^{(l)}$ 다. 여기서 $\mathbf{h}^{(0)} = \mathbf{x}$ 로 두면, 네트워크는 다음과 같이 표현할 수 있다.

  \[\mathbf{h}^{(l)} = f_l (\mathbf{h}^{(l-1)}) \textrm{ and thus } \mathbf{o} = f_L \circ \cdots \circ f_1(\mathbf{x})\]

• 모든 hidden layer 출력과 입력이 vector 라면, 임의의 parameter $\mathbf{W}^{(l)}$ 에 대한 $\mathbf{o}$ 의 gradient 는 다음과 같이 쓸 수 있다.

  \[\partial_{\mathbf{W}^{(l)}} \mathbf{o} = \underbrace{\partial_{\mathbf{h}^{(L-1)}} \mathbf{h}^{(L)}}_{ \mathbf{M}^{(L)} \stackrel{\textrm{def}}{=}} \cdots \underbrace{\partial_{\mathbf{h}^{(l)}} \mathbf{h}^{(l+1)}}_{ \mathbf{M}^{(l+1)} \stackrel{\textrm{def}}{=}} \underbrace{\partial_{\mathbf{W}^{(l)}} \mathbf{h}^{(l)}}_{ \mathbf{v}^{(l)} \stackrel{\textrm{def}}{=}}\]
• 즉, 이 gradient 는 $L-l$ 개의 행렬 $\mathbf{M}^{(L)} \cdots \mathbf{M}^{(l+1)}$ 와 gradient vector $\mathbf{v}^{(l)}$ 의 곱이다.
  • 여기서 $\mathbf{M}^{(i)} = \partial_{\mathbf{h}^{(i-1)}}\mathbf{h}^{(i)}$ 은 각 layer 의 출력이 이전 layer 의 출력에 대해 어떻게 변하는지를 나타내는 행렬이다.
  • $\mathbf{v}^{(l)} = \partial_{\mathbf{W}^{(l)}}\mathbf{h}^{(l)}$ 은 layer $l$ 의 출력이 해당 layer 의 weight 에 대해 어떻게 변하는지를 나타내는 벡터다.
• 이렇게 많은 수의 행렬 곱셈 연산으로 인해서 많은 확률들을 곱할 때 자주 발생하는 수치적 under-flow 문제의 위험을 내포하고 있다.
• 확률을 다룰 때는 보통 로그 공간으로 변환해 숫자 표현의 지수 부분에 부하를 주는 방법을 사용한다.
  • 수치 데이터를 다룰 때, 예를 들어 1.23456e-2 정수부(Significand) 는 1, 가수부(Mantissa) 는 23456, 지수부(Exponent) 는 -2 다.
• 그러나 위의 문제는 더 심각하다. 각 행렬 $\mathbf{M}^{(l)}$ 는 매우 다양한 고유값(eigenvalue)을 가질 수 있다. 이 값들은 매우 작거나 매우 클 수 있으며, 그들의 곱은 매우 크거나 매우 작을 수 있다.
• 이러한 상황에서 이 행렬의 고유값들이 gradient vector 에 곱해지면 gradient 가 불안정해진다.
• 불안정한 gradient 가 야기하는 위험은 numerical representation 문제를 넘어서기도 한다. 즉 gradient 의 예측 불가능한 크기는 최적화 알고리즘의 안정성에도 위협이 된다.
• 우리는 다음과 같은 두 가지 상황에 직면할 수 있다.
  • 지나치게 큰 parameter 업데이트로 인해 모델이 망가지는 경우(exploding gradient problem)
  • 너무 작은 업데이트로 인해 parameter 가 거의 움직이지 않아 학습이 불가능해지는 경우 (vanishing gradient problem)

Vanishing Gradients

• vanishing gradient 문제를 자주 일으키는 한 가지 원인은 각 layer 의 linear operation 이후에 통과하는 활성화함수 $\sigma$ 의 선택이다.
• 역사적으로, Sigmoid 함수 $1/(1+\exp(−x))$ 는 경계 함수(thresholding function)처럼 보인다는 이유로 인기가 많았다.
  • 초기 인공 neural network 는 생물학적 신경망에서 영감을 받았기 때문에, 생물학적 뉴런처럼 인공 뉴런이 (threshold 에 따라) 완전히 발화하거나 전혀 발화하지 않는 아이디어는 매력적으로 보였다.

• Sigmoid 가 왜 Vanishing gradient 를 일으키는지 더 자세히 살펴보자.

  

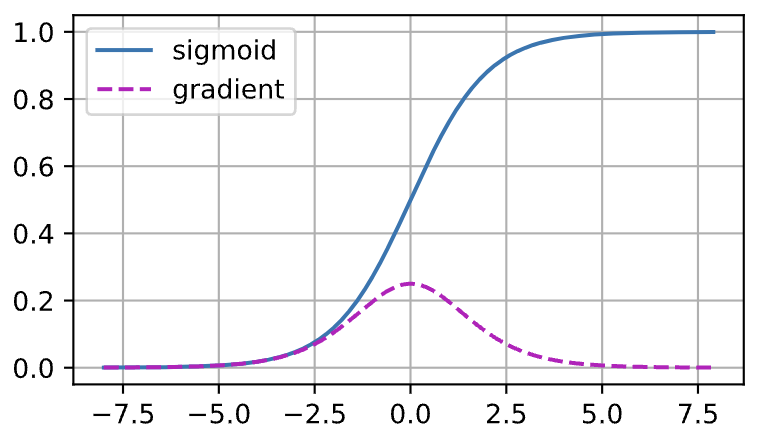
• 위 그래프를 보면 Sigmoid 의 기울기는 입력($x$ axis)이 크거나 작을 때 사라지는 것을 볼 수 있다.
• 더구나, 여러 layer 을 거쳐 역전파(backpropagation)를 할 때, 많은 Sigmoid 의 입력이 0 에 가까운 골디락스 구역(Goldilocks zone)에 있지 않으면 기울기의 전체 곱이 소실될 수 있다.
• 따라서 Sigmoid 를 활성화함수로 쓰는 경우, 네트워크가 많은 층을 가지고 있을 때 주의하지 않으면 어느 층에서든 기울기가 끊어질 가능성이 높다.
• 실제로 이 문제는 깊은 네트워크의 학습을 괴롭혔다. 결과적으로, 생물학적으로 덜 그럴듯하지만 더 안정적인 ReLU 함수가 실무에서 기본 선택으로 자리잡게 되었다.

Exploding Gradients

• Exploding gradient 문제도 vanishing gradient 문제만큼이나 성가실 수 있다.
• 이를 예시로 보기 위해서 100 개의 Gaussian 랜덤 행렬을 뽑아서 초기 행렬과 곱해본다.
• 그렇게 되면 우리가 선택한 분산 $\sigma^2 = 1$ 에서 행렬 곱은 폭발한다.

• 이러한 일이 deep network 의 초기화 단계에서 발생하면, gradient descent 최적화 알고리즘은 수렴할 기회를 가지지 못한다.

    M = torch.normal(0, 1, size=(4,4))
    print('a single matrix \n',M)
    for i in range(100):
        M = M @ torch.normal(0, 1, size=(4,4))
    print('after multiplying 100 matrices\n', M)
  

  100 번의 행렬곱 이후 gradient 가 exploding 함을 확인할 수 있다.

Breaking the Symmetry

• neural network 설계에서 또 하나의 문제는 parameterization 에서 발생하는 대칭성이다.
• 간단한 하나의 hidden layer 와 두 개의 유닛을 가지고 있는 MLP 를 가정해보자.
• 이 경우, 첫번째 층의 가중치 $\mathbf{W}^{(1)}$ 를 순열로 바꾸고 마찬가지로 출력층의 가중치도 순열로 바꾸면 동일한 함수를 얻을 수 있다.
• 첫번째 hidden 유닛과 두번째 hidden 유닛을 구분할 아무런 특별한 것이 없다. 즉, 각 층의 hidden 유닛들 사이에는 순열 대칭(permutation symmetry)이 존재한다.
• 이 문제는 단순히 이론적 불편함에 그치지 않는다. 위에서 가정한 은닉 유닛이 두 개 있는 하나의 은닉층을 가진 MLP 를 생각해보자. 이 때 설명을 위해, 출력층이 두 개의 은닉 유닛을 하나의 출력 유닛으로 변환한다고 가정하자.
• 만약 hidden layer 의 모든 parameter 를 $\mathbf{W}^{(1)} = c$ 와 같이 일정한 상수 $c$ 로 초기화한다고 생각해보자.
• 이 경우, 순전파 과정에서 두 은닉 유닛은 동일한 입력과 parameter 를 사용하여 동일한 activation 을 생성하고, 이것이 출력 유닛으로 전달된다.
• 역전파 과정에서, 출력 유닛을 parameter $\mathbf{W}^{(1)}$ 에 대해 미분하면 모든 요소가 동일한 값을 가지는 gradient 를 얻게 된다.
• 따라서 gradient 를 기반으로 한 업데이트(e.g. mini-batch SGD)를 거친 후에도 $\mathbf{W}^{(1)}$ 의 모든 요소는 여전히 동일한 값을 유지한다.
• 이러한 업데이트는 대칭성을 스스로 깨지 못하며, 네트워크가 표현할 수 있는 잠재력을 실현하지 못할 수 있다. 즉 은닉층은 마치 하나의 유닛만 있는 것처럼 동작하게 된다.
• mini-batch SGD 는 이 대칭성을 깨지 못하지만, 이후에 소개될 dropout regularization 은 이를 해결할 수 있다.

Parameter Initialization

• 위에서 언급한 문제를 해결하거나 최소한 완화하기 위한 방법 중 하나는 신중한 초기화를 사용하는 것이다.
• 아래에서 다루겠지만, 최적화 중 주의 깊은 처리와 적절한 regularization 을 통해 안정성을 더욱 높일 수 있다.

Default Initialization

• 이전에 우리는 가중치 값을 초기화할 때 normal distribution 을 사용했다.
• 만약 초기화 방법을 명시하지 않으면, 프레임워크는 default 랜덤 초기화 방법을 사용한다. 이는 종종 적당한 문제 크기에서 잘 동작한다.

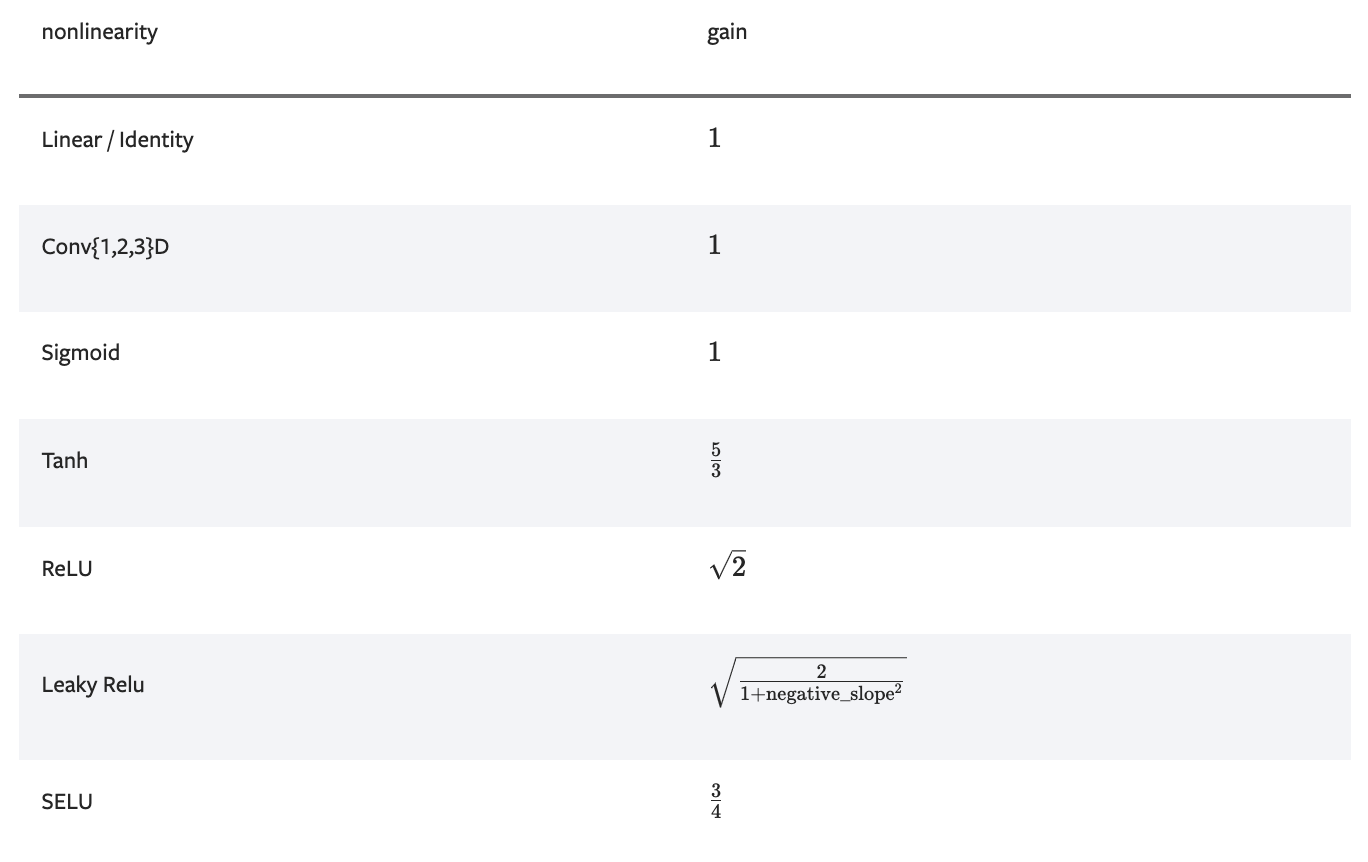
• Pytorch 에서는 Kaiming Uniform initialization 을 default 로 하고 있다. 아래 그림은 Pytorch 공식문서에서 가져왔다.

  

  

Xavier Initialization

• 비선형성(nonlinearity) 없이 fully connected layer 의 출력 $o_i$ 의 scale distribution 을 살펴보자.

• 이 fully connected layer 는 $n_{\text{in}}$ 개의 입력 $x_j$ 과 이에 대응하는 가중치 $w_{ij}$ 가 주어졌을 때, 출력은 다음과 같이 주어진다.

  \[o_{i} = \sum_{j=1}^{n_\textrm{in}} w_{ij} x_j\]
• 모든 가중치 $w_{ij}$ 는 동일한 분포에서 독립적으로 추출된다. 더 나아가, 이 동일한 분포가 평균이 0 이고 분산이 $\sigma^2$ 라고 가정해보자.
  • 이것은 분포가 Gaussian 이어야 한다는 의미는 아니고, 단지 평균과 분산이 존재해야 한다는 뜻이다.
• 이제 layer 에 들어가는 input $x_j$ 또한 평균이 0 이고 분산이 $\gamma^2$ 이며, $w_{ij}$ 와 서로 독립적이고 서로 간에도 독립적이라고 가정하자.

• 이 경우, $o_i$ 의 평균을 계산할 수 있다.

  \[\begin{aligned} E[o_i] & = \sum_{j=1}^{n_\textrm{in}} E[w_{ij} x_j] \\&= \sum_{j=1}^{n_\textrm{in}} E[w_{ij}] E[x_j] \\&= 0 \end{aligned}\]

• 그리고 분산을 계산하면 다음과 같다.

  \[\begin{aligned} \textrm{Var}[o_i] & = E[o_i^2] - (E[o_i])^2 \\ & = \sum_{j=1}^{n_\textrm{in}} E[w^2_{ij} x^2_j] - 0 \\ & = \sum_{j=1}^{n_\textrm{in}} E[w^2_{ij}] E[x^2_j] \\ & = n_\textrm{in} \sigma^2 \gamma^2 \end{aligned}\]
• 분산을 고정하기 위한 한 가지 방법은 $n_{\text{in}}\sigma^2 = 1$ 로 설정하는 것이다.
• 이제 역전파를 고려해보자. 역전파 과정에서는 출력에 가까운 층에서부터 기울기가 전파된다.
• 순전파에서 살펴본 것과 같은 이유로, 기울기의 분산도 폭발할 수 있으며, 이를 방지하려면 $n_{\text{out}}\sigma^2 = 1$ 이어야 한다. 여기서 $n_{\text{out}}$ 은 해당 층의 출력 수를 의미한다.

• 이러한 두 조건을 동시에 만족할 수 없기 때문에 다음을 만족시키려 한다.

  \[\begin{aligned} \frac{1}{2} (n_\textrm{in} + n_\textrm{out}) \sigma^2 = 1 \textrm{ or equivalently } \sigma = \sqrt{\frac{2}{n_\textrm{in} + n_\textrm{out}}} \end{aligned}\]
• 이것이 현재 표준으로 자리 잡은 Xavier initialization 의 이론적 근거이며, 실제로도 유용하게 작동한다.
• 보통 Xavier 초기화는 평균이 0 이고 분산이 $\sigma^2 = \frac{2}{n_\textrm{in} + n_\textrm{out}}$ 인 Gaussian 분포에서 가중치를 샘플링한다.
• 또한, 가중치를 Uniform(균등) 분포에서 샘플링할 때의 분산을 선택하기 위해 이 방식을 조정할 수 있다.

• Uniform 분포 $U(-a, a)$ 의 분산이 $\frac{a^2}{3}$ 임을 고려하면, 이를 $\sigma^2$ 조건에 대입하여 다음과 같은 초기화 방법을 얻는다.

  \[U\left(-\sqrt{\frac{6}{n_\textrm{in} + n_\textrm{out}}}, \sqrt{\frac{6}{n_\textrm{in} + n_\textrm{out}}}\right)\]
• 위 수학적 추론에서 비선형성(nonlinearity)을 고려하지 않았다는 점은 neural network 에서 쉽게 위반될 수 있지만, Xavier 초기화는 실제로 매우 잘 작동한다.
• 이처럼 Xaiver initialization 은 비선형 함수(ex. sigmoid, tanh)에서 효과적인 결과를 보여준다.
• 그러나 이를 ReLU 함수와 사용하면, 출력값이 0 으로 수렴하게 되는 현상을 확인 할 수 있다. 따라서 ReLU 함수에는 또 다른 초기화 방법을 사용해야 한다.

He Initialization

• ReLU 와 함께 많이 사용되는 weight initialization 방법으로 들어오는 노드의 수 $n_{\text{in}}$ 만 고려한다. Kaiming He 가 만들었다.

• Gaussian 분포에서는 아래와 같은 분포에서 가중치를 샘플링한다.

  \[W \sim N(0, \text{Var}(W)), \quad \text{Var}(W) = \sqrt{\frac{2}{n_{\text{in}}}}\]

• Uniform 분포에서는 아래의 분포에서 가중치를 샘플링한다.

  \[W \sim U\left(-\sqrt{\frac{6}{n_\textrm{in}}}, +\sqrt{\frac{6}{n_\textrm{in}}}\right)\]

Beyond

• 위 논의는 parameter initialization 에 대한 현대적 접근법의 일면만을 다룬다. 딥러닝 프레임워크는 여러 가지의 다른 휴리스틱을 구현하고 있다.

  torch 의 parameter initialization 방법들

• 더 나아가, parameter initialization 은 여전히 딥러닝에서 중요한 연구 주제이다. 여기에는 convolution kernel 과 같은 shared parameter, super-resolution, sequence model 등의 상황에 특화된 휴리스틱이 포함된다.
• 예를 들어, Xiao 는 신중하게 설계된 초기화 방법을 사용하여 10,000 layer 의 neural network 를 아키텍처 트릭 없이도 학습할 수 있음을 보여주었다.

Summary

• Vanishing gradient 와 Exploding gradient 는 깊은 neural network 에서 흔히 발생하는 문제다.
• 이러한 문제를 방지하기 위해 parameter initialization 에 매우 신중해야 하며, gradient 와 parameter 가 적절하게 제어될 수 있도록 해야 한다.
• 초기 기울기가 너무 크거나 너무 작지 않도록 하기 위해 초기화 휴리스틱이 필요하다.
• Random initialization 은 최적화 전에 대칭을 깨는 데 중요한 역할을 한다.
• Xavier initialization 은 각 layer 의 출력 분산이 입력의 개수에 영향을 받지 않도록 하며, 기울기의 분산이 출력의 개수에 영향을 받지 않도록 한다.
• ReLU 활성화함수는 Vanishing gradient 문제를 완화하여 수렴 속도를 가속화할 수 있다.
• parameter initialization 에 대해서는 이 블로그에 조금 더 자세하게 기술되어 있다.

맨 위로 이동 ↑