[Deep Learning, d2l] MLP (Multi Layer Perceptron) (2)

지금까지 우리는 mini-batch SGD 를 사용해 모델을 학습시켰다. 그러나 알고리즘을 구현할 때는 모델을 통해 순방향 전파(forward)를 계산하는 것만 신경썼고, 기울기를 계산할 때는 딥러닝 프레임워크가 제공하는 역전파 함수(backward())를 호출하기만 했다.

기울기를 자동으로 계산하는 기능은 딥러닝 알고리즘 구현을 매우 간단하게 해준다. 자동 미분(automatic differentiation)이 나오기 전에는 복잡한 모델에 작은 변화를 주더라도 복잡한 도함수를 일일이 손으로 다시 계산해야 했다. 따라서 과거의 학술 논문에서는 업데이트 규칙을 도출하는 데 여러 페이지를 할애하는 경우가 많았다. 우리는 앞으로도 딥러닝 프레임워크를 이용해서 역전파를 손쉽게 이용하겠지만, 딥러닝에 대한 얕은 이해를 넘어가려면 기울기가 어떻게 계산되는지 알아야 한다.

여기서는 역전파(backpropagation)에 대해 깊이 탐구한다. 기법과 구현에 대한 insight 를 위해 기본적인 수학과 계산 그래프(computational graph)를 사용한다. 먼저, weight decay($\ell_2$ regularization)를 사용하는 one-hidden-layer MLP 를 중심으로 설명을 시작한다.

Forward Propagation

• 순전파(forward propagation 또는 forward pass)는 neural network 에서 입력층부터 출력층까지 중간 변수들(출력 포함)의 계산과 저장을 의미한다.
• 하나의 은닉층을 가진 neural network 의 동작을 단계별로 살펴보자. 이 과정을 이해하면 딥러닝에 대한 얕은 이해를 벗어나는 첫걸음이 된다.

• input example 이 $\mathbf{x}\in \mathbb{R}^d$ 라고 가정하고, 은닉층에는 bias term 이 포함되지 않는다고 해보자. 여기서 중간 변수는 다음과 같다.

  \[\mathbf{z} = \mathbf{W}^{(1)} \mathbf{x}\]
• 여기서 $\mathbf{W}^{(1)} \in \mathbb{R}^{h \times d}$ 는 은닉층의 weight parameter 다.

• 중간 변수 $\mathbf{z}\in \mathbb{R}^h$ 를 활성화함수 $\phi$ 에 통과시키면 길이(차원)가 $h$ 인 hidden activation vector 를 얻는다.

  \[\mathbf{h} = \phi (\mathbf{z})\]

• 은닉층의 출력 $\mathbf{h}$ 도 중간 변수다. 출력층의 parameter 가 $\mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}$ 의 weight 만 포함된다고 가정하면, 길이가 $q$ 인 출력층 변수를 얻을 수 있다.

  \[\mathbf{o} = \mathbf{W}^{(2)} \mathbf{h}\]

• loss function 을 $l$ 이라 하고, example 의 label 이 $y$ 라고 가정하면, 하나의 데이터 예제에 대한 loss 를 다음과 같이 계산할 수 있다.

  \[L = l(\mathbf{o}, y)\]

• 이 때 $\ell_2$ regularization 의 정의를 보면, 하이퍼파라미터 $\lambda$ 가 주어졌을 때, regularization term 은 다음과 같다.

  \[s = \frac{\lambda}{2} \left(\|\mathbf{W}^{(1)}\|_\textrm{F}^2 + \Vert \mathbf{W}^{(2)} \Vert_\textrm{F}^2\right)\]
• 여기서 행렬의 Frobenius Norm($\Vert \cdot \Vert_\textrm{F}$) 은 matrix 를 vector 로 평탄화한 후 적용된 $\ell_2$ norm 이다.

• 마지막으로, 주어진 데이터 예제에 대한 모델의 regularized loss 는 다음과 같다.

  \[J = L + s\]
• 앞으로 $J$ 는 목적 함수(objective function)라고 부른다.

Computational Graph of Forward Propagation

• 계산 그래프를 그리면 연산자와 변수들 간의 의존성을 시각화하는 데 도움이 된다.

• 아래 그림은 위에서 예시로 든 간단한 네트워크에 대한 계산 그래프다. 사각형은 변수(variable)를, 원은 연산자(operator)를 나타낸다.

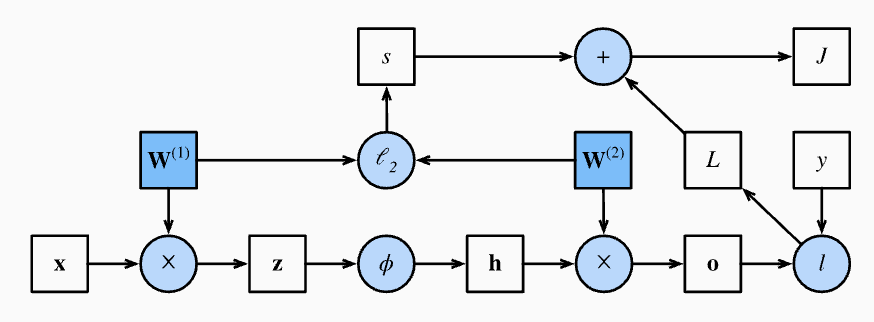  Computational graph of forward propagation

• 왼쪽 하단 모서리는 input 을, 오른쪽 상단 모서리는 output 을 나타낸다.
• 화살표의 방향(데이터 흐름)이 주로 오른쪽과 위쪽을 향하고 있다는 점에 주목하자.

Backpropagation

• 역전파(backpropagation)는 neural network parameter 에 대한 gradient 를 계산하는 방법을 의미한다.
• 간단히 말해서, 이 방법은 미분법에서의 연쇄법칙(chain rule)에 따라 네트워크를 출력층에서 입력층으로 역순으로 순회하는 방식이다.
• 이 알고리즘은 일부 parameter 에 대한 gradient 를 계산할 때 필요한 편미분(partial derivatives)을 저장한다.
• 함수 $\mathsf{Y}=f(\mathsf{X})$ 와 $\mathsf{Z}=g(\mathsf{Y})$ 가 있고, 입력과 출력 $\mathsf{X}, \mathsf{Y}, \mathsf{Z}$ 가 임의의 shape 을 가진 tensor 라고 가정하자.

• 연쇄법칙을 사용하여 $\mathsf{Z}$ 에 대한 $\mathsf{X}$ 의 미분을 다음과 같이 계산할 수 있다.

  \[\frac{\partial \mathsf{Z}}{\partial \mathsf{X}} = \textrm{prod}\left(\frac{\partial \mathsf{Z}}{\partial \mathsf{Y}}, \frac{\partial \mathsf{Y}}{\partial \mathsf{X}}\right)\]
• 여기서 $\textrm{prod}$ 연산자는 전치(transposition,$\top$)연산이나 입력의 위치변경(swapping)과 같은 필요한 연산을 수행한 후 인수들을 곱하는 역할을 한다.
  • vector 의 경우 이는 간단히 matrix-matrix 곱셈으로 처리된다. 반면에 고차원 tensor 의 경우 적절한 연산을 사용하는데, $\textrm{prod}$ 연산자는 이러한 수식적 부담을 덜어준다.
• 위에서 예시로 든 one hidden layer 을 가진 간단한 네트워크의 계산 그래프에서 parameter 는 $\mathbf{W}^{(1)}$ 와 $\mathbf{W}^{(2)}$ 다.
• 역전파의 목적은 $\partial J/\partial \mathbf{W}^{(1)}$ 와 $\partial J/\partial \mathbf{W}^{(2)}$ 의 gradient 를 계산하는 것이다. 이를 달성하기 위해 연쇄법칙을 사용하고 각 중간 변수와 parameter 의 gradient 를 차례로 계산한다.

• 계산 순서는 순전파(forward propagation)에서 수행된 것과 반대로, 계산 그래프의 결과에서 parameter 로 거슬러 올라가며 계산이 이루어진다. 다시 한번 그림을 보고 아래의 단계를 천천히 따라가보자.

  Computational graph of forward propagation

• 첫번째 단계는 loss term $L$ 과 regularization term $s$ 에 대한 objective function $J=L+s$ 의 기울기를 계산하는 것이다.

  \[\frac{\partial J}{\partial L} = 1 \; \textrm{and} \; \frac{\partial J}{\partial s} = 1\]

• 다음으로, 연쇄법칙에 따라 출력층 변수 $\mathbf{o}$ 에 대한 objective function 의 기울기를 계산한다.

  \[\frac{\partial J}{\partial \mathbf{o}} = \textrm{prod}\left(\frac{\partial J}{\partial L}, \frac{\partial L}{\partial \mathbf{o}}\right) = \frac{\partial L}{\partial \mathbf{o}} \in \mathbb{R}^q\]

• 다음으로, regularization term 에 대한 두 parameter 의 기울기를 계산한다.

  \[\frac{\partial s}{\partial \mathbf{W}^{(1)}} = \lambda \mathbf{W}^{(1)} \; \textrm{and} \; \frac{\partial s}{\partial \mathbf{W}^{(2)}} = \lambda \mathbf{W}^{(2)}\]

• 이제 출력층에 가까운 모델 parameter 에 대한 기울기 $\partial J/\partial \mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}$ 를 계산한다. 연쇄법칙을 사용하면 다음과 같은 결과를 얻는다.

  \[\frac{\partial J}{\partial \mathbf{W}^{(2)}}= \textrm{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{W}^{(2)}}\right) + \textrm{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(2)}}\right)= \frac{\partial J}{\partial \mathbf{o}} \mathbf{h}^\top + \lambda \mathbf{W}^{(2)}\]
  • 여기서 hidden activation vector $\mathbf{h}$ 의 전치행렬($\top$)이 나오는 이유는 행렬곱셈 규칙 때문이다.
  • 수식적으로 $\mathbf{o} = \mathbf{W}^{(2)} \mathbf{h}$ 를 $\mathbf{W}^{(2)}$ 로 편미분 하면 $\mathbf{h}$ 가 나와야 하지만, 차원 맞춤을 위해 행 벡터(전치된 형태)로 나타내야 한다.
  • 즉 $\frac{\partial J}{\partial \mathbf{o}} \in \mathbb{R}^q$ 이기 때문에 $q \times 1$ vector 이고, $\mathbf{h}^\top$ 은 $1 \times h$ vector 이므로, 이 둘을 곱하면 $q \times h$ 크기의 행렬이 나온다. 이는 $\mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}$ 의 크기와 일치하게 된다.

• $\mathbf{W}^{(1)}$ 에 대한 기울기를 얻기 위해서는 출력층에서 은닉층으로 역전파를 계속해야 한다. 은닉층 출력에 대한 기울기 $\partial J/\partial \mathbf{h} \in \mathbb{R}^h$ 는 다음과 같다.

  \[\frac{\partial J}{\partial \mathbf{h}} = \textrm{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{h}}\right) = {\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}\]

• 활성화함수 $\phi$ 는 element-wise 로 적용되므로, 중간 변수 $\mathbf{z}$ 에 대한 기울기 $\partial J/\partial \mathbf{z} \in \mathbb{R}^h$ 를 계산하기 위해서는 element-wise multiplication 연산자($\odot$)를 사용한다.

  \[\frac{\partial J}{\partial \mathbf{z}} = \textrm{prod}\left(\frac{\partial J}{\partial \mathbf{h}}, \frac{\partial \mathbf{h}}{\partial \mathbf{z}}\right) = \frac{\partial J}{\partial \mathbf{h}} \odot \phi'\left(\mathbf{z}\right)\]

• 마지막으로, 입력층에 가까운 모델 parameter 에 대한 기울기 $\partial J/\partial \mathbf{W}^{(1)} \in \mathbb{R}^{h \times d}$ 를 얻을 수 있다. 연쇄법칙에 따르면 다음과 같은 결과를 얻는다.

  \[\frac{\partial J}{\partial \mathbf{W}^{(1)}} = \textrm{prod}\left(\frac{\partial J}{\partial \mathbf{z}}, \frac{\partial \mathbf{z}}{\partial \mathbf{W}^{(1)}}\right) + \textrm{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(1)}}\right) = \frac{\partial J}{\partial \mathbf{z}} \mathbf{x}^\top + \lambda \mathbf{W}^{(1)}\]

Training Neural Networks

• neural network 를 학습할 때, 순전파와 역전파는 서로 의존적이다.
• 순전파는 계산 그래프의 의존성(연결) 방향을 따라 변수를 계산하며, 이러한 변수는 역전파에서 다시 사용된다. 역전파에서는 그래프에서의 계산 순서를 반대로 하여 기울기를 계산한다.
• 앞서 언급한 간단한 네트워크를 예로 들어보자.
  • 순전파에서 regularization term 을 계산할 때 모델 parameter $\mathbf{W}^{(1)}$ 와 $\mathbf{W}^{(2)}$ 의 현재 값에 의존한다. 여기서 현재 값은 가장 최근의 iteration 에서 역전파를 통한 최적화 알고리즘에 의해 업데이트된 값이다.
  • 역전파에서 parameter 의 gradient 계산은 순전파에 의해 계산된 은닉층 출력 $\mathbf{h}$ 의 현재 값에 의존한다.
• 따라서 neural network 를 학습할 때, 맨 처음 모델 parameter 가 초기화되면 순전파와 역전파를 번갈아 가며 실행하고, 역전파에서 제공된 gradient 를 사용해 모델 parameter 를 업데이트한다.
• 이 때 역전파는 중복 계산을 피하기 위해 순전파에서 저장된 중간 값을 재사용한다. 이로 인해 중간 값을 역전파가 완료될 때까지 유지해야 한다.
• 이는 학습이 단순한 예측보다 더 많은 메모리를 요구하는 이유 중 하나다.
• 또한 이러한 중간 값의 크기는 네트워크 layer 의 수와 batch size 에 비례한다. 따라서 더 깊은 네트워크를 더 큰 batch size 로 학습하면 out-of-memory(메모리 부족) 오류가 발생할 가능성이 커진다.

Summary

• 순전파(forward propagation)는 neural network 가 정의한 계산 그래프 내에서 중간 변수를 순차적으로 계산하고 저장하며, 입력층에서 출력층으로 진행된다.
• 역전파(backward propagation)는 중간 변수와 parameter 의 gradient 를 neural network 내에서 역순으로 순차적으로 계산하고 저장한다.
• deep learning 모델을 학습할 때 순전파와 역전파는 상호 의존적이며, 학습 시에는 예측보다 더 많은 메모리가 필요하다.

맨 위로 이동 ↑