[Deep Learning, d2l] MLP (Multi Layer Perceptron) (1)

앞에서 linear regression 과 더불어 softmax regression 을 공부했다. 이 과정에서 데이터를 다루고, 모델의 출력값을 유효한 확률 분포로 변환하며, 적절한 loss function 를 적용하고, 모델의 parameter 에 대해 loss 값을 최소화하는 방법을 배웠다. 이제 이러한 기초적인 linear model 의 메커니즘을 기억하면서 우리가 관심있는 Deep Neural Network 에 대해 공부해보자.

즉 여기서부터 딥러닝의 시작이라고 볼 수 있다. 가장 단순한 딥러닝 네트워크는 Multi Layer Perceptron(MLP) 이다. MLP 는 각각의 뉴런이 아래 layer 에 있는 뉴런들과 완전히 연결되어 input 을 받고, 위 layer 에 있는 뉴런들과도 완전히 연결되어 영향을 주고받는다.

자동 미분(automatic differentiation)은 딥러닝 알고리즘 구현을 상당히 단순화하는데, 딥러닝 네트워크에서 이러한 gradient 가 어떻게 계산되는지 깊이 있게 다룰 것이다. 그런 다음 딥러닝 네트워크를 성공적으로 학습시키는 데 핵심적인 수치적 안정성 및 parameter 초기화(initialization) 문제를 논의해보자.

또한 딥러닝처럼 고용량(high-capacity) 모델을 학습할 때는 over-fitting 의 위험이 언제나 있다. 따라서 딥러닝 네트워크에 대한 Regularization 및 Generalization 문제를 다시 살펴볼 것이다.

Hidden Layers

• 우리는 linear regression 에서 bias 를 추가한 linear transformation 으로 affine transformation 을 다뤘다.
• 즉 affine transformation 은 linear transformation 에 translation term 이 추가된 형태다.

• 아래는 affine transformation 의 일반식과 우리가 linear regression 에서 만들었던 모델이다.

  \[y = Ax + b, \quad \hat{\mathbf{y}} = \mathbf{X}\mathbf{w} + b\]

• 또한 softmax regression 에서 만든 모델은 아래와 같다.

  \[\mathbf{o} = \mathbf{W}\mathbf{x} + \mathbf{b}\]
• 위 모델을 다이어그램으로 표현한 것을 떠올려보면, 모델의 input 은 single affine transformation 을 통해 output 으로 바로 연결된다. 그 이후 softmax 연산을 수행한다.
• 만약 label 이 하나의 affine transformation 으로 input 과 연결된다면 이 접근만으로 충분하다. 그러나 affine transformation 에서 선형성(linearity)은 강한 가정이다.
• 선형대수학에서는 아래 가정을 만족하는 함수 $f$ 를 선형성을 갖는 함수라고 정의한다.
  • 가산성(Additivity): $f(x+y) = f(x) + f(y)$
  • 동질성(Homogeneity): $f(\alpha x) = \alpha f(x) \; \text{for scalar} \; \alpha$

Limitations of Linear Models

• 선형성(linearity)은 단조성(monotonicity)이라는 더 약한 가정을 포함한다.
  • 즉, feature 의 값이 증가하면 모델 output 이 항상 증가(weight 가 양수인 경우)하거나 항상 감소(weight 가 음수인 경우)해야 한다는 것이다.
• 이런 가정은 타당하다. 예를 들어, 개인이 대출을 상환할지 예측하려 한다면, 다른 조건이 모두 동일할 때 소득이 더 높은 신청자가 소득이 더 낮은 신청자보다 상환 가능성이 더 높다고 가정하는 것은 합리적일 수 있다.
  • 하지만 이러한 관계는 단조적일 수는 있어도 상환 가능성과 선형적으로 관련되지는 않을 것이다.
  • 소득이 0 달러에서 5 만 달러로 증가하는 것이 상환 가능성을 크게 높일 수 있지만, 100 만 달러에서 105 만 달러로 증가하는 것은 그만큼의 영향을 미치지 않을 가능성이 높다. 이 문제를 해결하는 한 가지 방법은 logistic map 을 사용하여 결과에 대한 log 확률로 변환해 선형성을 더 그럴듯하게 만드는 것이다.
• 단조성을 위반하는 예시는 쉽게 생각해낼 수 있다.
  • 예를 들어, 체온을 함수로 하여 건강 상태를 예측하려 한다고 해보자.
  • 정상 체온인 37°C(98.6°F) 이상인 경우, 체온이 높을수록 위험이 증가한다. 그러나 체온이 37°C 이하로 떨어져 체온이 낮을수록 마찬가지로 위험이 증가한다.
  • 다시 말해, 이 때는 37°C 에서의 거리를 feature 로 사용하여 이 문제를 해결할 수 있다.
• 그렇다면 고양이와 강아지 이미지를 분류할 때는 어떨까? (13, 17) 위치의 픽셀 강도가 증가하면 강아지일 가능성이 증가해야 할까, 아니면 감소해야 할까?
• linear model 을 사용하면 고양이와 강아지를 구별하는 유일한 기준이 개별 픽셀의 밝기라는 암묵적인 가정을 하게 된다. 하지만 이미지를 뒤집어도 카테고리가 유지되는 세상에서 이 접근 방식은 실패할 수밖에 없다.
• 또한 단순한 전처리 방식으로 문제를 해결할 수 있을지 여부는 분명하지 않다. 그 이유는 각 픽셀의 중요성이 주변 픽셀 값과 복잡하게 얽혀 있기 때문이다.
• linear model 에 적합하도록 feature 간의 관련 상호작용을 고려한 데이터 표현이 존재할 수는 있지만, 이를 손으로 계산하는 방법을 알기 어렵다.
• 따라서 linear model 은 단조성을 위반하는 예시 등 세상의 복잡한 비선형적 문제를 푸는데 한계가 있고 표현력이 부족하다.
• 그러나 Deep Neural Network 에서는 hidden layer 를 통해 representation 을 학습하고, 그 representation 에 작용하는 linear 모델을 함께 학습한다.
• 비선형성(nonlinearity) 문제는 오랫동안 연구되어 왔다. 예를 들어, Decision Tree 는 기본적으로 binary decision 을 사용해 클래스 멤버십을 결정하는 방식이다.
• 마찬가지로, Kernel Method 은 비선형 종속성을 모델링하기 위해 수십 년 동안 사용되어 왔다. 이는 nonparametric spline 모델과 Kernel Method 로 이어졌다.
• 이는 또한 뇌가 자연스럽게 해결하는 문제이기도 하다. 결국, 뉴런은 다른 뉴런에 신호를 전달하고, 또 다시 다른 뉴런에 신호를 전달한다.
• 그 결과로 우리는 비교적 단순한 변환들의 연속을 얻게 된다.

Incorporating Hidden Layers

• 우리는 하나 이상의 hidden layer 를 도입함으로써 linear model 의 한계를 극복할 수 있다.
• 가장 쉬운 방법은 여러 개의 fully connected layer 를 쌓는 것이다.
• 각 layer 는 그 위의 layer 로 신호를 전달해 최종적으로 출력을 생성한다.
• 이 때 처음 $L-1$ 개의 layer 는 데이터를 representation 하고, 마지막 layer 는 그 representation 을 이용해 선형 예측을 한다고 생각할 수 있다.

• 이 구조는 다층 퍼셉트론(multi layer perceptron)이라 불리며 MLP라고 약칭된다.

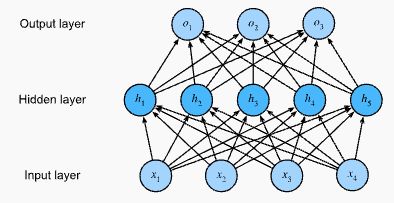  An MLP with a hidden layer of five hidden units

• 위 MLP 는 4 개의 입력, 3 개의 출력, 그리고 5 개의 은닉(hidden) 유닛을 가진 hidden layer 를 포함하고 있다.
• 입력 layer 는 계산을 포함하지 않으므로, 이 네트워크로 출력을 생성하려면 hidden layer 와 출력 layer 에서의 계산을 구현해야 한다.
• 따라서 이 MLP 의 layer 수는 두 개이다. 두 layer 모두 fully connected 되어 있다는 점에 유의해야 한다.
• 즉, 모든 입력이 hidden layer 의 모든 뉴런에 영향을 미치고, 그 뉴런들이 다시 출력 layer 의 모든 뉴런에 영향을 미친다.

From Linear to Nonlinear

• 이전과 마찬가지로, $d$ 차원의 입력(feature)을 가지는 $n$ 개의 데이터 example 로 이루어진 mini-batch 를 $\mathbf{X} \in \mathbb{R}^{n \times d}$ 로 나타낸다.
• $h$ 개의 은닉 유닛을 가진 하나의 hidden layer 를 가진 MLP 의 경우, hidden layer 의 출력을 hidden representation 이라고 하며, 이를 $\mathbf{H} \in \mathbb{R}^{n \times h}$ 로 나타낸다.
• hidden layer 와 출력 layer 모두 fully connected 되어 있기 때문에, hidden layer 의 weight 는 $\mathbf{W}^{(1)} \in \mathbb{R}^{d \times h}$, bias 는 $\mathbf{b}^{(1)} \in \mathbb{R}^{1 \times h}$ 로 나타내고, 출력 layer 의 weight 는 $\mathbf{W}^{(2)} \in \mathbb{R}^{h \times q}$, bias 는 $\mathbf{b}^{(2)} \in \mathbb{R}^{1 \times q}$ 로 나타낸다.

• 이를 통해 하나의 hidden layer 를 가진 MLP 의 출력 $\mathbf{O} \in \mathbb{R}^{n \times q}$ 을 아래와 같이 계산할 수 있다.

  \[\begin{aligned} \mathbf{H} & = \mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}, \\ \mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}. \end{aligned}\]
• 이렇게 MLP 모델은 hidden layer 를 추가한 후 추가적인 parameter 집합을 추적하고 업데이트해야 한다.
• 그러면 우리가 얻는 것은 무엇일까? 위에서 정의된 모델에서는 아무런 이득도 얻지 못한다.
• 그 이유는 간단하다. 위에서 설명한 hidden 유닛은 입력의 affine transformation 으로 주어지고, softmax 이전의 출력은 hidden 유닛의 affine transformation 일 뿐이다.
• 즉 선형 변환의 선형 변환은 여전히 선형 변환이다. 다시 말하면 선형 함수의 선형 함수는 여전히 선형 함수라는 것이다. 게다가, linear model 은 이미 모든 affine function 을 표현할 수 있다.
• 이를 더 직관적으로 보기 위해서는 위 정의에서 hidden layer 를 제거하면 된다.

• 그러면 parameter $\mathbf{W} = \mathbf{W}^{(1)}\mathbf{W}^{(2)}$ 와 $\mathbf{b} = \mathbf{b}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)}$ 를 가진 single layer model 과 동일해진다.

  \[\mathbf{O} = (\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})\mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W}^{(1)}\mathbf{W}^{(2)} + \mathbf{b}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W} + \mathbf{b}\]
• 따라서 multi layer architecture 의 잠재력을 실현하기 위해서는 중요한 요소가 하나 더 필요하다.
• 바로 각 hidden unit 에 affine transformation 후 적용되는 비선형 활성화함수 $\sigma$ 이다.
• 예를 들어, ReLU(rectified linear unit) 는 오늘날 가장 인기 있는 활성화함수다.
• ReLU 는 $\sigma(x) = \mathrm{max}(0, x)$ 로 정의되며, element-wise 로 각 요소에 대해 독립적으로 작동한다.
• 활성화함수 $\sigma(\cdot)$ 의 출력은 activations 라고 부른다.

• 일반적으로 활성화함수가 적용된 경우, 우리의 MLP 는 더 이상 linear model 로 축소될 수 없고 복잡한 문제를 풀 수 있는 표현력을 가지게 된다.

  \[\begin{aligned} \mathbf{H} & = \sigma(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}), \\ \mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}.\\ \end{aligned}\]
• $\mathbf{X}$ 의 각 행이 mini-batch 에서 하나의 데이터 포인트를 나타내므로, notation 에서 약간 잘못된 부분이 있지만 비선형 함수 $\sigma$ 가 입력에 행 단위로 적용된다고 정의할 수 있다.
  • 이는 softmax vectorization 에서 softmax 를 행 단위 연산(row-wise operation)으로 표현했을 때와 같은 방식이다.
• 활성화함수는 종종 row-wise 가 아니라 element-wise 로 적용된다. 즉, layer 의 선형 부분을 계산한 후 각 activation 값을 다른 hidden 유닛의 값과 상관없이 계산할 수 있다.
• 더 일반적인 MLP 를 구축하려면 이러한 hidden layer 를 계속 쌓을 수 있다.
• 예를 들어, $\mathbf{H}^{(1)} = \sigma_1(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})$ 와 $\mathbf{H}^{(2)} = \sigma_2(\mathbf{H}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)})$ 를 하나씩 쌓아가며, 점점 더 표현력이 높은 모델을 만들 수 있다.

Universal Approximators

• 우리의 뇌는 매우 정교한 통계적 분석을 할 수 있다. 그렇다면, Deep Neural Network 는 얼마나 강력할까?
• 이 질문은 여러 번 답변된 적이 있다. 예를 들어, Cybenko 는 MLP 의 맥락에서, 그리고 Micchelli1 는 단일 hidden layer 를 가진 RBF(radial basis function) 네트워크로 볼 수 있는 재생 커널 힐베르트 공간(RKHS)의 맥락에서 답을 내놓았다.
• 이 연구들 및 관련 결과들은 충분히 많은 노드와 적절한 가중치 집합을 주면 단일 hidden layer 네트워크만으로도 어떤 함수든 모델링할 수 있다고 제안한다. 하지만 실제로 이 함수를 학습하는 것은 어려운 부분이다.
• Nueral Network 를 C 프로그래밍 언어와 비슷하게 생각할 수 있다. C 언어는 다른 현대 언어들처럼, 계산 가능한 어떤 프로그램도 표현할 수 있지만, 요구 사항을 충족하는 프로그램을 실제로 만들어내는 것이 어려운 부분이다.
• 게다가, 단일 hidden layer 네트워크가 어떤 함수든 학습할 수 있다고 해서 모든 문제를 이를 통해 해결해야 한다는 뜻은 아니다.
• 사실 이 경우 kernel method 가 훨씬 더 효과적이다. kernel method 는 무한 차원 공간에서도 정확히 문제를 해결할 수 있기 때문이다.
• 실제로 더 wider 한 것이 아니라 더 deeper 한 네트워크를 사용함으로써 더 많은 함수를 근사할 수 있다.
• 이에 대해서는 다음에 더 자세히 다뤄보자. 해당 포스트에도 UAT 에 대해 정리해놓았다.

Activation Functions

• 활성화함수는 뉴런이 활성화 될지 말지를 결정한다. 이를 위해 weighted sum 을 계산하고, 그 합에 추가적인 bias 를 더한다.
• 이 함수들은 입력 신호를 출력으로 변환하는 미분 가능(differentiable)한 연산자이며, 비선형성을 추가한다.
• 활성화함수는 딥러닝에서 매우 중요한 역할을 하기 때문에 여기에서 일반적인 활성화함수들을 간략히 살펴보자.

ReLU

• 가장 많이 사용되는 활성화함수는 ReLU(rectified linear unit)이다. 이는 구현이 간단하고, 다양한 예측 작업에서 좋은 성능을 보이기 때문이다.

• ReLU 는 매우 간단한 비선형 변환을 제공한다. ReLU 는 주어진 element $x$ 에 대해 해당 element 와 0 중 더 큰 값을 취한다.

  \[\operatorname{ReLU}(x) = \max(x, 0)\]
• 따라서 ReLU 함수는 양의 요소만을 유지하고, 음의 요소는 0 으로 설정하여 모든 음의 요소를 버리는 효과를 가진다.

• 아래는 ReLU 함수를 그래프로 그린 것이다. 아래 그림을 보면 ReLU 활성화함수는 구간별로 선형이다.

  

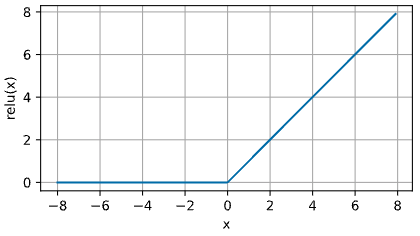
• 입력 $x$ 가 음수일 때, ReLU 함수의 기울기는 0 이다. 반면, 입력이 양수일 때는 기울기가 1 이다.
• 따라서 ReLU 는 입력이 정확히 0 일 때 미분 불가능하다. 이러한 경우, 음수일 때의 기울기를 기본값으로 사용하여 입력이 0 일 때 기울기가 0 이다. 이는 입력이 실제로 0 이 될 가능성이 적기 때문에 가능하다.
• (진정한)수학을 하고 있을 때는 경계 조건이 중요하겠지만, 우리는 Engineering 을 하고 있다.

• 아래 그림은 ReLU 의 기울기(도함수)를 그래프로 나타낸 것이다.

  

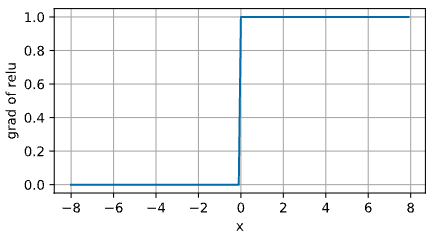
• ReLU 를 사용하는 이유는 그 도함수가 특히 잘 작동하기 때문이다. 즉 기울기가 소멸하거나, 혹은 그대로 통과시키기 때문에 최적화 과정이 더 잘 진행된다.
• 따라서 ReLU 는 과거 Neural Network 에서 문제가 되었던 gradient vanishing 문제를 완화한다. 이에 대해서는 더 자세히 다룰 것이다.
• ReLU 함수에는 여러 변형이 있다. 그 중 하나는 parameterized ReLU (pReLU) 함수다.

• 이 변형은 ReLU 에 linear term 을 추가하여 입력이 음수일 때도 소멸하는 것이 아니라 일부 정보가 여전히 통과하게 만든다.

  \[\operatorname{pReLU}(x) = \max(0, x) + \alpha \min(0, x)\]

Sigmoid

• Sigmoid 함수는 값이 실수 범위 $\mathbb{R}$ 에 속하는 입력을 받아서, 출력을 0 과 1 사이의 값으로 변환한다.

• 이러한 이유로 Sigmoid 는 종종 squashing(압축) function 이라고 불리는데, 이는 (-inf, inf) 범위의 모든 입력을 (0, 1) 범위의 값으로 압축하기 때문이다.

  \[\operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)}\]
• 초기 neural network 에서 과학자들은 생물학적 뉴런이 발화하거나 발화하지 않는 현상을 모델링하는 데 관심이 있었다.
• 따라서 이 분야의 선구자들은, 인공 뉴런의 발명자들인 McCulloch 과 Pitts 까지 거슬러 올라가서, thresholding units 에 집중했다.
• 임계값(threshold) 활성화는 입력이 특정 임계값 이하일 때 0 값을 취하고, 입력이 그 임계값을 초과할 때는 1 값을 취한다.
• gradient-based 학습으로 관심이 옮겨가면서, Sigmoid 함수는 임계값 유닛을 근사하면서 매끄럽고 미분 가능했기 때문에 자연스럽게 선택되었다.
• Sigmoid 는 아직도 binary classification 문제에서 출력을 확률로 해석할 때, 출력 유닛의 활성화함수로 널리 사용된다. 이러한 Sigmoid 는 Softmax 의 특별한 case 라고 생각할 수 있다.
• 하지만 Sigmoid 는 hidden layer 에서 더 간단하고 훈련이 쉬운 ReLU 에 의해 대체되었다.
• 그 이유는 Sigmoid 가 최적화할 때 문제를 야기하기 때문이다. Sigmoid 는 절대값이 큰 양수와 음수의 입력에서 gradient vanishing 문제가 발생하여, 빠져나오기 어려운 평탄한 영역(plateaus)을 만들어낸다.
  • 이는 아래 Sigmoid 의 그래프를 보면 알 수 있다.
• 그럼에도 불구하고 Sigmoid 는 여전히 중요하다. 예를 들어 RNN 에서 시간에 따른 정보 흐름을 제어하기 위해 Sigmoid 유닛을 사용하는 아키텍처, LSTM 에서 사용된다.

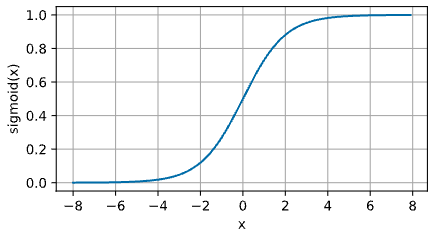
• 아래 그래프는 Sigmoid 함수를 나타낸 것이다. 입력이 0 에 가까워지면, Sigmoid 함수는 linear transformation 에 가까워진다.

  

• Sigmoid 함수의 도함수는 다음과 같이 주어진다. 즉 Sigmoid 함수의 미분은 자기 자신이 포함되어 있다.

  \[\frac{d}{dx} \operatorname{sigmoid}(x) = \frac{\exp(-x)}{(1 + \exp(-x))^2} = \operatorname{sigmoid}(x)\left(1-\operatorname{sigmoid}(x)\right)\]

• 아래 그래프는 Sigmoid 함수의 도함수를 나타낸 그래프다.

  

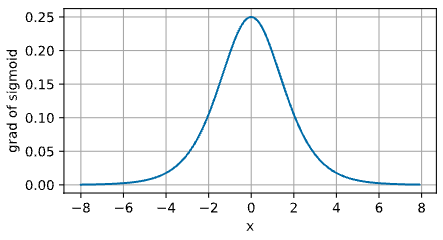
• 입력이 0 일 때 Sigmoid 함수의 도함수는 최대값인 0.25 에 도달한다.
• 입력이 0 에서 멀어질수록, 도함수는 0 에 가까워진다. 따라서 절대값이 큰 양수나 음수의 입력에서 gradient vanishing 문제가 발생하는 것이다.

Tanh

• Tanh 함수(hyperbolic tangent)는 Sigmoid 함수와 마찬가지로 입력을 변환하여 $-1$ 과 $1$ 사이의 값으로 만든다.

  \[\operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}\]

• 아래 그래프는 tanh 함수를 그래프로 나타낸 것이다.

  

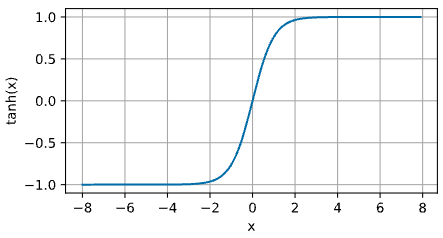
• 입력이 0 에 가까워질수록, tanh 함수는 linear transformation 에 가까워진다.
• Sigmoid 함수와 모양이 비슷하지만, tanh 함수는 좌표축 원점 $(0, 0)$ 에 대해 대칭적인 특성을 보인다.

• tanh 함수의 도함수는 아래와 같다.

  \[\frac{d}{dx} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x)\]

• 아래 tanh 함수의 도함수 그래프를 보면 알 수 있듯이, 입력이 0 에 가까워질수록 최대값인 1 에 도달한다. 또한 Sigmoid 함수에서와 마찬가지로, 입력이 0 에서 멀어질수록 tanh 함수의 도함수는 0 에 가까워진다.

  

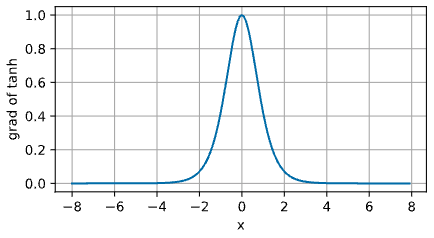
Summary

• 이 포스트를 통해서 비선형성(nonlinearity)을 포함하여 표현력이 높은 mulit layer neural network 아키텍처에 대해 알게 되었다.
• 오늘날은 오픈소스 딥러닝 프레임워크를 사용하여 몇 줄의 코드만으로도 빠르게 모델을 구축할 수 있다.
  • 이전에는 이 neural network 를 훈련시키기 위해 연구자들이 C, Fortran, 심지어 Lisp 로 layer 와 도함수를 명시적으로 코딩해야 했다.
• 또한 ReLU 는 Sigmoid 나 tanh 함수보다 최적화가 훨씬 더 용이하다는 부가적인 이점이 있음을 알았다.
• 이는 딥러닝이 다시 부상하게 된 주요 혁신 중 하나로 볼 수 있다.
• 그러나 활성화함수에 대한 연구는 멈추지 않는다. 예를 들어, GELU(Gaussian error linear unit) 활성화함수 $x \Phi(x)$ 는 Hendrycks 과 Gimpel 에 의해 제안되었다.
  • GELU 는 transformer 류 모델에서 활발히 사용되고 있다.
  • 여기서 $\Phi(x)$ 는 standard Gaussian cumulative distribution function 이다.
• 또한 Swish 활성화함수 $\sigma(x) = x \operatorname{sigmoid}(\beta x)$ 는 Ramachandran 의 논문에서 제안되었으며 많은 경우에 더 나은 정확도를 제공한다.
• 다양한 활성화함수는 Activation 카테고리에서 더 자세하게 다룰 것이다.

맨 위로 이동 ↑