[Deep Learning, d2l] Linear Neural Networks for Classification (1)

2024-04-08

앞에서 다룬 Linear Regression 과 Linear Classification 은 전통적인 머신러닝 방식이고 이를 이해하면 딥러닝에 대한 한층 더 심도있는 이해를 할 수 있다. 따라서 전 포스트에 이어 Linear Classification 을 정리해보자.

Classification task 에서도 데이터를 로드하고, 모델을 통과시키고, 출력을 생성하고, loss 를 계산하고, weight 에 대한 기울기를 취하고, 모델을 업데이트하는 대부분의 과정은 그대로 유지된다. 그러나 target 의 형태, 출력 layer 의 parameterization 및 loss function 의 선택은 classification task 에 맞게 조정된다.

Computer Vision 분야의 Image Classification 뿐만 아니라, Object Detection 이나 Segmentation 도 결국에는 Classification(분류)다. 물론 Object Detection 에서는 물체의 위치를 regression 으로 예측하지만, 그 안에 있는 class 에 대해서는 classification 을 통해 결과가 나온다. 따라서 앞으로의 무궁무진한 Classification 을 이해하기 위해서 반드시 정복하고 가자.

Classification

Regression 은 “얼마나 많이?” 혹은 “몇 개?” 와 같은 질문에 답하고자 할 때 사용하는 도구다.
- 집이 얼마에 팔릴지(가격), 야구팀이 몇 승을 할지, 혹은 환자가 퇴원하기 전 병원에 며칠 동안 머무를지 예측하려고 한다면, 아마도 regression 모델을 사용할 것이다.
- 하지만 regression 모델 내에서도 중요한 차이점들이 있다. 예를 들어, 집값은 절대 음수가 될 수 없으며, 변화는 종종 가격적으로 상대적일 수 있다. 따라서 가격의 로그값을 이용해 예측하는 것이 더 효과적일 수 있다.
- 마찬가지로 환자가 병원에 머무는 일수는 이산적이고 음수가 될 수 없는 확률변수다.
- 따라서 최소제곱법(least mean squares)이 이상적인 접근 방식이 아닐 수도 있다.
- 여기서 중요한 점은 단순히 squared error 를 최소화하는 것 외에 많은 추정 방법이 있다는 것이다.
- 더 나아가, Supervised learning 은 regression 외에도 훨씬 더 다양한 영역을 다룬다.
회귀(Regression)와 분류(Classification) 모두 학습 시 정답값(label)이 있는 Supervised Learning 에 속한다.
- 회귀 모델은 예측값으로 연속적인 값을 출력하고, 분류 모델은 예측값으로 이산적인 값을 출력한다. 쉽게, 회귀는 값 예측이고 분류는 클래스 예측이다.
- 현실에서는 어떤 카테고리에 해당하는지를 예측하는 문제를 더 많이 접하게 된다. “그렇다”, “그렇지 않다” 의 이진 분류를 수행할 수도 있고, 여러가지 클래스를 분류하는 다중 분류일 수도 있다.
카테고리 별로 값을 할당하거나, 어떤 카테고리에 속할 확률이 얼마나 되는지를 예측하는 것이 바로 Classification이다.
이 포스트에서는 “얼마나 많이?” 라는 질문을 제쳐두고, “어떤 카테고리인가?” 에 초점을 맞춘 Classification 문제에 집중한다. 예를 들어 아래의 질문들이 해당한다.
- 이 이메일은 스팸 폴더에 들어가야 할까 아니면 받은편지함에 들어가야 할까?
- 이 고객은 구독 서비스에 가입할 가능성이 더 높은가, 아니면 가입하지 않을 가능성이 더 높은가?
- 이 이미지는 당나귀, 개, 고양이, 아니면 수탉을 묘사하고 있는가?
- A 가 다음에 어떤 영화를 볼 가능성이 가장 높은가?
머신러닝/딥러닝 전문가들은 “classification” 이라는 단어를 두 가지 미묘하게 다른 문제를 설명하는 데 사용한다.
- 데이터 example 을 카테고리(클래스)로 확정적으로 할당(hard assignment)하는 것에만 관심이 있는 경우
- 각 카테고리가 적용될 확률을 평가하는 것처럼 확률적으로 할당(soft assignment)을 하는 경우
이 두 경우는 종종 혼동되는데, 그 이유는 우리가 확정적인 할당을 원할 때조차도 종종 확률적 할당을 하는 모델을 사용하기 때문이다.
더 나아가, 여러 label 이 동시에 참일 수 있는 경우도 있다. 이 문제는 multi-label classification 이다.
예를 들어, 한 뉴스 기사가 동시에 엔터테인먼트, 비즈니스, 우주 비행 주제를 다루고 있을 수 있지만, 의학이나 스포츠 주제는 다루지 않을 수 있다. 따라서 이 기사를 단일 카테고리로만 분류하는 것은 별로 유용하지 않을 것이다.
간단한 Image Classification 문제로 시작해보자.
- 여기서 각 입력은 $2\times2$ 의 grayscale 이미지로 구성된다.
- 각 픽셀 값은 하나의 스칼라 값으로 표현할 수 있으니, 네 개의 feature $\lbrace x_1, x_2, x_3, x_4 \rbrace$ 를 가지게 된다.
- 또한, 각 이미지는 “cat”, “chicken”, “dog” 중 하나의 카테고리에 속한다고 가정하자.
다음으로, label 을 어떻게 표현할지 선택해야 한다. 회귀 문제와 마찬가지로 분류에는 해당 데이터가 무엇으로 분류되어야 하는지 정답 레이블(label)이 필요하다.
컴퓨터는 인간의 언어를 이해하지 못하기 때문에 이 label 을 컴퓨터가 이해할 수 있는 숫자형으로 Encoding한다. 그 방식에는 두 가지가 있다.
가장 자연스러운 방법은 $y \in \lbrace 1, 2, 3 \rbrace$ 을 선택하는 것이다. 이는 Label Encoding 이다.
- 문자열의 Unique 값을 숫자로 바꿔주는 방법이다. 강아지, 고양이, 닭을 각각 숫자 1,2,3 으로 바꿔주는 것이다.
- 여기서 각 숫자는 $\lbrace \textrm{dog}, \textrm{cat}, \textrm{chicken} \rbrace$ 을 나타낸다. 정보를 이렇게 저장하는 것은 컴퓨터에게 좋은 방법이다.
- 만약 카테고리 간에 자연스러운 순서(order)가 있다고 해보자.
- 예를 들어 $\lbrace \textrm{baby}, \textrm{toddler}, \textrm{adolescent}, \textrm{young adult}, \textrm{adult}, \textrm{geriatric} \rbrace$ 을 예측하는 것이라면, 이를 순서형 회귀 문제(ordinal regression)로 다루고, label 을 이 형식으로 유지하는 것이 의미가 있을 수 있다.
- 숫자를 이용하여 label 의 순서를 따질 수 있기 때문이다.
그러나 일반적으로 classification 문제는 클래스 간에 자연스러운 순서를 가지고 있지 않다.
또한 label encoding 은 숫자의 크기(ordinal 특성)가 반영되기 때문에 숫자값을 가중치로 잘못 인식하여 값에 왜곡이 생길 수 있다.
따라서 통계학자들은 범주형 데이터를 표현하는 간단한 방법을 발명했는데, 바로 one-hot encoding 이다.
- one-hot encoding 은 우리가 가진 카테고리 개수만큼의 성분을 갖는 vector다.
- 즉 long-type 으로 구성된 변수들을 wide-type 으로 바꾸어 변수의 차원을 늘려준다.
- 특정 instance 의 카테고리에 해당하는 성분은 1 로 설정하고, 나머지 성분은 모두 0 으로 설정한다.
- 위 예제에서 label $y$ 가 3 차원의 vector 로 표현되며, $(1, 0, 0)$ 은 “cat”, $(0, 1, 0)$ 은 “chicken”, $(0, 0, 1)$ 은 “dog”를 의미한다.
\[y \in \lbrace (1,0,0), (0,1,0), (0,0,1) \rbrace\]

Linear Model

가능한 class 에 대해 conditional probabilities($P(Y\vert X)$) 를 계산하기 위해서, 우리는 가능한 class 에 맞게 여러 output 을 가지는 모델이 필요하다.
분류 task 를 Linear Model 로 다루기 위해서, class 개수 만큼의 affine function 이 필요하다.
affine function 은 일반적인 linear function 으로 선형변환과 평행이동을 결합한 함수다.
엄밀히 말하면, 마지막 카테고리는 1 과 다른 카테고리의 합 간의 차이가 되기 때문에 식이 하나 더 적어도 되지만, 대칭상의 이유로 약간 중복된 parameter 를 사용한다.
output layer 의 각 output 은 자기 자신과 연결된 affine function 과 호환된다.
위 예제에서 우리는 4 개의 feature 와 3 개의 category 를 가지고 있기 때문에, weight 를 나타내기 위해서 12 개의 scalar 값이 필요하고, 각 카테고리별 bias 가 필요하다.
따라서 Classification 문제를 풀기 위해 아래의 linear model 을 사용할 수 있다.
\[\begin{aligned} o_1 &= x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1,\\ o_2 &= x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2,\\ o_3 &= x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3 \end{aligned}\]
이를 다이어그램으로 표현하면 아래와 같다. linear regression 과 같이 single-layer neural network 로 나타낼 수 있다.

Softmax regression is a single-layer neural netwokr
각 출력($o_i$)은 모든 입력($x_j$)을 사용해서 계산되기 때문에 fully connected layer 다.
vector 와 matrix 의 notation 을 사용하면 아래와 같이 나타낼 수 있다.
\[\mathbf{o} = \mathbf{W}\mathbf{x} + \mathbf{b}\]
이 때 weight 는 $3 \times 4$ matrix 이며 모든 bias 는 3차원의 벡터($\mathbf{b}\in \mathbb{R}^3$)다.

Linear Regression 으로 분류를 하지 않는 이유

Linear Regression 을 사용하여 분류 task 를 수행할 수 있지만, 권장되지 않는다. 왜 그럴까?
바로 앞 포스트처럼 Squared Error 를 사용하는 Linear Regression 의 경우, 제곱 형식으로 큰 Loss 를 크게 반영하여 학습에 도움이 되지만 이상치에 영향을 많이 받는다.
새로운 데이터가 들어왔는데 그게 이상치에 해당하면, 찾아낸 최적의 선이 크게 영향을 받게 된다. 또한 분류 task 는 Regression 과 달리 이산적인 값(e.g. 남자/여자, 강아지/고양이 등)의 출력을 필요로 한다.
또한 분류를 수행할 때는 0 에서 1 사이의 확률의 형태로 해석하게 되는데 Linear 함수의 경우 선이기 때문에 0 밑으로도 떨어지고 1 위로도 올라간다. 따라서 태생적으로 한계가 존재한다.
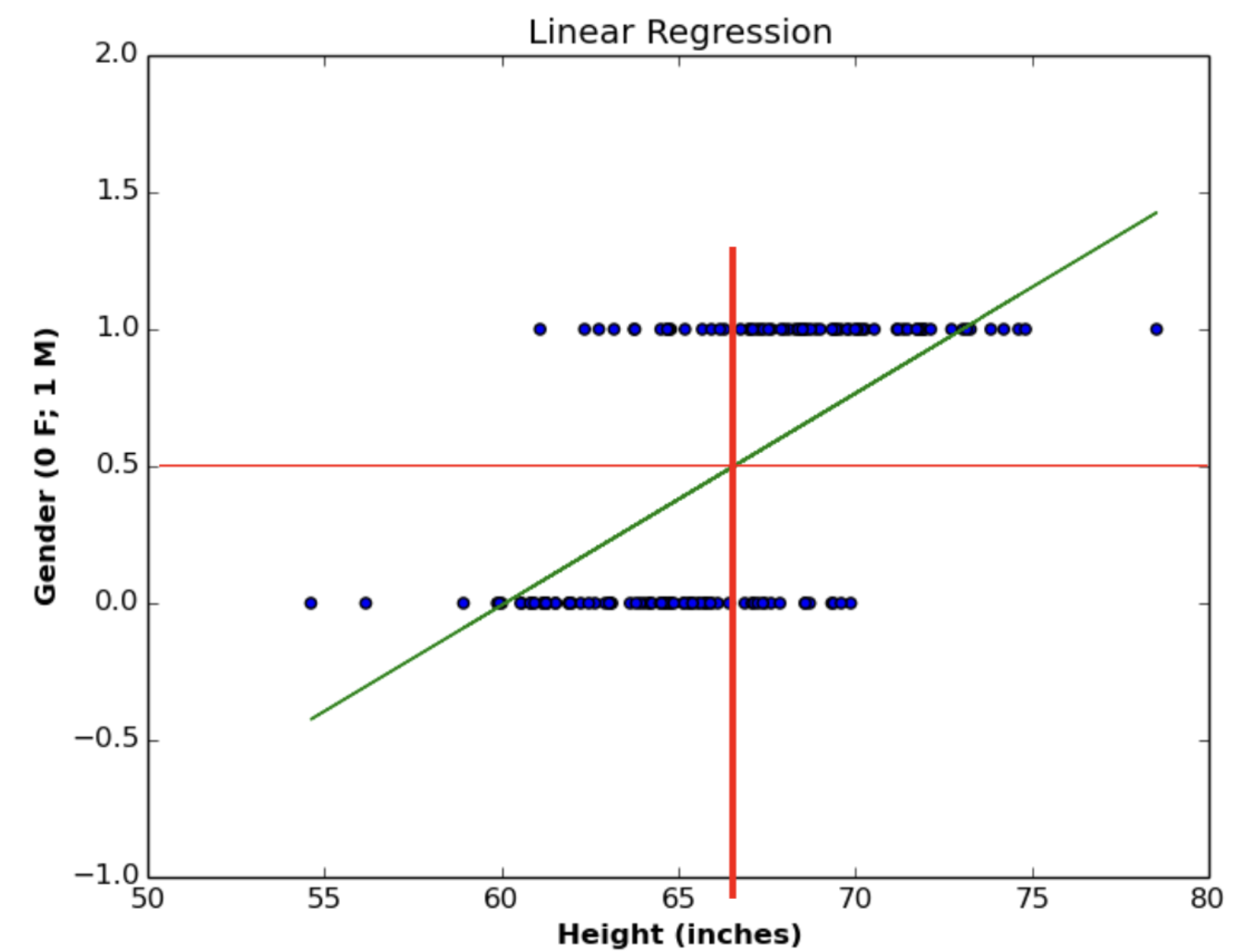
위 그림처럼 선이 단조롭게 증가할 때 기울기가 항상 동일해서 특징을 잘 잡아낼 수 없고, outlier, noise 에 쉽게 영향을 받을 수 있다.
따라서 Linear Regression 은 optimal 한 classifier 가 되기에는 한계가 있다.
이에 따라 Classification task 에서는 이진 분류에 사용되는 Logistic Regression 과 다중 분류로 일반화된 Softmax Regression 을 사용한다.

Logistic Regression

예컨대 “여자/남자”를 분류하거나 “참/거짓”을 분류하는 문제는 label 이 $y \in \lbrace 0, 1 \rbrace$ 라고 할 수 있다. 이러한 이진 분류는 Logistic Regression 을 사용한다.
Logistic Regression 도 구성 자체는 Linear Regression 과 크게 다르지 않다.

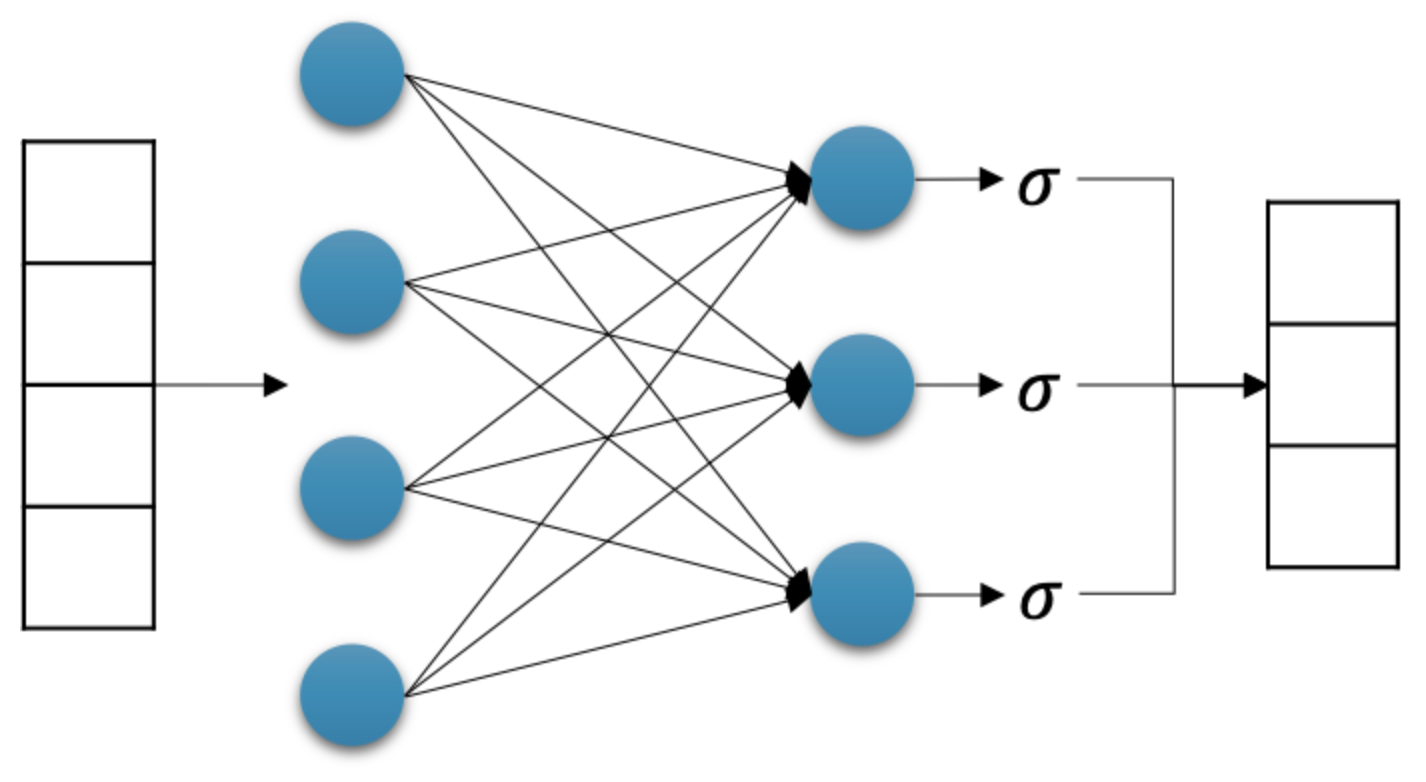출처: https://kh-kim.github.io/
위 그림에서 보이는 $\sigma$ 는 Sigmoid 함수를 뜻한다. 활성화함수로 Sigmoid(Logistic) function 을 사용한다.
- 활성화함수는 이 카테고리에서 자세히 정리한다.
💡 Linear Regression 에서는 활성화함수를 쓰지 않았을까?
활성화함수는 입력 신호의 총합을 출력 신호로 변환하는 함수다. 이를 통해 이전 층(layer)의 결과값을 변환하여 다른 층의 뉴런으로 전달할 수 있다. 그러나 딥러닝에서 일반적으로 이야기하는 활성화함수는 미분 가능한 비선형 함수다.

세상은 복잡하기 때문에 선형으로만 설명할 수 없고, 비선형의 표현력이 필요하기 때문에 딥러닝에서 만날 활성화함수는 비선형 함수이자, 학습을 위해 미분이 가능해야 한다. 그럼에도 불구하고, Linear Regression 에서도 가장 간단한 활성화 함수인 선형 함수가 쓰였다고 볼 수 있다. 물론 비선형 함수는 아니기 때문에 표현력이 부족하다고 할 수 있지만, 선형 함수는 입력과 동일한 값을 출력한다. 이러한 선형 함수도 입력 신호를 출력 신호로 변환하기 때문에 활성화함수라고 볼 수 있다. 다만 딥러닝에서 일반적으로 선형 함수만으로 모델을 구성하지는 않는다.
Logistic Regression 을 식으로 나타내면 아래와 같다.
\[\hat{y} = \sigma(\mathbf{o}) = \sigma(\mathbf{W}\mathbf{x} + \mathbf{b})\]
Sigmoid 함수를 이용하여 모델의 출력 값의 범위를 0 에서 1 사이로 고정할 수 있다. 이 점을 이용해서 확률로 해석할 수 있고, 참/거짓 등의 이진 분류를 할 수 있다.

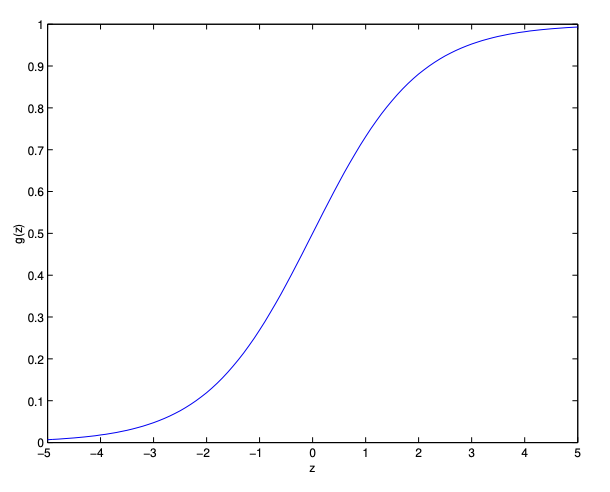Sigmoid 혹은 Logistic function 그래프. 출처: cs229 lecture note
Sigmoid 함수를 수식으로 보면 다음과 같다.
\[\sigma(x) = \frac{1}{1+e^{-x}}\]
수식과 그래프를 보면, Sigmoid 함수는 $+\infty$ 로 갈 경우 1 에 수렴하고 $-\infty$ 로 갈 경우 0 에 수렴한다. 또한 0.5 를 기준으로 참과 거짓을 판단할 수 있다.
만약 출력 vector $\mathbf{o}$ 의 어떤 요소의 값이 0.5 보다 같거나 클 경우 해당 요소에서 참을 예측했다고 결론지을 수 있으며, 반대로 0.5 보다 작을 경우 거짓을 예측했다고 결론내릴 수 있다.

Optimization

Sigmoid 의 미분은 아래와 같이 유도될 수 있다.
- 먼저 분수의 미분은 다음처럼 유도된다.
\[\begin{aligned} \frac{1}{g(x)^\prime} &= \lim_{h\rightarrow0}\frac{\frac{1}{g(x+h)} - \frac{1}{g(x)}}{h} = \lim_{h\rightarrow0}\frac{\frac{g(x)-g(x+h)}{g(x+h)g(x)}}{h} \\ &= \lim_{h\rightarrow0}-\frac{g(x+h)-g(x)}{hg(x+h)g(x)} = \lim_{h\rightarrow0}-\frac{g(x)^\prime}{g(x+h)g(x)} \\ &= -\frac{g(x)^\prime}{g(x)^2} \end{aligned}\]
- 또한 지수의 미분은 다음처럼 유도된다.
\[f(x) = e^{\alpha x}, \; f^\prime(x)=e^{\alpha x}\cdot(\alpha x)^\prime\]
- 이를 활용하여 Sigmoid 함수를 미분하면,
\[\begin{aligned} \sigma(x)^\prime &= -\frac{(1+e^{-x})^\prime}{(1+e^{-x})^2} = -\frac{e^{-x}\cdot(-1)}{(1+e^{-x})(1+e^{-x})} \\ &= \frac{1 - 1 + e^{-x}}{(1+e^{-x})(1+e^{-x})} = \displaystyle\frac{1}{1+e^{-x}}\cdot\frac{-1 + e^{-x}}{1+e^{-x}} \\ &= \sigma(x)(1 - \sigma(x)) \end{aligned}\]
- 즉 Sigmoid 함수를 미분하면 자기 자신과 1 에서 자기 자신을 뺀 값을 곱한 것과 같다.
이제 Logistic Regression 모델을 어떻게 최적화 시키는지 알아보자. 그러기 위해서는 loss function 을 정의해야 한다.
Linear Regression 에서는 오차항이 정규분포를 이룬다는 가정으로 $\hat{y}$ 도 정규분포를 이룬다고 할 수 있었다. Logistic Regression 에서는 어떨까?
Logistic Regression 에서는 $\hat{y}$ 이 정규분포를 따르지 않는다. $\hat{y}$ 는 범주형 이기 때문이다.
따라서 Logistic Regression 은 $\hat{y}$ 값이 베르누이 분포의 형태를 띈다.
- 결과가 두 가지 중 하나로만 나오는 실험이나 시행을 베르누이 시행(Bernoulli trial)이라고 한다.
- 이 때 베르누이 시행의 결과를 실수 0 또는 1 로 바꾼 것을 베르누이 확률변수(Bernoulli random variable)라고 한다.
- 베르누이 확률변수는 두 값 중 하나만 가질 수 있으므로 이산확률변수(discrete random variable)다.
- 베르누이 분포의 확률질량함수는 다음과 같다. 1 이 나올 확률을 의미하는 $\mu$ 라는 parameter(모수)를 가지며 0 이 나올 확률은 $1-\mu$ 이다.
\[\text{Bern}(x;\mu) = \mu^x(1-\mu)^{(1-x)} = \begin{cases} \mu & \text{if} \; x=1, \\ 1-\mu & \text{if} \; x=0 \end{cases}\]
💡 왜 베르누이 분포를 가정할까?

Linear Regression 에서 정규분포를 가정한 것처럼, Logistic Regression 또한 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아내는 것이 불가능하여 근사적으로 확률분포를 추정할 수 밖에 없다. 그러나 Logistic Regression 의 $y$ 는 범주형이기 때문에 정규분포를 가정할 수 없다. 따라서 2 가지 값만을 가지는 베르누이 분포를 가정한다. 즉 이진 분류 문제에서 종속변수가 베르누이 분포를 따른다는 가정 하에, 예측을 확률적으로 표현하며 이를 통해 “예측값이 실제값일 확률이 높지만, 확률적으로 아닐 수도 있다”는 해석이 가능하다.

이를 다르게도 해석할 수 있을 것이다. 성공확률이 $\mu$ 인 베르누이 시행을 $N$ 번 반복하는 경우, $N$ 번 중 성공한 횟수를 확률변수 $X$ 라고 한다면 $X$ 의 값은 0 부터 $N$ 까지의 정수 중 하나가 될 것이다. 이런 확률변수를 이항분포(binomial distribution)를 따르는 확률변수라고 한다. 이항분포 확률변수 $X$ 의 확률질량함수는 $N$ 개의 표본 값이 모두 0(실패) 아니면 1(성공)이라는 값을 가지기 때문에 $N$ 번 중 성공한 횟수는 $N$ 개의 표본값의 합이 된다.

즉 베르누이 확률변수를 전체 시행 횟수만큼 더하면 이항분포의 확률변수가 된다. 여기서, 이항 분포는 시행횟수 $N$ 이 커질수록 중심극한정리에 의해 Gaussian 의 가까운 형태가 된다. 따라서 Logistic Regression 은 베르누이 분포를 따르는 각각의 개별 데이터를 모델링하고, 여러 시행을 거쳐 베르누이 확률변수를 전체 시행 횟수만큼 더하면 이항분포이기 때문에 정규분포(Gaussian)로 근사된다는 것이다!

그렇게 되면 Linear Regression 처럼 정규분포를 가정할 수는 없어도, 정규분포에 근사하게 되는 이항분포의 각 시행인 베르누이 분포를 가정함으로써, “실제값은 내 예측값일 확률이 가장 높지만, 아닐 수도 있다!” 라고 말할 수 있을 것이다.
먼저 Logistic Regression 을 수행하는 Neural Network 에서 input $x$ 와 weight $\theta$ 가 연산되어 들어온다고 보면 아래처럼 나타낼 수 있다.
\[h_\theta(x) = g(\theta^\top x) = \frac{1}{1+e^{-\theta^\top x}}\]
- $\theta$ 는 weight 를 뜻하고 $g$ 는 sigmoid 함수를 뜻한다.
이제 Logistic Regression 은 이진 분류(binary classification)에서 사용되고 $y \in \lbrace 0, 1 \rbrace$ 이라고 했으므로, 아래와 같이 가정할 수 있다. 이는 베르누이 분포이다.
\[\begin{aligned} P(y=1 \mid x;\theta) &= h_\theta(x) \\ P(y=0 \mid x;\theta) &= 1-h_\theta(x) \end{aligned}\]
이 두 수식을 합쳐 아래와 같은 Likelihood 함수를 만들 수 있다. $y$ 에 0 과 1 을 대입해보면 알 수 있다.
\[p(y|x;\theta) = (h_\theta(x))^y(1-h_\theta(x))^{1-y}\]
각 시행은 독립 시행이므로 확률의 곱 형태로 나타낼 수 있는데, 여기에 계산의 효율성을 위해 $\log$ 를 씌운다. 이 식이 Logistic Regression 의 loss function 이 된다.
- $\log$ 를 씌우는 자세한 이유는 이 포스트에서 확인할 수 있다.
\[l(\theta) = \sum^n_{i=1}y^{(i)}\log h(x^{(i)})+(1-y^{(i)})\log(1-h(x^{(i)}))\]
위 식을 가지고 Linear Regression 에서 했던 것처럼 Maximum Likelihood Estimation 을 진행할 수 있다. Log Likelihood 가 최대값이 되는 지점을 찾기 위해 로그 가능도 함수를 미분하면 아래와 같다.

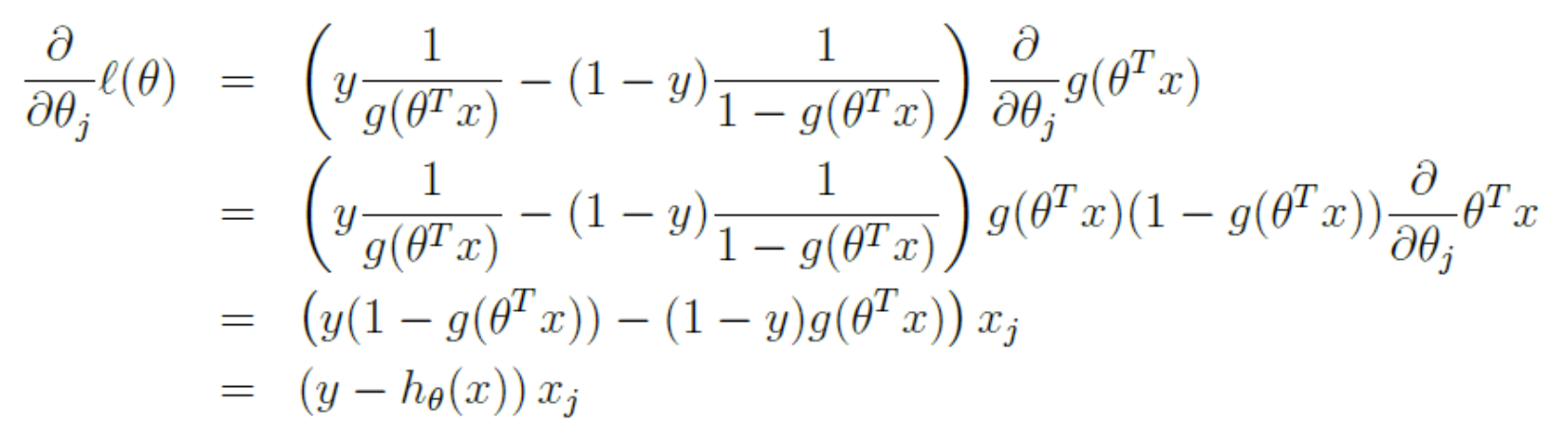chain rule 이 사용된다.
이처럼 Logistic Regression 의 loss function 은 기존 Linear Regression 의 MSE 와 다른 함수를 사용한다.
위 loss 를 Binary Cross Entropy(BCE) 라고 부른다. 이러한 Cross Entropy 는 아래에서 softmax regression 을 다룰 때 언급할 것이다.
linear regression 과 마찬가지로 loss 식을 parameter 로 미분하게 되면, loss 값이 낮아지는 방향으로 경사하강법을 수행할 수 있다.

Softmax Regression

linear regression 처럼 $\mathbf{o}$ 와 $\mathbf{y}$ 사이의 차이를 최소화하는 것은 분류에서 아래와 같은 이유로 적절하지 않다.
- 출력값($o_i$)을 확률로 해석하는데, 출력값의 총합이 1 이 되지 않을 수 있다.
- 출력값($o_i$)이 음수가 아닌 값이더라도 더해서 1 이 되지 않거나 1 이 초과하지 않을 거란 보장이 없다.
이 두 가지 문제는 추정 문제를 해결하기 어렵게 만들고, outlier 에 매우 취약하게 만든다.
예를 들어, 침실 개수와 집을 살 가능성 사이에 양의 선형 관계가 있다고 가정하면 대저택을 살 때 그 확률이 1 을 넘을 수도 있다. 따라서 출력값을 “압축“하는 메커니즘이 필요하다.
출력값을 압축하는 방법은 여러가지가 있다.
먼저 출력 $\mathbf{o}$ 가 $\mathbf{y}$ 의 변형된 버전이라고 가정할 수 있다. 즉 noise 가 더해진 것이고, 이 noise $\epsilon$ 는 정규분포에서 추출된 값이다.
\[\mathbf{y} = \mathbf{o} + \epsilon, \quad \text{where} \; \epsilon_i \sim \mathcal{N}(0, \sigma^2)\]
이를 probit model 이라고 한다. 1860년 Fechner 가 처음 소개한 방법으로, 이 방법은 매력적이지만 딥러닝에서 softmax 와 비교했을 때 잘 작동하지 않거나 최적화 문제가 복잡해지는 경향이 있다.
wiki 에서는 아래와 같이 probit model 을 설명한다.

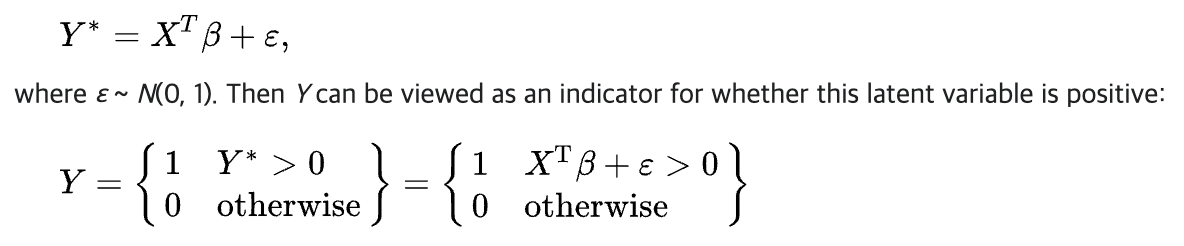Probit Model 출처: https://en.wikipedia.org/wiki/Probit_model
따라서 다른 방법으로 지수함수 $P(y = i) \propto \exp o_i$ 를 사용한다.
즉 출력값이 음수가 아닌 수이고 출력값의 합이 1 이 되도록 하기 위해서, 지수함수를 사용한다.
- 지수함수를 사용하면 $o_i$ 가 증가함에 따라 조건부 클래스 확률도 증가한다. 즉 해당 클래스가 할당될 확률도 증가한다는 것을 의미한다.
- 지수함수는 단조증가함수이며, 지수함수를 통한 확률은 음이 아닌 값이다.
지수함수의 결과를 지수함수의 총합으로 나누는 Normalization 을 통해 총합이 1 이 되고, 이를 수식화한 것이 softmax function 이다.
\[\hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o})\quad \text{where}\quad \hat{y}_i = \frac{\exp(o_i)}{\sum_j \exp(o_j)}\]
이 때, $\mathbf{o}$ 의 가장 큰 값의 위치가 $\hat{\mathbf{y}}$ 에서 가장 높은 확률을 갖는 클래스를 의미한다.
또한, softmax 연산은 인자의 순서를 유지하기 때문에, 가장 높은 확률을 가진 클래스를 결정하기 위해 softmax 를 계산할 필요는 없다. 즉 아래 식과 같다.
\[\operatorname*{argmax}_j \hat y_j = \operatorname*{argmax}_j o_j\]
Softmax 는 현대 물리학에서 기체 분자의 에너지 상태에 대한 분포를 모델링하기 위해 사용한 볼츠만 분포 등에서 사용된 기법이다.
열역학 앙상블에서 특정 에너지 상태가 발생할 빈도는 $\text{exp}(-E/kT)$ 에 비례한다고 한다.
여기서 $E$ 는 상태의 에너지, $T$ 는 온도이며, $k$ 는 볼츠만 상수다.
통계학자들이 통계 시스템에서 “온도” 를 높이거나 낮춘다고 말할 때, $T$ 를 조정하여 낮은/높은 에너지 상태를 선호하도록 만든다는 것을 의미한다.
또한 에너지는 오차에 해당한다. 딥러닝에서 energy-based 모델들은 문제를 묘사할 때 이 관점을 사용한다.

Vectorization

계산 효율성을 높이기 위해, 우리는 mini-batch 로 데이터를 vectorize 하여 계산한다.
$n$ 개의 mini-batch $\mathbf{X} \in \mathbb{R}^{n \times d}$ 가 주어졌다고 가정하자. 여기서 $n$ 은 샘플 개수, $d$ 는 입력의 차원 수(dimensionality)를 의미한다. 또한 출력에 $q$ 개의 범주가 있다고 가정하자.
그러면 weight 는 $\mathbf{W} \in \mathbb{R}^{d \times q}$ 를 만족하고, bias 는 $\mathbf{b} \in \mathbb{R}^{1 \times q}$ 를 만족한다.
\[\begin{aligned} \mathbf{O} &= \mathbf{X} \mathbf{W} + \mathbf{b}, \\ \hat{\mathbf{Y}} & = \mathrm{softmax}(\mathbf{O}) \end{aligned}\]
이렇게 하면 대부분의 연산이 matrix-matrix 곱셈 $\mathbf{X} \mathbf{W}$ 로 가속화된다.
또한 $\mathbf{X}$ 의 각 행이 하나의 데이터 example 을 나타내므로, softmax 연산은 행 단위로 계산(row-wise)할 수 있다.
즉, $\mathbf{O}$ 의 각 행에 있는 모든 항목에 대해 지수화(exponentiate)를 수행한 다음 그 합으로 정규화하면 된다.
하지만 큰 수를 지수화하거나 로그를 취할 때는 수치적인 overflow 또는 underflow 가 발생할 수 있으니 주의해야 한다.
- 이는 컴퓨터가 표현할 수 있는 데이터의 한계 수치를 넘거나, 최소 한계값 보다 작은 값이 등장하는 문제다.
- 딥러닝 프레임워크는 이 문제를 자동으로 처리해준다.
- 이러한 overflow 와 underflow 를 pytorch 에서 어떻게 해결하는지는 이 포스트에 정리했다.

Logit, Sigmoid, Softmax 의 관계

우리는 분류를 하고자 할 때 아래와 같이 데이터를 보고 난 후인 사후확률을 기준으로 삼는다.
\[X : Y_1 \; \text{if} \; P(Y_1 \vert X) > P(Y_2 \vert X) \\ X : Y_2 \; \text{if} \; P(Y_1 \vert X) < P(Y_2 \vert X)\]
이처럼 두 개의 클래스가 있는 binary(2-class) classification 인 경우, 판별 기준인 사후확률(posterior)을 베이즈 정리에 따라 전개해보자.
\[P(Y_1 | X) = \frac{P(X | Y_1) P(Y_1)}{P(X)} \\ P(Y_2 | X) = \frac{P(X | Y_2) P(Y_2)}{P(X)}\]
이 때 분모의 Evidence 는 아래와 같다.
\[P(X) = P(X | Y_1)P(Y_1) + P(X | Y_2)P(Y_2)\]
이처럼 사후확률은 Likelihood 와 Prior 의 곱으로 결정된다. 그러면 각 클래스($k$)별로 Likelihood 와 Prior 의 곱을 정의하는 것은 의미가 있다.
\[a_k = \log(P(X|Y_k)P(Y_k))\]
여기서 $\log$ 를 쓰는 것은 $\log$ likelihood 를 쓰는 것과 같은 이유다.
따라서 클래스 1 의 사후확률은 아래처럼 나타낼 수 있다.
\[P(Y_1 | X) = \frac{P(X | Y_1) P(Y_1)}{P(X | Y_1)P(Y_1) + P(X | Y_2)P(Y_2)} = \frac{e^{a_1}}{e^{a_1}+e^{a_2}}\]
이 식을 분자로 분모와 분자를 모두 나눠주면 아래와 같다.
\[P(Y_1 | X) = \frac{1}{1+e^{a_2 - a_1}}\]
여기서 $a_2 - a_1$ 를 분모 분자를 뒤집으면 Log Odds 라고 부르는 식이 나온다.
\[\begin{aligned} a_2 - a_1 &= \log( \frac{P(X | Y_2)P(Y_2)}{P(X | Y_1)P(Y_1)} ) \\ a = -(a_2 - a_1) &= \log(\frac{P(X | Y_1)P(Y_1)}{P(X | Y_2)P(Y_2)}) \end{aligned}\]
- Odds 는 사건이 발생할 확률을 사건이 발생하지 않을 확률로 나눈 비율이다.
- 즉 $P(Y_1 \vert X)$ 를 $1 - P(Y_1 \vert X)$ 로 나눈 값이다. 이 때 Odds 는 0 < Odds < $\infty$ 의 범위에 속하기 때문에 범위에 제약이 있다. 또한 확률값과 Odds 값은 비대칭성(Asymmetirc)을 띈다.
- 이러한 한계를 극복하기 위해 Odds 에 $\log$ 를 씌울 수 있다. 이를 logit 이라 부르고, logit(Log Odds)은 범위가 실수 전체가 된다.
  
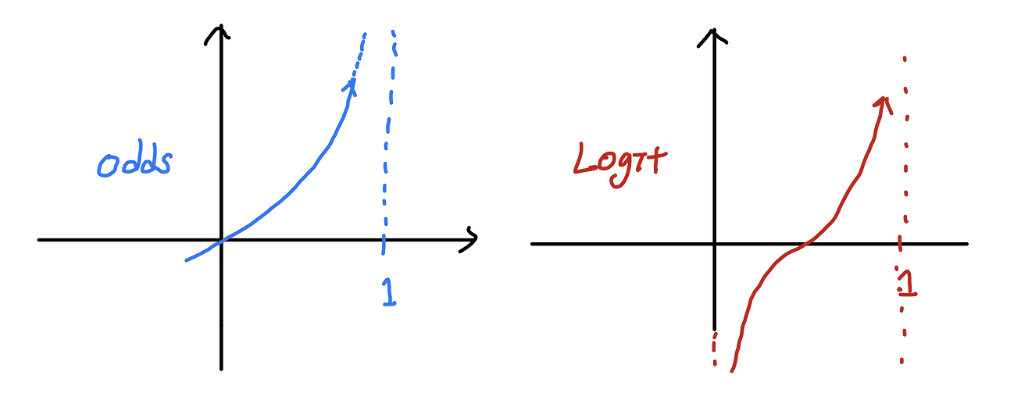  출처: https://csm-kr.tistory.com/43
- binary classification 에서는 단순 선형함수 $\mathbf{y}=\mathbf{W}\mathbf{x} + \mathbf{b}$ 로는 풀기 힘들다. 따라서 최종 예측값이 0.5 보다 작으면 0 으로, 0.5 보다 크면 1 로 판단하는 확률로 해석하는 것이 용이하다.
- 그러면 Odds 는 그 값이 1 보다 큰 지가 결정기준이 되고, logit 은 $\log$ 를 씌웠으므로 0 보다 큰 지가 결정기준이 된다.
- 이를 이용하면 단순 선형함수로 풀기 힘든 binary classification 문제를 $\log(\text{Odds}(\mathbf{y})) = \mathbf{W}\mathbf{x} + \mathbf{b}$ 로 풀 수 있다.
이를 위 Log Odds 를 이용해서 다시 사후확률을 정의하면 아래와 같다.
\[P(Y_1 | X) = \frac{1}{1+e^{-a}}\]
이를 $a$ 에 대한 함수로 그려보면 Sigmoid Function 이 나온다. 이를 $\mathbf{W}\mathbf{x} + \mathbf{b}$ 로 다시 정리해보자.
즉 실수 전체의 범위를 가지는 linear regression 의 식($\mathbf{W}\mathbf{x} + \mathbf{b}$)을 logit 으로 하여 위 식의 $a$ 대신에 넣어주면, 그 값을 0 에서 1 사이의 값으로 변환시켜주는 sigmoid(logistic) funtion 인 것이다.
\[\begin{aligned} \log(\text{Odds}(\mathbf{y})) = \mathbf{W}\mathbf{x} + \mathbf{b} \; &\rightarrow \; \text{Odds}(\mathbf{y}) = e^{\mathbf{W}\mathbf{x} + \mathbf{b}} \\ \frac{P(Y | X)}{1 - P(Y | X)} = e^{\mathbf{W}\mathbf{x} + \mathbf{b}} \; &\rightarrow \; \frac{1- P(Y | X)}{P(Y | X)} = e^{-(\mathbf{W}\mathbf{x} + \mathbf{b})} \\ \frac{1}{P(Y | X)} &= e^{-(\mathbf{W}\mathbf{x} + \mathbf{b})} + 1 \\ \therefore \; P(Y | X) &= \frac{1}{1+e^{-(\mathbf{W}\mathbf{x} + \mathbf{b})}} \end{aligned}\]
2 개의 클래스인 Binary Classification 이 아닌 K-Class Classification 도 마찬가지로 Likelihood 와 Prior 의 곱으로 정의할 수 있다.
\[P(Y_1 | X) = \frac{P(X|Y_1)P(Y_1)}{P(X|Y_1)P(Y_1) + P(X|Y_2)P(Y_2) + \ldots + P(X|Y_k)P(Y_k)}\]
위 식에서 우리가 사후확률의 분포로 판단을 하고, 그것은 Likelihood 와 Prior 의 곱에 비례했기 때문에 정의한 $a_k=\log(P(X \vert Y_k)P(Y_k))$ 를 이용하면 아래와 같다.
\[P(Y_1 | X) = \frac{e^{a_1}}{e^{a_1}+e^{a_2}+ \ldots +e^{a_k}} = \frac{e^{a_1}}{\sum _{j}^{}{e^{a_j}}}\]
이는 결국 Softmax Function 이 된다.
따라서 베이즈 정리를 통해 Classification 문제에서 결정 기준을 사후확률로 잡고, 이를 이용하여 binary 에서는 Sigmoid 를, k-class 에서는 Softmax 를 유도할 수 있다.
또한 일반적인 linear function 으로는 Classification 문제에 접근하기 어렵기 때문에, linear function 을 이용할 수 있도록 Odds 와 logit 같은 확률적 해석을 적용했고, 이를 이용해서 Sigmoid 와 Softmax 를 유도했다.

Loss function(Cross Entropy)

Classification 에서 사용되는 Loss function 에 대해 알아보자.
우리는 위에서 feature $\mathbf{x}$ 를 확률 $\mathbf{\hat{y}}$ 로 mapping 했으니, 이 mapping 의 정확도를 최적화하는 방법이 필요하다.
이 때 MSE Loss 를 확률적으로 정당화할 때도 사용했던 Maximum Likelihood Estimation 을 사용한다.

Log-Likelihood

softmax 함수를 통해 $\hat{\mathbf{y}}$ 라는 vector 를 얻을 수 있다.
이 vector 는 주어진 입력 $\mathbf{x}$ 에 대해 각 클래스의 조건부확률을 추정한 값으로 해석할 수 있다.
- 예를 들어 $\hat{y}_1 = P(y=\textrm{cat} \mid \mathbf{x})$ 가 될 수 있다.
이제 feature $\mathbf{X}$ 를 가진 데이터셋에서 label $\mathbf{Y}$ 가 one-hot encoding 된 vector 로 표현된다고 가정해보자.
우리는 주어진 feature 에서 모델에 의해 실제 클래스가 얼마나 가능성이 있는지 확인함으로써 추정치와 실제 데이터를 비교할 수 있다.
\[P(\mathbf{Y} \mid \mathbf{X}) = \prod_{i=1}^n P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)})\]
우리는 각 label 이 독립적으로 각각의 분포 $P(\mathbf{y}\mid\mathbf{x}^{(i)})$ 에서 추출된다고 가정하기 때문에 이 factorization 을 사용할 수 있다.
- factorization 은 곱하기로 쪼개는 것을 뜻한다.
- wiki 에는 a product of several factors 라고 정의되어 있으며 여러 factor 들의 곱으로 숫자나 수학적인 객체들을 만드는 것이다.
여러 항의 곱을 최적화하는 것은 어려우므로, 음의 로그를 취해서 negative log-likelihood 를 최소화하는 문제로 변환할 수 있다.
\[-\log P(\mathbf{Y} \mid \mathbf{X}) = \sum_{i=1}^n -\log P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)}) = \sum_{i=1}^n l(\mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)})\]
여기서 $q$ 개의 클래스가 있을 때 label $\mathbf{y}$ 와 모델의 예측 $\hat{\mathbf{y}}$ 간의 loss function $l$ 은 아래와 같다.
\[l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j\]
위 loss function 은 cross entropy loss 라고 부른다. 위 logistic regression 에서 본 loss function 과 식의 형태는 다르지만 같은 뜻을 가진다.
- logistic regression 에서는 두 경우만 존재하는 베르누이 분포를 가정하기 때문에 풀어쓴 것이고, $h(x^{(i)})$ 와 $\hat{y}_j$ 가 본질적으로 같은 것이기 때문이다.
$\mathbf{y}$ 는 길이가 $q$ 인 one-hot vector 이므로, 모든 좌표 $j$ 에 대한 합은 한 항목을 제외한 모든 항목에서 0 이 된다.
loss $l(\mathbf{y}, \hat{\mathbf{y}})$ 은 $\hat{\mathbf{y}}$ 가 확률 vector 이기 때문에 $0$ 이상으로 하한이 설정된다.
즉 $\hat{\mathbf{y}}$ 의 어떤 항목도 $1$ 을 넘지 않으므로, 그들의 negative log 는 $0$ 이하로 갈 수 없고, loss function $l(\mathbf{y}, \hat{\mathbf{y}}) = 0$ 인 경우는 모델이 실제 label 을 확실하게 예측할 때만 발생한다.
그러나 $l(\mathbf{y}, \hat{\mathbf{y}}) = 0$ 인 경우는 weight 가 유한한 값일 때 절대 발생할 수 없다.
왜냐하면 softmax 출력값을 1 로 만들기 위해서는 해당 입력 $o_i$ 를 무한대로 보내거나 혹은 $j \neq i$ 인 나머지 모든 출력값 $o_j$ 를 음의 무한대로 보내야 한다.
설령 모델이 출력 확률을 0 으로 할당할 수 있더라도, 그렇게 높은 확신을 가질 때 발생하는 오류는 무한의 loss 를 초래할 것이다. ($-\log 0 = \infty$)

Softmax and Cross-Entropy Loss

softmax 함수와 이에 대응하는 cross entropy loss 는 아주 많이 사용된다. 이것들이 어떻게 계산되는지 조금 더 이해할 필요가 있다.
loss function 의 정의에 softmax 정의를 대입하면 아래와 같은 식을 얻는다.
\[\begin{aligned} l(\mathbf{y}, \hat{\mathbf{y}}) &= - \sum_{j=1}^q y_j \log \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} \\ &= \sum_{j=1}^q y_j \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j \\ &= \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j \end{aligned}\]
그리고 임의의 logit $o_j$ 에 대한 미분은 아래와 같다.
\[\partial_{o_j} l(\mathbf{y}, \hat{\mathbf{y}}) = \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} - y_j = \color{red}{\mathrm{softmax}(\mathbf{o})_j} - \color{blue}{y_j}\]
위 식을 보면, 미분의 결과는 모델이 softmax 연산으로 할당한 확률(빨간색)과 실제로 일어난 결과(파란색)인 one-hot label vector 의 항목 간($j$)의 차이를 나타낸다.
이것은 regression 에서 관찰값 $y$ 와 예측값 $\hat{y}$ 의 차이를 구했던 방식과 매우 유사하다.
이는 우연이 아니다. 모든 지수족(exponential) 모델에서는 log-likelihood 함수의 미분값이 이 차이를 구하는 식에 의해 주어진다. 이 사실 덕분에 실제로 gradient 계산이 쉽게 이루어진다.
이제 단일 결과가 아닌 모든 결과에 대한 전체 분포를 관찰하는 경우를 생각해보자.
우리는 label $\mathbf{y}$ 를 이전과 동일한 방식으로 표현할 수 있다. 유일한 차이점은 vector 가 $(0, 0, 1)$ 과 같은 이진 항목만 포함하는 대신, $(0.1, 0.2, 0.7)$ 과 같은 일반적인 확률 vector 를 가지게 된다는 점이다.
앞에서 정의한 loss function $l$ 을 사용하면서 약간 일반화하여 해석해보자. 즉 우리가 정의한 loss function $l$ 의 값은 label distribution 에 대한 loss 의 기대값이다.
이 loss 는 cross entropy loss 라고 불리며, classification 문제에서 가장 일반적으로 사용되는 loss 중 하나다.
cross entropy 는 아래에서 다룰 정보이론을 이해하여 명확히 할 수 있다.
- 간단히 말하면 데이터셋의 label $\mathbf{y}$ 를 encoding 하는 데 필요한 bit 수를, 우리가 예측한 결과 $\hat{\mathbf{y}}$ 와 비교하여 측정하는 것이다.

Exponential Family

지수족(exponential family)은 지수함수와 연관되어 있는 특정 확률분포 종류를 가리키는 말이다.
정규 분포나 감마 분포, 다항 분포 등 일반적으로 널리 사용되는 분포들이 다수 포함되어 있다.
일반적으로, 확률분포가 다음의 형태로 나타나는 경우 지수족이라고 부른다.
\[p(y \mid \eta) = h(y)\text{exp}(\eta^\top T(y) - A(\eta))\]
여기서 $y$ 는 관찰값, $\eta$ 는 매개변수(parameter), $T(y)$ 는 충분통계량, $A(\eta)$ 는 정규화 항, $h(y)$ 는 기준 측도다.
정규화 항 $A(\eta)$ 는 확률분포가 적분해서 1 이 되도록 만드는 항이다. 즉 $A(\eta)$ 는 $\eta$ 에 의존하는 모든 $y$ 에 대해 분포가 제대로 정규화되도록 도와주는 역할을 한다. 아래 식은 확률분포를 1 로 만드는 정규화 항을 $\log$ 취한 형태로 나타낸 것이다.
\[A(\eta) = \log \left( \int h(y) \text{exp}(\eta^\top T(y))dy \right)\]
지수족 분포의 log-likelihood 함수는 아래와 같이 나타낼 수 있다.
\[\log p(y \mid \eta) = \log h(y) + \eta^\top T(y) - A(\eta)\]
그리고 이 지수족 분포의 log-likelihood 함수를 parameter $\eta$ 에 대한 미분을 계산하면 아래와 같다.
\[\frac{\partial}{\partial \eta}\log p(y \mid \eta) = \frac{\partial}{\partial \eta}(\eta^\top T(y) - A(\eta))\]
첫번째 term $\eta^\top T(y)$ 은 $\eta$ 에 대해 선형이므로 쉽게 미분 가능하다.
\[\frac{\partial}{\partial \eta}(\eta^\top T(y)) = T(y)\]
두번째 term $A(\eta)$ 는 정규화 항으로, $\eta$ 에 대한 미분은 기대값에 해당한다.
\[\frac{\partial}{\partial \eta}A(\eta) = \mathbb{E}_p(y \mid \eta)[T(y)] = \hat{T}(y)\]
따라서 log-likelihood 함수의 미분은 아래와 같이 얻을 수 있다.
\[\frac{\partial}{\partial \eta}\log p(y \mid \eta) = T(y) - \mathbb{E}_p(y \mid \eta)[T(y)] = T(y) - \hat{T}(y)\]
즉, 지수족 분포의 log-likelihood 함수의 미분은 실제 관찰된 값 $T(y)$ 와 모델의 예측값 $\hat{T}(y)$ 간의 차이로 표현된다.
이는 지수족 모델에서 gradient descent 와 같은 최적화 방법이 예측값과 실제값 간의 차이를 기반으로 동작함을 보여준다.
이 원리는 MSE 혹은 softmax 와 cross entropy loss function 에서도 유사하게 적용된다.

Information Theory

많은 딥러닝 논문에서 정보이론의 직관과 용어를 사용한다.
이를 이해하기 위해서 공통된 언어가 필요하다. 정보이론은 정보(=data)를 encoding, decoding, transmitting, manipulating 하는 문제를 다룬다.
AI Math 와 Loss 카테고리에서 정보이론을 자세하게 정리하고, 여기서는 d2l 에 나온 정도로만 이해하고 넘어가자.
- 정보이론에 대한 더 자세한 설명은 이 포스트에 잘 정리했다.

Entropy & Surprisal

정보이론의 핵심 아이디어는 데이터에 담긴 정보의 양을 정량화하는 것이다. 이는 데이터를 압축할 수 있는 능력의 한계를 설정한다.
분포 $P$ 에 대해 그 분포의 entropy $H[P]$ 는 아래와 같이 정의된다.
\[H[P] = \sum_j -P(j)\log P(j)\]
정보이론의 근본적인 개념 중 하나는 분포 $P$ 에서 무작위로 추출된 데이터를 인코딩하려면 최소한 $H[P]$ “nats” 가 필요하다는 것이다.
‘nat’ 은 bit 와 동등한 단위지만 base 가 2 가 아닌 $e$ 인 코드를 사용한다. 따라서, 1 nat 은 $\frac{1}{\log(2)} \approx 1.44$ bit 다.
데이터를 압축하는 것과 모델이 예측하는 것은 어떤 관계가 있을까?
만약 압축하려는 데이터 스트림이 있을 때, 다음 토큰을 항상 쉽게 예측할 수 있다면 이 데이터는 쉽게 압축된다.
예를 들어 모든 토큰이 항상 같은 값을 갖는 상황을 생각해보자. 이것은 매우 지루한 데이터 스트림이고 예측하기도 쉽다.
즉, 토큰이 항상 같기 때문에 스트림의 내용을 전달하기 위해 아무 정보도 전송할 필요가 없다. 이처럼 예측이 쉬운 데이터는 압축도 쉽다.
그러나 모든 사건을 완벽하게 예측할 수 없다면 가끔 놀라움(surprisal)을 느낄 때가 있다.
우리는 어떤 사건에 할당한 확률이 낮을수록 그 사건이 발생했을 때 놀람이 커진다.
Claude Shannon 은 사건 $j$ 에 주관적으로 확률 $P(j)$ 를 할당하고 이를 관찰했을 때의 놀라움을 아래의 식과 같이 정량화했다. 이를 정보량이라고도 한다.
\[\log \frac{1}{P(j)} = -\log P(j)\]
그렇다면 위에서 정의한 entropy는 올바른 확률을 할당했을 때 놀라움(정보량)의 기대값이다.

Cross Entropy

entropy 가 올바른 확률을 아는 사람이 경험하는 놀라움의 수준이라면, cross entropy 는 무엇일까?
$H(P, Q)$ 로 표기되는 $P$ 에서 $Q$ 로의 cross entropy 는 주관적인 확률 $Q$ 를 가진 관찰자(모델)가 실제로 $P$ 에 따라 생성된 데이터를 봤을 때의 entropy 의 기대값이다.
이는 아래와 같이 식으로 나타낼 수 있다.
\[H(P, Q) \stackrel{\textrm{def}}{=} \sum_j - P(j) \log Q(j)\]
cross entropy 는 $P=Q$ 일 때 0 이 된다. 즉 이러한 경우에 $P$ 에서 $Q$ 로의 cross entropy 는 $H(P, P)= H(P)$ 다.
쉽게 말해서, cross entropy 를 활용한 classification 의 목적은 두 가지 방식으로 생각할 수 있다.
- (i) 관찰된 데이터의 가능성을 최대화한다.
- (ii) label 을 전달하는 데 필요한 놀라움(즉, bit 수)을 최소화한다.

Summary

여기서 우리는 discrete output space 를 최적화할 수 있게 해주는 loss function 에 대해 다뤘다.
핵심은 확률론적 접근 방식을 취하고, 이산 범주를 확률분포에서 추출된 사례로 취급했다는 것이다.
이에 우리는 softmax 를 사용했다. softmax 는 일반적인 neural network layer 의 출력을 유효한 이산확률분포로 변환하는 편리한 활성화 함수다.
그리고 softmax 와 결합된 cross entropy loss 의 미분이 MSE 의 미분과 매우 유사하게 작동한다는 것을 확인했다.
- 즉, 기대 행동(실제값)과 예측된 행동(예측값) 간의 차이를 계산하는 방식으로 나타난다.
또한 통계 물리학과 정보이론과의 흥미로운 연결점이 있음을 봤다.
한편 우리는 여기서 computational 고려사항을 건너뛰었다.
특히, $d$ 개의 입력과 $q$ 개의 출력을 가진 fully connected layer 의 경우, parametrization 과 computational cost(계산복잡도) 는 $O(dq)$ 이며 이는 실제로 매우 오래 걸리는 정도이다.
다행히 $d$ 개의 입력을 $q$개 의 출력으로 변환하는 비용은 근사화(approximation)와 압축(compression)을 통해 줄일 수 있다.
예를 들어 Deep Fried Convnets 에서는 순열, 푸리에 변환, 스케일링의 조합을 사용하여 비용을 제곱(quadratic) 대신 log-linear 하게 줄였다. 더 발전된 구조적 행렬 근사에서도 유사한 기술이 사용된다.
마지막으로, quaternion 분해를 사용하여 계산 비용을 $O(\frac{dq}{n})$ 으로 줄일 수 있으며, 약간의 정확도를 희생하면 계산 및 저장 비용을 줄일 수 있다. 이것은 압축 factor $n$ 에 기반한 것이다.
그러나 우리는 가장 컴팩트한 표현이나 최소한의 부동 소수점 연산을 추구하는 것이 아니라, 현대의 GPU 에서 가장 효율적으로 실행할 수 있는 솔루션을 찾고 있다.

맨 위로 이동 ↑

Bkkhyunn