[Deep Learning, d2l] Linear Neural Networks for Regression (3)

여기까지 over-fitting 문제에 대해 알아봤으니 첫번째 정규화(regularization) 기법을 알아보자. 더 많은 학습 데이터를 수집함으로써 항상 over-fitting 을 완화할 수 있었다. 그러나 데이터셋을 더 많이 수집하는 것은 비용이 많이 들거나 시간이 많이 소요되거나 데이터셋을 구할 수 없는 경우일 수 있다. 따라서 일반적으로 어렵고 단기적으로 불가능하다.

그렇기 때문에 사용하는 모델의 복잡도를 조정하는 것이 선호된다. polynomial regression(다항식 회귀) 예제에서 우리는 다항식의 차수(degree)를 조정하여 모델의 복잡도를 조절할 수 있었다. 실제로 특징 수를 제한하는 것은 over-fitting 을 완화하는 데 널리 사용되는 기법이다. 그러나 단순히 feature 를 줄이거나 제거하는 것은 명확한 근거가 없으면 안 좋을 수 있다.

polynomial regression 에서 high-dimensional 입력이 들어올 때를 고려해보자. 다항식을 이러한 다변량 데이터로 자연스럽게 확장해주는 것은 단항식(monomials)이다. 단항식은 단순히 변수의 곱이다. 또한 단항식의 차수는 변수의 거듭제곱($n$ 승)의 합이다. 예를 들어 $x^2_1x_2$ 와 $x_3x^2_5$ 의 경우 차수가 3인 monomials 다.

$d$ 차수에서 항의 개수는 $d$ 가 커질수록 빠르게 증가한다. $k$ 개의 변수가 주어졌을 때, $d$ 차수의 monomials 의 개수는 $\binom{k-1+d}{k-1}$ 가 된다. 2차에서 3차로 변하는 것처럼 차수에서 작은 변화가 일어나도 모델의 복잡도는 급진적으로 증가한다. 따라서 우리는 모델의 복잡도를 조정할 수 있는 보다 정교한 툴이 필요하다.

Norms and Weight Decay

• parameter 의 수를 바로 조절하기보다 weight decay 는 parameter 가 가질 수 있는 값을 제한하면서 모델 복잡도에 영향을 미친다.
• 딥러닝에서는 $L_2$ regularization 이라 불리며 mini-batch SGD 로 최적화할 때 weight decay 는 parameteric 모델들을 정규화하기 위해 널리 사용된다.
• 이 방법은 모든 함수 $f$ 들 중에서 $f=0$ 이 가장 간단한 형태라는 것에 착안한다. 따라서 0 과 얼마나 가까운가를 이용해서 함수의 복잡도를 측정할 수 있다.
• 이 때 어떻게 함수와 0 사이의 거리를 정확하게 측정할 수 있을까? 여기에 맞는 정답은 없다.
• 사실 이를 측정하는 방법은 다양하여 별도의 수학 분야가 존재하기까지 한다. 예를 들어 Banach 공간 이론 등이 있다.
• 우리의 목적을 위해서는 아주 간단한 것을 사용해도 충분하다.
• linear function $f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x}$ 의 복잡도를 weight vector 의 norm(예를 들어 $\Vert \mathbf{w}\Vert^2$) 으로 측정하는 것이다.
  • norm 에는 $L_1, L_2, L_p$ norm 등이 있다. $L_p$ norm 은 일반화된 형태다.
• 우리는 weight vector 가 작을 경우 “이 함수는 간단하다” 라고 간주한다.
  • weight vector 의 크기는 모델의 복잡도를 어느 정도 반영하는데, 가중치가 작다는 것은 모델이 입력 데이터에 대해 덜 민감하고, 더 부드럽고 단순한 함수일 가능성이 크다는 것이다.
  • 이는 과적합(over-fitting) 위험을 줄이고, 모델이 일반화(generalization)를 더 잘할 수 있게 도와준다.
  • 가중치가 크면 모델은 특정 데이터 포인트에 매우 민감하게 반응하게 되어 학습 데이터에 과적합할 가능성이 커진다.
  • 반면, 작은 가중치는 모델이 전체 데이터에 대해 더 일반적인 패턴을 찾도록 하여 복잡도를 줄인다.
• weight vector 를 작게 유지하는 방법은 loss 를 최소화하는 문제에 penalty term 인 norm 을 더해주는 것이다.
• 따라서 우리의 원래 목표인 “training label 에 대해 예측 loss 를 최소화” 하는 것이 “예측 loss 와 penalty term 의 합을 최소화” 하는 새로운 목표로 대체되는 것이다.
• 이제 weight decay 가 추가된 learning algorithm 은 weight vector 가 너무 커졌을 때 training error 를 최소화하는 것보다 weight norm 인 $\Vert \mathbf{w} \Vert^2$ 를 최소화하는 것에 집중하게 된다. 이것이 우리가 원하는 것이다.

• linear regression 에서 loss 는 아래와 같았다.

  \[L(\mathbf{w}, b) = \frac{1}{n}\sum^n_{i=1}\frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2\]
• $\mathbf{x}^{(i)}$ 는 feature 이고 $y^{(i)}$ 는 $i$ 번째 데이터의 label 이다. $(\mathbf{w}, b)$ 는 parameter 인 weight 와 bias 다.
• weight vector 의 크기에 대한 penalty 를 주기 위해서 우리는 위 loss function 에 $\Vert \mathbf{w} \Vert^2$ 를 더해준다.
• 이 때 모델이 기존의 loss 와 새롭게 추가된 penalty 사이의 trade off 를 어떻게 다룰까?

• 우리는 이 trade-off 를 음이 아닌 하이퍼파라미터 regularization constant $\lambda$ 로 조절하고 validation data 를 사용하여 fit 한다.

  \[L(\mathbf{w}, b) + \frac{\lambda}{2}\Vert \mathbf{w} \Vert^2\]
• $\lambda$ 가 0 이면 우리는 원래의 loss function 을 사용하는 것과 같고, 0 보다 크면 weight vector 의 크기를 제한한다.
• 위 식을 보면 $\lambda$ 이외에 2 로 나눠주게 되는데, 이는 이차 함수의 미분을 수행할 때 차수 2 와 1/2 가 상쇄되어 식이 깔끔하고 간단하게 보이게 하기 위해서다.
• 여기서 Euclidean distance($L_2$ norm) 같은 표준 norm $\Vert \mathbf{w} \Vert$ 가 아니라 제곱된 norm 을 사용하는 이유는 계산의 편의성을 위한 것이다.
• $L_2$ norm 을 제곱함으로써 원래 식의 제곱근을 제거하고, weight vector 각 성분의 제곱의 합을 남길 수 있다. 이렇게 하면 미분의 합은 합의 미분과 같기 때문에 penalty term 의 미분을 쉽게 계산할 수 있다.
• 그러면 왜 weight decay 는 $L_2$ norm 을 사용하고 $L_1$ norm 은 사용하지 않을까? 사실 다른 norm 을 선택하는 것도 통계학에서 유용하고 널리 사용된다.
• $L_2$ 정규화된 linear model 은 ridge regression 을 구성하고, $L_1$ 정규화된 linear model 은 lasso regression 으로 잘 알려져 있다.
• $L_2$ norm 을 사용하는 이유 중 하나는 weight vector 의 큰 성분에 대해 과도한 penalty 를 부과하기 때문이다. 즉 weight vector 의 크기가 크면 클수록 더 큰 penalty 를 부과한다.
• 이는 학습 알고리즘이 많은 수의 feature 에 weight 를 고르게 분산시키도록 만든다. 실제로 이를 통해 모델이 단일 변수에서 발생할 수 있는 error 에 대해 더 강건(robust)하도록 만들어준다.
• 반면에 $L_1$ penalty 는 모델이 weight 를 일부 feature 에 집중시키고 나머지 weight 를 0 으로 만든다. 이는 feature selection 을 위한 효과적인 방법이 된다.
• 즉 $L_1$ regularization 을 쓰면 feature selection 의 효과가 있다는 것인데, 이렇게 되면 모델이 일부 feature 에 의존하게 되어 제거된 feature 에 대한 데이터를 수집, 저장 또는 전송할 필요가 없어진다.

• 아래의 식은 mini-batch SGD 에 $L_2$ regularization 을 추가한 식이다.

  \[\mathbf{w}\; \leftarrow \; \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)\]
• 이전과 마찬가지로 추정치($\mathbf{w}^\top \mathbf{x}^{(i)} + b$)가 관찰값($y^{(i)}$)과 다른 정도에 따라 $\mathbf{w}$ 를 업데이트한다.
• 그러나 $L_2$ regularization 이 적용되었으므로 $\mathbf{w}$ 의 크기를 0 에 가깝게 줄인다. 이 때문에 weight decay 라고 불리는 것이다. 그도 그럴것이 penalty term 만 남아있다고 한다면, 위 최적화 알고리즘은 학습의 각 단계에서 가중치를 감소(decay)시킨다.
• $L_1$ regularization 의 feature selection 과는 대조적으로, weight decay 는 함수의 복잡성을 지속적으로 조정할 수 있는 메커니즘을 제공한다.
• $\lambda$ 의 값이 작을수록 $\mathbf{w}$ 에 대한 제약이 적고, $\lambda$ 의 값이 클수록 $\mathbf{w}$ 에 대한 제약이 더 커진다.
• bias penalty $b^2$ 를 포함할지는 구현에 따라 다를 수 있고, 이는 신경망의 각 층에서도 달라질 수 있다. 하지만 일반적으로 bias term 은 정규화하지 않는다.
• $L_2$ regularization 이 다른 최적화 알고리즘에서 weight decay 와 동일하지 않더라도, weight 의 크기 축소를 통한 정규화 아이디어는 여전히 유효하다.

High-Dimensional Linear Regression

• 아래와 같은 식으로 데이터를 만들어보자.

  \[y = 0.05 + \sum^d_{i=1}0.01x_i + \epsilon \quad \text{where} \; \epsilon \sim \mathcal{N}(0, 0.01^2)\]
• label $y$ 는 평균이 0 이고 표준편차가 0.01 인 Gaussian noise 를 가지는 linear function 에 의해 만들어진다.
• weight decay 의 효과를 보기 위해서, over-fitting 을 만들기 위해 $d = 200$ 으로 high-dimensionality 를 만들어준다. 그리고 학습 시 20 개의 example 만 사용한다.

• 아래는 $\lambda$ 에 따른 train loss 와 validation loss 를 그래프로 나타낸 것이다.

  

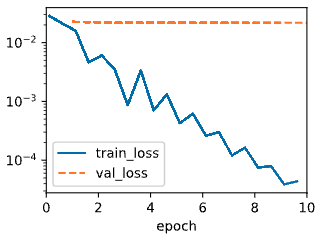
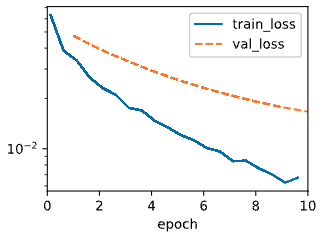
• 좌측 그림은 $\lambda = 0$ 으로 기존 loss function 을 사용한 것이고, 우측 그림은 $\lambda = 3$ 의 결과다.
• $\lambda = 0$ 일 때는 training error 가 감소하지만 validation error 는 그렇지 않다. over-fitting 이 일어난 것이다.
• $\lambda=3$ 일 때 training error 는 $\lambda = 0$ 일 때보다 증가(y축 단위 주목)하지만, validation error 는 감소하는 것을 확인할 수 있다. 즉 regularization 으로 over-fitting 을 완화하는 효과를 본 것이다.

Implementation

• weight decay 는 neural network 최적화(optimization)에 보편화되어 있기 때문에, 딥러닝 프레임워크는 weight decay 를 최적화 알고리즘에 포함해서 모든 loss function 과 쉽게 결합하여 사용할 수 있도록 한다.
• 따라서 추가적인 computational overhead 없이 알고리즘에 weight decay 를 추가하여 사용할 수 있다.
• weight 업데이트에서 weight decay 부분은 각 parameter 의 현재 값에만 의존하기 때문에, optimizer 는 각 parameter 를 한번씩 터치해야 한다.
• 기본적으로 PyTorch 는 weight 와 bias 를 동시에 감쇠하지만, 서로 다른 정책에 따라 서로 다른 parameter 를 처리하도록 optimizer 를 구성할 수 있다.
• 단순한 nonlinear function 의 경우 훨씬 더 복잡할 수 있다.
• Reproducing kernel Hilbert space(RKHS)의 개념을 사용하면 nonlinear context 에서 linear function 에서 사용하는 도구를 적용할 수 있다.
• 그러나 안타깝게도 RKHS 기반 알고리즘은 large and high-dimensional 데이터로 잘 확장되지 않는 경향이 있다.
• 따라서 이 책에서는 deep neural network 의 모든 layer 에 weight decay 를 적용하는 일반적인 휴리스틱을 채택할 것이다.

Summary

• Regularizatoin 은 over-fitting 을 처리하는 일반적인 방법이다.
• 고전적인 정규화 기법은 학습된 모델의 복잡도를 줄이기 위해서 학습 시 loss function 에 penalty term 을 추가한다.
• 모델을 단순하게 유지하기 위한 한 가지 선택은 $L_2$ penalty 를 loss function 에 더해주어 $L_2$ regularization 기법을 사용하는 것이다.
• 이는 mini-batch SGD 알고리즘의 업데이트 단계에서 weight decay 효과를 적용시킨다.
• 실제로 weight decay 기능은 딥러닝 프레임워크의 optimizer 에서 제공된다. parameter 의 서로 다른 세트마다 동일한 학습 loop 내에서 서로 다른 업데이트 동작을 가질 수 있다.

맨 위로 이동 ↑