[Deep Learning, d2l] Linear Neural Networks for Regression (2)

두 명의 대학생이 기말고사를 열심히 준비하고 있다고 가정해보자. 일반적으로 이전 해에 시행된 시험을 풀어보면서 연습하고 실력을 테스트하며 준비할 것이다. 그러나, 과거의 시험에서 잘 본다고 해서 반드시 실제 시험에서 잘 볼 것이라는 보장은 없다. 예를 들어, A 학생이 이전 해 시험 문제의 답을 암기하는 것만으로 준비했을 때, A 가 기억력이 좋아서 이전에 본 문제의 답을 완벽하게 기억할 수 있다 하더라도, 새로운(이전에 본 적 없는) 문제를 마주하면 얼어붙을 수 있다.

반면에, B 라는 또 다른 학생은 암기력이 좋지 않지만, 패턴을 잘 찾아내는 능력을 가지고 있다고 가정해보자. 만약 시험이 실제로 과거 문제를 재사용한 것이라면, A 가 B 보다 훨씬 더 잘할 것이다. B 가 찾아낸 패턴이 90% 정확성을 가지고 있다 해도, A 의 100% 기억력과는 비교할 수 없다. 그러나 시험이 전부 새로운 문제로 이루어졌다면, A 는 문제를 잘 풀지 못하지만 B 는 여전히 패턴 정확도 90% 의 평균을 유지할 수 있을 것이다.

위 예시가 머신러닝/딥러닝에서 이야기하는 Generalization 에 대한 예시다. 딥러닝의 목표는 데이터를 잘 설명할 수 있는 parameter $w$ 를 찾는 것이지만, 궁극적인 목표는 학습 과정에서 보지 못한 새로운 데이터에도 높은 성능을 보일 수 있는 Generalization, 즉 일반화 능력이다.

이러한 Generalization 에 대해서 다뤄보자.

Generalization

• 머신러닝의 목표는 패턴을 발견하는 것이다. 그러나 데이터만 단순히 외운 것이 아니라 general 한 패턴을 발견했는지 어떻게 확신할 수 있을까?
• 대부분의 경우, 우리의 모델이 general 한 패턴을 발견해야만 예측이 유용하다.
• 예를 들어 우리는 어제의 주식 가격을 예측하는 것이 아니라, 내일의 주식 가격을 예측해야 한다. 또한 이전에 진단된 환자의 이미 진단된 질병을 인식하는 것이 아니라, 보지 못한 환자의 새로운 질병을 진단할 수 있어야 한다.
• 이렇게 과거의 일어난 일로 모델이 학습에 사용하는 데이터가 아니라, 새로운 데이터를 대상으로 의미있는 예측을 만들어내야 한다. 이것이 가능하려면 모델은 general 한 패턴을 발견해야 한다.
• general 한 패턴을 어떻게 발견할 것인가 하는 문제는 머신러닝/딥러닝의 근본적인 문제이며, 통계학의 모든 문제라고 해도 과언이 아니다.
• 실제로 우리는 유한한 데이터를 사용하여 모델을 맞춰야 한다.
• 데이터의 규모는 domain 에 따라 매우 다양하다. 의료 문제의 경우 개인정보 문제 등에 의해 몇 천개의 데이터 포인트에 접근할 수 있을 것이다. 또한 희귀 질병을 연구할 때는 수백 개의 데이터에 접근할 수 있으면 다행이다.
• 그러나 ImageNet 과 같은 대규모 공공 데이터셋은 수백만 장의 이미지로 구성되어 있다. 오늘날 이러한 대규모 공공 데이터셋이 점점 더 선택지가 많아지는 상황이다.
• 하지만 이렇게 큰 규모의 데이터셋에서도, 이용 가능한 데이터 포인트의 수는 megapixel 해상도의 모든 가능한 이미지 공간에 비하면 극히 미미하다.
• 따라서 우리는 언제나 유한한 표본과 작업하므로, generalizable pattern 을 발견하는 것이 아니라 학습 데이터에 fit 한 모델을 만든다는 위험이 있다.
• 학습 데이터에 과하게 맞추는(fit), 즉 실제의 데이터 분포보다 학습 데이터의 분포에 더 가까이 맞추는 현상을 over-fitting(과적합)이라고 한다.
• 이러한 과적합을 방지하는 기술을 정규화(regularization) 기법이라고 한다.

Training Error and Generalization Error

• 일반적인 Supervised Learning 에서는 학습 데이터와 테스트 데이터가 동일한(identical) 분포에서 독립적(independently)으로 추출된다고 가정한다. 이를 i.i.d. 가정이라고 부른다.
• i.i.d. 가정은 매우 강력하고 제한적인 가정이지만, 이러한 가정 없이는 아무것도 할 수 없다.
• 왜 우리는 $P(X, Y)$ 분포에서 샘플링된 학습 데이터셋으로 다른 분포 $Q(X,Y)$ 에서 생성된 테스트 데이터에 대한 예측을 할 수 있다고 믿어야 할까?
• 이러한 도약을 가능하게 하려면 $P$ 와 $Q$ 가 어떻게 연관되어 있는지에 대한 강한 가정이 필요하다.
• 나중에 우리는 분포의 변화(shift)를 가능하게 하는 가정에 대해 논의할 것이지만, 우선은 $P(\cdot) = Q(\cdot)$ 인 i.i.d. case 를 이해해야 한다.
• 먼저, training error $R_{\text{emp}}$ 와 일반화 오류(generalization error) $R$ 을 구분해야 한다.
  • training error 는 empirical error 로, 학습 데이터셋에서 계산된 통계량이다.
  • 일반화 오류는 실제 분포에 대한 기대값(expectation)이다.
• 일반화 오류는 같은 실제 데이터 분포에서 추출된 수많은 추가 데이터 example 을 모델에 적용했을 때 나타날 결과로 생각할 수 있다.

• training error 는 아래와 같이 급수(sum) 형태로 나타낼 수 있다.

  \[R_{\text{emp}}[\mathbf{X, y}, f] = \frac{1}{n}\sum^n_{i=1}l(\mathbf{x}^{(i)}, y^{(i)}, f(\mathbf{x}^{(i)}))\]

• generalization error 는 아래와 같이 integral 형태로 나타낼 수 있다.

  \[R[p, f] = \mathbb{E}_{(\mathbf{x}, y) \sim P}[l(\mathbf{x}, y, f(\mathbf{x}))] = \int \int l(\mathbf{x}, y, f(\mathbf{x}))p(\mathbf{x}, y)d\mathbf{x}dy\]
• 우리는 generalization error $R$ 을 정확하게 계산할 수 없다. 그리고 density function 인 $p(\mathbf{x}, y)$ 의 정확한 형태 또한 절대 알 수 없다. 더욱이 우리는 실제의 전체 데이터를 사용할 수도 없다.
• 따라서 우리는 $\mathbf{X}^\prime$ 와 label $\mathbf{y}^\prime$ 으로 구성된 test set 을 우리 모델에 적용시킴으로써 generalization error 를 추정할 수 밖에 없다.
• 이는 우리가 empirical training error 를 구하는 방식와 같은 방식으로 적용되지만 test set $\mathbf{X}^\prime, \mathbf{y}^\prime$ 을 사용하는 것과 같다.
• 우리가 test set 에서 모델(classifier)을 평가할 때 test set 의 sample 에 따라 달라지지 않는 fixed classifier 로 작업한다. 실제로 training 과 inference 의 차이는 학습에서는 weight 를 업데이트 하지만 test 에서는 업데이트 하지 않는다.
• 따라서 generalization error 를 추정하는 것은 단순히 평균 추정의 문제다. 그러나 training set 에 대해서는 같은 말을 할 수 없다.
• 우리가 최종적으로 사용하게 되는 모델은 training set 의 선택에 명시적으로 의존한다. 따라서 training error 는 일반적으로 실제 모집단에 대한 실제 오류의 편향된 추정치(biased estimate)가 될 것이다.
• 그렇다면 Generalization 의 핵심 질문은 우리가 “언제 training error 가 모집단의 오류(generalization error)에 근접할 것으로 예상해야 하는지?” 가 된다.

Model Complexity

• 고전적인 이론으로는 단순한 모델과 충분한 데이터를 사용할 경우, training error 와 generalization error 는 서로 가깝게 나타나는 경향이 있다.
• 그러나 더 복잡한 모델을 사용하거나 데이터가 적을 때는 training error 가 감소하지만 generalization error 와의 간극이 커지는 경향이 있다. 이는 놀라운 일이 아니다.
• 표현력이 매우 풍부(복잡한)해서 어떤 데이터셋에 대해 임의의 label 을 완벽하게 맞출 수 있는 parameter set 을 가진 모델을 생각해보자.
• 이 경우, training 데이터에 대해서 완벽하게 맞췄다(fit)고 하더라도, generalization error 에 대해서는 어떤 결론을 내릴 수 있을까? 우리는 generalization error 가 무작위 추측(random guessing)보다 더 낫다고 말할 수 없다.
• 일반적으로, 모델에 대한 제약이 없는 상황에서 training 데이터를 맞췄다는 것만으로 그 모델이 일반화 가능한 패턴을 발견했다고 결론지을 수 없다.
• 반대로 모델이 임의의 레이블을 fitting 할 수 없다면, 패턴을 발견했을 가능성이 크다. 이게 무슨 말일까?
• 모델 복잡성에 대한 학습 이론적인 아이디어들은 반증 가능성의 기준을 공식화한 칼 포퍼의 사상에서 영감을 받았다.
  • 포퍼에 따르면, 모든 관측치를 설명할 수 있는 이론은 과학적인 이론이 아니다.
  • 결국, 특정 이론이 그 어떤 가능성도 배제하지 않았다면, 그 이론은 세상에 대해 아무것도 말해주지 못한 셈이다.
  • 따라서 우리가 원하는 것은 상상 가능한 모든 관측치를 설명할 수 없으면서도, 우리가 실제로 관측한 것과 호환되는 가설이다.
• 모델 복잡성의 적절한 개념이 무엇인지는 복잡한 문제다. 일반적으로 더 많은 parameter 를 가진 모델이 임의로 할당된 label 을 더 잘 맞출 수 있다. 그러나 이것이 항상 참은 아니다.
  • 예를 들어, Kernel Methods 는 무한한 수의 parameter 공간에서 작동하지만, Kernel Methods 의 복잡성은 parameter 가 아닌 다른 방식으로 제어된다.
• 복잡성을 측정할 때 유용한 개념 중 하나는 parameter 가 가질 수 있는 값의 범위다.
  • 여기서 parameter 가 임의의 값을 취할 수 있는 모델은 더 복잡하다고 볼 수 있다. 이에 관해서는 후에 regularization 방법 중 하나인 weight decay 부분에서 다시 다룰 것이다.
• 서로 크게 다른 모델 클래스(ex. Decision Tree 와 Neural Net)를 비교할 때 모델 복잡성을 비교하는 것은 어려울 수 있다.
• 여기서 딥러닝에 대해 본격적으로 다룰 때 다시 강조하게 될 중요한 점이 있다.
• 임의의 label 을 맞출 수 있는 모델의 경우, 낮은 training error 가 반드시 낮은 generalization error 를 의미하지는 않는다. 그러나 동시에 높은 generalization error 를 의미하지도 않는다.
• 우리가 확신할 수 있는 유일한 것은, 낮은 training error 만으로는 낮은 generalization error 를 보증할 수 없다는 것이다.
• 딥러닝 모델은 실제로 일반화가 어느정도 되지만, training error 만으로 일반화 성능에 대해 결론을 내리기에는 너무 강력한 모델들이다.
• 이러한 경우, 사후적으로 holdout 데이터를 사용하여 일반화 성능을 검증해야 한다. holdout data 는 바로 validation set 이며, 검증 데이터에서의 오류를 검증 오류(validation error)라고 한다.

Underfitting & Overfitting

• training error 와 validation error 를 비교할 때, 우리는 두 가지 상황을 염두한다.
• 먼저 training error 와 validation error 모두 크지만 둘 사이에 격차가 작은 경우다.
  • 만약 모델이 training error 를 줄일 수 없다면, 이는 우리 모델이 너무 간단하여 표현력이 불충분하고 우리가 모델링하고자 하는 패턴을 잘 포착하지 못한다는 것이다.
  • 또한 training error 와 generalization error 사이의 Generalization gap($R_{\text{emp}} - R$) 이 작은 상황이기 때문에 우리는 더 복잡한 모델을 통해 해결할 수 있다.
  • 이러한 현상을 under-fitting(과소적합) 이라고 한다.
• 또 다른 상황은 training error 가 validation error 보다 현저히 작은 경우다. 이는 over-fitting(과대적합) 을 시사한다.
  • over-fitting 은 항상 나쁜 것은 아니다. 딥러닝에서는 좋은 성능의 예측 모델이 validation data 보다 training data 에서 훨씬 잘 예측할 때가 많다.
  • 궁극적으로 우리는 generalization error 를 낮추는 것에 관심을 가져야 하고, 여기에 장애물이 될 때 두 격차에 관심을 가진다.
  • training error 가 0 이면 generalization gap 은 generalization error 와 정확하게 동일하며 이 격차를 줄여야서 진전을 이룰 수 있다.

Polynomial Curve Fitting

• over-fitting 과 모델 복잡성에 관한 직관을 위해서 다음을 고려해보자.
  • single feature $x$ 와 이에 대응하는 label $y$ 로 구성된 학습데이터가 있다.
  • 우리는 label $y$ 를 추정하는 $d$ 차 다항식을 아래와 같이 정의할 수 있다.
  \[\hat{y} = \sum^d_{i=0}x^iw_i\]
• 위 식은 linear regression 이므로 loss function 으로 squared loss 를 사용할 수 있다.
• 고차 다항식은 더 많은 parameter 를 가지고 있고 모델 함수의 선택 범위가 더 넓기 때문에 저차 다항식보다 더 복잡하다.
• 학습 데이터셋을 고정하면, 고차 다항식은 저차 다항식 보다 항상 더 낮은(최악의 경우 동일한) training error 를 얻어야 한다.
• 실제로 고유한 feature $x$ 값을 가진 각 데이터 예제가 있을 때, 데이터 예제의 수와 같은 차수의 다항식 함수는 training set 에 완벽하게 fit 할 수 있다.

• 아래 그림에서 우리는 다항식의 차수(모델 복잡도)와 under-fitting, over-fitting 간의 관계를 비교할 수 있다.

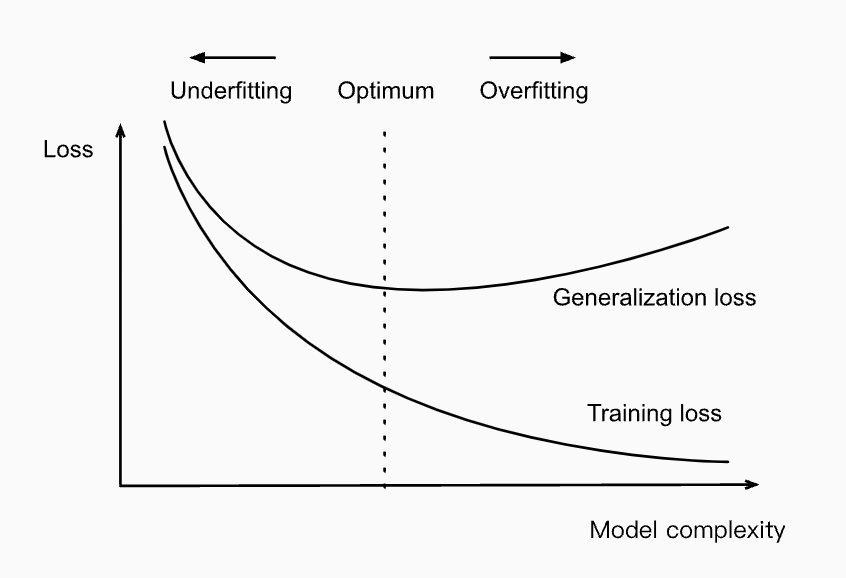  Influence of model complexity on under-fitting and over-fitting

Dataset Size

• 우리가 염두에 두어야 할 또 다른 큰 고려사항은 데이터셋의 크기다.
• 학습 데이터셋에 샘플이 적을수록 과적합이 발생할 가능성이 높아지고 더 심각해진다. 학습 데이터의 양이 증가할수록 generalization error 는 일반적으로 감소한다.
• 또한 일반적으로 더 많은 데이터는 결코 해롭지 않다. 즉 데이터가 많으면 언제나 좋다.
• 풀 문제와 데이터의 분포가 정해져 있을 때, 모델 복잡도가 데이터의 양보다 더 빠르게 증가해서는 안된다.
• 더 많은 데이터가 주어지면 우리는 더 복잡한 모델을 만들려고 할 수 있다. 그러나 충분한 데이터가 없으면 더 간단한 모델이 더 어려워질 수 있다.
• 많은 작업에서 딥러닝은 수천 개의 학습 데이터를 사용할 수 있을 때 linear model 을 능가한다.
• 따라서 현재 딥러닝의 성공은 인터넷 기업에서 발생하는 방대한 데이터셋의 풍부함, 저렴한 스토리지, 연결된 장치 등에서 기인한다.
• 즉 많은 데이터셋이 딥러닝의 성공을 이끌었다.

Model Selection

• 일반적으로, 우리는 서로 다른 방식(다양한 아키텍처, 학습 목표, 선택된 feature, 데이터 전처리, 학습률 등)으로 차이가 나는 여러 모델을 평가한 후에 최종 모델을 선택한다.
• 이렇게 여러 모델 중에서 선택하는 과정을 모델 선택(model selection)이라고 부른다.
• 원칙적으로, 우리는 모든 하이퍼파라미터를 선택한 후에 테스트셋을 사용해야 한다.
• 만약 모델 선택 과정에서 테스트 데이터를 사용하게 되면, 테스트 데이터에 과적합(over-fitting)할 위험이 있다. 이 경우 큰 문제가 발생할 수 있다.
• 학습 데이터에 과적합하게 되면, 테스트 데이터에서 평가함으로써 그 문제를 발견할 수 있다. 그러나 테스트 데이터에 과적합하게 되면, 그 사실을 어떻게 알 수 있을까?
• Ong et al.(2005) 의 연구는 복잡도를 엄격하게 제어할 수 있는 모델에서도 이 문제가 어떻게 터무니없는 결과를 초래할 수 있는지를 보여준 사례다.
• 따라서 모델 선택에 테스트 데이터를 절대 사용해서는 안된다.
• 그러나 모델 선택을 위해 학습 데이터에만 의존할 수 없다. 왜냐하면 학습에 사용한 데이터에서 generalization error 를 추정할 수 없기 때문이다.
• 실제 상황에서는 이 문제가 더 복잡해진다.
• 이상적으로는 테스트 데이터를 한 번만 사용하여 최고의 모델을 평가하거나 소수의 모델을 비교해야 한다.
• 그러나 실제로는 테스트 데이터가 한 번의 사용 후에 폐기되는 경우는 드물다. 매 실험마다 새로운 테스트셋을 구할 수 있는 경우가 거의 없기 때문이다.
  • 실제로 Image Classification 과 OCR 같은 알고리즘의 발전에 있어서 수십 년간 벤치마크 데이터를 재사용하는 것이 중요한 영향을 미쳤다.
• 테스트셋을 학습에 사용하는 문제를 해결하기 위한 일반적인 방법은 데이터를 세 가지로 나누는 것이다.
  • 학습 데이터와 테스트 데이터 외에 검증 데이터셋(validation set)을 추가로 사용하는 것이다.
• 그러나 이 결과로 검증 데이터와 테스트 데이터 간의 경계가 불분명해지는 애매한 상황이 발생하기도 한다.
• 특별한 언급이 없는 한, 이 책(d2l)의 실험에서 사용되는 데이터는 실제로는 학습 데이터와 검증 데이터일 뿐, 진정한 테스트셋은 아니다.
• 따라서 이 책의 각 실험에서 보고된 정확도는 실제 테스트셋의 정확도가 아니라 검증 정확도(validation accuracy)이다.

Cross-Validation

• 학습 데이터가 부족할 때는 충분한 데이터를 남겨 적절한 검증 데이터를 구성하는 것이 어려울 수 있다.

• 이 문제를 해결하기 위한 좋은 방법 중 하나는 k-fold cross-validation 을 사용하는 것이다.

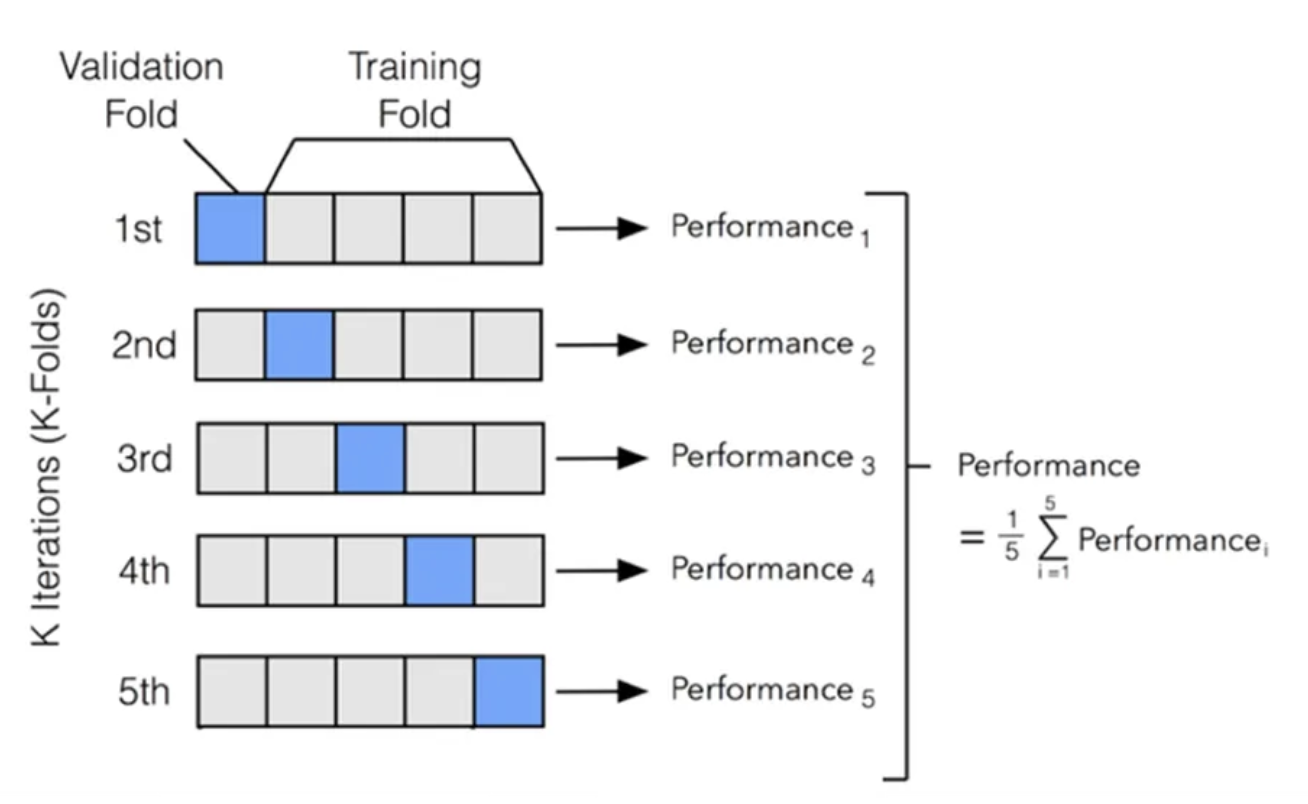  $k=5$ 일 때 k-fold cross-validation

  • 원래의 학습 데이터를 $k$ 개의 겹치지 않는 부분 집합으로 나눈다.
  • 그 후 모델 학습과 검증을 $k$ 번 실행하는데, 각 실행에서는 $k-1$ 개의 부분 집합을 사용해서 학습하고, 학습에 사용되지 않은 나머지 하나의 부분 집합을 사용해 검증한다.
  • 마지막으로, training error 와 validation error 는 $k$ 번의 실험 결과를 평균하여 추정한다.

Summary

• 여기서는 머신러닝/딥러닝에서 일반화의 기초를 알아보았다.
• 일반화에 대한 것은 더 깊은 모델로 나아갈수록 복잡하고 직관에 어긋나는 경우가 있다.
• 더 깊은 모델들은 데이터를 심각하게 over-fitting 할 수 있고, parameter 가 더 많은 더 큰 architecture 가 더 일반화가 잘되는 경우도 있다.
• 아래는 잘 알려진 경험 법칙이다.
  1. model selection 을 위해 validation set 을 꼭 사용하자. 또는 $K$-fold cross-validation 을 사용하자.
  2. 더 복잡한 모델은 더 많은 데이터를 필요로 한다.
  3. 모델 복잡도의 관련 개념에는 parameter 의 수와 parameter 가 가질 수 있는 값의 범위가 포함된다.
  4. 다른 조건이 동일할 때, 더 많은 데이터는 거의 항상 더 나은 Generalization 성능을 가져온다.
  5. Generalization 관련 논의는 모두 i.i.d. 가정에 기반한다. 이 가정을 완화하여 학습과 테스트 동안 분포가 변화할 수 있도록 허용한다면 또 다른 가정 없이는 일반화에 대해 아무것도 말할 수 없다.

맨 위로 이동 ↑