[Deep Learning, d2l] Linear Neural Networks for Regression (1)

머신러닝/딥러닝 task 중 가장 기본이 되는 Regression 은 numerical value 를 예측하고자 할 때 사용한다. 예를 들어 집 값을 예측하거나, 수요량/공급량을 예측하거나 할 때 사용한다. Linear Regression 은 이러한 Regression 문제를 푸는데 가장 간단하고 표준이 되는 도구다.

오늘날에는 매우 복잡한 architecture 를 가진 모델들이 수도 없이 개발되고 있다. 여기서는 앞으로 모델들에 대한 이해를 높이기 위해서 parameterizing, 데이터 처리, loss function, model training 등 기본에 집중해보자. 또한 얕은 Neural Network 는 linear 및 softmax regression 을 포함한 많은 고전적인 통계 예측 방법을 포함하는 linear model 집합으로 구성된다. 따라서 linear regression 과 같은 고전적 방법은 많은 맥락에서 널리 사용되며 더 멋진 architecture 의 사용을 정당화할 때 종종 기준선으로 사용해야 하기 때문에 이해하는 것이 매우 중요하다.

이러한 Linear Regression 을 Dive into Deep Learning 교재를 통해 자세히 알아보고, Neural Network 에서 Linear Regression 이 어떻게 수행될 수 있는지 보자. 여기서 등장하는 수학적 개념들은 AI Math 카테고리에서 더 자세히 다룬다.

선형 회귀(Linear Regression)

• 회귀 문제는 주어진 데이터 $x$ 에 해당하는 실제 값으로 주어지는 타겟 $y$ 를 예측하는 과제이다. 즉, 독립변수 $𝑥$ 에 대응하는 종속변수 $𝑦$ 와 가장 비슷한 값 예측값 $\hat{y}$ 을 출력하는 함수 $f^{\ast}(x)$ 를 찾는 과정이다.
• 이는 선형 회귀 모델을 통해서 내가 풀고자 하는 어떤 함수 $f(x)$ 를 근사하는 함수 $f^{\ast}(x)$ 를 찾는 것이다.

• Linear Regression 은 “예측하고자 하는 종속변수 $y$ 와 독립변수 $\mathbf{x}$ 간에 선형성을 만족한다는 가정” 을 따른다. 즉 조건부기대값 $\mathbb{E}[Y\vert X= \mathbf{x}]$ 가 $\mathbf{x}$ 의 가중합(weighted sum)으로 표현될 수 있다.

  \[\mathbb{E}[Y\vert X] = w_1x_1 + w_2x_2 + \cdots + w_nx_n + b\]
• $w_1, w_2, \ldots, w_n$ 은 독립변수 $x_1, x_2, \ldots, x_n$ 에 대응하는 가중치(회귀계수)이고, $b$ 는 절편(편향)이다.
  • 일반적으로 우리는 $n$ 개의 데이터셋을 사용하고, $\mathbf{x}^{(i)}_j$ 는 $i$ 번째 sample 의 $j$ 번째 값을 나타낸다.
• 주의할 점은 기대값이라고 해서 산술평균이 아니다. $\mathbf{x}$ 의 값 $x_i$ 를 가지고 가장 대표성이 있는 하나의 값이 되어야하므로 일반적으로 조건부확률분포의 기대값인 조건부기대값을 Regression 문제의 답으로 하는 경우가 많다.
• 따라서 $X$ 가 주어졌을 때 $Y$ 의 기대값이 선형결합을 통해 나온다는 것이다. 그러나 이러한 가정은 observation noise 때문에 예측값이 정확하게 실제값이 되지 않는다.
• 그러한 이유로 두번째 가정은, “noise 가 Gaussian 분포를 따라 잘 작용한다는 가정” 을 부과한다. 뒤에서 자세히 알아보자.

Model

• 모델은 feature 가 어떻게 target 추정값으로 변환될 수 있는지를 정의한다. 집 값 예측을 예로 들어보자. 이 때 feature 는 area(지역) 와 age(건축년수) 다.

• 위에서 본 선형가정 은 target(price) 의 기대값이 feature(area, age) 의 가중합으로 표현될 수 있다는 것이었다. 따라서 아래와 같이 모델이 정의될 수 있다.

  \[\text{price} = w_{\text{area}} \cdot \text{area} + w_{\text{age}} \cdot \text{age} + b\]
• $w$ 는 weight(가중치) 이고 $b$ 는 bias(or offset or intercept) 다.
• weight 는 각 feature 가 우리의 예측값에 미치는 영향의 정도를 나타낸다. bias 는 모든 feature 가 0 일 때 추정값이 된다. 이러한 bias 가 필요한 이유는 feature 로 이루어진 선형함수를 표현하기 위해서다.
• 위 집 값 예측 모델은 input feature 에 대한 affine transformation 이라고 볼 수 있다. 엄밀히 말하면 feature 를 weighted sum(가중합) 을 통해 선형변환하고, bias 를 더해줌으로써 translation 이 결합된 형태의 affine transformation 이다.
• 이 모델의 목표는 평균적으로 예측값이 데이터셋의 실제값과 최대한 가깝도록 $\mathbf{w}$ 와 $b$ 를 선택하는 것이다.
• 머신러닝/딥러닝에서는 high-dimensional 데이터셋을 사용하고 linear algebra notation 을 쓰는 것이 효율적이고 일반적이다. 고차원에 정의된 벡터와 행렬 그리고 그 연산 등을 다루는 것이기 때문이다.

• 우리의 input 이 $d$ 차원의 feature 로 구성되어 있고, 실제값을 $y$, 예측값을 $\hat{y}$ 라고 할 때 아래처럼 나타낼 수 있다.

  \[\hat{y} = f(x) \approx y \\ \hat{y} = w_1x_1+w_2x_2+\cdots+w_dx_d+b=w^Tx+b$\]

• 그리고 input feature 와 그에 대응한 weight 들은 vector 로 나타낼 수 있다.

  \[\hat{y} = \mathbf{w}^T\mathbf{x} + b, \quad \mathbf{x}, \mathbf{w} \in \mathbb{R}^d\]
• 위 식에서 vector $\mathbf{x}$ 는 데이터 셈플 하나의 feature vector 다. 우리는 전체 $n$ 개의 데이터로 이루어진 데이터셋의 feature 를 matrix 로 표현한다. 즉 이 matrix 는 row 에 모든 데이터 샘플을 포함하고 각 column 이 feature 를 나타내게 된다.

• 그러면 모든 데이터의 feature 를 matrix 로 나타내고, 예측값 또한 데이터 샘플마다 나오게 되므로 아래와 같이 matrix-vector 의 곱으로 나타낼 수 있다. 합하는 과정에서는 broadcasting 이 일어난다.

  \[\hat{\mathbf{y}} = \mathbf{Xw} + b, \quad \mathbf{X} \in \mathbb{R}^{n \times d}, \; \mathbf{w} \in \mathbb{R}^d, \; \hat{\mathbf{y}} \in \mathbb{R}^n\]
• 위 식이 일반적인 선형 모델이 된다. 가중치 벡터 $\mathbf{w}=(w_1,\cdots,w_d)$ 와 편향(bias) $b$ 는 함수 $f(x)$ 의 계수(coefficient)이자 이 선형회귀모형의 모수(parameter)다.
• linear regression 의 목표는 $\mathbf{X}$ 와 같은 분포에서 sampled 된 새로운 데이터를 넣었을 때 가장 적은 error 를 가진 예측값을 출력하는 parameter 를 찾는 것이다.
• 그러나 아무리 모델의 성능이 뛰어나도 real-world 에서 예측값과 실제값이 절대 동일할 수 없다. 반드시 작은 양이라도 error 가 포함될 수밖에 없다.
• 이러한 이유로 우리가 선형모델을 정의할 때, 위와 같이 우리가 해결할 수 없는 error 를 표현하는 noise term 을 포함해야 한다.
• parameter $\mathbf{w}, b$ 를 찾기 위해서 두 가지를 더 알아야 한다.
  • 1) 현재 모델의 성능, 품질을 측정하는 방법 $\rightarrow$ Loss function
  • 2) 성능, 품질을 향상시킬 수 있는 방법, 즉 학습 $\rightarrow$ 최적화 알고리즘
• 결국 우리가 하고자 하는 것은 모델의 예측과 실제값 사이의 차이를 최소화하는 모델 parameter $\mathbf{w}, b$ 를 찾는 것 이다. 이를 통해 풀고자 하는 어떤 함수 $f(x)$ 를 근사하는 함수 $f^{\ast}(x)$ 를 찾을 수 있다.

Loss function(Mean Squared Error)

• 모델 학습을 위해서 모델의 예측과 실제 사이의 오차(거리)를 측정해야 한다. 오차는 0 또는 양수값이고 값이 작을수록 오차가 적음을 의미한다.
• Linear Regression 에서 가장 일반적인 Loss function 은 squared error 다.

• $i$ 번째 샘플에 대한 loss($l$) 계산은 $l^{(i)}(\mathbf{w}, b)=\frac{1}{2}(\hat{y}^{(i)}-y^{(i)})^2$ 로 나타낼 수 있다.

  Fitting a linear regression model to one-dimensional data
  출처: Dive into Deep Learning

• 수식에 곱해진 1/2 상수값은 2차원인 loss(squared error)를 미분했을 때 값이 1 이 되도록 만들어서 수식을 조금 더 간단하게 만들기 위해 사용된 값이다. 상수를 나누는 것은 모델의 성능에 영향이 거의 없다.
• 데이터셋은 이미 구했거나 주어져있기 때문에, empirical error 인 loss 값은 모델 paramter 인 $\mathbf{w}, b$ 에만 의존한다. 즉 내가 구한 데이터가 전체 데이터를 충분히 대표한다고 했을 때, 모델 parameter 가 이 데이터들을 잘 fit 할 수 있는 함수가 되도록 만들어야 한다.
• 위와 같은 squared loss 는 제곱 형식이기 때문에, 큰 loss 를 더 크게 반영하여 학습에 도움이 되지만 이는 이상치에 큰 영향을 받을 수 있다는 것을 의미한다. (d2l 에서는 양날의 검이라 표현한다.)

• 전체 데이터셋에 대해서 모델의 품질을 측정하기 위해서, 학습 데이터셋 $n$ 개에 대한 loss 의 평균값을 사용할 수 있다. 이는 Mean Squared Error 즉 MSE 이다.

  \[L(\mathbf{w}, b) = \frac{1}{n}\displaystyle\sum_{i=1}^nl^{(i)}(\mathbf{w},b) = \frac{1}{n}\displaystyle\sum_{i=1}^n\frac{1}{2}(\mathbf{w}^T\mathbf{x}^{(i)}+b-y^{(i)})^2\]

• 이 MSE 를 최소화하는 모델 parameter $\mathbf{w}^\ast$ 와 $b^\ast$ 를 찾는 것이 바로 모델을 학습시키는 과정이다.

  \[\mathbf{w}^\ast, b^\ast = \underset{\mathbf{w}, b}{\mathrm{argmin}} \; L(\mathbf{w}, b)\]

최적화 알고리즘(학습)

• 앞서 정의한 Linear Regression 모델과 loss 함수의 경우, loss 를 최소화하는 방법은 역행렬을 사용해서 수식으로 표현할 수 있다.
  • 먼저 bias $b$ 또한 우리가 구해야 하는 값이기 때문에, input matrix 에 1 로 구성된 column 을 하나 추가하고 $b = w_0$ 와 같이 생각하면 $\mathbf{w}$ 안에 포함시킬 수 있다.

  • 그러면 우리는 아래의 loss 식을 최소화하는 문제를 다루면 된다.

    \[\Vert \mathbf{y} - \mathbf{Xw} \Vert ^2\]
  • $\mathbf{X}$ 는 feature 들이 서로 선형독립인 full rank matrix 이므로 역행렬이 존재하는 가역(invertible)행렬이다. 따라서 loss surface 에 하나의 critical point(극점)이 존재하고 이는 loss 의 minimum 이 된다.
  • 이 때 $\mathbf{X}$ 는 주어진 데이터로서 바뀔 것이 없고 $\mathbf{y}$ 는 모델 입장에서 모르는 값이다. 따라서 위 식을 최소화하는 $\mathbf{w}$ 를 어떻게 잘 찾을 것이냐로 귀결된다.

  • 이 minimum 을 찾기 위해 $\Vert \mathbf{y} - \mathbf{Xw} \Vert^2$ 를 $\mathbf{w}$ 에 대하여 미분하여 0 이 되는 지점을 찾으면 된다. 따라서 아래처럼 식을 전개한다. $\theta$ 는 $\mathbf{w}$ 를 뜻한다.

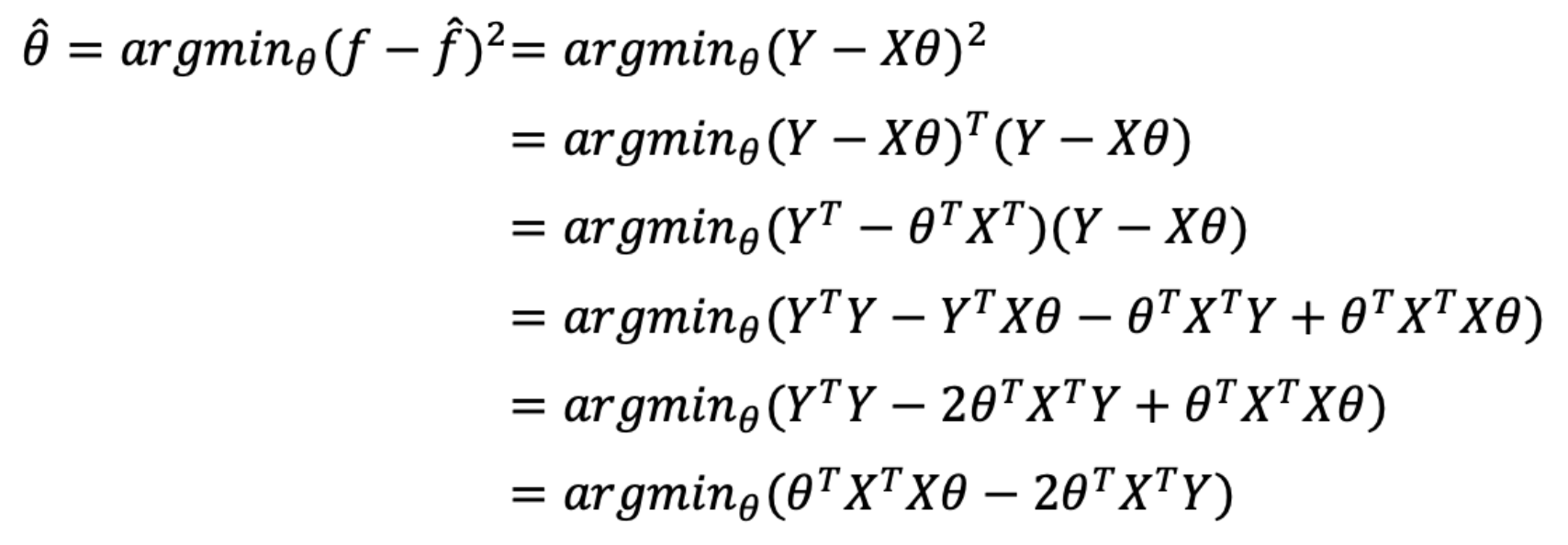    먼저 loss 를 풀어준다.

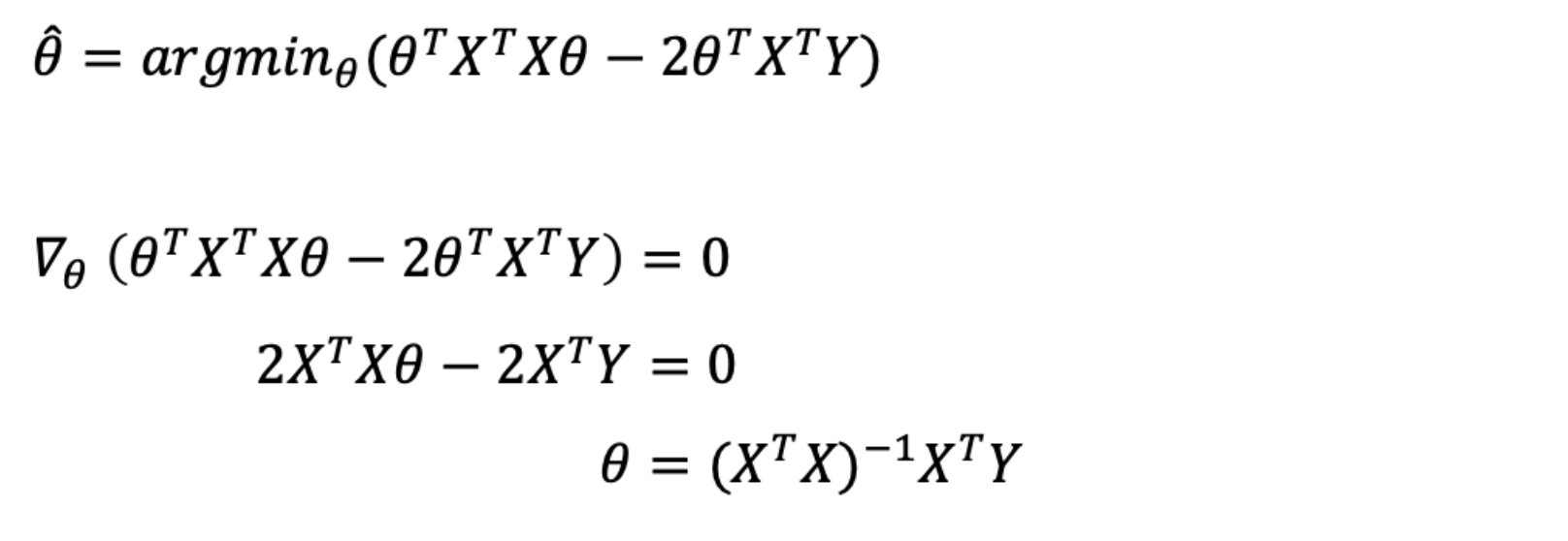    $\theta(\mathbf{w})$ 로 미분하여 0 이 되는 점을 찾는다.

  • 따라서 아래의 식이 우리가 찾는 optimal solution 이 된다.

    \[\mathbf{w}^\ast = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}\]
  • 주의할 점은 이 solution 은 $\mathbf{X^TX}$ 가 역행렬이 존재(invertible)해야 한다. 즉 matrix 의 column(features) 가 서로 선형독립이어야 한다.
• 이처럼 역행렬을 이용한 위 solution 제약적이기 때문에 딥러닝에서 사용하기 어렵다. 왜냐하면 복잡한 현실세계의 함수는 대부분 비선형이기 때문에 역행렬을 이용한 최적화는 한계가 있기 때문이다.
• 즉 위 optimization solution 은 Multi Layer Perceptron 이나 비선형 layer 가 있으면 적용할 수 없는 한계가 있다. 따라서 대부분의 딥러닝 모델은 이러한 역행렬을 이용한 분석적 방법을 적용할 수 없다.

Mini-batch SGD

• 다행히 딥러닝에서는 모델의 parameter 를 어떤 최적화 알고리즘을 사용해서 점진적으로 업데이트하여 loss 를 줄여나갈 수 있다. 그 알고리즘이 바로 gradient descent(GD, 경사하강법)이다.
• GD 는 거의 모든 딥러닝 모델의 핵심 technique 으로, 학습 과정동안 loss 값이 낮아지는 방향으로 점진적으로 parameter 를 업데이트하여 error 를 줄인다.
• 이러한 GD 는 매 학습 iteration 마다 전체 데이터셋에 대해 loss func 을 계산하고 loss func 을 $\mathbf{w}$로 편미분한 값을 활용한다.
• 그러나 이렇게 parameter 를 업데이트하는 것은 매우 느리다. 이렇게 한 번의 업데이트를 위해 전체 데이터를 가지고 계산하는 것은 정확한 값을 구할 수는 있지만 학습 속도가 매우 느리다.
• 또한 이론적으로 gradient descent 는 미분 가능하고 볼록(convex)한 함수에 대해서 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어 있다.

• 그러나 딥러닝과 같은 비선형회귀의 문제인 경우 많은 경우에 목적식(loss func)이 볼록하지 않을 수 있으므로 수렴이 항상 보장되지는 않는다.

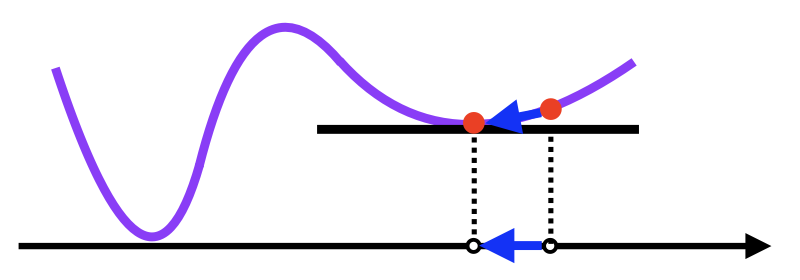  non-convex 목적식

• 이를 해결하기 위해 SGD(Stochastic Gradient Descent) 를 활용한다.
  • SGD 는 한번의 iteration 에 single example 을 이용하여 가중치를 업데이트한다.(one observation one update step)
  • 볼록이 아닌(non-convex) 목적식은 SGD 를 통해 최적화할 수 있다. 만능은 아니지만 딥러닝의 경우 SGD 가 일반적인 GD 보다 실증적으로 더 낫다고 검증되었다.
• 그러나 SGD 에도 단점이 있다.
  • 1) 컴퓨터의 프로세서는 main memory 에서 processor cache 로 데이터를 옮기는 것보다 계산하는 것이 훨씬 빠르다. 또한 matrix-vector 곱이 vector-vector 연산보다 더 효율적이다. 이는 프로세스 측면에서 sample 을 하나씩 처리하는 것이 모든 sample(full-batch) 을 한번에 처리하는 것보다 느릴 수도 있다는 것을 의미한다.
  • 2) 자주 사용되는 Batch Normalization 과 같은 layer 는 한 개 이상의 sample 이 있어야 잘 동작한다.
  • 3) 데이터 한 개씩만 계산하기 때문에 gradient 의 추정값이 너무 noise 해진다.
• 이러한 이유들을 종합하여, full-batch 와 one single sample 을 이용하는 것이 아닌 mini-batch 를 사용한다.
• 이 때 mini-batch 의 size 는 dataset 의 크기, memory, workers 등에 따라 다르게 설정할 수 있는 하이퍼 파라미터다.
• 일반적으로 32 에서 256 사이의 2의 제곱수로 시작하는 것이 좋다고 알려져 있다.

• 이를 minibatch stochastic gradient descent 라고 한다. 딥러닝에서 일반적으로 쓰이는 방식이다.

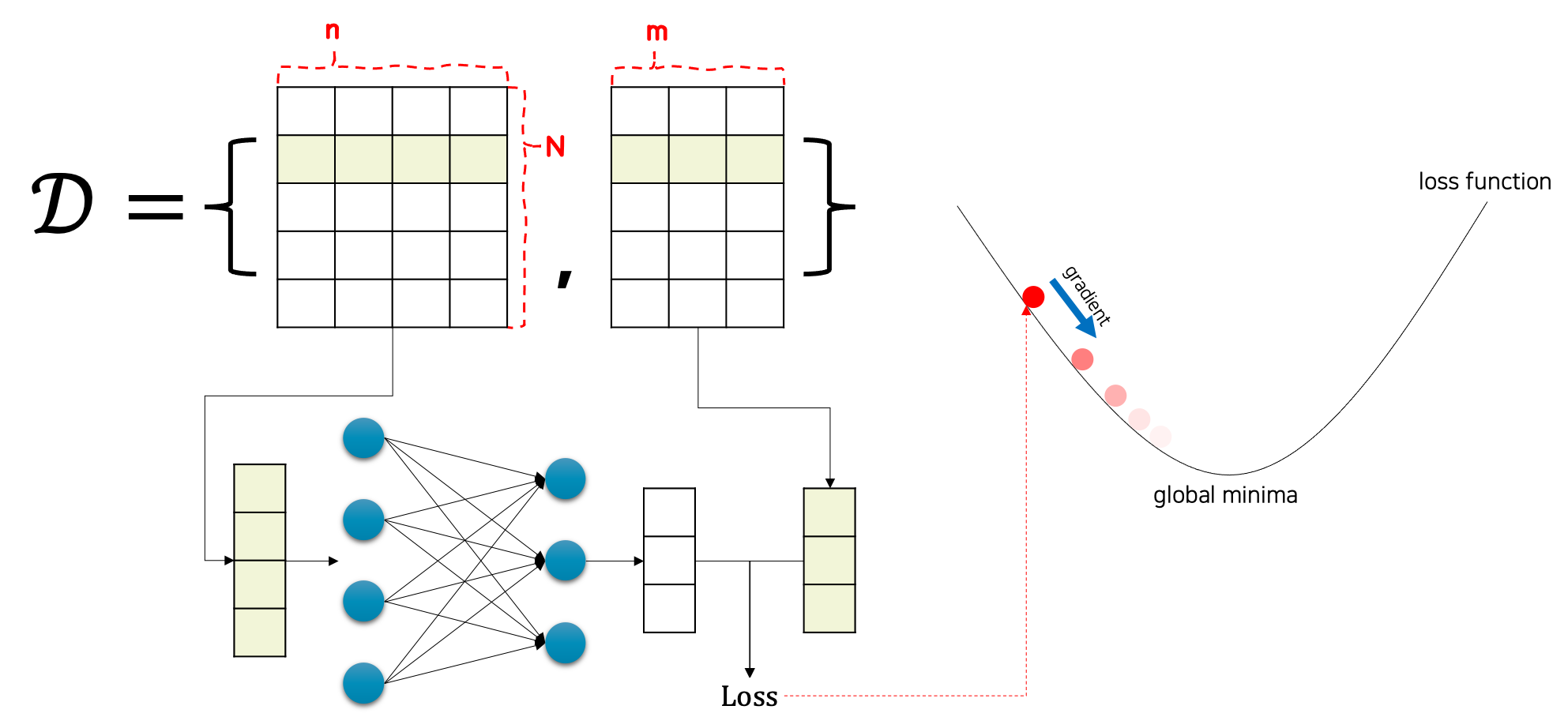  출처: https://kh-kim.github.io
  위 그림에서는 mini-batch 가 아닌 one sample 이지만,
  32 에서 256 사이의 2의 제곱수 만큼의 sample 을 이용하여 위와 같은 방식으로 모델이 학습된다.

• 각 iteration $t$ 마다 random(stochastic) 하게 선택된 mini-batch sample 을 가지고 모델 parameter 에 대한 loss 의 평균을 미분하여 gradient 를 구한다. 이러한 gradient 를 학습률(learning rate)과 곱하고 현재의 parameter 에 빼주게 된다.

• 이를 식으로 나타내면 다음과 같다.

  \[(\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{\vert\mathcal{B}\vert}\sum_{i \in \mathcal{B}_t}\partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b)\]
• 즉 mini-batch SGD 를 사용하여 아래의 과정으로 학습이 진행된다.
  1. (일반적으로)난수를 이용해서 모델 parameter 를 초기화한다.
  2. 학습 데이터에서 batch size($\mathcal{B}$) 만큼의 sample 들을 균일한 방식으로 뽑아서 mini-batch 를 구성한다. mini-batch 를 구성하는 sample 은 다양한 방식을 사용할 수 있다. 클래스 간 균형을 위해 Startified Sampling 등을 사용할 수 있다.
  3. mini-batch 의 데이터를 모델에 통과(feed-forward)시키고 나온 출력 $\mathbf{Xw}$ 과 실제값 $\mathbf{y}$ 을 비교한 뒤 평균 loss 값을 얻는다. 이를 모델 parameter($\mathbf{w}$)로 편미분한다.
  4. 3 의 결과와 미리 정의된 학습률(learning rate = step size, $\eta>0$)을 곱해서 loss 값이 최소화되는 방향으로 parameter 를 update 한다.
  \[\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{\vert\mathcal{B}\vert}\sum_{i \in \mathcal{B}_t}\partial_{\mathbf{w}} l^{(i)}(\mathbf{w},b) \quad &&= \mathbf{w} - \frac{\eta}{\vert \mathcal{B} \vert}\sum_{i \in \mathcal{B}_t}\mathbf{x}^{(i)}\left(\mathbf{w}^T\mathbf{x}^{(i)} + b - y^{(i)}\right) \\ b &\leftarrow b - \frac{\eta}{\vert\mathcal{B}\vert}\sum_{i \in \mathcal{B}_t}\partial_{b} l^{(i)}(\mathbf{w},b) \quad &&= b - \frac{\eta}{\vert \mathcal{B} \vert}\sum_{i \in \mathcal{B}_t}\left(\mathbf{w}^T\mathbf{x}^{(i)} + b - y^{(i)}\right) \end{aligned}\]
• 여기서 batch size($\mathcal{B}$)와 learnig rate($\eta$)는 모델 학습을 통해서 찾아지는 값이 아니라 우리가 직접 선택 해야하는 하이퍼파라미터(hyper parameters) 이다.
  • 이러한 하이퍼파라미터는 Bayesian Optimization 이나 Grid Search 와 같은 technique 으로 적절한 값을 찾을 수도 있다.
• mini-batch 는 batch size 에 따라 확률적으로 선택하므로 매 iteration 마다 목적식 모양이 바뀌게 된다. 즉 매번 다른 mini-batch 를 사용하기 때문에 곡선 모양이 바뀌는 것이다.

• 따라서 SGD 는 non-convex 한 목적식에서도 사용 가능해져 학습에 더 효율적이게 된다. 매번 다른 곡선으로 gradient 를 계산하기 때문에 이전 iter 에서 gradient 값이 0 이 더라도 다음 iter 에서 값이 생겨 update 가 가능하다.

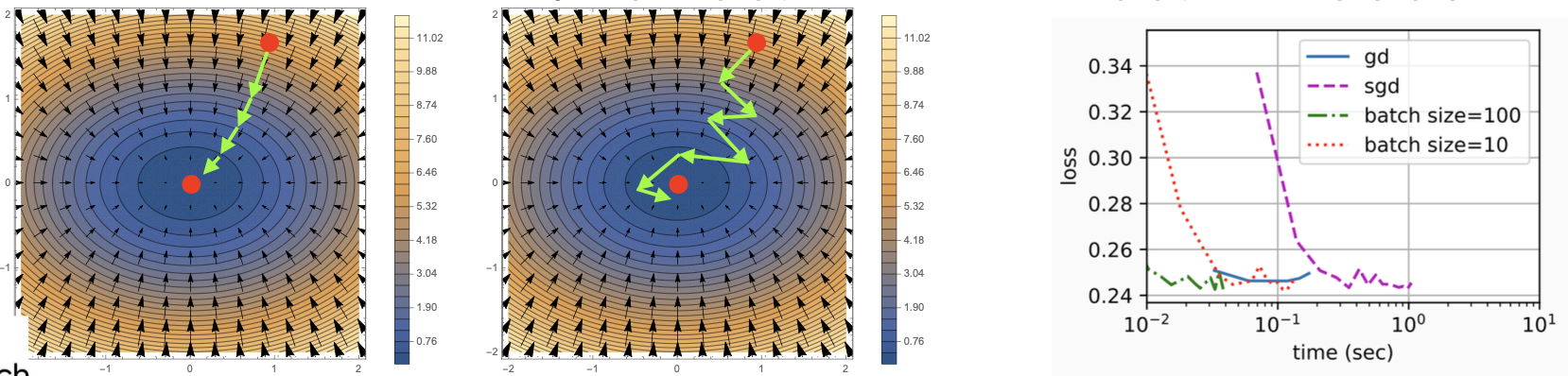  좌: 경사하강법(GD), 가운데: 확률적 경사하강법(SGD), 우: GD vs. SGD vs. mini-batch SGD

• 모델 학습이 끝나면 모델 parameter $(\mathbf{w}, b)$ 에 대해 추정된 값인 $\hat{\mathbf{w}}$ 와 $\hat{b}$ 을 저장한다.
• 그러나 이 추정된 값들이 loss 함수를 최소화 시키는 최적의 값(minimizer) $\mathbf{w}^{\ast}, b^{\ast}$ 이 정확하게 될 수 없다.
• 이 알고리즘이 minimizer 를 향해 천천히 수렴한다고 하더라도 우리는 유한한 횟수의 학습을 진행하고, mini-batch 가 매 순간 random 하게 선택되기 때문이다.
• 우리가 위에서 역행렬을 통해 optimal solution 을 찾을 때는 global minimum 이 있다고 했지만, 딥러닝에서의 loss surface 는 매우 많은 saddle points(안장점) 와 local minima 들을 포함한다.
• 그러나 우리는 정확한 parameter 추정값을 찾기보다 낮은 loss 값과 정확한 예측값을 찾으면 된다. 실제로 많은 딥러닝 적용과정은 학습 데이터셋에 대한 loss 를 최소화시키는 parameter 를 찾는다.
  • local minima 문제는 실생활과 같은 고차원의 공간에서는 발생하기 힘든 매우 희귀한 경우다. 즉 고차원의 공간에서 모든 축의 방향으로 오목한 형태가 형성될 확률은 거의 0 에 가깝다.
  • 실제 딥러닝 모델에는 weight 가 수도 없이 많으며 그 수많은 weight 가 모두 local minima 에 빠져야 weight update 가 정지되기 때문에 크게 문제되지 않는다.
  • 고차원의 공간에서 대부분의 극점(critical point)은 local minima 가 아니라 saddle point 다.
  • 설령 고차원의 공간에서 local minima 가 있다고 하더라도 이는 global minima 거나 global minima 와 거의 유사한 수준의 loss 값을 가진다.
  • 따라서 우리는 학습을 통해서 이 최적의 값(global minima)에 근접하는 값(local minima)을 찾는 것으로 충분하다.
• 이보다 더 중요한 문제는 바로 학습 과정에서 보지 못한 새로운 데이터에 대해서도 올바른 예측값을 낼 수 있는 일반화(generalization) 능력이다. 이는 다음 포스트에서 살펴보자.

Inference

• 학습이 완료된 모델($\hat{\mathbf{w}}^T\mathbf{x} + \hat{b}$)이 주어지면 우리는 새로운 example 에 대해 새로운 예측값을 만들어낼 수 있다.
• 이를 “모델 예측(prediction)” 또는 “모델 추론(inference)” 이라고 하고, validation 혹은 test 단계에서 진행한다.

Vectorization

• 딥러닝 연산을 할 때 보통 numpy 를 활용한 연산을 진행한다.
• 일반적으로 사용되는 딥러닝 프레임워크인 torch 나 tensorflow 역시 numpy 를 base 로 만들어져 있다.

• numpy 는 일반 python 의 for 문 보다 훨씬 빠른데, 그 이유는 numpy 는 각 element 에 대해 for 문을 수행하는 것이 아니라 전체 array 에 대해 vectorization 연산을 수행하기 때문이다. 따라서 torch 의 연산도 빠르다.

  n = 10000
  a = torch.ones(n)
  b = torch.ones(n)
  c = torch.zeros(n)
  t = time.time()
  for i in range(n):
      c[i] = a[i] + b[i]
  print(f'for loop: {time.time() - t:.5f} sec')
  t = time.time()
  d = a + b
  print(f'vectorization {time.time() - t:.5f} sec')
  

  'for loop: 0.17802 sec'
  'vectorization 0.00036 sec'
  

• vectorization 은 하드웨어 상의 SIMD (Single Instruction Multiple Data) 동작과 관련이 있다.
• 최신 64비트 프로세서들은 정수에 대해 수치 연산을 수행하는 64 bit register 16 개를 포함하고 있다. 이러한 register 들은 한번에 하나의 값만 가질 수 있기 때문에 scalar register 라고도 불린다.
• 이러한 칩들은 256 bit register 16 개를 추가적으로 포함하도록 발전했다. register 용량이 커져 64 비트값 4개, 32 비트값 8개 등을 동시에 저장할 수 있으니 vector register 라 불린다.
• 따라서 register 에 올라가 있는 여러 값들을 한번에 수치 연산할 수 있는 instruction 이 가능해지게 된 것이다. 즉, single instruction 에 multiple data 를 처리할 수 있게 된 것이다.
• 결과적으로 vectorization 은 scalar register 대신 vector register 를 이용하여 수치 연산을 더 빠르게 하는 과정을 의미한다.
• scipy 나 numpy 등이 vectorization 을 활용하는 대표적인 라이브러리이고, numpy 의 built-in 함수를 쓰는 것이 vectorization 관련해서 최적화가 되어 있으니 훨씬 빠르다.
• 따라서 이를 이용하여 mini-batch 학습이 빠르게 진행될 수 있는 것이다.

정규분포(Normal Dist)와 Squared Loss

• 우리는 위에서 선형 회귀의 일반적인 목적식인 squared error loss 를 사용했다.
  • 이 때 최적의 parameter 를 가진 선형모델은 조건부기대값 $\mathbb{E}[Y \vert X]$ 을 반환한다.
  • 이는 수학적으로 증명되어 있고 이 블로그에서 증명을 확인할 수 있다.
  • squared error loss 는 outlier 에 대해 더 큰 패널티를 부과한다.
• 이러한 squared error loss 를 noise 의 분포에 대해 확률적인 가정을 줌으로써 다르게 바라볼 수 있다.
• 확률분포는 데이터공간의 초상화로서, 데이터를 바라보고 해석하는데 굉장히 중요한 도구이다.

• 이 중 조건부확률 $P(y \vert \mathbf{x})$ 는 입력변수 $\mathbf{x}$ 에 대해 정답이 $y$ 일 확률을 의미한다. 단, 선형회귀와 같은 연속확률분포에서는 확률이 아니라 밀도로 해석한다.

  💡 딥러닝은 확률론 기반의 머신러닝 이론에 기반을 두고 있다. 위에서 본 loss func 의 작동원리는 데이터 공간을 통계적으로 해석해서 유도하게 된다. 이렇게 유도된 loss func 을 가지고 학습을 통해서 예측이 틀릴 위험(risk)을 최소화하도록, 즉 데이터에서 관찰되는 분포와 모델 예측의 분포의 차이를 최소화하는 방향으로 유도한다. AI Math 포스트에서 자세히 다루겠지만, loss 를 최소화하기 위해서는 측정하는 방법을 알아야 하고, 이 측정하는 방법을 통계학에서 제공하기 때문에 머신러닝, 딥러닝을 이해하려면 확률론의 기본 개념을 알아야 한다.
  
  머신러닝/딥러닝은 최적의 parameter 를 찾는 것이 목표인데, 이 parameter 를 보는 관점은 크게 두 가지가 존재한다.
  1) Frequentist View : Model 의 parameter 들을 Fixed Value 로 취급하여 데이터로부터 그 값을 구한다.
  2) Bayesian View : Model 의 parameter 들을 각각 하나의 Random Variable 로 취급하여 그 parameter 의 Distribution 을 구한다.
  
  우리가 Classification, Object Detection, Segmentation 등 일반적인 딥러닝을 사용할 때는 Frequentist View 로 본다. 그러나 Bayesian View 도 “불확실성” 을 알 수 있다는 점에서 자율주행 등에서 유용하게 사용되고 있다.

• 기대값은 데이터를 대표하는 통계량으로 사용할 수 있으면서, 모델링하고자 하는 확률분포에서 계산하고 싶은 다른 통계적 범함수를 사용하는데 이용되는 도구다.
  • 평균과 동일한 개념으로 사용할 수 있지만 머신러닝, 딥러닝에서는 더 폭넓게 사용된다.
  • 목적으로 하는 함수가 있을 때 그 함수의 기대값을 계산하는 것을 통해서 데이터를 해석할 때 여러 방면에서 사용할 수 있다.
• 딥러닝을 포함한 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표다. 그러나 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하므로, 근사적으로 확률분포를 추정할 수 밖에 없다.
  • 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적(parametric) 방법론이라 한다.
  • 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론이라 부른다. SVM, Decision Tree, KNN 등 머신러닝의 많은 방법론은 비모수 방법론에 속한다.
• 딥러닝에서도 MLP 를 사용하여 데이터로부터 특징 패턴 $\phi(\mathbf{x})$ 를 추출하고 가중치행렬 $\mathbf{W}$ 를 통해 조건부확률을 계산하거나 혹은 조건부기대값을 추정하는 식으로 학습을 하게 된다.
• 다시 돌아와서, 정규분포(Gaussian)와 Squared loss 를 활용하는 Linear Regression 은 관련이 깊다.

• 먼저, squared loss 는 간단한 편미분이라는 특징으로 gradient 가 예측값과 실제값의 차이로 계산된다.

  \[\text{squared loss}\; : \; l(y,\hat{y})=\frac{1}{2}(y-\hat{y})^2 \; \rightarrow \; \partial_{\hat{y}}\;l(y,\hat{y})=(\hat{y}-y)\]

• 다음으로, 평균이 $\mu$, 분산이 $\sigma^2$ 일 때 정규분포는 다음과 같이 나타낸다.

  \[p(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (x - \mu)^2\right)\]

  

• 평균을 변경하면 $x$ 축을 따라 이동하는 것과 일치하고, 분산을 늘리면 분포가 확산되어 peak(높낮이)가 낮아진다.
• Squared Error(Squared Loss) 를 적용한 선형 회귀모델에서 중요한 가정은 관측값(데이터)을 얻는 것은 noise 가 있기 마련이고, 그 noise $\epsilon$ 는 정규분포 $\mathcal{N}(0, \sigma^2)$ 를 따른다는 것이다.
  • 이는 전통적인 머신러닝의 선형회귀모델의 가정 중 하나다. 이 블로그에 잘 정리되어 있다.

  • 데이터에 noise 가 있음을 모델에 반영한다.

    \[y = \mathbf{w}^\top \mathbf{x} + b + \epsilon \; \text{where} \; \epsilon \sim \mathcal{N}(0, \sigma^2)\]
  • 이러한 noise 는 우연 오차(random error)로, 존재할 수 밖에 없는 오차이며 사람이 조정할 수 없는 오류다.
• 또한 오차의 분산이 $\mathbf{x}$ 에 관계없이 일정하다. 등분산성(homoscedasticity) 가정이다.
• 이러한 가정들을 종합하면 아래와 같이 생각할 수 있다.
  • 정규분포($\epsilon$)에 상수($\mathbf{w}^\top\mathbf{x}+b$)를 더하더라도 정규분포다. 단지 평균이 0 에서 $\mathbf{w}^\top\mathbf{x} +b$ 로 이동했다고 볼 수 있다. 또한 오차의 분산도 상수항을 더하더라도 일정하다.

  • 그러면 우리는 아래처럼 모델을 나타낼 수 있다.

    \[y \sim \mathcal{N}(\mathbf{w}^\top\mathbf{x} +b, \sigma^2)\]

  💡 왜 정규분포를 가정할까?
  
  예측을 할 때는 “내 예측값이 실제값과 정확히 일치한다!” 라고 말할 수 없다. 언제나 예외는 존재하는 법이고, 정확히 예측할 수 있다면 머신러닝과 딥러닝이 필요없을 것이다.
  
  따라서 “실제값은 내 예측값일 확률이 가장 높지만, 아닐 수도 있다!” 라고 말하는 것이 현명하다. 여기서 “아닐 수도 있다” 는 것은 바로 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아내는 것이 불가능하여 근사적으로 확률분포를 추정할 수 밖에 없기 때문이다. 이는 근본적으로 발생하는 불확실성이다.
  
  이 때, 실제값은 내가 모르기 때문에 Random Distribution 인데, 내가 예측한 값을 평균으로 하는 정규분포(가우시안분포)를 따른다고 볼 수 있다고 말하는 것이 앞선 현명한 말과 비슷한 의미가 된다. 왜냐하면 정규분포는 평균에서 확률밀도가 가장 높기 때문이다. 즉 이를 다시 말하면 “실제값의 분포는 나의 예측값을 평균으로 하고 $\sigma^2$ 를 분산으로 하는 정규분포를 따른다!” 라고 말할 수 있는 것이다.
  
  또 다른 이유로 중심극한정리(Central Limit Theorem, CLT)를 들 수 있다. 이는 “표본의 수가 충분히 많으면, 모집단의 분포 형태와 상관없이 그 표본들의 (표본)평균의 분포가 정규분포에 점점 근사한다.”는 것을 뜻한다. 이를 이용해 어느 정도의 표본 수만 확보되면 “오차항이 정규분포를 이룬다” 를 증명할 수 있다. 또한 오차항의 정규성을 가정하지 않더라도 중심극한정리에 의해서 정규분포의 성질을 이용한 계산이 가능하다.
  
  참고로, 중심극한정리와 헷갈릴 수 있는 개념인 대수의 법칙(Law of large numbers)은 어떤 모집단에서 표본 집단들을 추출할 때, 추출한 데이터의 크기가 커질수록 그 표본집단들의 평균은 모평균과 같아지고, 표본집단들의 분산은 0 에 가까워진다는 것이다. 즉 표본크기가 무한히 커짐에 따라 표본평균이 실제 모평균으로 “확률수렴“한다는 것이다. 반면 중심극한정리는 표본 크기가 무한히 커짐에 따라 표본평균의 분포가 표준정규분포로 “분포수렴“하는 개념이다.

• 이제 선형회귀모델의 모수(parameter)를 추정해야 하는데, 이 때 추정해야 할 모수가 바로 $\mathbf{w}$ 와 $b$ 가 된다.
• 모수를 추정할 때는, 가정된 확률분포에 대응하는 모수의 값으로 관측값이 설명될 수 있는 가능성을 가지고 추정한다. 이를 가능도 추정법(likelihood estimation)이라고 한다.
• 즉, 가능도 함수는 모수 $\theta$ 를 따르는 분포가 $\mathbf{x}$ 를 관찰할 가능성을 뜻한다.
  • 확률밀도함수에서는 모수 $\theta$ 가 이미 알고 있는 상수 벡터이고 $x$ 가 변수(벡터)다. 하지만 모수 추정 문제에서는 이름이 내포하는 것과 같이 어떤 분포에 대해 이미 실현된 표본값 $x$ 는 알고 있지만 역으로 모수 $\theta$ 를 모르고 있는 상황이며 이 모수를 추정하는 것이 관심사이다.
  • 따라서 확률밀도함수와는 반대로 $x$ 를 이미 알고 있는 상수 벡터로 놓고 $\theta$ 를 변수(벡터)로 생각한다. 물론 함수의 값 자체는 여전히 동일하게, 주어진 $x$ 에 대해 나올 수 있는 확률밀도이다.
  • 달라진 것은 원래의 확률밀도함수가 $x$ 를 변수로 하는 함수였다면 가능도 함수는 $\theta$ 를 변수로 하는 함수가 된 것이다.
  • 이렇게 확률밀도함수에서 모수를 변수로 보는 경우에 이 함수를 가능도함수(likelihood function)라고 한다.
  • 같은 함수를 확률밀도함수로 보면 $p(y\vert X;\theta)$ 로 표기하지만 가능도 함수로 보면 $L(\theta;X,y)$ 기호로 표기한다. 동일한 대상이지만 바라보는 관점의 차이를 반영하는 표기인 것이다.
  • 참고로 위 표기에서 “;”는 parameterized, “,”는 conditioning 이라는 뜻을 가지고 있다. $\theta$ 는 학습에 의해 결정되는 값이지 Random variable 이 아니므로 “;”가 된다.

  💡 그렇다면 딥러닝 입장에서, 가능도(likelihood)는 고정된 training data($X, y$)를 가지고 학습을 통해서 다양한 $\theta$ 값 중에서 하나를 고르는 것이다. 다르게 얘기하면, 고정된 parameter($\theta$) $w$ 가 주어졌을 때 입력변수($X$)에 대해 정답이 $y$ 일 확률이다.

• 이제 우리가 할 일은 맨 처음 난수로 초기화하거나 학습을 진행하면서 업데이트된 parameter($\theta$) $w$ 를 가지고, 가능한 모든 데이터 $x$ 에 대하여 예측값이 실제값에 최대한 가깝게 위치하도록 하는 것이다.

• $\mathbf{x}$ 가 주어졌을 때 $y$ 의 가능도 함수는 아래와 같이 표현될 수 있다. 다시 한번 짚어보면 여기서 모수, 즉 parameter 는 $\mathbf{w}$ 와 $b$ 가 된다.

  \[P(y \vert \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right)\]
• 일반적으로 모수의 추정을 위해 확보하고 있는 확률변수 표본의 수는 하나가 아니라 여러 개 $x=(x_1,x_2,\ldots,x_n)$ 이므로, 가능도함수 또한 복수의 표본값에 대한 결합확률밀도가 된다.

• 또한 표본 데이터 $x_1,x_2,\ldots,x_n$ 는 같은 확률분포에서 나온 독립적인 값들이므로 결합확률 밀도함수는 독립사건의 확률 계산에 의해 다음처럼 곱으로 표현된다.

  \[P(\mathbf{y} \vert \mathbf{X}) = \prod^n_{i=1} p(y^{(i)} \vert \mathbf{x}^{(i)})\]
• 위 식의 값(가능도)이 가장 커지는 $\mathbf{w}$ 및 $b$ 가 전체 데이터셋의 가능도를 최대화하는 값이고 최적의 값이 된다.
• 왜냐하면 가능도가 최대값이 될 때, 가정한 확률분포에 대응하는 모수의 값이 관측값을 설명할 수 있을 가능성이 가장 높기 때문이다.
• 같은 말로 가능도가 최대값이 되는 parameter 에서 입력변수($X$)에 대해 정답이 $y$ 일 확률이 가장 높다는 것이다. 이 방식을 Maximum Likelihood Estimation (MLE) 라고 부른다.
• 가능도의 최대값은 로그를 취한 후 최대값을 찾는다. 또한 최적화는 최대화보다는 최소화로 표현되는 경우가 더 많기 때문에(경사하강법은 최소값을 찾는다), 음의 로그 가능도 $-\log P(\mathbf{y} \vert \mathbf{X})$ 를 최소화한다.
  • 로그가능도를 최적화하는 모수 $\theta$ 는 가능도를 최적화하는 MLE 가 된다.
  • 로그를 사용하는 이유는, 데이터의 숫자가 적으면 상관없지만 만일 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로는 기존의 가능도를 계산하는 것은 불가능하다.
  • 또한 데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있기 때문에 컴퓨터로 연산이 가능해진다. 더욱이 가능도가 최대면 로그가능도도 최대이기 때문에 문제가 발생하지 않는다.
  • 경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하게 되는데, 로그가능도를 사용하면 연산량을 $O(n^2)$ 에서 $O(n)$ 으로 줄여준다.
  • 대게의 손실함수의 경우 경사하강법을 사용하므로 음의 로그가능도(negative log-likelihood)를 최적화하게 된다.
  \[-\log P(\mathbf{y} \vert \mathbf{X}) = \sum^n_{i=1} \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2\]
• 위 공식을 활용하여 $-\log P(\mathbf{y} \vert \mathbf X)$ 를 최소화 해보자.
  • $\sigma$ 와 $\pi$ 는 상수값이라 로그 가능도를 최대화하는 $\mathbf{w}$ 와 $b$ 값에 영향을 주지 않는다.
  • 음의 부호가 붙어 최대화를 위해서는 최소화를 해야하므로, $\left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2$ 이 식을 최소화시키는 $\mathbf{w}$ 와 $b$ 를 찾으면 된다.

• 잘 보면, 이는 Squared Error 다. 즉, Gaussian noise 를 갖는 선형 모델의 likelihood 를 최대화하는 것은 선형 회귀의 squared loss 를 최소화 시키는 것과 동일한 문제로 정의될 수 있는 것이다.

  💡 이렇게 MLE 를 이용하면 Regression task 에서 L2 Loss(MSE) 를 쓰는 이유를 증명해 낼 수 있다. 반대로 생각하면, 우리가 앞으로 Deep Learning 에서 L2 Loss 를 이용한다는 것은 주어진 Data 로부터 얻은 Likelihood 를 최대화 시키겠다는 뜻으로 해석할 수 있을 것이다. 왜냐하면 위에서 본 것처럼 L2 Loss 를 최소화 시키는 일은 Likelihood 를 최대화 시키는 일이기 때문이다!
  
  그러면, 딥러닝에서 목표는 내가 풀고자 하는 함수를 잘 근사하는 함수를 찾아내는 것이고, 이를 위해 loss 를 측정하는데 Regression 에서는 이 loss 를 최소화시키는 가중치가 실제값에 가장 높은 확률로 맞는 예측값을 낼 수 있도록 한다는 것이다!
  
  참고로 Classification 문제에서는 Bernoulli Distribution 을 이용하면 비슷한 방법으로 Cross Entropy Error 를 유도할 수 있다.

• 이 로그가능도를 최소화하는 지점은 미분계수가 0 이 되는 지점을 찾으면 된다.
• 찾고자 하는 parameter 에 대하여 로그를 취한 로그 가능도 함수를 편미분하고 그 값이 0 이 되도록 하는 parameter 를 찾는 과정을 통해 가능도 함수를 최대화시켜줄 수 있다.

Linear Regression as a Neural Network

• 위에서 본 단순한 linear model 들은 현실세계의 복잡한 문제들을 표현하기에 충분하지 않다. 그러나 Neural Network 는 가능하다. 이러한 Neural Network 에서는 Linear Regression 을 어떻게 다룰까?

• Neural Network 구조로 선형 회귀를 표현해보면, 아래 그림과 같이 Neural Network 다이어그램을 이용해서 선형 회귀 모델을 도식화 할 수 있다.

  Linear Regression is a single-layer neural network

• 위 Neural Network 에서 입력값의 개수를 feature dimension 이라고 부르기도 한다.
• 따라서 위 그림에서 입력값의 개수는 $d$ 개이고, 선형 회귀의 결과인 출력값($o$)의 개수는 1 개이다.
• input layer 에는 어떤 비선형이나 어떤 계산이 적용되지 않기 때문에 이 네트워크의 총 layer 의 개수는 1이다.
• 모든 입력들이 모든 출력(이 경우는 한개의 출력)과 연결되어 있기 때문에, 이 layer 는 fully connected layer 또는 dense layer 라고 불린다.

Reference

• https://d2l.ai/chapter_linear-regression/linear-regression.html
• https://hongl.tistory.com/282
• https://hyeongminlee.github.io/post/bnn002_mle_map
• https://laoonlee.tistory.com/5

맨 위로 이동 ↑