[Deep Learning] Deep Learning, Neural Network (2)

딥러닝을 공부하는 이유, 즉 내가 딥러닝에 매력을 느끼고 이를 공부하는 이유를 정리하고자 한다. 남들이 하니까 하는 게 아니라, 어느 부분에서 딥러닝이 정말 효과적이고 사람들에게 서비스할 수 있는지 그 근본적인 이유를 알아보자.

Universal Approximation Theorem (범용 근사 정리, UAT)

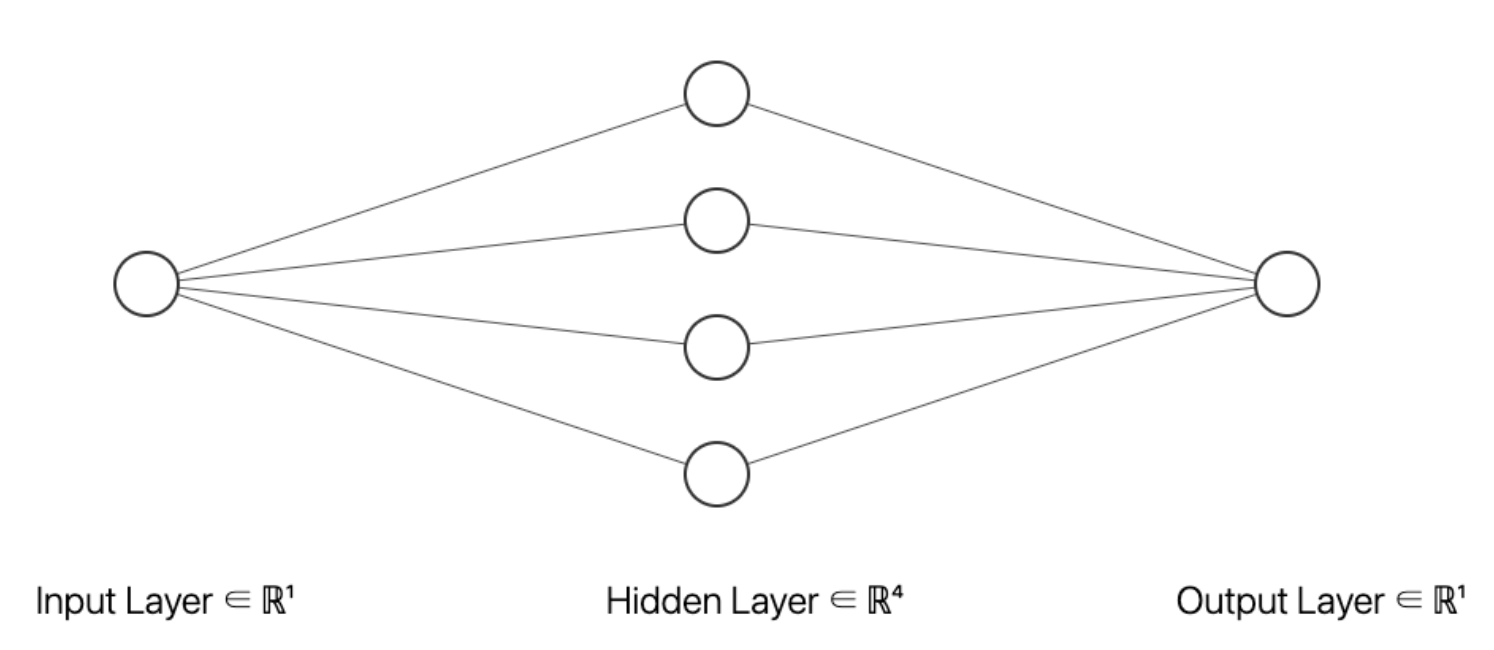
• UAT 는 1개의 hidden layer 로 모든 함수를 근사할 수 있다는 이론이다.

  

• 위와 같은 NN 이 임의의 모든 함수를 근사할 수 있다는 것인데, 어떻게 그럴 수 있을까?

Sigmoid to Step function

• 먼저 Sigmoid 함수를 딥러닝의 차원에서 고민해볼 수 있다.
• 보통의 입력값($x$)은 $wx+b$ 의 형태로 들어간다. 이후 활성화 함수로 Sigmoid($\sigma(x)=\frac{1}{1+e^{-x}}$)를 통과시킨다고 해보자.

• $e$ 를 대략 3 이라 생각했을 때, $wx+b$ 가 0 이면 1/2 이고 $wx+b$ 가 1이면 3/4 이 된다.

  

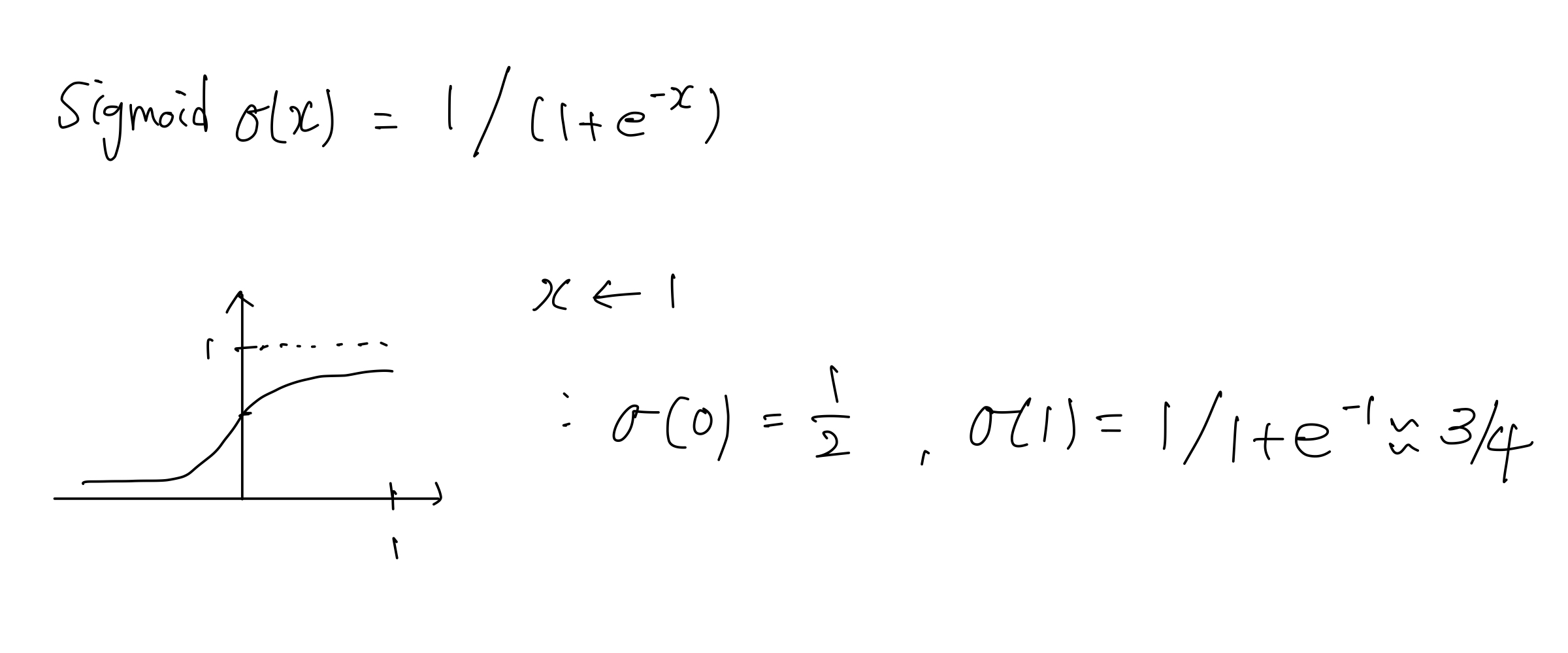
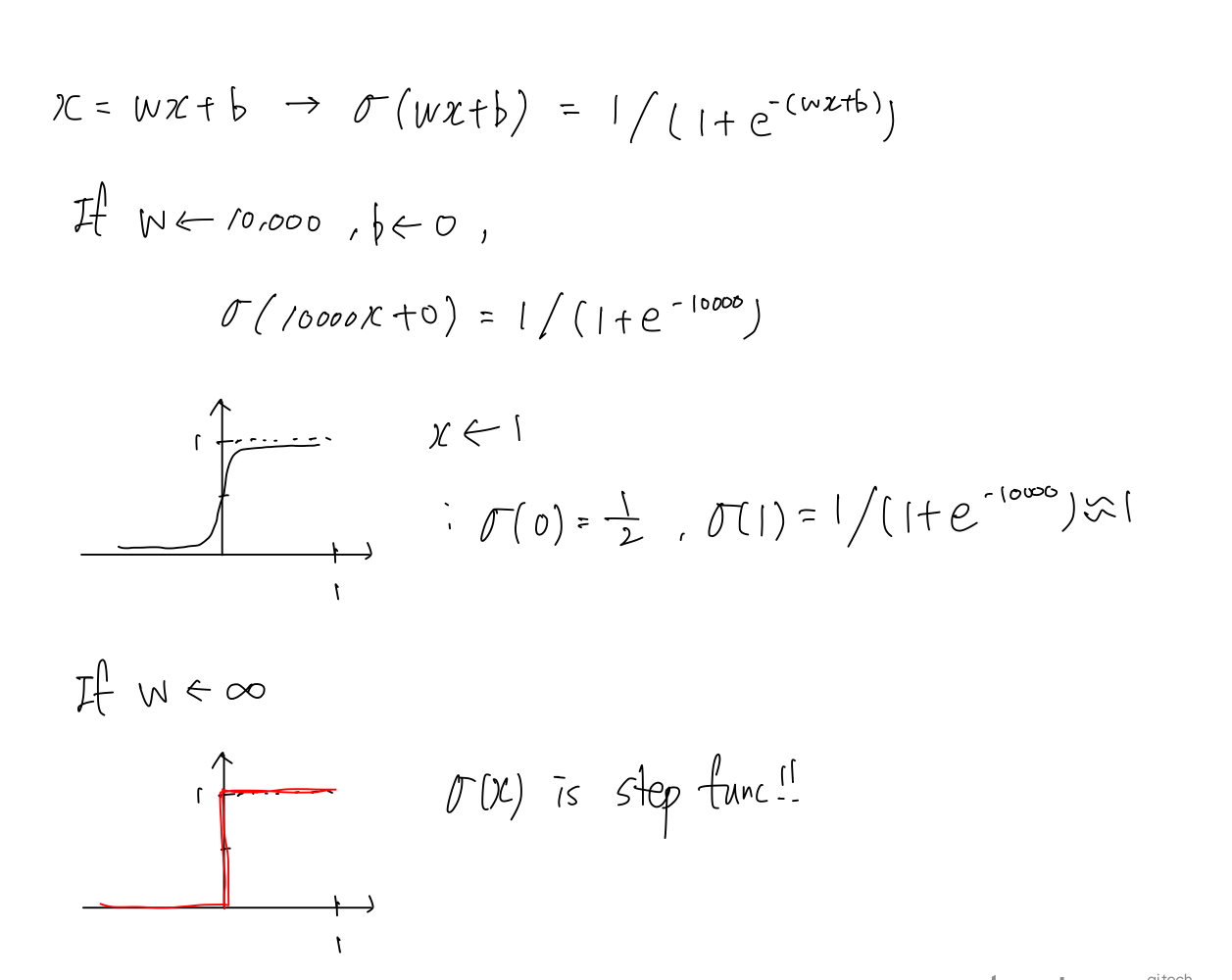
• 이 때 $w$ 가 큰 값이고 $b$ 가 0 이라면, $x$ 가 0 일 때 1/2 이고, $x$ 가 1 일 때 $e^{-x}$ 가 0 에 수렴하여 1 이 된다.
• 이를 통해 $x$ 가 0 에서 1 사이일 때 모두 Sigmoid 함수를 거친 값이 1 에 가깝게 됨을 알 수 있다.

• 즉 $w$ 를 굉장히 큰 수로 보내는 것은, 아래 그림과 같이 Sigmoid 함수를 Step 함수로 만드는 것과 같다고 생각할 수 있다.

  

Bump function for approximation

• 이제 Bump function 을 생각해보자.
• Bump func 은 많은 경우에 근사할 때 쓰이는데, 딥러닝에서의 근사에도 사용될 수 있다. 딥러닝에서 근사는 일반적으로 실제 데이터의 확률분포를 우리가 설정하여 모델링한 분포를 통해 근사한다.
• 이 때 분포 간의 거리를 측정해주는 도구인 KL-div(Kullback-Leibler Divergence), JSD(Jensen-Shannon Divergence), MMD(Maximum Mean Discrepancy) 등으로 근사한다. 해당 개념들은 따로 포스트를 두어 정리할 것이다.
• 예를 들어 실제 분포는 복잡한데 Gaussian 의 평균과 표준편차를 조정해서 근사할 수 있다. 실제의 분포와 근사하는 분포 사이의 Gap 이 많이 존재함에도, 이를 이용하는 VAE 나 GAN 은 이미지를 잘 생성해낸다.

• 따라서 우리가 설정해주는 사전분포로도 충분히 잘 근사됨을 확인할 수 있다.

  

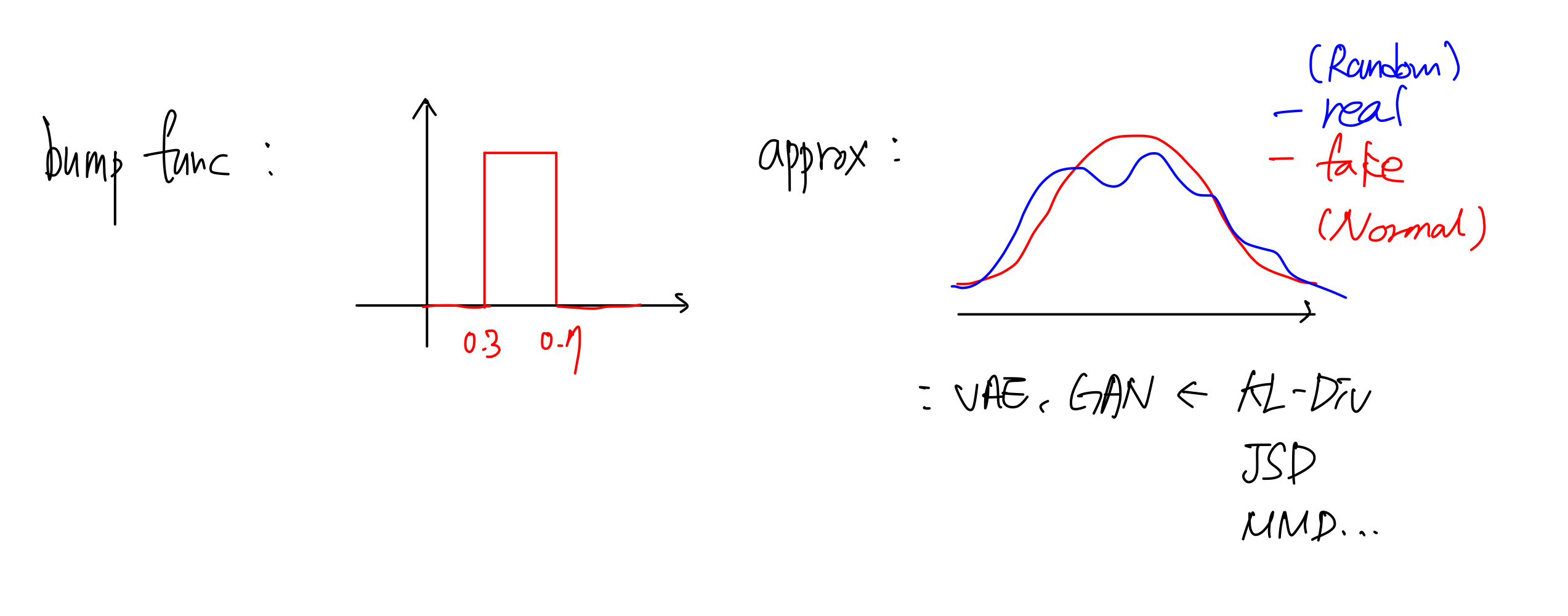
• 즉 위 그림처럼 복잡한 분포를 꼭 복잡하게 모델링하지 않고도 우리가 알고 있는 Gaussian 분포로도 충분히 잘 근사함을 시사하는 것이다.

• 근사는 우리가 일정 오차를 정하고 그 오차 내에서 fitting 은 아니더라도 충분히 근사가 된다는 것을 뜻한다.

  

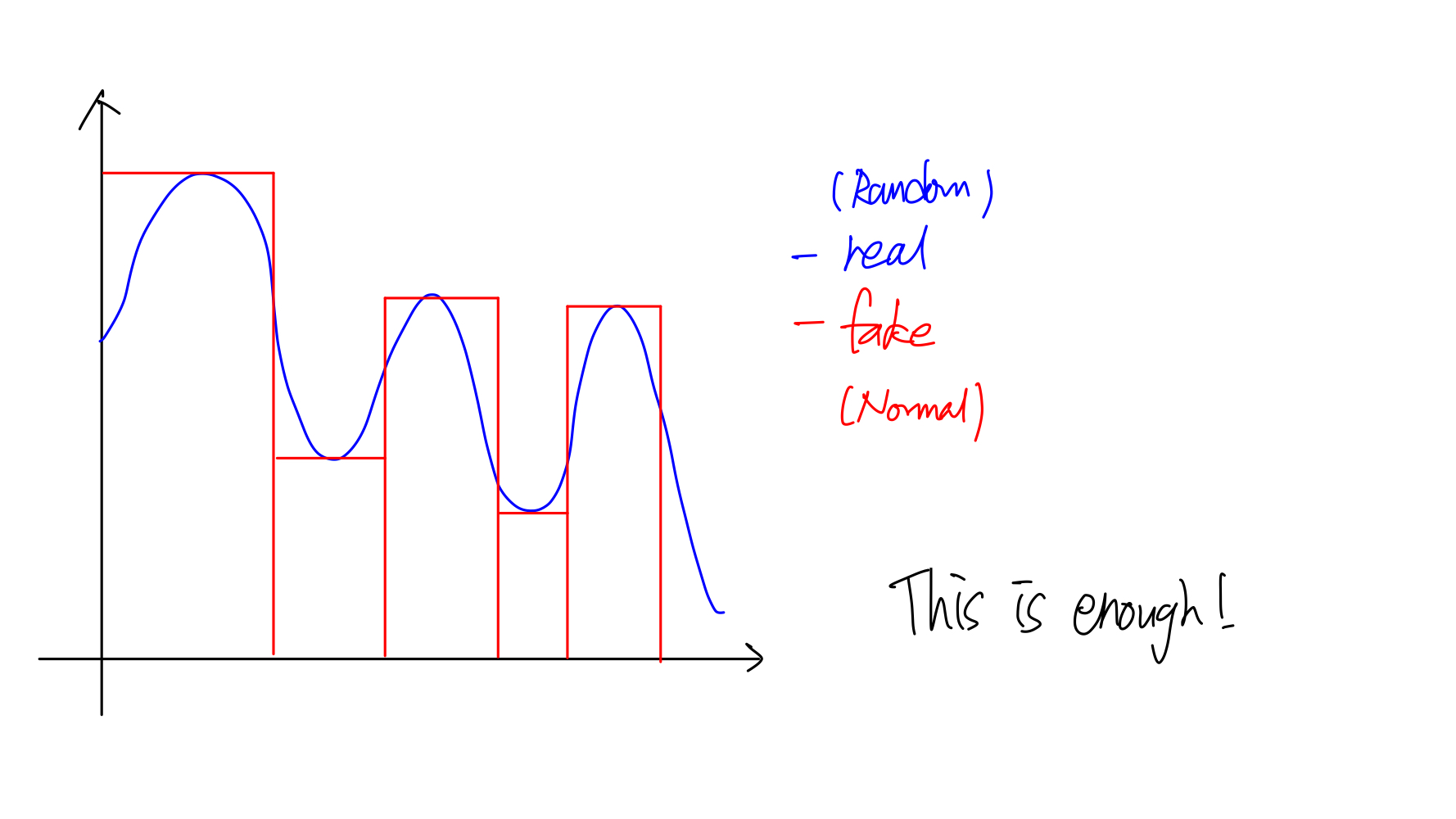
• 임의의 파란색 실선과 같은 함수가 주어질 때 빨간색 bump func 의 조합으로 근사할 수 있다. 위와 같은 근사는 우리에게 자연스럽다. 왜냐하면 적분과 같기 때문이다.
• 오차가 더 적게 근사하고 싶다면 bump func 을 더 잘게 쪼개면 된다. 이렇게 충분히 잘 근사시킬 수 있다.

Step function to Bump function

• 여기까지 Sigmoid 가 Step func 이 될 수 있고, Bump func 을 가지고 임의의 함수를 근사가 가능함을 확인했다.
• 이 때, Step func 은 Bump func 이 될 수 있다. 이렇게 하면 UAT 에 좀 더 근접해볼 수 있다.

• 어떤 함수를 오차범위를 허용하는 함수로 근사한다고 했을 때, 아래처럼 생긴 NN 을 사용한다고 해보자.

  

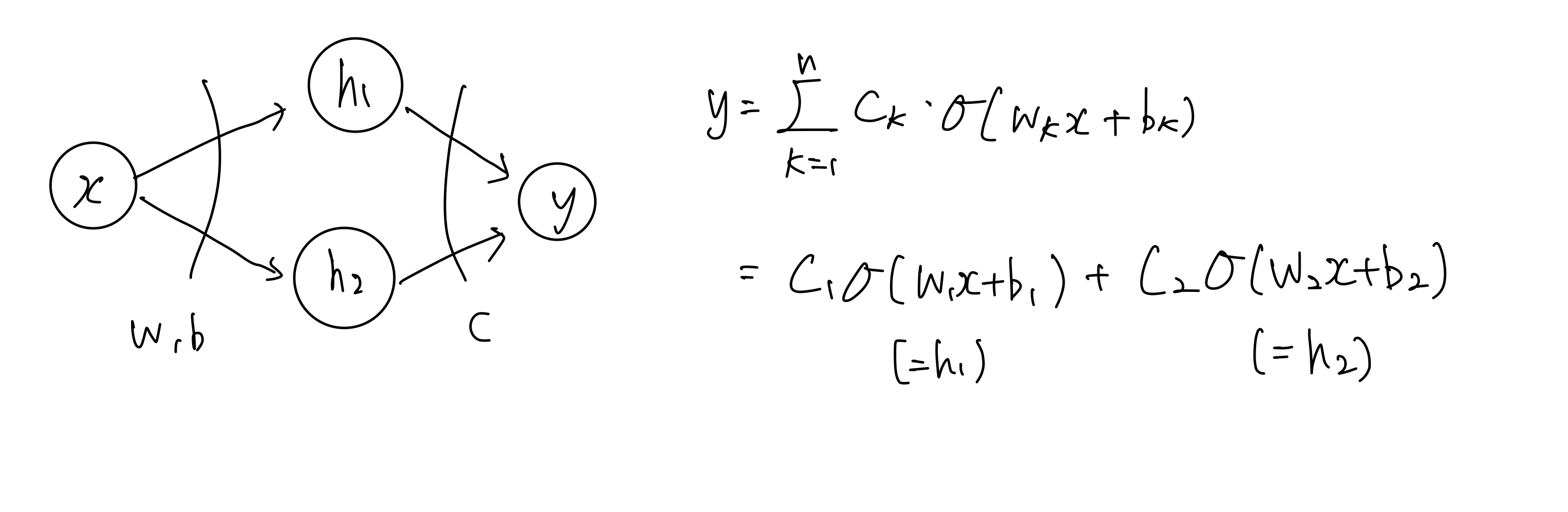
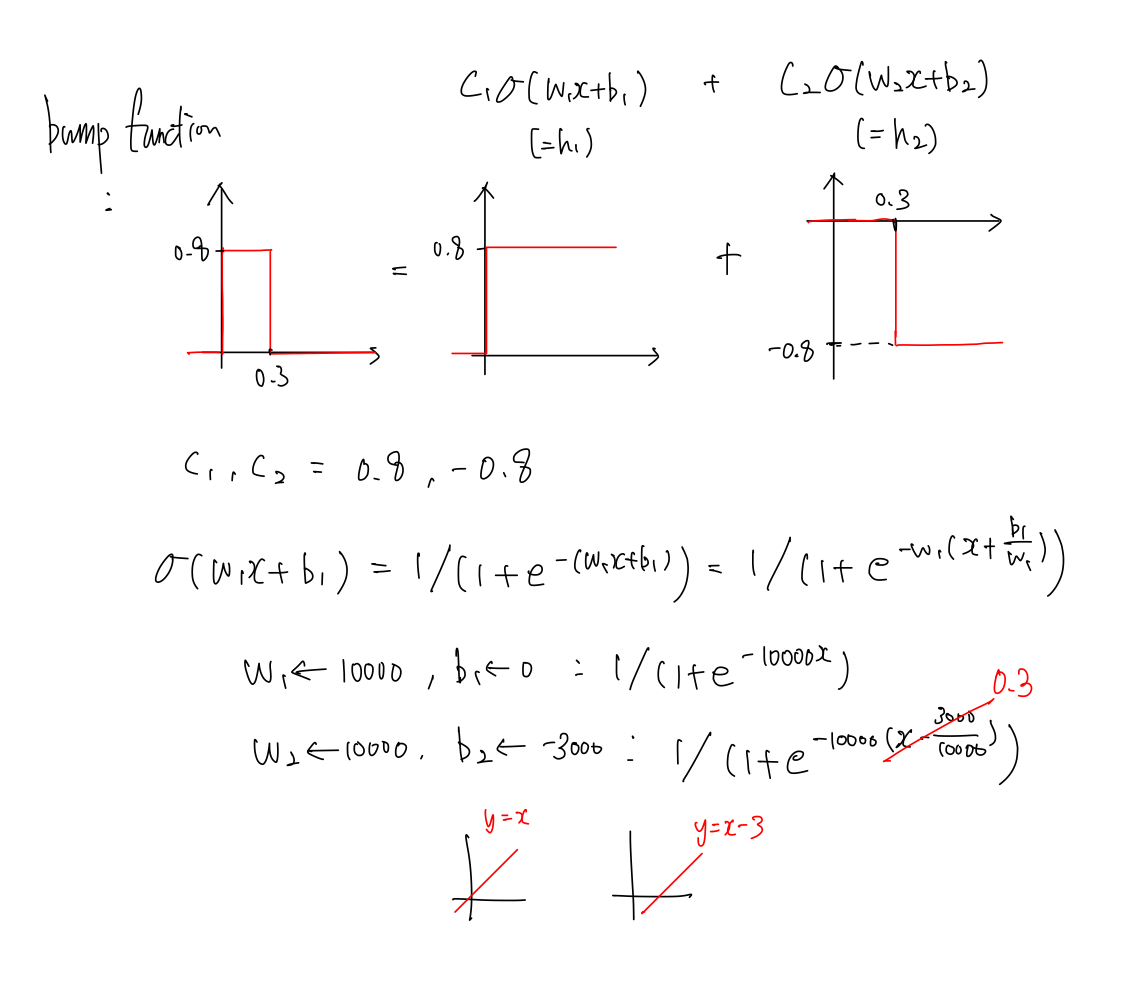
• 내가 만들려는 Bump func 이 아래 그림과 같을 때, Sigmoid 함수의 값의 범위는 0~1 이고 $c_1$ 과 $c_2$ 는 Sigmoid 앞에 곱해지기 때문에 각각 0.8, -0.8 로 정의할 수 있다.

• 또한 Bump func 에 따라 $b_1$ 과 $b_2$ 도 각각 구해낼 수 있다.

  

• 얻어낸 값들을 활용해서 식을 전개하기만 하면 내가 원하는 Bump func 을 만들어낼 수 있다.

  

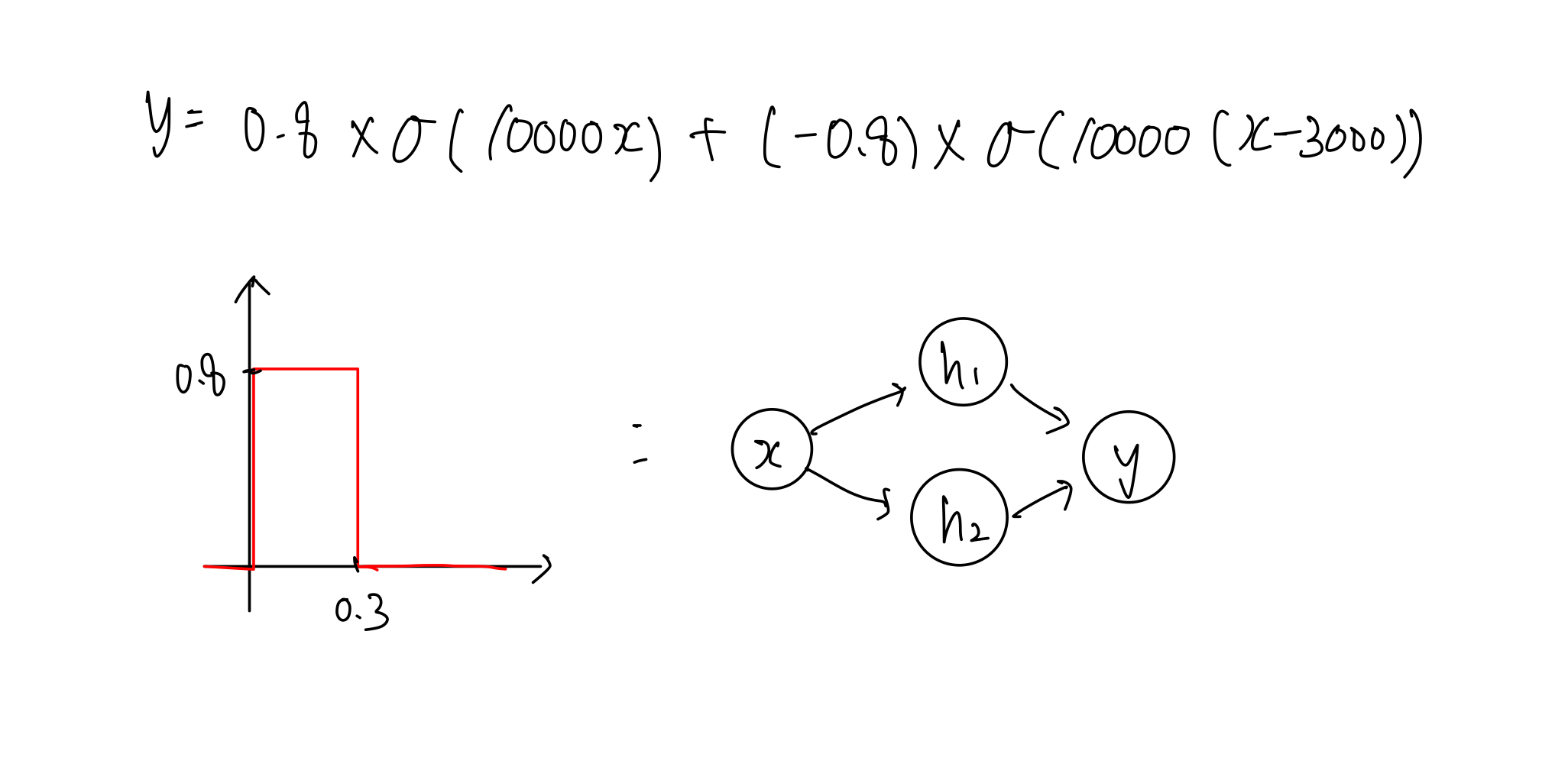
• 이처럼 2개의 step func 이 존재하면 하나의 bump func 을 만들어냄을 확인할 수 있다.
• 그러면, 우리는 $2n$ 개의 hidden layer 를 가진 심플한 NN 이 있으면 적어도 $n$ 개의 bump func 을 가지는 함수로 근사할 수 있는 것이다.
• 만약 layer 가 2만 개 있다면 1만 번 쪼갠 정도의 오차범위 내로 임의의 함수를 근사할 수 있는 것이다.
• 그러면 우리는 NN 을 가지고 복잡한 함수를 근사할 수 있다는 것이 된다!

UAT 의 한계

• 그러나 UAT 는 굉장히 한정적이고 최소한의 당위성만을 부여해주고 있다. 왜 그럴까?
• 이미 많은 모델들은 깊은 layer 를 많이 가지고 있다. 이 정도면 아주 복잡한 함수도 근사할 수 있다. 그러나 크게 2가지의 이슈를 가지고 있다.
• 첫번째로 위에서 전개한 식은 적당한 가중치가 이미 주어졌을 때 잘 성립한다.
  • 우리는 풀고자 하는 문제를 잘 풀 수 있는 가중치를 찾기 위해 딥러닝을 하는데 이 가중치가 어떻게 주어지느냐가 UAT 에서 부족하다.
• 두번째로 1층의 layer 로는 3차원에서 voxel 형태의 bump func 을 만들 수 없다.
  • 위에서 본 것처럼 2차원, 평면좌표 상의 bump func 을 만들어낼 수는 있지만, 3차원에서도 이렇게 성립하는지는 아직 모른다.
• 즉 실생활은 굉장히 고차원이고, 가중치를 구하기 어려운 상황이다. 모든 조건들이 잘 충족되면 위처럼 근사가 가능하지만 현실에서는 한계가 있다는 것이다.

Deep? Wide?

• 하나의 layer 에 여러 개를 쌓는 것처럼 전개가 되었는데, 왜 우리는 wide 가 아니라 deep NN 을 하는 형태로 발전했을까?
• layer 가 깊어질수록 좀 더 고차원의 데이터를 표현하는데, 모델링하는 것들을 잘 할 수 있다.
• 같은 개수의 노드가 존재했을 때 layer 를 deep 하게 쌓으면 고차원의 표현을 더 잘할 수 있다.
  • 4개의 노드가 있다고 했을 때, 하나의 layer 에 4개 모두 존재한다면 2개의 bump func 이 만들어지고 4개의 path 가 존재한다.
  • 그러나 층을 deep 하게 쌓으면 path 가 더 복잡해지기 때문에 고차원 표현을 더 잘할 수 있는 것이다.
  • 9개의 노드를 1 layer (1x9) 로 두기보다 3 layer (3x3) 으로 두면 복잡한 데이터를 표현하는데 적합한 것이다.
  • 이러한 이유로 wide 가 아닌 deep 으로 발전하게 된 것이다.

• 또한 층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 개수가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능하다고 한다. 층이 얇으면 wide 하게 뉴런(노드)의 개수가 기하급수적으로 증가하기 때문이다.

  💡 이 UAT 를 통해서 왜 딥러닝을 공부하고 있는지, ‘딥’러닝이 왜 합리적인 방향인 것인지를 직관적으로 알 수 있다. 현재 딥러닝은 wide 하기도, deep 하기도 하다. 이는 엄청 복잡한 차원의 엄청 복잡한 함수를 잘 근사할 수 있을 것이라는 믿음으로 보인다. 아직 우리가 근사하려는 현실은 너무도 복잡하지만, 이는 아직 잘 안되는 것이지 언젠가 가능할 것이다.

딥러닝은

• 머릿속으로 생각하는 아이디어를 구현하고 결과를 뽑는 Implementation Skills(TF, Pytorch)도 중요하지만, 동시에 Math Skills(Linear Algebra, Probability) 도 당연히 중요하다.

  

• 앞으로 데이터, 모델, loss function, 알고리즘(optimizer) 이 4가지 항목에 비추어서 논문을 보자!
• loss function 은 모델을 어떻게 학습시킬지에 대한 것(파라미터 업데이트를 위한 기준값)이다.
• 즉 loss 는 이루고자 하는 것에 proxy(근사치)이다. 이 loss 를 왜 사용해야 하는지, 이 loss 가 줄어드는 것이 내가 풀고자 하는 문제를 어떻게 푸는지 이해해야 한다.

• 또한 loss function 의 목적은 단순히 줄이는 것이 아니라, 내 모델이 학습하지 않은 데이터에 잘 동작하도록 하는 것이다!

  

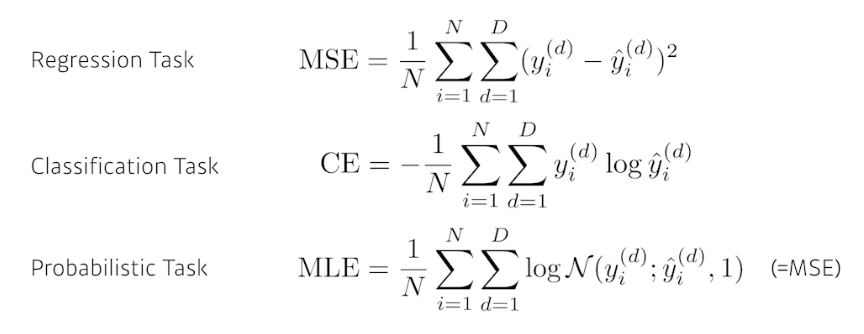
• Optimization Algorithm 은 다양한 테크닉이 있다.
  • Dropout, Early Stopping, k-fold validation, Weight decay, Batch Normalization, Mixup, Ensemble, Bayesian Optimization 등이 있다.
  • 네트워크가 단순히 학습 데이터가 아닌 실환경에서 잘 동작하도록 도와준다!
• 다음은 임팩트가 있던 딥러닝 방법론들이다. 다른 포스트에서 모두 다룰 것이다.
  • AlexNet(2012): 딥러닝 패러다임의 시작을 알렸다. 딥러닝이 실제로 성능을 발휘한 것을 보여준 논문이다.
  • DQN(2013): 강화학습 방법론이다. Q-Learning. 딥마인드를 있게 한 방법론이다.
  • Encoder/Decoder(seq2seq), Adam(optimizer): 오늘날 가장 흔하게 사용되는 Optimizer 인 Adam 은 웬만하면 잘된다.
  • GAN, ResNet(2015): 특히 ResNet 은 딥러닝이 왜 딥러닝인지, 네트워크를 깊게 쌓을 수 있게 만들어준 방법론이다.
  • Transformer(Attention Is All You Need, 2017): Transformer 구조는 정말 중요하다. MHA(Multi Head Attention) 등의 구조를 이해해야 하고, 다른 기존의 RNN 에 비해 어떤 장점, 좋은 성능이 있는지 이해해야 한다.
  • Bert(2018): fine-tuned NLP models.
  • Big Language Models(GPT-X, 2019)
  • Self-Supervised Learning (SimCLR, 2020): 내 학습 데이터 외에 추가 데이터(라벨이 없는)까지 활용해서 visual representation 이미지를 컴퓨터가 잘 이해할 수 있는 벡터로 바꾸는 방법론이다.

맨 위로 이동 ↑