[Deep Learning] Deep Learning, Neural Network (1)

앞으로 Loss, Activation function, Optimization 등 딥러닝을 구성하는 여러 부분들에 대해 공부한 기록을 남긴다. 각각의 파트에 대해서 세세하게 정리하기 전에, 딥러닝이 어떤 식으로 발전했는지를 알아보자.

딥러닝의 역사

• 딥러닝이 어떻게 발전해왔고 어떻게 지금의 방향으로 흘러오게 되었는지를 이해하면 도움이 된다.

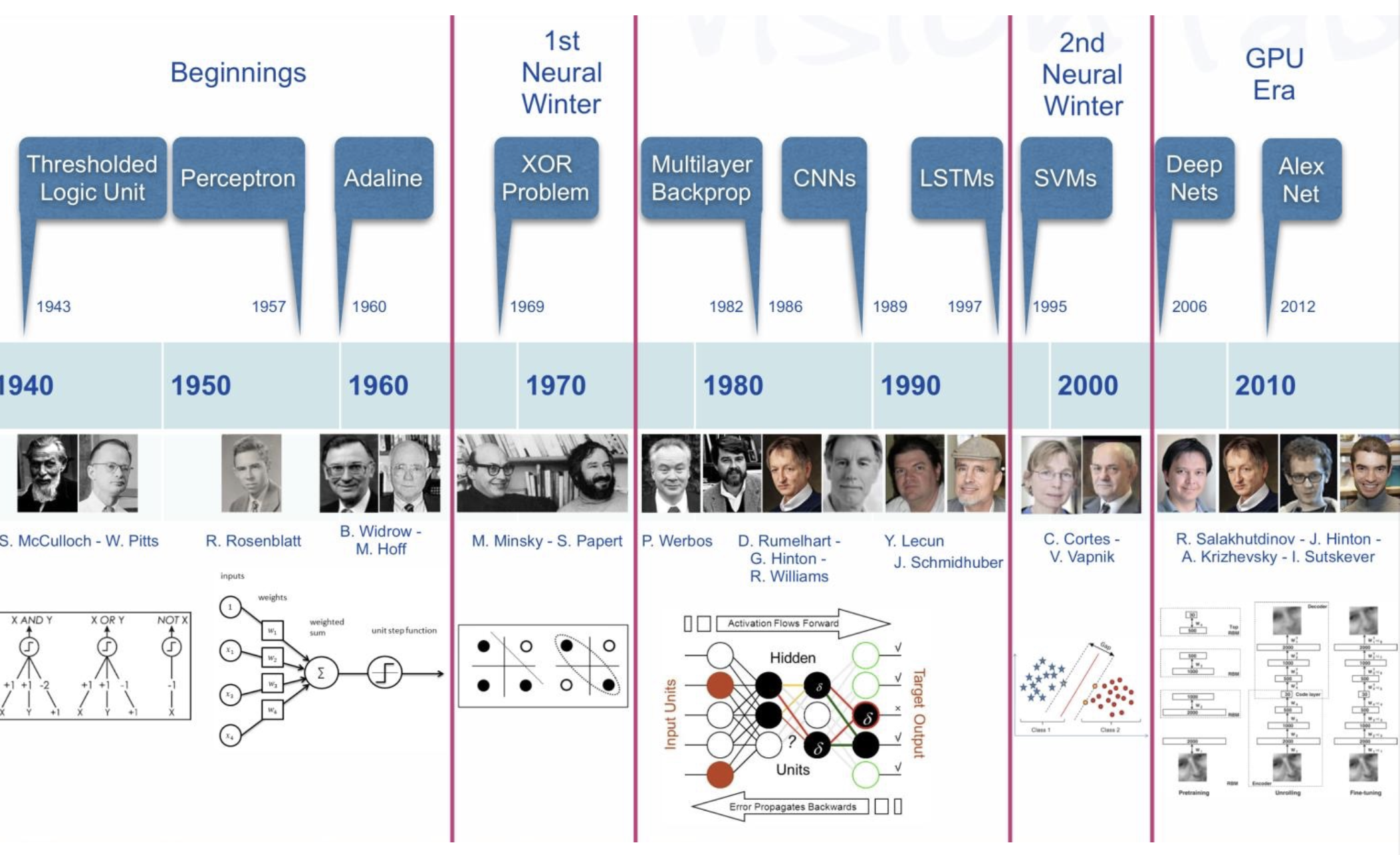  딥러닝의 연혁

Neural Network

• Neural Networks 란 사람의 뇌를 모방한 컴퓨팅 시스템으로, 딥러닝의 근간이 된다.
• 계산 신경과학 분야에서는 뇌를 정확히 모델링하는 것에 도전하면서 인공 신경망의 핵심 유닛을 단순화된 생물학적 뉴런으로 비유했다.
• 기존의 선형 분류(Classification)나 회귀(Regression) 모델에서 1) 활성화 함수(activation func)의 추가와 2) 층(layer) 으로 뉴런을 연결하는 구조를 통해서 완전한 신경망을 만들 수 있다.
• 초기 Neural Network 인 퍼셉트론부터 시작해서, MLP(multi layer perceptron), 오늘날에는 Neural Network 를 복잡하게 쌓아올린 딥러닝이 뜨겁게 발전하고 있다!

Perceptron

• 1950 년대 후반에 프랭크 로젠블라트가 제안한 초기의 인공 신경망으로, 다수의 신호를 입력으로 받아 하나의 결과를 내보내는 알고리즘이다.
• 즉, 입력 신호를 받아 그 신호의 가중합을 계산하고, 임계값에 따라 출력을 결정하는 알고리즘이다.

• 개별 신경세포는 간단한 연산능력이 있다고 알려져 있는데, 이 신경세포 하나하나가 서로 연결되어 동작하면 고도의 인지, 판단 능력이 생성된다. 이러한 동작과 비슷하게 수학적으로 모델링한 것이 퍼셉트론이라 볼 수 있다.

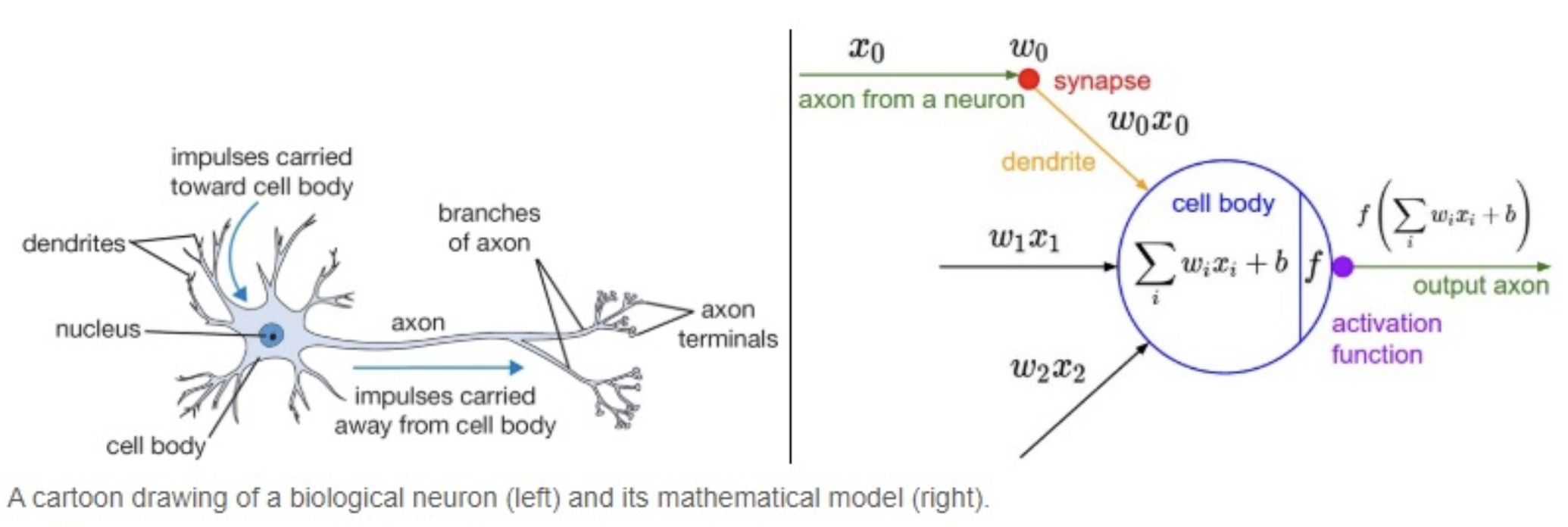  뉴런과 퍼셉트론

• 퍼셉트론 신호는 1 또는 0 의 두 가지 값을 가질 수 있다. 즉, 어떠한 임계값을 기준으로 하여 신호를 활성화(1)하거나, 비활성화(0)할 수 있다.
• 각 입력값과 그에 해당하는 가중치의 곱의 전체 합이 임계치(threshold)를 넘으면, 종착지에 있는 인공 뉴런은 출력 신호로서 1 을 출력하고 그렇지 않을 경우에는 0 을 출력한다.

• 또한 입력값 외에 편향(bias) 도 입력으로 포함되며, 일반적으로 입력값을 1 로 하고 가중치와 곱해진다. 이는 퍼셉트론이 얼마나 쉽게 활성화될지를 조정하는 매개변수 역할을 한다.

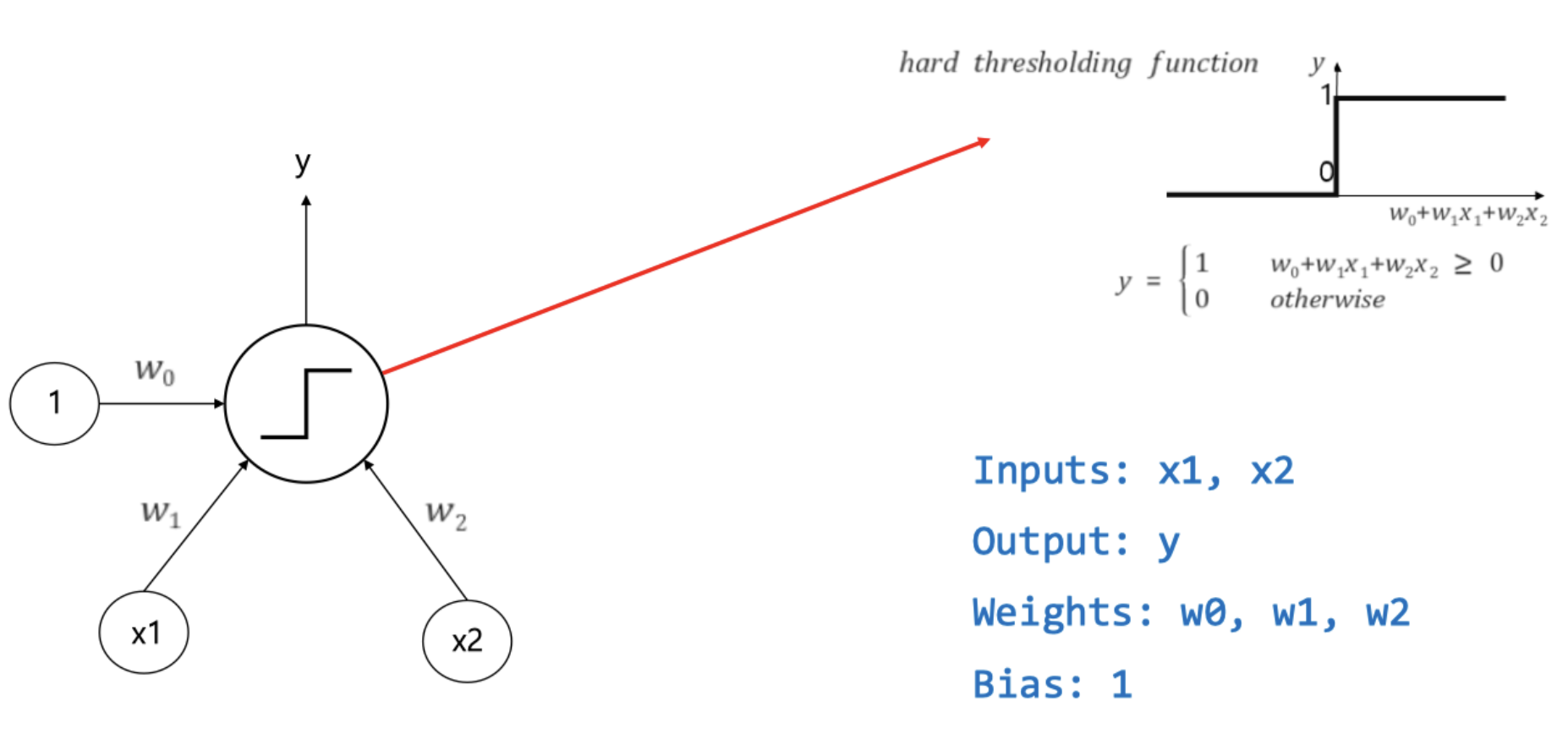  $x$ 는 입력값, $w$ 는 가중치(weight), $y$ 는 출력값. bias 또한 $w_0$ 와 곱해지는 입력값이다.

• 아래 그림과 같이 퍼셉트론의 식을 나타낼 수 있고, 이 퍼셉트론을 활용하여 and, or 연산이 가능하다. 즉 퍼셉트론이 $w$ 와 $bias$($b$) 에 따라서 and 와 or 을 흉내낼 수 있다는 것이다.

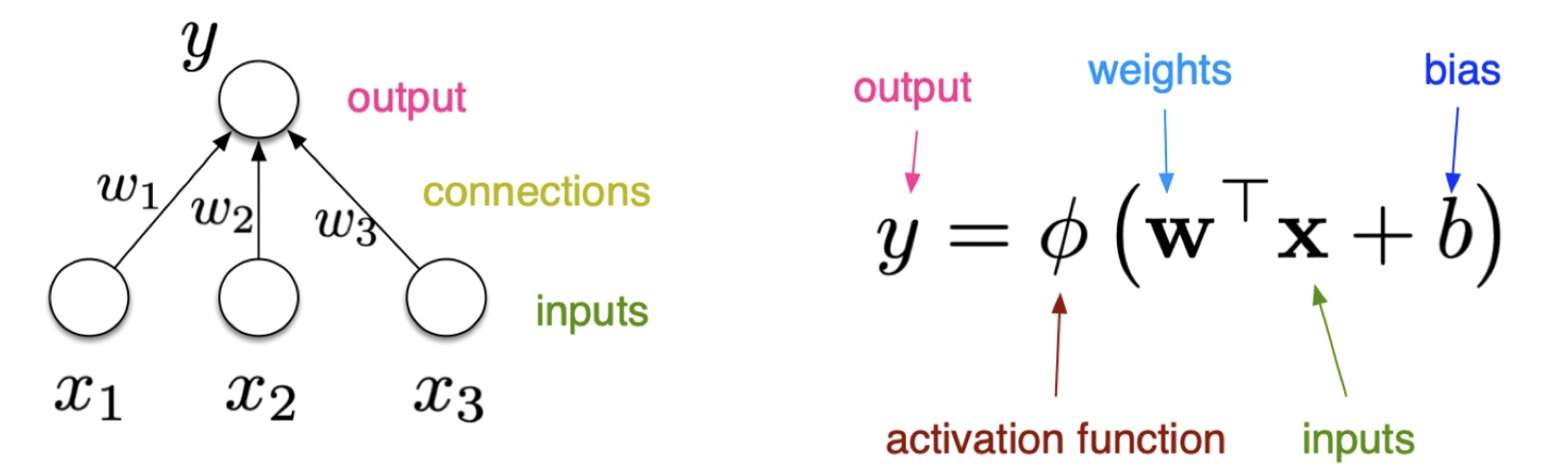  퍼셉트론 그림(좌), 퍼셉트론 식(우)

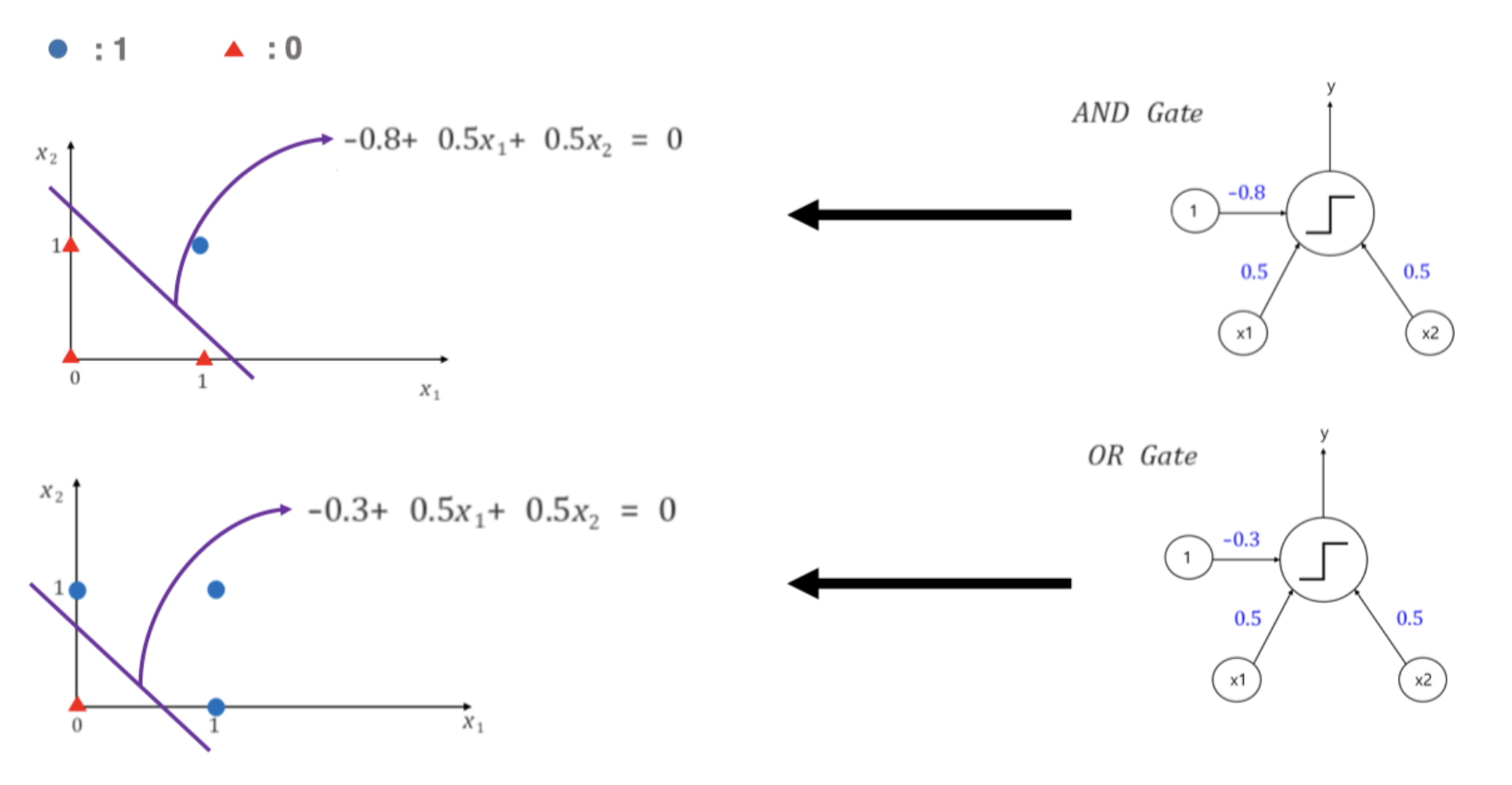  하나의 퍼셉트론으로 and 와 or 연산을 수행할 수 있다.

• 여기서 임계값을 결정하여 퍼셉트론의 출력값을 변경시키는 함수가 활성화 함수(activation function, $\phi$)다. 초기 퍼셉트론은 hard thresholding func, 즉 step function 을 사용했다.
• 실제 신경 세포 뉴런에서의 신호를 전달하는 축삭돌기의 역할을 퍼셉트론에서는 가중치(weights)가 대신한다. 각 입력값에 대응하는 가중치의 값이 크면 클수록 해당 입력 값이 중요하다는 것을 의미한다.
• 편향(bias)은 해당 퍼셉트론(뉴런)이 얼마나 쉽게 활성화 되는지를 조절하는 매개변수 정도로 생각할 수 있다. 즉 임계값을 넘어 출력이 1 이 되기 위해 필요한 신호의 크기를 조정하는 역할을 한다.
• step function 을 생각해볼 때, 입력과 가중치 곱의 합이 0 보다 크거나 같으면 1 이고 작으면 0 이 된다. 이 때 임계값 0 은 보통 $\theta$ 로 표현된다.
• 따라서 임계값 $\theta$ 를 기준으로 활성화 여부를 따질 때, 이 $\theta$ 가 입력과 가중치 곱의 합 변으로 이항되어 편향 $b$ 로 표현하는 것이다. 이러한 편향 $b$ 도 퍼셉트론의 입력으로 사용되며 딥러닝이 최적의 값을 찾아야 할 변수 중 하나가 된다.
• 그렇게 보면, 편향이 클수록 더 큰 입력이 필요하고 편향이 작을수록 더 쉽게 활성화된다.

활성화 함수(Activation Function)

• 활성화 함수는 선형에 비선형성을 추가하여 네트워크의 표현력을 늘려주는 역할을 한다.
• 초기 인공 신경망 모델인 퍼셉트론은 활성화 함수로 계단 함수(step func)를 사용했지만, 그 뒤에 등장한 여러가지 발전된 신경망들은 계단 함수 외에도 여러 다양한 활성화 함수를 사용하기 시작했다.
• 시그모이드(sigmoid) 함수는 대표적인 활성화 함수 중 하나로, 이진 분류 문제에서 사용된다. 소프트맥스(softmax) 함수는 다중 클래스 분류에서 사용되는 활성화 함수다.
• 퍼셉트론의 활성화 함수를 계단 함수에서 시그모이드 함수로 변경하면, 이 퍼셉트론은 곧 이진 분류를 수행하는 로지스틱 회귀와 동일해진다.
• 다시 말하면 로지스틱 회귀 모델이 인공 신경망에서는 하나의 인공 뉴런으로 볼 수 있으며, 로지스틱 회귀를 수행하는 인공 뉴런과 위의 퍼셉트론의 차이는 오직 활성화 함수의 차이이다. 즉, 퍼셉트론은 계단 함수를 사용하고, 로지스틱 회귀는 시그모이드 함수를 사용하여 출력값을 확률로 해석한다.
• 따로 포스트를 두어 Relu 등의 다양한 Activation Function 에 대해 정리한다. 여기서는 아래와 같은 활성화 함수들이 있다는 것만 알고 넘어가자.

• 중요한 점은 활성화 함수가 신경망에 비선형성을 추가하여 표현력을 늘려주어 더 복잡한 패턴을 학습할 수 있도록 돕는다는 것이다.

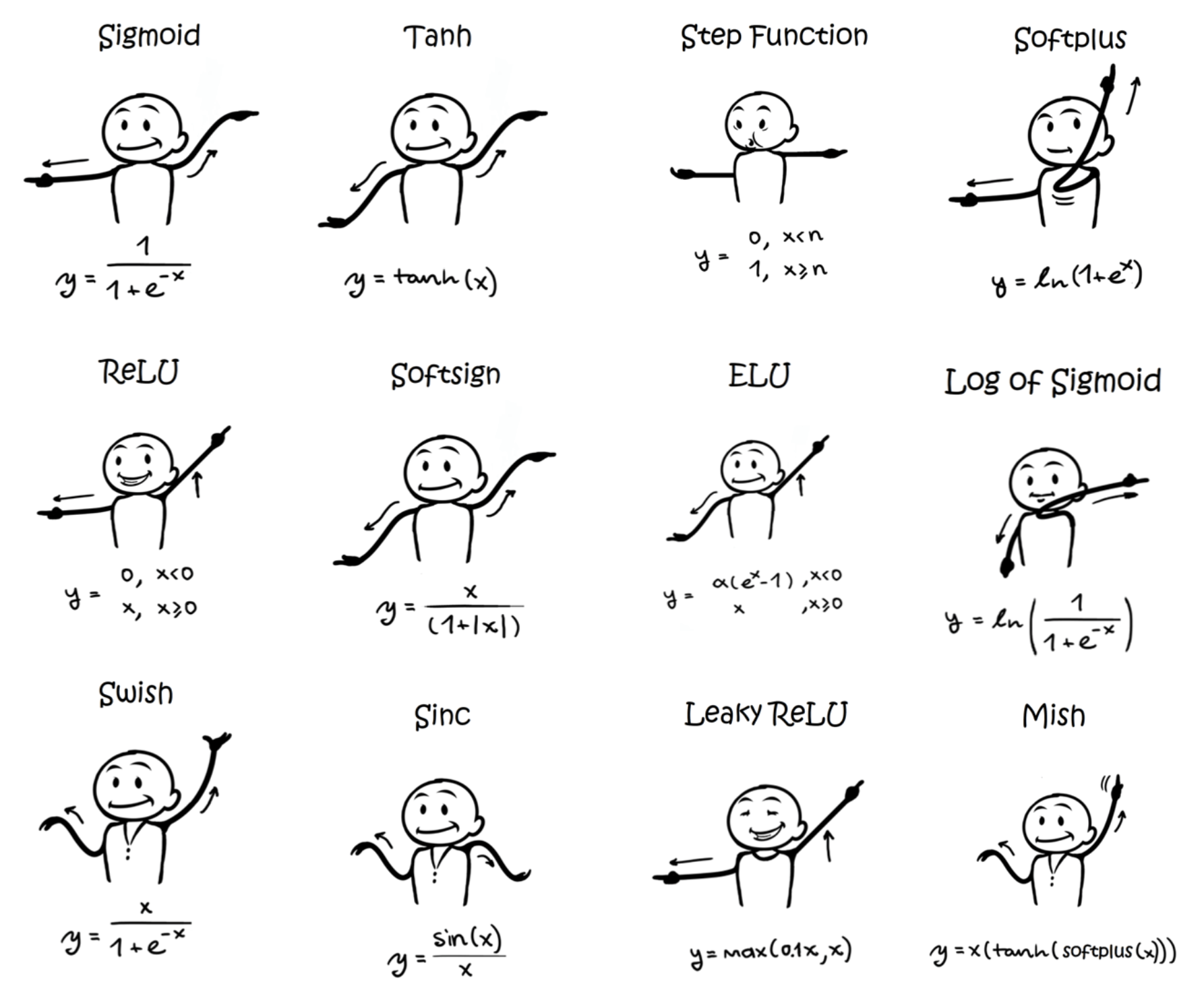  활성화함수에는 다양한 종류가 있다.

단층 퍼셉트론(single layer perceptron)

• 지금까지 살펴본 Perceptron 은 단층 퍼셉트론이다. 단층 퍼셉트론은 입력층(input layer)과 출력층(output layer) 두 단계로만 이루어져 있다.

  단층 퍼셉트론

• 이 단층 퍼셉트론은 위에서 봤듯 AND, OR, NAND 문제를 풀 수 있지만, 선 하나로 XOR 문제는 풀 수 없다. 즉 단층 퍼셉트론은 linear 문제만 풀 수 있고, XOR 과 같은 non-linear 문제는 풀 수 없는 것이다.

• 중요한 것은 실생활을 근사할 수 있는 함수들은 대부분이 non-linear 다. 따라서 단층 퍼셉트론만으로는 절대적으로 한계가 있다.

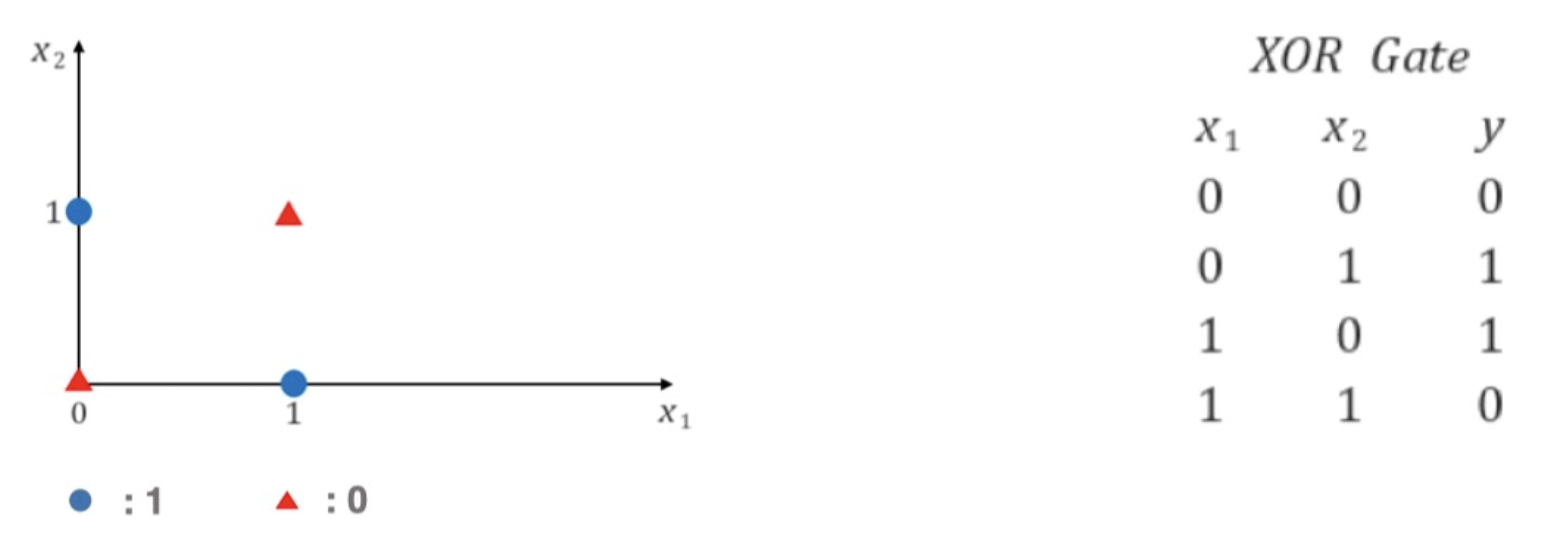  XOR Problem

• 위 문제를 풀기 위해서는 적어도 두 개의 선이 필요한데, 이에 대한 해답이 다층 퍼셉트론(MLP)이다.

다층 퍼셉트론(MLP, multi layer perceptron)

• 다층 퍼셉트론과 단층 퍼셉트론의 차이는 단층 퍼셉트론은 입력층과 출력층만 존재하지만, 다층 퍼셉트론은 중간에 층을 더 추가했다.

• 입력층과 출력층 사이에 존재하는 층을 은닉층(hidden layer)이라 한다. 이 은닉층이 어떻게 구성되었는가에 따라 딥러닝 모델의 성능을 좌우할 수 있다.

  

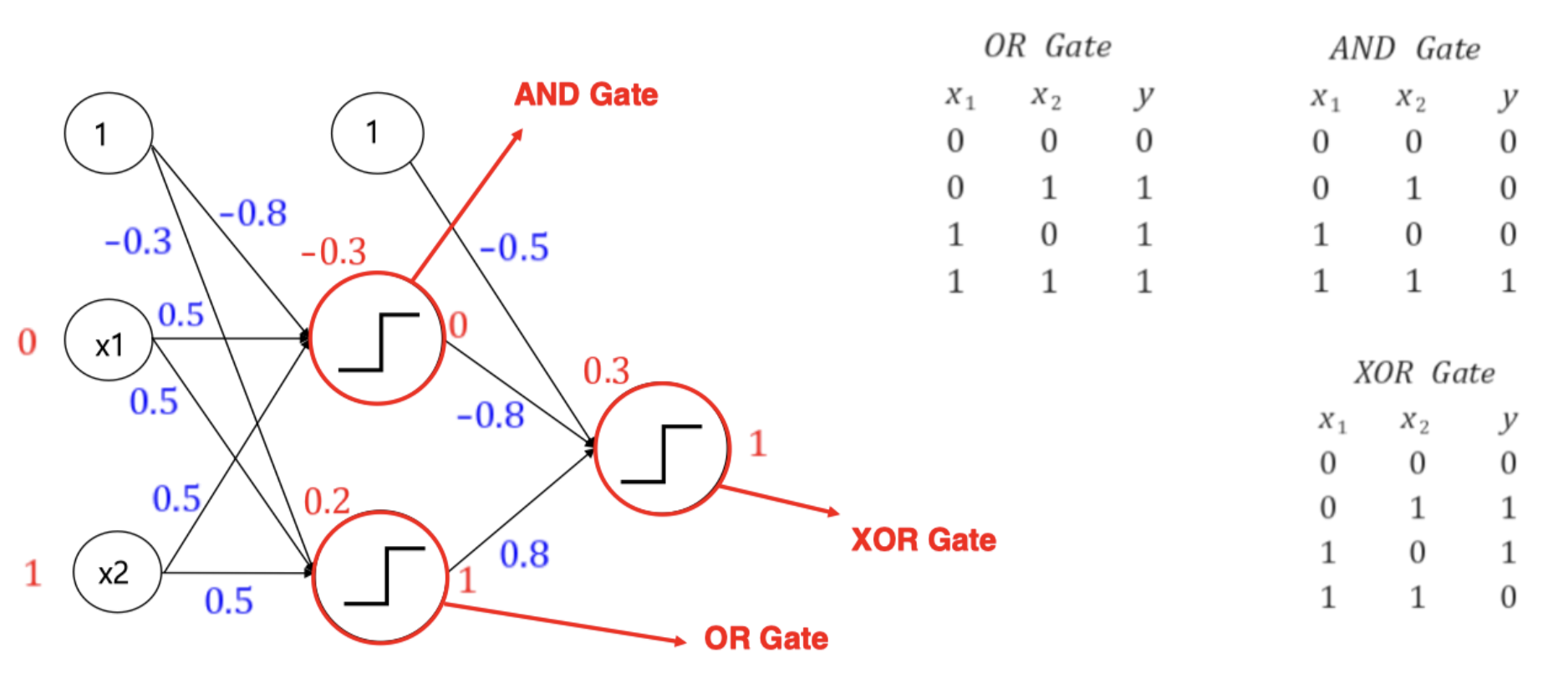
• 단순히 퍼셉트론 두 개를 stacking 하면 XOR 문제가 풀린다.
• MLP 부터는 ANN(Artificial Neural Network) 이라고도 불리고, hidden layer 가 2개 이상인 신경망을 DNN(Deep Neural Network) 이라고 부른다.

신경망 학습방법

• 위처럼 퍼셉트론이 OR, AND, XOR 문제를 풀 때 가중치를 바꿔가면서 풀었는데, 기계가 가중치를 스스로 찾아내도록 자동화시키기 위해서 training 혹은 learning 단계가 필요하다.
• 이 때 다음 포스트에서 다룰 선형, 로지스틱 회귀에서 사용되는 손실 함수(loss func)와 옵티마이저(optimizer)가 사용된다. 학습시키는 인공 신경망이 DNN 일 경우 딥러닝(Deep Learning)이라고 한다.
• 딥러닝 모델의 학습은 역전파라는 과정이 근간을 이루고 있다. 다른 포스트에서 중요한 역전파(Back propagation)에 대해 자세히 정리하자.

• 여기서는 딥러닝의 흐름을 이해하고 어떻게 학습이 되는지 이해하기 위해서 과거의 신경망 학습방법이 어떻게 발전되어 왔는지 간단히 보자.

  Hebb’s rule (Hebbian Learning)

  • 신경망에서 뉴런 사이의 weight 들을 업데이트 시켜주는 메커니즘 중 하나다. Hebb 이 신경망을 학습시키기 위해 제안했다.
  • Hebbian learning 을 요약하면, “cell A 가 cell B 를 자극시키는 데 충분하고 지속적인 원인으로 작용한다면, cell B 에 대한 cell A 의 작용력이 내부적으로 변화를 일으켜 증가하게 된다.” 라고 말할 수 있다.

  • 즉 만일 어떤 신경세포의 활성이 다른 신경세포가 활성하는 데 계속적으로 공헌한다면, 두 신경세포 간의 연결 가중치를 증가시켜야 한다는 것이다.

    \[W_{ij}^{new} = W_{ij}^{old}+{\alpha}\;{\cdot}\;a_ib_j\]
  • $\alpha$ 는 학습률이고, $a_i$ 와 $b_j$ 가 A 와 B 뉴런의 활성화 여부(1 또는 0)다. 두 뉴런이 같이 활성화가 되면 두 뉴런 사이의 가중치가 계속해서 업데이트 된다.
  • 즉 Hebb’s rule 에서 학습은 뉴런들 간의 연결을 만드는 활동이고 하나의 퍼셉트론 입장에서 input 과 output 을 가지고 가중치를 업데이트한다. 이는 Unsupervised Learning 이다. 왜냐하면 정답을 주지 않고 뉴런 활성화 여부가 가중치를 업데이트 하기 때문이다.
  • Hebbian Learning 은 이처럼 Unsupervised Learning 이지만, 이후 목적이 되는 정답값을 이용하면서 Supervised Learning 으로 발전하고, 오늘날 딥러닝 학습의 근간이 되었다.

  Perceptron learning rule

  • Perceptron learning rule 의 핵심 아이디어는 만일 어떤 신경세포의 활성으로 잘못된 출력을 낸다면, 연결 가중치를 오차에 비례하여 조절하여 올바른 예측을 한다는 것이다.

    

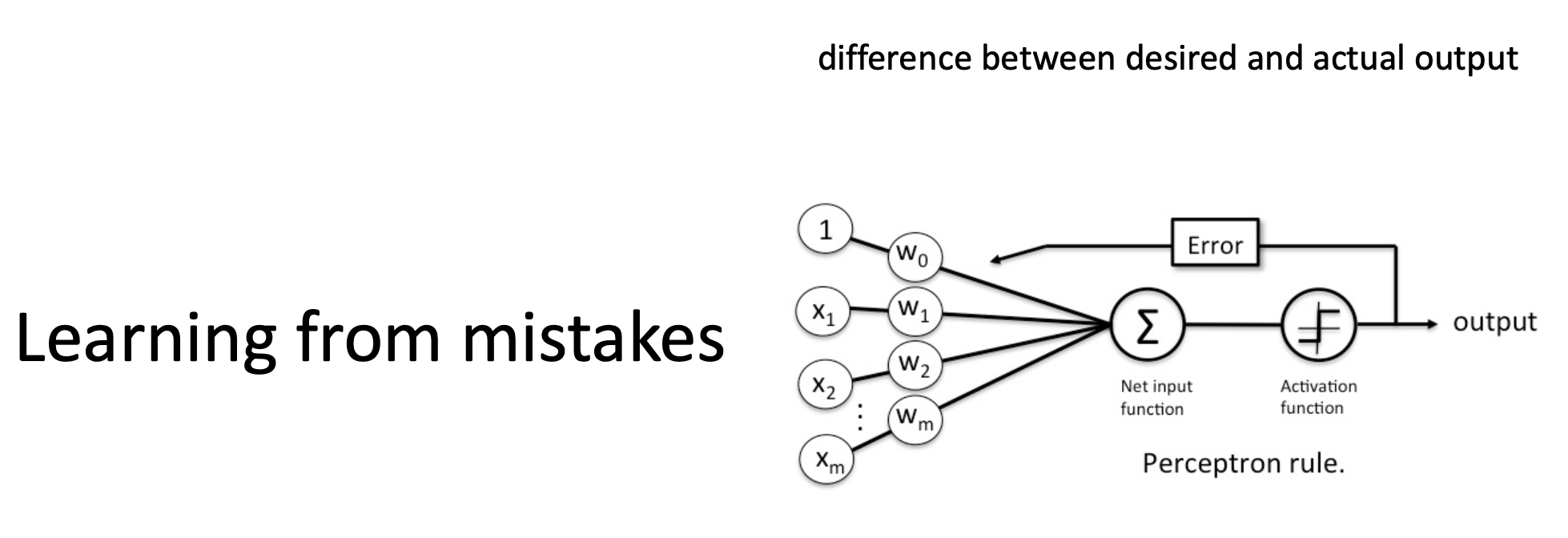
  • 즉 weight 를 학습할 때 목적패턴(정답값)과 예측값을 이용하는 학습 방법이다.

  • 목적패턴과 예측값이 다를 때 입력이 1인 뉴런(활성화된 뉴런)에 대해서만 오차만큼 학습을 시킨다. 이 때 같은 데이터를 여러 번 반복해서 해를 찾는 과정을 거친다.

    $t$ 는 실제값, $z$ 는 예측값. 활성화 함수는 step func 이다.

  • Perceptron learning rule 은 기존의 Hebbian Learning 에서 목적 패턴(정답값)이라는 개념을 도입하여 Supervised Learning 을 한 것으로 보인다. 그렇게 잘못된 출력에 대해서만 가중치를 조정한다.
  • 그러나 이 Perceptron rule 은 단층 퍼셉트론에서 사용되었기 때문에 XOR같은 선형 분리가 불가능한 문제에 대해서는 적절히 학습할 수가 없었다.
  • 즉 Perceptron learning rule 에서는 모든 training example 들이 linearly separable 해야 한다. 만약 linearly separable 하지 않다면, 잘 수렴할지 확신할 수 없다.

  Delta rule (Widrow Hoff Learning Algorithm)

  • 다층 퍼셉트론과 같은 신경망의 학습에 사용된다.

  • delta rule 의 핵심은 gradient descent를 이용하는 것이다. gradient descent 는 이후 포스트에서 다룰 역전파(backpropagation)의 근간이기 때문에 중요하다.

    

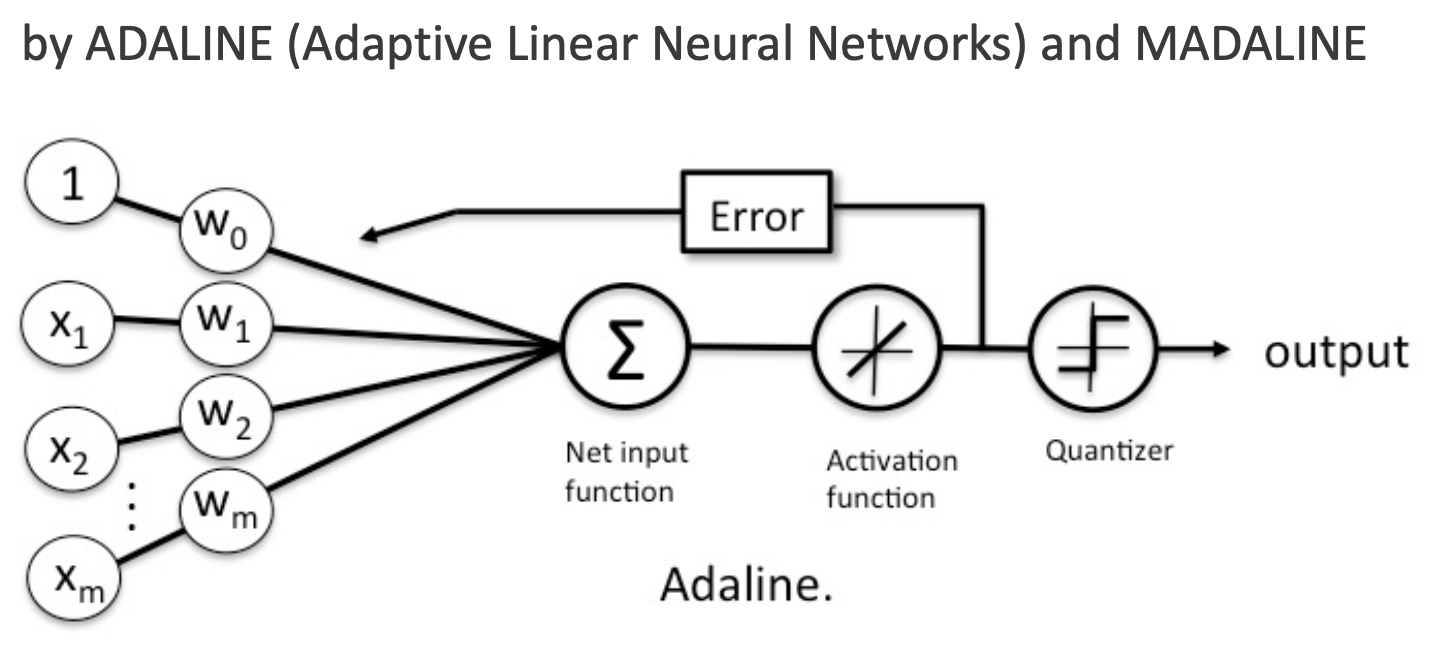
  • Adaline 은 Perceptron 을 발전시킨 인공 신경망이다.
    • Perceptron 의 경우에는 순입력 함수의 출력값을 임계값을 기준으로 1과 -1(혹은 1, 0)로 분류한다.
    • 위에서 본 것처럼 가중치의 업데이트는 입력에 대한 활성함수의 출력값(1 또는 -1)과 실제 결과값이 같은지 다른지에 따라 이루어진다.

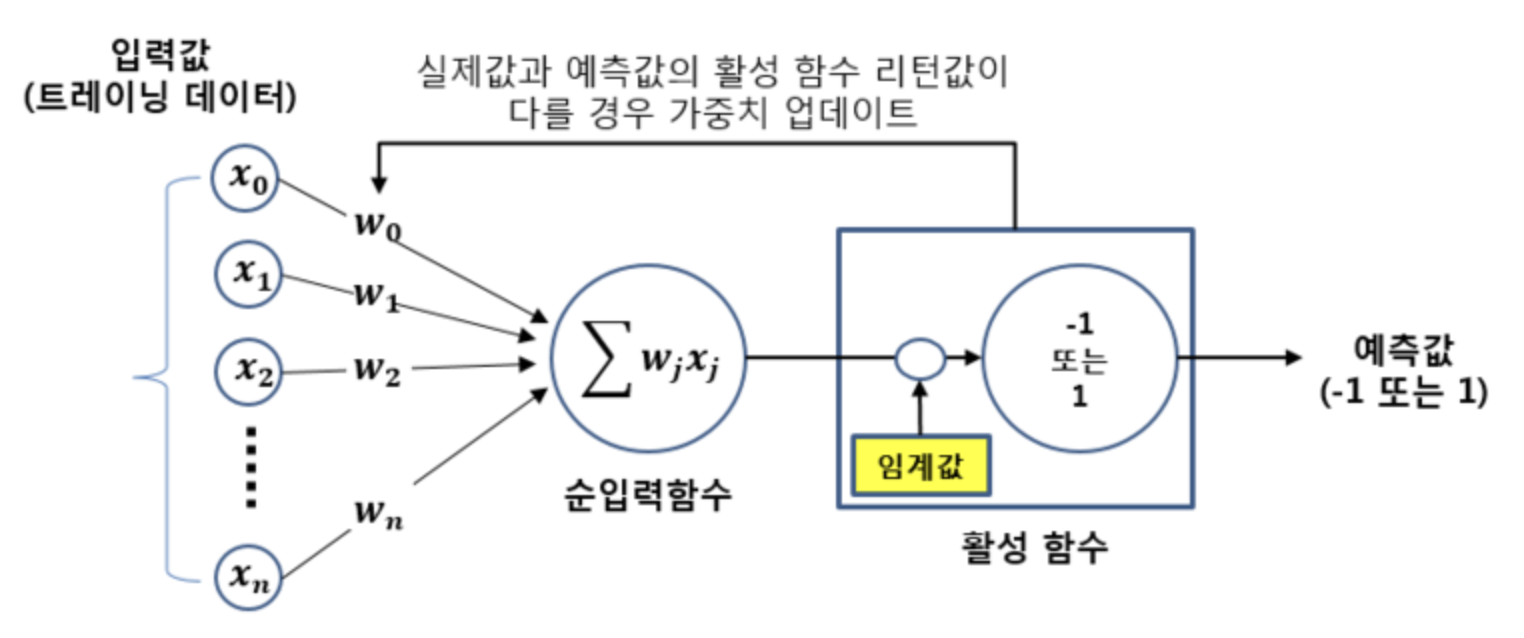    Perceptron

    • 반면에 Adaline은 순입력 함수의 리턴값과 실제 결과값의 오차(Error)가 최소화 되도록 가중치를 조정하게 된다.
    • 또한 Adaline 은 활성화 함수를 거치면 Continous value 를 가진다. 활성화 함수를 거친 출력(예측값)을 실제값과 비교할 때 loss func 으로 MSE 를 활용했다.

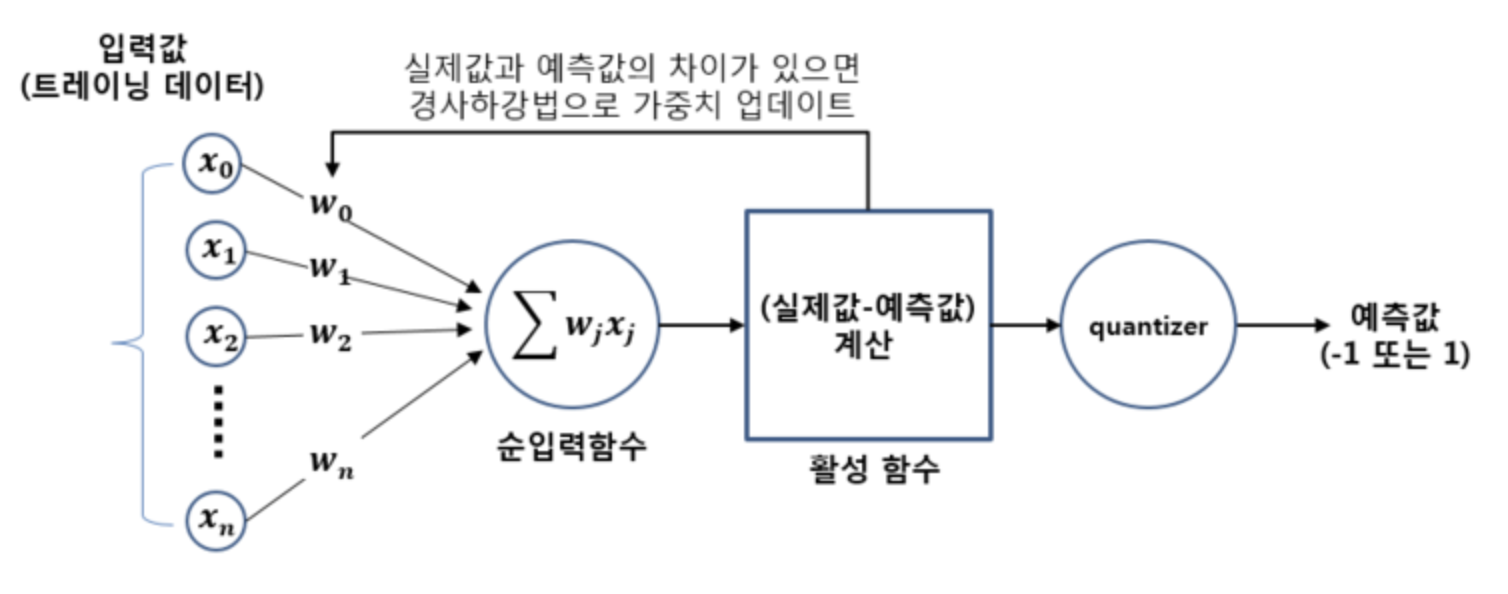    Adaline

  • Gradient Descent는 파라미터 $W$에 대한 error 를 계산하는 목적함수(Objective Func, Loss Func)를 잘 정의하고, 이 함수가 최소화되는 방향을 찾아서 점점 나아가는 것이다.
  • 구체적으로 loss func 을 각 파라미터로 편미분하여, 각 파라미터에 대한 기울기를 구해 local minima 를 향하도록 움직여간다.
  • 이처럼 Delta Rule 은 Perceptron Rule 과 거의 유사하나, 전체 학습 데이터에 대한 오차를 최소화하는 방법이다.
• 이렇게 발전하여 오늘날 gradient descent, back propagation 이 활용되고 있다.

다시 Neural Network

• Neural Network 는 풀고자 하는 문제를 풀도록 설계되는 모델이자 딥러닝에서 계속 해서 등장하는 모델 모두를 아우른다.
• 이러한 Neural Network 는 선형 & 비선형 연산이 반복적으로 일어나는 function approximators 다. 즉, 내가 풀고자 하는 어떤 문제이자 함수를 근사하는 함수이다.
• 그리고 Neural Network 의 학습은 나의 파라미터가 어느 방향으로 움직였을 때 loss func 이 줄어드는 지를 찾고 그 방향으로 파라미터를 바꾸는 것이 목적이다.

• 이 때 업데이트되는 파라미터는 가중치 $w$ 와 편향 $b$ 다.

  

  

  

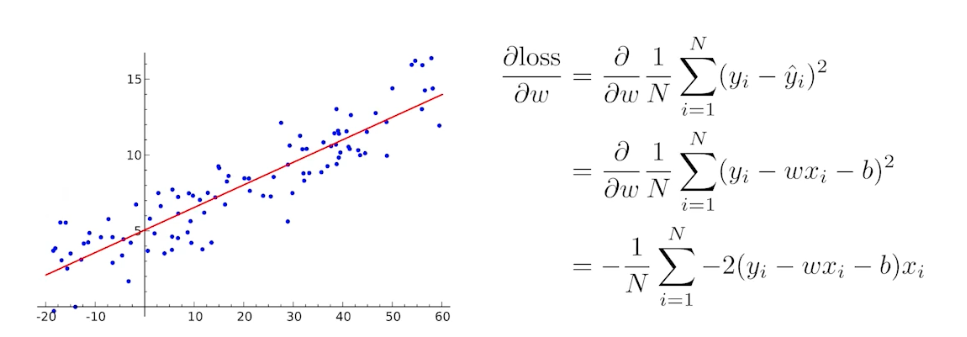
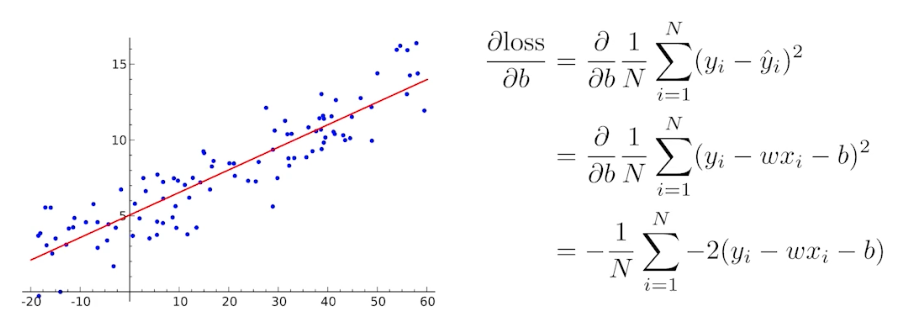
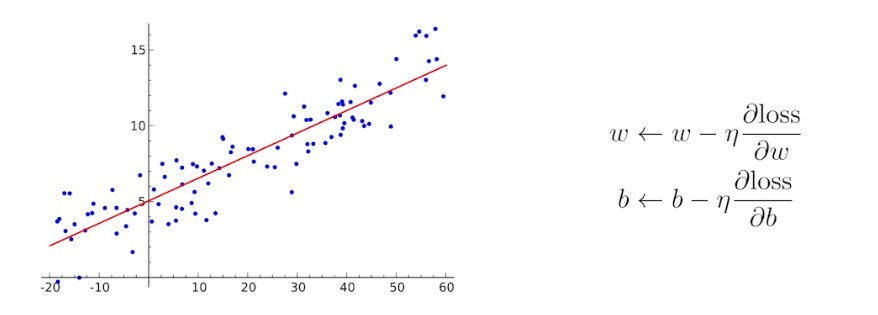
• 딥러닝이 어려운 점은 단순히 linear 한 변환만 있는 것이 아니라는 점이다.
• 딥러닝에서는 loss func 이 local minima 로 향하도록 하는 파라미터($W$, weights)들을 찾는 것이 목적이고, 이 파라미터들은 행렬로 표현된다.

• 행렬은 두 개의 벡터 스페이스 사이의 변환이라고 해석할 수 있다. 즉 선형성을 가지는 변환이 있을 때, 그 변환은 항상 행렬로 표현된다. 어떤 행렬을 찾겠다는 것은 두 개의 벡터 스페이스(두 차원) 사이에 선형 변환을 찾겠다는 것이다.

  

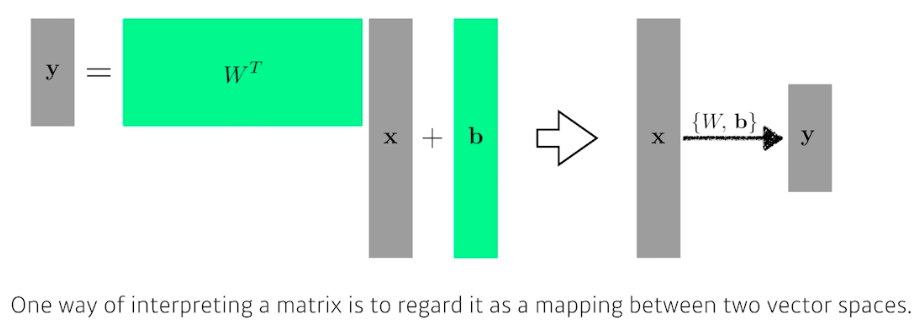
• 이 때 현실세계의 문제를 더 잘 근사하고 표현하기 위해서는 non-linearity 가 필요하고 이를 위해 MLP 에서는 퍼셉트론을 2개 이상 stack 했다.

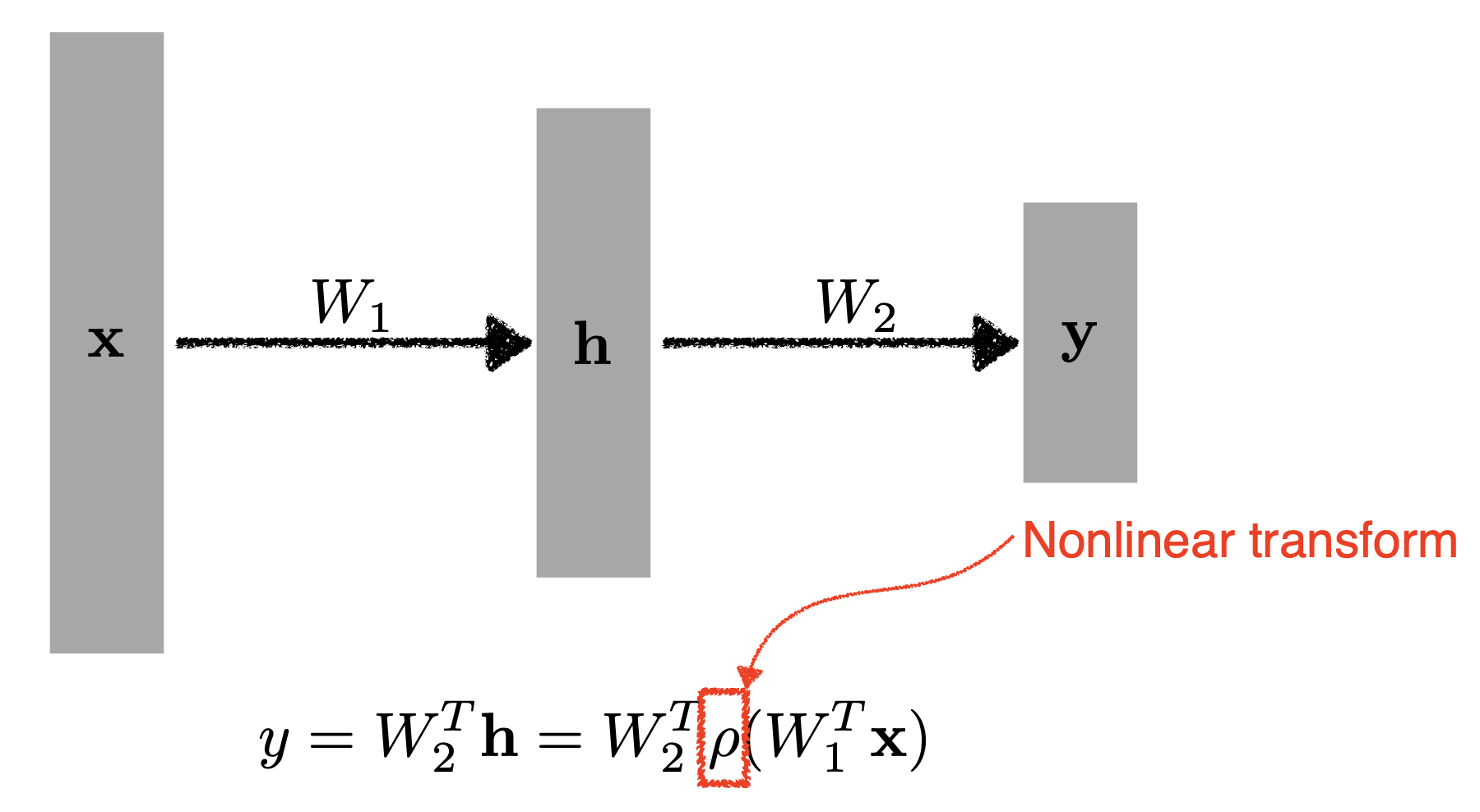  $\rho$ 는 activation func 이다.

• 이처럼 네트워크가 표현하는 표현력을 극대화하기 위해서 단순히 선형결합을 $n$ 번 반복하는 게 아니라, 한번 선형변환(affine)이 오면 activation func 을 이용해서 Non-linear transform 을 거친다.
• 그렇게 얻어지는 feature vec 를 다시 선형변환, 비선형변환 거치는 것을 $n$ 번 반복하면 더 많은 표현력을 가진다. 이것이 보통의 Neural Network 이다!
• 어떤 활성화 함수(비선형 변환)가 있어야 딥러닝에서 의미가 있지만, 어떤 함수가 좋은지는 모른다. 상황마다 다르기 때문에 공부와 경험이 필요하다.
• 앞으로 공부할 때는 어떤 loss func 이 어떤 성질을 가지고, 이게 왜 내가 원하는 결과를 얻어낼 수 있는지를 반드시 알아야 한다! 모든 loss 가 내가 원하는 문제를 완벽히 푼다고 할 수 없기 때문이다.
• 예를 들어 회귀에서 보통 사용되는 MSE 는 이상치가 있을 때 그 이상치를 맞추려고 하다 보면 네트워크가 망가질 수도 있다!
• 또한 분류 문제에서 MSE 보다 Cross Entropy 가 더 많이 사용되는 이유도 알면 좋다.

맨 위로 이동 ↑