[Algorithm] 4. Priority Queue

우선순위 큐(Priority Queue)

• 우선순위 큐는 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조이다.
• 즉, 우선순위 큐는 데이터를 우선순위에 따라 처리하고 싶을 때 사용한다.
• 예시로, 물건 데이터를 자료구조에 넣었다가 가치가 높은 물건부터 꺼내서 확인해야 하는 경우를 들 수 있다.
• 구현 방법은 아래와 같다.
  • 리스트를 이용해서 구현할 수 있다.
  • 힙(heap)을 이용해서 구현할 수 있다.
  • 데이터의 개수가 N 개일 때, 구현 방식에 따라서 시간 복잡도를 비교하면
    • 리스트 : 삽입시간 $O(1)$, 삭제시간 $O(N)$
    • 힙(Heap) : 삽입시간 $O(logN)$, 삭제시간 $O(logN)$
  • 힙 자료구조를 이용하면, 단순히 N 개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일하다. 이 경우 시간 복잡도는 $O(NlogN)$ 이다.

힙(Heap)

• 힙(Heap)의 특징
  • 힙은 완전 이진 트리 자료구조의 일종이다.
  • 힙에서는 항상 루트 노드를 제거한다.
  • 최소 힙(min heap)
    • 루트 노드가 가장 작은 값을 가진다.
    • 따라서 값이 작은 데이터가 우선적으로 제거된다.
  • 최대 힙(max heap)
    • 루트 노드가 가장 큰 값을 가진다.
    • 따라서 값이 큰 데이터가 우선적으로 제거된다.
  • 완전 이진 트리
    • 힙은 완전 이진 트리를 따른다.
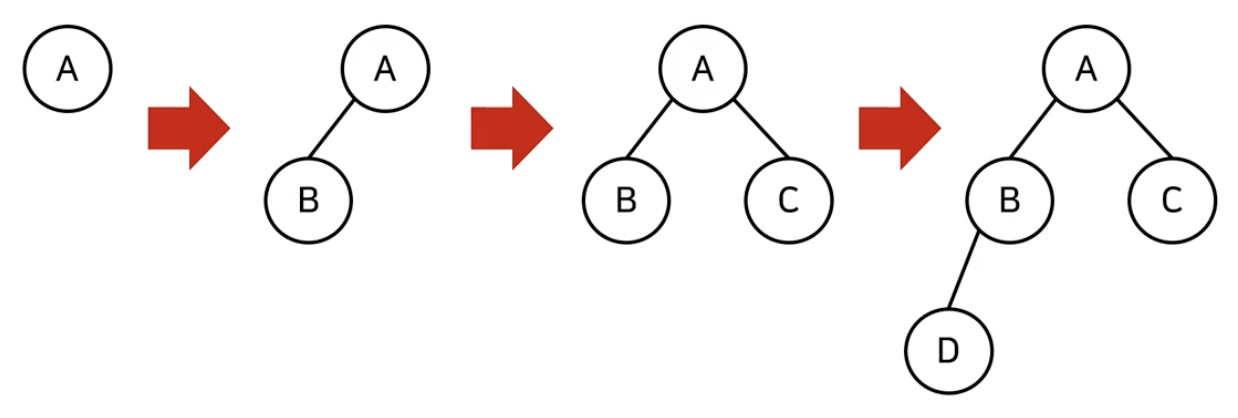
    • 완전 이진 트리란 루트 노드부터 시작하여 왼쪽 자식노드, 오른쪽 자식노드 순서대로 데이터가 차례대로 삽입되는 트리를 의미한다.

    

최소 힙 구성 함수

• 어떠한 데이터를 힙에 넣었을 때, 그 힙 자료구조가 힙의 성질을 가지도록 만드려면 어떻게 해야할까?
• 일반적으로 힙을 구성하기 위한 함수의 이름을 보통 heapify 라고 부른다.
• 이 때 heapify 는 상향식과 하향식으로 구현할 수 있다.
• 실제로 상향식에서는 하나의 데이터가 들어왔을 때 들어온 데이터로부터 부모 쪽으로 거슬러 올라가면서 매번 부모보다 자신의 값이 더 작은 경우에 위치를 바꿀 수 있도록 한다.
• 예를 들어, 새로운 데이터가 최소 힙 성질을 만족하지 않으면(부모보다 자식이 크면) 최소 힙 성질을 만족하도록 서브 트리가 구성된다.
• 새로운 원소가 들어왔을 때 heapify 를 이용하면 $O(logN)$ 의 시간복잡도로 힙의 성질을 유지하도록 할 수 있다.
• 기본적으로 힙 자료구조는 완전 이진트리를 따르기 때문에 균형잡힌 트리로서 동작한다. 그렇기 때문에 항상 부모쪽으로 거슬러 올라가거나, 다시 부모에서 자식으로 내려올 때 최악의 경우에도 $O(logN)$ 의 시간복잡도를 보장할 수 있다.
• 힙에서 원소가 제거될 때는 $O(logN)$ 의 시간복잡도로 힙 성질을 유지하도록 할 수 있다.
• 원소를 제거할 때는 가장 마지막 노드가 루트 노드의 위치에 오도록 한다.
• 이후 루트 노드에서부터 하향식으로(더 작은 자식 노드로) heapify() 를 진행한다.
• 파이썬의 경우 기본적으로 heap 자료구조가 min heap 형태로 동작한다. max heap 으로 동작하고자 한다면 데이터를 넣을 때와 데이터를 꺼낼 때 - 를 붙여서 데이터를 꺼내면 max heap 으로 동작한다.

• 아래의 코드는 우선순위 큐(힙 자료구조)를 이용한 오름차순 정렬이다.

    import heapq
      
    def heapsort(iterable):
        h = []
        result = []
        # 모든 원소를 차례대로 힙에 삽입
        for value in iterable:
            heapq.heappush(h, value)
        # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
        for i in range(len(h)):
            result.append(heapq.heappop(h))
        return result
  

• 내림차순 정렬

    import heapq
      
    def heapsort(iterable):
        h = []
        result = []
        # 모든 원소를 차례대로 힙에 삽입. max heap 으로 동작해야 하기 때문에 - 를 붙인다.
        for value in iterable:
            heapq.heappush(h, -value)
        # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
        for i in range(len(h)):
            result.append(-heapq.heappop(h))
        return result
  

맨 위로 이동 ↑