[Algorithm] 19. Graphs - Markov Chain

마르코프 체인

• 마르코프 체인(Markov Chain)은 마르코프 성질을 가진 이산확률과정이다.
• 마르코프 성질은 ‘특정 상태의 확률은 오직 과거의 상태에 의존한다’라는 것으로, $n+1$회의 상태(state)는 $n$회의 상태나 그 이전 $n-1, n-2, \cdots$ 의 상태에 의해 결정된다.
• 즉 현재 상태가 미래 상태에 영향을 주는 유일한 변수이다.
• 예를 들어 오늘의 날씨가 맑다면 내일의 날씨는 맑을지 비가 내릴지를 확률적으로 표현할 수 있다. 물론 실제 날씨 예보라는 건 굉장히 복잡한 변수들과 모델링을 거쳐서 생성되지만 이러한 연속적인 현상을 단순히 표현할 때는 마르코프 체인을 가정하고 쓸 수 있고, 종종 단순한 모델이 강력한 효과를 발휘할 때도 있다.
• 마르코프 체인은 주로 베이지안 통계학이나 강화학습에 사용되며, MCMC(Markov Chain Monte Carlo)와도 연결되어 사용된다.

마르코프 체인 예시

• 마르코프 성질 여부에 대한 흔한 예시로는 동전 앞뒤 예측과 날씨 예측이 있다.
• 동전 앞뒤를 예측하는 것은 독립시행이기 때문에 $n$번째 상태가 $n+1$번째 상태에 영향을 주지 않으므로 마르코프 성질이 없다.

• 반면 날씨 예측과 같이 직관적으로 오늘 날씨에 의해 내일 날씨가 결정될 수 있으므로 마르코프 성질이 있다고 할 수 있다. 만약 오늘을 기반으로 하루 뒤를 예측한다면 1차 마르코프 모델이라하고 이틀 뒤를 예측한다면 2차 마르코프 모델이라 한다.

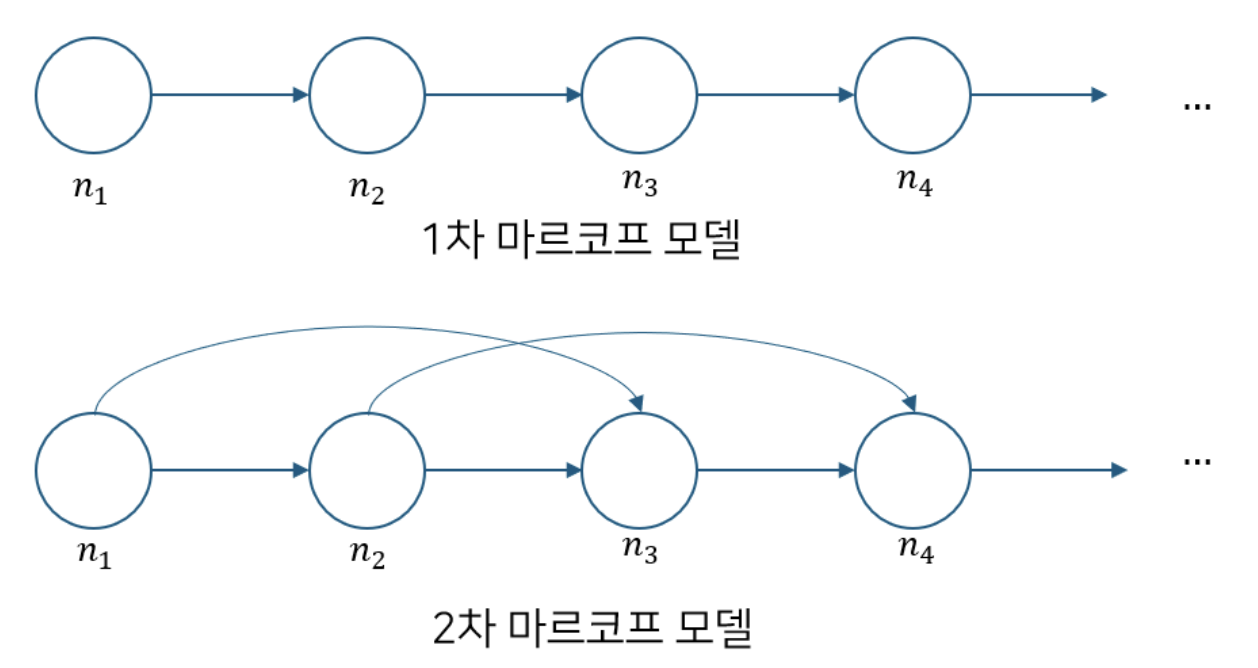  이미지 출처: https://roytravel.tistory.com/358

마르코프 모델

• 마르코프 모델이란 마르코프 체인을 기반으로 만든 확률 모델이다. 즉 상태가 시간에 따라 변화하는 확률적 과정을 나타내는 모델이다.내일 날씨를 예측하는 마르코프 모델을 만들어보자.
• 마르코프 모델을 만들기 위해선 가장 먼저 각 상태를 정의해야 한다. 그리고 이 상태는 상태 전이 확률로 나타낸다. 상태 전이 확률이란 어떤 상태에서 다른 상태로 이동할 확률을 의미한다.
• 상태 전이 확률을 행렬로 표현한 것을 전이 행렬(Transition Matrix)라고 한다.
• 상태 전이 행렬의 원소 $P[i][j]$는 상태 $i$에서 상태 $j$로 전환될 확률을 나타낸다.

• 현재 상태에서 다음 상태로 전환하는 과정은 현재 상태에 기반한 확률적 선택이다. 예를 들어, 현재 상태가 $i$라면, $P[i]$행의 값들을 기반으로 다음 상태를 확률적으로 선택한다.

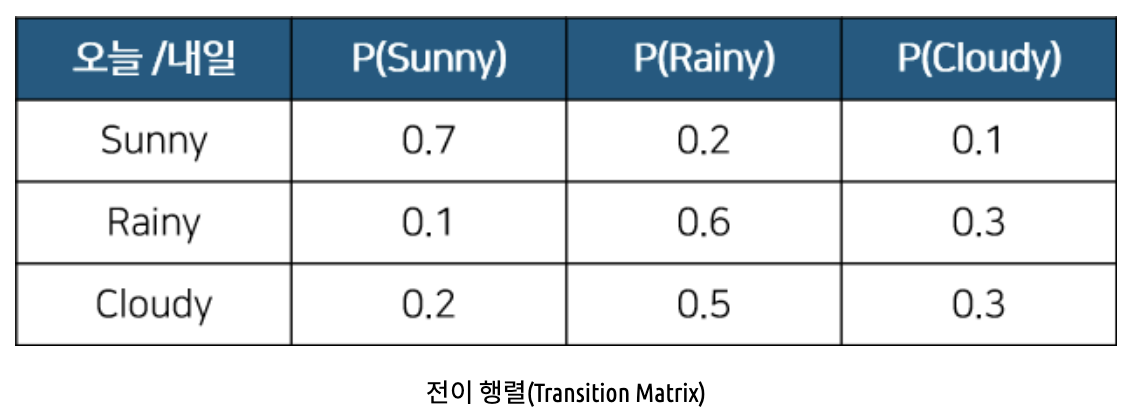  이미지 출처: https://roytravel.tistory.com/358

• 위 전이 행렬을 해석하면, 오늘 날씨가 Sunny 일 때 내일 Suuny일 확률이 0.7, Rainy일 확률이 0.2, Cloudy일 확률이 0.1이라 예측한다.
• 이를 기반으로 오늘이 어떤 특정 날씨일 때 내일이 어떤 특정 날씨일 확률을 구하기 위해서는 오늘 날씨가 $P[i]$라고할 때 내일의 날씨 $P[i][j]$ 를 구할 수 있다.
• 만약 오늘 날씨를 기반으로 이틀 뒤 날씨를 예측하고 싶다면 $P[P[i][j]][j]$ 를 계산하면 된다.
• 참고로 전이 행렬을 거듭 곱하다보면 더 이상 전이 행렬의 값이 변하지 않고 수렴하는 상태가 오는데 이를 안정 상태(Steady State)라고 한다. 즉 행렬 $P$는 거듭곱을 통해 어떤 행렬 $P^\prime$이 되지만 수렴한 뒤에는 $P$가 된다.

• 또 전이 행렬은 도식화 가능하다. 이 도식화한 것을 상태 전이도(State Transition Diagram)라고 하며 아래와 같다.

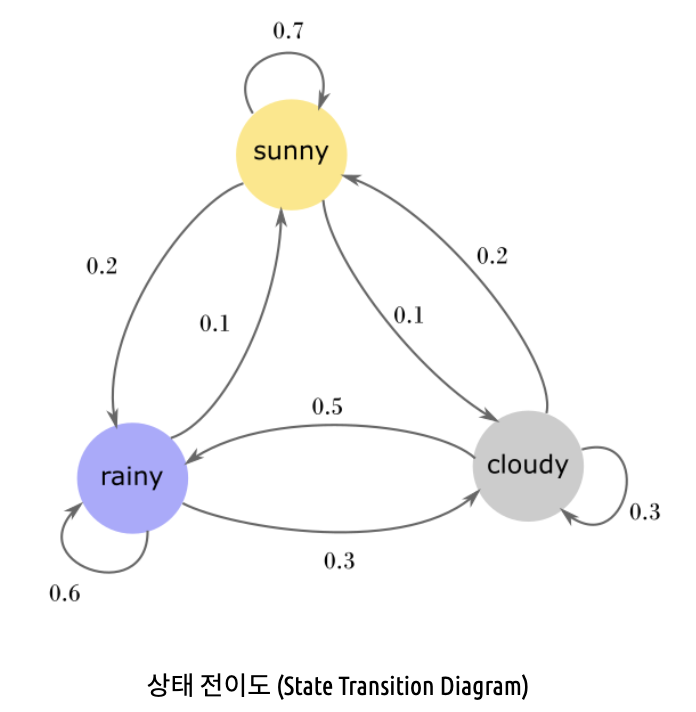  이미지 출처: https://roytravel.tistory.com/358

마르코프 체인 구현

import numpy as np

class MarkovChain:
    def __init__(self, transition_matrix, states):
        # 상태 전이 행렬
        self.transition_matrix = np.array(transition_matrix)
        self.states = states
        self.num_states = len(states)

    # step 별 상태를 기록하는 함수
    def generate_sequence(self, start_state, steps):
        state_sequence = [start_state]
        current_state = start_state

        for _ in range(steps):
            next_state = np.random.choice(self.states, p=self.transition_matrix[self.states.index(current_state)])
            state_sequence.append(next_state)
            current_state = next_state

        return state_sequence

    # 특정 step 의 상태를 출력하는 함수
    def transition_at_step(self, start_state, steps):
        current_state = start_state

        for _ in range(steps):
            current_state = np.random.choice(self.states, p=self.transition_matrix[self.states.index(current_state)])

        return current_state

    # 특정 step 후 특정 상태의 확률을 출력하는 함수
    def probability_of_state_after_steps(self, start_state, target_state, steps):
        current_state = start_state
        state_index = self.states.index(target_state)
        
        for _ in range(steps):
            current_state = np.random.choice(self.states, p=self.transition_matrix[self.states.index(current_state)])

        return self.transition_matrix[self.states.index(current_state), state_index]

# 예제
if __name__ == "__main__":

    states = ['Sunny', 'Rainy', 'Cloudy']
    transition_matrix = [
        [0.7, 0.2, 0.1],
        [0.1, 0.6, 0.3],
        [0.2, 0.5, 0.3]
    ]

    mc = MarkovChain(transition_matrix, states)

    start_state = 'Sunny' # 오늘 날씨

    # 오늘이 Sunny 일 때 5일 동안의 날씨 확률
    steps = 5
    sequence = mc.generate_sequence(start_state, steps)
    print(f"오늘 상태가 {start_state} 일 때 {steps} 동안의 날씨 확률")
    print(sequence)

    # 오늘이 Sunny 일 때 3일 후의 날씨
    steps = 3
    final_state = mc.transition_at_step(start_state, steps)
    print(f"{steps}일 후 날씨는 {final_state}")

    # 오늘이 Sunny 일 때 2일 후에 Cloudy 일 확률
    target_state = 'Cloudy'
    steps = 2
    probability = mc.probability_of_state_after_steps(start_state, target_state, steps)
    print(f"{steps}일 후에 {target_state} 일 확률은 {probability:.4f}")

맨 위로 이동 ↑