[Algorithm] 18. Graphs - Hamilton Path
해밀턴 경로, 해밀턴 회로
- 오일러 경로, 오일러 회로와 같이 그래프 이론에서 중요한 개념이다.
- 해밀턴 경로(Hamiltonian Path)는 그래프의 모든 정점을 한 번씩 지나는 경로다. 이 때 정점은 중복 방문하지 않는다.
-
해밀턴 회로(Hamiltonian Circuit)는 해밀턴 경로 중 시작점과 마지막점이 같은 경우이다.
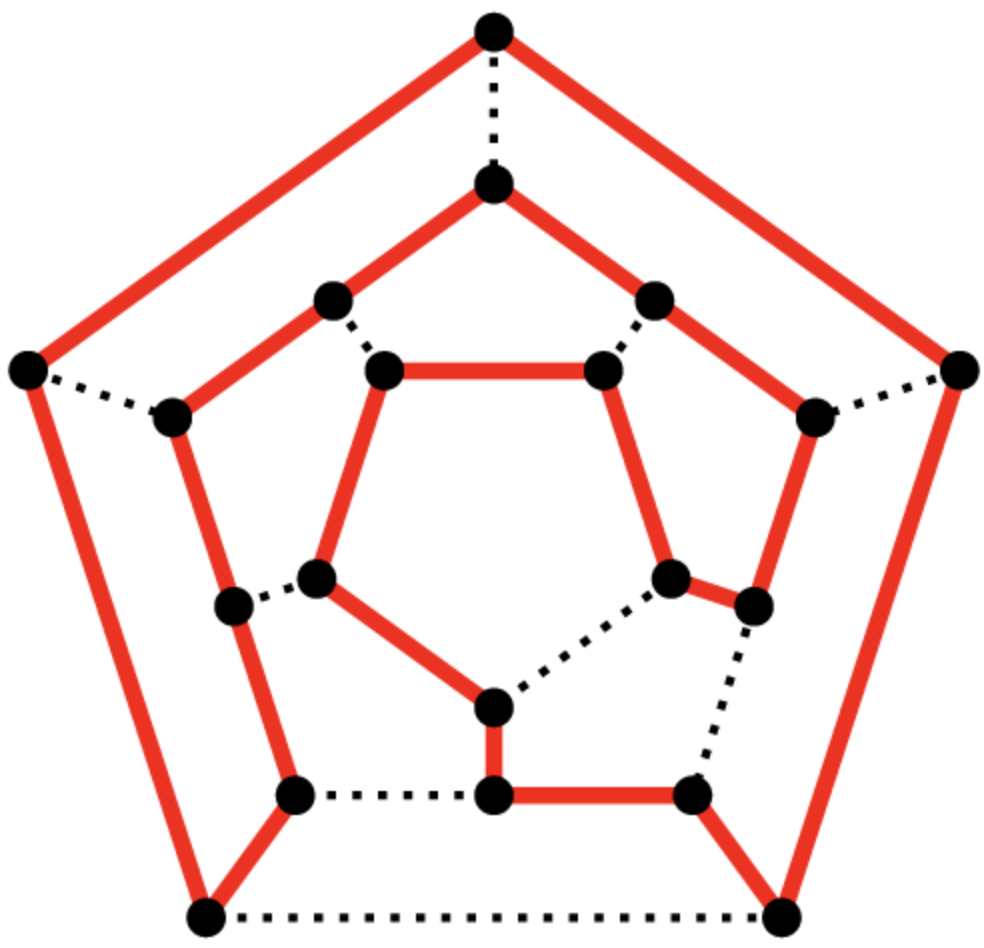해밀턴 회로. 이미지 출처: https://torbjorn.tistory.com/240 - 오일러 회로와는 다르게 어떤 그래프가 해밀턴 경로인지, 해밀턴 회로인지 여부를 묻는 문제는 NP-Complete 문제다.
- 오일러 그래프와 해밀턴 그래프 사이에는 관계가 없다.
- NP-Complete 문제는 다항시간 내에 풀 수 없는 NP-hard 문제이다. 즉 정확한 해결을 위해서는 모든 경우를 탐색하는 경우의 수 알고리즘을 사용해야 한다.
- 일반적으로 해밀턴 경로와 해밀턴 회로를 찾기 위해서는 백트래킹(Backtracking)을 기반으로 하는 방법이 사용된다.
- 현재 NP-complete 문제를 위한 모든 알려진 알고리즘들은 문제의 크기에서 지수적인 (exponential) 시간을 요구한다.
- NP-complete에 대해서는 완전한 진짜 정답을 찾기 보다는 훨씬 적은 양의 계산을 통해서 정답에 가까운 값을 찾는데 만족한다. 어떤 더 빠른 알고리즘이 있는지는 모른다.
해밀턴 경로
- 해밀턴 경로는 출발 정점에 따라 값이 다르다.
- 한 정점에서 출발해서 모든 정점을 한 번씩 방문하면 그때의 방문 순서가 해밀턴 경로이다.
- 해밀턴 경로가 존재하기 위한 조건은 그래프의 정점의 수가 $n$ 일 때, 정점 1개 또는 2개는 $\frac{n}{2}$ 미만의 차수를 가져야 한다. 그러나 이러한 조건은 여러 조건들 중 하나일 뿐이며, 해밀턴 경로 존재의 필요조건이 아닌 충분조건이다.
- 즉 위 조건을 만족하는 그래프가 있으면 해밀턴 경로가 존재하지만, 위 조건을 만족하지 않는다고 해도 해밀턴 경로가 존재할 수 있다.
- 따라서 백트래킹 등 알고리즘으로 완전탐색 하는 접근이 좋다.
- 해밀턴 회로와 다르게 마지막 정점에서 다시 출발 정점으로 갈 필요는 없다.
def hamiltonian_path(graph): n = len(graph) path = [-1] * n # 경로를 저장할 배열 visited = [False] * n # 방문 여부를 저장할 배열 # pos는 현재 경로에서 몇 번째 정점을 방문하고 있는지를 나타낸다. # 재귀 함수 hamiltonian_util이 호출될 때마다 pos가 1씩 증가하며, 모든 정점을 방문했는지 확인. # path 배열의 pos 위치에 현재 방문한 정점을 기록 def is_valid(v, pos): # v가 현재위치(pos)에서 유효한 정점인지 확인한다. if not visited[v]: # 방문하지 않은 정점이고 전 위치(pos-1)에서 현재정점(v)로의 간선이 있으면 유효하다. if pos == 0 or graph[path[pos-1]][v]: return True return False def hamiltonian_util(pos): ''' 백트래킹을 사용하여 모든 정점을 방문하는 경로를 찾는다. 재귀적으로 호출하여 경로를 찾고, 실패하면 이전 상태로 돌아간다. ''' # 모든 정점을 방문한 경우 해밀턴 경로를 찾은 것 if pos == n: return True for v in range(1, n): # 시작 정점은 0이므로 1부터 시작 if is_valid(v, pos): path[pos] = v visited[v] = True if hamiltonian_util(pos + 1): return True # Back tracking path[pos] = -1 visited[v] = False return False # 시작 정점 0. -> 해밀턴 경로가 존재하지 않으면 다른 정점에서 시작해봐야 할 수도 있다. path[0] = 0 visited[0] = True if not hamiltonian_util(1): print("해밀턴 경로가 없다.") return False print("해밀턴 경로:", path) return True # 예제 graph = [ [0, 1, 1, 1, 0], [1, 0, 1, 0, 1], [1, 1, 0, 1, 0], [1, 0, 1, 0, 1], [0, 1, 0, 1, 0] ] hamiltonian_path(graph)
해밀턴 회로
- 한 정점에서 출발해서 모든 정점을 딱 한 번씩 방문하고 다시 출발 정점으로 돌아와야 한다.
- 출발 정점과 해밀턴 회로는 무관하다.
- 해밀턴 회로의 존재는 정점 차수와 관계가 없으며 모든 정점의 차수가 짝수라 하더라도 존재하는 경우도 있고 그렇지 않은 경우도 있다. 결과적으로 해밀토니언 회로를 찾기 위한 조건은 아직 밝혀지지 않았으며 시행착오에 의해 찾아야만 한다.
def hamiltonian_circuit(graph): n = len(graph) path = [-1] * n # 경로를 저장할 배열 visited = [False] * n # 방문 여부를 저장할 배열 def is_valid(v, pos): # v가 pos 위치에서 유효한 정점인지 확인 if not visited[v]: # pos-1에서 v로의 간선이 있으면 유효 if pos == 0 or graph[path[pos-1]][v]: return True return False def hamiltonian_util(pos): # 모든 정점을 방문한 경우 해밀턴 회로를 찾은 것 if pos == n: # 경로를 찾는 과정은 해밀턴 경로와 유사하지만, 마지막에 시작 정점으로 돌아오는 조건을 추가 # 시작 정점으로 돌아오는지 확인 if graph[path[pos-1]][path[0]]: return True else: return False for v in range(1, n): # 시작 정점은 0이므로 1부터 시작 if is_valid(v, pos): path[pos] = v visited[v] = True if hamiltonian_util(pos + 1): return True # Backtrack path[pos] = -1 visited[v] = False return False # 시작 정점을 0 path[0] = 0 visited[0] = True if not hamiltonian_util(1): print("해밀턴 회로가 없습니다.") return False print("해밀턴 회로:", path + [path[0]]) return True # 예제 graph = [ [0, 1, 1, 1, 0], [1, 0, 1, 0, 1], [1, 1, 0, 1, 0], [1, 0, 1, 0, 1], [0, 1, 0, 1, 0] ] hamiltonian_circuit(graph)
directed 해밀턴 경로, 해밀턴 회로
- 해밀턴 경로, 해밀턴 회로는 정점을 한번씩만 지나는 그래프이기 때문에 그래프를 만들 때 인접행렬로 만들어주면 undirected 해밀턴 알고리즘과 유사하게 쓸 수 있다.
- 전 정점 위치(pos-1)에서 현재 정점(v)으로 간선이 있는지 확인하기 때문이다.
해밀턴 경로, 해밀턴 회로 시간복잡도
- 해밀턴 경로 알고리즘은 백트래킹을 기반으로 하며, 모든 가능한 경로를 탐색한다.
- 각 단계마다 선택할 수 있는 정점의 수는 $n-1$개이다. (시작 정점을 제외)
- 경로를 구성하는 각 단계마다 최대 $n−1$개의 선택지가 있으며, 이는 $n−1$번의 재귀 호출이 이루어질 수 있음을 의미한다.
- 따라서 모든 가능한 순열을 생성하고 검사하는 과정에서 $O(n!)$의 시간 복잡도가 필요하다.
- 정리하면, 해밀턴 경로와 해밀턴 회로를 찾는 알고리즘은 모든 가능한 순열을 탐색하며 정확한 해를 찾기 때문에 시간 복잡도가 $O(n!)$이고, 이는 입력 그래프의 크기가 커질수록 계산 시간이 급격히 증가하는 것을 의미한다.
- 따라서 큰 그래프에 대해서는 효율적인 해결책을 찾기 위해 다른 방법이나 최적화 기법을 사용해야 한다.
댓글 남기기