Bkkhyunn

Bkkhyunn

배움과 경험을 기록하고,
세상과 사람을 매개하는
AI 개발자가 되기까지

[Algorithm] 17. Graphs - Euler Path

오일러 경로, 오일러 회로

  • 그래프 이론에서 중요한 개념이다.
  • 무향(undirected)이나 유향(directed) 그래프가 있을 때, 그래프에 존재하는 모든 간선을 정확히 1번씩만 방문하는 연속된 경로가 오일러 경로이고, 오일러 경로에서 시작점과 도착점이 같으면 오일러 회로가 된다.

오일러 경로

오일러 경로(Eulerian Path)에 대해 알아보자.

오일러 경로 조건
  • 오일러 경로는 무향 그래프에서 다음과 같은 조건을 만족해야 한다.
    1. 그래프의 모든 간선을 한 번씩만 지나야 한다.
    2. 유향/무향 관계없이 연결 그래프(모든 정점이 서로 연결되어 있는 그래프)여야 한다. 즉 서로 다른 간선이 있는 컴포넌트가 존재해서는 안된다.
      • 그러나 간선이 없이 떨어져 있는 정점이 있다면 오일러 경로는 존재할 수 있다.
    3. 정확히 두 개의 정점이 홀수 차수를 가져야 한다. 두 정점은 시작점과 끝점이며 각각 홀수 차수의 간선을 가진다.
  • 차수란 정점에 부속되어 있는 간선의 수를 의미한다.
  • 오일러 경로는 시작점을 어느 지점으로 하느냐에 따라 몇몇의 간선을 지나지 못할 수도 있다.

  • 아래의 그림이 오일러 경로의 조건을 만족한다.

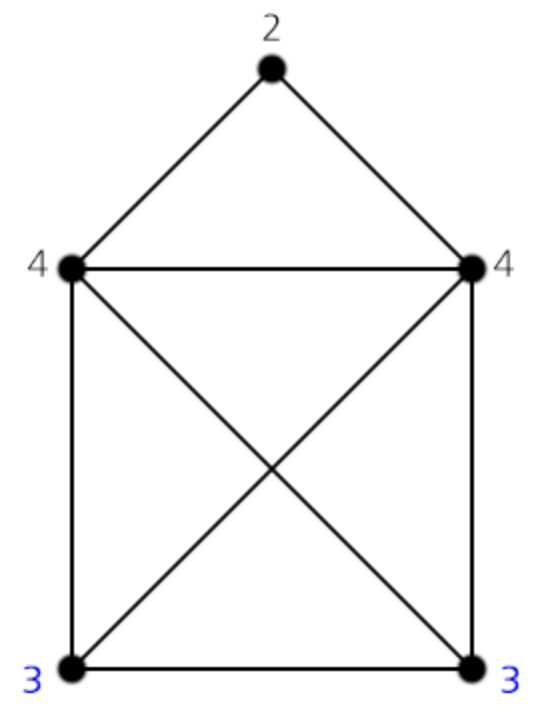    Untitled이미지 출처: https://velog.io/@ddochi132/w26d5a3f

  • 유향 그래프에서 오일러 경로가 존재하려면 indegree(진입차수)가 1 적은 정점 하나가 시작점, outdegree(진출차수)가 1 적은 정점 하나가 끝점으로 정해진다.
  • 또한 다른 indegree와 outdegree가 불일치하는 정점이 더 있으면 안되고, 1씩 차이가 나지 않아도 안된다.

오일러 회로

오일러 회로(Eulerian Circuit)에 대해 알아보자.

오일러 회로 조건
  • 오일러 회로는 무향 그래프에서 다음과 같은 조건을 만족해야 한다.
    1. 그래프의 모든 간선을 한 번씩만 지나야 한다.
    2. 유향/무향 관계없이 연결 그래프여야 한다. 즉 서로 다른 간선이 있는 컴포넌트가 존재해서는 안된다.
    3. 모든 정점이 짝수 차수를 가져야 한다. 즉, 시작점과 끝점이 동일하기 때문에 모든 정점의 차수가 짝수여야 한다.

  • 오일러 회로는 존재만 한다면 그 어떤 정점을 시작점으로 뽑아도 만드는 것이 가능하다.

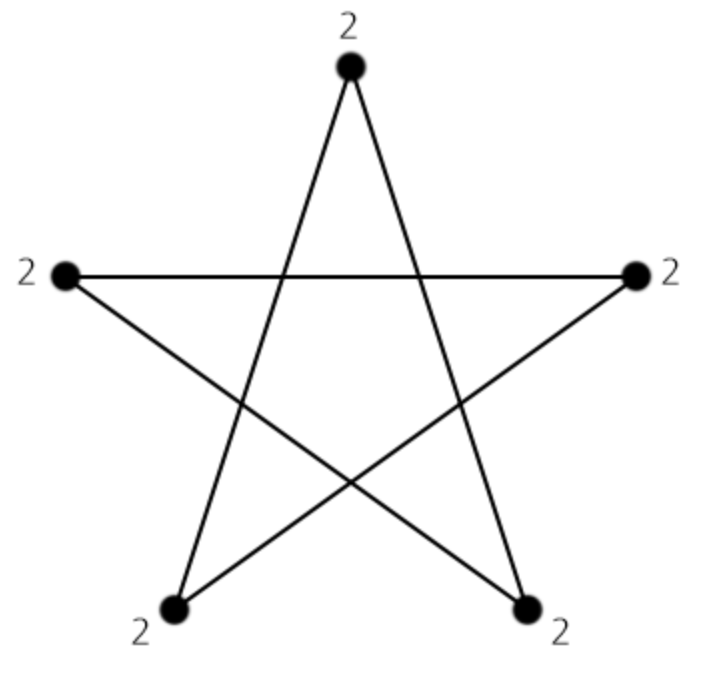    Untitled이미지 출처: https://velog.io/@ddochi132/w26d5a3f

  • 유향 그래프에서 오일러 회로가 존재하려면 모든 정점에 대해 indegree와 outdegree가 일치해야 한다.

Hierholzer’s Algorithm

  • 오일러 경로와 오일러 회로를 찾는 알고리즘이다.
  • 다음과 같은 형태로 동작한다.
    1. 시작 정점에서 출발하여 가능한 모든 경로를 탐색한다.
      1. 오일러 경로를 찾는 경우, 시작점은 홀수 차수를 가진 정점 중 하나가 된다.
      2. 오일러 회로를 찾는 경우, 시작점은 임의의 정점이 될 수 있다.
    2. 이미 지나온 간선을 제거하면서 경로를 계속 따라간다.
    3. 경로가 끊길 때마다 남은 그래프에서 새로운 시작점을 찾아 경로를 탐색한다.
    4. 모든 간선을 탐색할 때까지 반복한다.
  • 무향 그래프에서의 Hierholzer’s Algorithm
    • 간선을 추가할 때 양방향으로 추가하며, 홀수 차수를 가진 정점의 수를 세어 시작 정점을 결정한다. 
      from collections import defaultdict

def find_eulerian_path_or_circuit_undirected(graph):
    # 간선을 추가하는 함수
    def add_edge(u, v):
        graph[u].append(v)
        graph[v].append(u)

    # 정점의 차수 초기화
    degree = defaultdict(int)
    for u in graph:
        for v in graph[u]:
            degree[u] += 1

    # 시작 정점 찾기 - 홀수 차수를 가진 정점(오일러 경로) 또는 임의의 정점(오일러 회로)
    start_node = None
    odd_count = 0
    for node in graph:
        if degree[node] % 2 != 0:
            odd_count += 1
            if start_node is None:
                start_node = node

    # 그래프가 유효한 오일러 경로 또는 회로를 갖고 있는지 확인
    if odd_count != 0 and odd_count != 2:
        return None

    # 홀수 차수가 없는 경우 임의의 정점을 시작 정점으로 설정
    if start_node is None:
        start_node = next(iter(graph))

    # 방문 여부를 체크하기 위한 set
    visited = set()

    # 연결 그래프인지 확인하는 DFS
    def dfs(node):
        stack = [node]
        while stack:
            u = stack.pop()
            for v in graph[u]:
                if v not in visited:
                    visited.add(v)
                    stack.append(v)

    # 시작 정점부터 DFS를 수행하여 연결된 모든 정점을 방문.
    visited.add(start_node)
    dfs(start_node)

    # 모든 정점을 방문했는지 확인
    for node in graph:
        if node not in visited:
            return None  # 연결되지 않은 정점이 있으면 오일러 경로나 회로가 없음

    # 방문된 간선을 추적하기 위해 사용되는 set
    visited_edges = set()
        
    # Hierholzer's Algorithm (dfs - stack)
    stack = [start_node]
    path = []

    while stack:
        u = stack[-1]
        if graph[u]:
            v = graph[u][-1]
            edge = (min(u, v), max(u, v))  # 정렬된 간선 사용 -> 추적에 용이
            if edge not in visited_edges:
                visited_edges.add(edge)
                stack.append(v)
                graph[u].pop()
                graph[v].remove(u)  # 무향 그래프이므로 양방향 간선을 제거
            else:
                stack.pop()
        else:
            path.append(stack.pop())

    # 경로 반환
    return path[::-1]

# 예제
graph = {
    0: [1, 2],
    1: [0, 2, 3],
    2: [0, 1, 3],
    3: [1, 2]
}

result = find_eulerian_path_or_circuit_undirected(graph)
if result is None:
    print("오일러 경로 또는 회로가 없다.")
else:
    print("오일러 경로 또는 회로:", result)
  • 유향 그래프에서의 Hierholzer’s Algorithm
    • 각 정점의 진입 차수와 진출 차수를 계산하고, 이를 바탕으로 시작 정점과 끝 정점을 결정한다. 
      from collections import defaultdict

def find_eulerian_path_or_circuit_directed(graph):
    # 정점의 진입 차수와 진출 차수를 계산
    in_degree = defaultdict(int)
    out_degree = defaultdict(int)
    for u in graph:
        out_degree[u] = len(graph[u])
        for v in graph[u]:
            in_degree[v] += 1

    # 시작 정점과 끝 정점을 찾기
    start_node, end_node = None, None
    for node in graph:
        if in_degree[node] == out_degree[node] + 1:
            if end_node is not None:
                return None  # 오일러 경로가 두 개 이상 존재하는 경우
            end_node = node
        elif out_degree[node] == in_degree[node] + 1:
            if start_node is not None:
                return None  # 오일러 경로가 두 개 이상 존재하는 경우
            start_node = node
        elif out_degree[node] != in_degree[node]:
            return None  # 오일러 경로가 존재하지 않는 경우

    # 시작 정점이 없는 경우 임의의 정점을 시작 정점으로 설정
    if start_node is None:
        start_node = next(iter(graph))

    # Hierholzer's Algorithm (dfs - recursion)
    def dfs(node):
        while graph[node]:
            neighbor = graph[node].pop(0)
            dfs(neighbor)
        path.append(node)

    # Hierholzer's Algorithm을 시작 정점에서 호출
    path = []
    dfs(start_node)

    # 경로 반환
    return path[::-1] if len(path) == sum(out_degree.values()) + 1 else None

# 예제
graph = {
    0: [1],
    1: [2, 3],
    2: [0],
    3: [4],
    4: [1]
}

result = find_eulerian_path_or_circuit_directed(graph)
if result is None:
    print("오일러 경로 또는 회로가 없습니다.")
else:
    print("오일러 경로 또는 회로:", result)
Hierholzer’s Algorithm 시간복잡도
  • 시간복잡도는 $O(V+E)$ 를 가진다. DFS 를 노드의 개수($V$), 간선의 개수($E$)만큼 실행하기 때문이다.
맨 위로 이동 ↑

댓글 남기기

관련 게시글