[Algorithm] 13. Tree

2024-06-29

트리(Tree) 자료 구조

트리는 가계도와 같은 계층적인 구조를 표현할 때 사용할 수 있는 자료구조이다. 대표적인 예시는 가계도 이다.
트리 관련 용어
- 루트 노드(Root node) : 부모가 없는 최상위 노드
- 단말 노드(Leaf node) : 자식이 없는 노드
- 크기(Size) : 트리에 포함된 모든 노드의 개수
- 깊이(Depth) : 루트 노드부터의 거리. 루트 노드의 깊이는 0이 된다.
- 높이(Height) : 깊이 중 최댓값
- 차수(Degree) : 각 노드의 (자식방향) 간선 개수. 자식이 몇 개인지가 차수가 된다.
기본적으로 트리의 크기가 N 일 때, 전체 간선의 개수는 N-1 개 이다.

이진 탐색 트리(BST, Binary Search Tree)

이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조의 일종
이진 탐색 트리의 특징
- 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드
- 부모 노드보다 왼쪽 자식 노드가 작다.
- 부모 노드보다 오른쪽 자식 노드가 크다.
이러한 특징이 유지될 수 있도록 트리를 구성한 것이 이진 탐색 트리이다.
이진 탐색 트리에서 어떻게 데이터를 조회할 수 있을까?
1. 루트 노드부터 방문하여 탐색을 진행한다.
2. 현재 노드와 찾는 원소를 비교한다.
3. 찾는 원소가 더 크면 오른쪽, 더 작으면 왼쪽을 방문한다.
4. 현재 노드와 값을 비교한다.
5. 현재 노드와 찾는 원소를 비교한다.
6. 찾는 원소가 더 크면 오른쪽, 더 작으면 왼쪽을 방문한다.
7. 원소를 찾으면 탐색을 종료한다.
탐색 과정을 진행하면서 탐색 범위가 이상적인 경우 절반 가까이 줄어드는 것을 확인할 수 있다.
이진 탐색 트리는 이진 탐색이 가능한 형태로 탐색을 수행할 수 있도록 하기 위해서 고안된 트리 자료구조의 일종으로서, 이상적인 경우에 데이터를 탐색하는 경우, $O(logN)$ 에 비례하는 연산이 소요될 수 있도록 한다.
다만 그렇게 빠르게 탐색이 가능한 경우는 이진 탐색 트리가 왼쪽과 오른쪽에 대해서 균형이 잡혀있는 형태로 트리가 구성되어 있을 때에만 가능하다.
실제로는 트리 자료구조를 활용한 다양한 종류의 자료구조가 존재한다.

트리의 순회(Tree Traversal)

트리 자료구조에 포함된 노드를 특정한 방법으로 한 번씩 방문하는 방법을 의미한다.
트리의 정보를 시각적으로 확인할 수 있다. 따라서 트리 자료구조를 코드로 구현할 때 트리의 순회도 같이 구현해서 사용하는 경우가 많다.
대표적인 트리 순회의 방법
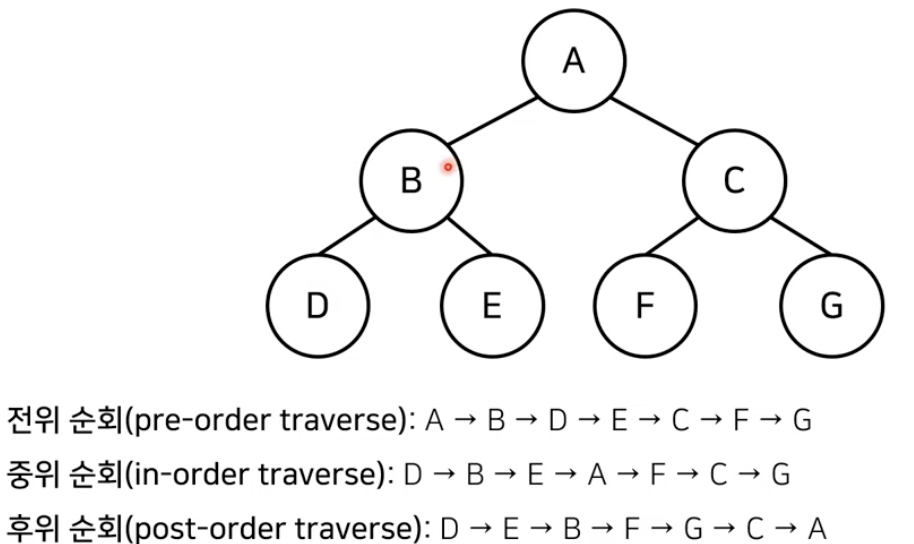
- 전위 순회(pre-order traverse) : 루트(자기 자신)를 먼저 방문(출력)한다. 이후 왼쪽, 오른쪽 차례로 방문을 진행한다.
- 중위 순회(in-order traverse) : 왼쪽 자식을 방문한 뒤에 루트(자기 자신)를 방문한다. 이후 오른쪽 노드를 방문한다.
- 후위 순회(post-order traverse) : 왼쪽 자식을 방문하고 오른쪽 자식을 방문한 뒤에 마지막으로 루트(자기 자신)를 방문(출력)한다.

트리 순회 구현

class Node:
    def __init__(self, data, left_node, right_node):
        self.data = data
        self.left_node = left_node
        self.right_node = right_node

# 전위 순회(Preorder Traversal)
def pre_order(node):
    # 자기 자신(루트)의 데이터를 먼저 출력
    print(node.data, end=' ')
    if node.left_node != None:
        pre_order(tree[node.left_node])
    if node.right_node != None:
        pre_order(tree[node.right_node])

# 중위 순회(Inorder Traversal)
def in_order(node):
    if node.left_node != None:
        in_order(tree[node.left_node])
    # 왼쪽을 먼저 방문한 뒤에 자기 자신의 데이터를 출력
    print(node.data, end=' ')
    if node.right_node != None:
        in_order(tree[node.right_node])

# 후위 순회(Postorder Traversal)
def post_order(node):
    if node.left_node != None:
        post_order(tree[node.left_node])
    if node.right_node != None:
        post_order(tree[node.right_node])
    # 왼쪽, 오른쪽 차례대로 방문한 뒤 마지막으로 자기 자신의 데이터를 출력
    print(node.data, end=' ')

n = int(input())    
tree = {}

for i in range(n):
    data, left_node, right_node = input().split()
    if left_node == "None":
        left_node = None
    if right_node == "None":
        right_node = None
    tree[data] = Node(data, left_node, right_node)

세그먼트 트리(Segment Tree)

세그먼트 트리(Segment Tree)는 구간의 합, 구간의 최솟값, 구간의 최댓값 등을 빠르게 구할 때 사용한다.
누적합과 비슷하지만 누적합은 합계를 구할 때에만 사용할 수 있고, 하나의 값이 업데이트 되면 해당 숫자 뒤의 모든 숫자가 모두 업데이트 되어야 한다. 반면에 세그먼트 트리는 구간 내의 다양한 값들을 구할 수 있고, 업데이트 되더라도 몇개의 숫자만 업데이트 하면 되기 때문에 훨씬 유용하게 사용할 수 있다.
어떠한 데이터들이 주어지고 그 데이터의 구간 합을 구하는 문제라면 누적합(Prefix Sum)을 사용하지만 중간에 값이 업데이트 되거나, 합계가 아닌 최대값, 최소값 등을 구해야 한다면 세그먼트 트리를 사용한다.
세그먼트 트리는 완전 이진 트리 형태로 구현된다.

세그먼트 트리 만들기

세그먼트 트리는 아래의 과정으로 만들 수 있다.
위처럼 숫자들이 있을 때, 이 숫자들의 구간 합을 구하기 위해서 2개씩 합계를 구한다.
위 예제에서는 데이터가 짝수개이기 때문에 2개씩 합계를 구할 수 있지만, 홀수개인 경우에는 마지막에 0이라는 숫자가 있다고 생각하고 합계를 구한다. 이후 또 2개씩 묶어 합계를 구한다.
똑같이 2개씩 묶는다. 마지막에 앞의 2개를 묶으면 하나가 남는데, 뒤에 0으로 되어있는 합계가 있다고 생각하고 실행한다.
마지막으로 2개의 합계를 구하면 세그먼트 트리가 완성된다.

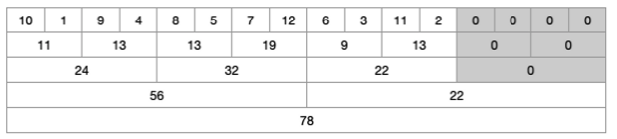
구간 합 구하기

4번째 숫자인 4부터 11번째 숫자인 11 까지 합계를 구해보자.
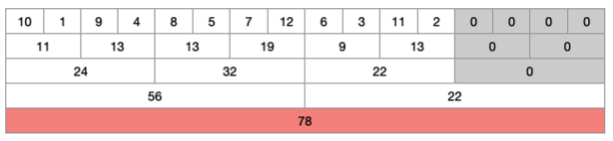
먼저 전체 범위인 1부터 16까지를 확인한다. 4부터 11까지이기 때문에 범위를 줄여줄 필요가 있다. 이 때 이분 탐색처럼 두 부분으로 나누어 다시 탐색한다.
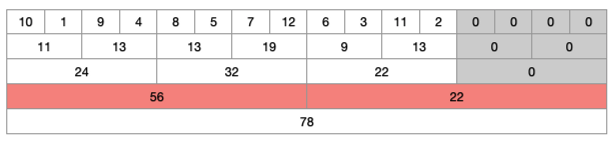
1부터 8까지 범위와 9부터 16까지 범위 확인 결과, 아직 4와 11 범위 밖의 값이 존재하기 때문에 한 단계 안으로 더 들어간다.
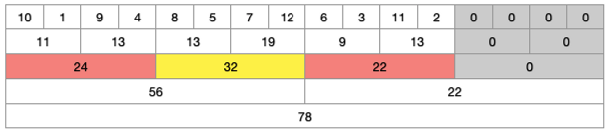
1부터 4까지 범위 안에는 4가 포함 되어 있기 때문에 한 단계 더 들어가야 한다. 그러나 5부터 8까지는 전체 구하려는 범위인 4와 11 사이 범위에 포함되어 있기 때문에 더 이상 탐색할 필요가 없다. 9부터 12까지는 구하려는 범위 11보다 크기 때문에 한 단계 더 들어가야 한다. 13부터 16은 범위 밖에 있기 때문에 더이상 탐색할 필요가 없다.
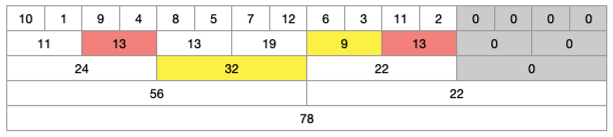
1부터 2는 범위 밖에 있기 때문에 탐색을 중지한다. 3부터 4는 3이 범위 밖에 있기 때문에 한 단계 더 탐색이 필요하다. 이미 범위 안을 확인했던 5부터 8은 넘어가고, 9부터 10은 범위 안에 있기 때문에 포함한다. 11부터 12는 12가 범위 밖에 있기 때문에 한 단계 더 탐색한다.
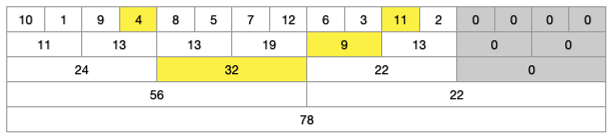
이로써 최종적으로 모든 범위를 구할 수 있다. 이제 4 + 32 + 9 + 11을 하면 4부터 11까지 범위의 합계를 구할 수 있다.
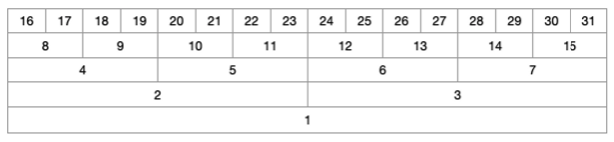
세그먼트 트리에서는 맨 아래부터 1번 인덱스로 하는 트리 형태를 떠올려야 한다.
위 그림처럼 전체 범위를 뜻하는 가장 밑의 루트 트리가 1번 인덱스가 된다. 위 예제에서는 전체가 16개의 범위를 뜻하지만 데이터의 개수에 따라 전체의 범위가 변한다. 데이터가 4개라면 전체가 1부터 4까지가 되는 것이고, 데이터가 100개라면 전체 범위는 데이터 100개를 포함할 수 있는 2의 제곱수인 128개가 된다. 이처럼 세그먼트 트리는 가변적인 범위를 가지고 있다.
위 예제에서 전체 범위의 값은 1번 인덱스에 저장되고 1번 부터 8번까지는 2번 인덱스가 된다. 또한 9번부터 16번 까지는 3번 인덱스가 된다. 이처럼 어떤 범위가 $n$번 인덱스라면 그 하위 인덱스는 $2n$ 과 $2n + 1$번 인덱스가 된다.

값 업데이트 하기

구간의 값을 변경할 때는 어떻게 할까?
누적합(Prefix Sum)을 사용해서 구간합(Interval Sum)을 구하는 것은 세그먼트 트리보다 빠를 수 있다. 그러나 값의 변경이 생긴다면 누적합으로는 해결이 불가능하다. 어떤 값이 변경될 때마다 매번 누적합을 다시 구해줘야 하기 때문이다.
하지만 세그먼트 트리를 이용하면 몇개의 숫자만 변경하면 된다.
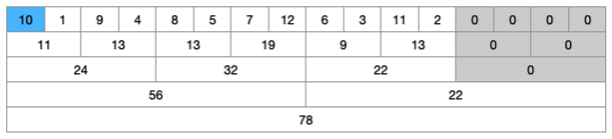
위 예제에서 첫번째 값인 10을 15로 변경해보자. 값이 10에서 15로 5가 커진다. 따라서 10이 포함된 라인의 값 모두에 5씩 더해주면 된다.
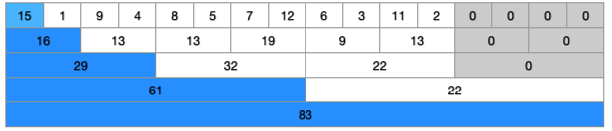
이렇게 자신의 포함된 범위의 숫자들만 변경된 값만큼 반영해주면 문제가 해결된다.
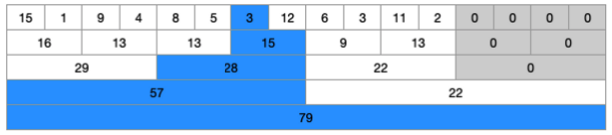
중간의 7번째 인덱스의 값인 7을 3으로 변경해보면, 7보다 4 작아졌기 때문에 해당 라인의 숫자들만 변경해주면 된다.

세그먼트 트리 구현

'''
- 어떤 데이터가 존재할 때, 특정 구간의 결과값을 구하는데 사용하는 자료구조이다. 즉 구간합에 사용된다.
- 단순한 구간합 뿐만 아니라주어진 쿼리에 대해 빠르게 응답하기 위한 자료구조이기도 하다.
- 세그먼트 트리는 이진트리를 기본으로 한다.
- 발전된 세그먼트 트리가 바이너리 인덱스 트리다.
'''

class SegmentTree:
    def __init__(self, nums):
        self.n = len(nums)
        self.tree = [0] * (4 * self.n)  # 세그먼트 트리를 저장할 배열
        self.build(nums, 1, 0, self.n - 1)

    def build(self, nums, idx, left, right):
        if left == right:
            self.tree[idx] = nums[left]
        else:
            mid = (left + right) // 2
            self.build(nums, 2 * idx, left, mid)
            self.build(nums, 2 * idx + 1, mid + 1, right)
            self.tree[idx] = self.tree[2 * idx] + self.tree[2 * idx + 1]

    def update(self, idx, val):
        """
        세그먼트 트리의 idx번째 값을 val로 업데이트하는 메서드
        """
        self._update(1, 0, self.n - 1, idx, val)

    def _update(self, tree_idx, left, right, idx, val):
        if left == right == idx:
            self.tree[tree_idx] = val
            return
        mid = (left + right) // 2
        if idx <= mid:
            self._update(2 * tree_idx, left, mid, idx, val)
        else:
            self._update(2 * tree_idx + 1, mid + 1, right, idx, val)
        self.tree[tree_idx] = self.tree[2 * tree_idx] + self.tree[2 * tree_idx + 1]

    def query(self, ql, qr):
        """
        세그먼트 트리에서 구간 [ql, qr]의 합을 반환하는 메서드
        """
        return self._query(1, 0, self.n - 1, ql, qr)

    def _query(self, idx, left, right, ql, qr):
        if qr < left or right < ql:  # 현재 노드가 구간에 완전히 벗어날 경우
            return 0
        elif ql <= left and right <= qr:  # 현재 노드가 구간에 완전히 포함될 경우
            return self.tree[idx]
        else:
            mid = (left + right) // 2
            return self._query(2 * idx, left, mid, ql, qr) + self._query(2 * idx + 1, mid + 1, right, ql, qr)

# 테스트
nums = [1, 3, 5, 7, 9, 11]
seg_tree = SegmentTree(nums)

print("Original Array:", nums)
print("Segment Tree:", seg_tree.tree)

print("Query [1, 3]:", seg_tree.query(1, 3))
seg_tree.update(2, 6)
print("After Update [2, 6]:", seg_tree.tree)

바이너리 인덱스 트리(Binary Indexed Tree, BIT, 펜윅 트리)

바이너리 인덱스 트리(BIT)는 2진법 인덱스 구조를 활용해 구간 합 문제를 효과적으로 해결해줄 수 있는 일종의 트리 자료구조를 의미한다.
펜윅 트리(fenwick tree) 라고도 한다.
정수에 따른 2진수 표기는 2의 보수로 표현한다.
- 7 : 00000000 00000000 00000000 00000111 (4+2+1)
- -7 : 11111111 11111111 11111111 11111001 (7의 2진수 표기법에서 모든 비트에 대해 flip 하고, 1을 더한 값과 동일한 비트를 가진다.)
0 이 아닌 마지막 비트를 찾는 방법
- 특정한 숫자 K 의 0이 아닌 마지막 비트를 찾기 위해서 K & -K 를 계산하면 된다.
- 예를 들어 8 은 2진수로 00000000 00000000 00000000 00001000 이기 때문에, 마지막 비트는 K & -K 의 결과인 8($2^3$) 이 나온다.
```
n = 8
    
for i in range(n+1):
    print(i, "의 마지막 비트:", (i & -i))
```
- 파이썬에서는 & 연산을 사용하면 자동으로 특정 정수를 2의 보수로 표기한 결과에서의 비트단위 And 연산을 수행할 수 있다.
어떠한 양의 정수를 2의 보수로 표기했을 때 0이 아닌 마지막 비트를 찾는 과정이 어디에 사용될까?
바로 바이너리 인덱스 트리(BIT)에서 매우 효과적으로 사용될 수 있다.

세그먼트 트리 vs. BIT(펜윅 트리)

데이터 업데이트가 가능한 상황에서의 구간 합(Interval Sum) 문제는 세그먼트 트리와 바이너리 인덱스 트리로 해결할 수 있다.
- 문제 : 어떤 N 개의 수가 주어져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려고 한다. 만약에 1, 2, 3, 4, 5 라는 수가 있고, 3번째 수를 6으로 바꾸고 2번째부터 5번째까지의 합을 구하라고 한다면 17을 출력하면 되는 것이다. 그리고 그 상태에서 다섯번째 수를 2로 바꾸고 3번째부터 5번째까지 합을 구하라고 한다면 12가 될 것이다.
- 데이터 개수: N(1≤N≤1,000,000)
- 데이터 변경 횟수: M(1≤M≤10,000)
- 구간 합 계산 횟수: K(1≤K≤10,000)
- 시간복잡도를 단축할 수 있는 솔루션을 사용해야 한다. 구간 합을 계산할 때마다 데이터를 선형적으로 탐색하면 $O(NK)$ 만큼의 시간복잡도가 소요되기 때문이다.
주요 차이점과 유사점
- 구조와 구현
  - 세그먼트 트리는 완전 이진 트리 형태로, 배열을 기반으로 트리 구조를 형성한다.
  - 펜윅 트리는 단일 배열과 비트 연산을 사용하여 부모와 자식 관계를 관리한다.
- 구간 쿼리와 업데이트
  - 두 트리 모두 구간 합 또는 특정 범위에 대한 쿼리와 업데이트를 $O(logN)$ 시간 복잡도로 처리할 수 있다.
  - 세그먼트 트리는 더 일반적인 쿼리와 업데이트(예: 구간 최소값, 최대값, 구간 합 등)를 지원한다.
  - 펜윅 트리는 주로 구간 합과 점 업데이트에 특화되어 있다.
- 메모리 사용
  - 두 트리 모두 $O(N)$의 공간 복잡도를 가진다.
- 구현 복잡도
  - 세그먼트 트리는 구현이 더 복잡하며, 트리의 각 노드와 관련된 구간을 명시적으로 관리해야 한다.
  - 펜윅 트리는 구현이 비교적 단순하며, 배열 인덱스와 비트 연산을 통해 쉽게 관리할 수 있다.

바이너리 인덱스 트리: 트리 구조 만들기

0 이 아닌 마지막 비트는 내가 저장하고 있는 값들의 개수가 된다.
데이터의 개수가 $N$개라고 하면, 하나의 배열을 만들고 이 배열은 BIT 에 대한 값의 정보를 담게 한다.
각각의 인덱스의 값은 0 이 아닌 마지막 비트를 뜻하고 이는 내가 담고 있는 값들의 개수다.
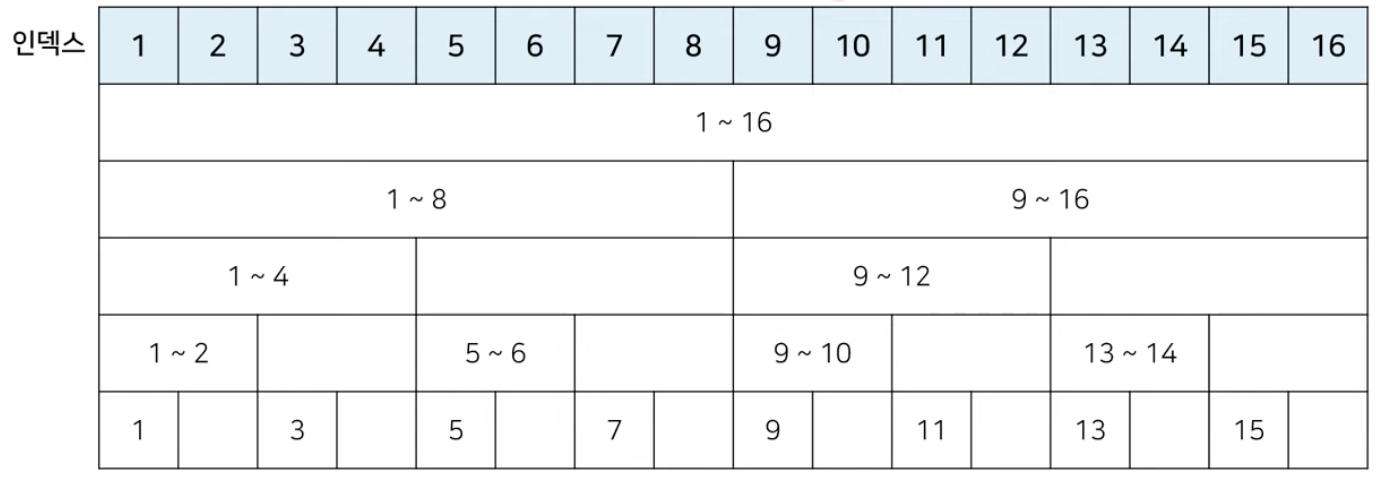
위 예시에서 16은 0이 아닌 마지막 비트가 16인 경우이다. 1~16 까지의 모든 데이터에 대한 값들의 합을 담겠다는 의미이다.
8 은 0이 아닌 마지막 비트가 8이다. 1~8 까지의 값들의 합을 담고 있다.
7 은 0이 아닌 마지막 비트가 1이다. 이 경우에는 7 자기 자신에 대한 정보만 담고 있다.
이런 식으로 0 이 아닌 마지막 비트는 해당 인덱스가 담고 있는 값들의 개수라고 볼 수 있다.
위 자료구조를 이용해서 특정 값을 변경할 때, 0이 아닌 마지막 비트만큼 더하면서 구간들의 값을 변경한다.
바꾸고자 하는 그 특정 위치의 값부터 시작해서 0 이 아닌 마지막 비트만큼 더하면서 구간들의 값을 변경하는 것이다.
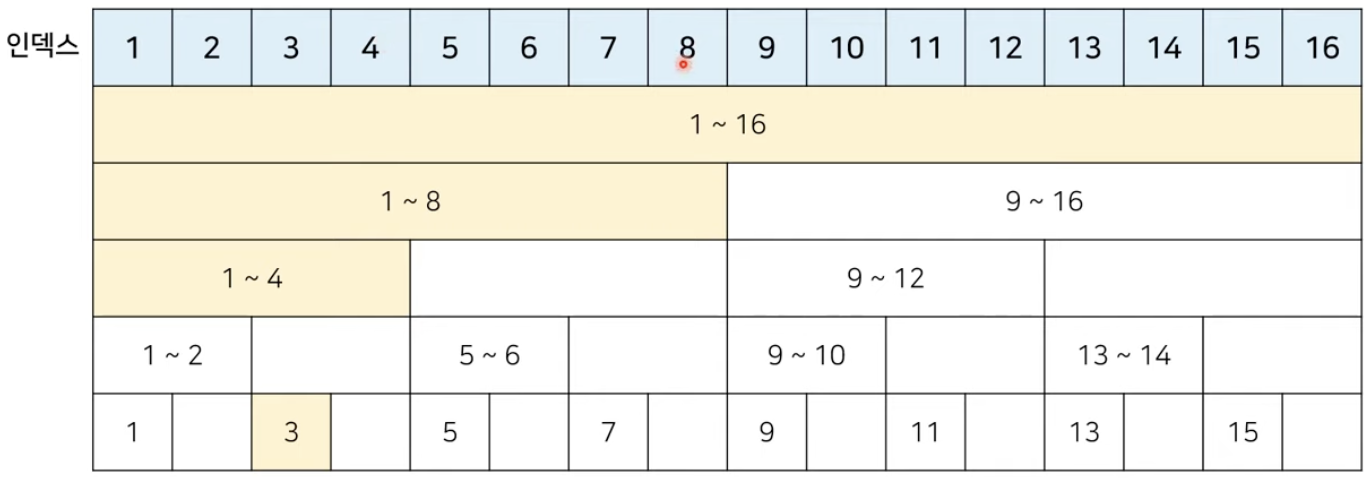
- 3번째 값이 바뀌었다면, 3의 마지막 비트는 1이기 때문에 한 칸 이동해서 4에 대한 값을 바꾸고, 4에서 8, 8에서 16에 대한 값을 바꾼다.
- 즉, 3, 4, 8, 16 은 모두 세번째 위치에 대한 값의 합 정보를 담고 있는 인덱스이다.
- 따라서 총 4번 값을 업데이트 하면 된다.
데이터의 개수가 N 개일 때 높이는 $O(logN)$ 으로 형성되기 때문에, 특정 위치의 값을 바꿀 때 시간 복잡도가 최악의 경우에도 $O(logN)$ 을 보장하도록 만들 수 있다는 것을 확인할 수 있다.

바이너리 인덱스 트리: 누적 합(Prefix Sum)

1부터 N 까지의 합(누적 합) 구하기
0이 아닌 마지막 비트만큼 빼면서 구간들의 값의 합을 계산한다.
누적합을 구하는 방법을 명시해야 하는 이유는 구간 합을 구할 때 누적합을 이용하면 더욱 효과적으로 구간합을 구할 수 있기 때문이다.
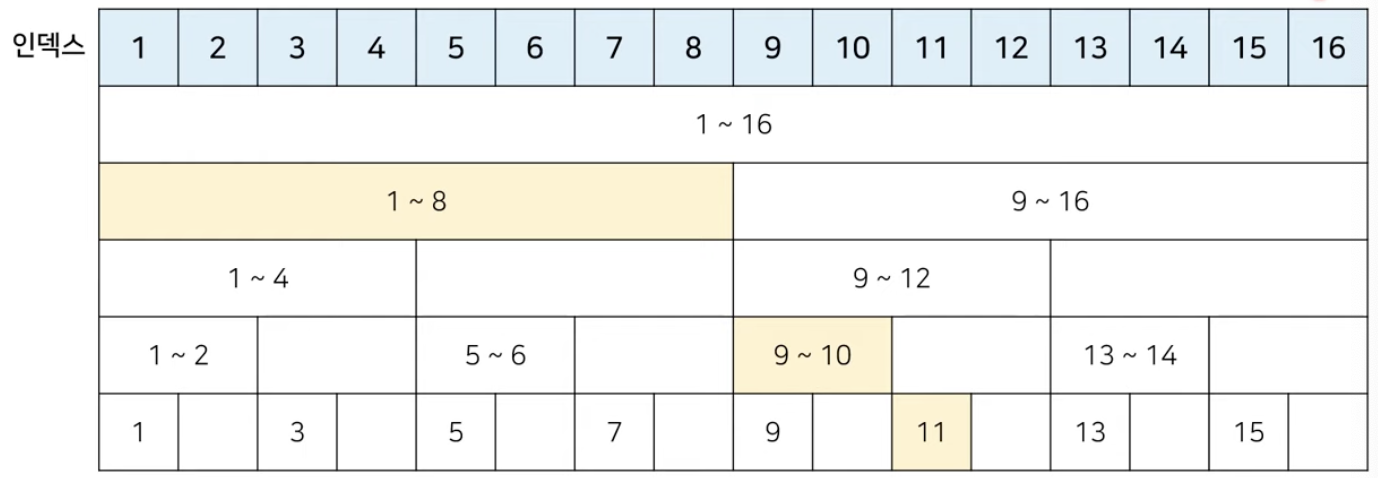
첫번째 원소부터 열한번째 원소까지 누적합을 구한다면, 11부터 출발하면 된다.
11은 11하나에 대한 값을 가지고 있다. 합계를 더하고 한칸 이동한다.
10은 9~10의 값의 합을 담고 있다. 합계를 더하고 두칸 이동한다.
8은 1~8의 값의 합을 담고 있기 때문에 모든 값의 합을 더한 합계를 더한다.
그러면 1 부터 11까지 총 11개의 원소에 대한 합계를 구할 수 있다.
이러한 방법을 이용하게 되면 최악의 경우에도 $O(logN)$ 에 해당하는 시간이 소요된다.

바이너리 인덱스 트리 구현

import sys
input = sys.stdin.readline()

# 데이터의 개수(n), 변경 횟수(m), 구간 합 계산 횟수(k)
n, m, k = map(int, input().split())

# 전체 데이터의 개수는 최대 1,000,000개
arr = [0] * (n+1)
tree = [0] * (n+1)

# i 번째 수까지의 누적 합을 계산하는 함수
def prefix_sum(i):
    result = 0
    while i > 0:
        result += tree[i]
        # 0이 아닌 마지막 비트만큼 뺴가면서 앞쪽으로 이동
        i -= (i & -i)
        
    return result
    
# i 번째 수를 dif 만큼 더하는 함수
def update(i, dif):
    while i <= n:
        tree[i] += dif
        # 0이 아닌 마지막 비트만큼 더해가면서 뒤쪽으로 이동
        i += (i & -i)
        
# start 부터 end 까지의 구간 합을 계산하는 함수
def interval_sum(start, end):
    return prefix_sum(end) - prefix_sum(start-1)
    
for i in range(1, n+1):
    x = int(input())
    arr[i] = x
    update(i, x)
    
for i in range(m+k):
    a, b, c = map(int, input().split())
    
    # 업데이트(update) 연산인 경우
    if a == 1:
        update(b, c-arr[b]) # 바뀐 크기(dif) 만큼 적용
        arr[b] = c
    
    # 구간 합(interval sum) 연산인 경우
    else:
        print(interval_sum(b, c))

맨 위로 이동 ↑

Bkkhyunn

[Algorithm] 13. Tree

트리(Tree) 자료 구조

이진 탐색 트리(BST, Binary Search Tree)

트리의 순회(Tree Traversal)

트리 순회 구현

세그먼트 트리(Segment Tree)

세그먼트 트리 만들기

구간 합 구하기

값 업데이트 하기

세그먼트 트리 구현

바이너리 인덱스 트리(Binary Indexed Tree, BIT, 펜윅 트리)

세그먼트 트리 vs. BIT(펜윅 트리)

바이너리 인덱스 트리: 트리 구조 만들기

바이너리 인덱스 트리: 누적 합(Prefix Sum)

바이너리 인덱스 트리 구현

댓글 남기기

관련 게시글

[Algorithm] 19. Graphs - Markov Chain

[Algorithm] 18. Graphs - Hamilton Path

[Algorithm] 17. Graphs - Euler Path

[Algorithm] 16. Sliding Window