[CNN] 3. CNN 의 구조와 parameter

CNN 의 구조

• 일반적인 CNN 은 convolution layer, pooling layer, fully connected layer 로 이루어져 있다.

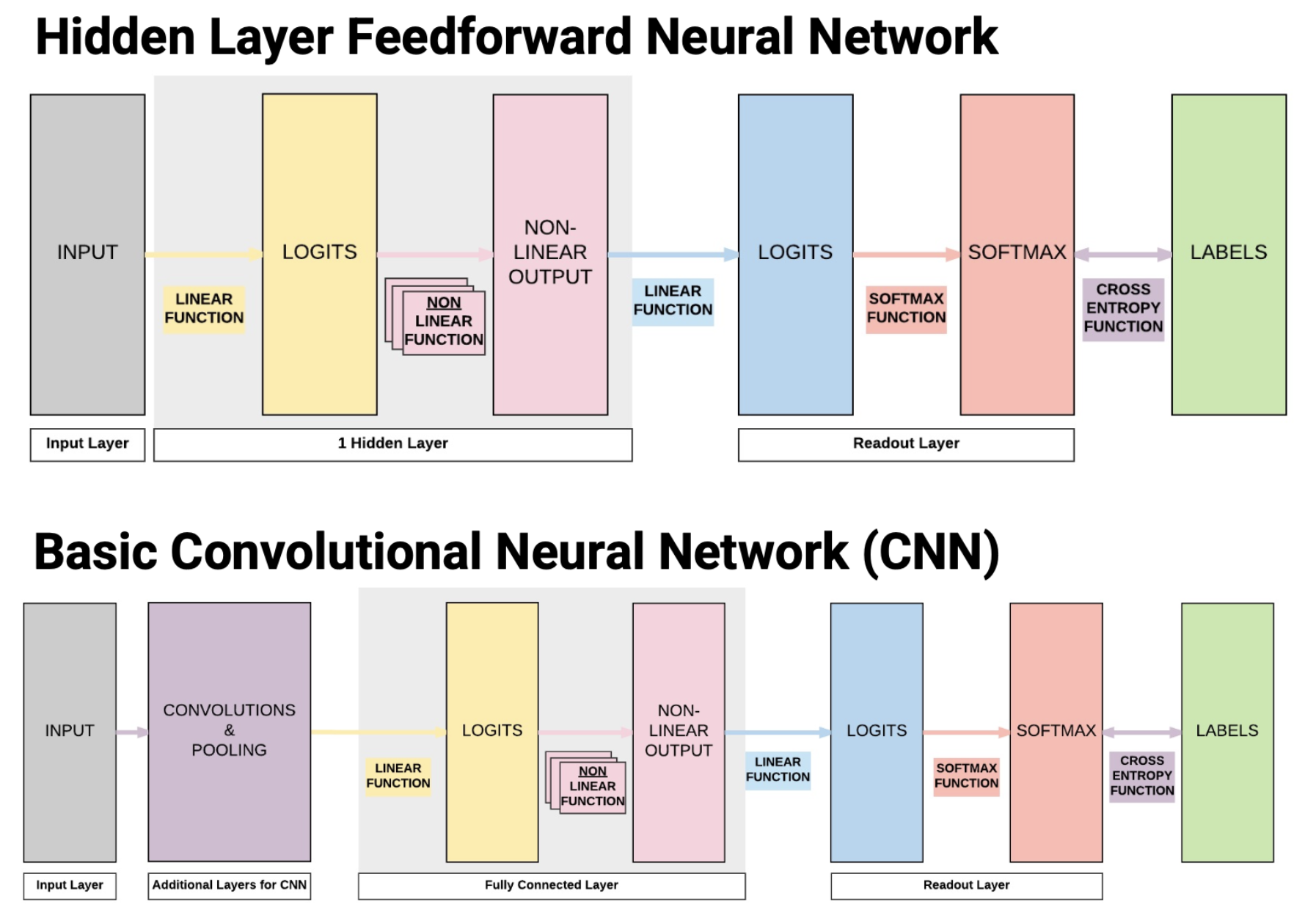  NN 과 CNN 의 모습

  • Convolution and pooling layers : feature extraction. 이미지에서 유용한 정보를 추출한다.
  • Fully connected layer : decision making. 분류를 하거나 회귀를 해서 내가 원하는 출력값을 얻도록 한다.

• input 으로 이미지를 받아서 convolution layer 와 pooling layer 를 반복적으로 거친 뒤 하나 이상의 fully connected layer 를 거친다. 이후 softmax 를 거쳐 이미지가 각 레이블에 속할 확률 값을 리턴하게 된다.

convolution layer

• convolution layer 는 입력받은 이미지의 특징을 추출하는 역할을 하는 CNN 의 핵심이다. CNN 은 이 convolution layer 를 여러 겹 쌓아 만들게 된다.

• convolution layer(conv layer) 에서는 filter 를 가지고 이미지를 순회하면서 특징을 추출하는데, 어떤 과정을 통해 추출하는지 알아보자.

  

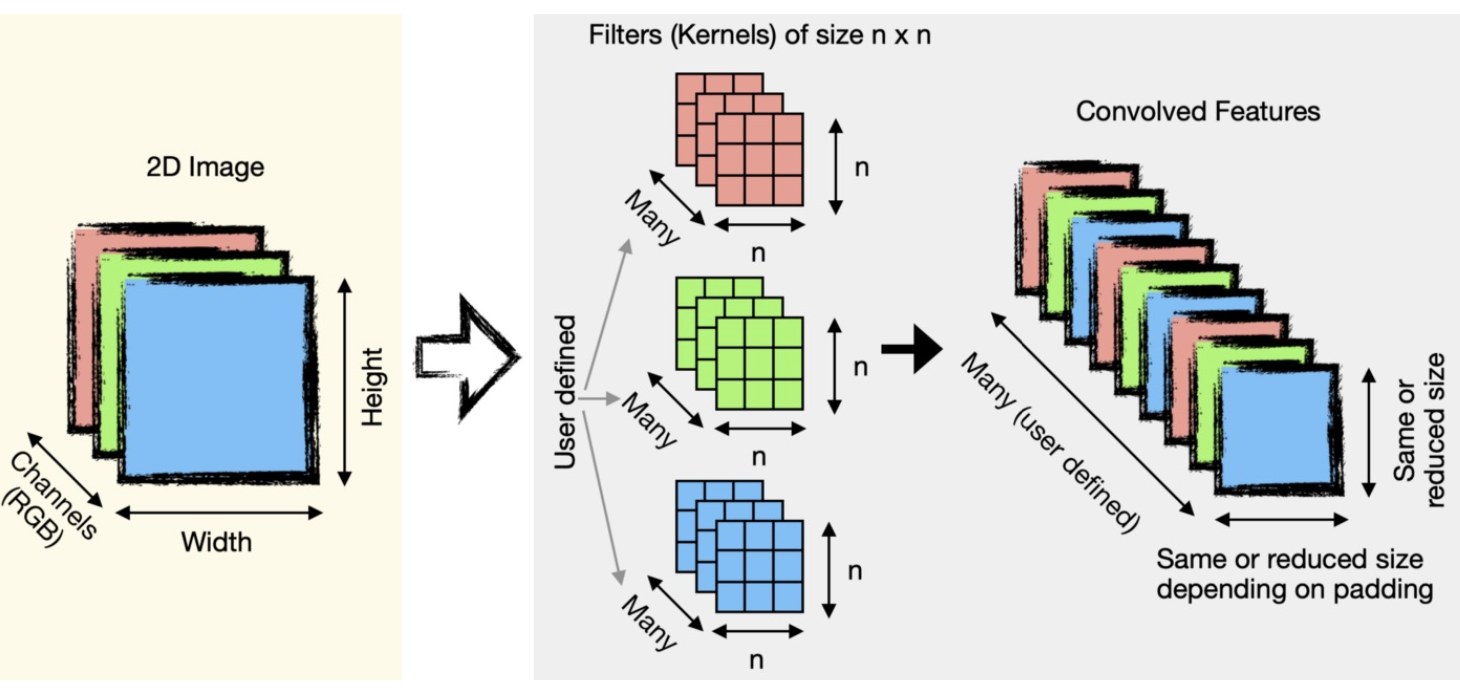
• 위처럼 conv layer 에서 filter 는 정해진 크기(n x n)와 input image 혹은 전 layer 의 feature map 의 channel 과 같은 channel 을 가진다. 그리고 filter 의 개수는 내가 정해주는 하이퍼 파라미터다.

• 여러 개의 filter 를 사용하는 것은 여러 filter 를 가지고 이미지의 여러 특징을 뽑아내겠다는 것이다.

  AlexNet - 96 개의 filter 시각화

• 위 그림처럼 서로 다른 filter 는 서로 다른 특징들을 추출하게 된다.
• 가중치를 가진 filter 가 이미지를 순회하면서 이미지의 점, 선과 같은 특징이 있는 부분과 곱해져 높은 값은 더 높게 낮은 값은 낮게 하여 픽셀 값을 뽑아내게 된다.
• filter 는 학습하면서 가중치를 계속 업데이트하고, 해당하는 특징을 더 극대화해서 추출한다. 이렇게 각 필터가 이미지를 순회하면서 추출한 특징은 feature map 에 mapping 된다. 그렇게 각 conv layer 에서 만들어진 feature map 은 다음 conv layer 에 보내지게 된다.

• 그러면 각 conv layer 는 이미지의 무엇을 보게 될까?

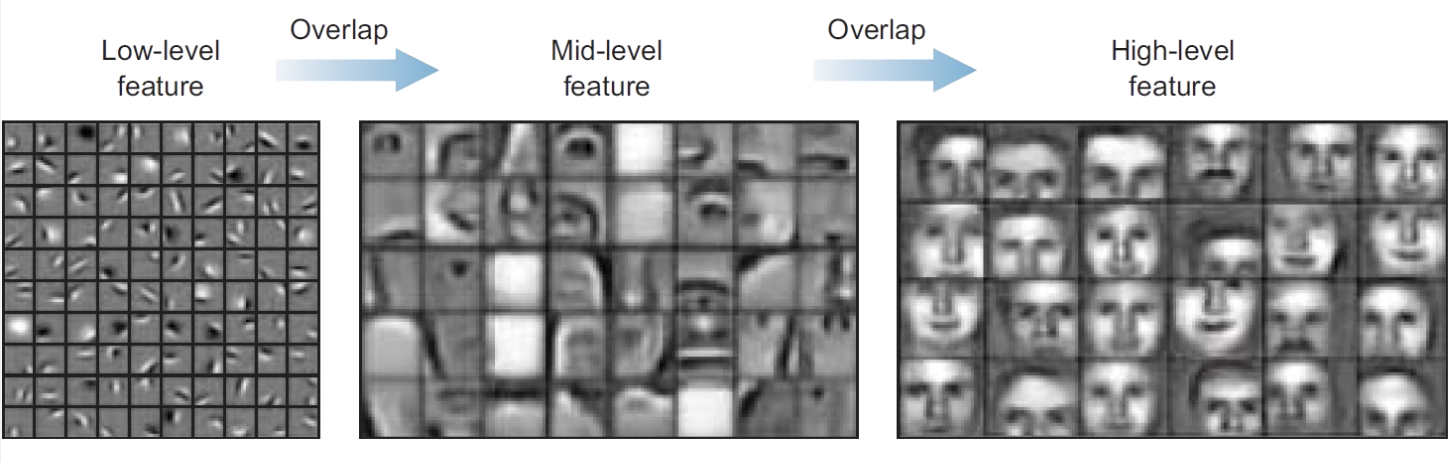  semantic level 에 따른 분류. low level(낮은, 앞 층) 에서 high level(높은, 뒤 층) 까지 feature 의 특징을 볼 수 있다.

• 여러 겹의 conv layer 중 가장 첫번째의 conv layer(low-level) 에서 filter 는 이미지의 세세한 부분(점, 선 등)을 보게 된다. 처음에는 이미지 크기에 비해 상대적으로 작은 filter 를 가지고 convolution 하게 되고, 이미지의 매우 작은 부분만 볼 수 있기 때문이다.
• 따라서 low-level 의 conv layer 일수록 점, 선과 같은 단순한 정보를 추출하게 된다.
• 그러나 conv layer 가 뒤로 갈수록(high-level) 더 복잡한 정보들을 추출한다. 또한 점점 pooling 에 의해 feature 의 size 가 줄어들고 다음에 다루게 될 receptive field 가 넓어지면서 filter 가 이미지의 전체적인 부분을 볼 수 있게 된다. ZFNet 에서 conv layer 층 마다 학습된 filter 를 이미지에 입혀 feature map 을 시각화했다.
• 위 이미지는 2013년 ZFNet 에서 conv layer 마다의 feature map 을 추출한 것이다(ZFNet 은 의미가 있는 논문으로 추후 다른 포스트에서 정리할 것).

• 실제 pytorch 에서 구현한 convolution layer 를 보자.

  

• torch.nn 에서 불러올 수 있으며 input 의 channel 과 output 의 channel 을 정해준다. 이 때 전자는 해당 conv layer 가 받는 input 의 channel 이고, 후자는 해당 conv layer 의 filter 개수를 뜻한다.
• 또한 kernel size 도 정해준다.

pooling layer

• conv layer 를 지나면 pooling layer 를 지난다. pooling layer 는 이미지를 down sampling 하는 역할을 수행한다.

  

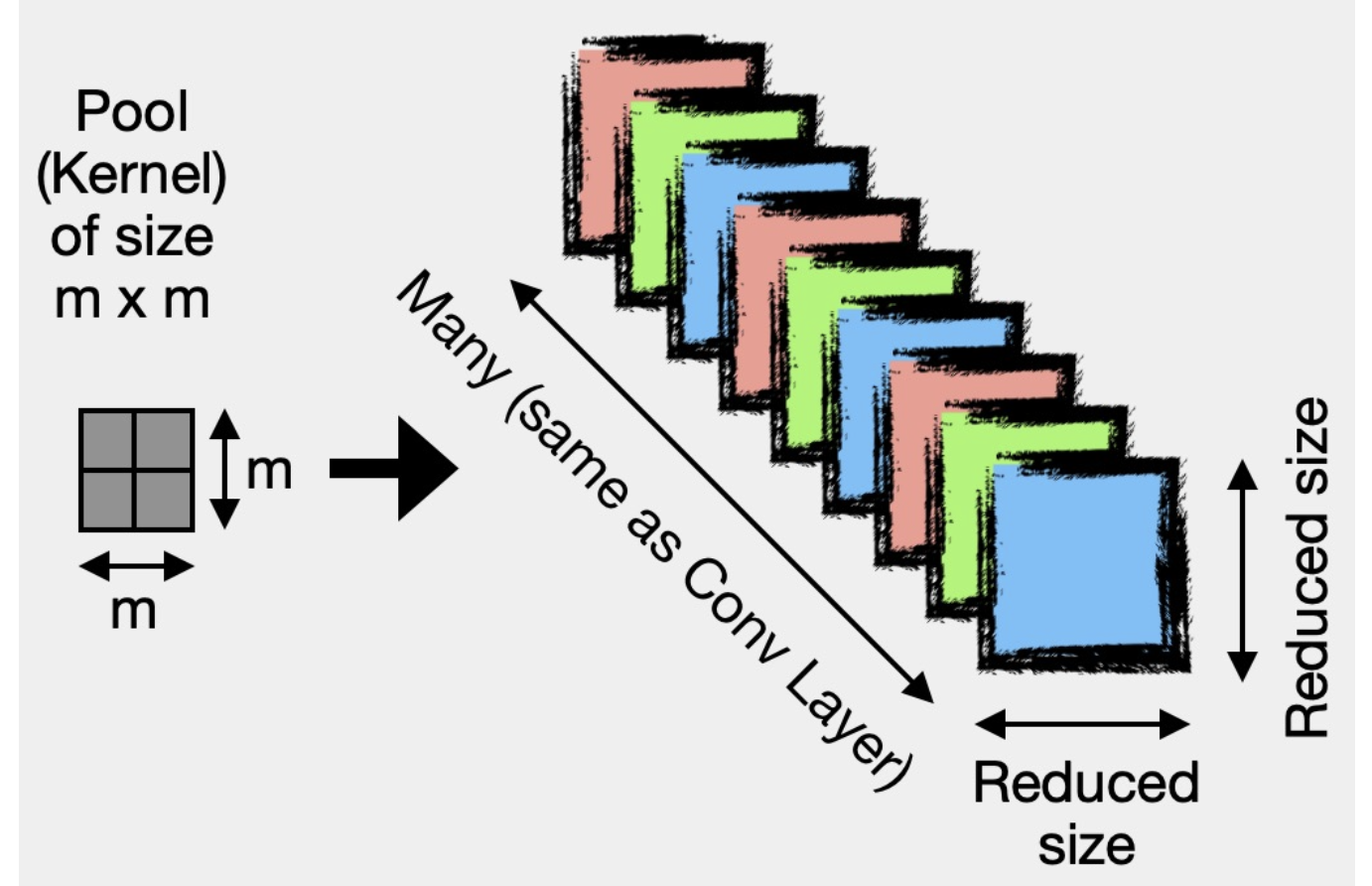
• 연산은 비교적 간단하다. 특정 크기의 filter 가 conv layer 를 거쳐 나온 feature map 을 순회하면서 해당 영역에서 조건에 맞는 값을 추출하는 것이다.

• 이 조건에 따라 pooling 방법이 다른데, 특정 영역에서 가장 큰 값을 추출하는 max pooling, 영역 내 값들의 평균을 추출하는 average pooling 등 여러 조건이 있다.

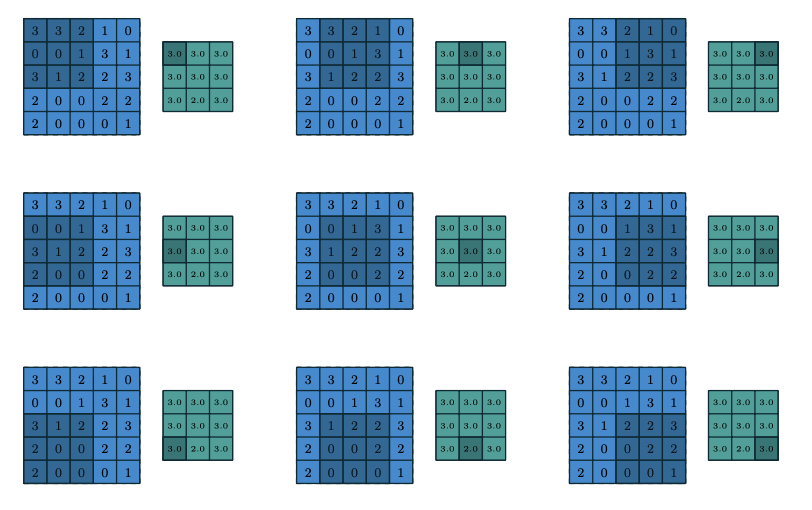  3x3 max pooling. stride 1

• max pooling 의 경우 영역 내에 가장 큰 값을 가져오기 때문에 특징이 더욱 뚜렷해지는 효과를 가져온다.
• 또한 pooling 을 수행하면 이미지의 형태는 유지하면서 크기만 작아지게 된다.
• 크기를 작게 만드는 이유는 이후 conv layer 에서 filter 가 이미지의 더 큰 부분을 볼 수 있도록 하기 위함이다.
• 예를 들어 conv layer 1 에서 만들어진 feature map 을 pooling 에 보내 resolution 을 줄이고, 이후 conv layer 2 에서 convolution 을 할 때,filter 가 보는 영역은 conv layer 1 의 filter 가 여러 번 움직여서 본 영역을 한 번에 볼 수 있게 된다.
• pooling layer 를 거쳐 down sampling 되면 이미지의 형태와 특징은 유지한 채 크기만 작아지므로, 이후 conv layer filter 는 좀 더 이미지 내 물체의 형태적인 특징을 잡아낼 수 있다. 즉, 더 추상적인 부분을 볼 수 있게 된다.
• 따라서 conv layer 와 pooling layer 를 반복적으로 거치면 뒤 쪽 layer 의 filter 들은 앞 쪽 layer 의 filter 들과 합성되어 input 이미지의 더 큰 영역을 보게 되고 더 추상적인 역할을 하게 된다.

• 실제 pytorch 에서 구현한 pooling layer(max pooling)를 보자.

  

• torch.nn 에서 불러올 수 있으며 kernel size 만 정해주면 된다.
• return_indices 와 같은 argument 는 Segmentation 에서 자주 쓰이는 UnPooling 을 위한 것이다.

conv layer + pooling layer

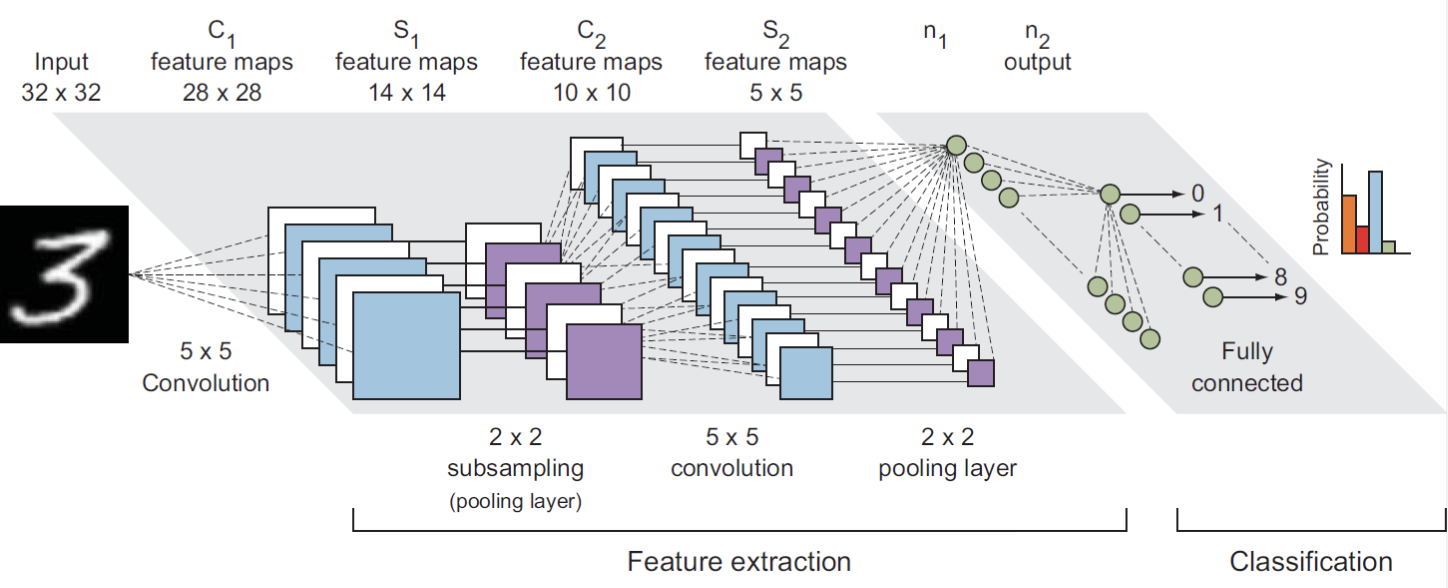
• 위의 그림을 보면, (1x32x32) 의 input image 가 주어진다. 채널이 1인 이유는 gray scale 이기 때문이다. RGB 로 이루어진 image 라면 채널이 3이 된다.
• 첫번째 conv layer 에서 5개의 5x5 filter(5x1x5x5) 를 사용하여 5개의 feature map(5x28x28)이 만들어진다($C_1$).
  • 이 때 filter 의 개수는 내가 정해주는 것이고, filter 의 channel 은 input image 의 channel 과 같다.
  • conv layer 의 output feature map 의 channel 은 filter 의 개수가 된다.
• 이후 2x2 pooling 을 통해 5개의 feature map 이 down sampling(5x14x14) 된다.($S_1$).
• 그리고 다음 conv layer 는 16개의 filter를 가지고 있다. 여기서 이 16개의 5x5 filter 를 가지고 5개의 feature map 에 동시에 conv 연산이 적용된다. 즉, (5x14x14) 의 feature map 에 (16x5x5x5) filter 를 가지고 conv 연산을 진행하고, (16x10x10) 의 feature map 이 나오게 된다. ($C_2$)

• 이후 2x2 pooling 을 거쳐 (16x5x5) 의 feature map 이 나오게 되고 이를 dense 하게 만들어 fully connected layer 를 통과시키게 된다.

  💡 왜 뒤로 갈수록 feature 의 개수 즉 filter 의 개수를 많이 쓸까?
  
  1) 첫번째는 연산량 때문이다. 첫번째 conv layer 에서는 큰 이미지가 입력되어 conv 연산을 수행해야 하므로 적은 수의 filter 만으로도 연산량이 많아지게 된다. 이후 layer 를 지날수록 down sampling 되므로 이미지의 크기가 계속 줄어들기 때문에 더 많은 수의 filter 를 사용해도 연산량은 크게 증가하지 않게 된다.
  
  2) 두번째 이유는 뒤 쪽 layer 로 갈수록 conv 의 대상이 되는 이미지가 더 추상적이기 때문이다. 일반적으로 conv filter 는 이미지의 특징 패턴을 잡아낸다. 초반에 위치한 layer 들은 주로 사물을 구성하는 edge 나 corner 와 같은 좀 더 상세한 패턴을 잡아낸다. 그러나 점, 선과 같은 단순한 정보들로부터는 추출할 특징이 많지 않으므로 여러 filter 를 사용하는게 큰 의미가 없다. 또한 점, 선과 같은 패턴만으로 이미지를 판별하기에는 부족하다. 오히려 이러한 상세 패턴은 다양한 유형으로 존재하면서 noise 나 over fitting 으로 적절한 이미지 분류로 동작하기 어렵다. 그래서 이들 상세화된 패턴들이 결합된 보다 일반적이고 추상적인 패턴으로 만들어 내기 위해서 conv filter 의 개수를 더욱 증가시키게 된다. 초기 CNN 을 연구하면서 filter 개수를 증가시키면 상세 정보는 손실되지만 보다 일반적이고 추상화된 패턴을 잡아낼 수 있다는 것이 밝혀지면서 이렇게 filter 수를 증가시키게 된 것이다. 이런 일반적이고 추상적인 패턴들을 뽑아내는 것이 개별적으로 상세화된 패턴을 뽑아내는 것보다 훨씬 복잡한 연산이 필요하다. 개별적으로 상세화된 패턴을 보다 복잡하게 결합하여 보다 일반화된 패턴을 뽑아내야 하기 때문이다. 그래서 더 많은 filter 의 개수를 가지게 된다.
  

  💡 왜 뒤로 갈수록 feature 의 size 가 작아질까?
  
  1) 첫번째는 보다 큰 receptive field 와 추상화 수준의 증가를 위해서다. 각 layer 에서 pooling 을 통해 image 의 resolution(공간적 해상도)을 줄이면 receptive field 가 커져 이후 layer 의 feature map 이 더 넓은 context 를 포함하게 된다. 또한 초기 layer 는 이미지의 선, 점, 색 같은 기본적인 특성을 포착하고 깊은 layer 로 갈수록 더 복잡하고 추상적인 특성을 학습하는데, image resolution 을 줄임으로써 더 높은 수준의 추상화를 가능하게 한다.
  
  2) 두번째는 계산 효율성이다. feature map 의 크기가 줄어들면 다음 layer 의 연산량이 감소하여 전체 네트워크의 계산 효율성이 향상된다. 또한 마지막 fully connected layer 에서 flatten 을 할 때 feature map 의 크기를 줄임으로써 파라미터 수가 감소하게 되고 이는 over-fitting 을 방지하는데 도움이 될 수 있다.

fully connected layer

• 앞서 이미지를 입력받아 conv layer 와 pooling layer 를 거쳐 feature extracion 을 반복했다.

• 최종적으로 물체와 유사한 feature map 을 가지고 이미지를 분류하게 되는데, 여기서 fc layer 를 사용한다.

  

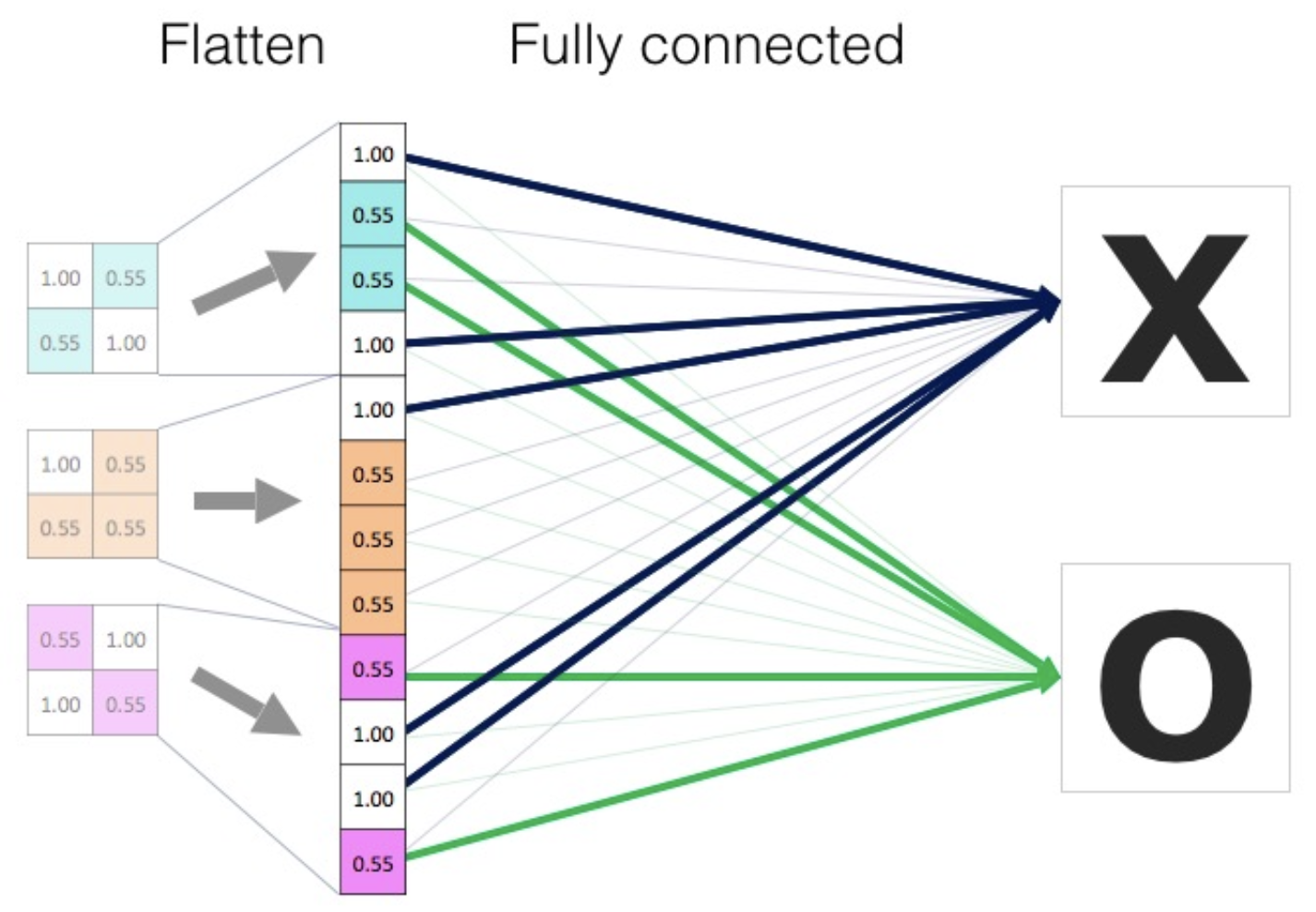
• 마지막 feature map 을 일렬로 flatten 하고 이것을 fc layer의 입력으로 준 뒤, 여러 hidden layer 를 거쳐 분류 문제를 해결하게 된다.

구현

• 실제 pytorch 에서 convolution layer, pooling layer, fully connected layer 를 어떻게 구현했는지 확인해보자.

• pytorch 의 torchvision 에서는 완성된 모델과 pretrained 된 모델을 제공한다. 아래는 그 중 AlexNet에 해당한다.

  class AlexNet(nn.Module):
      def __init__(self, num_classes: int = 1000, dropout: float = 0.5) -> None:
          super().__init__()
          _log_api_usage_once(self)
          self.features = nn.Sequential(
              nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
              nn.ReLU(inplace=True),
              nn.MaxPool2d(kernel_size=3, stride=2),
              nn.Conv2d(64, 192, kernel_size=5, padding=2),
              nn.ReLU(inplace=True),
              nn.MaxPool2d(kernel_size=3, stride=2),
              nn.Conv2d(192, 384, kernel_size=3, padding=1),
              nn.ReLU(inplace=True),
              nn.Conv2d(384, 256, kernel_size=3, padding=1),
              nn.ReLU(inplace=True),
              nn.Conv2d(256, 256, kernel_size=3, padding=1),
              nn.ReLU(inplace=True),
              nn.MaxPool2d(kernel_size=3, stride=2),
          )
          self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
          self.classifier = nn.Sequential(
              nn.Dropout(p=dropout),
              nn.Linear(256 * 6 * 6, 4096),
              nn.ReLU(inplace=True),
              nn.Dropout(p=dropout),
              nn.Linear(4096, 4096),
              nn.ReLU(inplace=True),
              nn.Linear(4096, num_classes),
          )
  
      def forward(self, x: torch.Tensor) -> torch.Tensor:
          x = self.features(x)
          x = self.avgpool(x)
          x = torch.flatten(x, 1)
          x = self.classifier(x)
          return x
  

• conv layer - activation function - pooling layer 가 여러번 반복되는 것을 확인할 수 있다.
  • 이 때 각 nn.Conv2d 의 argument 를 보면 이전 층의 output channel 과 현재 층의 input channel 이 같음을 확인할 수 있다.
• classifier 는 fully connected layer 다.

convolution 연산의 파라미터 수

• 항상 집중해서 봐야 할 것은 이 연산을 정의하는데 필요한 파라미터의 숫자를 잘 생각해야 한다.
• (convolution kernel 의 size x input 이미지의 channel x output channel) 로 convolution layer 의 파라미터의 숫자를 계산해낼 수 있다.
• 왜냐하면 Convolution 에서 학습되는 파라미터는 filter 이기 때문이다. 이 때 filter(kernel)의 size 는 내가 정해주는 것이고, 이 filter 가 input channel 과 같은 channel 을 가지고, output channel 만큼의 개수를 가지고 있다.
• 위에서 살펴본 일반적인 CNN 의 구조에서, 최근 들어서 뒷단의 FC(Fully Connected Layer) 가 점점 최소화되는 추세이다. 왜냐면 파라미터 숫자에 dependent 하게 되기 때문이다.

• 내가 학습하고자 하는 어떤 모델의 파라미터의 숫자가 늘어날수록 학습이 어렵고 일반화 성능이 떨어진다고 알려져 있다. 파라미터 숫자가 너무 많으면 내가 아무리 학습을 잘 시켜도 이 모델을 배포했을 때 성능이 안나올 수 있는 것이다. 더불어 서비스 특징에 따라 연산 속도가 중요할 수 있는데, 파라미터 수가 많으면 연산 속도가 오래 걸린다.

  💡 이처럼 CNN 이 발전하는 방향은 성능을 위해서 모델을 최대한 deep 하게 가져가지만 동시에 파라미터 숫자를 줄이는데 집중하게 된다. 이에 따라 파라미터 숫자를 줄이기 위한 테크닉들이 계속해서 시도되고 있다. AI 개발자로서 항상 유념해야 하는 것은, 어떤 뉴럴 네트워크 아키텍쳐를 봤을 때 네트워크의 레이어 별로 몇 개의 파라미터로 이루어져 있고, 전체 파라미터 숫자가 몇 개 인지를 보는 것이 중요하다. 그 감을 가지는 것이 중요하게 된 것이다.

• 따라서 어떤 뉴럴 네트워크에 대해서, 파라미터가 몇 개인지를 손으로 계산해 보는 것이 좋다.
• 이 때, output shape 이 어떻게 되는지는 fully connected layer 의 파라미터 수를 구하는 데 필요하다. convolution layer 의 출력 텐서를 flatten 한 값이기 때문이다.

• 따라서 output shape(dimension) 의 영향을 미치는 stride, padding 의 개념이 어떻게 적용되는지 알아야 한다.

  Stride

  • Stride 란 넓게 걷는다 라는 것이다.
  • Stride 가 1 이라는 것은 kernel(convolution filter)을 매 픽셀마다 찍고 바로 한 픽셀 옮겨서 찍는다. Stride 가 2이면 filter 를 하나 찍고 바로 옆으로 옮기는 것이 아니라 2칸 옮긴다.

  • 이처럼 Stride 는 내가 convolution filter를 얼마나 dense 혹은 sparse 하게 찍을 것이냐를 의미하게 된다.

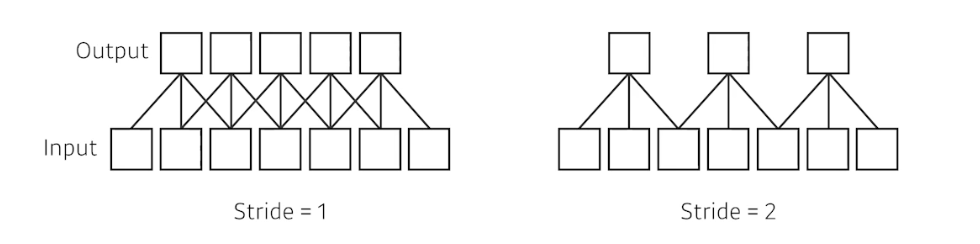    이 그림에서는 3x3 kernel 의 1D Convolution

  • 2D 로 가면 stride 의 파라미터가 width, height 방향으로 2개가 된다.

  💡 [Stride vs. Pooling]
  
  CNN 에서 feature 의 resolution(size)을 줄일 때, stride=2 또는 max/average pooling을 이용하여 resolution을 1/2 로 줄이는 방법을 많이 사용한다. 이런 stride 와 pooling 의 성질에 따라 선택하여 사용할 수 있다.
  
  1) convolution with stride
  convolution layer 를 이용하여 stride = 2로 feature 의 resolution 을 줄이면 학습 가능한 파라미터가 추가되기 때문에 학습 가능한 방식으로 resolution을 줄이게 되나 그만큼 파라미터의 증가 및 연산량이 증가하게 된다.
  ① 학습 가능한 파라미터가 추가되므로 네트워크가 resolution 을 잘 줄이는 방법을 학습할 수 있어서 pooling 보다 성능이 좋다.
  ② feature를 뽑기 위한 convolution layer 와 down sampling 을 위한 stride 를 동시에 적용할 수 있다. 이 경우 같은 3x3 크기의 filter 를 사용하더라도 stride 가 적용되기 때문에 더 넓은 receptive field 를 볼 수 있다.
  ③ STRIVING FOR SIMPLICITY: THE ALL CONVOLUTIONAL NET 라는 논문에서는 모든 pooling 을 convolution with stride로 변경 시 성능 상승의 효과가 있는 것을 확인했다.
  "We find that max-pooling can simply be replaced by a convolutional layer with increased stride without loss in accuracy on several image recognition benchmarks"
  
  2) pooling
  반면 pooling을 이용하여 resolution 을 줄이게 되면 학습과 무관해지며 학습할 파라미터 없이 정해진 방식(max, average)으로 resolution 을 줄이게 되어 연산 및 학습량은 줄어들지만 convolution with stride 방식보다 성능이 좋지 못하다고 알려져있다.
  ① convolution 연산 대비 연산량이 적으며 저장해야 할 파라미터의 숫자도 줄어드므로 학습 시간도 상대적으로 줄일 수 있고 inference 시 시간도 줄일 수 있다.
  ② FishNet 에서 제안한 내용 중에 skip connection 에서 convolution layer 가 계속 추가되면 backpropagation 시 gradient 가 잘 전달이 안될 수 있다고 하여 단순히 pooling 만을 사용한 기법이 적용된다. 즉, layer 를 줄여서 gradient 전파에 초점을 두려고 할 때 pooling 을 사용하는게 도움이 될 수 있다.

  Padding

  • 일반적으로 convolution 연산을 수행하면 이미지의 바운더리 정보가 버려진다. 즉 convolution filter 가 이미지의 가장자리를 넘어 적용되기 때문에 내가 가진 이미지의 가장 가장자리를 찍을 수 없다.
  • 그래서 가장자리를 새로 만들어주는 것이 padding 이다. 일반적으로 0-padding 은 가장자리에 덧대는 값이 0 이다.

  • padding 에 값을 주면 input 과 output 의 dimension 이 똑같게 된다.

    

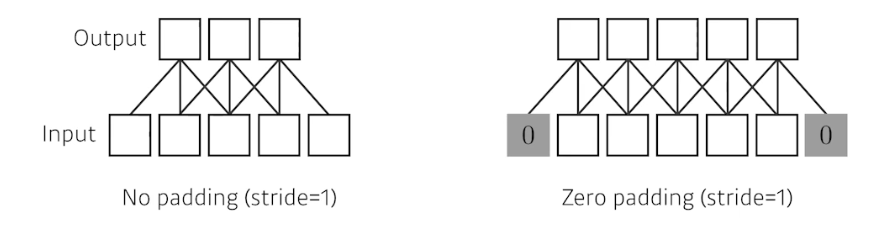
• 아래의 그림은 Stride 와 Padding 이 추가되었을 때 convolution 연산을 나타낸 것이다.

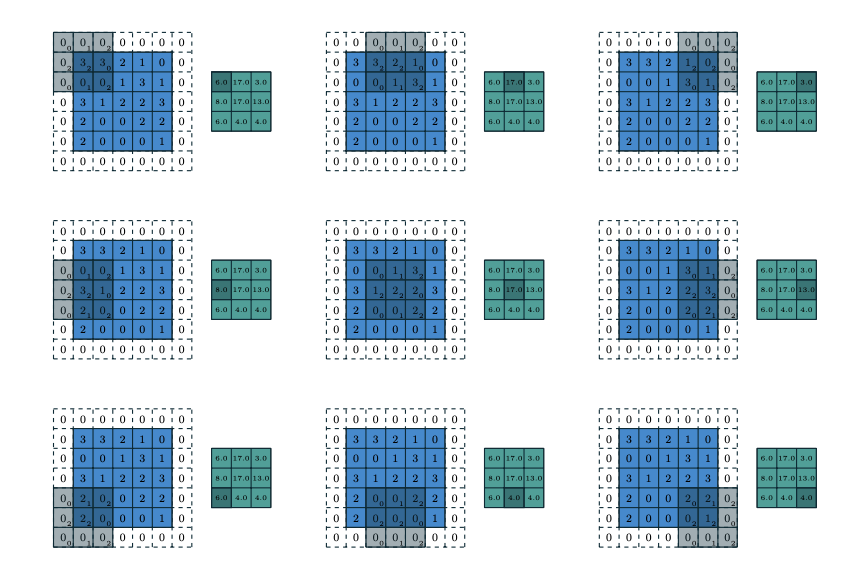  kernel size 3x3, stride 2, zero-padding 1

• 또한 적절한 크기의 padding 과 stride 가 1이면 어떤 input 과 convolution 연산의 출력으로 나오는 convolution feature map 의 dimension 이 같아지는 것을 알 수 있다.
• 예를 들어 input 과 feature map 의 dimension 이 같아질려면, kernel size 가 3x3 일 때는 padding 이 1, 5x5 일 때는 padding 이 2, 7x7 일 때는 padding 이 3이 필요하다.
• 즉 kernel size // 2 의 padding 과 stride 가 1이면 항상 입력과 출력이 같다!

• 아래처럼 convolution 연산을 할 때 내가 원하는 출력값에 맞춰서 padding 과 stride 를 줄 수 있다.

  

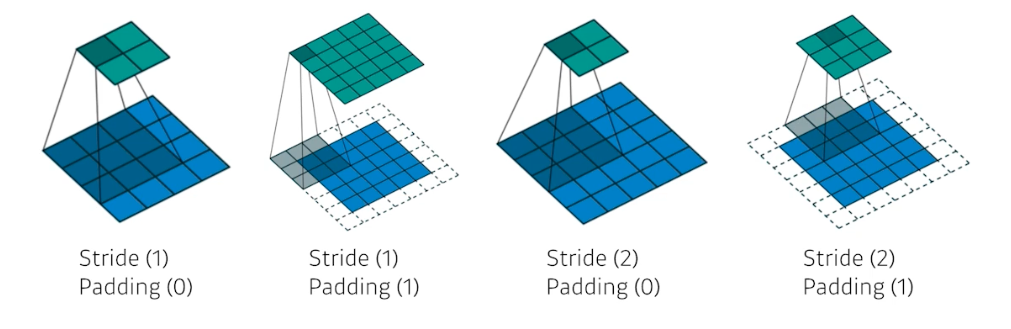
• 이제 output tensor(feature map) 의 dimension 을 계산해보자.

  • 먼저, convolution 연산 후 output image 의 크기(텐서 크기)는 input size + (2*padding) - filter size / stride + 1 이다.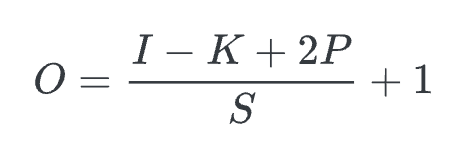

    input size($I$), filter size($K$), padding($P$), stride($S$)

  • pooling 연산 후 output image 의 크기(텐서 크기)는 input size - pooling size / stride + 1 이다.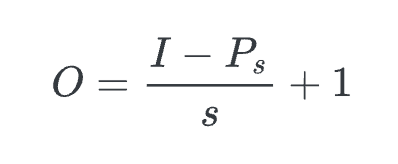

    input size($I$), pooling size($P_s$), stride($S$)

• 이제 예시를 통해 convolution 연산의 파라미터 수와 convolution 후 output 의 dimension(shape)을 구해보자.

  

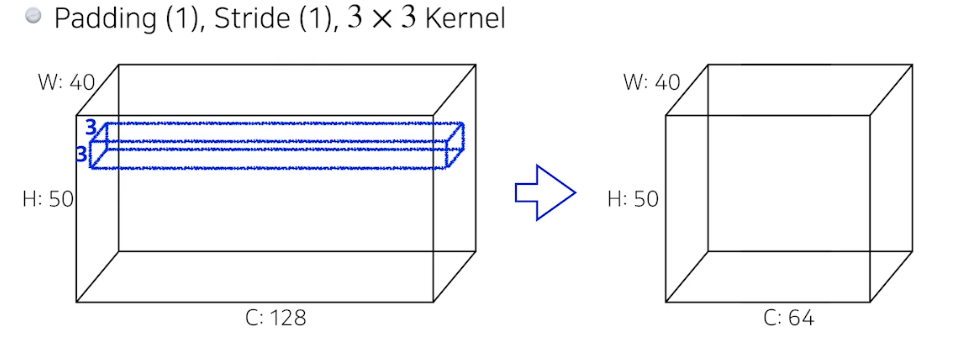
  • convolution feature map(output)의 하나의 channel(한 겹)을 만들기 위해서는, 내가 convolution 하고 싶은 filter(kernel) 의 spatial dimension(위에서는 3x3) 과 input 의 channel dim 과 kernel 의 channel 을 가지고 convolution 연산을 수행한다.
  • 즉 convolution filter(kernel)의 channel 은 input 이미지 channel 과 같다.
  • kernel 의 spatial dimension 이 3x3 이고, input 이미지의 spatial dimension 이 40x50 이다. input 이미지와 kernel 의 channel 수는 같고, padding 이 1, stride 가 1 이다.
  • output dimension 은 output width = (40 - 3 + 2) / 1 + 1 = 40, output height = (50 - 3 + 2) / 1 + 1 = 50 이다. 따라서 input 이미지의 spatial dimension 과 같은 convolution output feature 가 1겹(1 channel) 나오게 된다.

  • 그러나 우리가 궁극적으로 원하는 feature map 의 channel 은 64 이기 때문에, convolution filter(kernel)의 개수가 64개 필요하다. 따라서 convolution 연산에서 필요한 파라미터 숫자는 아래와 같이 된다.

    \[3 \times 3 \times 128 \times 64 = 73,728\]
• padding 이나 stride 는 convolution layer 의 파라미터 숫자와는 무관하다.
• 그러나 fully connected layer 에서는 마지막 convolution feature map 을 flatten 해야 하기 때문에 파라미터 수를 알기 위해서 tensor shape 를 알아야 한다. 따라서 output tensor shape 을 구하는 공식을 알아야 한다.
• pooling 의 경우 파라미터가 없다. 그러나 max pooling 과 같이 가장 큰 값을 고르거나 평균값을 고르는 등 파라미터 수에 직접적인 연관은 없지만, 마찬가지로 output tensor shape(dimension) 이 달라지기 때문에 알아야 한다.
• 따라서 CNN 에서 하나의 layer 의 파라미터 숫자는 오로지 input 의 dimension 과 내가 convolution operation 하는 filter 혹은 kernel 이 몇 개 있는지에 dependent 하다.
• 이런 계산이 자동으로 되어야 한다. 네트워크의 파라미터 숫자를 네트워크 모양만 봐도 감이 생겨야 한다. 이게 10000단위 인지 등 단위 개념에서 감이 생기면 좋은 무기가 된다.
• input, output 의 spatial dimension 은 convolution 연산에서 각각의 spatial 위치에 가해지는 filter 가 동일하기 때문에 파라미터 숫자와 상관이 없지만, input image 의 size(spatial dimension)가 커지면 kernel 이 sliding window 해야 하는 부분이 많아지기도 하고, fc layer 에서의 파라미터 수 증가와도 직접적 관계가 있기 때문에 유의하자.

맨 위로 이동 ↑