[CNN] 2. Convolutional Neural Network(CNN)

CNN(Convolutional Neural Network)

• Computer Vision 의 많은 모델의 기본이 되는 CNN(Convolutional Neural Network) 에 대해 살펴보자.
• 특히 CNN 이 왜 이미지를 대상으로 성능이 좋은지 보자.

convolution

• Convolution 은 원래 신호처리에서 사용되던 개념이다. 입력함수(입력)와 대상함수를 연산하여 출력함수를(출력) 계산하는 연산으로, 합성곱으로 정의된다.
• 즉 convolution 연산은 신호처리에서 시스템의 출력을 구할 때 쓰는 하나의 연산인데, 두 가지 신호가 겹쳐지는 부분의 넓이(적분)로 구해진다.

• 엄밀하게 convolution 은 대상함수를 반번하여 입력함수 위를 이동하면서 곱한 다음, 구간에 대해 적분하여 출력함수를 계산한다.

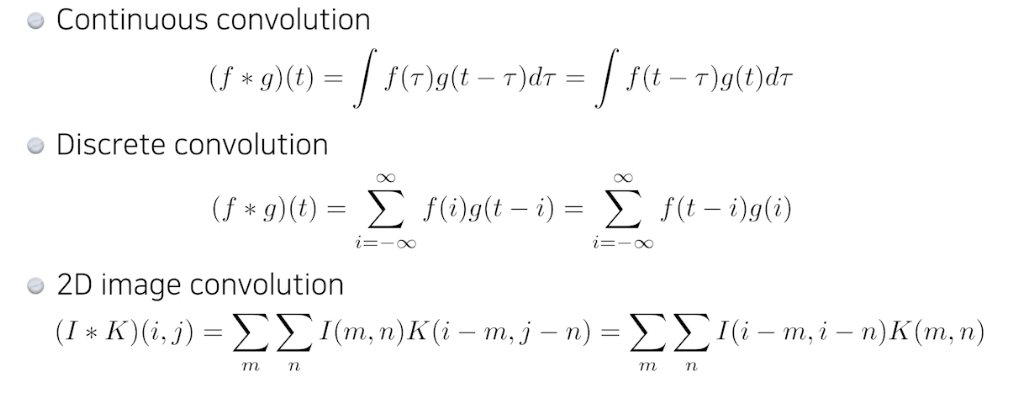  본래 신호처리에서 사용되던 convolution 연산

• CNN 에서는 이러한 convolution 연산을 2D 이미지에 적용시키는 것이다.
• 이미지를 입력함수로 보고, 앞으로 수없이 등장할 convolution filter 를 대상함수로 보면 이미지 위에 작은 필터를 이동시키면서 각 위치의 이미지 영역과 필터를 convolution 하여 feature map 을 출력하는 것이다.
• 이 Convolution 연산은 이미지의 특정 부분과 필터를 내적하는 것으로 볼 수도 있다. 두 벡터가 유사할수록 큰 값을 출력하는 내적의 특성에 의해 필터는 이미지에 있는 패턴들과 유사한 형태로 학습이 되는 것이다.
• 많은 머신러닝/딥러닝 프레임워크에서는 필터를 반전하는 것을 제외하고는 Convolution 과 완전 동일한 연산인 Cross-correlation 을 통해 convolution 연산을 구현한다.
• 어차피 필터의 값을 학습하려는 것이 목적이기 때문에 뒤집어서 convolution 을 하나 그냥 하나 동일하다. 학습과 추론 시에 필터만 일정하면 된다. 따라서 딥러닝 프레임워크들은 convolution 이 아니고 그냥 cross-correlation 으로 구현되어 있다. 그러나 관습상 합성곱이라고 부른다.

convolution 연산

• convolution 연산 시 적용하고자 하는 filter의 모양, 값에 따라서 같은 이미지에 대한 출력이 달라진다. 이를 잘 활용하면 convolution 연산으로 이미지 blur 처리나 강조 등을 수행할 수 있다.

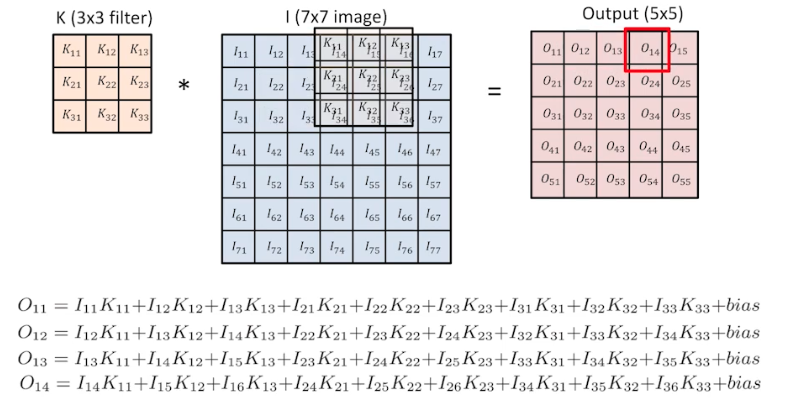  같은 위치에 있는 값끼리 곲한 값을 모두 다 더한 값이 $O$ 가 된다.

• output feature map 의 한 칸은 input image 에서 convolution filter 가 움직이면서 filter 와 겹쳐지는 영역의 같은 위치에 있는 값들을 곱한 후, 모두 더한 값으로 정해진다. (위 그림 참고)
• convolution 연산의 결과인 feature map 의 channel 수는 convolution filter 의 개수이다.
• 즉, convolution filter 가 여러 개 있다고 보고, filter 한 개의 연산 결과가 output feature 의 한 channel 이 된다. convolution filter 가 1개 있으면 output feature 의 channel 은 1이고, 4개가 있으면 4이다.
• 따라서 output feature map 의 channel 을 알면, 여기에 적용되는 convolution filter 의 개수 역시 계산할 수 있다.
• RGB 이미지는 3개의 channel(Red, Green, Blue)을 가지므로, 이 이미지에 적용되는 convolution filter 도 3개의 channel 을 가져야 한다. 이렇게 하여 각 filter의 channel 이 입력 이미지의 해당 channel 과 연산된다. 그 후 모든 channel 의 결과가 합쳐져 최종 output feature map 을 생성한다.

• 정리하면, convolution 레이어에서 filter(또는 kernel)의 개수는 출력 데이터의 channel 수를 결정한다. 각 filter 는 입력 데이터에 독립적으로 적용되며, 각 filter 의 출력은 출력 데이터의 하나의 channel 을 형성한다.

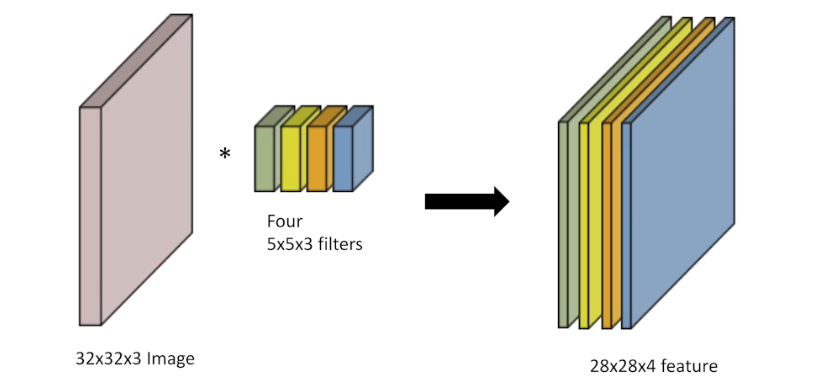  filter가 4개 이므로, output feature map 의 channel도 4이다.

• convolution filter 는 여러 개 있을 수도 있다. 단, 한 번 convolution 을 거치고 나면 그 다음에는 non-linear activation 를 거치게 된다.

• 즉, 입력 이미지(32x32x3)가 convolution filter(4x5x5x3)를 거쳐서 나온 convolution feature map(28x28x4)의 각 element 별로 ReLU 등의 activation func 혹은 non-linear activation 을 거친다.

  

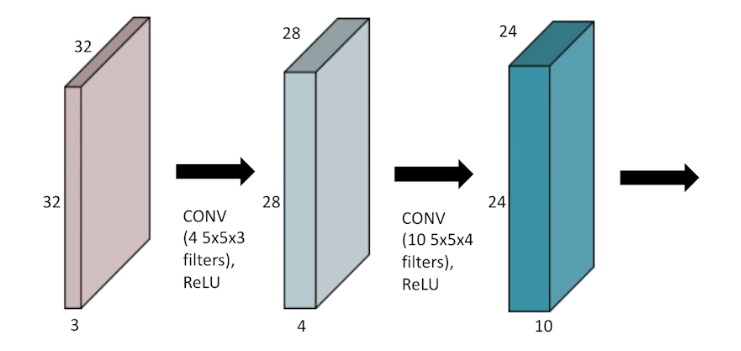
• convolution filter 의 channel 은 내가 지금 convolution 을 하는 feature(input 이미지)의 channel dimension 이 된다. 즉 convolution 의 대상이 되는 feature(혹은 input) 와 convolution filter 의 channel 은 같아야 한다.

CNN 이 사용되는 이유 파헤치기

• 역사적으로 보면, 맨 처음 인공신경망의 초창기 모델은 MLP 이다. 가장 오래된 것은 perceptron, 그 다음 MLP 순이다. 물론 perceptron 은 1층짜리 NN 과 같아서 이 녀석으로는 XOR 문제를 풀 수 없었다.
• 이후 여러 층을 쌓고 비선형성(non linear)함수, 즉 activation func 을 주입했더니 XOR 등 여러 문제를 풀 수 있었다. 이것이 60년대 쯤이다.
• 이후 얀 누쿤의 LeNet 이 90년대 초에 등장했다. CNN 은 이 LeNet 과 함께 등장했으며 아직까지도 사용된다.
• 그렇다면 왜 우리는 MLP 에서 CNN 으로 넘어간 것일까? MLP 에서 뭐가 부족하고 CNN 에서 어떤 점이 좋았던 것일까?

CNN 의 장점

• MLP 에서 CNN 으로 넘어갔을 시기에 가장 주요한 MLP 의 단점은 계산량과 파라미터 수가 많다는 것이다.
• 파라미터 수가 많다는 것은 계산량이 많다는 것과 모델을 훈련하기 어려워짐을 뜻한다. 또한 파라미터 수가 많기 때문에 데이터가 많이 필요했다. 그러나 90년대 초반에는 데이터가 많지 않았다.
• 그 당시 CNN 의 가장 큰 장점은 데이터 효율성에 있다. MLP 를 훈련하기 위해서 10만개의 데이터가 필요할 때, CNN 은 2~3만개면 훈련이 가능했다.
• 이런 데이터 효율성이라는 CNN 의 엄청난 장점은 훈련이나 학습에 큰 이점을 가져왔다. 또한 필요한 데이터의 수도 줄어든 것 뿐만 아니라 translation equivariance, translation invariance 라는 특성이 CNN 을 사용함으로써 동반되는 개념으로 따라왔다.
• translation invariance, translation equivariance 는 사실 말장난 같은 개념이다.

• 먼저, CNN 의 일반적인 구조는 convolution layer - pooling layer - activation function 으로 이루어지는데, convolution layer 는 동일한 weight 를 가진 일정한 filter size 를 가지고 sliding window 로 연산을 하면서 이미지의 특징을 학습한다.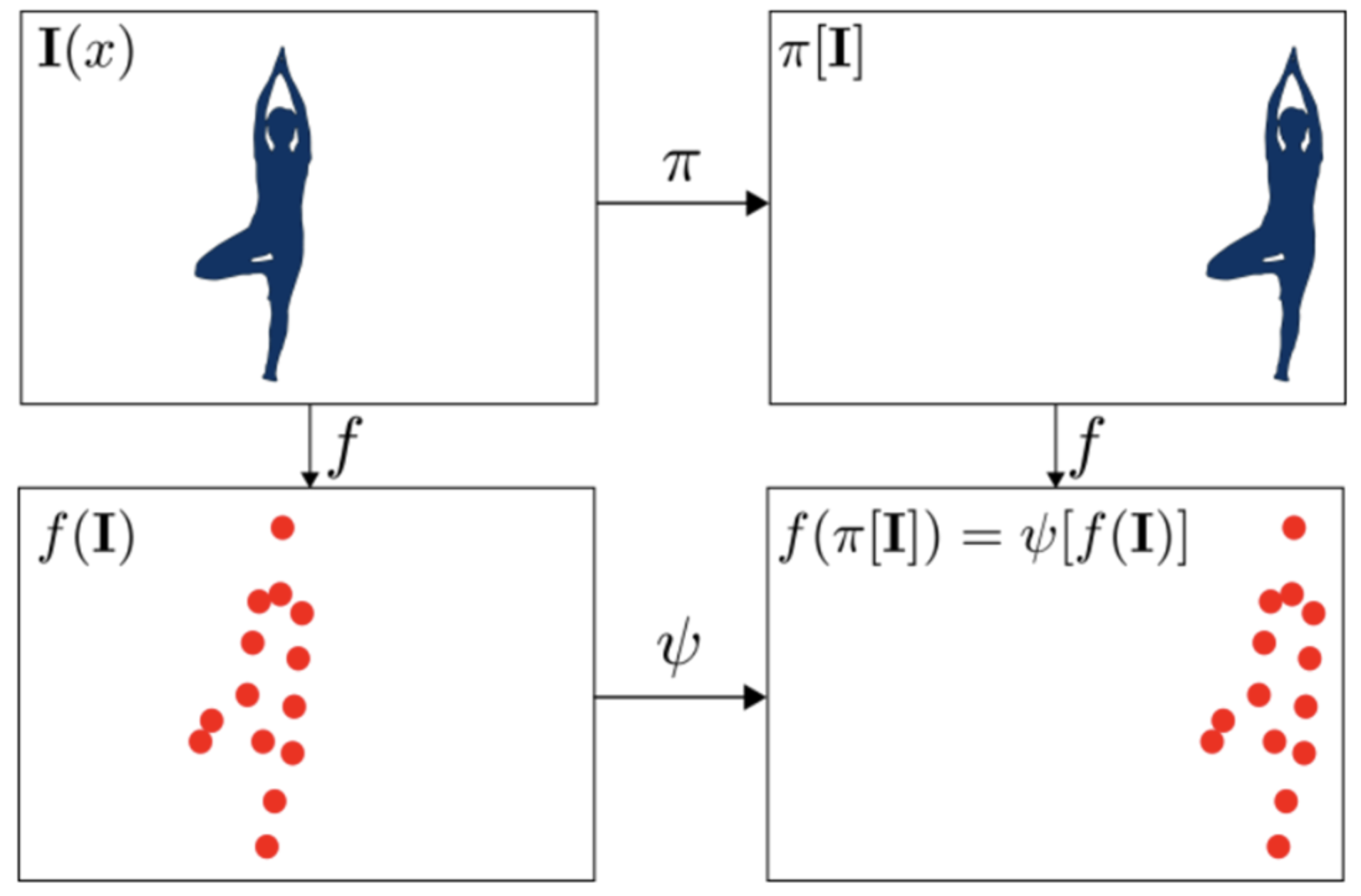

  

• 위 예제처럼 사람이 정면에 있는 경우, 오른쪽으로 치우친 경우가 있다. 이 이미지를 convolution layer 를 통과시킨다면 같은 weight 를 가진 filter 가 통과되면서 사람이 있는 곳에서 동일한 빨간색 점의 패턴이 학습된다.
• 즉 사람이 이미지의 어디에 위치해있던 상관없이 동일 패턴이 학습되는 것이다.

• 여기서 우리는 translation equivariance 와 translation invariance 에 대해서 깊게 생각해볼 수 있다.

  Translation Equivariance

  • Equivariance 는 Variance 즉 가변성을 뜻한다. 이러한 성질은 convolution layer 에서 잘 나타난다. 즉 넣는 input 값에 따라 output 값이 변한다는 것이다.
  • 위치를 이동시키는 함수 $f$ 가 있고, 데이터가 $x$ 일 때, $Conv(f(x)) = f(Conv(x))$ 이다.
  • 즉 어떤 input 의 위치를 바꿨을 때 다른 결과는 다 똑같고 위치만 달라지면 위치에 따른 equivalance 가 있다고 한다. 이 특성으로 얻을 수 있는 이점은 물체가 어디에 있든 위치만 달라진 똑같은 값을 뽑기 때문에 그 물체를 feature vector 로 정확히 뽑을 수 있다.
  • 쉽게 이야기 하면, input 위치가 변하면 output 위치도 변하기 때문에 convolution filter 하나로 다양한 위치에서 특징 추출이 가능하며 이렇게 추출된 특징들은 동일하다는 것이다.

  Translation Invariance

  • Invariance 는 불변성을 뜻한다. 다른 input 에 대하여 어떤 함수를 통과시키면 같은 output 으로 나올 수 있다는 것이다.
  • 즉 translation invariance 는 물체의 위치가 어디에 있든 출력이 변하지 않는다는 것이다. 패치 단위로 연산을 함으로써 어디에 있든 출력 관점에서 같다는 것인데, 위치를 바꿔도 결과값은 항상 동일하다는 것이다.
  • 이는 convolution layer 와 쌍으로 붙는 pooling layer 에서 수행된다. pooling filter size 내에서는 위치에 상관없이 동일한 값을 추출한다.
  • max pooling 을 생각하면 쉽다. 2x2 filter 내에 큰 값이 어디에 있든 max pooling 을 거치면 가장 큰 값이 동일하게 나온다.
  • 또한 convolution layer 에서는 각 위치마다 동일한 filter 를 사용하여 parameter(weight)를 share 하기 때문에 위치에 상관없이 같은 객체는 같은 값을 추출한다. 이를 두고 translation invariance learning 이라고 한다. 이미지의 특징을 학습할 때, 동일한 weight 를 가진 kernel 을 가지고 훑어가며 학습하기 때문에 위치는 결과값에 영향을 주지 않는다는 것이다.
  • 엄밀하게, CNN 자체는 translation equivariant 한 네트워크이고 translation invariance 성질은 가지고 있지 않다. convolution filter 내에 object 의 위치가 바뀌면 값의 위치도 바뀌는 equivariant 하기 때문이다.
  • 그러나 convolution layer 와 pooling layer 가 반복되고 fully connected layer 를 거치면서 결과값을 얻게 되면 translation invariant 하게 된다.
  • filter size 내에서 위치에 따라 값이 변하긴 하지만 convolution 은 weight 를 공유하고, local 한 영역을 sliding window 방식으로 훑으면서 object 의 위치와 상관없이 동일한 패턴을 학습한다.
  • 또한 translation equivariant 한 feature map 들을 fully connected layer 에 넣었을 때도 아직까지는 equivariant 하게 된다. fc layer 의 입력값은 마지막 feature map 을 flatten 한 것이기 때문이다.
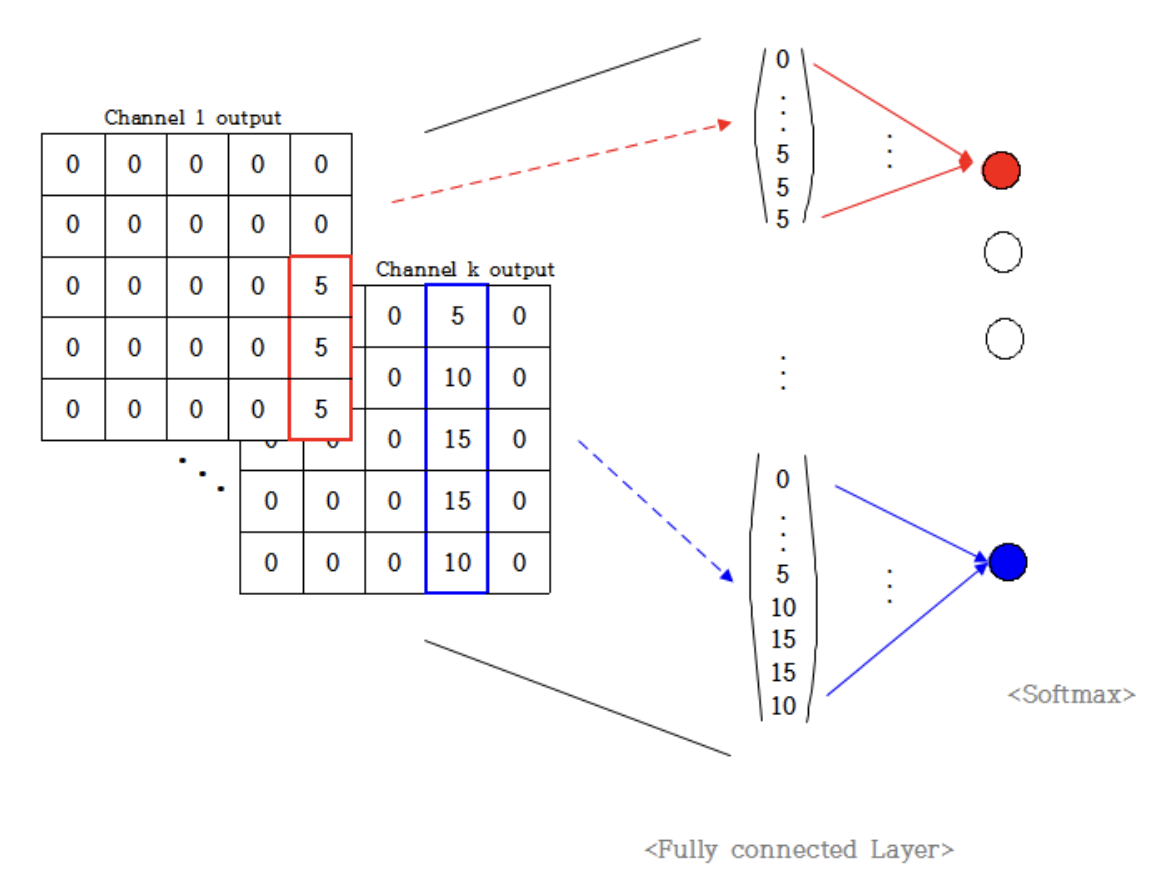
  • 그러나 fc layer 의 값을 softmax 연산 하여 결과값을 받으면 위치와 상관없이 동일한 패턴을 가진 같은 object 는 같은 결과값을 가진다. object 가 있는 쪽의 값이 크게 나오고 큰 값이 결국 softmax 의 결과값으로 나오기 때문이다.
    
• 이처럼 두 개념은 비슷하면서도 다른데, feature vector 상에서 연결된다.
• 공간의 관점에서 image 공간과 feature 공간의 위치가 대응하여 공간상으로 같은 공간에 input 과 output 이 mapping 이 된다는 것이 translation equivalance 이고, 이 때 위치에 상관없이 같은 object 에 대한 output 값이 같다는 것이 translation invariance 이다.
• CNN 을 사용하면 이 두가지 특징을 가져갈 수 있다는 장점이 생긴다.
• convolution layer 가 equivariant 한 성질을 갖기 때문에 다양한 위치에서 특징 추출이 가능한데, pooling layer 와 parameter sharing 을 통해 invariant 하게 모델을 학습한다. 이를 통해 fully connected layer 를 거쳐 softmax 를 한 결과값은, 동일한 object 는 위치와 상관없이 동일한 값을 가지게 된다.

inductive bias

• inductive bias 는 지금은 많이 등장하는 용어는 아니지만, 1~2 년 전까지만 해도 굉장히 중요했던 개념이다. inductive bias 는 딥러닝의 발전 흐름과 완전 직결된다.
• inductive bias 는 모델을 선택하고 훈련해서 결과를 얻는 과정 속에서 인간이 개입하는 정도를 뜻한다.
• 머신러닝/딥러닝의 모델은 1) 데이터의 input 이 조금만 바뀌어도 모델의 결과가 망가지게 되고, 2) 데이터 본연의 의미를 학습하는 것이 아닌 결과와 편향을 학습하게 된다는 일반적인 문제를 가지고 있다.
• 이러한 문제를 해결하기 위한 것이 inductive bias 다. 학습 시에는 만나보지 않았던 상황에 대하여 정확한 예측을 하기 위해 사용되는 추가적인 가정(assumption)이다. 즉 모델이 목표 함수를 학습하고 훈련 데이터를 넘어서 일반화된 성능을 가질 수 있도록 만든 가정인 것이다.
• 이렇게 머신러닝/딥러닝의 모델들은 “나는 이런 특성을 가진 데이터를 주로 다루겠다.” 는 식의 가정 하에서 만들어진다. 그래서 각 모델의 가정과 데이터 특성에 맞는 모델을 잘 선택하는 것이 중요하다.

• 머신러닝과 딥러닝이 주어진 데이터에 맞는 함수를 가방에서 찾는 과정이라고 비유할 때, inductive bias 는 그 가방의 크기와 반비례한다. 모델에 적용되는 inductive bias 가 많을수록 가방의 크기는 작아진다. 그 가정에 맞는 모델을 선택해야 하기 때문이다.

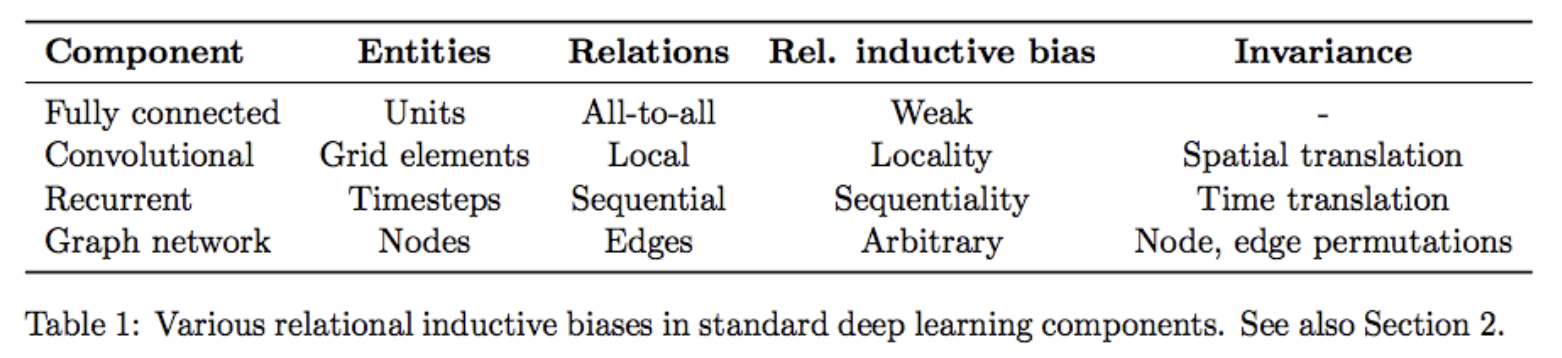  딥러닝에서의 다양한 inductive bias

• 거의 모든 함수를 표현할 수 있는 MLP 의 경우 엄청 큰 가방(inductive bias 가 weak)이라 생각할 수 있고, CNN 은 MLP 보다 작은 크기의 가방이다.
• CNN 의 inductive bias는 locality 다.
• CNN 에 대한 inductive bias 에 translation equivariance 와 translation invariance 가 포함된다고 보기도 하는데, convolution 개념은 신호처리에도 쓰였기 때문에 convolution 을 NN 에 도입했더니 따라온 두 현상이라고 보는 해석도 있다.
• inductive bias 는 결국 내가 주입한 것이라고 볼 때, 3x3 같은 kernel(filter) 크기만 주입한 것이지 “위치에 따라 값이 같게 해” 이렇게 주입한 것은 아닐 것이기 때문이다.
• 따라서 CNN 은 locality 라는 inductive bias 가 주입이 된 상황이다. 그러나 CNN 은 그 당시에 데이터 효율이 좋아서 사용한 것에 불과하다. 그런데 최근에는 데이터가 부족하지 않고 너무나도 많다.
• 그러다 보니 inductive bias 를 많이 주입할 필요가 없어졌다. 그래서 사람들은 다시 MLP 로 돌아가는 움직임을 보였다. 이 MLP 로 돌아가는 시기와 NLP 에서 트랜스포머가 대세가 되는 시기가 겹친다. 이 트랜스포머가 MLP 이기 때문이다.
• Computer Vision 에서 트랜스포머는 CNN 으로 패치 단위로 임베딩을 얻고 이 임베딩으로 MLP 하는 것과 구조가 같다.
• 트랜스포머에서는 다시 돌아가서 패치 단위 연산으로 임베딩을 뽑고 이 임베딩에 MLP 를 태운다. 적당한 가중치에 제약(소프트맥스)을 건 것이 트랜스포머이고, 이 제약이 빠지면 MLP 와 구조적으로 동일하다.
• 위에서 본 것처럼 MLP 는 inductive bias 가 굉장히 적은 형태다. 뉴런을 한 레이어에 몇 개로 할 것인지, 레이어를 몇 층으로 구성할 것인지가 끝이다. 즉 사람은 레이어 내의 뉴런의 개수, 레이어 층의 개수만 정해주면 끝인 것이다.
• 반면에 CNN 은 3x3 conv layer 와 같이 local 한 feature 만 보라는 강력한 inductive bias 가 들어간다.
• 결국은 inductive bias 가 빠진 형태가 지금(2024)의 대세라고 볼 수 있다. 이전에는 데이터가 부족해서 inductive bias 를 강력하게 주입한 CNN 이 대세였고, 이제는 데이터가 부족하지 않아 inductive bias 가 그렇게 필요하지 않아서 MLP, 트랜스포머(MLP 와 구조적 동일) 가 대세가 된 것이다.
• 다르게 비유해보자. inductive bias 는 모델에게 시험 범위에 대한 사전지식을 주는 것으로 비유할 수 있다. 우리는 시험에서 사전지식을 알려주지 않은 녀석과 사전지식을 알려준 녀석을 비교할 때, 사전지식이 포함된 범위에서 누가 더 실력적으로 뛰어난 지 판단이 불가하다. 사전지식의 영향이 있기 때문이다.
• 그러나 갑자기 전범위로 시험을 내면, 사전지식이 없는 녀석이 시험을 잘 본다. 내부적인 연결과정에서 무언가 패턴을 찾아낸 녀석과, local 한 feature 만 보라고 사전지식을 준 녀석 사이에 성능 차이가 나기 시작하는 것이다. 이게 MLP → CNN → MLP, Transformer 의 흐름과 비슷하지 않은가?
• inductive bias 는 ViT 논문에도 등장한다. 이 ViT 는 Computer Vision 분야에서 워낙 중요한 논문이라 inductive bias 가 동시에 중요하게 됐다.
• 결국 inductive bias 같은 인사이트를 들고 있으면 나중에 모델을 선택할 때도 도움이 된다.
  • 사전지식이 충분하고 문제가 어렵지 않고 데이터가 많지 않으면 CNN 이 제일 좋다.
  • 만약 inductive bias 개념이 별로 필요하지 않은 문제라면, 어떤 지표를 봐도 트랜스포머가 높은 곳에 스코어링하고 있다.
  • 내가 다뤄야 할 문제의 난이도, 데이터셋 이런 것들을 고려해서 CNN 과 트랜스포머를 선정하는 것이 모델을 선정하는데 중요한 요소가 된다.
• 딥러닝에서의 inductive bias 에 대한 감을 유지하자. 모델을 선정하는 것도 전체 큰 틀에서 보면 inductive bias, 즉 인간의 지식이 주입되는 것이기 때문이다.

CNN 의 가정

• 위에서 CNN 의 inductive bias 가 locality 임을 보았는데, 더 자세히 살펴보자.
• CNN 은 어떻게 가정을 두었길래 image 에서 가장 좋은 성능을 보였을까?
• 다른 포스트에서 살펴볼 것이지만, LeNet 과 구조적으로 거의 동일한 AlexNet 논문에서 이미지가 가진 특성에 대한 CNN 의 가정이 언급된다.

• 바로 stationarity of statistics 와 locality of pixel dependencies 다.

  Stationarity

  • stationarity 는 시계열 데이터의 통계적인 특성이 시간이 지나도 변하지 않는다는 뜻이다.
  • 쉽게 말해 시간이 변해도 동일한 패턴이 반복된다는 뜻인데, 동일한 패턴이 반복되면 분석도 쉬워진다.
  • 이미지는 시간 대신에 위치에 관계없이 동일한 패턴들이 반복되는 특징을 가지고 있다. 여러 사람이 있는 이미지는 위치에 관계없이 발견될 수 있는 사람의 동일한 패턴이 있다.
  • 이는 달리 말하면 이미지의 특정 위치에서 학습한 파라미터를 이용해서 다른 위치에 있는 동일한 특징을 추출할 수도 있다는 뜻이다.
  • 그리고 위에서 살펴보았지만, CNN 의 핵심이 되는 연산인 convolution 연산은 오래전부터 시계열 데이터를 다루는 신호처리에서 1-d convolution 을 널리 사용했다. 이 관점에서 이미지도 영상신호의 하나로 보고 2-d convolution 을 이용하는 것이다.
  • 이미지에 convolution 을 사용하면서 여러 이점이 따라온다.
    • 이미지를 convolution filter 가 sliding window 방식으로 훑으면서 feature map 을 출력한다. 이 convolution 연산을 filter 안에 있는 이미지의 특정 부분과 convolution 의 weight 를 내적하는 것으로 볼 수 있다. 두 벡터가 유사할수록 큰 값을 출력하는 내적의 특성에 의해 filter 는 이미지에 있는 패턴들과 유사한 형태로 학습될 수 있다.
    • convoltuion 이 weight 를 공유하는 것은 효율을 가져온다. 바로 위에서 본 convolution filter 의 parameter sharing 이 가져오는 효율이다. 동일하더라도(같은 object 라도) 위치에 따라 다른 특징으로 인식한다면 모두 다른 filter 를 사용해야 하기 때문에 비효율적이다.
    • 여기서 CNN 의 데이터 효율이 설명된다. parameter sharing 은 feature map 하나를 출력하기 위해 한 장의 filter 만을 이용하기 때문에 Fully Connected Layer 보다 훨씬 적은 파라미터 수를 사용한다. 따라서 메모리를 아낄 수 있고 연산량도 적으며 데이터 수를 더 적게 학습시켜도 더 좋은 성능을 낼 수 있다. 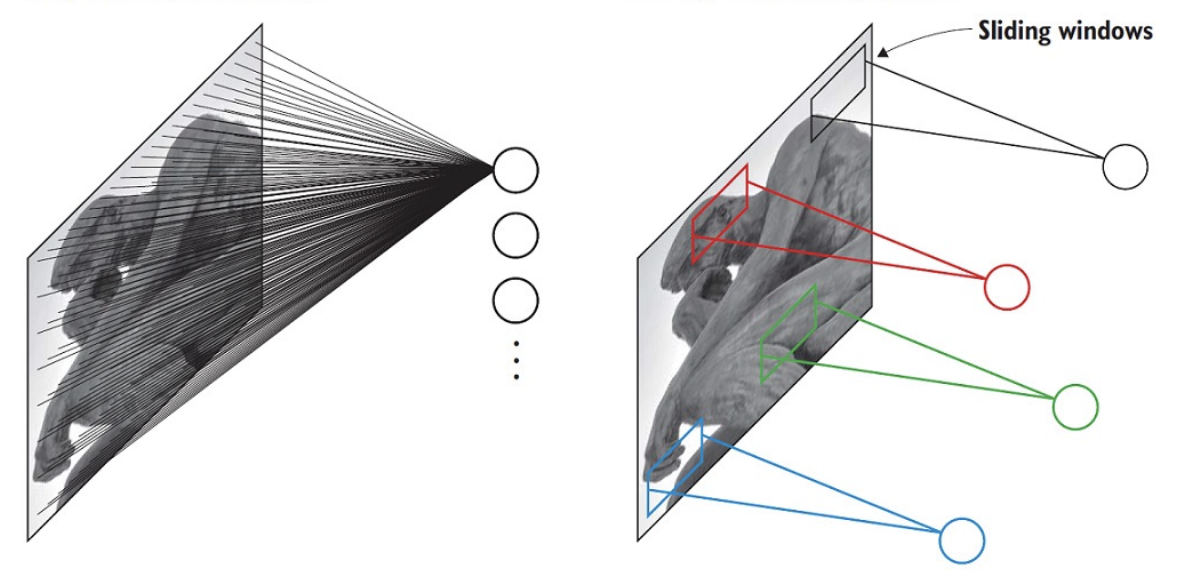좌: FCN 우: CNN
    • statistical efficiency 란 예측 모델의 품질 측정방법으로 더욱 효율적인 모델은 상대적으로 데이터 수를 적게 학습시켜도 더 좋은 성능을 내야한다는 의미로 사용되는데, convolution 은 하나의 filter 로 동일한 특징을 여러 곳에서 볼 수 있기 때문에 FC layer 에 비해 동일한 학습 데이터셋 상황에서도 더 많은 데이터를 학습한 효과를 갖게 되고 결국 statistical efficiency 가 향상된다.
    • 이게 무슨 말이냐면, filter 하나가 input 의 여러 곳을 보기 때문에 마치 더 많은 데이터를 보게 되는 것처럼 통계적인 효율성이 올라간다. 반면에 FC layer 와 같이 weight 를 공유하지 않으면 input size 와 동일한 크기의 weight 를 갖게 되고 모든 입력 하나하나가 전체 weight 와 연결된다. 즉 weight 가 전체적으로 데이터를 한번만 보게 되는 것으로 convolution 보다 비교적 데이터를 적게 보게 되는 것이다.
  • 이러한 Stationarity 는 이미지 위치에 상관없이 동일한 패턴, 특징들이 존재한다는 가정이기 때문에 parameter sharing 을 하는 convolution 연산에 매우 적합하다. convolution 이 stationarity 가정을 잘 살리면서 비교적 연산량은 더 적고 메모리를 아끼며, 데이터 효율도 더 높다.
  • 또한 convolution 이 가진 입력의 위치가 바뀌면 출력도 동일하게 위치가 변하는 translation equivariance 특성은 이미지의 stationarity 와 매우 잘 맞는다. filter 하나로 다양한 위치의 특징들을 추출하는 것이기 때문에.
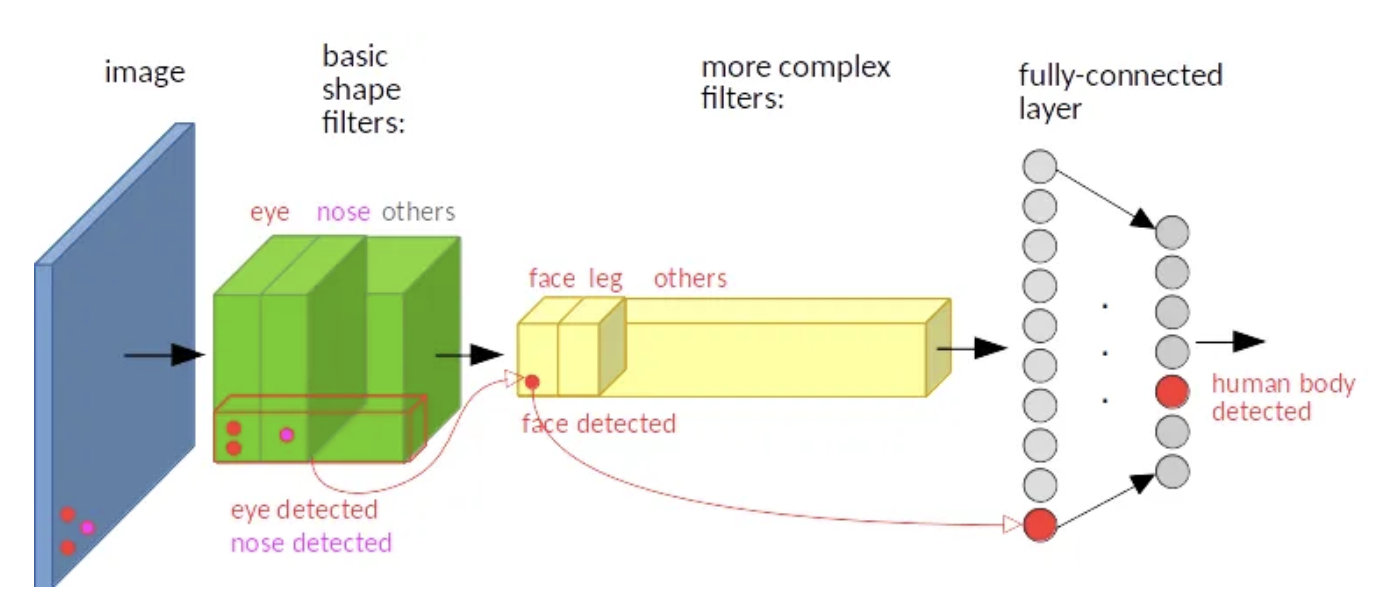
  • 중요한 것은, 위에서 살펴본 것처럼 pooling layer 와 더불어 parameter sharing 이 translation invariance 를 가져온다는 것이다. 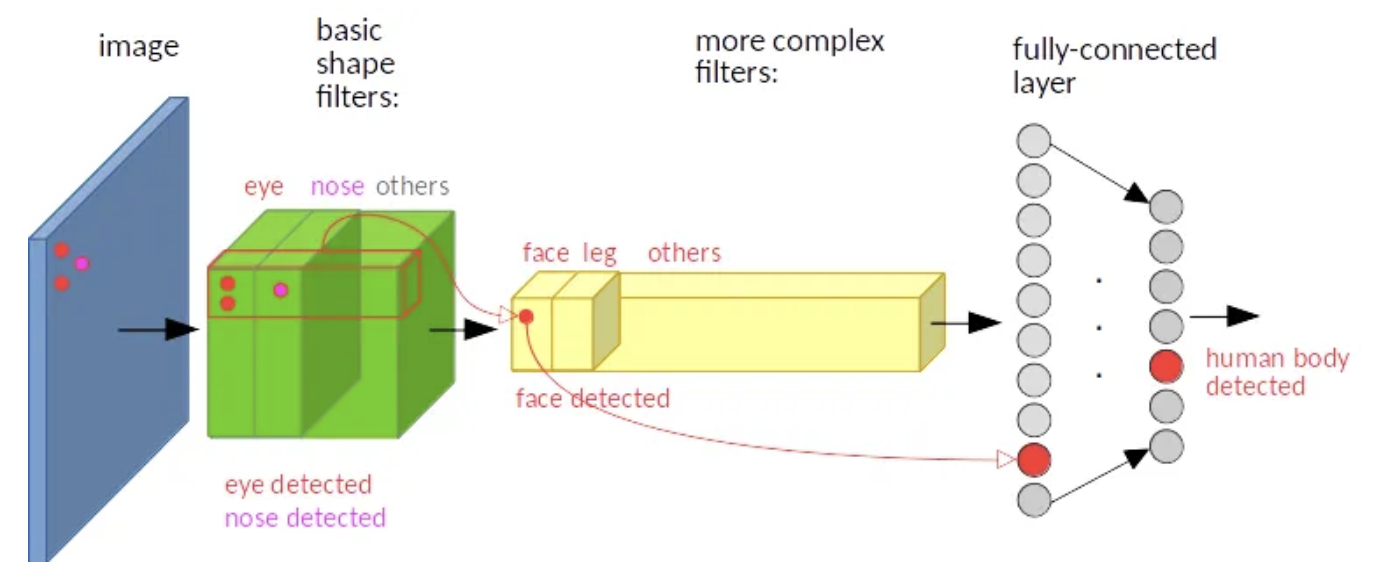input image 의 다른 위치에서 eye 와 nose 의 특징을 추출하는 것인데, 마지막 fc layer 이후 분류 결과를 보면 동일하게 human body detected 결과를 가져옴을 알 수 있다(translation invariance).
  • CNN 을 classification 에서 사용할 때, 각 class 의 확률을 출력하는 하나의 커다란 함수로 본다면, 그 안에 포함된 convolution 연산은 equivariant 해서 서로 다른 위치에 있는 특징을 입력으로 넣으면 feature map 에서도 각 특징을 서로 다른 위치에 배치시킨다.
  • 하지만 convolution layer 들을 지나서 fc layer 와 softmax 를 거친 결과는 특징의 서로 다른 위치와는 상관없이 같은 값을 높게 출력한다.
  • 즉, feature map 상에서 서로 다른 위치를 가지더라도 parameter sharing 을 하나는 한장의 filter 가 같은 object 에 대해 어느 위치에 있건 동일한 결과값을 가져오기 때문에 CNN 자체가 translation invariance 특성을 갖게 된다.
  • 이러한 CNN 의 translation invariance 특성은 단점을 비판 받기도 한다. 위치에 관계없이 같은 값을 출력한다면 엉망인 순서의 이목구비를 보고 사람 얼굴이라고 할 수 있지 않느냐는 비판이 그 중 하나이다. 그러나 이후 포스트에서 다루겠지만, 더 깊은 convolution layer 일수록(high-level), 더 큰 형태의 특징들을 뽑아내기 때문에 CNN 의 구조가 적절하다면 충분히 커버 가능하다.

  Locality

  • locality 는 이미지에서 한 점과 의미있게 연결된 점들은 주변에 있는 점들로만 국한된다는 뜻이다.
  • 즉 이미지는 작은 특징들로 구성되어 있기 때문에 픽셀의 종속성은 특징이 있는 작은 지역으로 한정된다.
  • 예를 들어 사람 얼굴에서 코 라는 특징은 코를 구성하는 픽셀값에서만 표현되고 눈 위의 픽셀에서는 관계가 없다. 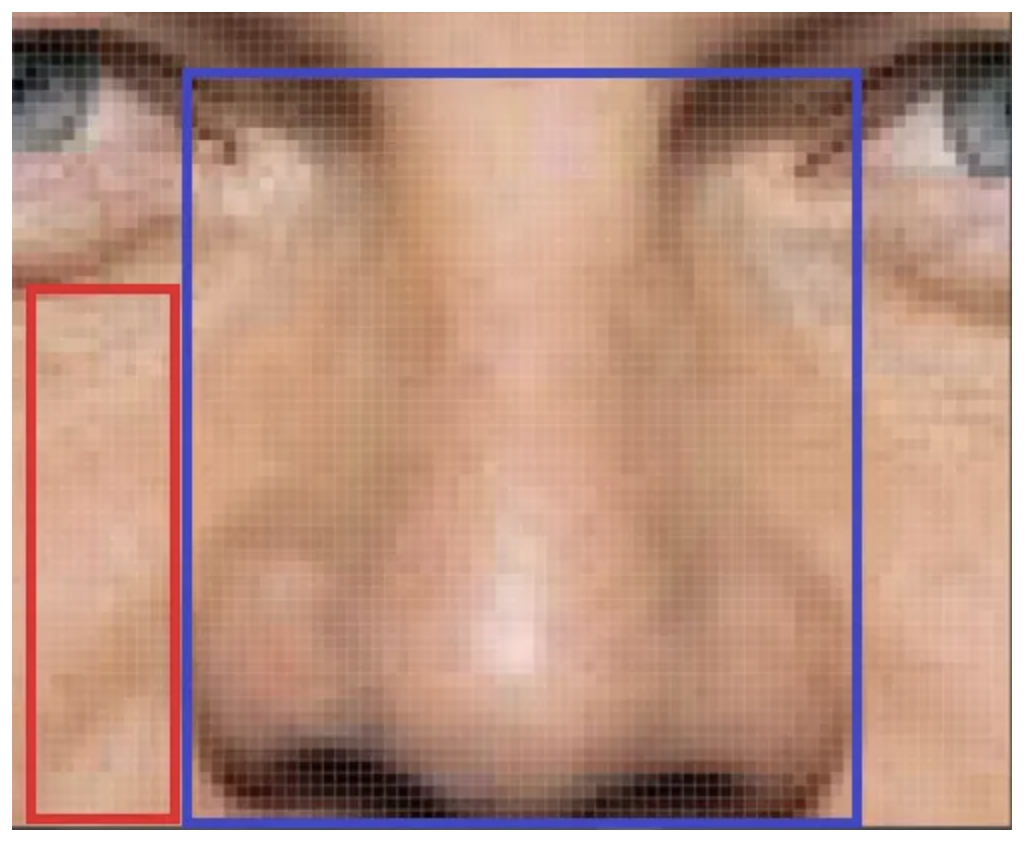파란색 영역의 픽셀들은 빨간색 영역의 픽셀과는 관계가 없다.
  • 다시 말해, 이미지를 구성하는 특징들은 이미지 전체가 아닌 일부 지역에 근접한 픽셀들로만 구성되고 근접한 픽셀들끼리만 종속성을 가진다는 가정이다.
  • 이러한 가정은 convolution filter 가 Sparse interactions 특성을 갖는다는 점에서 잘 맞는다.
  • Sparse interactions 란 하나의 출력 유닛이 입력의 전체 유닛과 연결되어 있지않고 입력의 일부 유닛들과만 연결되어 있다는 의미이다. 이미지를 conv filter 가 sliding window 방식으로 훑어가면서 feature map 을 만들어가는 과정을 생각하면 쉽게 이해된다. 이 또한 주변 픽셀들과만 연관이 있다는 가정인 locality 와 딱 들어 맞는다.
• 마무리하면, CNN 은 이미지의 특성인 Stationarity 와 Locality 를 가정하여 만들어진 모델인 만큼 당연하게 이미지에서 좋은 성능을 거둔다.
• 특히 동일한 특징이 이미지 내 여러 지역에 있을 수 있고, 작은 지역안에 픽셀 종속성이 있다는 가정 때문에 parameter sharing, sparse interaction 의 특성을 가지는 CNN 의 근간이 되는 convolution 연산이 아주 잘 들어맞음을 알 수 있다.

맨 위로 이동 ↑