[Activation] 4. Swish, Mish, SwiGLU, GEGLU

앞서 다양한 활성화 함수들을 봤다. 여전히 ReLU 는 가장 많이 사용되는 활성화 함수지만, 정답은 없다. 모델의 특성과 상황에 맞게 적절한 활성화 함수를 고르는 것이 실력이며, 무난하게 논문에서 사용하고 있는 활성화 함수를 사용하는 것도 좋은 방법이다. 실제로 바로 앞에서 살펴본 GELU 는 transformer 의 BERT 계열이나 ViT 에서 사용되었고, GLU 는 gating 에 Sigmoid 대신 다른 활성화 함수를 사용하여 최근 SOTA 모델에서 많이 사용되고 있다.

다시 한번 짚어보면, 비선형 활성화 함수는 deep neuarl networks 설계에 필수적인 요소다. 초창기에는 Sigmoid, Tanh 같은 함수가 주로 사용되었지만 bounded 되어있는 특성상 gradient saturation 이 발생하여 gradient vanishing 문제가 있었다.

현재는 ReLU 함수가 거의 대부분의 (특히, CNN 계열) neural networks 에서 대표적인 비선형 활성화 함수로 사용되고 있다. ReLU 는 Sigmoid, Tanh 함수에 비해 gradient vanishing 문제를 해결하고 일반화 성능 및 수렴 속도가 좋다고 알려져 있다. 그러나 ReLU 도 만능은 아니다. ReLU 의 대표적인 문제로는 ReLU 함수 자체가 음수값을 아예 0 으로 만들어버리기 때문에 값이 한 번 음수가 되어버리면 그 부분에 대해서는 기울기 또한 0 이 되어 학습이 되지 않는 현상인 dying ReLU 다.

이를 극복하기 위해 음수 부분을 살짝 다르게한 Leaky ReLU, ELU, SELU 등이 등장했지만 ReLU 에 비해 성능 향상이 거의 미미하고 데이터셋이나 모델에 따라 성능 향상이 일관되지 않아 주로 사용되지 않는 실정이다. 아래에서 소개할 Swish 와 Mish 는 각 논문에서 ReLU 보다 성능 측면에서 확실히 향상되는 활성화 함수라고 검증되었다.

그리고 Swish 와 앞서 살펴본 GLU 가 결합된 SwiGLU 는 Meta 의 LLaMA 에서 사용되었고, GELU 와 GLU 가 결합된 GEGLU 는 구글의 Gemma 에 사용되었다. 이처럼 다양한 activation function 이 사용되는 가운데, 각 함수들의 차이점과 공통점을 이해하는데 Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark 해당 논문에서 세분화한 activation function 분류 체계가 개인적으로 도움이 됐다.

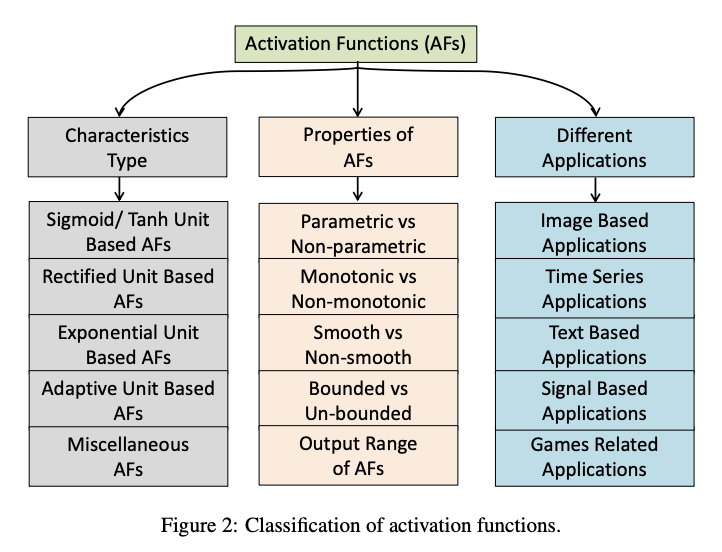
이 포스트까지 하면 2024년 10월 기준으로 굵직한 Activation Function 을 정리했다. 앞으로 특정 Activation Function 이 사용되는 이유, 성능이 잘 나오는 이유, 장점/단점 등을 숙지하고 원하는 곳에서 어렵지 않게 꺼내 쓸 수 있도록 하자.

Swish(SiLU, Sigmoid Linear Unit)

• Swish 와 SiLU 는 같은 활성화 함수다. 구글이 논문에서 Swish 라는 함수로 정의했기 때문에 Swish 라고도 불린다. 다만 차이점은 trainable parameter $\beta$ 의 유무다.

• SiLU 는 Sigmoid Linear Unit 의 줄임말로 입력 $x$ 에 sigmoid 를 씌운 값과 입력의 곱으로 이루어져있다.

  \[\text{SiLU}(x) = x \sigma(x)\]
• 이러한 SiLU 는 2016 년 GELU 를 제안한 논문에서 처음 소개되었다. GELU 가 표준 Gaussian CDF 를 사용하는데, 이를 표준 Logistic CDF 로 바꾸면 SiLU 가 나온다.
• SiLU 또한 1) bounded below, 2) non-monotonic, 3) unbounded above, 4) smooth 한 특성을 가지고 있다.

• Swish 함수는 SiLU 에 trainable parameter 인 $\beta$ 를 추가한 것이다.

  \[\text{Swish}(x) = x \sigma(\beta x)\]

• $\beta$ 값에 따른 Swish 와 그 도함수를 그래프로 그리면 아래와 같다.

  

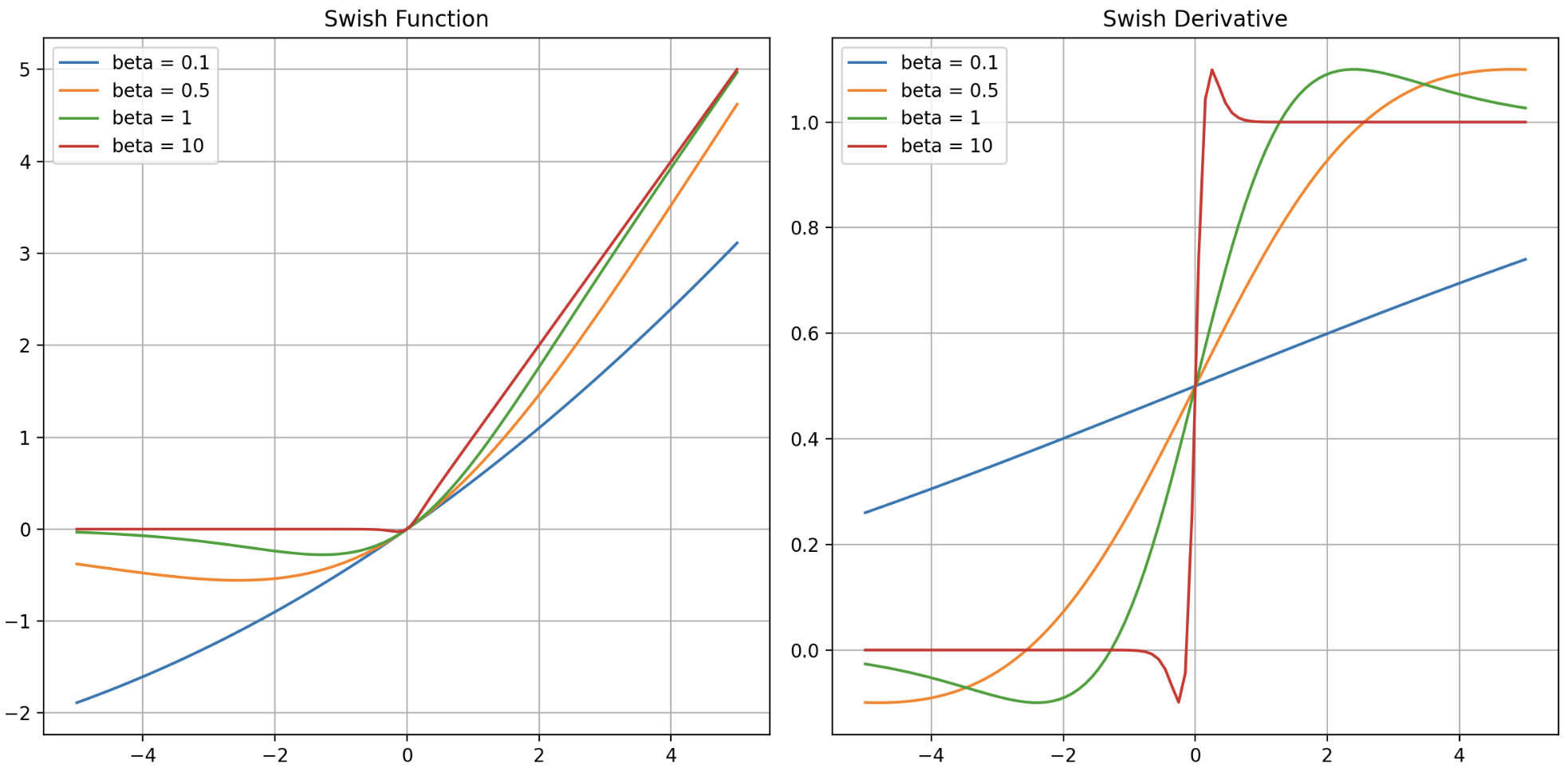
• 위 그래프에서 볼 수 있듯, $\beta$ 가 0 에 가까울수록 선형 함수가 되며 무한에 가까울수록 ReLU 와 같아진다. 그리고 $\beta = 1$ 인 경우 SiLU 와 Swish 는 같은 함수다. 이 $\beta$ 값에 따라 $\text{Swish}_\beta$ 로 표현하기도 한다.
• 이 $\beta$ 가 학습에 따라 변하는 parameter 이기 때문에, 선형 함수, Swish, ReLU 의 사이를 왔다 갔다 하며 최적의 activation function 을 찾아간다고 이해할 수 있다.
• Swish 는 activation function 만 바꾼 모든 실험에서 ReLU 를 압도한다고 한다. 이는 GELU, SiLU 와 마찬가지로 아래의 특성을 가지고 있기 때문이다.
• bounded below $x < 0$
  • 해당 특성은 많은 activation function 이 가지고 있다. 즉 너무 큰 음수값은 0 으로 보내서 regularization 을 하는 효과가 있다.
  • 그러나 ReLU 는 모든 음수값에 대해 0 이 되므로 Dying ReLU 문제에 직면했고, 이에 따라 Leaky ReLU 나 ELU 등이 나왔다.
  • Swish 도 마찬가지로 어느 정도 작은 음수값을 허용하여 Dying Neuron 현상을 막고, 너무 큰 음수값은 0 이 되도록 하고 있다.
• non-monotonic
  • Swish 는 약간의 음수를 허용하고 있고 양수 영역도 완전한 직선 그래프가 아니다. 이 때문에 ReLU 와 비슷하게 생겼지만 오히려 표현력이 좋다.
  • 위 도함수 그래프에서 0 근처를 보면 ReLU 와의 차이점이 확연히 보인다.
  • 이처럼 단조증가함수가 아니기 때문에 역전파 과정에서도 gradient 가 작은 음수더라도 온전히 이전 layer 에 전달할 수 있어 학습이 잘 된다.
• unbounded above
  • Sigmoid 나 Tanh 는 입력이 0 에서 멀어지면 Saturated 되어 gradient vanishing 되는 문제가 있었고, ReLU 는 양수 영역에서 입력이 그대로 출력되는 unbounded above 특성을 통해 gradient vanishing 문제를 해결했다.
  • 이러한 특성은 다른 activation function 에서도 이어지고, 마찬가지로 Swish 도 가지고 있다.
• smooth
  • Smooth 는 Generalization 과 Optimization 에서 중요한 이슈다. Swish 는 ReLU 와 달리 Smooth 한 형태를 가진 함수로, Initialization 과 learing rate 에 덜 민감하다. 또한 모든 점에서 미분이 가능하다.

  • 아래 그림은 6-layer 를 가진 임의의 neural network 에서 output layer 의 activation map 을 나타낸 것이다.

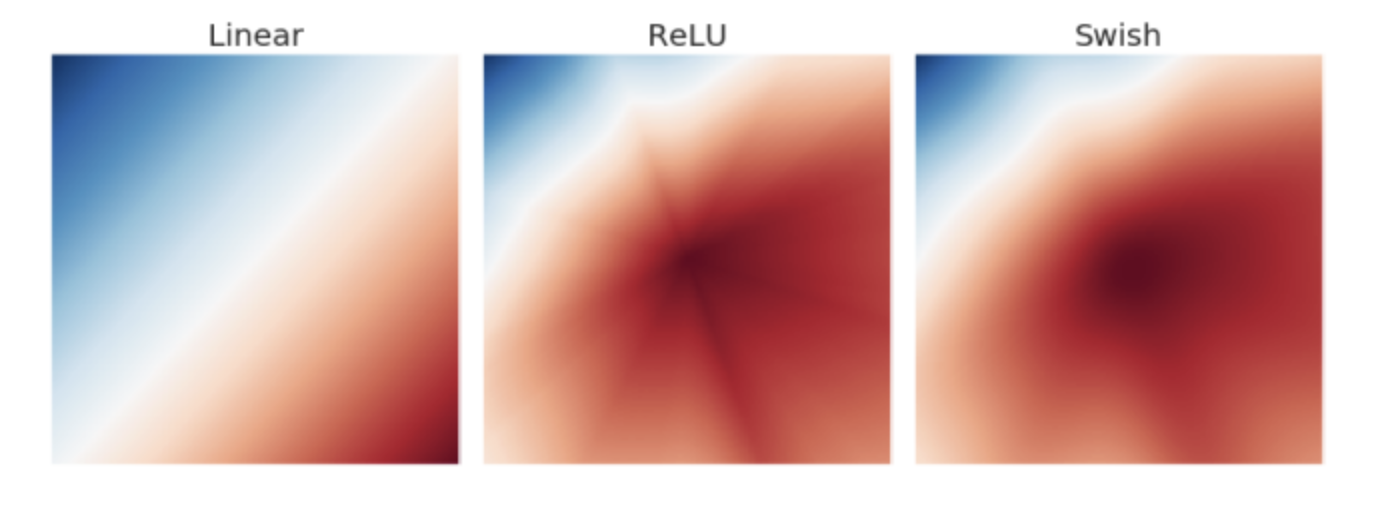    출처 : https://velog.io/@iissaacc/Swish-function

  • ReLU 의 activation map 을 보면 별모양이 나타나 있다. 이는 activation map 상에서 갑작스러운 변화를 의미한다. 딥러닝에서 작은 변화에도 민감하게 반응하는 것은 모델 학습을 어렵게 하는 원인이다.
  • Swish 와 같이 경계가 흐릿(smooth)하면 ReLU 와는 반대로 작은 변화에는 작게, 큰 변화에는 크게 반응하게 해서 optimizer 가 제대로 minima 를 찾아가게 한다.
• 또한 Swish 는 GELU 와 마찬가지로 Sigmoid 의 gating 을 활용하는 함수라고도 볼 수 있다. 실제로 이전 포스트에서 봤듯 GELU 의 식을 근사하면 Swish 와 같은 함수가 나왔다.
  • 이처럼 자기 자신 $x$ 에 비선형 함수를 거친 값을 곱하는 것을 self-gating 이라고 한다. 이는 LSTM 에서의 gating 모델링에서 유래된 것이다.
  • 또한 이러한 self-gating 은 element-wise(=point-wise) 하게 연산되기 때문에 다른 활성화 함수와 마찬가지로 치환이 쉽다.
• 이러한 Swish 는 매우 깊은 Neural Network 에서 ReLU 보다 높은 정확도를 달성하지만, Sigmoid 연산으로 ReLU 보다 연산 비용이 많이 든다.

Mish

• Mish 함수는 Swish 함수를 연장하여 아래와 같은 식으로 정의된다.

  \[\text{Mish}(x) = x \cdot \text{Tanh}(\text{Softplus}(x))\]
• 위 식 내의 tanh 와 softplus 는 앞선 포스트에서 다루었다.
• 그리고 Mish 또한 $x$ 에 비선형 함수를 거친 값을 곱하는 self-gating 함수다.

• 이러한 Mish 함수를 미분한 식은 아래와 같다. $\text{Tanh}$ 의 미분이 $\text{Sech}^2$ 가 되는 것은 여기에 잘 증명되어 있다.

  \[\frac{d}{dx}\text{Mish}(x) = \text{Sech}^2(\text{Softplus}(x))x\text{Sigmoid}(x) + \frac{\text{Mish}}{x}\]

• 위 식에서 $x\text{Sigmoid}(x)$ 는 $\text{Swish}_1$ 함수이며 $\text{Sech}^2(\text{Softplus}(x))$ 는 $\Delta x$ 가 된다.

  \[\frac{d}{dx}\text{Mish}(x) = \Delta(x) \text{Swish}(x) + \frac{\text{Mish}}{x}\]
• ReLU 함수는 gradient 를 그대로 유지하는 반면 Mish 는 추가적인 스칼라 요소 $\Delta(x)$ 가 최적화 과정에서 기울기를 smooth 하게 만들어 수렴을 더 쉽게 해주는 역할로 동작한다.
  • 이 부분이 바로 Mish 를 제안한 논문에서, Mish 가 Swish 와 비슷한 형태를 가지고 있지만 Swish 보다 더 좋은 성능을 내는 이유라고 설명한다.
  • $\text{Swish}(x)$ 앞에 존재하는 $\Delta(x)$ 값이 최적화 문제에서 많이 연구되었던 preconditioner 처럼 작용하여 강력한 정규화 효과를 제공하고 gradient 를 더 smooth 하게 만든다고 한다.

• Mish 함수와 그 도함수를 그래프로 그리면 아래와 같다. 그래프의 형태가 Swish 와 매우 비슷한 형태다.

  

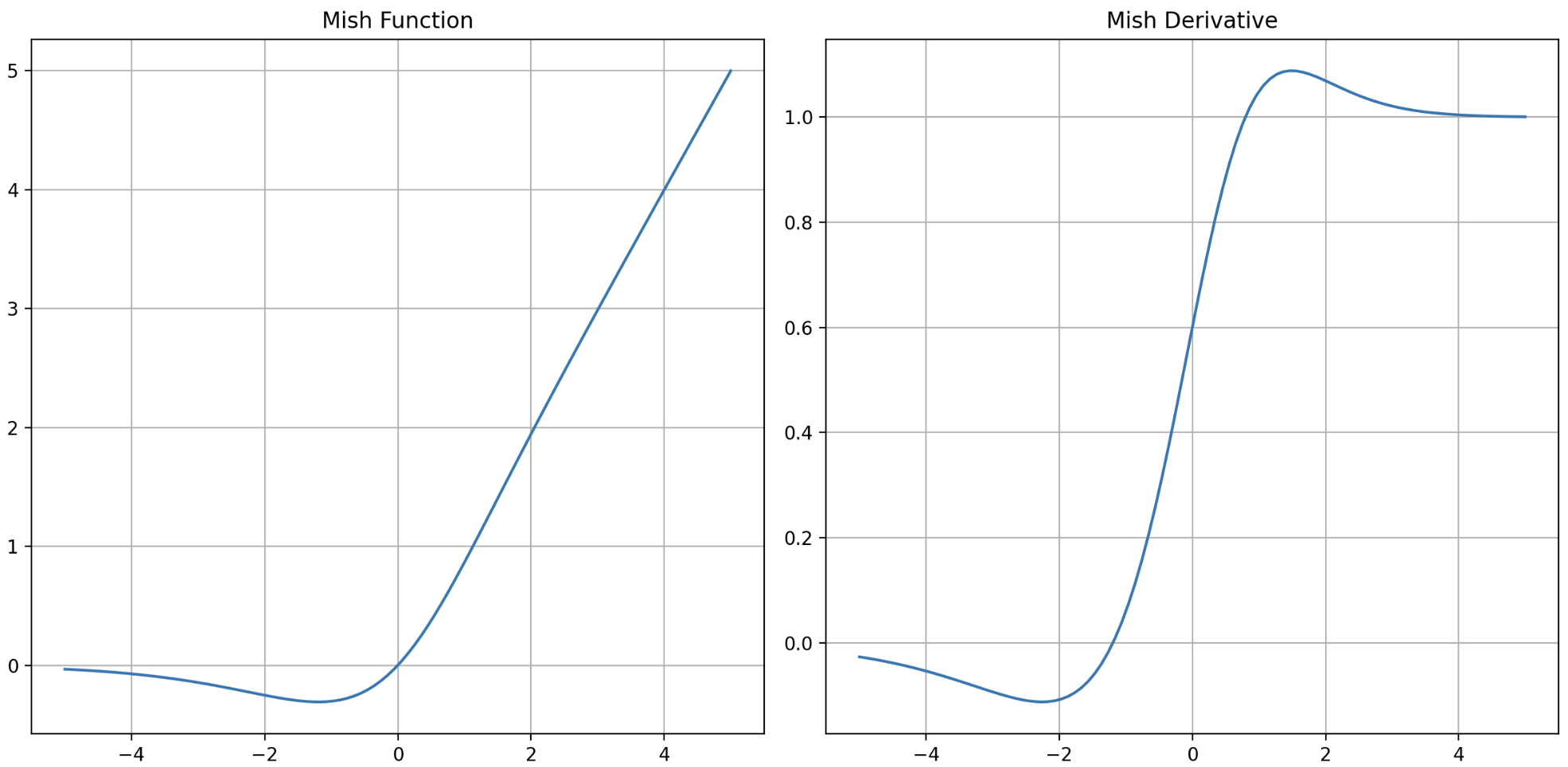
• Mish 함수도 GELU, Swish 함수와 마찬가지로 1) bounded below, 2) non-monotonic, 3) unbounded above, 4) smooth(모든 구간 미분 가능) 한 특성을 가지고 있다. 즉 Swish 의 장점을 모두 가진다.
  • 작은 음수의 값을 보존하여 Dying Neuron 현상을 방지하고 gradient 가 작은 음수더라도 온전히 이전 layer 에 전달할 수 있어 학습이 잘 된다.
  • ReLU 와 마찬가지로 unbounded above 이므로 값이 saturated 되지 않아 gradient vanishing 을 방지한다.
  • bounded below 이므로 neural network 의 parameter 가 급격하게 증가하지 않고 너무 큰 음수값은 $-0.31$ 로 제한되어 강력한 Regularization 효과를 가지고 있다.
  • 또한 도함수 그래프를 보면 모든 구간에서 연속이고 미분 가능(smooth)하여 initialization 이나 learning rate 에 덜 민감하면서 최적화와 generalization 에 효과적이다.
• 모든 구간에서 연속이고 미분 가능한 특징은 gradient base 로 parameter 를 업데이트하는 최적화에서 기울기가 정의되지 않아 발생하는 불안정한 요소를 제거하여 neural networks 가 깊어지더라도 정보 손실을 최대한 방지하고 전 layer 로 전파하는 역할을 수행한다.

• 이를 통해 깊은 neural networks 에서도 안정적인 학습과 높은 성능을 달성할 수 있다.

  

• 위 그림은 랜덤하게 초기화된 5-layer neural networks 출력의 activation map 을 각 활성화 함수 별로 분석한 결과다.
• ReLU 의 출력은 급격히 변하지만 Mish 의 출력은 굉장히 부드러운 형태를 가지고 있으며 이를 통해 최적화가 상대적으로 용이할 것임을 유추할 수 있다.

• 또한 Mish 의 논문에서는 ReLU 나 Swish 보다 Mish 가 훨씬 loss surface 를 더 부드럽게 만든다고 소개한다.

  

• 위 그림을 보면 ReLU 함수는 local minima 가 여기저기 존재하지만 Mish 함수는 loss surface 가 굉장히 부드럽고 넓은(flat) minima 를 가지고 있다. 이를 통해 더 안정적인 학습이 가능하다.
• 이 Mish 는 ReLU, Swish 보다 더 좋은 성능을 보이고 있으며 각각의 실험 결과에 대한 자세한 결과는 Mish: A Self Regularized Non-Monotonic Activation Function 논문을 확인해보자.
• 그러나 Mish 는 Swish 에 비해 수학적으로 무거운, 즉 복잡한 연산이 들어가 있어 계산 비용이 많이 든다는 단점이 있다.

SwiGLU

• SwiGLU 를 자세히 보기 전에, 기본적인 선형 변환과 ReLU 활성화 함수의 조합을 다시 한 번 짚어보자.

  \[\text{max}(0, xW_1 + b_1)W_2 + b_2\]
• 이 과정은 neural network 가 비선형성을 가지게 하며, 주어진 입력 $x$ 에 대해서 더 복잡한 표현을 학습할 수 있게 한다.
• 앞선 포스트에서 살펴본 GLU 는 위 개념에서 한 단계 더 나아간 것이다.

• GLU 는 두 개의 선형 변환을 사용하며, 그 중 하나는 Sigmoid 함수로 활성화 된다.

  \[\text{GLU}(x, W, V, b, c) = \sigma(xW + b) \otimes (xV + c)\]

• 이 GLU 의 과정을 예를 들어보자. 편의상 bias term 은 생략하고 아래와 같이 $x, W, V$ 가 주어진다.

  \[x = \begin{pmatrix} 1 \\ 2 \end{pmatrix}, \quad W = \begin{pmatrix} 0.5 & 0.3 \\ 0.7 & 0.2 \end{pmatrix}, \quad V = \begin{pmatrix} 0.4 & 0.6 \\ 0.8 & 0.1 \end{pmatrix}\]

• 그러면 $xW$ 와 $xV$ 는 아래와 같이 계산된다.

  \[xW = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \begin{pmatrix} 0.5 & 0.3 \\ 0.7 & 0.2 \end{pmatrix} = \begin{pmatrix} 1.9 & 0.7 \end{pmatrix}\\ xV = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \begin{pmatrix} 0.4 & 0.6 \\ 0.8 & 0.1 \end{pmatrix} = \begin{pmatrix} 2.0 & 0.8 \end{pmatrix}\\\]
• 이제 Sigmoid 함수는 $xW$ 를 0 과 1 사이로 Scaling 하며 최종 element-wise 곱셈 결과에 영향을 미치게 된다.
• 즉, $\sigma(xW)$ 행렬에서 특정 요소의 값이 크다면 Sigmoid 는 1 에 가까운 값을 반환하고, 작다면 0 에 가까 운 값을 반환하므로 $xV$ 행렬의 요소의 값이 크게 감소하거나 유지될 수 있다.

• SwiGLU 는 위 GLU 에서 Sigmoid($\sigma$) 대신 Swish 함수가 쓰인 것이다. 즉 Sigmoid Gate 대신 Swish Gate 를 사용하는 것이다.

  \[\begin{aligned} \text{SwiGLU}(x, W, V, b, c) &= \text{Swish}_1(xW+b) \otimes (xV + c) \\ &= (xW + b)\sigma(xW + b) \otimes (xV + c) \end{aligned}\]
• SwiGLU 논문에서는 transformer 의 FFN(Feed Forward Network) 에서 SwiGLU 를 사용할 때 변형한 FFN layer 를 사용한다.
• original FFN 에서는 두 개의 가중치 행렬을 사용하지만, GLU 의 변형을 활성화 함수로 사용하는 FFN 에서는 세 개의 행렬을 사용한다는 점이 특징이다.
• 이 때 학습 대상이 되는 행렬의 수를 늘려도 computation 은 일정하게 가져가기 위해, hidden units 의 개수는 2/3 으로 줄인다.
• SwiGLU 는 구글의 PaLM 과 Meta 의 Llama2 를 포함한 여러 유명한 LLM 에서 활발하게 사용하고 있다.
• 그러나 해당 논문은 이러한 GLU 의 (gate)변형 접근 방식이 더 나은 성능 지표를 제공하는 이유에 대해 전혀 설명하지 않고, 단순히 이를 신의 은혜라고 표현하고 있다.
• Sigmoid 활성화 함수의 형태를 고려했을 때, Swish 와 GELU 가 가지는 더 좋은 특징들이 성능 향상과 관련이 있을 것이다.
• 즉 Sigmoid 에 비해 unbounded above 한 것이 더 중요한 정보는 더 중요하게 반영하도록 하면서도, bounded below 하여 중요하지 않은 정보는 걸러낼 수 있고, saturated 되어 있지 않아 gradient vanishing 도 방지할 수 있기 때문이라고 추측한다.
• 또한 연속적으로 미분 가능하다는 점은 gradient base 최적화 알고리즘에 중요한 역할을 하기 때문에 SwiGLU 의 smooth 한 특성은 더 빠르고 안정적으로 수렴하도록 도울 수 있을 것이다.
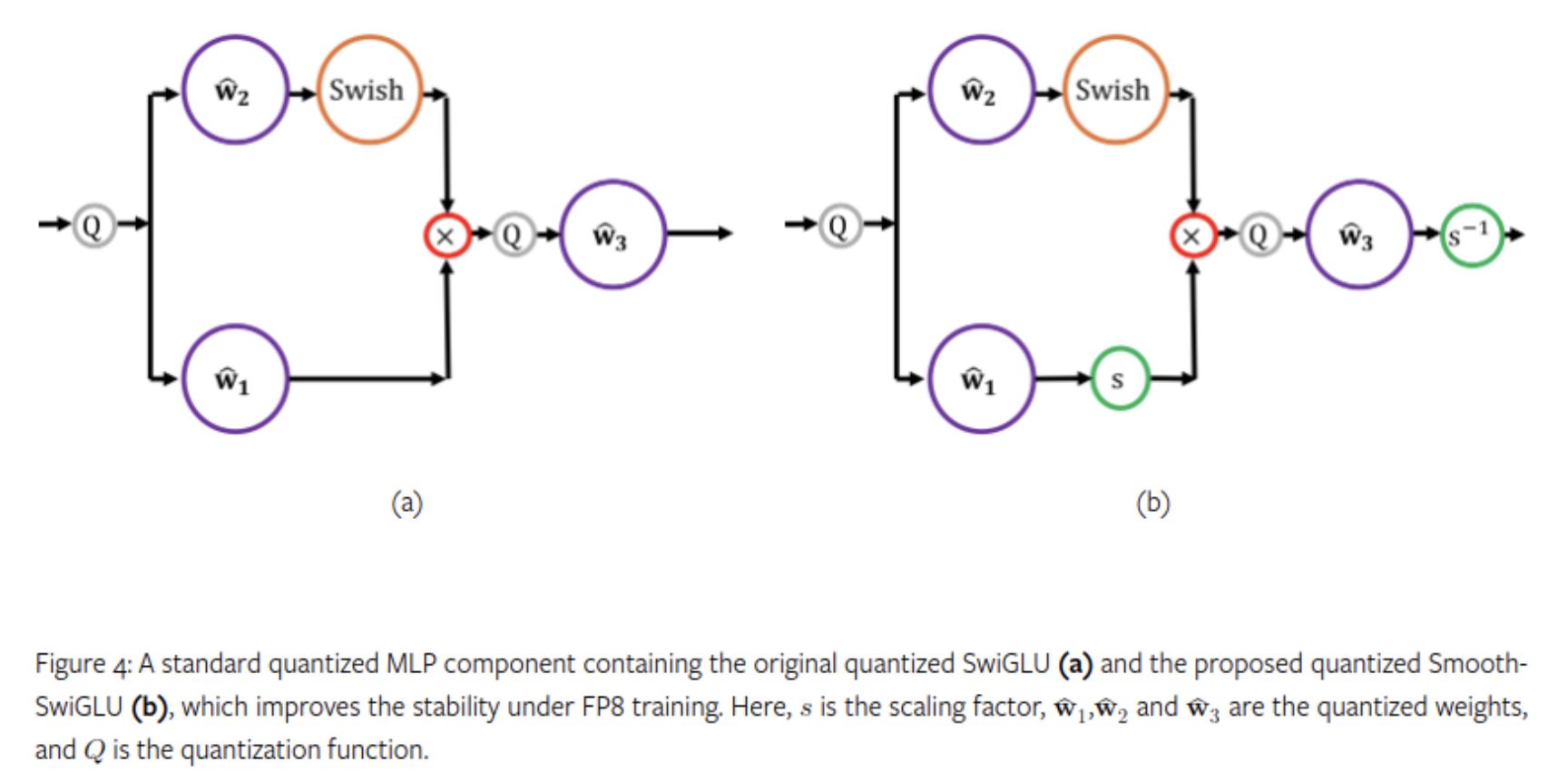
• 그러나 2024 년 9월 Intel 의 Habana Labs 는 2조 개의 토큰을 사용해 FP8 LLM 을 훈련하는 과정에서 치명적인 불안정함을 발견했는데, 이 문제는 SwiGLU 사용으로 인한 것으로 밝혀졌다. 2000 억 개의 토큰에 도달한 이후, 이상값들이 증폭되는 경향이 있던 것이다.

• 이를 해결하기 위해 Scaling factor 를 도입한 Smooth-SwiGLU 라는 새로운 활성화 함수를 개발했다.

  

GEGLU

• GEGLU 또한 SwiGLU 와 마찬가지로 GLU 에서 Sigmoid 대신 GELU 를 사용한 변형이다. 즉 Sigmoid Gate 대신 GELU Gate 를 사용하는 것이다.

  \[\text{GEGLU}(x, W, V, b, c) = \text{GELU}(xW+b) \otimes (xV + c)\]
• GELU 는 입력값을 통계적으로 변환하여 ReLU 보다 더 부드러운 비선형성을 제공한다. 또한 Swish 와 마찬가지로 unbounded above, bounded below 특징을 가지고 있다.
• 이러한 특징으로 Sigmoid 를 활용한 gating 보다 더 성능이 좋을 것이라고 추측된다. 실제로 GEGLU 는 구글의 Gemma 에 사용되었다.

Activation Function Tip

• Activation function 은 어떤 함수를 써야하는지 정답은 없고 상황에 따라, 모델이 개발된 배경에 따라 써야하는 activation function 이 다르다.
• 그럼에도 특정 상황에서 주로 사용되거나 특정 분야에서 성능이 좋다고 검증된 activation function 이 있는 만큼 가이드를 간단하게 정리할 수 있겠다.
• 하지만 이 또한 일반적인 경우를 위한 참고사항일 뿐 시간이 허락된다면 성능을 올리기 위해 activation function 을 바꿔보거나, 논문에서 사용하고 있는 activation function 을 그대로 써도 좋은 방법이다.
• 앞선 포스트에서 activation function 은 hidden layer 와 output layer 에서 사용되는 계열들이 있다고 언급했다.
• 각 모델 계열 별로 hidden layer 에서 주로 사용되는 activation function 은 다음과 같다.
  • MLP(Multi-Layer Perceptron) : ReLU 계열
  • CNN(Convolutional Neural Network) : ReLU 계열, Swish, Mish
  • RNN(Recurrent Neural Network) : Sigmoid / Tanh
  • Transformer(NLP, Vision) : GELU, SwiGLU, GEGLU
  • Image Generative(Diffusion 등) :
• Output layer 는 task 에 따라 activation function 을 다르게 선택한다.
  • Regression : Linear activation
  • Binary classification : Sigmoid
  • Multi classification : Softmax
• 층이 깊어질수록 최근 SOTA 모델에서 자주 사용되는 GELU, SwiGLU 혹은 Swish, Mish 를 사용해보자. 그 외에는 ReLU 와 ELU 를 비교하며 사용해도 좋다.
• 그러나 모델을 처음부터 구현하는 것이 아니라면 논문이나 공개된 코드에서 사용하고 있는 활성화 함수를 그대로 써도 좋다.
• 개인적으로 성능을 올리기 위한 선택지 중에서 오늘날은 질 좋은 데이터의 중요성이 강해지고 있고, 모델링 부분에서는 activation function 보다 모델 구조(backbone 등)나 Optimization, Regularization 기법들을 비교 실험하는 것이 더 중요하다고 생각한다.

Reference

• https://velog.io/@iissaacc/Swish-function
• https://hongl.tistory.com/213
• https://velog.io/@tobigs-nlp/PaLM-Scaling-Language-Modeling-with-Pathways-1#31-swiglu-activation
• https://junhan-ai.tistory.com/m/271
• https://arxiv.org/pdf/2002.05202

맨 위로 이동 ↑