[Activation] 3. ELU, SELU, CELU, GELU, GLU

지금까지 Sigmoid, Tanh, ReLU 계열의 활성화 함수를 다뤘다. 여기서부터는 ReLU 의 단점을 해결하기 위해 Exponential 을 취한 ELU 와 ELU 의 변형인 SELU, CELU 를 살펴보자. 그리고 Transformer 와 같은 Language 모델링에서 쓰이고 있는 GELU 와 GLU 를 정리할 것이다.

중요한 것은, 각 활성화 함수가 어떤 특징 때문에 사용되고 있고, 활성화 함수로서 기능할 수 있는 이유가 무엇인지를 잘 생각하자. 활성화 함수 정리의 첫 시작 에 정리한 내용들을 잘 유념해야 한다.

ELU(Exponential Linear Units)

• 2015 년에 나온 비교적 최근의 activation function 으로, ReLU 의 단점을 해결한 대표적인 대안 방법 중 하나다.

• ELU 는 0 을 기준으로 각져 있는 ReLU 를 $\exp$ 를 사용해서 부드럽게(smooth) 만든 활성화 함수다. 또한 ReLU 가 음의 값에서 0 이 되는 문제를 아래의 식처럼 해결한다.

  \[\begin{aligned} \text{ELU}(x) &= \begin{cases} \alpha(\exp(x)-1) & \text{if} \; x \leq 0 \\ x & \text{if} \; x > 0 \end{cases} \\ \end{aligned}\]

• 이를 그래프로 그리면 아래와 같다.

  

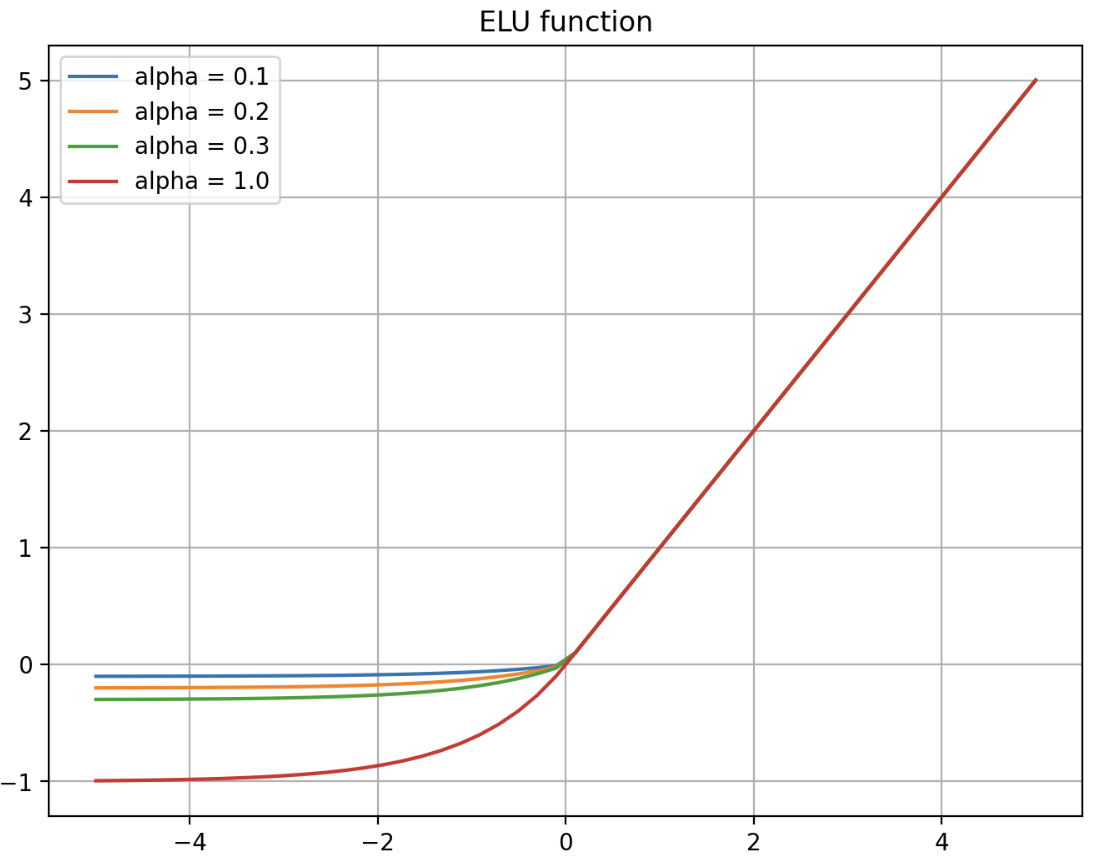
• 위 식에서 $\alpha$ 는 하이퍼파라미터이며 일반적으로 1 로 설정한다. 이 경우 $x=0$ 에서 급격하게 변하지 않고 모든 구간에서 매끄럽게 변하므로, 경사하강법에서 수렴 속도가 빠르다.
• 이러한 ELU 의 장점은 아래와 같다.
  • ELU 는 ReLU 의 장점을 모두 가지고 있다.
  • ReLU 와 유사하게 생겼으면서도 ReLU 와 달리 미분 하더라도 부드럽게 이어진다. 또한 ReLU 와 달리 음의 출력을 생성할 수 있다. 이를 통해 dying ReLU 현상을 해결할 수 있다.
  • 출력값이 거의 zero-centered 에 가깝다. 위 ELU 의 그래프를 보면 0 을 기준으로 smooth 하다. 이에 따라 모델이 더 빠르게 수렴할 수 있다. 즉 ELU 가 0 중심의 출력을 제공하므로, neural network 의 weight 업데이트가 더 안정적이게 이루어져 학습 속도가 빠를 수 있다.
  • ELU 는 ReLU 나 PReLU 와 달리 negative regime 에서도 비선형적이기 때문에 복잡한 분류에서도 사용할 수 있다.
• 또한 larger negative input 에 대해서 saturate 하는 것을 통해 noise 에 robustness 를 추가해준다.
  • 음수 구간이 $\alpha(\exp(x)-1)$ 와 같이 지수함수 형태로 정의되어 $x$ 값이 음수 방향으로 커지더라도 함수값이 0 에 가까운 일정한 음수값으로 포화(saturate)한다.
  • 따라서 아주 큰 음수값이 입력되어도 출력값이 커지지 않으므로 noise 에 덜 민감해진다. 그리고 위 그림을 보면 알 수 있지만 $\alpha$ 가 입력이 큰 음수값일 때 수렴할 값을 정의하는 것과 같다.
  • ELU 를 제안한 논문에서는 이런 deactivation 이 좀 더 강인함을 줄 수 있다고 주장한다. 해당 논문에 자세히 나와있으니 참고하자.
• 이렇게 보면 ELU 는 ReLU 와 Leaky ReLU 의 중간 정도라고 생각할 수 있다. Leaky ReLU 처럼 zero-centered 한 출력을 낼 수 있고 ReLU 처럼 Saturation 특성도 가지고 있기 때문이다.
• 그러나 ReLU 에 비해 성능이 크게 증가한다는 이슈가 없으며, $\exp$ 의 존재로 오히려 연산량이 늘어났기에 학습 속도가 ReLU 에 비해 느리다.
• 또한 $\alpha$ 값이 1 로 고정되어있다는 단점도 있다. 그러나 사실 $\alpha \neq 1$ 인 경우 음수 영역에서 미분이 불연속적인 부분이 있다.

CELU(Continuously Differentiable Exponential Linear Units)

• CELU 는 ELU 가 $\alpha = 1$ 이 아니면 음수 영역에서 미분이 불연속적인 부분이 존재한다는 점을 해결하기 위해서 $x$ 가 음수값일 때 $\alpha$ 로 나눠준다.

  \[\begin{aligned} \text{CELU}(x) &= \begin{cases} \alpha(\exp(x / \alpha)-1) & \text{if} \; x \leq 0 \\ x & \text{if} \; x > 0 \end{cases} \\ \end{aligned}\]
• 즉 CELU 는 ELU 의 변형으로, 연속적으로 미분 가능하게 만들어진 활성화 함수다. CELU 에서도 $\alpha$ 값은 하이퍼파라미터이다.

• 그래프로 그리면 아래와 같다.

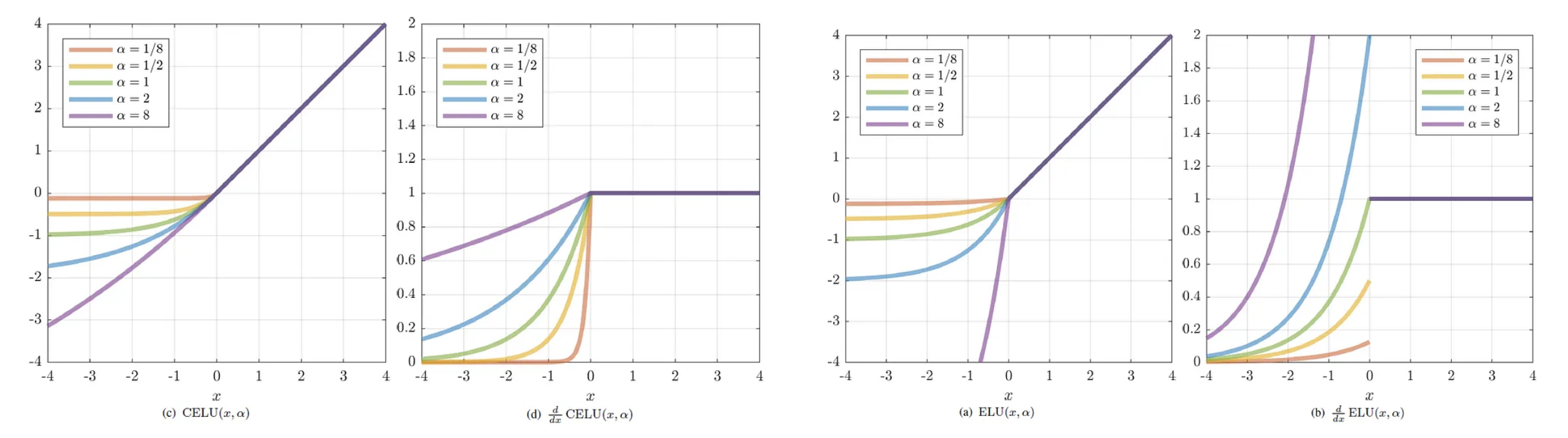  출처 : https://towardsdatascience.com/google-continuously-differentiable-exponential-linear-units-with-interactive-code-manual-back-fcbe7f84e79

• 위 그래프에서 왼쪽 두 그래프는 $\alpha$ 값에 따른 CELU 그래프와 그 도함수 그래프다. 오른쪽 두 그래프는 ELU 에 해당한다.
• 이처럼 CELU 는 ELU 의 장점을 가지고 있으면서 어떤 $\alpha$ 에도 연속적인 미분 가능한 함수가 된다. 따라서 ELU 의 특성을 유지하면서도 하이퍼파라미터 $\alpha$ 를 보다 유연하게 설정할 수 있다.

SELU(Scaled Exponential Linear Units)

• SELU 또한 ELU 함수의 변형으로서 출력에 스케일링 요소를 도입한다. 2017 년 Klambauer 등이 제안했다.

  \[\begin{aligned} \text{SELU}(x) &= \lambda \begin{cases} \alpha(\exp(x)-1) & \text{if} \; x \leq 0 \\ x & \text{if} \; x > 0 \end{cases} \\ \end{aligned}\]
• 위 식에서 $\alpha$ 와 $\lambda$ 는 하이퍼파라미터로서, 논문에서 제안된 값인 $\alpha \approx 1.6733$, $\lambda \approx 1.0507$ 을 사용한다.

• 그래프로 그리면 아래와 같다.

  

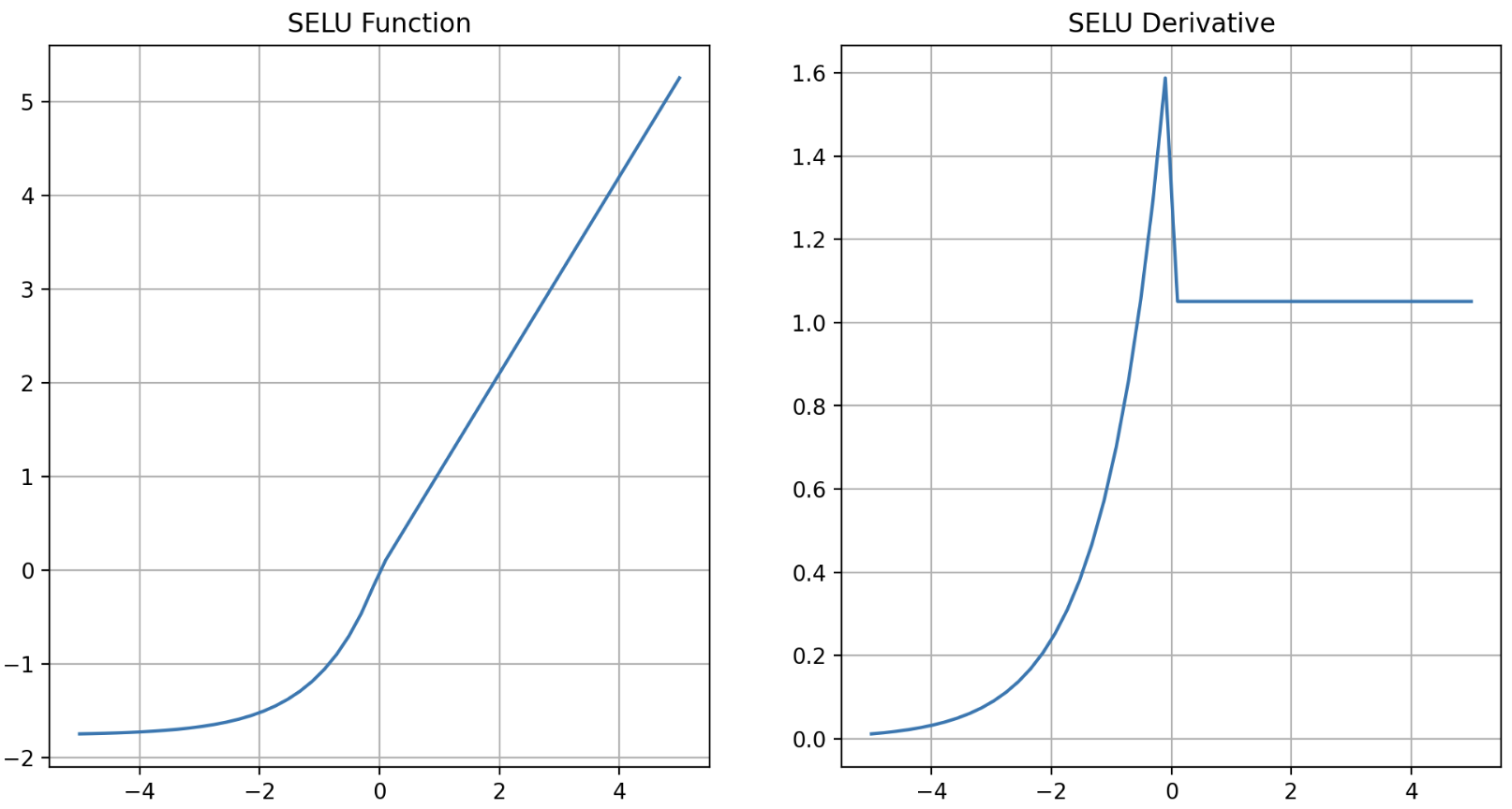
• 저자는 fully connected layer 만 쌓아서 neural network 를 만들고 모든 hidden layer 가 SELU 활성화 함수를 사용하면 네트워크가 자기 정규화(self-normalized) 된다고 주장한다.
  • Neural Network 를 학습할 때, layer 가 쌓일수록 각 layer 의 출력값들이 그 전 layer 의 출력에 의존하게 된다. 이 과정에서 출력값의 평균과 분산이 적절히 유지되지 않으면, 네트워크가 안정적으로 학습하기 어렵다.
  • 출력값의 분산이 너무 작아지면, 역전파 과정에서 기울기가 점점 작아져 네트워크가 학습을 제대로 못하는 상황이 발생한다. 즉 gradient vanishing 이 발생한다.
  • 반대로, 출력값의 분산이 너무 커지면 역전파 중 기울기가 매우 커져 학습이 불안정해지거나 발산할 수 있다. 즉 gradient exploding 이 발생할 수 있다.
• 이 때 SELU 는 학습 중 네트워크의 layer 에서 출력의 평균과 분산이 각각 0 과 1 로 유지되도록 설계되었다.
• 이는 gradient vanishing 과 exploding 문제를 막아준다. 이러한 특성을 통해 neural network 의 학습 속도와 수렴 성능을 향상시킬 수 있다.
• 이것을 가능하게 하는 것은 하이퍼파라미터 $\alpha$ 와 $\lambda$ 다.
  • $\lambda$ 는 스케일링 parameter 다.
  • $\alpha$ 는 자기 정규화를 보장하는 fixed-point 방정식에서 유도된 parameter 다.
• 이러한 $\alpha$ 와 $\lambda$ 는 평균과 분산이 layer 간에 불변으로 유지되도록 정의되며, 이는 neural network 에서 소실되거나 폭발하는 기울기 문제를 방지하는 데 중요한 요소다.
• 또한 SELU 가 자기 정규화를 이루기 위해서 필요한 몇가지 조건이 존재한다.
  • input 데이터가 반드시 표준화(평균 0, 표준편차 1)되어야 한다.
  • 모든 hidden layer 의 weight 는 LeCun Normal Initialization 으로 초기화되어야 한다.
  • 네트워크는 일렬로 쌓여진 layer, 즉 feed-forward network 로 구성되어야 한다. RNN 이나 Skip Connection 과 같은 순차적이지 않은 구조에서 사용하면 자기 정규화되는 것을 보장하지 않는다.
• 이처럼 SELU 를 사용하는 네트워크는 SELU 의 자기 정규화를 통해 학습이 안정적으로 진행될 수 있으며, 학습 속도와 수렴 성능이 개선될 수 있다.
• 특히 딥러닝 모델에서 layer 가 많이 쌓일수록 gradient vanishing 이나 exploding 문제를 겪을 확률이 높아지는데, SELU 는 이를 근본적으로 해결하는 데 도움이 된다.
• 그러나 SELU 는 $\alpha$ 값에 따라 활성화 함수의 결과값이 일정하지 않아 층을 많이 쌓을 수 없다고 한다.
• 또한 SELU 의 성능은 초기화의 정확성과 하이퍼파라미터에 민감하다. 그리고 모든 구조가 SELU 에서 동일한 이점을 얻는 것은 아니며, SELU 는 다른 정규화나 regularization 기법과 호환되지 않을 수 있다.
• 그리고 SELU 역시 ReLU 에 비해 성능이 그리 뛰어나지 않고 연산만 늘어나기 때문에, SELU 보다 ELU 를 추천하기도 한다. 더구나 오늘날 딥러닝 모델에서 skip connection 기법은 정말 많이 쓰이고 있기 때문에 SELU 사용에 유의해야 한다.

GELU(Gaussian Error Linear Unit)

• GELU 는 BERT, GPT, ViT 등 모델에서 encoder block 안의 2-layer MLP 구조의 활성화 함수로 사용되는 함수다.
• 입력 $x$ 의 부호에 대해서 self-gating 하는 ReLU 와 달리 GELU 는 $x$ 와 Gaussian distribution CDF($\Phi$) 에 $x$ 를 넣어준 값을 곱해준다. 이를 통해 $x$ 가 다른 입력과 비교했을 때 얼마나 큰 지, 즉 가중치를 부여하는 효과를 얻는다.

• 즉 GELU 는 입력값이 클수록 출력값을 더 크게 만들어, 입력값의 “중요도”에 따라 다른 처리를 하게 한다. 이는 기존의 ReLU 가 제공하는 “단순한 긍정 값의 선형 전달”과 비교하여, 더 복잡한 데이터의 특성을 모델링할 수 있는 가능성을 열어준다. 아래에서 자세히 보자.

  \[\text{GELU}(x) = x \ast \Phi(x)\]
• GELU 는 dropout, zoneout, ReLU 함수의 특성을 조합하여 유도된 것이다.
• ReLU 는 입력 $x$ 의 부호에 따라 1 이나 0 을 deterministic 하게 곱하고, dropout 은 1 이나 0 을 stochastic 하게 곱한다.
• 따라서 GELU 에서는 이 두 개념을 합쳐 $x$ 에 0 또는 1 로 이루어진 mask 를 stochastic 하게 곱하면서도 stochasticity 를 $x$ 의 부호가 아닌 값에 의해서 정하고자 하는 것이다.
  • 이 때 구체적으로 $x$ 에 mask 역할을 하는 $m \sim \text{Bernoulli}(\Phi(x))$ 를 곱한다. 즉 Bernoulli Distribution 의 함수(dropout 대체)와 input $x$(ReLU)의 곱으로 표현한 것이 바로 GELU 다.
• $\Phi(x) = P(X \leq x), \; X \sim \mathcal{N}(0,1)$ 는 표준 Gaussian 분포의 CDF(Cumulative Distribution Function) 이다.
  • GELU 에서 이 CDF 를 이용하는 이유는 batch normalization 이후에 $x$ 가 일반적으로 정규분포 양상을 띄기 때문에 $X$ 의 분포로 선택했다고 한다.
  • 또한 입력값의 크기에 따라 확률적으로 가중치를 부여하기 위함이다. 이를 통해 neural network 는 입력 데이터의 중요도를 더 세밀하게 판단할 수 있게 된다.

  

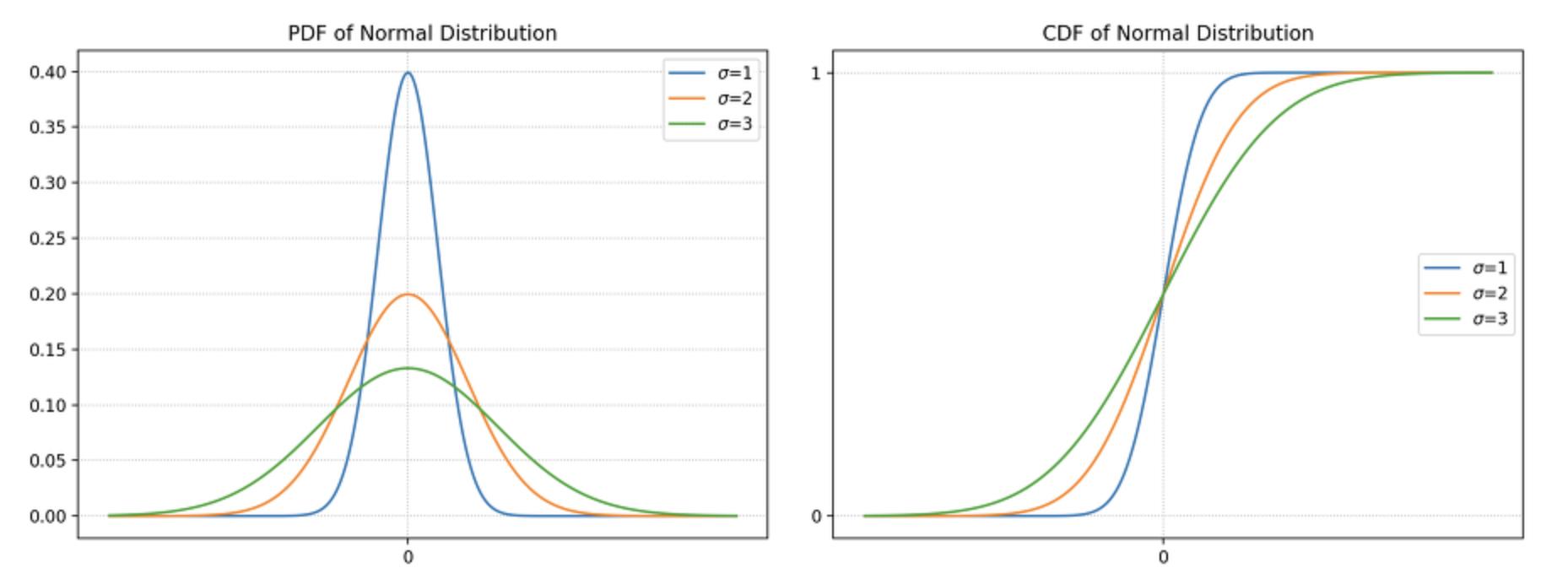
  • 여담으로 위 정규분포의 CDF 가 Sigmoid 와 비슷하게 생겼는데, Logistic Regression 에서 Sigmoid 대신 정규분포의 CDF 를 사용하는 모델을 Probit Regression 이라고 한다.
  • 그러나 이 CDF 를 사용하는 것은 최적화 관점에서 쉬운 일이 아니기 때문에, 다소 오차는 있지만 CDF 와 모양이 거의 흡사하면서도 계산은 매우 쉬운 Sigmoid 를 사용한다고 한다.
• $x$ 가 줄어들수록 $\Phi(x)$ 가 줄어드므로 $x$ 가 dropped 될 확률이 높아진다. 즉 초기 의도대로 stochastic 특성을 유지하면서 그 특성이 입력값에 의존하도록 만든 것이다.

• 이제 neural network 에서 활성화 함수로 사용되기 위해 deterministic 함수로 변환해준다. Dropout 처럼 확률에 따른 평균을 취하면 $\Phi(x) \times x + (1 - \Phi(x)) \times 0 = x\Phi(x)$ 가 된다. 또한 CDF 함수는 수학적으로 복잡한 형태의 error 함수($\text{erf}$)로 정의할 수 있다.

  \[\text{GELU}(x) = xP(X \leq x) = x\Phi(x) = x \cdot \frac{1}{2}\left[1 + \text{erf}(x / \sqrt{2})\right]\]

• 위 식에서 $\text{erf}$ 로 정의되는 CDF 는 정확하게 계산하기 복잡하므로 아래와 같이 근사할 수 있다.

  \[\begin{aligned} \text{GELU}(x) = x \cdot \frac{1}{2}\left[1 + \text{erf}(x / \sqrt{2})\right] &\approx 0.5x\left(1 + \tanh\left[\sqrt{\frac{2}{\pi}}(x + 0.044715x^3)\right]\right) \\ &\approx x\sigma(1.702x) \end{aligned}\]
• 이 근사식은 계산이 더 간단하면서도 원래 GELU 함수의 성질을 잘 유지한다. 이를 그래프로 나타내면 아래와 같다.

• 추가로 Sigmoid 를 통해 근사한 것($x\sigma(x)$)은 SiLU(Sigmoid Linear Unit) 라고 불린다. 이는 Swish 활성화 함수와 같다. 즉 Swish 의 입력값에 미세한 값을 곱해준 것과 같다.

  

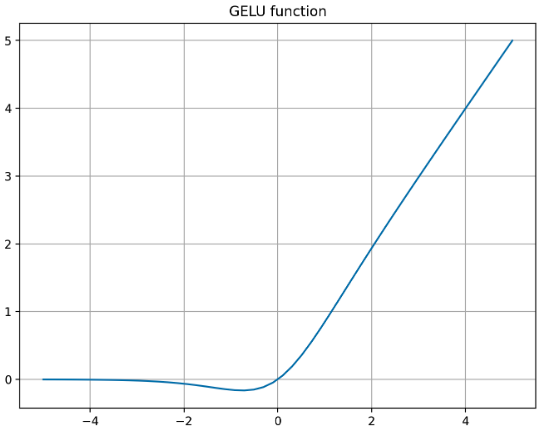
• 위 그래프를 보면 GELU 는 1) bounded below, 2) non-monotonic, 3) unbounded above, 4) smooth 한 특성을 가지고 있음을 알 수 있다.
  • 즉 GELU 는 모든 점에서 미분 가능하고, 단조증가함수가 아니며 비선형 활성화 함수 목적에 맞게 더욱 복잡한 전체 함수를 모델링하는데 더 도움이 된다.

  • 또한 ReLU 처럼 $x$ 의 부호에 대해서 gating 이 되는 것과 달리 GELU 는 $x$ 가 다른 입력에 비해 얼마나 큰지에 대한 비율로 gating 이 되기 때문에 확률적인 해석이 가능해지고 함수 형태가 미분 가능하게 된다.

    

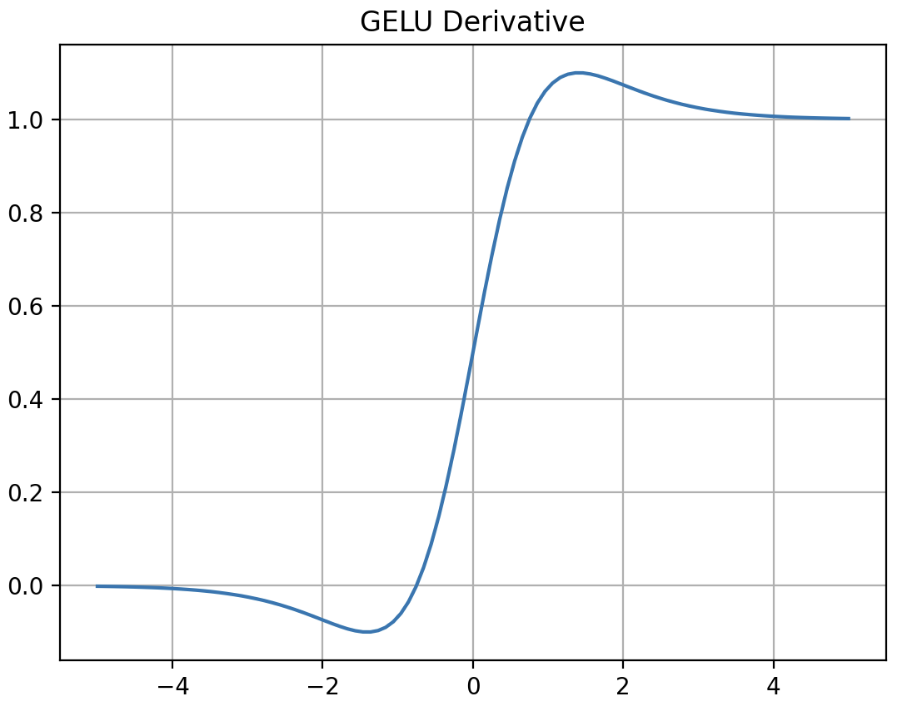
  • ReLU 의 단점을 해결하기 위해 나온 Leaky ReLU 와 같은 함수들은 음수 부분에서 bounded below 되어 있지 않은 선형 함수이기 때문에 발산할 수 있었다. 이는 feature 학습에 부정적인 영향을 끼칠 가능성이 있다.
  • 그러나 GELU 는 음수 부분이 값을 가지지만 너무 커지지 않게 bounded 하면서 기울기가 잘 정의되어 있는 함수다.

• 이러한 GELU 를 ReLU, ELU 와 비교해서 그리면 아래와 같다.

  

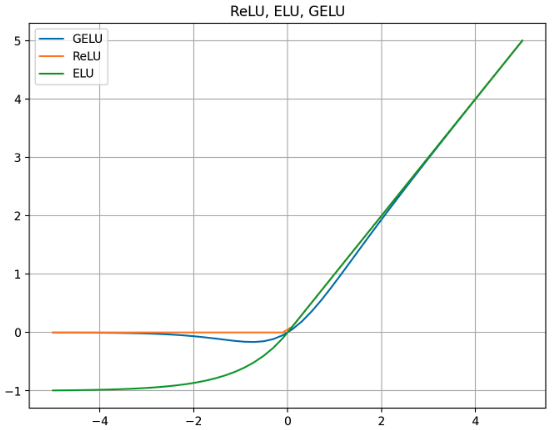
  • GELU 는 입력값에 따라 출력이 부드럽게 증가하고, $x$ 가 커질수록 $\Phi(x)$ 의 값도 커져 출력이 선형적으로 증가하는 경향을 보인다. 음수 영역에서도 완전히 0 으로 수렴하지 않고, 작은 음수 값을 유지하면서 부드러운 형태를 유지한다. 이러한 bounded below 특징은 gradient vanishing 에서 자유롭게 해준다.
  • ReLU 는 0 보다 작은 모든 $x$ 에 대해 출력이 0 이 되며, $x$ 가 0 을 초과하는 지점에서는 입력값과 동일한 출력값을 가진다. 음수값에서 전혀 활성화되지 않는 문제는 Dying ReLU 문제로 이어진다.
  • ELU 는 음수값에서 ReLU 와 달리 완전히 평평하지 않고, 일정한 음의 값으로 수렴한다. 이는 음수 입력에 대해 작은 음수 값을 출력하여 네트워크가 음수 입력에서도 일부 정보를 유지할 수 있도록 하는 것이다. 또한 $x$ 가 양수인 영역에서는 ReLU 와 유사하지만 더 부드러운 곡선을 그린다.
• GELU 에서 CDF 함수를 정의할 때 사용한 $X \sim \mathcal{N}(0, \sigma)$ 에서 $\sigma = 0$ 이면 ReLU 가 된다.
• 따라서 GELU 는 ReLU 의 smoothing 버전 이라고 볼 수 있다. 또한 ELU 의 경우도 GELU 에서 CDF 함수를 Standard Cauchy distribution 에 대해서 정의하면 유도할 수 있다.
• 이처럼 GELU 는 음수와 양수의 입력 모두에 대해 더 많은 정보를 유지하려는 시도가 나타나있고, 이는 모델이 보다 복잡한 패턴을 학습하는 데 유용할 수 있다. ReLU 는 계산적으로 효율적이며, ELU 는 음수값에서도 일부 정보를 유지하려는 시도를 보여준다.
• ReLU, ELU 와 GELU 를 비교했을 때 GELU 가 일관적으로 성능이 더 좋다는 실험 결과가 있다. 최근 NLP(BERT 등) 와 Vision 분야(ViT 등)가 점점 더 모델이 커지고 깊어지면서 GELU activation 을 많이 사용하고 있다.
• 그러나 복잡하고 큰 모델에서 매우 효과적이긴 하지만 작은 네트워크나 단순한 작업에서는 항상 더 나은 성능을 보이지 않을 수도 있다. 복잡한 gating 이 필요하지 않은 상황에서는 ReLU 와 같은 단순한 활성화 함수가 더 적합할 수 있다.

GLU(Gated Linear Unit)

• GLU 는 NLP 분야에서 처음 소개되었으며 neural network layer 로 정의된다. 이 layer 는 입력에 대한 두 개의 linear transformation(matrix multiplication)의 element-wise 곱을 수행한다.

• 그 중 하나는 Sigmoid 가 적용된다. 그것이 gate 로서 동작한다.

  \[\text{GLU}(x, W, V, b, c) = \sigma(xW + b) \otimes (xV + c)\]
• 여기서 $W, V$ 는 학습 가능한 행렬(텐서)이고, $\otimes$ 연산은 element-wise 곱셈을 의미한다.

• bias 행렬 $b$ 와 $c$ 를 제외한 행렬 연산의 관점에서 GLU 를 시각화하면 아래와 같다.

  

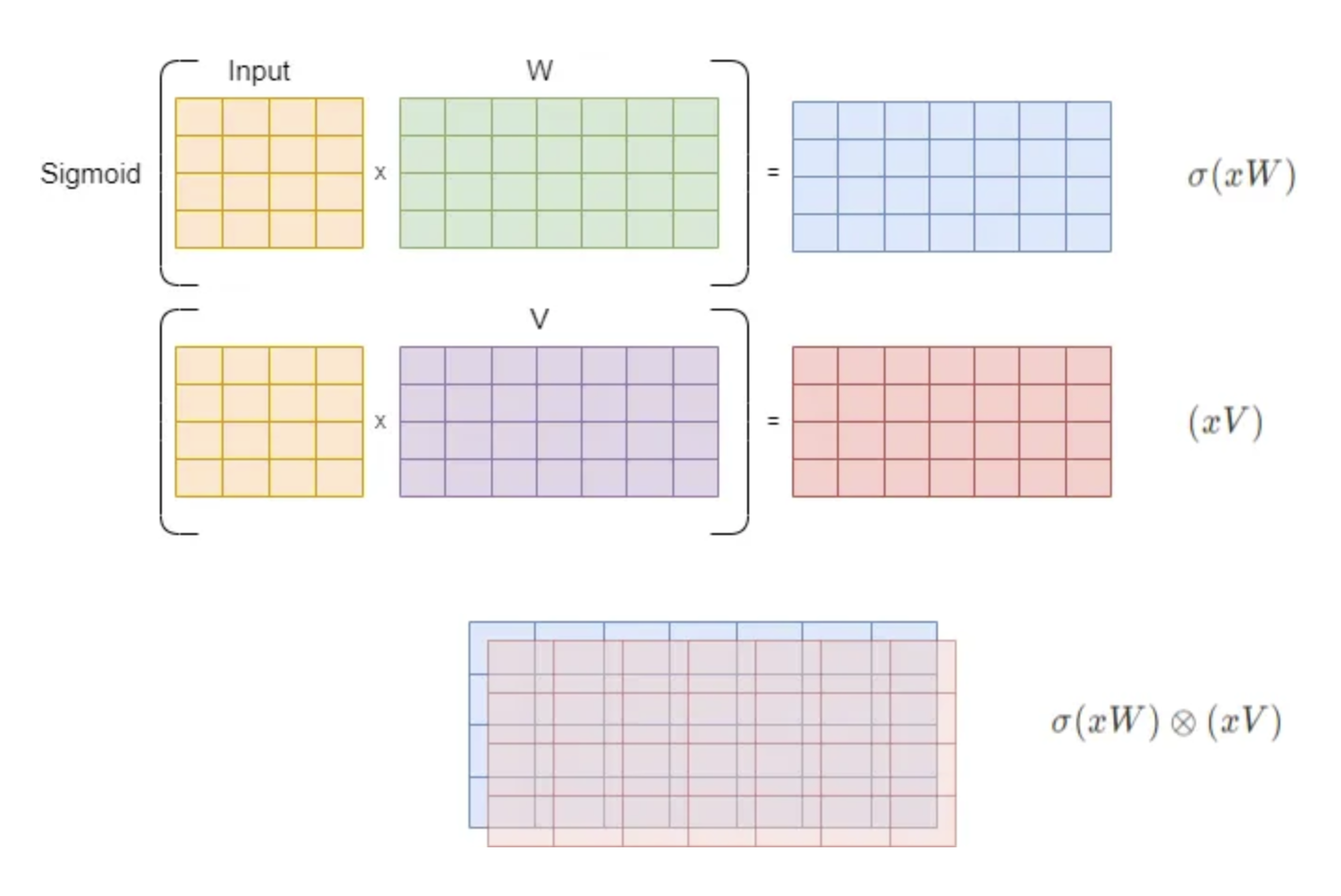
• 위 그림에서 마지막 연산처럼 겹치는 element 들이 서로 곱해지며, 결과적으로 $\sigma(xW + b)$ 의 출력은 $(xV + c)$ 에 대한 filter 이자 gate 로 동작한다. 그리고 이 filter 는 학습 중에 자동으로 조정된다.
• 즉 Sigmoid 활성화 행렬이 구성하는 값에 따라 선형 변환된 행렬의 같은 위치에 있는 값이 두드러지거나 감소하게 된다. 이를 통해 정보의 흐름을 조절하여 중요한 정보는 통과시키고 불필요한 정보는 차단할 수 있다.
• 이는 LSTM 에서 사용된 gate 와 같은 개념이다. LSTM 에서 Sigmoid 를 gate 로 사용한 것과 같이 GLU 에서도 Sigmoid 를 gate 로 사용한 것이다.
• 다만, LSTM 의 gate 는 상태(state)를 조절하는 데 중점을 두고 있고, GLU 의 gate 는 활성화 출력을 제어하는 차이가 있다. 이를 통해 input 의 정보를 얼만큼 사용할 것인지를 조절하는 것이다.

• 이처럼 GLU 의 가장 큰 장점은 아래 그림과 같은 gate 메커니즘이다.

  

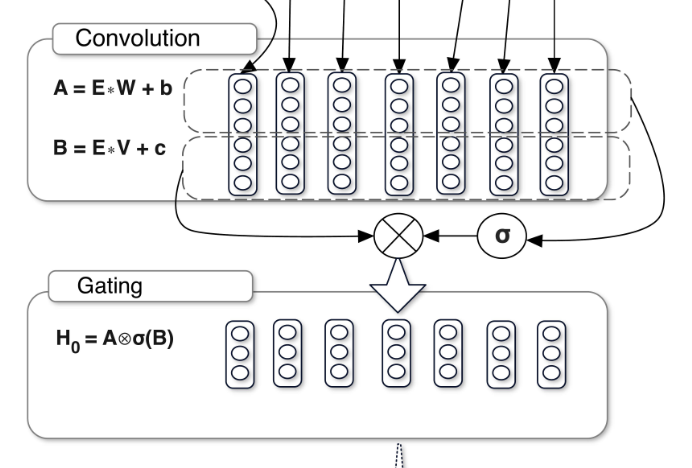
• 이 메커니즘은 학습 과정에서 입력 데이터의 특정 부분을 강화하거나 억제할 수 있다.
• Sigmoid 함수로 활성화된 gate 는 각 입력에 가중치를 부여하고, 이를 다른 행렬과 element-wise 곱해서 중요한 정보는 강조하고 덜 중요한 정보는 억제하여 모델이 더 유용한 패턴을 학습할 수 있게 한다. 이는 정보 처리에 있어서 매우 유연한 제어를 가능하게 한다.
• 또한 학습 효율성이 좋다. 입력이 단순히 통과되는 것이 아니라 입력과 gate 가 곱해지는 형태로 정보가 처리되기 때문에, 학습 중에 불필요한 정보나 잡음을 억제하는 효과를 얻을 수 있다.
• 이러한 특성 덕분에 GLU 는 복잡한 데이터셋에서도 모델이 더 효율적으로 학습할 수 있고, gradient vanishing 문제 해결과 수렴을 도와준다.
• 추가적으로 Sigmoid 활성화 함수는 비선형성을 도입해 주며, 이는 선형 변환만을 사용하는 것보다 더 복잡한 함수 형태를 모델링할 수 있게 만든다.
• GLU 는 두 개의 선형 변환을 사용하기 때문에, 일반적인 활성화 함수에 비해 더 많은 학습 가능한 parameter 를 제공한다. 그러나 그만큼 추가적인 연산이 필요하여 계산 비용이 늘어난다.
• 또한 GLU 는 단순하면서도 gate 를 통해 입력을 필터링하기 때문에, 상대적으로 가벼운 구조로 더 강력한 성능을 발휘할 수 있다.
• 이는 Transformer 구조가 등장하기 이전, LSTM 과 같은 복잡한 RNN 모델을 사용하지 않고도 비슷한 수준의 성능을 달성할 수 있었던 이유 중 하나다.
• 그리고 GLU Variants Improve Transformer 논문에서 소개하듯이, Sigmoid 부분에 다른 활성화 함수를 조합해서 다양한 ReGLU, GEGLU, SwiGLU 등 GLU 시리즈들을 만들어낼 수 있다.

Reference

• https://pod3275.github.io/paper/2019/03/27/SELU.html
• https://velog.io/@greensox284/Activation-Scaled-Exponential-Linear-Unit-SELU
• https://hongl.tistory.com/236#google_vignette
• https://jik9210.tistory.com/14
• https://medium.com/@tariqanwarph/activation-function-and-glu-variants-for-transformer-models-a4fcbe85323f

맨 위로 이동 ↑